スポンサードリンク
こんにちは、ももやまです。
皆さんはプリントを番号順に並べなおしたり、小学校や中学校で「身長順」や「学生番号が小さい順」に整列したりしましたね。
実は、整列を行うアルゴリズムには様々なものがあり、基本的なものから応用まで様々なものがあるため、非常に奥が深いテーマとなっています。
今回はそんな整列を行うアルゴリズム(ソートアルゴリズムと呼ばれます)の中でも基本的な3つのソートについて説明していきたいと思います。
なお、基本3ソートは基本情報でも頻出なので必ず仕組み、プログラムを理解しておくことを強くおすすめします。
目次
スポンサードリンク
1.バブルソート
(1) バブルソートとは
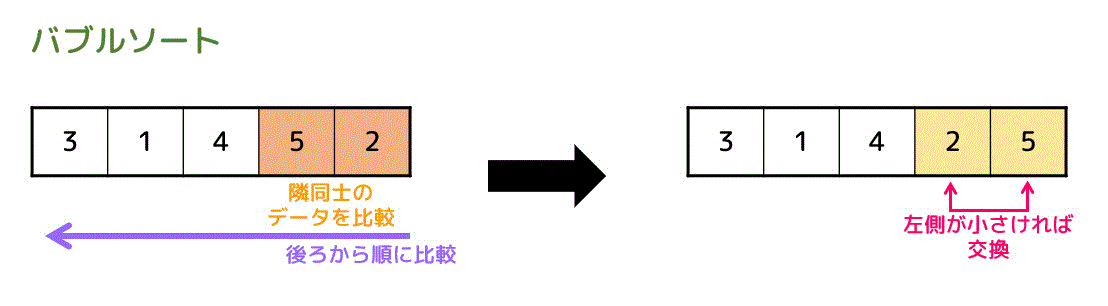
隣り合ったデータを右から*1順番に比較していき、右のほうが小さければ(昇順になっていなければ)データを入れ替えていき、整列させる方法をバブルソートと呼びます*2。
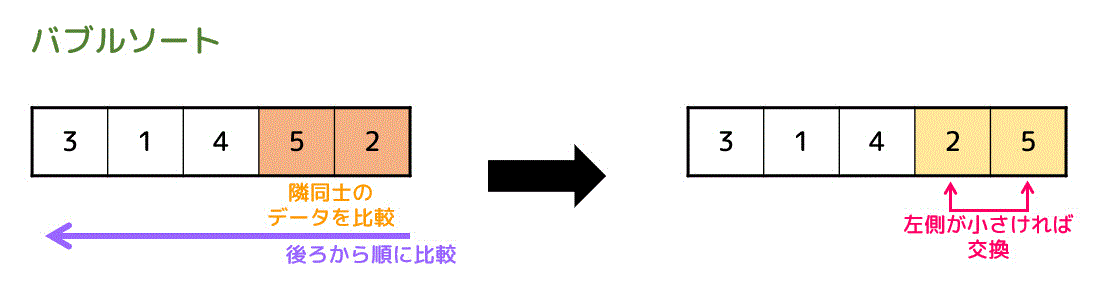
例えば、下の4つのデータを昇順にバブルソートしてみましょう。

後ろから順番に隣同士を比較していき、正しい順番になっていなければ2つのデータを入れ替えていきます。
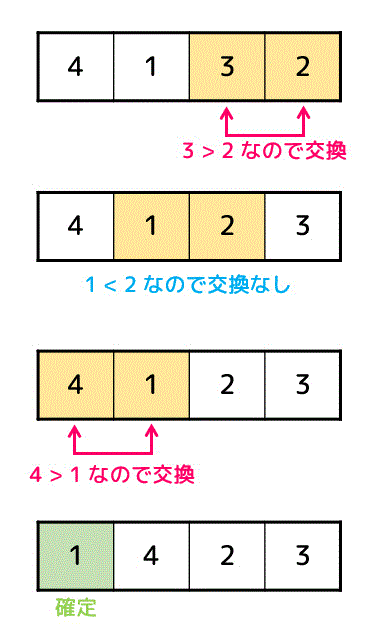
左端まで比較していくと、一番左側のデータの値が確定します。
さらにデータを確定させていくために再び右から順番にデータを比較していき、正しい順番(昇順)になっていなければ入れ替えます。
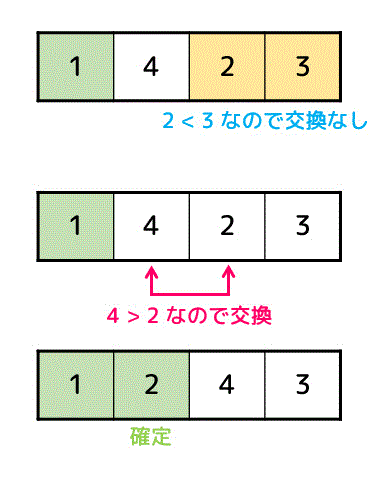
左端まで比較したので、未確定データの一番左側のデータが確定します。
再び右から比較していきます。
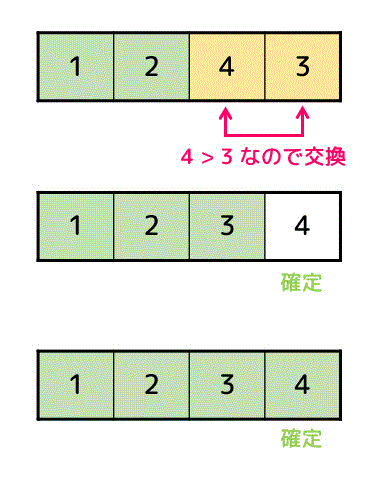
未確定データの一番左側のデータが確定し、自動的に残り1つのデータも確定するのでソート完了です!
(2) バブルソートのプログラム
要素数が n の配列 data を昇順にバブルソートするプログラムは、下のように書くことができます。
void bubble_sort(int data[],int n) {
int tmp;
for(int i = 0; i < n - 1; i += 1) {
for(int j = n - 1; j >= i + 1; j -= 1) {
// 配列の右側から順番に比較、昇順でなければ入れ替え
if(data[j-1] > data[j]) { // 条件を data[j-1] < [j] に変えると降順ソートに
// data[j-1] と data[j]の入れ替え
tmp = data[j-1];
data[j-1] = data[j];
data[j] = tmp;
// 入れ替え終わり
}
}
}
}
なお、if(data[j-1] > data[j]) の部分を if(data[j-1] < data[j]) に変えると降順ソートを行うことができます。
(3) バブルソートの比較・交換回数
n個のデータをバブルソートするときにif文で比較する回数とデータの最大交換回数を考えましょう。
バブルソートでは、1番目の要素を確定させるときに n-1 回、2番目の要素の確定時に n-2 回、………、最後(n-1 番目)の要素を確定時に 1 回比較するため、比較回数、および最大の交換回数は\[
\frac{1}{2} ( 1 + n - 1) \cdot (n-1) = \frac{1}{2} n (n-1)
\]となります*3。
そのため、バブルソートの計算量をオーダーで表すと \( O(n^{2}) \) となります。
スポンサードリンク
2.選択ソート
(2) 選択ソートとは
まだ整列が終わってないデータから最小値*4のデータを取り出し、最小値と確定データの右隣*5と入れ替えることで整列させていく方法を選択ソートと呼びます。
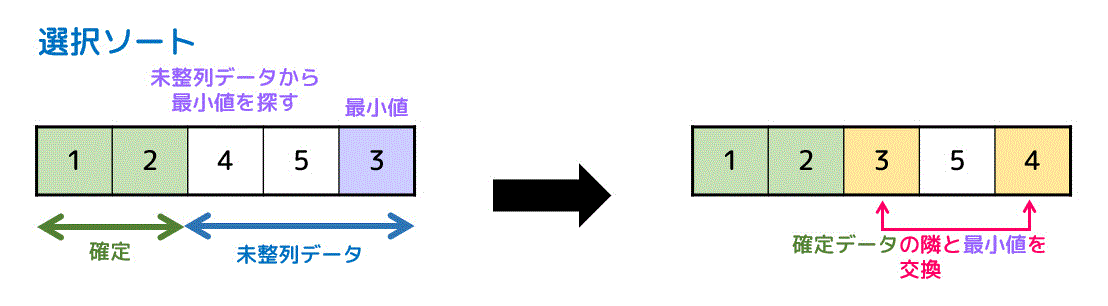
例えば、下の4つのデータを昇順に選択ソートしてみましょう。
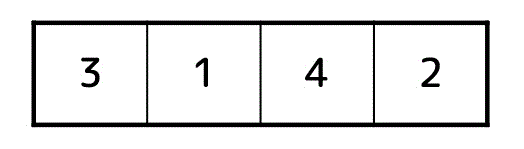
まず、未確定データ(全部)から最小値を探し、左端のデータと入れ替えます。
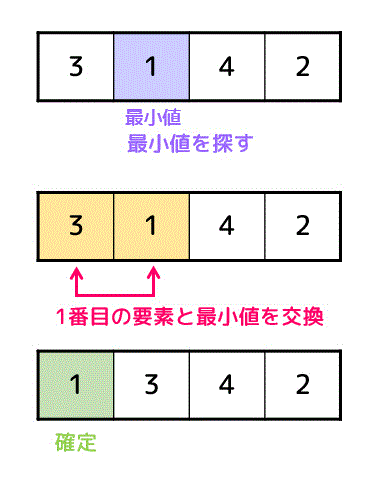
すると、左端のデータ「1」の場所が確定します。
再び確定していない残りの3つのデータから最小値を探し、確定データの右隣(2番目)のデータと入れ替えます。
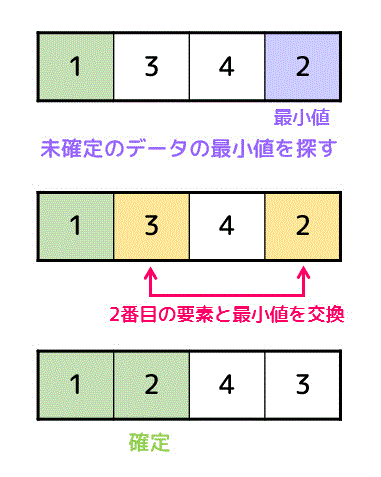
すると、左から2番目のデータ「2」の場所が確定します。
再び残り2つのデータから最小値を探し、確定データの右隣(3番目)のデータと入れ替えます。
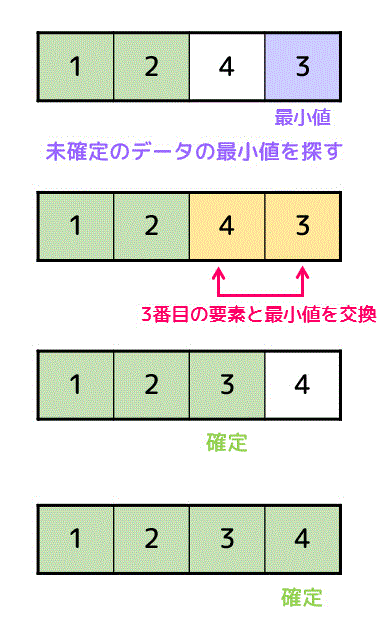
すると、左から3番目のデータ「3」が確定し、残りのデータ「4」の場所も確定し、ソート完了です!
(2) 選択ソートのプログラム
要素数が n の配列 data を昇順に選択ソートするプログラムは、下のように書くことができます。
void selection_sort(int data[],int n) {
int tmp, min;
for(int i = 0; i < n - 1; i += 1) {
min = i; // 配列の先頭を最小値の要素
for(int j = i + 1; j < n; j += 1) {
if(data[j] < data[min]) { // 暫定の最小値以下なら最小値を更新
min = j; // 最小値を持つ
}
} // min は最小値の要素
// data[i] と data[min] の入れ替え
tmp = data[i];
data[i] = data[min];
data[min] = tmp;
// 入れ替え終わり
}
}
参考までに降順ソートの場合は、下のようなプログラムとなります。
void selection_sort(int data[],int n) {
int tmp, max;
for(int i = 0; i < n - 1; i += 1) {
max = i; // 配列の先頭を最大値の要素と仮定
for(int j = i + 1; j < n; j += 1) {
if(data[j] > data[max]) { // 暫定の最大値以上なら最大値を更新
max = j; // 最大値を持つ
}
} // max は最大の要素
// data[i] と data[max] の入れ替え
tmp = data[i];
data[i] = data[max];
data[max] = tmp;
// 入れ替え終わり
}
}
(3) 選択ソートの比較・交換回数
n個のデータを選択ソートするときにif文で比較する回数とデータの交換回数を考えましょう。
選択ソートでは、最小値(or最大値)を探すために自分以外の未確定の要素を比較して最小値を探します。
そのため、1番目の要素を確定させるときにn-1回、2番目の要素を確定させるときにn-2回、……、n-1番目の要素を確定させるときに1回比較を行います*6。
そのため、選択ソートの比較回数、および最大の交換回数は\[
\frac{1}{2} ( 1 + n - 1) \cdot (n-1) = \frac{1}{2} n (n-1)
\]となります
また、交換は最小値を見つけたときにのみ行うので、n-1回の交換で済みます。
よって選択ソートの計算量は \( O(n^{2}) \) となります。
同じ \( O(n^{2}) \) ですが、交換回数がバブルソートよりも基本的に少ないため選択ソートはバブルソートより早いです。
スポンサードリンク
3.挿入ソート
[2022/8/11 修正] 挿入ソートの説明で使用していた画像に誤りがあったため、修正いたしました。(1) 挿入ソートとは
データを整列済と未整列の2つに分類し、未整列データの先頭の要素を正しい場所に挿入していくことで整列済にしていく方法を挿入ソートと呼びます。
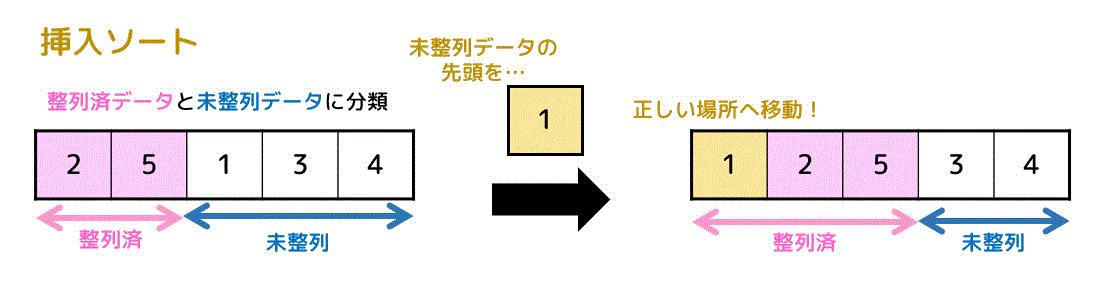
例えば、下の4つのデータを昇順に選択ソートしてみましょう。

まず、1つ目を整列済とします。
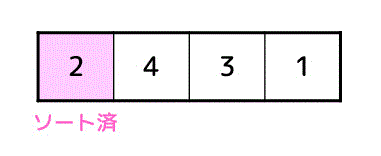
次に未整列のデータの先頭(2番目のデータ)を適切な位置に移動させます。
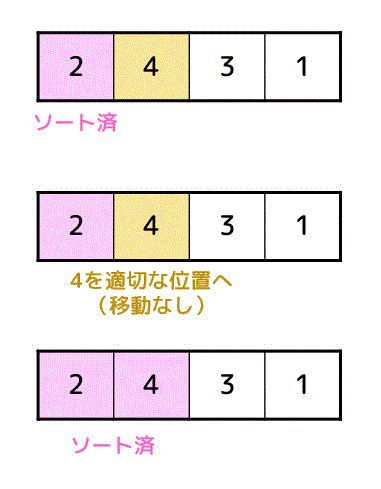
おや、偶然にも移動させなくても適切な位置でしたね。ということで2番目までのデータが整列できましたね。
どんどん整列済にしていきましょう。
つぎは3番目のデータを適切な位置に移動させます。
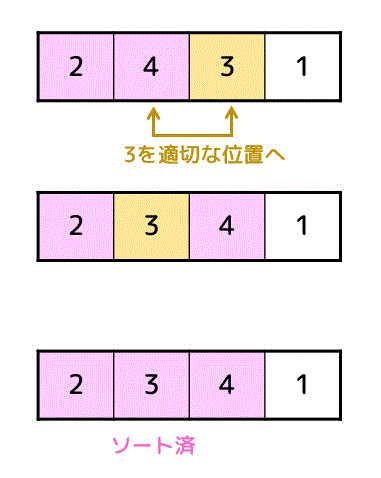
最後に4番目のデータを適切な位置に移動させればソート完了です。
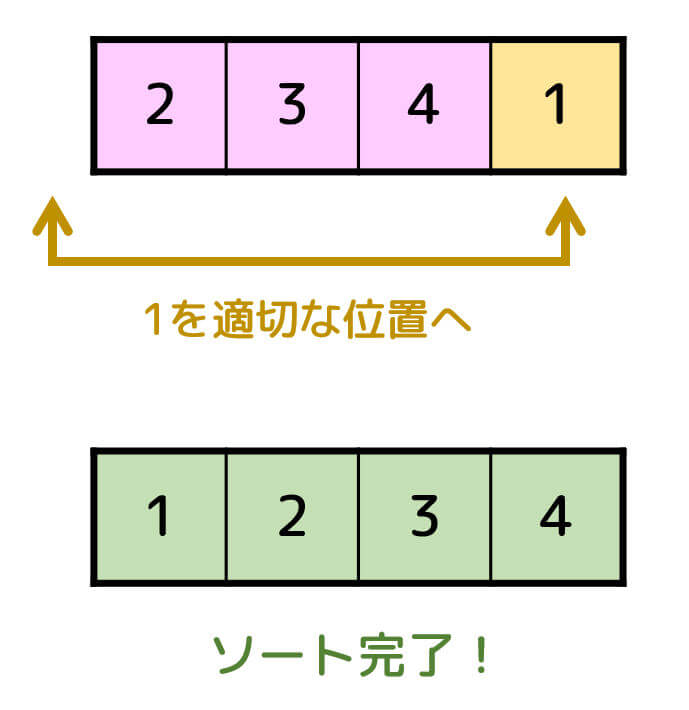
(2) 挿入ソートのプログラム
要素数が n の配列 data を昇順に挿入ソートするプログラムは、下のように書くことができます。
void insertion_sort(int data[], int n) {
int j, tmp;
for(int i = 1; i < n; i += 1) {
j = i;
// 適切な位置に入れ、整列済データを増やす
// while(j > 0 && data[j-1] < data[j]) に変えると降順ソートになる
while(j > 0 && data[j-1] > data[j]) {
// data[j-1] と data[j] の入れ替え
tmp = data[j-1];
data[j-1] = data[j];
data[j] = tmp;
// 入れ替え終わり
j -= 1; // 1つ左のデータへ
}
}
}
なお、while(j > 0 && data[j-1] > data[j]) の部分を while(j > 0 && data[j-1] < data[j]) に変えると降順ソートを行うことができます。
(3) 挿入ソートの比較・交換回数
n個のデータを選択ソートするときにif文で比較する回数とデータの最大交換回数を考えましょう。
1番目のデータは比較、交換をしなくても整列済にできますね。
2番目以降のデータは、値によっては1回の比較(交換なし)で済みますが、最もデータを比較・交換する場合、左端になるまでデータを交換していく必要があります。
2番目のデータであれば比較・交換回数は最大1回、3番目のデータであれば比較・交換回数は最大2回、n番目のデータであれば比較・交換回数は n-1 回となるので選択ソートの比較回数、および最大の交換回数は\[
\frac{1}{2} ( 1 + n - 1) \cdot (n-1) = \frac{1}{2} n (n-1)
\]となります。
よって挿入ソートの計算量は \( O(n^{2}) \) となります。
挿入ソートは、バブルソートや選択ソートに比べてデータが昇順に近ければ近いほど比較・交換回数が減少するため、他の単純ソートよりも速度が早いです。
4.ソートの安定性
(1) 安定ソートとは
同じ値が2つ以上あるときにソートしても同じ値の順番が変わらない(保存される)ソートのことを安定ソートと呼びます。
例えば下の6つのデータを数字が小さい順にソートすることを考えましょう。
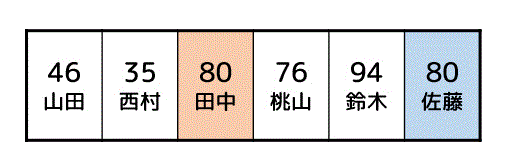
安定ソートであれば、下のように「80点の田中さん」と「80点の佐藤さん」の順序は必ず元のデータと同じになります。
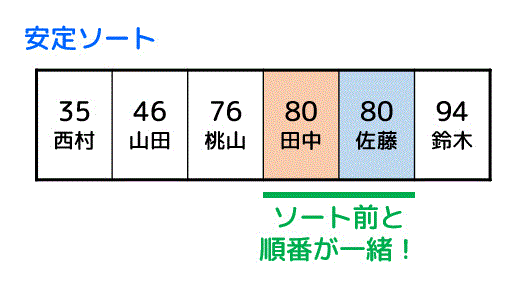
一方、安定でないソート(不安定ソート)の場合、下のように「80点の田中さん」と「80点の佐藤さん」の順序が入れ替わってしまうことがあります。
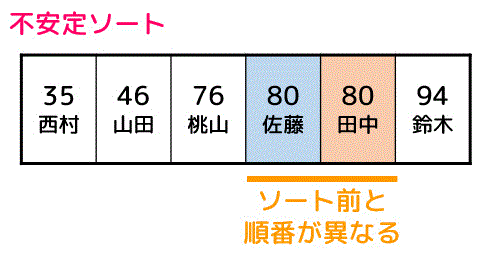
(2) 基本3ソートの安定性
今回紹介したソートの中でバブルソート・挿入ソートの2つは安定ソートです。
バブルソート、挿入ソートは隣同士のデータが正しい順番でなければ入れ替えるだけなので、隣同士に同じデータがあったとしても入れ替えは発生せず、元のデータと順序が変化しません。
一方選択ソートは、「隣同士のデータ」だけでなく、下のような「同じデータの順序を壊す」入れ替えを行う可能性があるため、安定ソートとはいえません。
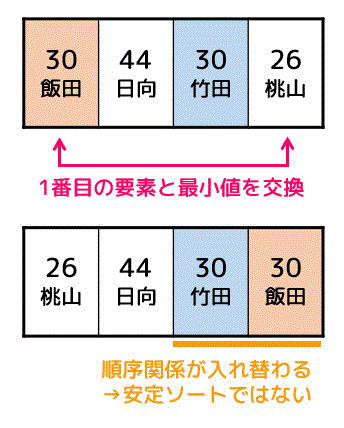
誤) 挿入ソート
正) 選択ソート
5.基本3ソートのまとめ
では、今回説明した3つのソートを簡単にですがまとめていきましょう。
(1) 基本3ソートの性質
バブルソート:隣り合ったデータを右側から比較し、正しい順番でなければ入れ替えていくことで左側から泡のようにソートしていく。
選択ソート:未整列のデータから最小値を探し、整列済みの最後尾に加えていくことでソートしていく。
挿入ソート:データを「整列済」・「未整列」の2つに分け、未整列のデータを整列済データの正しい場所に入れていくことでソートしていく。
(2) 計算量・安定性
| ソート名 | 最悪計算量 | 最良計算量 | 安定? |
|---|---|---|---|
| バブルソート | \( O(n^{2}) \) | \( O(n) \) | Yes |
| 選択ソート | \( O(n^{2}) \) | \( O(n^{2}) \) | No |
| 挿入ソート | \( O(n^{2}) \) | \( O(n) \) | Yes |
最悪計算量、平均計算量は3つのソートともに \( O(n^{2}) \) ですが、実際に計算が早い順番としては、
挿入ソート>選択ソート>バブルソート
となります。
6.練習問題
では、3問だけですが基本情報の過去問で練習していきましょう。
練習1
四つの数の並び(4, 1, 3, 2)を、ある整列アルゴリズムに従って昇順に並べ替えたところ、数の入替えは次のとおり行われた。この整列アルゴリズムはどれか。
[基本情報技術者平成14年春期 午前問14](1, 4, 3, 2)
(1, 3, 4, 2)
(1, 2, 3, 4)
ア:クイックソート
イ:選択ソート
ウ:挿入ソート
エ:バブルソート
練習2
未整列の配列Aiを,次のアルゴリズムで整列する。要素同士の比較回数のオーダを表す式はどれか。
[アルゴリズム]A[1]~A[n]の中から最小の要素を探し,それをA[1]と交換する。 A[2]~A[n] の中から最小の要素を探し,それをA[2]と交換する。 同様に,範囲を狭めながら処理を繰り返す。
ア:\( O(\log_{2} n) \)
イ:\( O(n) \)
ウ:\( O(n \log_{2} n) \)
エ:\( O(n^{2} ) \)
練習3
n個のデータをバブルソートを用いて整列するとき,データ同士の比較回数は幾らか。
ア:\( n \log n \)
イ:\( n (n+1) / 4 \)
ウ:\( n (n-1) / 2 \)
エ:\( n^{2} \)
7.練習問題の答え
(1) 解答1
解答:ウ
選択肢ごとに解説
ア:クイックソートは、ある基準値より大きいもの・小さいもののグループに振り分け、振り分けたグループの中でさらにグループ分け……を繰り返していくことでソートするアルゴリズム。(次回説明します)
イ:選択ソートであれば、左から順番にソートが完了していくので、(1, 4, 3, 2) → (1, 3, 4, 2) → (1,2,3,4) のような変化はしていかず、
(4,1,3,2) (1,4,3,2) # 1, 4を交換 (1,2,3,4) # 2, 4を交換
ウ:大正解。
エ:バブルソートであれば、隣り合ったデータしか比較し、交換することができないので
(1, 3, 4, 2) # 2番目と3番目のデータを交換 (1, 2, 3, 4) # 2番目と4番目のデータを交換
のよううな交換はしない。よって誤り。
解答2
解答:エ
上のアルゴリズムで探す場合、要素を探すために最大で約 n ステップ必要である。(要素を探すときのオーダー: \( O(n) \))
n 個のデータを確定させるためには要素を約 n 回*7探す必要があるので、オーダーは \[ O(n) \times O(n) = O(n^{2} ) \] となる。
よって答えはエとなる。
解答3
解答:ウ
バブルソートは、隣り合ったデータを比較していき、正しくなければ順番を入れ替えることで左側から順番に要素が確定していく。
比較するために必要な回数は1番目の要素のときに n-1 回、2番目で n 回、……、n番目の要素で1回となるので、バブルソートの比較回数は\[
\frac{1}{2} ( 1 + n - 1) \cdot (n-1) = \frac{1}{2} n (n-1)
\]で導出することができる。よって答えはウ。
8.さいごに
今回は基本的な3つのソートアルゴリズムとして、バブルソート、選択ソート、挿入ソートの3つを紹介しました。
できれば、基本的な3つのソートアルゴリズムは仕組みを理解するだけでなく、自分でプログラムが書けるようになることをおすすめします*8。
次回は、少し難しく、基本的なソートよりも高速にソートできるソートアルゴリズムを紹介していきたいと思います。
*1:正確には配列の添字が大きいほうから
*2:降順ソートをしたときには、降順になっていなければデータを入れ替えればOKです
*3:n = 4 のように具体例で考えてみるとよりわかりやすくなると思います。4個のデータの場合、最初のデータを確定させるまでに3回、2つ目のデータを確定させるまでに2回、3つ目のデータを確定させるために1回、合計6回比較を行います。
*4:降順に並び替える場合は最大値のデータを取り出せばOKです。
*5:確定データがないときは左端のデータと入れ替える。
*6:バブルソートと同じく n = 4 などで試してみるとわかりやすいと思います。
*7:実際には n-1回 だけどオーダーで考えるときはn回に対しての1回は誤差なので無視できる
*8:基本情報受けるだけなら仕組み理解するだけでもOKですが……
関連広告・スポンサードリンク