スポンサードリンク
こんにちは、ももやまです。
今回は2分探索木の4つの走査方法、具体的には
- 行きがけ順による走査
- 通りがけ順による走査
- 帰りがけ順による走査
- 幅優先探索による走査
の4つの違いについてわかりやすく説明していきたいと思います!
「2分探索木ってどんなやつだっけ」、「2分探索木忘れちゃったよ」という人は下にある記事でわかりやすく2分探索木について説明しているのでぜひご覧ください!
目次
スポンサードリンク
1.2分探索木の全探索
木構造にある各ノードを1度だけ訪問することを探索(走査)と呼びます。
全探索の仕方をおおまかに分けると、
- 深さ優先探索(DFS)
- 幅優先探索(BFS)
の2つとなります。
さらに、深さ優先探索はさらに
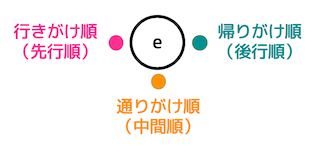
- 行きがけ順(先行順 / 前順 / preorder)
- 通りがけ順(中間順 / 間順 / inorder)
- 帰りがけ順(後行順 / 後順 / postorder)
の3つに分けることができます*1。
深さ優先探索、幅優先探索の2つで実際に(木以外のグラフなどを)探索した場合にどのような順番で探索できるかについてはこちらの記事にまとめているのでもし興味があればご覧ください。
スポンサードリンク
2.行きがけ順(先行順 / 前順 / preorder)
(1) 行きがけ順とは
行きがけ順は、「最初にノードを訪問する」タイミングが早い順に各ノードを探索していく方式です。
ノードを探索する具体的な順番は、
- まずデータを訪問
- 左側のノードに移動
- 右側のノードに移動
の順で探索を行います。
なお、先に進めなくなったときは、1つ戻って探索できるノードがあるか探します。
根まで戻ったときに探索できるノードがなくなったときが探索終了です。
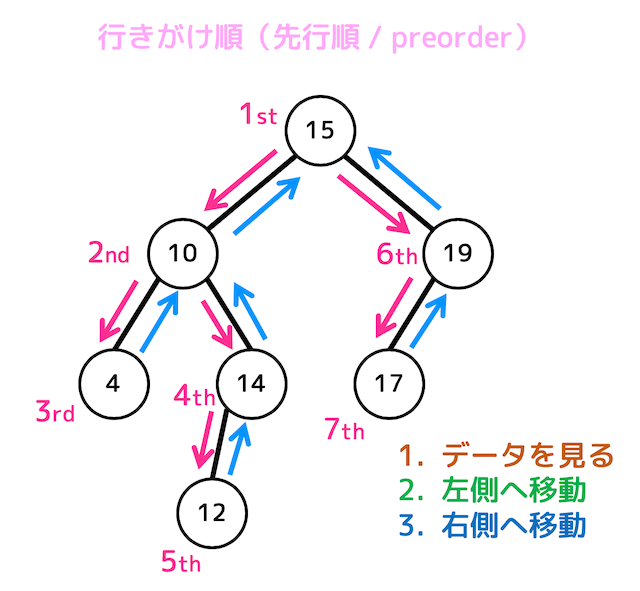
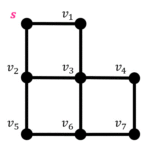
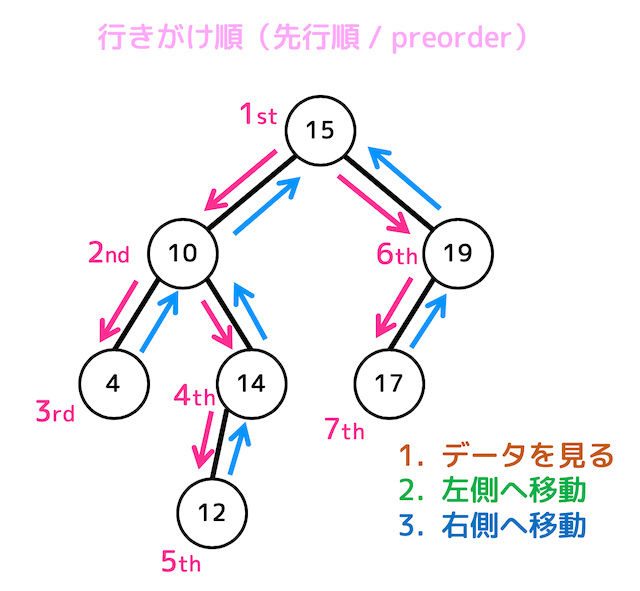
上の木構造の場合、行きがけ順による探索の過程は、
- まず15を訪問し、左側へ
- 10を訪問し、左側へ
- 4を訪問、左右両方なくなったので、1つ戻り10の右側をチェック
- 14を訪問、左側へ
- 12を訪問、左右両方なくなったので、3つ戻り15の右側をチェック
- 19を訪問、左側へ
- 17を訪問、全ノードチェック完了
のようになります。
(2) 行きがけ順を正しく求める魔法の一筆書き
試験ではよく「行きがけ順」を求めさせる問題が出題されます。
そこで、今回は簡単に行きがけ順を求めるテクニックを紹介したいと思います。
まず、下のように根からすべてのノードを反時計回りするように一筆書き(緑の線)をします。
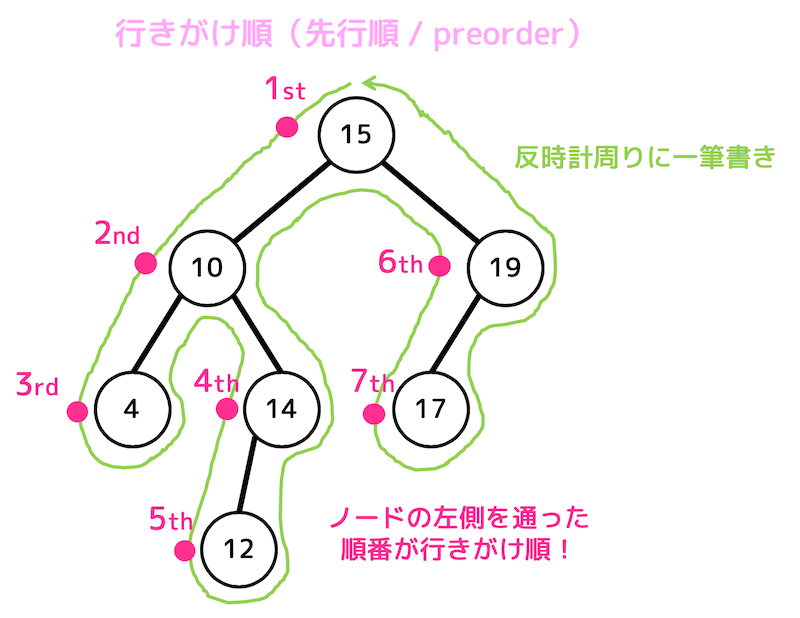
一筆書きをしたときに、ノードの左側(赤丸部分)を通った順番がなんとそのまま行きがけ順となります!
(3) 行きがけ順にデータを出力するプログラム
行きがけ順にデータを探索していく関数 preorder は、下のように再帰を用いることで簡単に記述することができます。
なお、引数 *p は木構造の根を指すポインタです。
void preorder(struct TREE *p) {
if(p != NULL) {
printf("%d ",p->data); // データの出力
preorder(p->left); // 左ノードへ移動
preorder(p->right); // 右ノードへ移動
}
}
スポンサードリンク
3.通りがけ順(中間順 / 間順 / inorder)
(1) 通りがけ順とは
通りがけ順は、途中(左側のノードに移動できなくなったタイミング)でノードを訪問するタイミングが早い順に各ノードを探索していく方式です。
具体的には、
- まず左側のノードに移動
- 左側に移動できなくなったらデータ出力
- 右側のノードに移動
の順で探索を行います。
なお、行きがけ順と同じように先に進めなくなったときは、1つ戻って探索できるノードがあるか探します。
根まで戻ったときに探索できるノードがなくなったときが探索終了です。
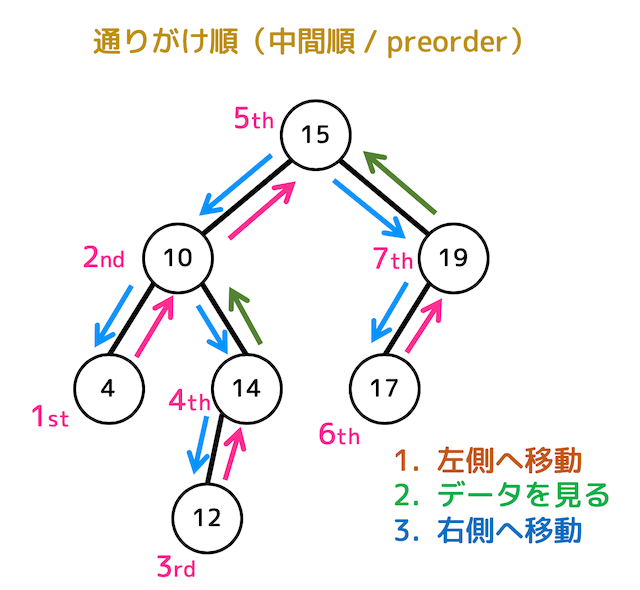
上の木構造の場合、行きがけ順による探索の過程は、
- まず左側に行けるだけ行き、4を出力
- 1つ戻り10を出力(左側にはもう行けないので)
- 右側に行き、14から左側に移動し、12を出力(14はまだ左側にいけるので出力しちゃダメ)
- 1つ戻り14を出力
- 1つ戻り10へ、しかし10は出力済みなのでさらに1つ戻り、15を出力
- 右側へ行き、さらに左側へ行き、17を出力(19は左側に行けるため出力できない)
- 1つ戻り19を出力、全ノード出力完了
のようになります。
(2) 通りがけ順を正しく求める魔法の一筆書き
「通りがけ順(中間順)」も一筆書きの魔法のテクニックで簡単に求めることができちゃいます!
まず、行きがけ順と同じように下のように根からすべてのノードを反時計回りするように一筆書き(緑の線)をします。
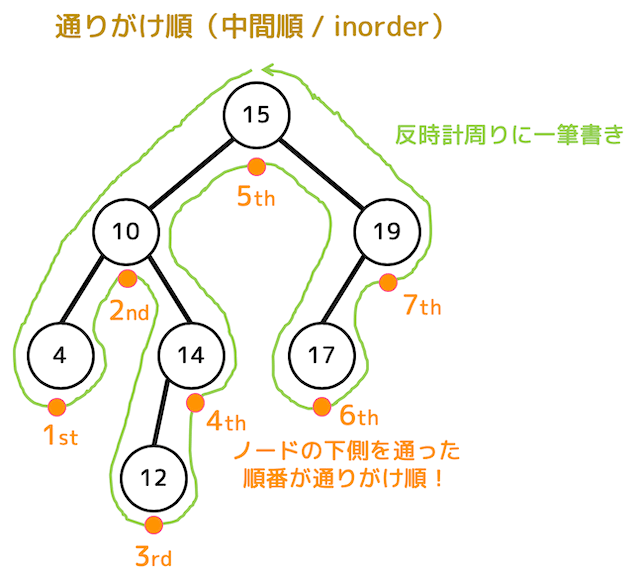
一筆書きをしたときに、ノードの下側(黄丸部分)を通った順番がなんとそのまま通りがけ順となります!
なお2分探索木の場合、通りがけ順は必ずデータの昇順となるので必ず頭に入れておきましょう。
(ただし試験では、「通りがけ順は昇順」とおぼえてきた人を落とすために、わざとデータが正しく入れられていない2分探索木 or 数値の代わりにa, b, cなどの文字になった2分探索木が出題されることがあります。なので通りがけ順の求め方(魔法の一筆書き)も頭にいれておきましょう。)
(3) 通りがけ順にデータを出力するプログラム
通りがけ順にデータを探索していく関数 inorder も、下のように再帰を用いることで簡単に記述することができます。
なお、引数 *p は木構造の根を指すポインタです。
void inorder(struct TREE *p) {
if(p != NULL) {
inorder(p->left); // 左ノードへ移動
printf("%d ",p->data); // データの出力
inorder(p->right); // 右ノードへ移動
}
}
4.帰りがけ順(後行順 / 後順 / postorder)
(1) 帰りがけ順とは
帰りがけ順は、最後(左右両方のノードに移動できなくなったタイミング)にノードを訪問するタイミングが早い順に各ノードを探索していく方式です。
具体的には、
- まず左側のノードに移動
- つぎに右側のノードに移動
- 移動できなくなったデータ出力
の順で探索を行います。
なお、行きがけ順、通りがけ順と同じように先に進めなくなったときは、1つ戻って探索できるノードがあるか探します。
根まで戻ったときに探索できるノードがなくなったときが探索終了です。
(2) 帰りがけ順を正しく求める魔法の一筆書き
「帰りがけ順(後行順)」も一筆書きの魔法のテクニックで簡単に求めることができちゃいます!
まず、行きがけ順、通りがけ順と同じように下のように根からすべてのノードを反時計回りするように一筆書き(緑の線)をします。
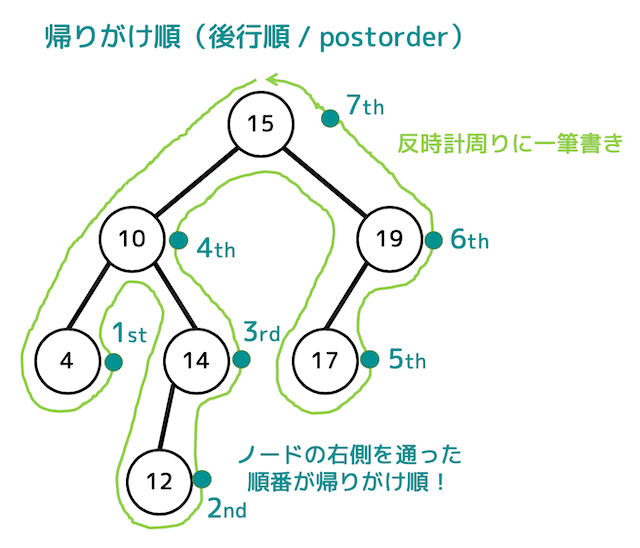
一筆書きをしたときに、ノードの右側(緑丸部分)を通った順番がなんとそのまま帰りがけ順となります!
(3) 帰りがけ順にデータを出力するプログラム
帰りがけ順にデータを探索していく関数 postorder も、下のように再帰を用いることで簡単に記述することができます。
なお、引数 *p は木構造の根を指すポインタです。
void postorder(struct TREE *p) {
if(p != NULL) {
postorder(p->left); // 左ノードへ移動
postorder(p->right); // 右ノードへ移動
printf("%d ",p->data); // 最後にデータ出力
}
}
5.幅優先探索
(1) 幅優先探索とは
幅優先探索は、深さごとに浅い順かつ左側から探索していく方式です。
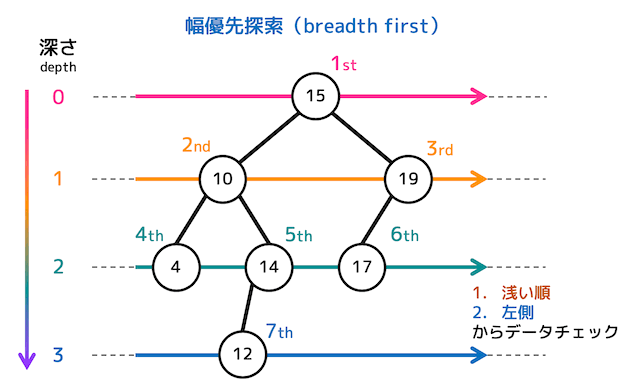
そのため、探索開始地点に近い点からまんべんなく探索が行われます。
(2) 幅優先探索で走査を行うプログラム
幅優先探索での走査は、深さ優先探索のように再帰を用いたプログラムでは表現できないので、下のようなデータ構造「キュー」を使って表現します*2。
#define SIZE 10 // キューの大きさ
struct QUEUE {
struct TREE* elm[SIZE]; // データの中身(ノード)
int start; // キューのデータの始まり
int end; // キューのデータの終わり
} ;
さらに、下のようにキューの操作関数を用意します。
// 初期化関数 QUEUEがポインタなのは参照渡しにするため
void init(struct QUEUE *q) {
q->start = 0;
q->end = 0;
}
// キューを環状と考え、次のキューの場所を計算する関数
// Ex. SIZE = 5 のとき、3番目の次は4番目、4番目の次は0番目
int nextStep(int x) {
return (x + 1) % SIZE;
}
// enqueue関数(ノードを入れていく)
void enqueue(struct TREE *x, struct QUEUE *q){
q->elm[q->end] = x;
q->end = nextStep(q->end);
}
// dequeue関数 出力するのはノードのポインタなので *dequeue となる
struct TREE *dequeue(struct QUEUE *q){
struct TREE* out_data = q->elm[q->start];
q->start = nextStep(q->start);
return out_data;
}
// キューが空か判定
int isEmpty(struct QUEUE *q){
if(q->start != q->end) {
return 0;
}
else {
return 1;
}
}
以上の操作関数を用いることで幅優先探索を行う関数 breadthfirst を下のように書くことができます。
なお、引数 *p は木構造の根を指すポインタ、引数 *q がキューを表します。
void breadthfirst(struct TREE *p, struct QUEUE *q) {
struct TREE *dq; // ノード取り出し用
if(p != NULL) {
enqueue(p,q); // 根の取り出し
while(! isEmpty(q)) {
dq = dequeue(q); // ノード取り出し
printf("%d ",dq->data); // 取り出したノードの値を出力
// 取り出したノードを展開し、左右のノードをキューへ
if(dq->left != NULL) {
enqueue(dq->left,q);
}
if(dq->right != NULL){
enqueue(dq->right,q);
}
}
}
}
6.練習問題
では、2問ほど2分探索木の走査練習をしてみましょう。
練習1
つぎの2分探索木がある。
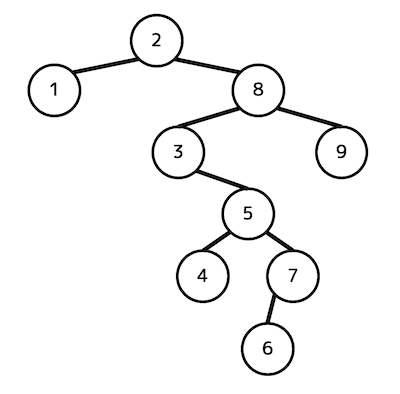
この2分探索木を、
- 行きがけ順
- 通りがけ順
- 帰りがけ順
- 幅優先探索による走査
したときにノードを走査する順番を答えなさい。
練習2
2分木の走査の方法には、その順序によって次の三つがある。
- 前順:節点,左部分木,右部分木の順に走査する。
- 間順:左部分木,節点,右部分木の順に走査する。
- 後順:左部分木,右部分木,節点の順に走査する。
図に示す2分木に対して前順に走査を行い,節の値を出力した結果はどれか。
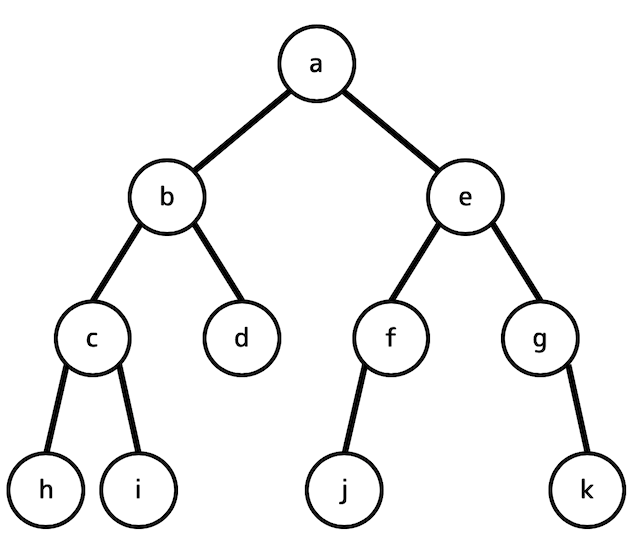
ア:abchidefjgk
イ:abechidfjgk
ウ:hcibdajfegk
エ:hicdbjfkgea
おまけ:間順(通りがけ順)、後順(帰りがけ順)、幅優先探索による走査もやってみよう!
7.練習問題の答え
練習1
魔法の一筆書きで順番を求めていきましょう。
行きがけ順
解答:2, 1, 8, 3, 5, 4, 7, 6, 9
魔法の一筆書きをしたときにノードの左側を通る順番がそのまま行きがけ順。
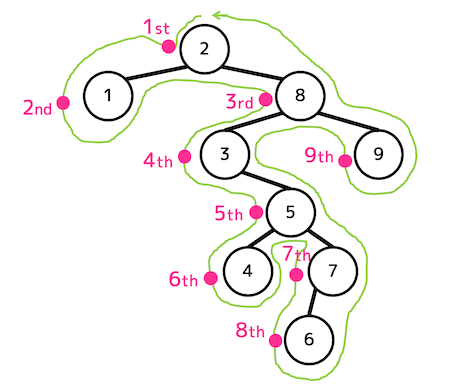
通りがけ順
解答:1, 2, 3, 4, 5, 6, 7, 8, 9
魔法の一筆書きをしたときにノードの下側を通る順番がそのまま通りがけ順。
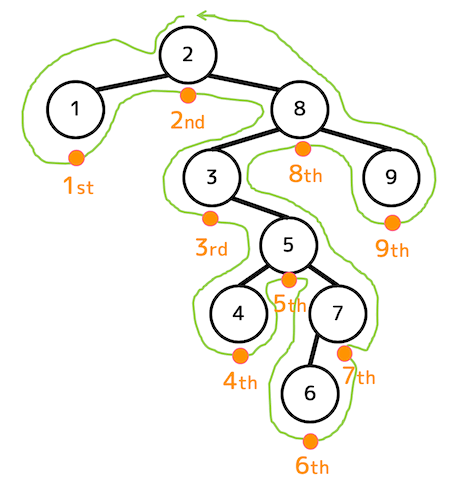
なお、通りがけ順を求めたときは解答が昇順になっていることを確かめること。
帰りがけ順
解答:1, 4, 6, 7, 5, 3, 9, 8, 2
魔法の一筆書きをしたときにノードの右側を通る順番がそのまま通りがけ順。
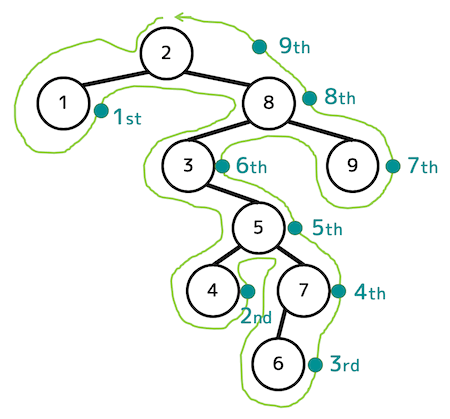
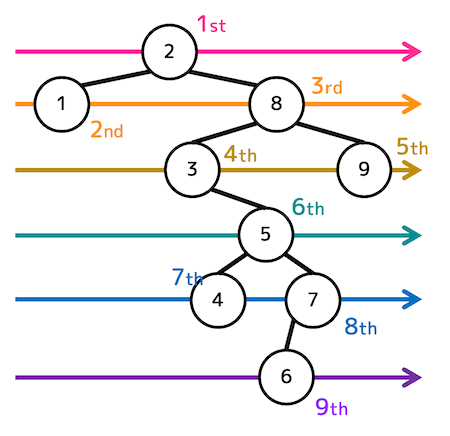
幅優先探索による走査
解答:2, 1, 8, 3, 9, 5, 4, 7, 6
深さごと(浅いところが先)に左側から順番に探索したものが幅優先探索。
練習2
解答:ア(順番:a, b, c, h, i, d, e, f, j, g, k)
練習1と同じく魔法の一筆書きで前順(行きがけ順)を求めていきましょう。
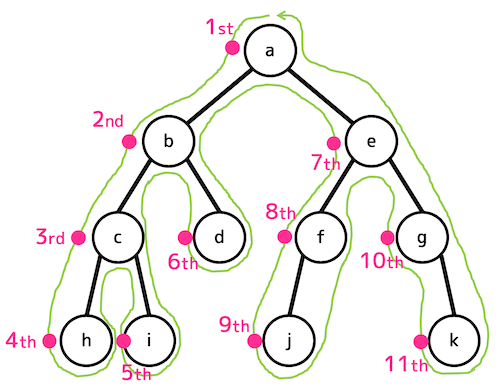
よって答えはアとなる。
おまけ:間順(通りがけ順)
通りがけ順:h, c, i, b, d, a, j, f, e, g, k
魔法の一筆書きをしたときにノードの下側を通る順番がそのまま間順(通りがけ順)。
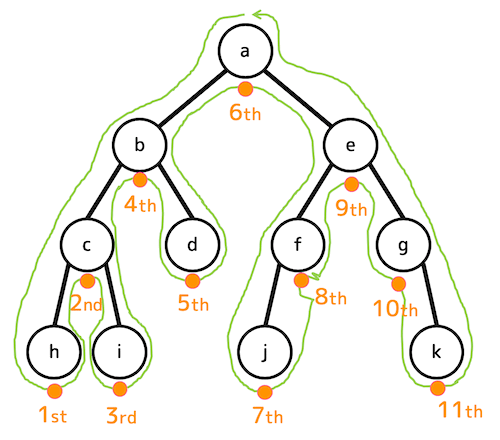
おまけ:後順(帰りがけ順)
後順:h, i, c, d, b, j, f, k, g, e, a
魔法の一筆書きをしたときにノードの右側を通る順番がそのまま後順(帰りがけ順)。
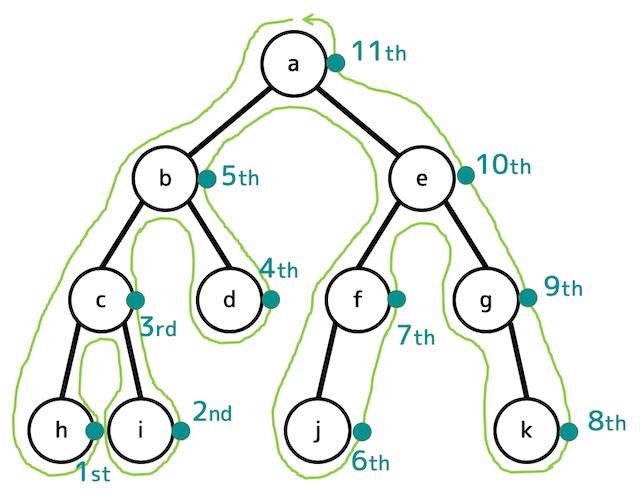
おまけ:幅優先探索による走査
解答:a, b, e, c, d, f, g, h, i, j, k
深さごと(浅いところが先)に左側から順番に探索したものが幅優先探索。
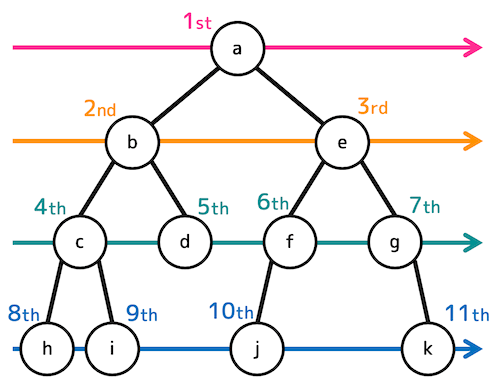
8.さいごに
今回は2分探索木の4つの走査方法についてまとめていきました。
行きがけ順、通りがけ順、帰りがけ順は、すべてのノードを反時計周りで囲って、特定の位置を通過する順番がそのまま走査順なるのでぜひ覚えておきましょう!
次回は基本的なソートアルゴリズムについてまとめていきたいと思います。
関連広告・スポンサードリンク