スポンサードリンク
こんにちは、ももやまです。
今回はオートマトンの演算についてまとめていきましょう。
皆さん、和集合、積集合、差集合については覚えていますか?
もし忘れてしまった人はこちらから復習しましょう!(少しだけですが使います)
前回のオートマトン「第02羽」はこちら↓
目次
スポンサードリンク
1.補集合演算
(1) 補集合演算 \( \overline{A} \), \( A^C \), \( \Sigma^{*} - A \)
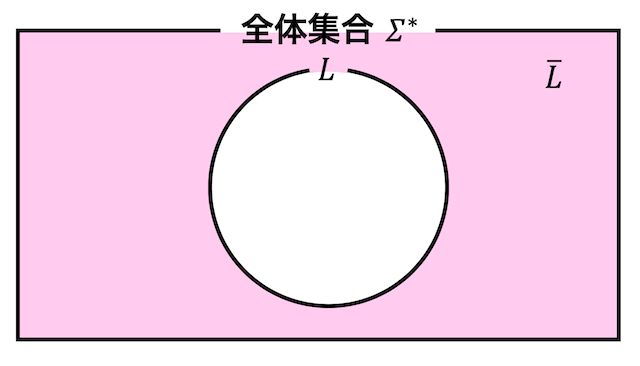
集合 \( L \) の補集合 \( \overline{L} \) とは、\( L \) に属さないもの全体を表しますね。
ベン図で表現すると、下のようになります。
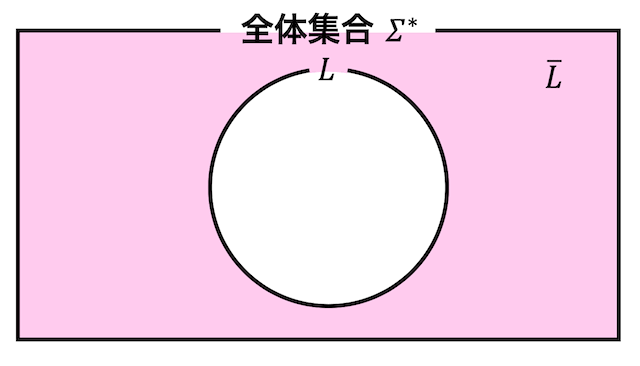
言語 \( L \) の補集合 \( \overline{L} \) とは、受理しない語(文字列)の集合を表します。つまり、言語 \( L \) に属さない文字列を受理するような集合となります。
言い換えると、今まで言語 \( L \) で受理した文字列は補集合では受理しなくなり、今まで言語 \( L \) で受理しなかった文字列は補集合では受理します。
また補集合を受理する言語 \( \overline{L} \) のことを、あとで説明する差演算を用いて、全体集合(すべての文字を受理する言語)からもとの言語の差 \( \Sigma^{*} - L \) と表されることもあります。
例として、次の状態遷移図で表されるような決定性オートマトンの補集合を考えてみましょう*1。(決定性というところがポイントです!)
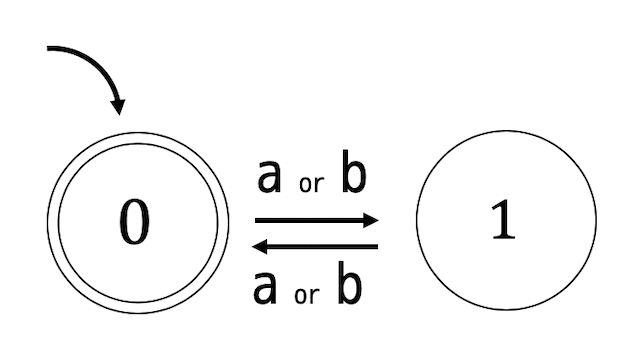
補集合ということは、今まで受理した文字列は受理しないように、今まで受理しなかった文字列は受理するようにすればOKですね。
つまり、とある決定性オートマトン \( L \) の補集合というのは、状態の受理状態◎と非受理状態○を入れ替えたオートマトンということができます。
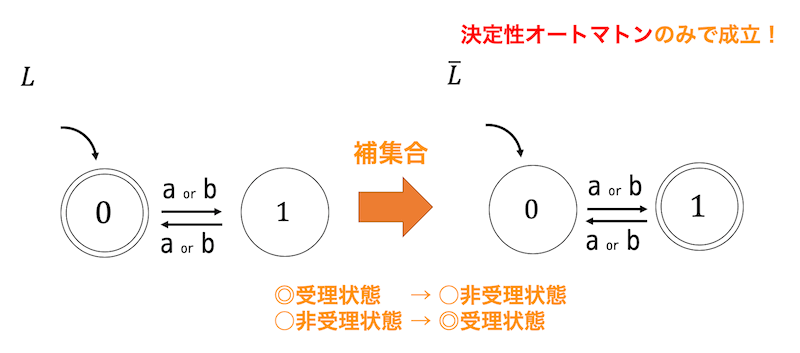
補集合演算における注意
補集合演算は必ず決定性オートマトンに変換した状態で行ってください。非決定性オートマトンのまま受理状態◎と非受理状態○を入れ替えても補集合を受理するオートマトンとはなりません。
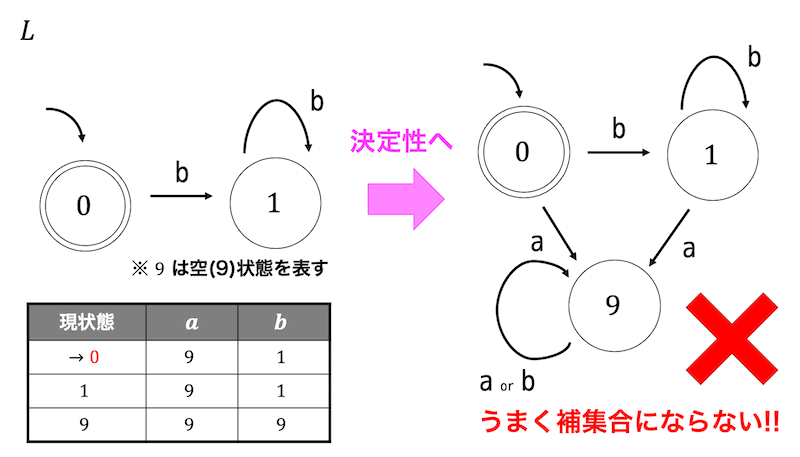
非決定性オートマトンの受理状態と非受理状態を入れ替えても補集合演算にならないことを確かめてみましょう。
例えば左側の状態遷移図で表される非決定性オートマトンを考えてみましょう。
まずは正しい手順で補集合を求めるために決定性オートマトンに変換を行います。
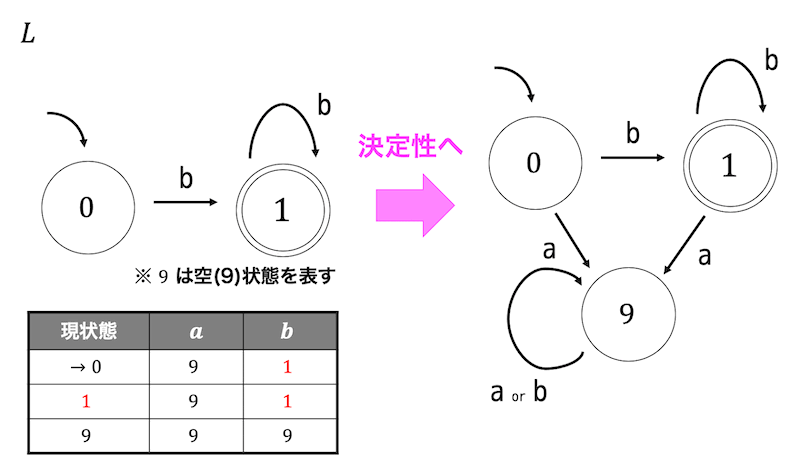
つぎに、決定性オートマトンの受理状態と非受理状態を入れ替えて補集合をとります。
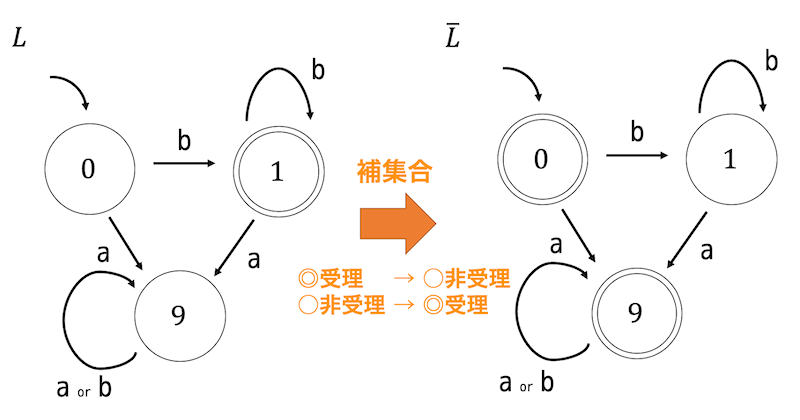
一方、非決定性の受理状態と非受理状態を入れ替えてから決定性オートマトンに変換すると、上の結果と異なった結果が出てきてしまい、正しく補集合を受理するオートマトンを求められません。
Step1:計算元のオートマトンが非決定性オートマトンなら決定性オートマトンに直す
Step2:決定性オートマトンの受理状態と非受理状態を入れ替える
以上の2ステップで補集合を受理するような決定性オートマトンが求められる。
補集合を受理するようなDFAの書き方
非決定性オートマトンを決定性オートマトンに直す方法がよくわからない(or忘れてしまった)という人はこちらから復習しましょう。
スポンサードリンク
2.2つの言語に対する演算(和・積・差演算)
ここからは2つの言語に対する演算(和、積、差の3つ)を紹介していきたいと思います。
具体例として、下の2つの状態遷移図、状態遷移表で表される言語を考えてみましょう。
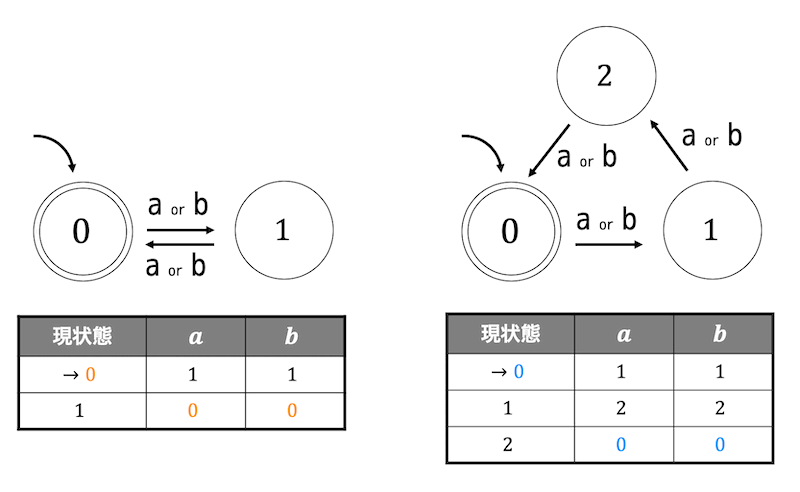
左側は2の倍数を受理するようなオートマトン \( L_1 \)
右側は3の倍数を受理するようなオートマトン \( L_2 \)
を表しています。
まずは、2つのオートマトンを1つとして、状態遷移表を書いていきます。
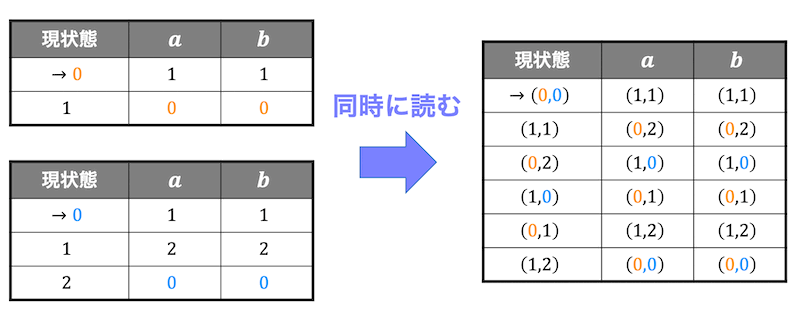
初期値を (\( L_1 \) の初期状態, \( L_2 \) の初期状態) とし(今回は(0,0) )、\( L_1 \) の状態遷移と \( L_2 \) の状態遷移を同時に読み取っていきます。
上の状態遷移表のように、\( L_1 \) の受理状態と \( L_2 \) の受理状態それぞれに色や記号などをつけておくと後々和集合、積集合、差集合を求めるときにわかりやすくなります。
1行目:\( L_1 \) の状態が0のとき \( a,b \) ともに1へ遷移する。また、\( L_2 \) の状態が0のとき \( a,b \) ともに1へ遷移する。よって、\( a \) も \( b \) も(1,1) となる。
2行目:\( L_1 \) の状態が1のとき \( a,b \) ともに0へ遷移する(受理状態)。また、\( L_2 \) の状態が0のとき \( a,b \) ともに2へ遷移する。よって、\( a \) も \( b \) も(0,2) となる。
………
というのを未知の状態遷移がなくなるまですべて調べていきます。
ここまでは和演算、積演算、差演算すべて同じ流れです。
では3つの演算で何が異なるかというと、和・積・差の演算で異なるのは受理状態の違いです。
(2) 和演算 \( L_1 \cup L_2 \)
和集合は下の図のように、2つの集合 \( L_1 \), \( L_2 \) のうちのどちらか一方、もしくは両方に属している要素の集合を表します。
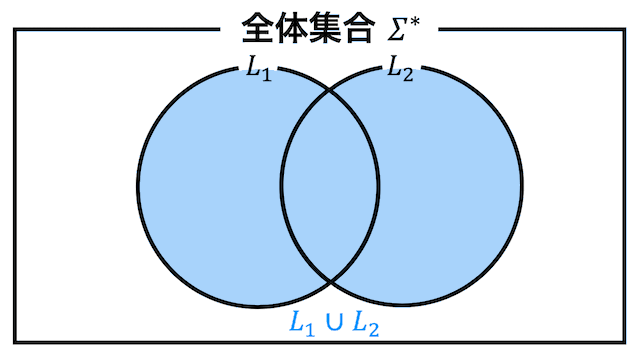
言語の和演算 \( L_1 \cup L_2 \) も同じように、2つの言語 \( L_1 \), \( L_2 \) のうちどちらか片方でも受理している状態であれば \( L_1 \cup L_2 \) も受理状態となります。
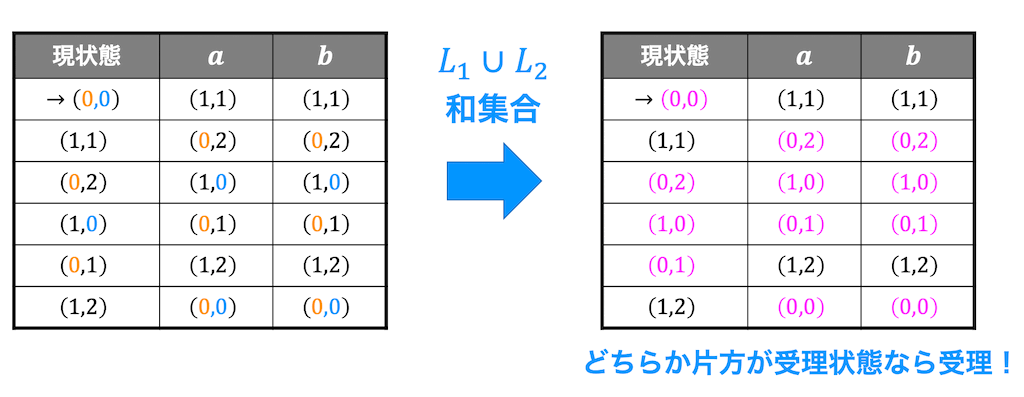
あとは表をみながら状態遷移図を記入するだけです!
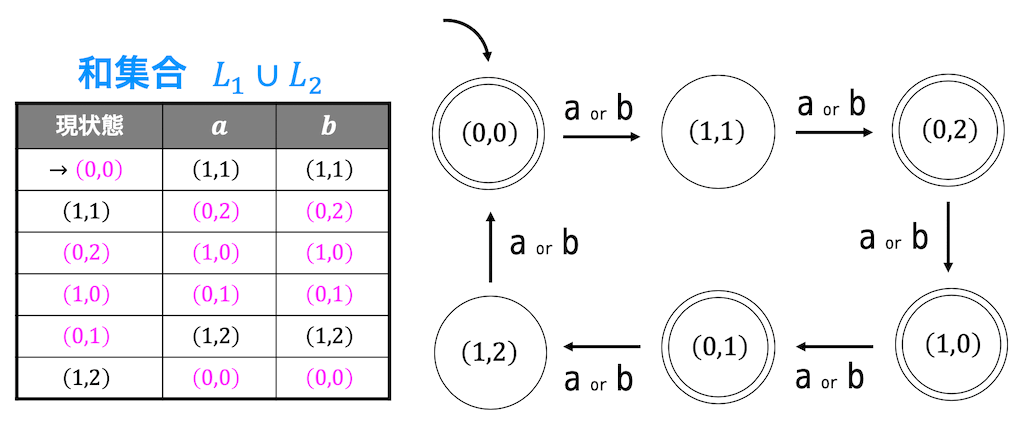
確認すると、文字数が2の倍数もしくは3の倍数のときに受理するような決定性オートマトンになっていますね。なので、正しく和演算が出来ていることがわかります。
(3) 積演算 \( L_1 \cap L_2 \)
積集合は下の図のように、2つの集合 \( L_1 \), \( L_2 \) のうちの両方に属している要素の集合を表します(片方だけではダメ)。
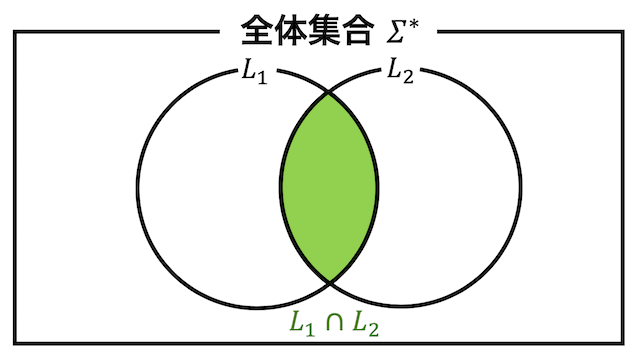
言語の積演算 \( L_1 \cap L_2 \) も同じように、2つの言語 \( L_1 \), \( L_2 \) の両方が受理している状態であれば \( L_1 \cup L_2 \) も受理状態となります。
(片方だけなら受理状態とはならない)
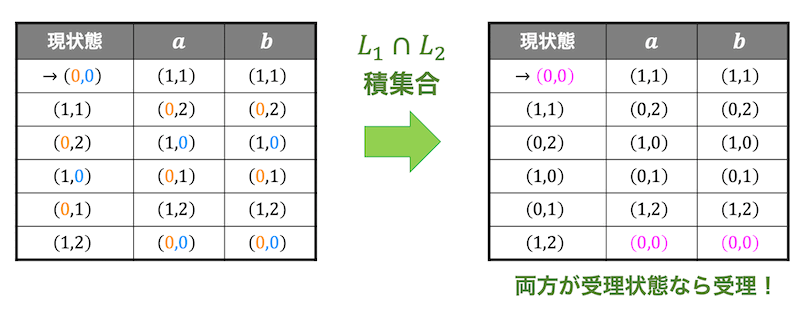
あとは状態遷移表を状態遷移図に直せばOKです!
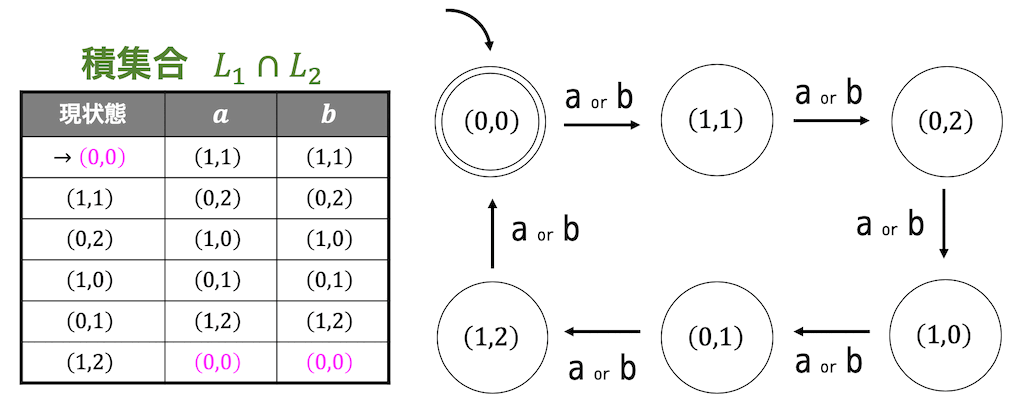
確認すると、文字数が2の倍数かつ3の倍数(つまり6の倍数)のときに受理するような決定性オートマトンになっていますね。なので、正しく積演算が出来ていることがわかります。
(4) 差演算 \( L_1 - L_2 \)
差集合は下の図のように、2つの集合 \( L_1 \) に含まれているが \( L_2 \) には含まれていない要素の集合を表します。つまり、\( L_1 \cap \overline{L_2} \) と同じです。
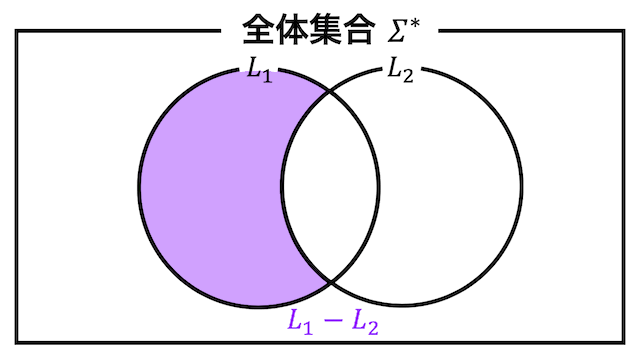
言語の積演算 \( L_1 - L_2 \) も同じように、\( L_1 \) が受理状態かつ \( L_2 \) が非受理状態であれば \( L_1 - L_2 \) も受理状態となります。
(\( L_1 \) で受理する文字列かつ \( L_2 \) で受理しない文字列が \( L_1 - L_2 \) で受理する文字列)
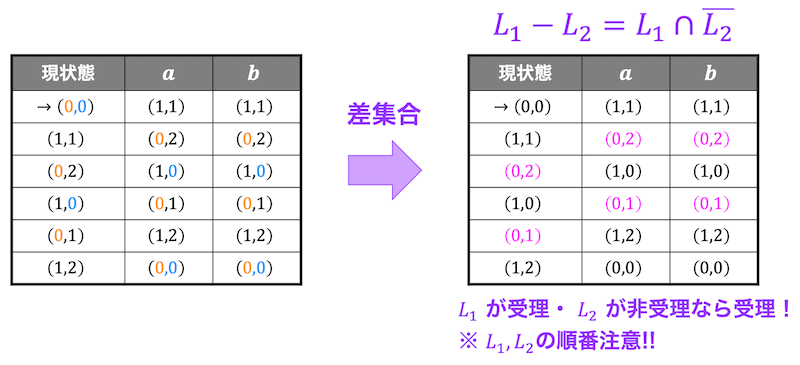
和演算や積演算と異なり、順番を入れ替えると(\( L_1 - L_2 \) と \( L_2 - L_1 \) のように) 結果が変わってしまう点に要注意です。
あとは状態遷移表から状態遷移図を書けば完成です。
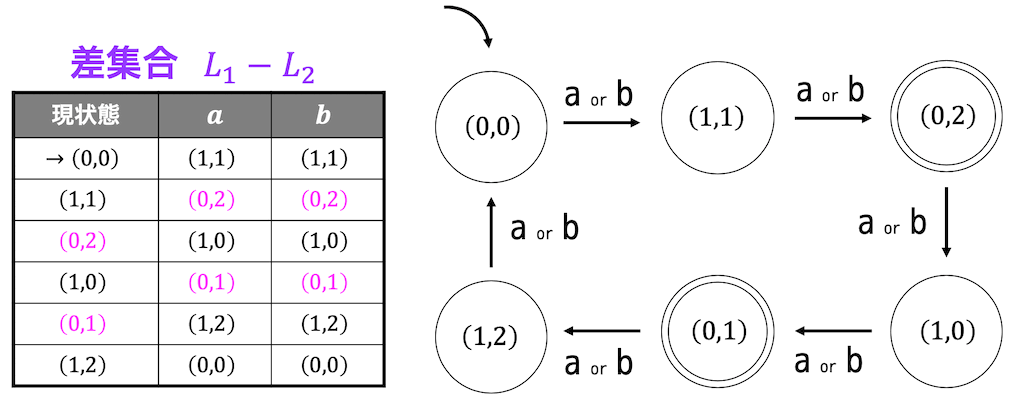
確認すると、文字数が2の倍数かつ3の倍数ではないときに受理するような決定性オートマトンになっていますね。なので、正しく差演算が出来ていることがわかります。
Step1:計算したい2つのオートマトン \( L_1 \), \( L_2 \) を決定性オートマトンに変換し、状態遷移表を書く
Step2:2つの状態遷移表を同時に読んでいき、新たな状態遷移表を書いていく
Step3:受理状態の確認↓(差演算は順番に要注意!)
和演算 \( L_1 \cup L_2 \)
\( L_1 \), \( L_2 \) どちらか片方が受理している状態を受理状態とする
積演算 \( L_1 \cap L_2 \)
\( L_1 \), \( L_2 \) 両方が受理している状態を受理状態とする
差演算 \( L_1 - L_2 \)
\( L_1 \) が受理していて \( L_2 \) が受理していない状態を受理状態とする
差演算 \( L_2 - L_1 \)
\( L_2 \) が受理していて \( L_1 \) が受理していない状態を受理状態とする
Step4:状態遷移表をみながら状態遷移図を書く。
以上の4ステップで和、積、差が求められる。
決定性オートマトンにおける和演算・積演算・差演算の求め方
スポンサードリンク
3.各種演算と正則言語
有限オートマトン(決定性非決定性限らず)を書くことをできるような言語を正則な言語と呼びます。
各種演算とオートマトンの正則性を下に示しておきます。
また、ある言語 \( L_1 \), \( L_2 \) がともに正則なとき、\( L_1 \cup L_2 \), \( L_1 \cap L_2 \), \( L_1 - L_2 \) は正則である。
\( L \) が正則ならば補集合 \( \overline{L} \) も正則はわかりやすいと思います。受理状態と非受理状態を入れ替えるだけなので補集合にした瞬間に有限オートマトンが書けなくなる、なんてことは起こりませんよね。
また、\( L \) の補集合の補集合、つまり \( \overline{\overline{L}} \) は元の言語 \( L \) に戻りますよね。なので補集合を取っても正則性は変わらないことがわかりますね。
また、ともに正則な(有限オートマトンが書ける)言語 \( L_1 \), \( L_2 \) に対して和演算、積演算、差演算を行っても必ず有限オートマトンが書けることが上の定理からわかりますね。
しかし、この逆( \( L_1 \cup L_2 \) が正則ならば \( L_1 \), \( L_2 \) が正則)は成り立つでしょうか? 少し考えてみましょう。
(練習問題に入れたのでぜひ考えてください、最後のほうに答えを載せています。)
4.練習問題
では、2問練習してみましょう。1問はオートマトンを実際に演算する問題、もう1問は定理を考えるような問題です。
練習1
つぎの非決定性オートマトン \( M_1 \) および決定性オートマトン \( M_2 \) で与えられる言語 \( L(M_1) \), \( L(M_2) \) がある。
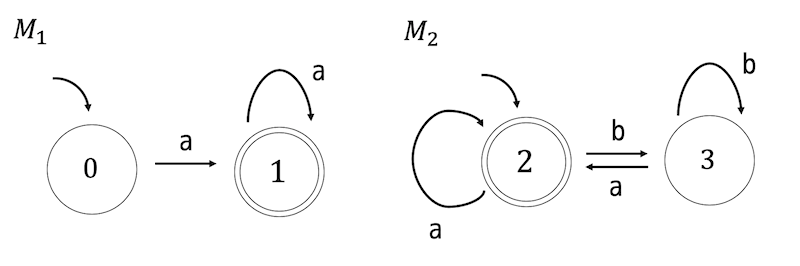
これについて、次の(1)〜(5)の問いに答えなさい。
(1) \( M_1 \) を決定性オートマトンに直しなさい。[前回の復習](2) \( \Sigma^{*} - L(M_1) \) を受理するような決定性オートマトンを書きなさい。
(3) \( L(M_1) \cup L(M_2) \) を受理するような決定性オートマトンを書きなさい。
(4) \( L(M_1) \cap L(M_2) \) を受理するような決定性オートマトンを書きなさい。
(5) \( L(M_2) - L(M_1) \) を受理するような決定性オートマトンを書きなさい。
練習2
つぎの(1)〜(10)の文章が正しければ○、誤っていれば×を答えなさい。簡単な理由も書くこと。
(1) 言語 \( L_1 \cup L_2 \) が正則ならば、当然 \( L_1 \), \( L_2 \) ともに必ず正則である。
(2) 言語 \( L_1 \cap L_2 \) が正則ならば、当然 \( L_1 \), \( L_2 \) ともに必ず正則である。
(3) 言語 \( L_1 \), \( L_1 \cup L_2 \) が正則ではないのに \( L_2 \) が正則となる場合が存在する。
(4) 言語 \( \Sigma^{*} - L \) が正則ならば、当然 \( L \) は必ず正則である。
(5) 言語 \( L_1 \), \( L_2 \) がともに正則でないならば、当然 \( L_1 - L_2 \) は正則でない。
(6) 言語 \( L_1 \), \( L_2 \) がともに正則でないならば、当然 \( L_1 \cap L_2 \) は正則でない。
(7) 言語 \( L_1 \), \( L_2 \) がともに正則でないならば、当然 \( L_1 \cup L_2 \) は正則でない。
(8) 言語 \( \overline{L} \) が正則でないならば、当然 \( L \) も正則ではない。
(9) 言語 \( L_1 \cup L_2 \) が正則でないならば、\( L_1 \), \( L_2 \) のうち少なくとも一方は正則ではない。
(10) 言語 \( L_1 \cap L_2 \) が正則でないならば、\( L_1 \), \( L_2 \) のうち少なくとも一方は正則ではない。
5.練習問題の答え
解答1
(1)
まずは復習。
状態遷移表を書いて状態遷移図に直せばOK。
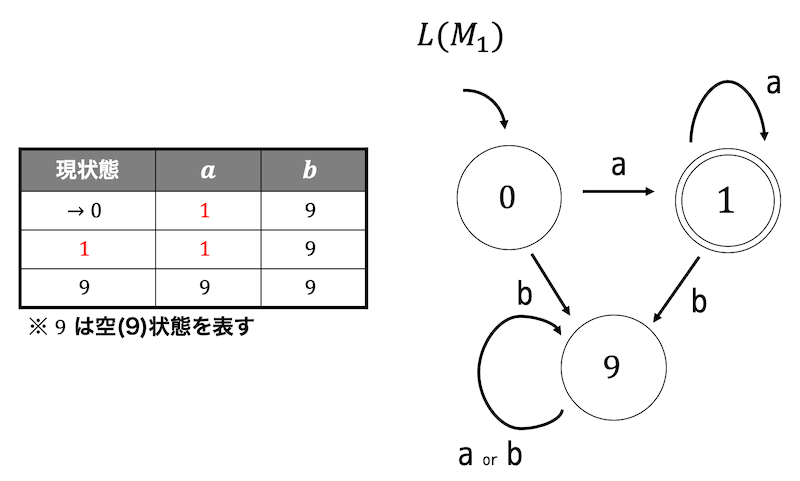
(2)
\( \Sigma^{*} - L(M_1) = \overline{L(M_1)} \) となるので、\( L(M_1) \) の補集合を受理するようなオートマトンを書けばOK。補集合は決定性オートマトンの受理状態と非受理状態を入れ替えるだけ。よって下のように書ける。
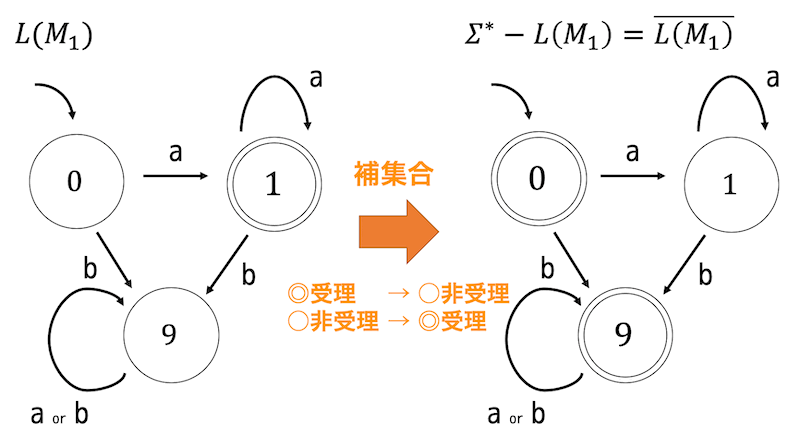
(3)〜(5)
まずは、\( L(M_1) \) と \( L(M_2) \) の状態遷移表を書き、同時に読んでいった状態遷移表を新たに書く。
(左側の数値が \( L(M_1) \) の状態、右側の数値が \( L(M_2) \) の状態を表す。)
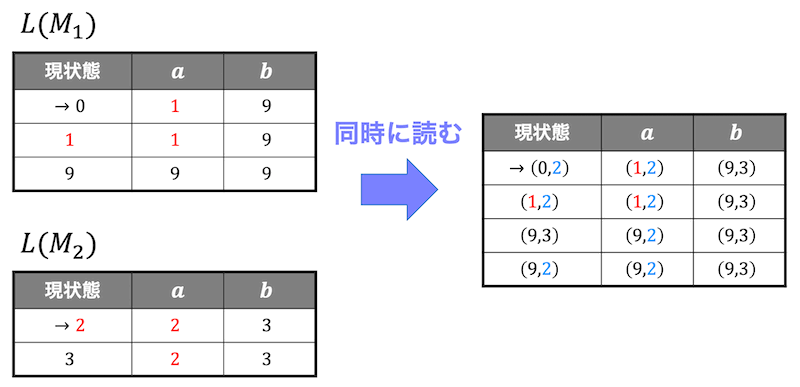
これで下準備が完了。
(3)
\( L(M_1) \cup L(M_2) \) なので(和演算)、どちらか片方でも受理状態であれば \( L(M_1) \cup L(M_2) \) においても受理状態となる。
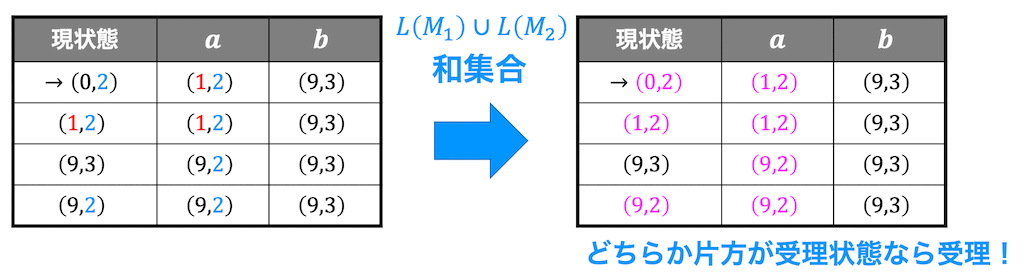
よって、状態遷移図は
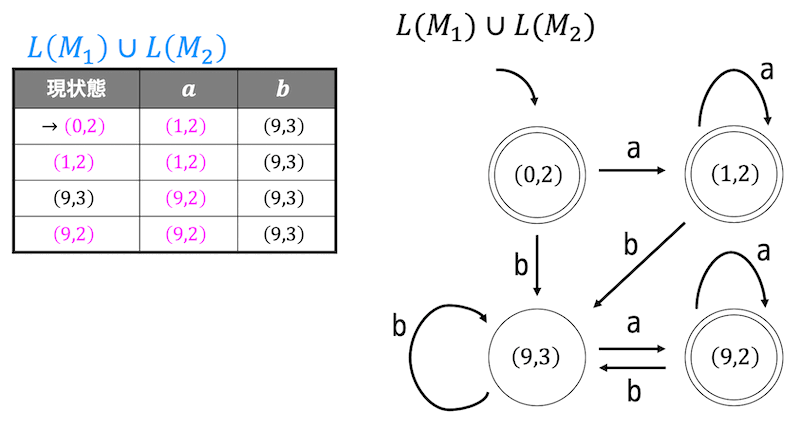
となる(状態遷移表を読むだけ)。
(4)
\( L(M_1) \cap L(M_2) \) なので(積演算)、両方が受理状態であれば \( L(M_1) \cap L(M_2) \) においても受理状態となる。
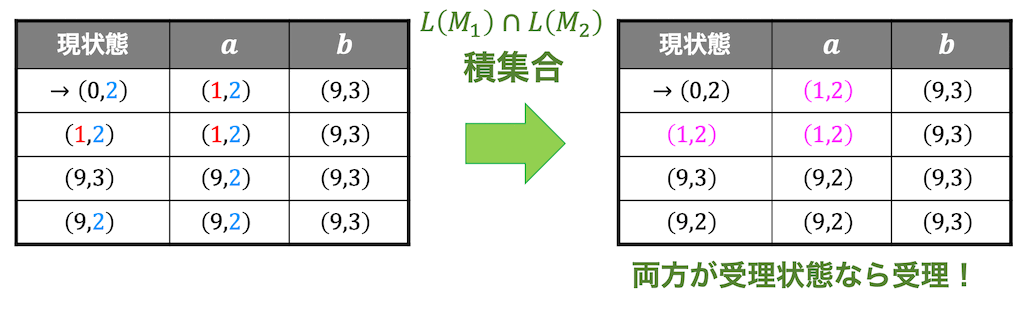
よって状態遷移図は
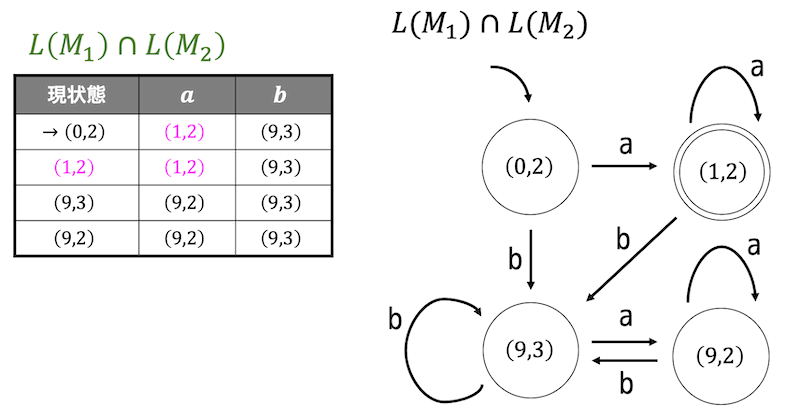
となる。
(5)
\( L(M_2) - L(M_1) \) なので(差演算)、\( L(M_2) \) が受理して \( L(M_1) \) が受理しないような状態が \( L(M_2) - L(M_1) \) においても受理状態となる。
(順番要注意!!)

よって状態遷移図は
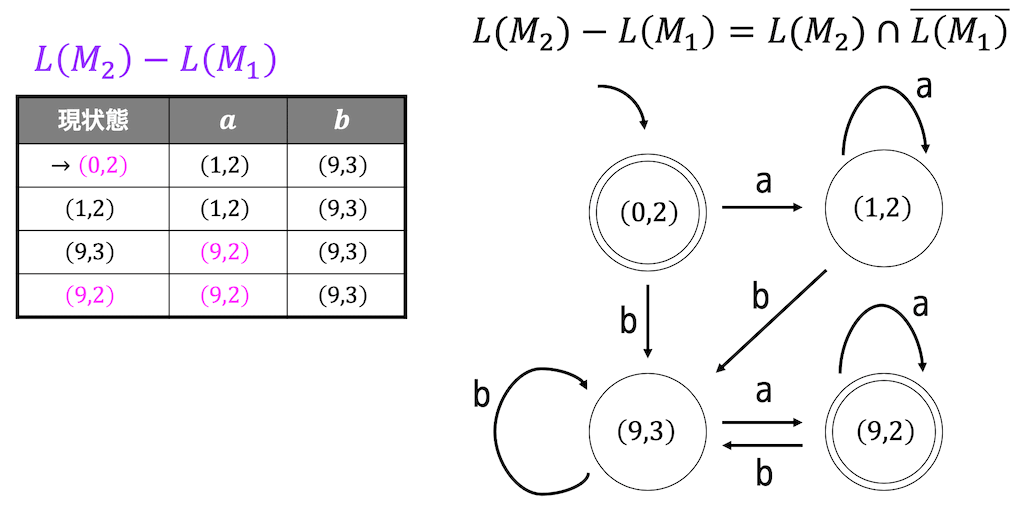
となる。
解答2
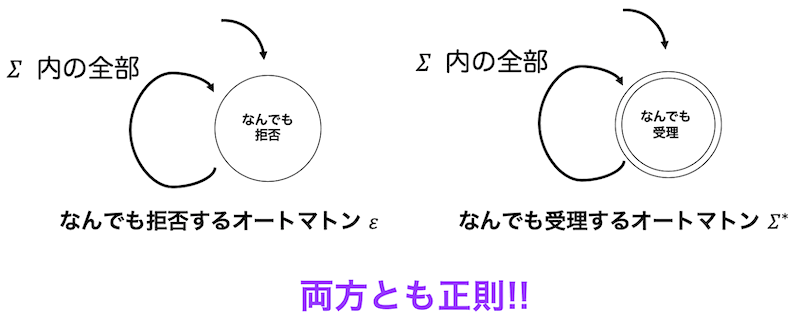
このような問題では \( \varepsilon \)(すべての文字を受理しないような言語)や \( \Sigma^{*} \)(すべての文字を受理するような言語)を例として考えるとかなり簡単に反例を考えることができます(\( \Sigma^{*} \) と \( \varepsilon \) は両方とも正則です)*2。
正則でない言語を \( N \) とおく。
(1)
解答:×
理由:例えば、\( L_1 = N \), \( L_2 = \overline{N} \) のとき、\( L_1 \cup L_2 = \Sigma^{*} \) となる。\( \Sigma^{*} \) が正則なのにも関わらず、 \( L_1 \), \( L_2 \) は正則な言語ではないのでこれが反例となる。
(2)
解答:×
理由:例えば、\( L_1 = N \), \( L_2 = \overline{N} \) のとき、\( L_1 \cup L_2 =\varepsilon \) となる。\( \varepsilon \) が正則なのにも関わらず、 \( L_1 \), \( L_2 \) は正則な言語ではないのでこれが反例となる。
(3)
解答:○
理由:例えば、\( L_1 = N \), \( L_2 = \varepsilon \) とすると、\( L_1 \cup L_2 = N \) となり、\( L_1 \), \( L_1 \cup L_2 \) が正則ではないのに \( L_2 \) が正則となる。
(4)
解答:○
理由:\( \Sigma^{*} - L \) は \( L \) の補集合を表している。
\( \overline{L} \) の補集合は \( \overline{\overline{L}} = L \) となる。正則な言語の補集合は正則なので○。
(5)
解答:×
\( L_1 = L_2 = N \) とすると、\( L_1 - L_2 = \varepsilon \) となり、\( L_1 \), \( L_2 \) が正則でないのに正則になってしまう。
(6)
解答:×
ほぼ(5)と同じ。\( L_1 =N \), \( L_2 = \bar{N} \) とすると、\( L_1 \cap L_2 = \varepsilon \) となり、\( L_1 \), \( L_2 \) が正則でないのに正則になってしまう。
(7)
解答:×
\( L_1 =N \), \( L_2 = \overline{N} \) とすると、\( L_1 \cup L_2 = \Sigma^{*} \) となり、\( L_1 \), \( L_2 \) が正則でないのに正則になってしまう。
(8)
解答:○
対偶を取ると「\( L \) が正則ならば \( \overline{L} \) も正則」となり、定義そのものになる。対偶が○なので元も○。
(9)
解答:○
対偶を取ると「\( L_1 \), \( L_2 \) がともに正則ならば \( L_1 \cup L_2 \) も正則である」となり、定義そのものになる。対偶が○なので元も○。
(10)
解答:○
対偶を取ると「\( L_1 \), \( L_2 \) がともに正則ならば \( L_1 \cap L_2 \) も正則である」となり、定義そのものになる。対偶が○なので元も○。
\( N \cup \overline{N} = \Sigma^{*} \)、\( N \cap \overline{N} = \varepsilon \) は典型的な反例として使いまくれるのでぜひ頭に入れておきましょう。
6.さいごに
今回はオートマトンの各種演算(前編)についてまとめていきました。
今までの項目とは違い、オートマトンの各種演算は発想力がなくても計算するだけで求めることができるので比較的点数を取りやすい部分だと言えます。なので必ずやり方を覚えておきましょう。
次回はオートマトンの連接、クリーネ閉包についてまとめていきたいと思います。
↓次回(第04羽)はこちら!
関連広告・スポンサードリンク