スポンサードリンク
こんにちは、ももやまです。
今回は決定性オートマトンを最小化する方法について説明していきたいと思います。
前回のオートマトン「第04羽」はこちら!↓
目次
スポンサードリンク
1.冗長な状態とは
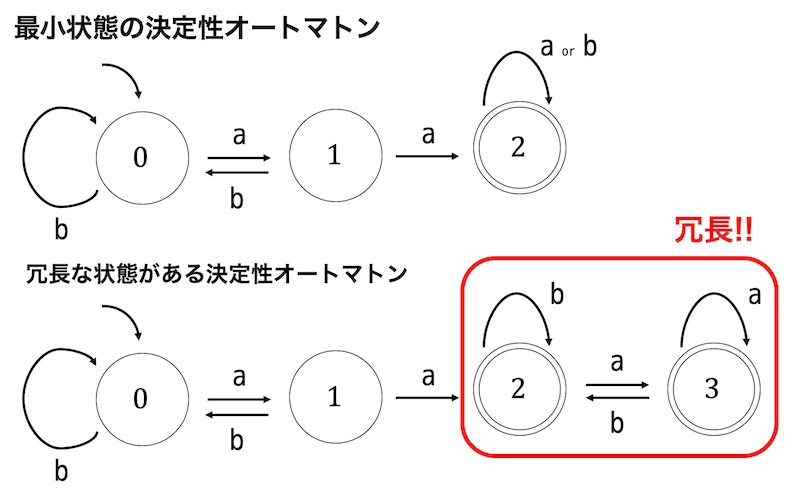
例えば同じ操作*1を行う下のような2つの決定性オートマトンがあったとします。
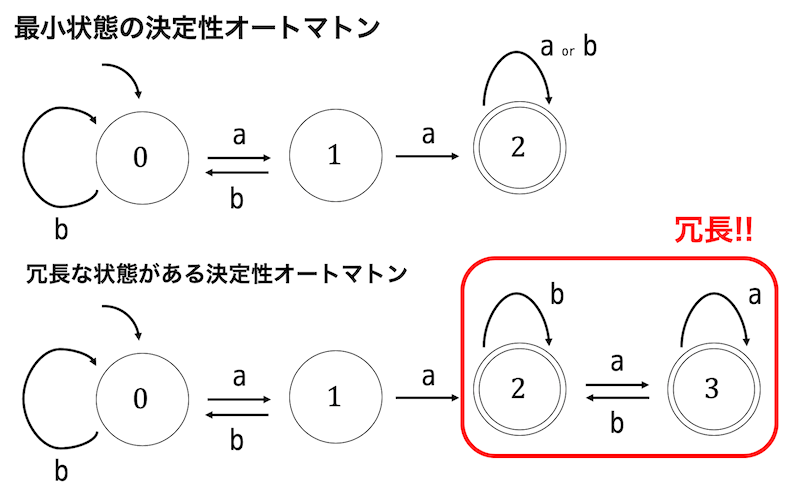
このとき、下のオートマトンは上のオートマトンに比べたら1つ余分な状態が含まれていますよね。
今回は、このような冗長な状態が含まれているオートマトンを冗長な状態がまったくない最小状態のオートマトンにする方法を考えていこうと思います。
スポンサードリンク
2.オートマトンの最小化の方法
オートマトンの状態数を少なくするというのは、等価な状態のグループを見つけて1つの状態にすると言い換えられます。
つまり、オートマトンを最小化するということは、等価な状態のグループをすべて見つけ、これ以上等価な状態のグループが見つからないようにすることを表します。
では、2つほど例題を使ってオートマトンを最小化する方法を説明していきましょう。
例題1
次の状態遷移図、状態遷移表で表される決定性オートマトンが最小状態オートマトンでなければ最小化しなさい。最小状態オートマトンであれば「最小状態である」と書くこと。
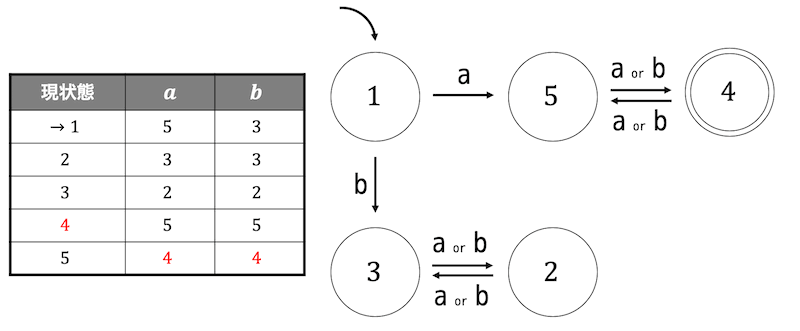
解説1
最小状態かどうかを判別するためにどの状態が等価であるかを判定していきます。
最小化する際には、一旦すべての状態が等価である(すべてが同じグループ)と仮定します。つぎに、等価ではないとわかった瞬間にグループを分離していきます。
まずは、受理状態と非受理状態は明らかに等価ではないのでグループを2つに分けます。
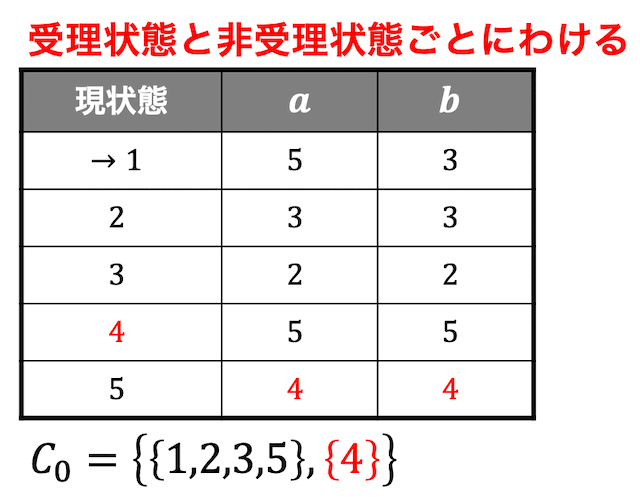
すると状態4とそれ以外でグループが分かれましたね。
ここからは、等価とは言えないグループを見つけ、分離する作業を行います。
そのため、(現在等価としている)状態1,2,3,5の \( a \), \( b \) のそれぞれの遷移先をチェックし、\( a \) の遷移先のグループ もしくは \( b \) の遷移先のグループが異なっているグループを探していきます。
今回の場合は、状態1, 2, 3については状態 \( a \), 状態 \( b \) ともに黒色のグループに遷移しているため、同じグループだといえます。しかし、状態5については状態 \( a \), \( b \) ともに赤色のグループ(状態1, 2, 3とは異なるグループ)に遷移していますね。
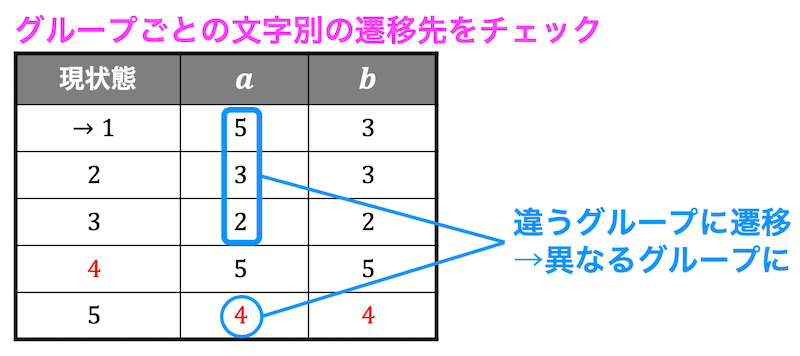
異なるグループに遷移するということは状態が区別できる、つまり等価ではないと言うことができるのでグループをわけます。
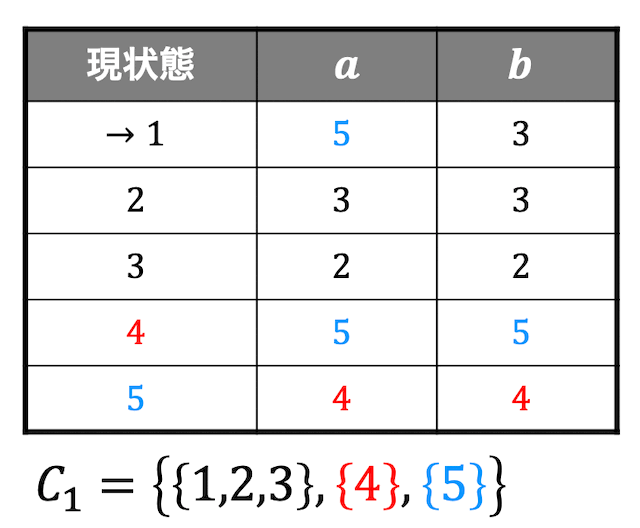
すると、状態1,2,3のグループ、状態4のグループ、状態5のグループの3つにわかれましたね。
この操作を他のグループに分けられなくなるまで続けます。
今度は状態1,2,3が異なるグループに分けられるかみていきましょう。
すると、状態1だけは状態2,3と違って \( a \) のときに青色のグループに遷移しますね。つまり、状態1と状態2,3は等価ではないといえます。
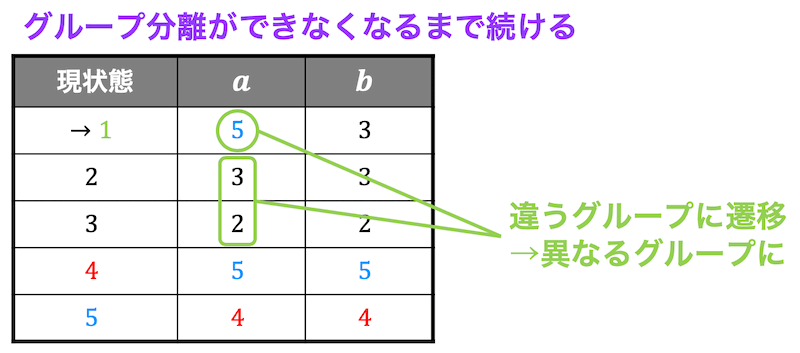
なので状態1、状態2,3でまたグループをわけます。
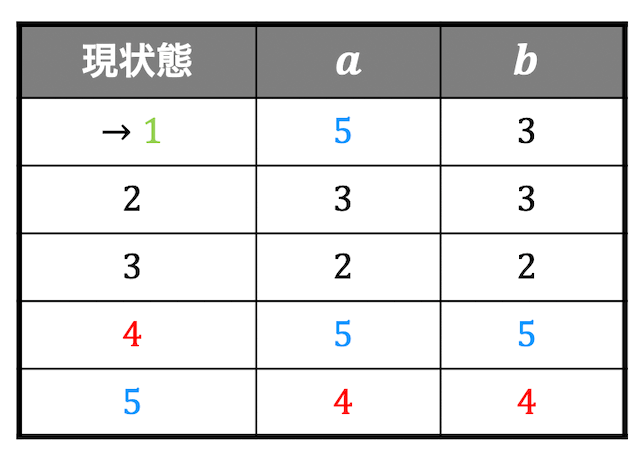
今度は残った状態2,3が分離できるかどうかを確認しますが、\( a \), \( b \) のときも同じグループ(黒)に遷移していますね。
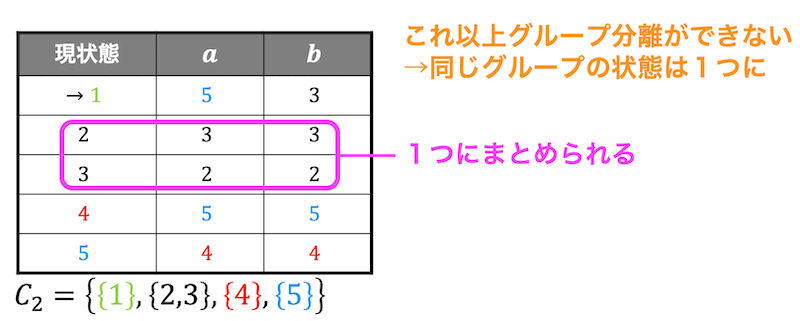
なので、これ以上グループが分離できませんね。なので、状態2,3は等価と言うことができます。
なので、状態2,3は1つの状態23とみることができます。
よって、最小状態決定性オートマトンの状態遷移表、状態遷移図は下のように書くことができます。
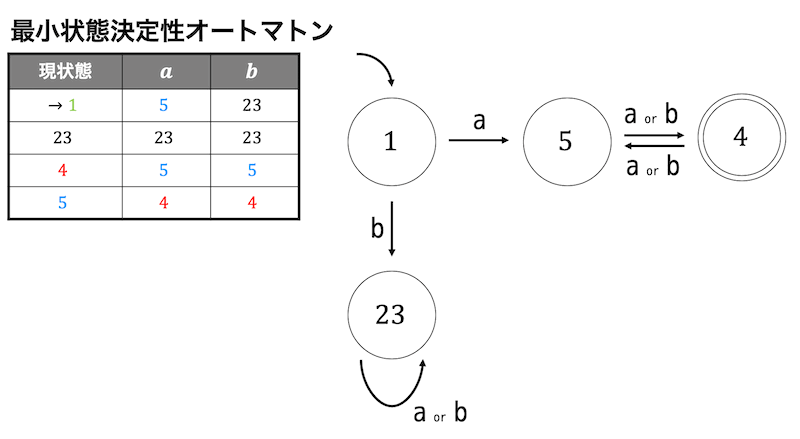
このような手順でオートマトンの最小化を行うことができます。
では、もともと最小状態オートマトンを最小化しようとするとどうなるかをやってみましょう。
例題2 もともと最小状態オートマトンの場合
次の状態遷移図、状態遷移表で表される決定性オートマトンが最小状態オートマトンでなければ最小化しなさい。最小状態オートマトンであれば「最小状態である」と書くこと。
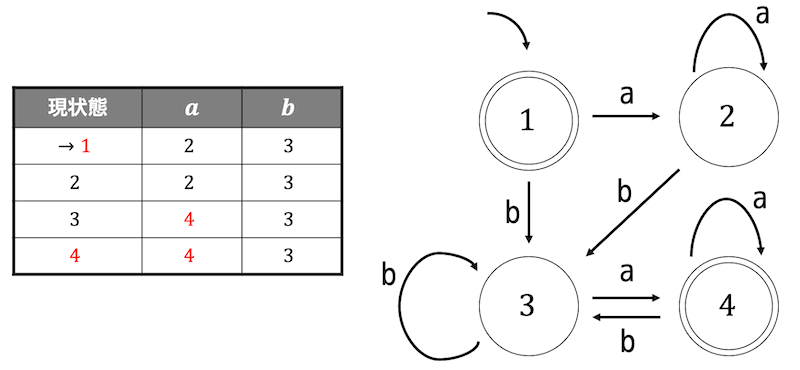
解説2
例題1と同じようにまずは受理状態と非受理状態を別のグループに分けます。
そしてグループごと(状態2,3と状態1,4)の遷移先を確かめ、同じグループ内で遷移先が異なるグループであるものを分離していきます。
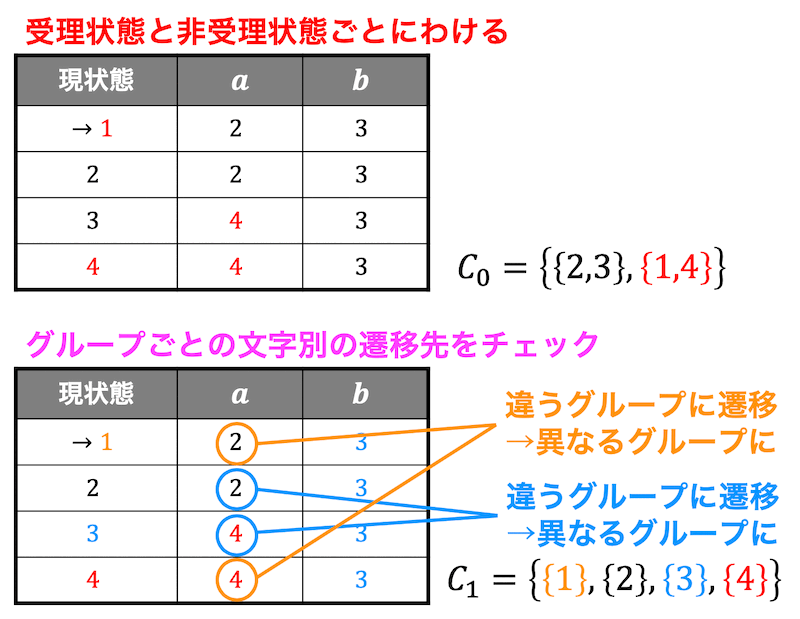
今回の場合、状態1,4の \( a \) における遷移先が黒のグループ、赤のグループと違うグループに遷移しているため、状態1,4は別々にできます。さらに状態2,3に関しても \( a \) における遷移先が黒のグループと赤のグループと異なるので状態2,3も別々にすることができます。
すると状態1,2,3,4すべてが別々のグループになってしまいましたね。
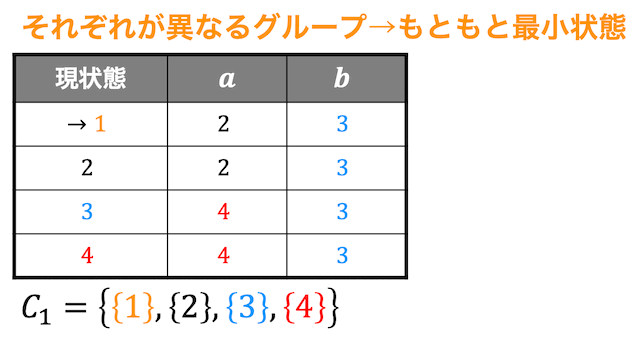
このように、すべての状態が別々のグループになった場合は等価な状態が1つもないということができるでもともと最小状態決定性オートマトンであったことを証明したことになります。
ちなみに最小状態オートマトンは必ず1通りしかありません。なので採点、チェックとかもらくらくですね。
スポンサードリンク
3.練習問題
では4問ほど練習してみましょう。いつもより気持ち程度多めです。
練習1
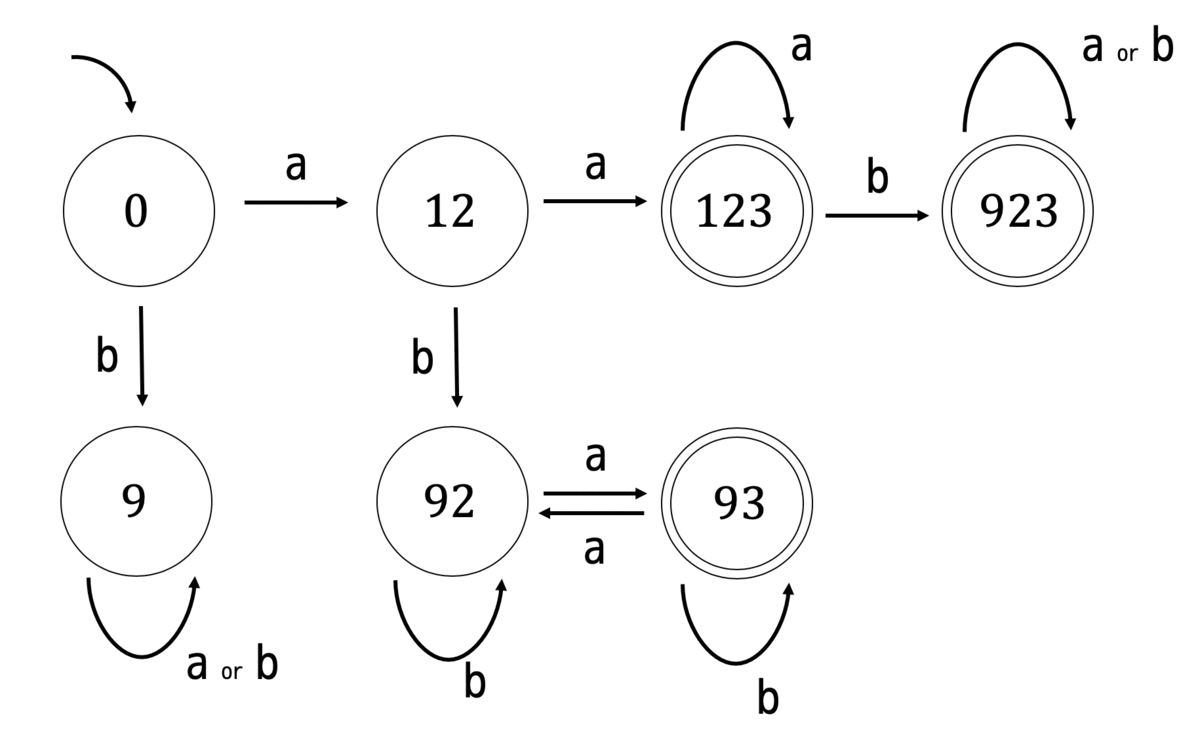
次の状態遷移図で表される決定性オートマトンが最小状態オートマトンでなければ最小化しなさい。最小状態オートマトンであれば「最小状態である」と書くこと。
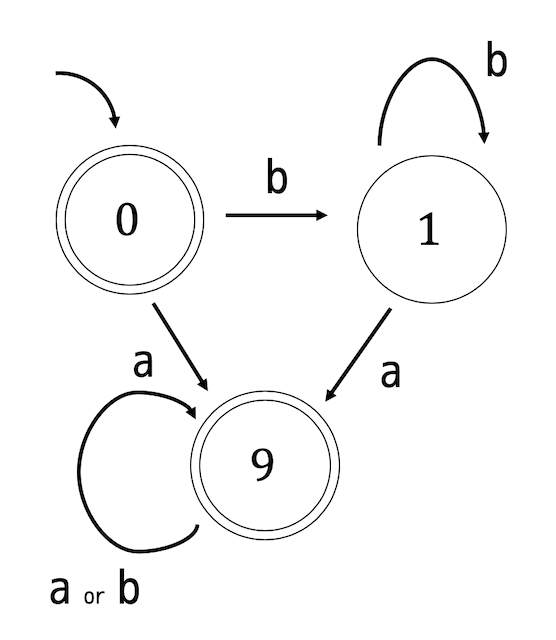
練習2
次の状態遷移図で表される決定性オートマトンが最小状態オートマトンでなければ最小化しなさい。最小状態オートマトンであれば「最小状態である」と書くこと。
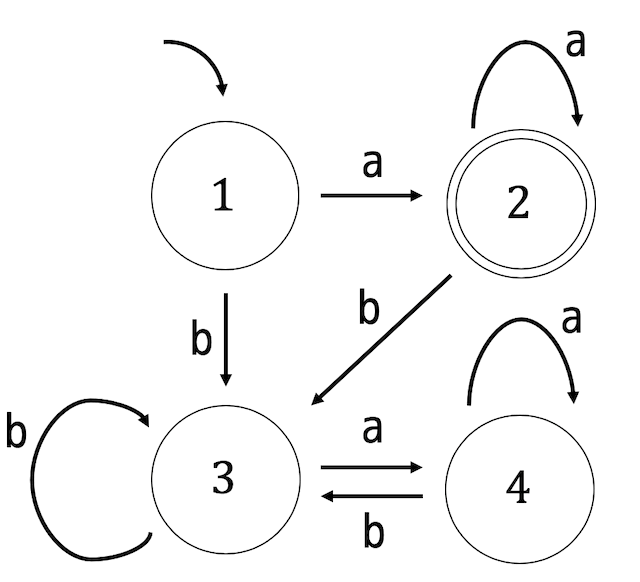
練習3
次の状態遷移図で表される決定性オートマトンが最小状態オートマトンでなければ最小化しなさい。最小状態オートマトンであれば「最小状態である」と書くこと。
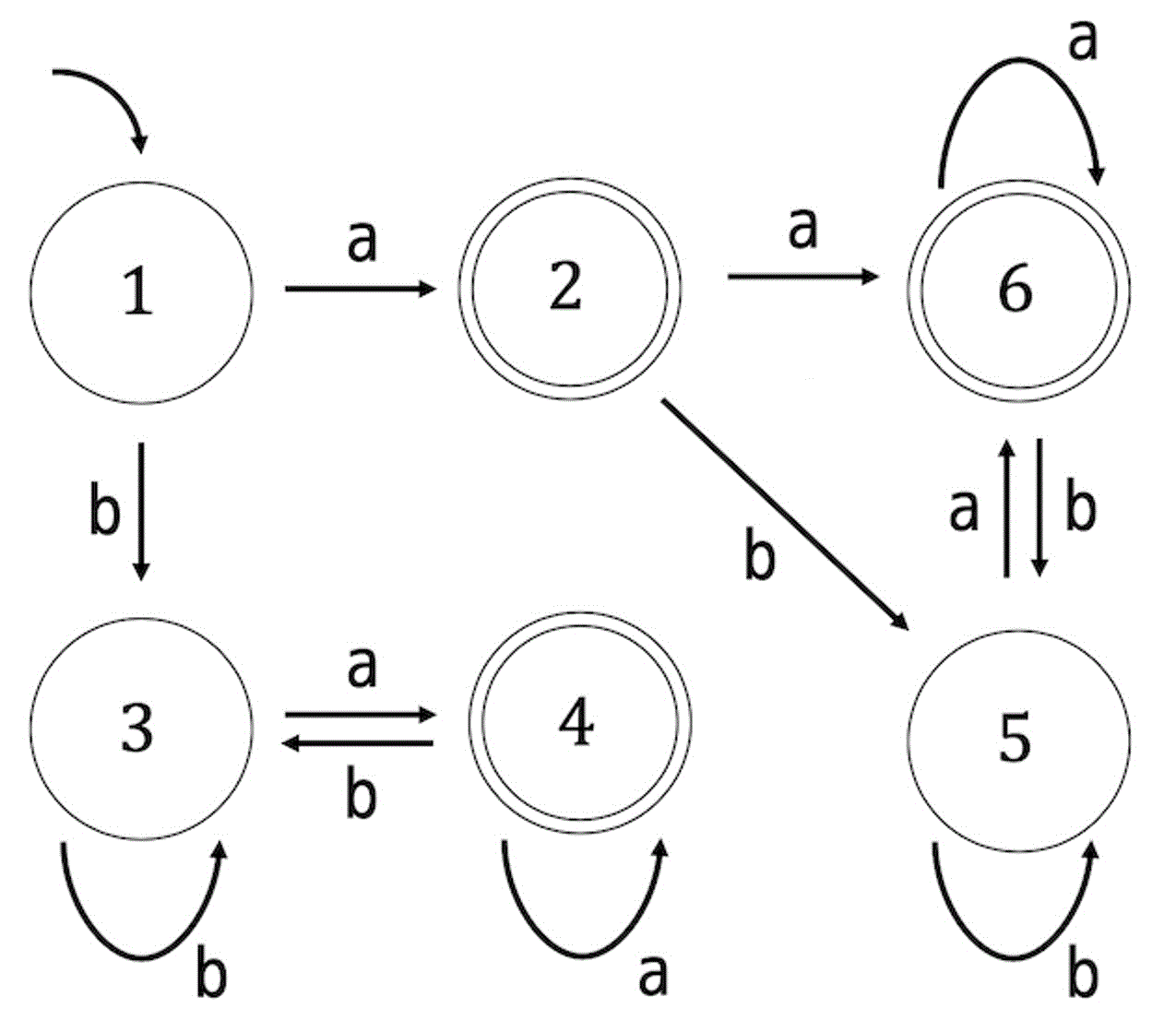
練習4
次の状態遷移図で表される決定性オートマトンが最小状態オートマトンでなければ最小化しなさい。最小状態オートマトンであれば「すでに最小状態である」と書くこと。
4.練習問題の答え
解答1
Step1:受理状態と非受理状態で別グループに
状態1と状態0,9にわけられます。\[
C_0 = \left\{ \{1 \}, \{0,9 \} \right\}
\]
Step2:グループごとの遷移先を確認し、分離されるか判定
状態0,9が分離可能かを判定する。
状態0と状態9の \( b \) における遷移先が異なるグループなので状態0と状態9は分離される。\[
C_1 = \left\{ \{1 \}, \{0 \} , \{ 9 \} \right\}
\]
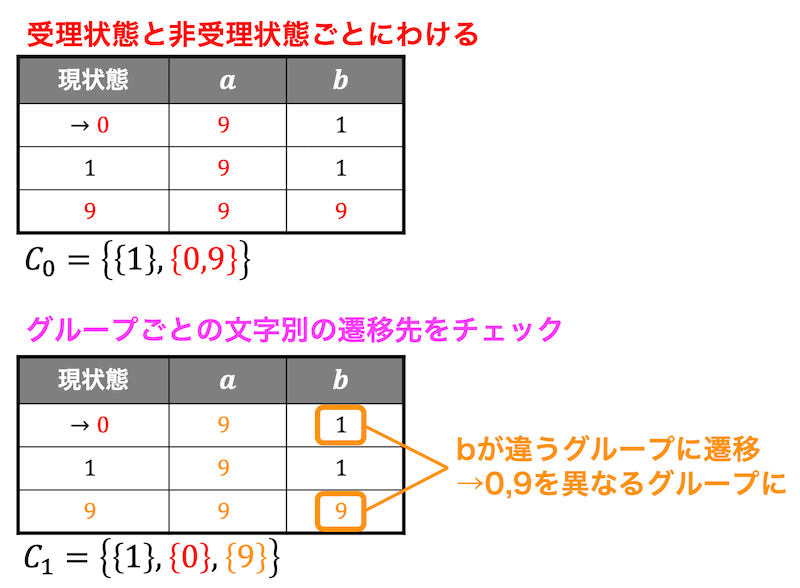
今回は状態0、状態1、状態9がすべて別々グループになりましたね。
なので、すでに最小状態である。
解答2
Step1:受理状態と非受理状態で別グループに
状態1,3,4と状態2にわけられます。\[
C_0 = \left\{ \{1,3,4\}, \{2 \} \right\}
\]
Step2:グループごとの遷移先を確認し、分離されるか判定
状態1,3,4が分離可能かを判定する。
状態1と状態3,4の \( a \) における遷移先が異なるグループなので状態1と状態3,4は分離される。\[
C_1 = \left\{ \{3,4 \}, \{2 \} , \{ 1 \} \right\}
\]
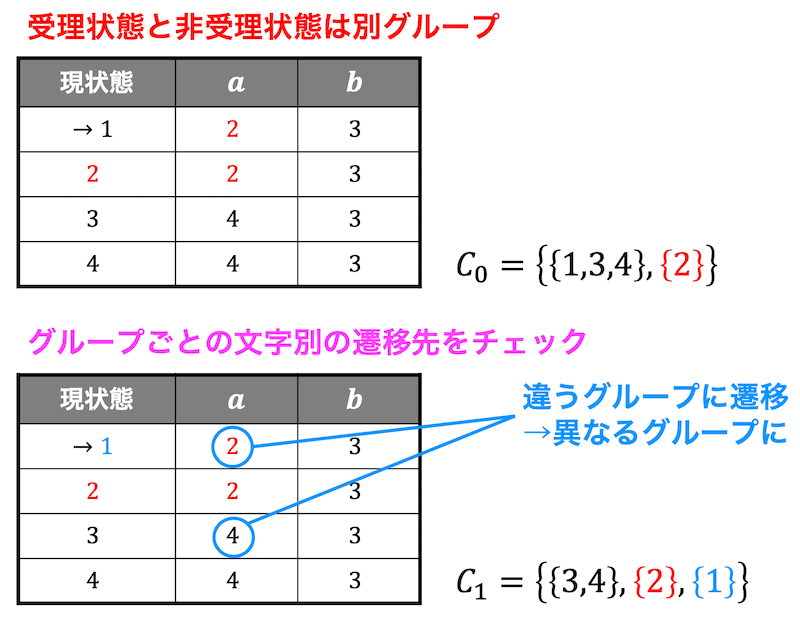
今度は状態3,4が分離できるかどうかを確認する。
しかし、どちらの状態も \( a \) の場合、\( b \) の場合両方で同じグループ(黒)に遷移していますね。
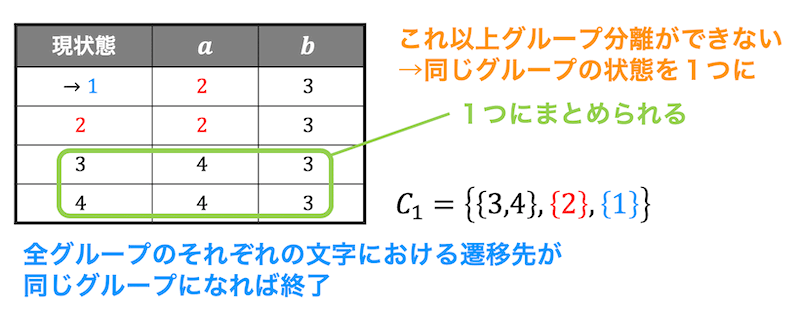
なので、状態3,状態4は等価な状態と言え、1つの状態にまとめることができます。
よって最小状態オートマトンは下のようになります。
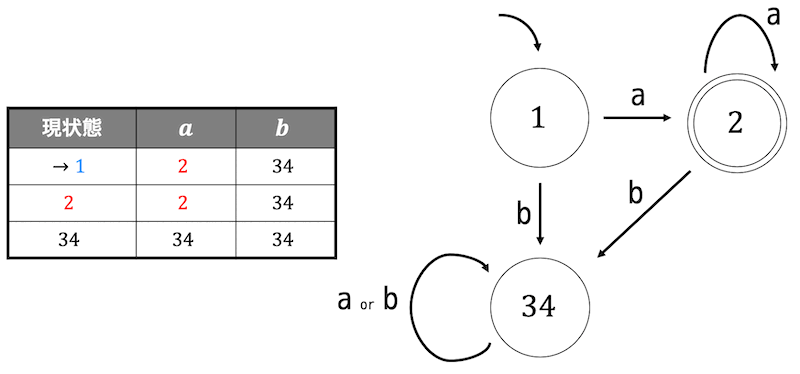
解答3
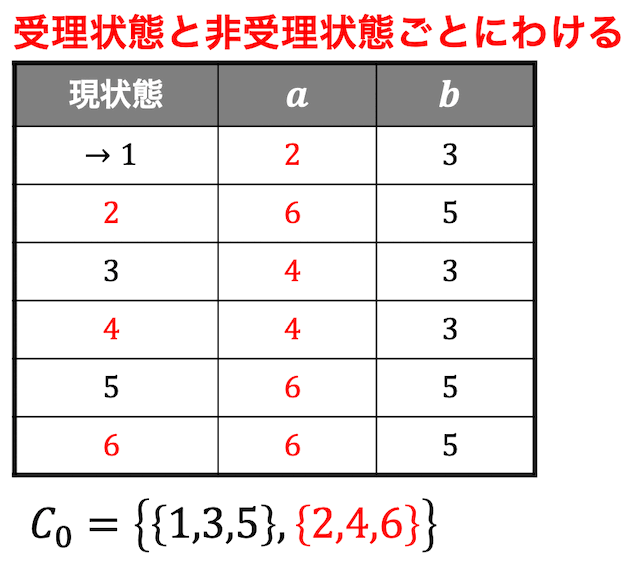
Step1:受理状態と非受理状態で別グループに
状態1,3,5と状態2,4,6にわけられます。\[
C_0 = \left\{ \{1,3,5\}, \{2,4,6 \} \right\}
\]
Step2:グループごとの遷移先を確認し、分離されるか判定
状態1,3,5および状態2,4,6がそれぞれ分離可能かどうかを調べる
しかし、状態1,3,5の \( a \) における遷移先、\( b \) における遷移先はすべて同じグループであり、状態2,4,6の \( a \) における遷移先、\( b \) における遷移先もすべて同じグループである。
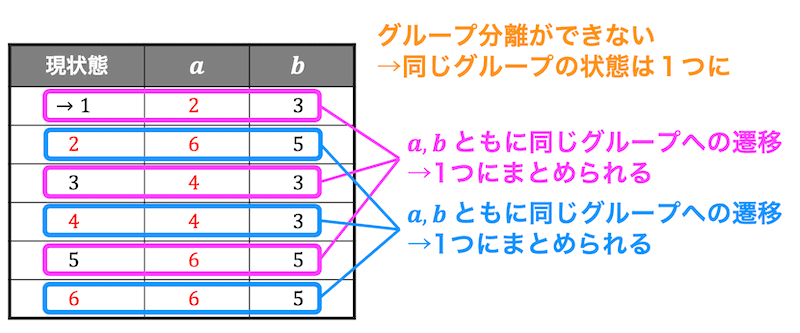
なので、グループ分離ができない。よって状態1,3,5および状態2,4,6はそれぞれ等価なので1つの状態と考えることができる。
最小状態決定性オートマトンの状態遷移表および状態遷移図は下のようになる。
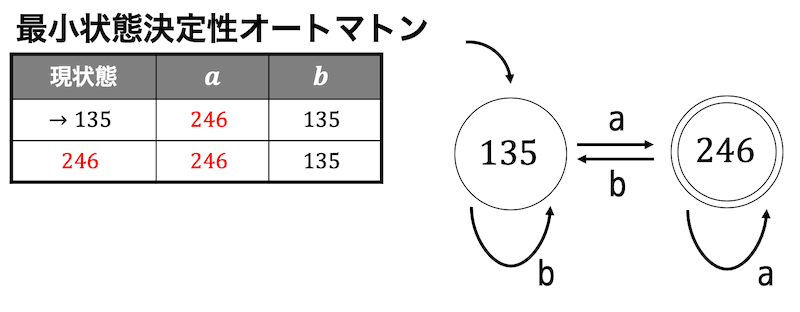
解答4
Step1:受理状態と非受理状態で別グループに
状態1,3,5と状態2,4,6にわけられます。\[
C_0 = \left\{ \{1,3,5\}, \{2,4,6 \} \right\}
\]
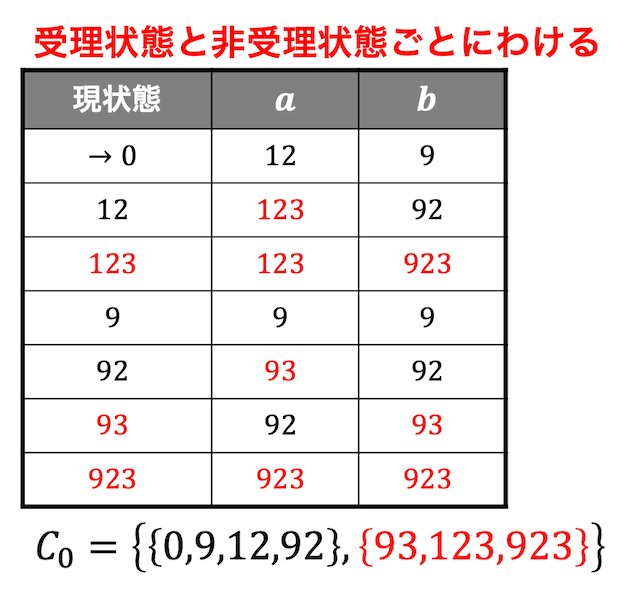
Step2:グループごとの遷移先を確認し、分離されるか判定
状態0,12,9,92および状態93,123,923がそれぞれ分離可能かどうかを調べる。
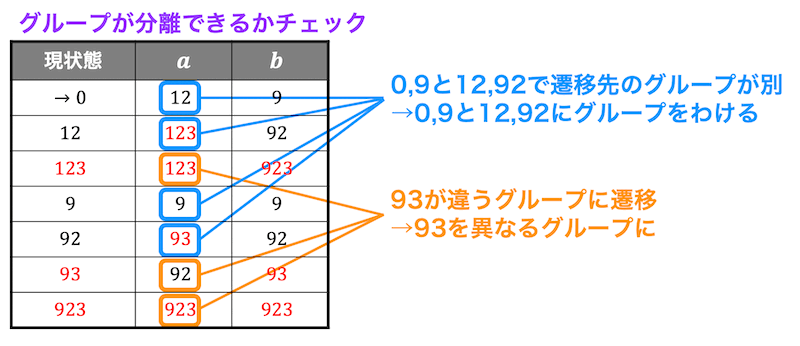
状態0,9,12,92に関しては \( a \) における遷移先のグループが0,9と12,92でそれぞれ異なるので状態0,9および状態12,92でグループを分けられる。
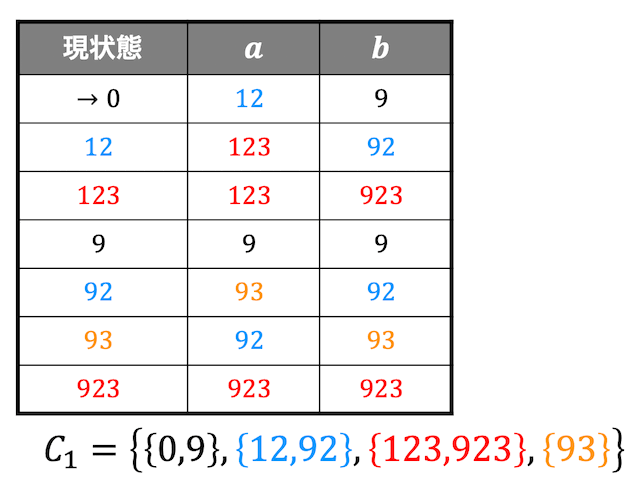
次に状態0,9のグループ、状態12,92のグループ、状態123,923のグループが分離できないかを調べます。
すると、状態0と状態9は \( a \) における遷移先のグループが異なりますね。また、状態12と状態92も \( a \) における遷移先のグループが異なりますね(状態123,923は遷移先のグループが \( a \) の場合、\( b \) の場合で同じなので分離できない)。
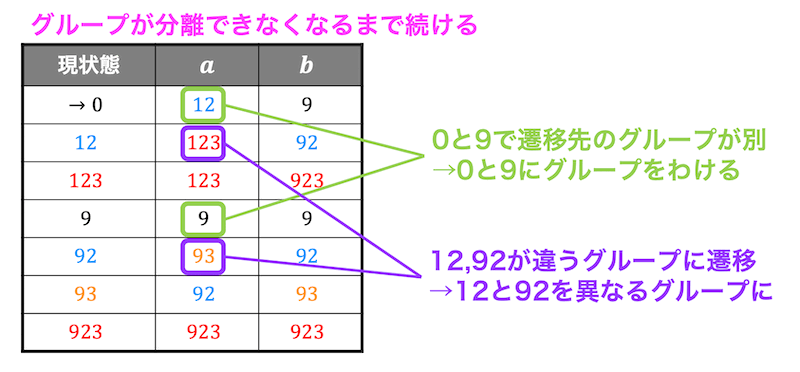
なので状態0、状態9のグループおよび状態12、状態92のグループは分離させることができます。
最後に状態123,923をもう1度みてみます。
しかし、\( a \), \( b \) ともに遷移先のグループは同じですね。
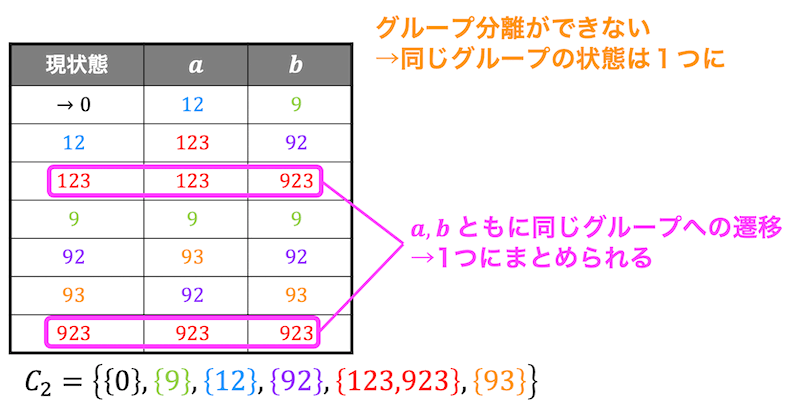
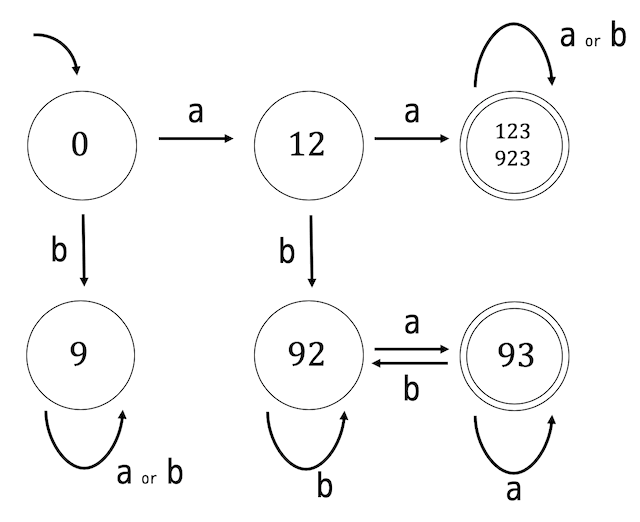
なので、1つにまとめることができます。よって状態遷移図は下のようになります。
5.さいごに
今回は決定性オートマトンを最小状態の決定性オートマトンにする方法についてまとめました。
実際に試験などでは採点を楽にするために最小状態のオートマトンで答えさせることが結構あるのでせっかく答えが出せても最小化を間違えて0点になりましたみたいなことがないように注意してください。
次回は皆さんが▂▅▇█▓▒░(‘ω’)░▒▓█▇▅▂ うわあああああああああってなる正則ではない言語の証明についてやっていきたいと思います。
ではまた次回、さらだばー!
Next「第06羽」はこちら!↓
*1:\( a \) が2連続で含まれるオートマトンを受理する操作である。
関連広告・スポンサードリンク