スポンサードリンク
こんにちは、ももやまです。
今回は正規表現についてまとめてみました。
ただ正規表現についてまとめただけでなく、正規表現を有限オートマトンの状態遷移図で表す方法についてもまとめているのでそちらもご覧ください!
(正規表現について知りたい人は2章を、正規表現をオートマトンに直す方法が知りたい人は3章をご覧ください)
前回のオートマトンの記事(総復習)はこちら!
第3章「正規表現と有限オートマトン」を読む人はこちらの記事の内容が理解できているとすんなりと理解できるかと思います。
目次
スポンサードリンク
1.正規表現とは
ある決まったパターンがあるいくつかの文字列を1つずつ記すのではなく、1つの形式でまとめて表現しちゃおう! というのが正規表現です*1。
正規表現を用いると「ある決まったパターン」に合致するような文字列すべてを一度にチェックすることができるので大変便利です。
パターンというと難しく聞こえるかもしれません。なのでパターンの例をいくつか紹介していきましょう。
例えば、
- 明日の天気は晴れです。
- 明日の天気は曇りです。
- 明日の天気は雨です。
- 明日の天気は雪です。
のような4つの文章があったとします。
正規表現がないと、これら4つの文章を1つずつチェック(検索)していく必要があります。
しかし、この文章には「明日の天気は」で始まり、「です。」で終わり、間に「晴れ / 曇り / 雨 / 雪」のいずれかが含まれる、というパターンがありますね。
なのでこれら4つの文章は正規表現を使うことで一度にチェックすることができるのです!
(実際にどのように記述するかは下のほうで紹介したいと思います。)
他にもパターンとしては、
- xxxで始まる(終わる)文字列
- 半角数字を4桁以上含むような文字列
- yyyが3回以上繰り返されているような文字列
などなど、様々なパターンがあり、これらはすべて正規表現で表すことができるのです!
では、よく出てくる正規表現の種類を説明していきましょう。
スポンサードリンク
2.よく使う正規表現の表記法
ではよく出てくる正規表現を少しですが紹介していきたいと思います。
その1 1文字を表す . (ドット)
まずは . (ドット)です。
ドットを使うとなんでもいい(任意の)1文字を表すことができます。
1文字分のワイルドカードといってもよいでしょう。
実際に正規表現の例と合致する文字列・合致しない文字列の例を示しています。
/* 正規表現の例 */ 吾輩は.である。 /* 〇 正規表現に合致する文字列の例 */ 吾輩は猫である。 吾輩は犬である。 吾輩は猿である。 吾輩は🐇である。 吾輩は膳である。 /* × 正規表現に合致しない文字列の例*/ 吾輩はネコである。 吾輩はイヌである。 吾輩はサルである。 吾輩はウサギである。 吾輩は人間である。
「吾輩は(1文字)である。」の(1文字)の部分が1文字(猫・犬・猿 etc.)のものは合致し、1文字以外のもの(ネコ・イヌ・ウサギ etc.)のものは合致していないことがわかりますね。
また、ドットを複数個組み合わせることで(複数文字)が含まれているかどうかを判定することもできます。
例えば、ドットを3つ ... と並べると、(3文字)が含まれているかどうか判定できます。再び例を見ていきましょう。
/* 正規表現の例 */ あなたは...県出身ですね!? /* 〇 正規表現に合致する文字列の例 */ あなたは神奈川県出身ですね!? あなたは和歌山県出身ですね!? あなたはとちぎ県出身ですね!? あなたはなごや県出身ですね!? /* × 正規表現に合致しない文字列の例*/ あなたは静岡県出身ですね!? あなたは福岡県出身ですね!? あなたはわかやま県出身ですね!? あなたは宮崎県出身ですね!?
ドットが3文字なので、「あなたは(3文字)県出身ですね!?」の(3文字)の部分が3文字のものだけが合致していますね。
その2 0回以上の繰り返しを表す *
つぎに * です。
* を文字の後につけると、0回以上の繰り返しを表現することができます。
例を見ていきましょう。
/* 正規表現の例 */ キミのこと、とっ*ても好き! /* 〇 正規表現に合致する文字列の例 */ キミのこと、とても好き! キミのこと、とっても好き! キミのこと、とっっても好き! キミのこと、とっっっても好き!
上の例の場合、*が「っ」の前についているので、「っ」が0回以上繰り返されているものすべてが合致していますね。
しかし、文字単体ではなく、複数文字のセットを繰り返したいときもあるかもしれません。
その場合は、繰り返したい文字のセットを括弧 ( ) でくくりましょう。
また例を示します。
/* 正規表現の例 */ うさぎって(本当に)*かわいいよね! /* 〇 正規表現に合致する文字列の例 */ うさぎってかわいいよね! うさぎって本当にかわいいよね! うさぎって本当に本当にかわいいよね! うさぎって本当に本当に本当にかわいいよね! /* × 正規表現に合致しない文字列の例*/ うさぎって本当かわいいよね! (「本当に」ではなく「本当」で切れてるため) うさぎって本当に本当かわいいよね!
セットを繰り返す場合、セットの途中で終わっているような文字列は受理しないことに注意してください。
その3 1回以上の繰り返しを表す +
+ を文字の後につけると、1回以上の繰り返しを表現することができます。
先程の * を使って表すと c+ = cc* と書くことができます。
まずは1文字の場合の例を見てみましょう。
/* 正規表現の例 */ やっほー!+ /* 〇 正規表現に合致する文字列の例 */ やっほー! やっほー!! やっほー!!! やっほー!!!!!!!!!!!!!!! /* × 正規表現に合致しない文字列の例*/ やっほー (!を1回も繰り返していないので)
2文字以上のセットを繰り返す場合もみてみましょう。
/* 正規表現の例 */ (ラーメン)+食べたい /* 〇 正規表現に合致する文字列の例 */ ラーメン食べたい ラーメンラーメン食べたい ラーメンラーメンラーメン食べたい ラーメンラーメンラーメンラーメンラーメンラーメンラーメンラーメン食べたい /* × 正規表現に合致しない文字列の例*/ ラーメンラー食べたい (セットの繰り返しになっていない) 食べたい (1回も繰り返していない)
その4 0回 or 1回の繰り返しを表す ?
? を文字の後につけると、0回または1回の繰り返しを表現することができます。
/* 正規表現の例 */ 了解でー?す。 /* 〇 正規表現に合致する文字列の例 */ 了解です。 了解でーす。 (ーの繰り返しが0回 or 1回なら合致) /* × 正規表現に合致しない文字列の例*/ 了解でーーす。 (ーを2回以上繰り返している)
その5 決められた回数を繰り返す {N} {M,N}
決められた回数を繰り返すような正規表現もあります。
{N} を文字の後につけると、N 回の繰り返しを表現できます。
また、{M,N} を文字の後に着けると、M 回以上 N 回以下の繰り返しを表現できます。
(M, N のどちらかは省略可)
/* 正規表現の例 */
(ねぇ){3} → ねぇねぇねぇ (「ねぇ」を3回繰り返す)
(先輩){3,5}!
→先輩先輩先輩
→先輩先輩先輩先輩
→先輩先輩先輩先輩先輩(「先輩」を3~5回繰り返す)
うわぁ…{,2}
→うわぁ
→うわぁ…
→うわぁ……(「…」を0~2回繰り返す、下限値省略パターン)
今日の最下位は~{3,} かに座!!
→今日の最下位は~~~ かに座!!
→今日の最下位は~~~~~ かに座!!
→今日の最下位は~~~~~~~~~~~~~~~~~~~~~~~~ かに座!!
(「~」を3回以上繰り返す、上限値省略パターン)
その6 いずれかを表す |
その2とその3で文字列を括弧でくくるとグループになると説明しましたね。
グループの文字列を | でくくることで | で区切ったいずれかの文字列を合致させることができます。
例えば、 XXX|YYY|ZZZ とすれば、XXX か YYY か ZZZ のいずれかの文字列が合致します。
最初の例で
- 明日の天気は晴れです。
- 明日の天気は曇りです。
- 明日の天気は雨です。
- 明日の天気は雪です。
のような4つの文章を紹介しましたね。この文章を正規表現で書いてみましょう。
/* 正規表現の例 */ 明日の天気は(晴れ|曇り|雨|雪)です。 /* 〇 正規表現に合致する文字列の例 */ 明日の天気は晴れです。 明日の天気は曇りです。 明日の天気は雨です。 明日の天気は雪です。
このように正規表現で表すことができます!
さらにいずれかを表す | を繰り返しを表す * や + などと併用することができます!
/* 正規表現の例 */ 注文は(ラーメン|チャーハン|餃子)+でお願いします。 /* 〇 正規表現に合致する文字列の例 */ 注文はラーメン餃子でお願いします。 注文はラーメン餃子チャーハン餃子でお願いします。 注文はチャーハンラーメン餃子餃子餃子でお願いします。
この場合、ラーメン・チャーハン・餃子のいずれか1つを選び、さらに1回以上繰り返していますね!
(「ラーメン餃子」のように違うものを繰り返してもOK)
その7 指定した文字を選ぶ文字クラス [ ]
「0,1,2,3のいずれかを合致させたい」のように指定した文字を合致させるときに使うのが [ ] です。 文字クラスとも呼ばれます。
[ ] に受理させたい文字を並べることで並べた文字のいずれかが来たときに受理させることができます。
/* 正規表現の例 */ [0123456789] /* 〇 正規表現に合致する文字列の例 */ 3 4 7 /* × 正規表現に合致しない文字列の例*/ 25 (たくさん数字が並んでいるので紛らわしいが、1文字の場合しか合致しないことに注意!)
上の例でいくと、0~9の半角数字のうちの1文字を合致させることができます。
一見たくさん文字があるので複数文字を合致させそうに見えるのですが、複数文字の場合は合致しないので要注意です。
複数文字を合致させる場合は + や * 記号を使って、[0123456789]**2 や [0123456789]+*3 と表記します。
省略記法 [ - ] (ハイフン)
しかし、[0123456789] といちいち書くのはめんどくさいですね。
正規表現では、ASCIIコードが連続していれば、合致させたい文字列を連続して表記することができます。
半角数字の0~9はすべてASCIIコードが連続しているので [0123456789] を [0-9] のように省略することができます。
ASCIIコードってなんだ? どこが連続しているんだ? と思った人は下の記事をご覧ください。ASCIIコードについてわかりやすくまとめています。
下に省略の例を載せてみたので参考までどうぞ。
/* 正規表現の例 */ [0-9] → 半角数字のいずれか1文字(例:3, 5, 6) [A-Z] → 大文字アルファベットのいずれか1文字(例:A, C, E) [a-z] → 小文字アルファベットのいずれか1文字(例:b, g, y) [A-z] → アルファベットのいずれか1文字(例:C, k, z) [A-C0-1] → A,B,C,0,1 のいずれか
もちろん * や + との併用もOKです!
/* 正規表現の例 */ 支払い料金は[0-9]*0円です。 /* 〇 正規表現に合致する文字列の例 */ 支払い料金は1100円です。 支払い料金は3340円です。 支払い料金は1000000000000000円です。 支払い料金は00100円です。
指定した文字「以外」を合致させる ^
指定した文字「以外」を合致させる場合は ^ を使うことで表現ができます。
例えば、[^0-9] と表現すると「半角数字以外の文字」を合致させることができます。
また、[^,]* と書くと、カンマ以外を含む文字列すべて合致させられます*4。
正規表現まとめ
よく使う正規表現の例は以上です。
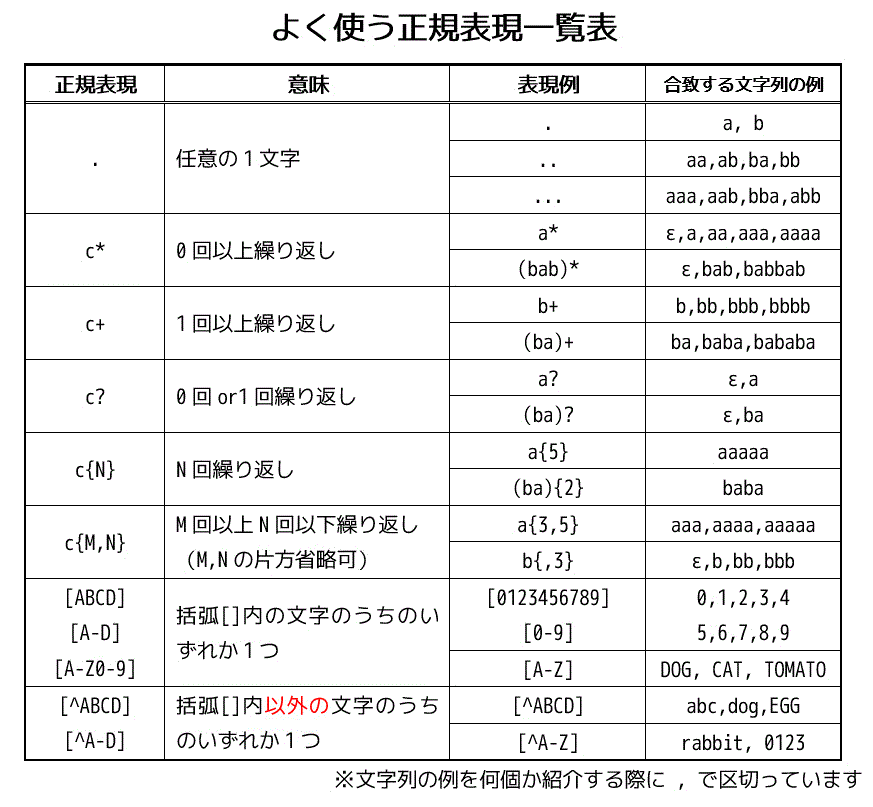
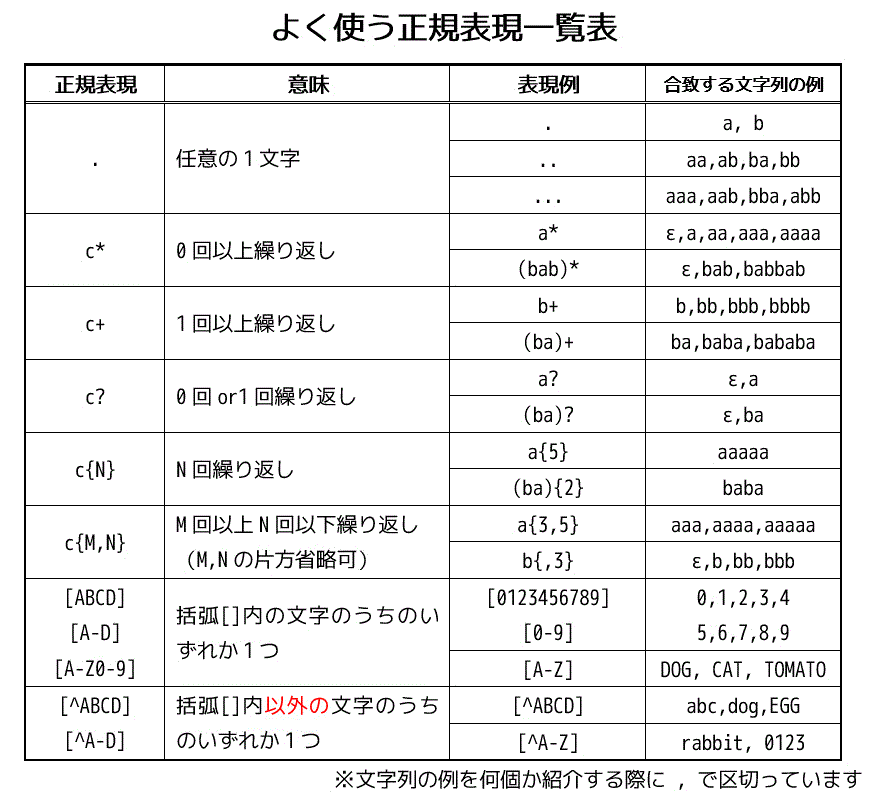
今までに出てきた正規表現を簡単にですが表にまとめてみました。
では実際に1問例題(基本情報の過去問)を解いてみましょう。
例題1
[基本情報技術者平成28年春期 午前問3]UNIXにおける正規表現 [A-Z]+ [0-9]* が表現する文字列の集合の要素となるものはどれか。
ア:456789
イ:ABC+99
ウ:ABC99*
エ:ABCDEF
解説1
解答:エ
[A-Z]+ は大文字アルファベット1文字以上の繰り返し、[0-9]* は半角数字1文字以上の繰り返しを表しますね。
ア:大文字アルファベットが1文字も存在しないのでNG
イ:+ は正規表現を表すための特殊な記号なので文字列に含まれている + は表現されないのでNG
ウ:イと同様に * は正規表現を表すための記号なので文字列に含まれているのはNG
エ:半角数字は含まれていないが [0-9]* なので半角数字はなくてもOK
スポンサードリンク
3.正規表現と有限オートマトン
有限オートマトンも正規表現と同様に「ある決まったパターン」に合致するような文字列すべてを一度にチェックする道具の1つでしたね。
実は、正規表現を用いて表すことができれば有限オートマトンを用いて表すこともできるのです!
もちろん有限オートマトンを正規表現に変換することもできます。
つまり、
- ある言語 \( L \) が正則
- \( L \) を受理するような正規表現が書ける
- \( L \) を受理するような非決定性オートマトンが書ける
- \( L \) を受理するような決定性オートマトン書ける
この4つは同等なものなのです!
ここからは今までに紹介した正規表現を非決定性有限オートマトンを用いて表してみましょう。
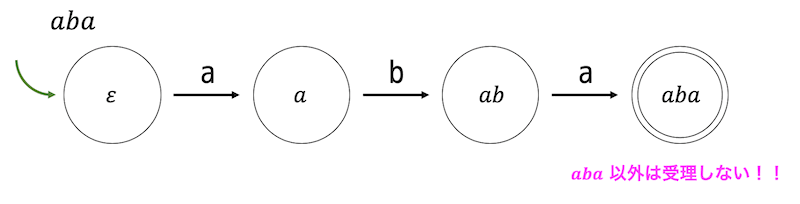
(1) ただの文字列
例えば aba のような * や + や | などの正規表現特融の記号がないような文字列はその文字列単体のみを受理します。今回の場合だと、aba 以外は受理しません。
非決定性オートマトンの状態遷移図は下のようになります。
(2) 0文字以上の繰り返しを表す *
* は直前の文字の0文字以上の繰り返しを表しましたね。
例えば文字列 \( b^* \) は下のような状態遷移図で表すことができます。
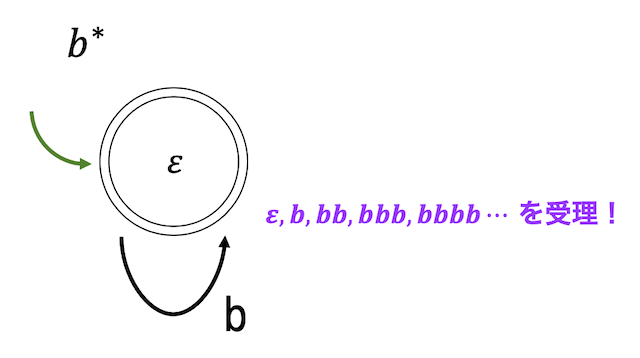
同様に文字列 \( (aba)^* \) のような複数文字の繰り返しも下のような遷移図で書くことができます。
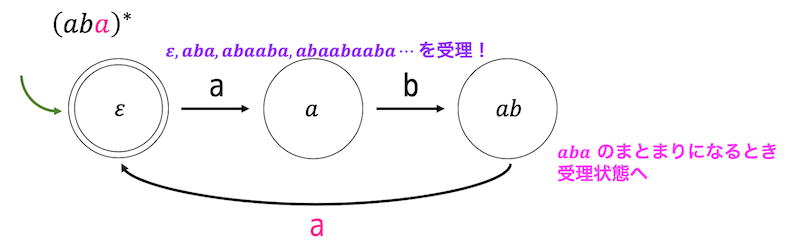
(3) 1文字以上の繰り返しを表す +
+ は直前の文字の1文字以上の繰り返しを表しましたね。
(2)の * を用いて書くと c+ = cc* となります。
例えば文字列 \( b^+ \) は下のような状態遷移図で表せます。
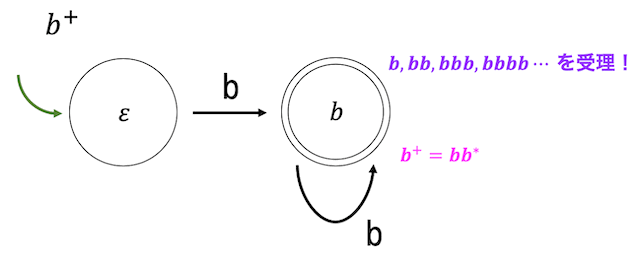
同様に文字列 \( (aba)^+ \) のような複数文字の繰り返しも下のような状態遷移図で表すことができます。
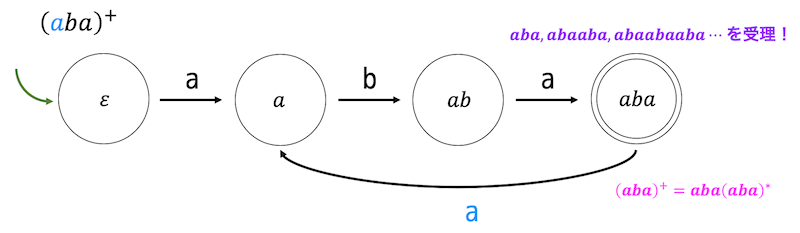
(4) いずれかを表す |
文字列を | で区切ることで | で区切ったいずれかの文字列を受理するような正規表現となります。
例えば、\( aba \) もしくは \( bab \) を受理するような正規表現は \( (aba|bab) \) と表すことができます。( \( (aba+bab) \) と表されることもあります。)
また、\( (aba|bab) \) の状態遷移図は下のようになります。
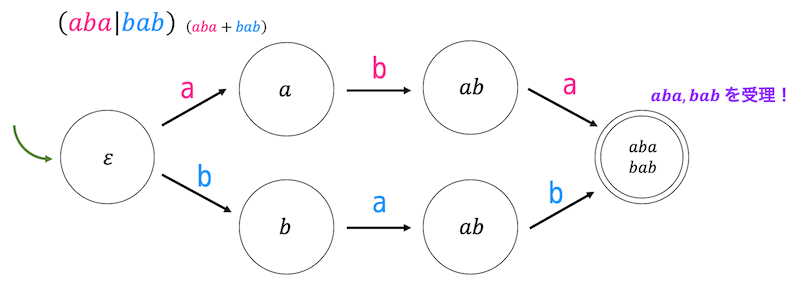
では、実際に今の(1)~(4)を踏まえて例題を解いてみましょう。
例題2
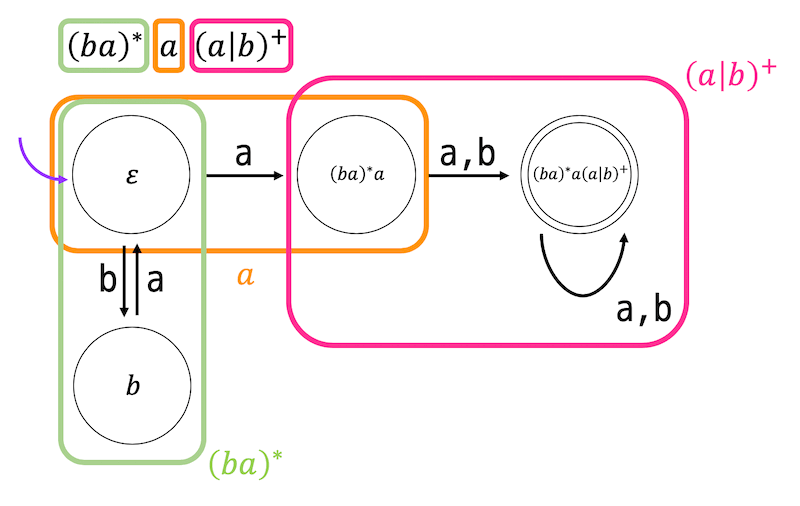
正規表現 \( (ba)^* a (a|b)^+ \) がある。つぎの問いに答えなさい。ただし、\( \Sigma = \{ a,b \} \) とする。
(1) \( (ba)^* a (a|b)^+ \) を受理するような文字列として適切なものを1~4の中から2つ選び、番号で答えなさい。
- \( ababa \)
- \( bbbb \)
- \( baba \)
- \( baaba \)
(2) 正規表現 \( (ba)^* a (a|b)^+ \) を受理するような非決定性オートマトンを書きなさい。
解説2
(1)
解答:1, 4
ポイントは正規表現の途中に含まれている \( a \) 単体。
- 1文字目の
a+ 2文字目以降のbabaを \( (a|b)^+ \) とすることで受理できる - \( a \) が1文字も含まれていないので受理しない。
- 途中にある \( a \) をどう頑張っても表せないのでNG。
- 2文字目までの
baを \( (ba)^* \)で、3文字目のa+ 4文字目以降のbaを \( (a|b)^+ \) とすることで受理できる
(2)
下のような状態遷移図となる。
4.練習問題
では2問ほど練習しましょう。
「オートマトンと正規表現」なので、オートマトンと正規表現を両方絡ませた問題。
練習1
[ソフトウェア開発技術者平成19年秋期 午前問8]次の有限オートマトンで受理する文全体を正規表現で表したものはどれか。
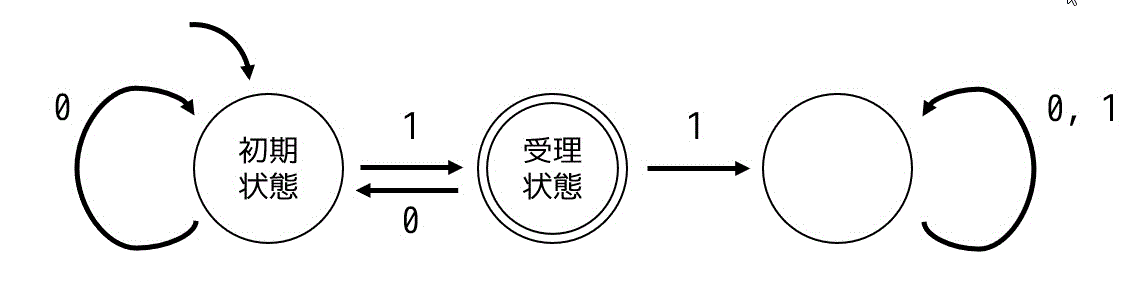
ア:\( (010)^* 1 \)
イ:\( (01|101)^* \)
ウ:\( (0|10)^* 1 \)
エ:\( (1|01)^* \)
練習2
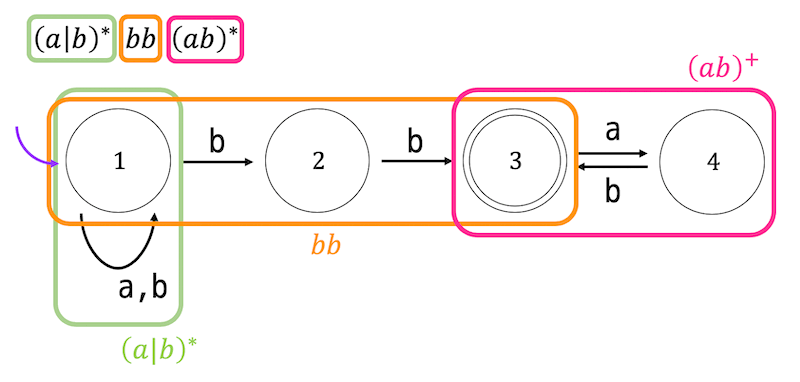
正規表現 \( (a|b)^* bb (ab)^* \) がある。つぎの問いに答えなさい。ただし、\( \Sigma = \{ a,b \} \) とする。
(1) \( (a|b)^* bb (ab)^* \) を受理するような文字列として適切なものを1~4の中から2つ選び、番号で答えなさい。
- \( abab \)
- \( bbbb \)
- \( abba \)
- \( bbbab \)
(2) 正規表現 \( (a|b)^* bb (ab)^* \) を受理するような非決定性オートマトンを書きなさい。
(3) (2)の非決定性オートマトンを最小状態決定性オートマトンに直しなさい。
5.練習問題の答え
解答1
解答:ウ
[普通に解く(選択肢がない場合の解き方)] 初期状態から再び初期状態に戻る文字列の組み合わせとしては、0の繰り返しか、10の繰り返しの2パターンがある。つまり、「0を繰り返す」or「10を繰り返す」のあとに1がくれば受理状態となる。これを正規表現で表現すると \( (0|10)^* 1 \) となる。よって答えはウ。
[消去法] 受理するためには必ず 1 で終わる必要がありますね。なので、空文字でも受理してしまうイとエは真っ先に選択肢から外れます。
あとはアかウかどうか。
ここで文字列 \( 01 \) は受理しなければならない。
しかし選択肢アは、\( (010)^* 1 \) となっていて \( 01 \) が受理されない。
よってアは誤りなので答えはウ。
解答2
(1)
解答:2, 4
ポイントは正規表現の途中に含まれている \( bb \) 単体。
bbが含まれていないのでダメ- \( (a|b)^* \) を最初の2文字とし、\( bb \) 単体は3文字目・4文字目とすれば受理する
- \( bb \) は含まれているが、 最後の1文字を \( (ab)^* \) に入れることはできないのでダメ。
- \( (a|b)^* \) を最初の1文字、\( bb \) 単体は2文字目・3文字目、残りの
abは \( (ab)^* \) に入れられるのでOK。
(2)
非決定性オートマトンは下のようになる。
(3)
※もし非決定性オートマトンを決定性オートマトンにする方法を忘れてしまった人はこちらをご覧ください。
www.momoyama-usagi.com
まずは非決定性オートマトンを決定性オートマトンにする。
すると、下のような状態遷移表と状態遷移図ができる。
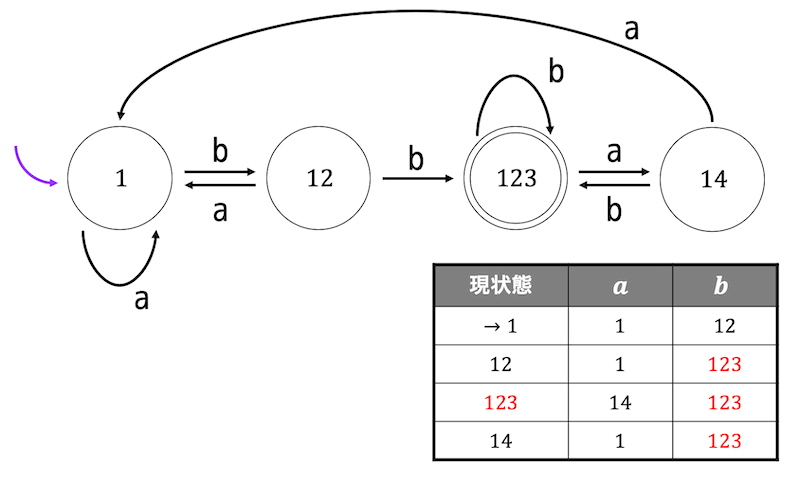
つぎに、最小化アルゴリズムに沿って最小状態かどうか判定し、最小状態でなければ最小化を行う。
※決定性オートマトンの最小化アルゴリズム・最小状態オートマトンかどうかの確認法を忘れてしまった人はこちらの記事をご覧ください↓
まずは状態を受理状態・非受理状態の2つのグループに分ける。
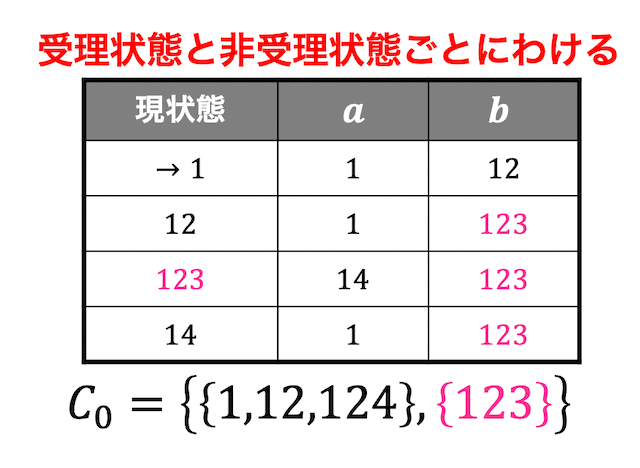
つぎにそれぞれのグループの「文字ごとの遷移先」をチェックし、異なるグループに遷移する場合があれば違うグループに隔離を行う。
今回の場合、状態1の \( b \) の遷移先が他のグループ(状態12,状態14)と異なるので、状態1を隔離する。
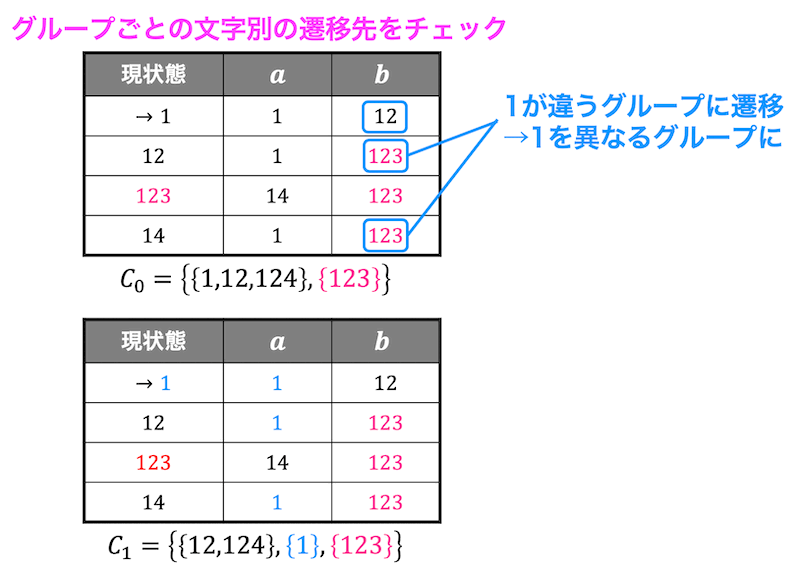
隔離後にもう1度それぞれのグループの「文字ごとの遷移先」をチェックする。
今回は異なるグループに遷移する場合が存在しないので、この時点での同じグループの状態を1つにまとめることができることがわかる。
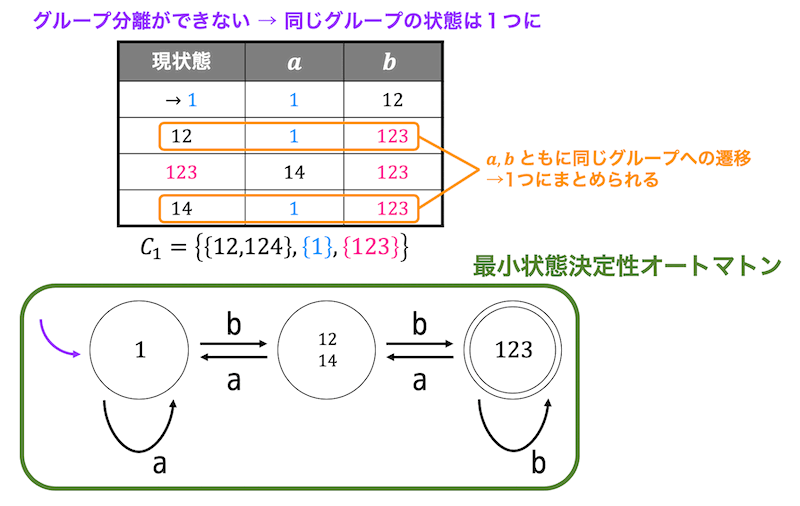
よって、最小状態決定性オートマトンは上のような状態遷移図で表せる。
6.さいごに
今回はよく使われる正規表現の一部を解説し、さらに正規表現を有限オートマトンで表記する方法についてまとめていきました。
実際にはまだまだ便利な正規表現がたくさんあるので、余力のある人はこの記事には載っていない正規表現も覚えてみるのもいいかもしれません。
正規表現自体は特に文字の置換の際に便利なのでぜひ使っていきましょう!
(例えば全角数字を半角数字に置換するときとかに使えますよ!)
関連広告・スポンサードリンク