うさぎでもわかる計算機システム　Part03　固定小数点・浮動小数点

2019年6月19日 2019年6月19日 22分45秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。
今回は2進数における小数点記法についてまとめたいと思います。

小数点記法には固定小数点記法と浮動小数点記法の2つがあります。
両者とも説明をしておきたいと思います。

１．固定小数点方式
- 数直線で表現可能な数を表すと……
２．浮動小数点方式
- 数直線で表現可能な数を表すと……
３．主要浮動小数点数の規格
４．２進数の小数点表記における誤差
５．練習問題
６．練習問題の解答
７．さいごに

スポンサードリンク

１．固定小数点方式

まず、皆さんが思い浮かぶのが固定小数点方式です。
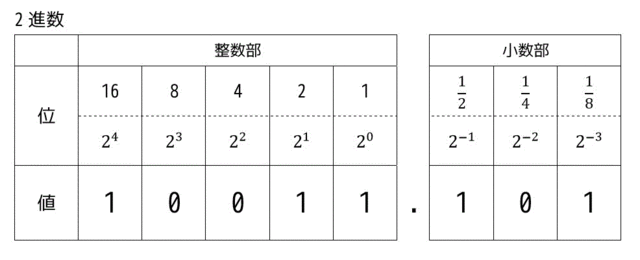
固定小数点は、図のように扱える桁の中の一部を整数部、残りを小数部と固定してしまう方式です。

例えば、8bitのうちの5bitを整数部、3bitを小数部とします。
すると、このような形で２進数を表現することができます。

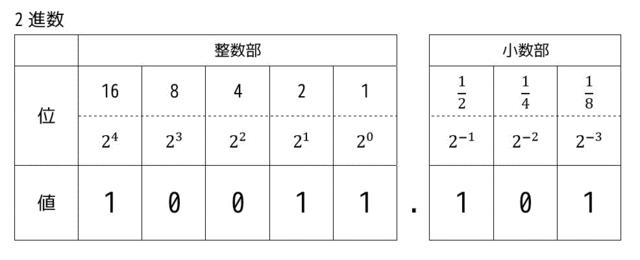
例えばこの場合は、10011101b は、19.625 となります。

数直線で表現可能な数を表すと……

小数点の部分を固定するため、それぞれ表せる小数は等間隔*1となります。

今回の場合だと、小数部は3ビットなので、1/8ずつ単位で表すことができます。

スポンサードリンク

２．浮動小数点方式

皆さんは化学や物理などで \( 6.02 \times 10^{23} \) のように「有効数字×10のべき乗」で答えを書いたことはありませんか？　これを浮動小数点方式といいます。

計算機上で小数を扱う際には、浮動小数点方式が使われています。
計算機上で浮動小数点を扱う際には、以下の3つの部分に分かれます。

符号部：正負を表す部分。必ず1bit。0なら正（もしくは0）、1なら負
仮数部：有効数字部分。必ず「1.XXX」と、整数部分が1になるようにする*2。これを正規化*3といいます。1.XXX の 1 を省略するケチ表現が使われることが多い。
指数部：2のべき乗（2進数なので）で表す。今回はわかりやすく2の補数で表現するが、実際の計算機上では比較などを楽にするために一定数（下で記述）を加算して計算を楽にする。

以上を踏まえると、2進数の浮動小数点表記は必ず次のような表記になります。

浮動小数点表記

浮動小数点表記は、\[ \pm \ \alpha \times 2^{\beta} \]の形となる。

\( \alpha \) ：仮数*4　\( \beta \) ：指数
基数：2（\( 2^{\beta} \) の2）

たとえば、-5.5を浮動小数点表記にしてみましょう。まずは、1.XXXの形に正規化をします。\[5.5 = 2^2 + 2^0 + 2^{-1} = 2^2 (2^0 + 2^{-2} + 2^{-3})\]と変形できます。

このときの括弧内の部分の最大項を \( 2^0 \) にするように2のべき乗でくくると、必ず 1.XXX の形に正規化することができるので必ずこの形にしましょう。

仮数部を10進数で求めると \[ 2^0 + 2^{-2} + 2^{-3} = 1 + 0.25 + 0.125 = 1.375\]となります。指数部は、くくったときに出てきた \( 2^2 \) となります。よって、指数部の形にすると、

となります。また、2進数で表現してみます。

符号：負の数なので1
指数部：2乗なので、010となる（2の何乗かを記録）。
仮数部：\( 2^0 + 2^{-2} + 2^{-3} \) の形で、ケチ表現なので \( 2^0 \) を省略し、4ビット、つまり \( 2^{-4} \) の値まで表せる。よって0110。

仮数部を2進数で表すと、以下のような形に変形することができます。

これらを踏まえ、上の8bit浮動小数点表記にすると、10100110b となります。

数直線で表現可能な数を表すと……

浮動小数点方式の場合、固定小数点方式の場合と異なり、表せる数の間隔は均一とはなりません。

0に近ければ近いほど密度は高く（大きく・濃く）なり、多くの小数を表すことができます。

逆に0に遠ければ遠いほど密度は低く（小さく・薄く）なり、少ない数の小数しか表せなくなります。

また、あまりにも0に近い数を表そうすると浮動小数点方式で表現できなくなります。これをアンダーフローといいます。

スポンサードリンク

３．主要浮動小数点数の規格

現在の主要な計算機では、IEEE754という浮動小数点の規格が用いられています。IEEE754では、単精度（float型）、倍精度（double型）、4倍精度（long double型）の3つにおいて、下の桁数だけ指数部、仮数部の領域が取られています。

	符号	指数部	仮数部
単精度	1bit	8bit	23bit
倍精度	1bit	11bit	52bit
4倍精度	1bit	15bit	112bit

IEEE754の浮動小数点表記では、上で説明した浮動小数点表記の仕様とは若干異なる仕様が追加されています。具体的にいうと、

指数部は、数値の大小を比較しやすくするために、２の補数表現を使わずに実際の指数に一定数（例：単精度なら127）足されている。
数字以外にも、NaN（数じゃない値）、\( \pm \infty \) なども表すことでオーバーフロー、アンダーフローなどの正常ではない結果にも対応できるようにしている（例外処理に対応）。

があります。

４．２進数の小数点表記における誤差

２進数の小数点表記における誤差の原因として、桁落ち・情報落ち・丸め誤差などがあります。

これらの誤差の原因は、プログラムを書く際には避けて通れない問題なので、必ず頭に入れておくようにしましょう。

これらの誤差については、こちらの記事に具体例を含めてわかりやすくまとめたのでこちらをご覧ください。
（基本情報や情報系大学の期末試験にも頻出項目です。）

www.momoyama-usagi.com

５．練習問題

では、練習していきましょう。

問題1

0.7を6bitの固定小数点方式と浮動小数点方式のそれぞれで表して誤差を比べる。つぎの問いに答えなさい。

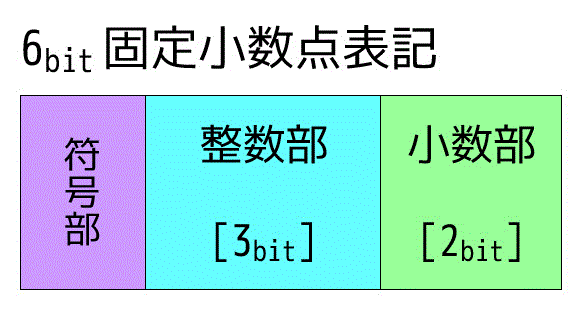
(1) 最下位ビットから2ビットを小数部、最上位ビットを符号部(0が正で1が負)、残りを整数部とする6ビット固定小数点方式の2進数で0.7を表しなさい。変換後の小数第3位以降は切り捨て、変換後の数値と0.7との誤差の大きさを10進数で答えなさい。

(2) 最下位ビットから3ビットを仮数部、最上位ビットを符号部、残り2ビットを指数部とする6ビット浮動小数点方式の2進数で0.7を表しなさい。
ただし、仮数部はケチ表現、（1.XXXの1を省略）、指数部は2の補数表現とする。

さらに変換後の数値と0.7との誤差の大きさを10進数で答えなさい。

問題2

つぎの中で誤っている文章を1つ選びなさい。
ただし、6bitの浮動小数点方式は、最下位ビットから3bitを仮数部（ケチ表現、1.XXXのXを省略）、最上位ビットを符号部、残り2bitを指数部（2の補数表現を用いる）とする。

固定小数点方式2進数を数直線上で考えると、表現できる小数の密度は均一となる。
浮動小数点表現では、数直線上において、0から遠くなればなるほど表現できる小数の密度は低く（小さく）なる。
2.875は丸め誤差なしに6bitの浮動小数点方式で表現できる。
0.75は丸め誤差なしに6bitの浮動小数点方式で表現できる。

問題3

3141.5を丸め誤差なしで浮動小数点で表現したい。
このとき、仮数部と指数部はそれぞれ何ビットずつ必要か答えなさい。
ただし仮数部はケチ表現（ 1.XXX… の 1を省略）、指数部は2の補数表現を用いるものとする。

問題4

浮動小数点表示法における仮数が正規化されている理由として，適切なものはどれか。
[基本情報技術者試験　平成19年春期問4]

ア：固定小数点数とみなして大小関係が調べられるようにする。
イ：四則演算のアルゴリズムが簡素化できる。
ウ：表現可能な数値の範囲を拡大する。
エ：有効数字のけた数を最大に保つ。

問題5

浮動小数点に関する次の記述を読んで、設問1～4に答えよ。
[基本情報技術者過去問題平成27年秋期　午後問2]

\( \alpha = 0 \)、または \( 1 \leqq | \alpha | \lt 2 \) を満たす \( \alpha \)、および \( -126 \leqq \beta \leqq 127 \) を満たす \( \beta \) を用いて \( \alpha \times 2^{\beta} \) の形で表記される浮動小数点数を、図1に示す32ビット単精度浮動小数点形式の表現（以下、単精度表現という）で近似する。

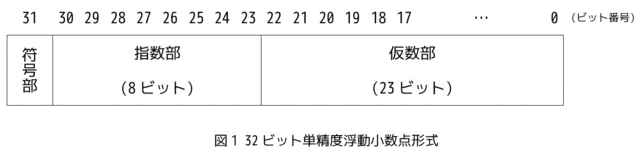
(1)：符号部（ビット番号31）
\( \alpha \) の値が正のとき0、負のとき1が入る。

(2)：指数部（ビット番号30～23）
\( \beta \) の値に127を加えた値が2進数で入る。

(3)：仮数部（ビット番号22～0）
\( | \alpha | \) の整数部分1を省略し、残りの小数部分がビット番号22に小数第1位が来るような2進数で入る。このとき、仮数部に格納できない部分については切り捨てる。

(4)：\( \alpha \) の値が0の場合、符号部、指数部、仮数部ともに0とする。

なお、値の記述として、単に \( \alpha \) と記述した場合は、\( \alpha \) は10進数表記であり、 \( (\alpha)_n \) と記述した場合は、\( \alpha \) が \( n \) 進数表記であることを示す。例えば、\( (0.101)_2 \) は 0.625 と同じ値を表す。また、 0…0 という表記は0が連続していることを表す。

設問1

0.625を単精度表現したときに指数部に入る値として正しい答えを解答群の中から選べ。

ア：\( \mathrm{(00)}_{16} \)　　イ：\( \mathrm{(7E)}_{16} \)　　ウ：\( \mathrm{(7F)}_{16} \)
エ：\( \mathrm{(FE)}_{16} \)　　オ：\( \mathrm{(FF)}_{16} \)

設問2

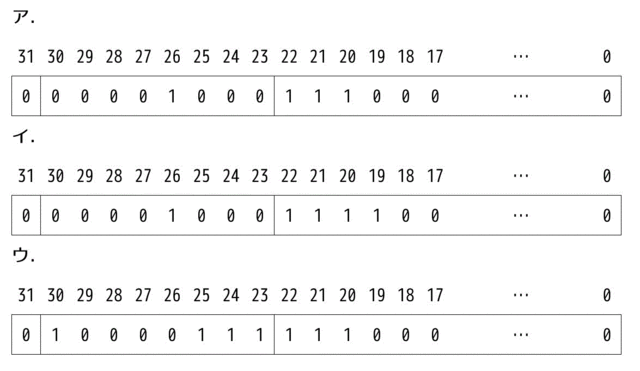
次の単精度表現された数値として正しい答えを、解答群の中から選べ。

値：0 | 0111 1110 | 100000…0

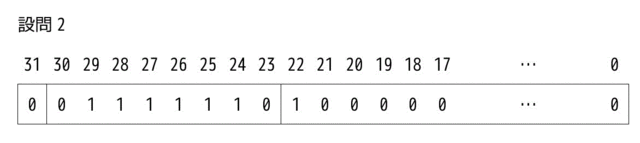
ア：0.125　　イ：0.25　　ウ：0.375　　エ：0.5
オ：0.75　　カ：1.5

設問3

次の記述中の \( \left[ \ \ \ \ \ \ \ \ \right] \) に入れる正しい答えを、解答群の中から選べ。

2つの浮動小数点AとBの加算を行う。

A: 0 | 1000 0100 | 100000…0
B: 0 | 1000 0011 | 100000…0

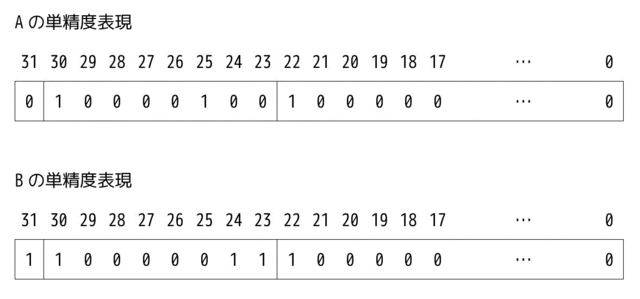
AとBの加算を次の①、②の手順で行う。

①　指数部の値の大きい方に合わせる。 Aが \( (1.1)_2 \times 2^5 \) であることから、Bを \( \left( - \left( \left[ \ \ \ a \ \ \ \right] \right)_2 \right) \times 2^5 \) とする。

②　加算を行う。\[
( (1.1)_2 + \left( - \left( \left[ \ \ \ a \ \ \ \right] \right)_2 \right) ) = (1.1)_2 \times 2^{\left[ \ \ \ b \ \ \ \right]}
\]

aに関する解答群
ア：0.001　　イ：0.01　　ウ：0.011　　エ：0.1　　オ：0.11　　カ：1.1

bに関する解答群
ア：3　　イ：4　　ウ：5　　エ：6　　オ：130　　カ：131　　キ：132

設問4

次の記述中の \( \left[ \ \ \ \ \ \ \ \ \right] \) に入れる正しい答えを、解答群の中から選べ。

設問3のAについて、A×10 の値は、次の①～③の手順で求めることができる。

①　A×8の値を求める。\[ A \times 8 = (1.1)_2 \times 2^5 \times 8 = (1.1)_2 \times 2^5 \times 2^3 = (1.1)_2 \times 2^8 \]

②　A×2の値を同様に求める。

③　①と②の結果を加算する。
加算結果を単精度表現すると、\( \left[ \ \ \ c \ \ \ \right] \) になる。

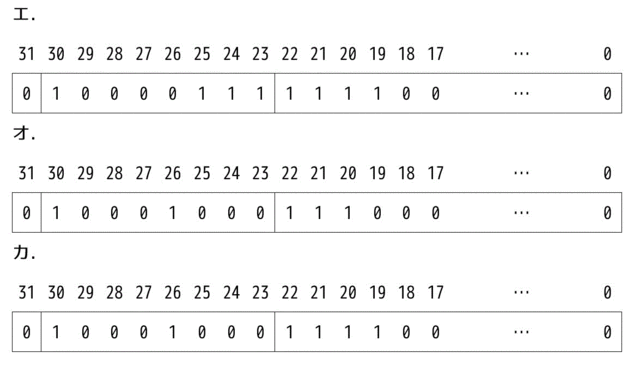
cに関する解答群

ア：0 | 0000 1000 | 111000…0
イ：0 | 0000 1000 | 111100…0
ウ：0 | 1000 0111 | 111000…0
エ：0 | 1000 0111 | 111100…0
オ：0 | 1000 1000 | 111000…0
カ：0 | 1000 1000 | 111100…0

６．練習問題の解答

問題1

0.7を2のべき乗で表す。\[0.7 = 2^{-1} + 2^{-3} + 2^{-4} + 2^{-7} + \cdots \]となる。

(1) 固定小数点表記を考える。整数部は0、小数部は2ビットなので \( 2^{-2} \) までの項を表すことができる。よって2進数に直すと、0000.10となる。また、この値を10進数に戻すと0.5となる。よって0.2の誤差が発生することがわかる。

(2) 0.7を2のべき乗で表したものを、\( 2^{-1} \) でくくることにより、1.XXXの形にする。 \[\begin{align*}
0.7 & = 2^{-1} + 2^{-3} + 2^{-4} + 2^{-7} + \cdots \\ & = 2^{-1} (2^{0} + 2^{-2} + 2^{-3} + 2^{-6} + \cdots)
\end{align*} \]となる。指数部は-1となるので、-1を2の補数表現で表すと11となる。

また、仮数部は上位3桁（整数の1は省略なので小数第3位）まで表せるため、\( 2^{-3} \) の項まで表すことができる。よって011となる。

0.7は正なので符号は0、よってこれを順番通りに並べると011011となる。
また、10進数に戻すと、\[2^{-1} (2^{0}+2^{-2}+2^{-3}) = \frac{11}{16}\]と変形できるので、\[\frac{7}{10} - \frac{11}{16} = \frac{1}{80}\]より、誤差は0.0125となる。

問題2

正解：3

それぞれの選択肢を見ていく。
6bit小数点の指数部は2の補数表現なので、\( 2^{-2} \leqq x \leqq 2^{1} \) の範囲で誤差なしで表せ、仮数部は3ビットあるため、\( 2^{-3} \) の項まで誤差なしで表せる。

正しい。固定小数点なので表現できる数値の密度は均一。
正しい。浮動小数点は0から遠ければ遠くなるほど表現できる数値の密度は小さくなる。
誤り。2.875は、\[2.875 = 2^1 + 2^{-1} + 2^{-2} + 2^{-3} = 2^1 (2^0 + 2^{-2} + 2^{-3} + 2^{-4})\]と変形できる。このとき指数部は \( 2^1 \) なので誤差なしで表せるが、仮数部が \( 2^{-4} \) の項まであるため、正しく計算することができない。
正しい。0.75は、\[0.75 = 2^{-1} + 2^{-2} = 2^{-1} (2^0 + 2^{-1}) \]と変形できる。このとき指数部は \( 2^{-1} \) なので誤差なしで表せ、仮数部が \( 2^{-1} \) の項まであるため、正しく計算ができる。

問題3

解答：仮数部12ビット　指数部5ビット。

まずは3141.5を 1.XXX × 2^Y の形にする。
2のべき乗の中で、一番大きい項は \( 2^{11} \) なので、全体を \( 2^{11} \) でくくりだし、括弧内を \( 2^{0} + 2^{-1} + \cdots \) （この形は必ず1.XXXになる）の形する。\[ \begin{align*}
3141.5 & = 2^{11} + 2^{10} + 2^6 + 2^2 + 2^0 + 2^{-1} \\ & = (2^0 + 2^{-1} + 2^{-5} + 2^{-9} + 2^{-11} + 2^{-12} ) \cdot 2^{11}
\end{align*}\]すると、指数部は \( 2^{11} \) となり、仮数部の中で一番小さな桁は \( 2^{-12} \) となる。

よって仮数部は \( 2^{-12} \) までの桁があれば表せることになるので12ビット必要。
また、指数部は11乗であり、\( 2^3 \leqq 11 \leqq 2^4 \) なので4ビット必要。

さらに補数表現なので符号を表す1ビットを付け足すので合計5ビット。

解答4

解答：エ

正規化は、有効桁数を最大に保つために行われる。

解答5

設問1

解答：イ\[0.625 = 1.25 \times 2^{-1} \] である。

このときの指数部は \( 2^{-1} \) 、つまり\( \beta = -1 \) である。
指数部は \( \beta \) の値に127を足せばよいので、126を16進数表記したものが答えとなる。まずは2進数に変換する。

すると、0111 1110 となる。あとはこれを16進数に変換するだけ。

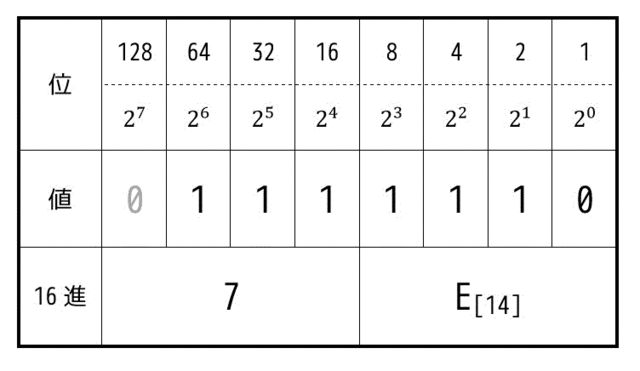
よって答えはイの \( \mathrm{(7E)_16} \) となる。

設問2

解答：オ

符号部：0
指数部：0111 1110
仮数部：1000…0

である。これを順番に10進数の形にする。

まずは指数部を10進数に直す。\[ 2^6 + 2^5 + 2^4 + 2^3 + 2^2 + 2^1 = 64 + 32 + 16 + 8 + 4 + 2 = 126\]となる。指数部は127足された値が格納されているため、127を引けばよい。すると \( \beta = -1 \) となる。なので、指数部は \( 2^{-1} \) となる。

つぎに仮数部を直す。1000…0 ということは、小数部分は \( (0.1)_2 \) となっている。これに整数部分の1をつけ足して \( (1.1)_2 \) となっていることがわかる。つまり、仮数部は1.5となる。\[ 1.5 \times 2^{-1} = 0.75\] より、答えはオの0.75。