うさぎでもわかる計算機システム　Part05　論理回路の基本編 [基本情報対応]

こんにちは、ももやまです。
今回は論理回路の基本についてまとめたいと思います。

NOT回路・AND回路・OR回路の基本3回路、XOR(Ex-OR)回路・NAND回路・NOR回路・XNOR(Ex-NOR)回路などの説明とその練習問題（基本情報の過去問もあります）を載せています。

 

論理演算（ブール代数）が出来ていることを前提に説明をするので、もし論理演算がまだ苦手だと思った人はこちらの記事をご覧ください。

www.momoyama-usagi.com

最後に論理回路を読む練習問題付きです。 

※注意

この記事では論理和のことを \( + \)、論理積のことを \( \cdot \) で表記しています。
人によっては論理和を \( \lor \) 、論理積を \( \land \) で表す人もいます。

例えば \( A \) と \( B \) の論理和は \( A + B \)、論理積は \( A \cdot B \) と表します。論理積の \( \cdot \) を省略して \( AB \) のように表すこともあります。

 

 

スポンサードリンク

１．基本的な確認

論理回路では、0か1の2つの状態だけを考えます。
0はFalse・偽・offの状態を表し、1はTrue・真・onの状態を表します。

さらに論理式を回路で表現します。

 

スポンサードリンク

２．基本的な3回路

まずは、基本的な3つの回路について説明します。
すべての論理式はこの3つの回路だけで表すことができます。

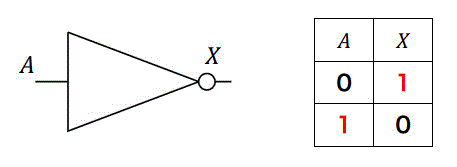
(1) NOT回路 \( \bar{A} \)

入力された回路が1であれば0を、0であれば1を出力する回路です。
言い換えると、入力の0,1を入れ替える回路とも言えます。インバーターと呼ばれることもあります。

 

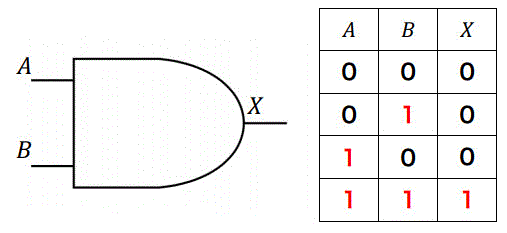
(2) AND回路 \( A \cdot B \)

2つの入力が両方とも1のときだけ1を出力し、それ以外のときは0を出力する回路です。

AND回路、OR回路をごっちゃに覚えてしまう人がいるので正しく覚えましょう。
AND回路はANDのDの形をしてるからANDだというと覚えやすいかもしれません……（ゴリ押しですが……）

 

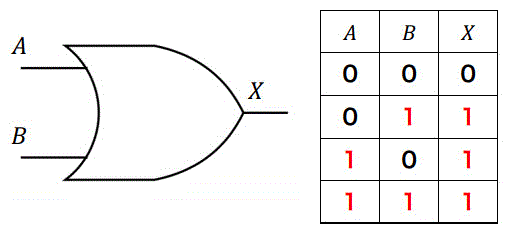
(3) OR回路 \( A + B \)

2つの入力のうちどちらか一方でも1であれば1を出力し、どちらとも0のときだけ0を出力する回路です。

 

スポンサードリンク

３．さらなる4回路

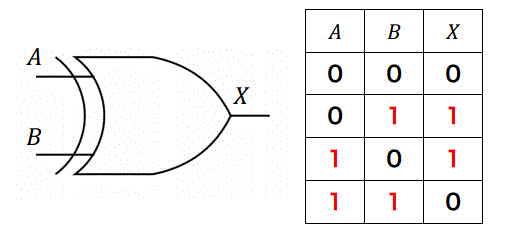
(1) XOR回路(Ex-OR回路) \( A \oplus B \)

2つの入力の排他的論理和(Exclusive or)、つまり2つの入力が異なれば1を、同じであれば0を出力する回路です。真理値表を示します。

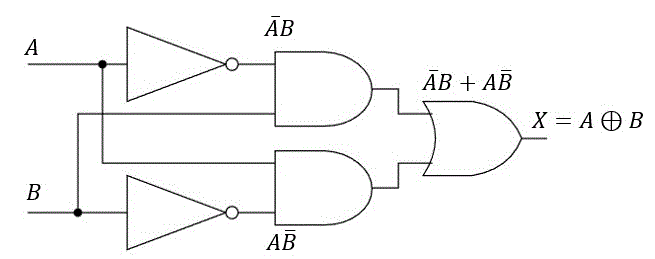
論理式を変形すると、\[ A \oplus B = A \bar{B} + \bar{A} B \] となり、基本3回路で表せます。 

 

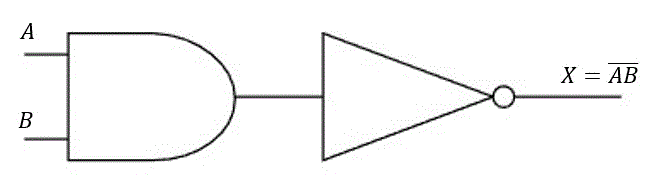
(2) NAND回路 \( \overline{A \cdot B} \)

AND回路の否定を取ります。つまり、両方とも1のときは0、それ以外のときは1を取る回路となります。出力側についている○はnot回路だと思ってください。

真理値表はこのようになります。

 

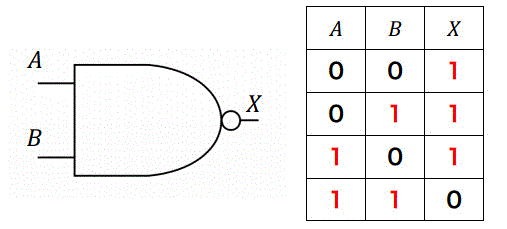
論理式の変形をすると、\[ \overline{A \cdot B} = \bar{A} + \bar{B} \]となり、NOT回路とOR回路で表現してあげることができます。

 

 

(3) NOR回路 \( \overline{A + B} \)

OR回路の否定を取ります。つまり、両方とも0のときは1、それ以外のときは0を取る回路となります。NANDと同じく出力側についている○はnotだと思ってください。

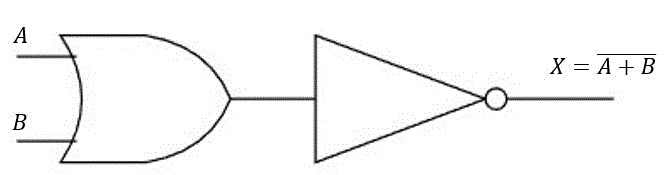
真理値表はこのようになります。

 

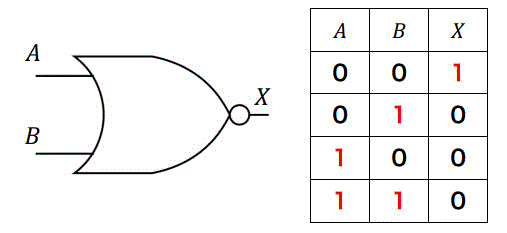
論理式の変形をすると、\[ \overline{A + B} = \bar{A} \cdot \bar{B} \]となり、NOT回路とAND回路だけで表現してあげることができます。

 

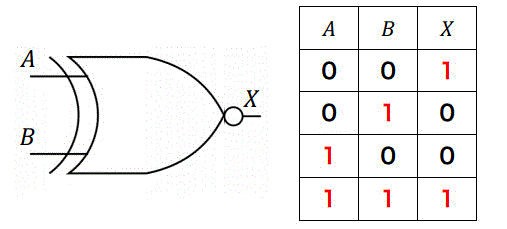
(4) XNOR回路(Ex-NOR回路) \( \overline{A \oplus B} \)

XOR回路の否定を取ります。つまり、2つの入力が同じのときに1を、異なるときに0を出力する回路だと思ってください。上の2つと同じく、出力側についている○はNOTだと思ってください。

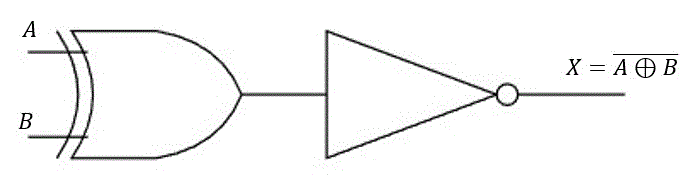
真理値表はこのようになります。

 

４．NAND回路で基本3回路の表現

NAND回路だけで基本的な3回路を表現してあげることができます。

NAND回路だけで回路を表現するメリット、基本的な3回路を用意する場合は、NOT回路だけ不足し、AND回路が余っているような現象が発生しますがNAND回路だけの場合は、どれか1つの回路だけが不足するようなことが起こらず、さらに素子が1つなのでコストを抑えられるなどがあります。

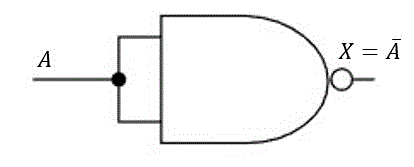
(1) NOT回路をNAND回路だけで表す

NAND回路の真理値表に注目してください。

A,Bともに0のときはANDの条件を満たさないため出力は1、A,Bともに1のときはANDの条件を満たすために出力は0になっていますね。

なので、自分自身のNANDを取ることでNOT回路を表現してあげることができます。

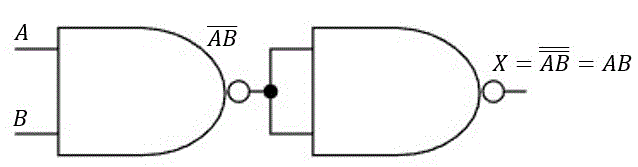
(2) AND回路をNAND回路だけで表す。

NAND回路はAND回路のNOTですね。

なので、NAND回路をさらにNOTするとAND回路が表現できます。

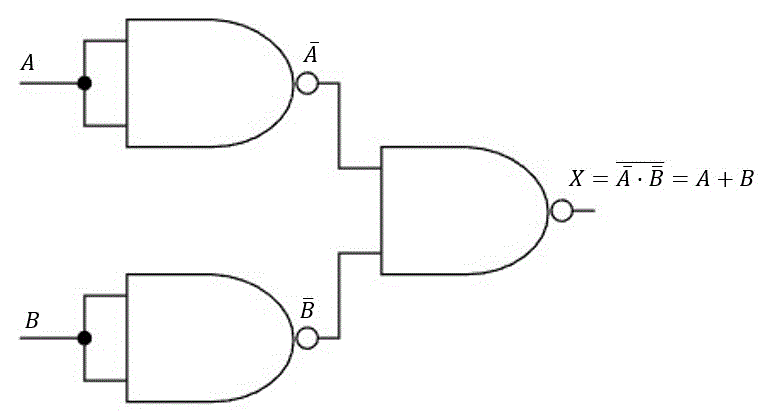
(3) OR回路をNAND回路だけで表す

\( A + B \) を変形すると、\( \overline{\bar{A} \cdot \bar{B}} \) となります。

つまり、AにNOT回路をつけたものとBにNOT回路をつけたもののNANDをとればいいことになります。

 

５．練習問題

では何問か練習してみましょう。

練習1

次の(1),(2)の論理回路の入力 \( A,B \) に対する出力 \( X \) を求めなさい。

(1)

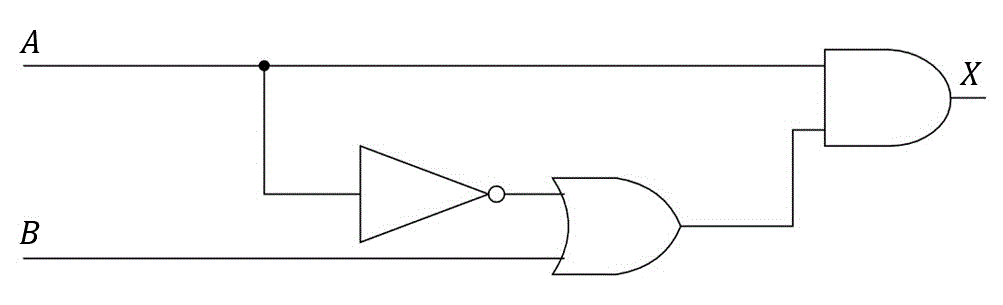
(2)

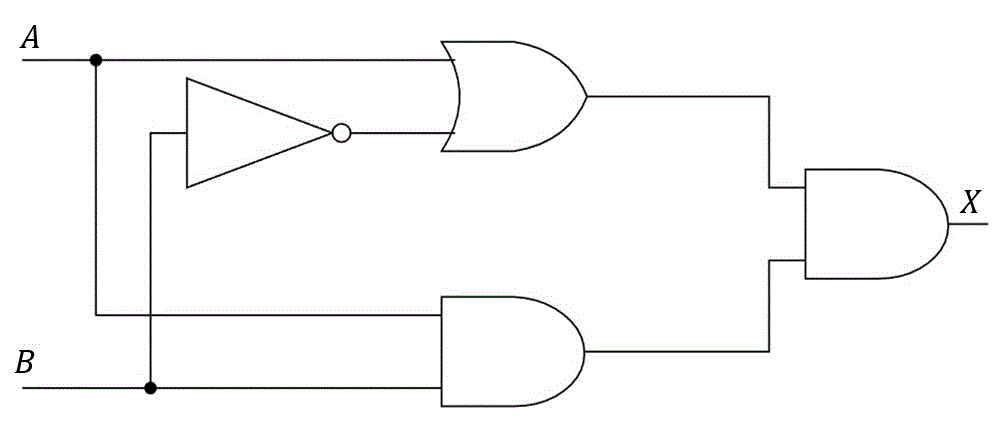
練習2

図に示すディジタル回路と等価な論理式はどれか。ここで、論理式中の \( \cdot \) は論理積、 \( + \) は論理和を表す。

[基本情報技術者平成29年秋期 午前問23]

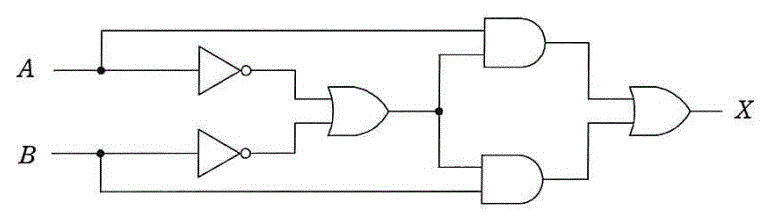
ア：\( X = A \cdot B + \overline{A \cdot B} \)
イ：\( X = A \cdot B + \bar{A} \cdot \bar{B} \)
ウ：\( X = \bar{A} \cdot B + A \cdot \bar{B} \)
エ：\( X = (\bar{A} + B) \cdot (A + \bar{B}) \)

 

練習3

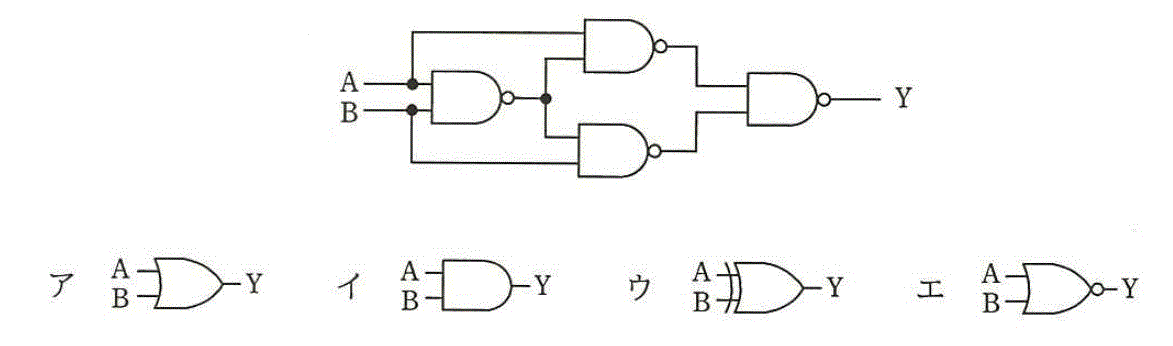
図の論理回路と同じ出力が得られる論理回路はどれか。

[基本情報技術者平成21年春期 午前問24]

 

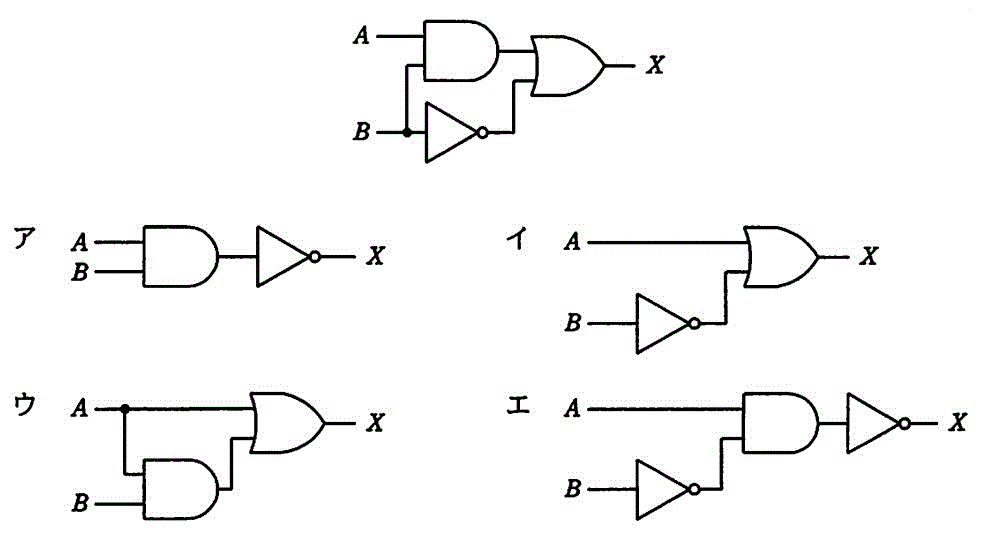
練習4

図の論理回路と等価な論理回路はどれか。

[基本情報技術者平成28年春期 午前問23]

６．練習問題の答え

解答1

(1)

解答

\( A \)	\( B \)	\( X \)
0	0	0
0	1	0
1	0	0
1	1	1

問題を解く際に下の画像のように真理値表や論理式のメモを書くと解きやすくなります。

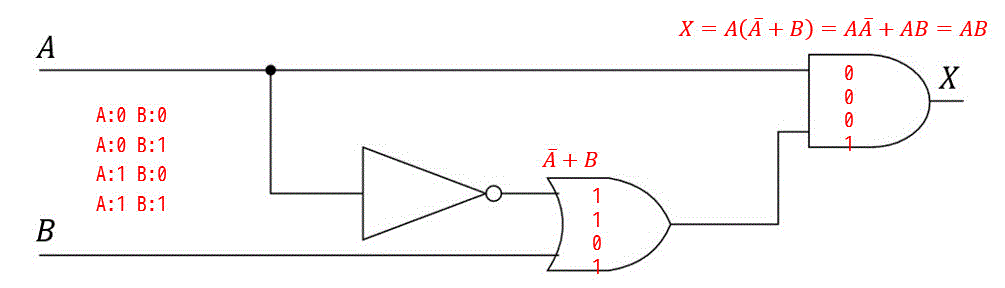
(2)

解答

\( A \)	\( B \)	\( X \)
0	0	0
0	1	0
1	0	0
1	1	1

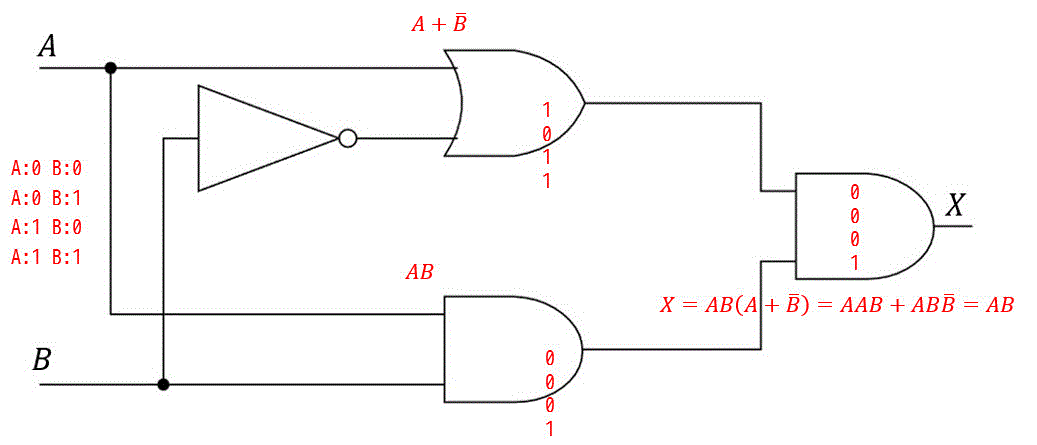
解答2

解答：ウ

おすすめは、問題の論理回路にこのようにメモ（真理値表・論理変形）をしながら解く方法です。

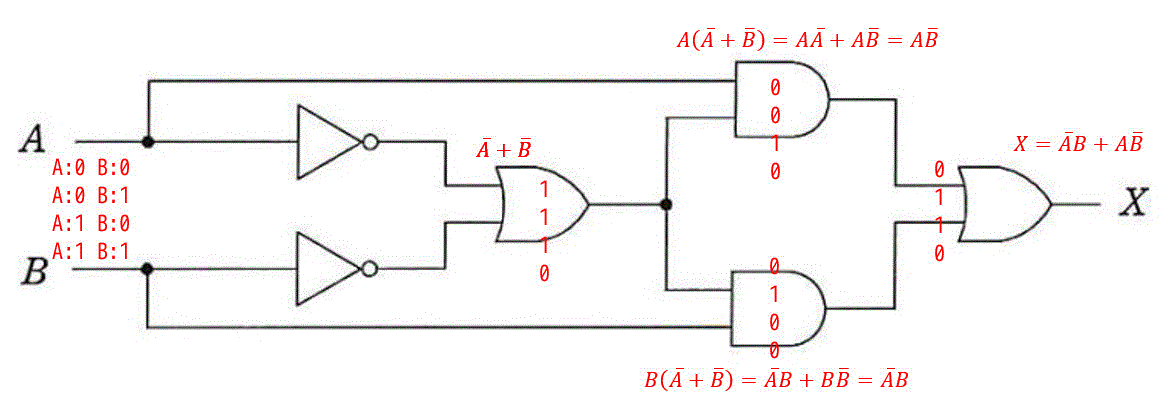
論理式の変形で解いた人は、答えがウとすぐに出せます。

 

真理値表で解いた場合は、選択肢のア〜エのそれぞれの論理式を真理値表になおしてあげる必要があります。

 

アの真理値表

\( A \cdot B = C \) とおくと、\( C + \bar{C} \) となり、常に1となることがわかります。

\( A \)	\( B \)	\( A \cdot B \)	\( \overline{A \cdot B} \)	ア
0	0	0	1	1
0	1	0	1	1
1	0	0	1	1
1	1	1	0	1

 

イの真理値表

\( A \)	\( B \)	\( A \cdot B \)	\( \bar{A} \cdot \bar{B} \)	イ
0	0	0	1	1
0	1	0	0	0
1	0	0	0	0
1	1	1	0	1

 

ウの真理値表

\( A \)	\( B \)	\( \bar{A} \cdot B \)	\( A \cdot \bar{B} \)	ウ
0	0	0	0	0
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

 

エの真理値表

\( A \)	\( B \)	\( \bar{A} + B \)	\( A + \bar{B} \)	エ
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	1	1	1

と書くことができます。よって真理値表が問題の回路（の真理値表）と一致するのは、ウとなります。 

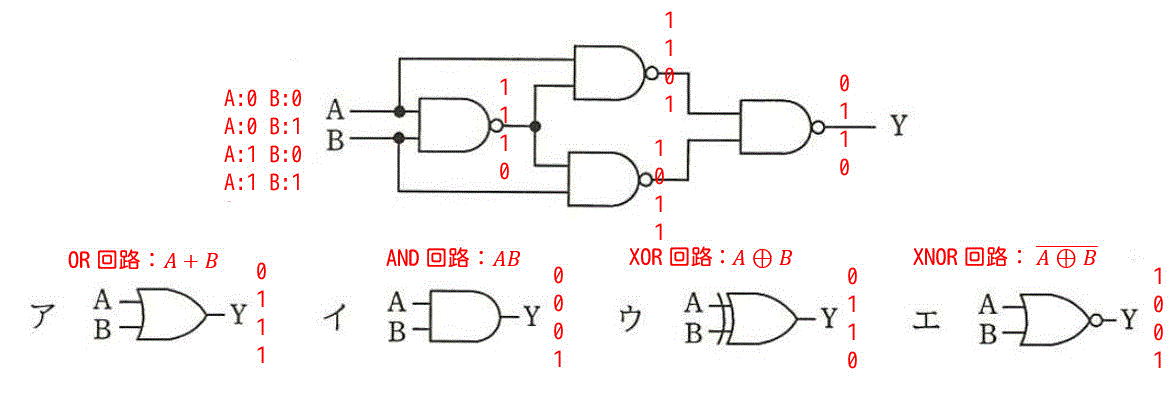
解答3

解答：イ

問題の真理値表はこのようになります。

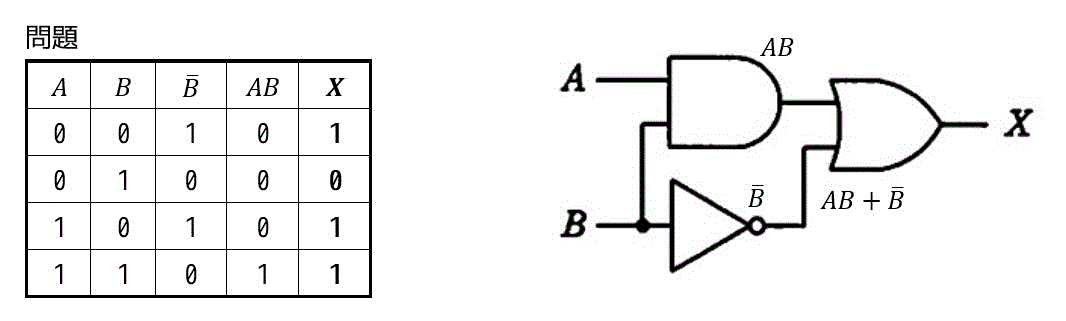
つぎにア～エの真理値表を記していきます。

 

 

 

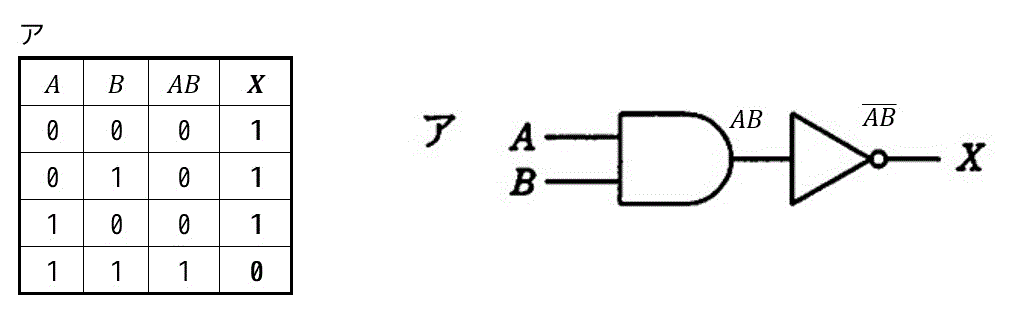
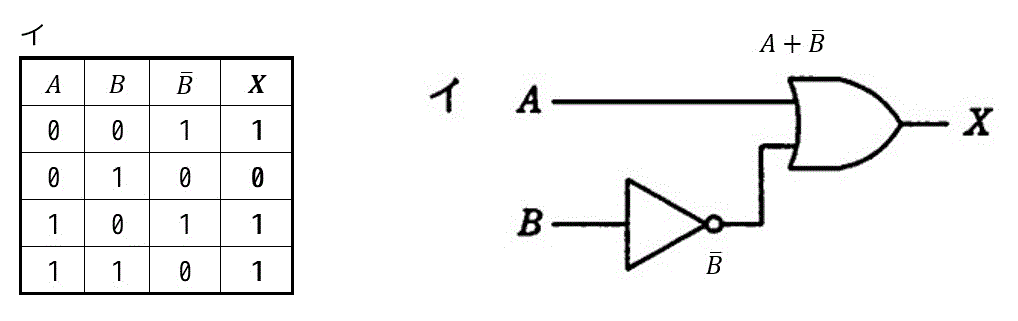
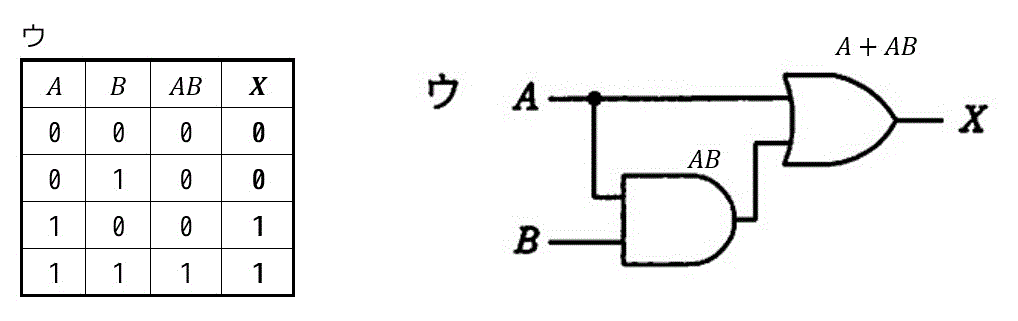
となり、出力 \( X \) が一致しているのはイとなり、イが答えになります。

 

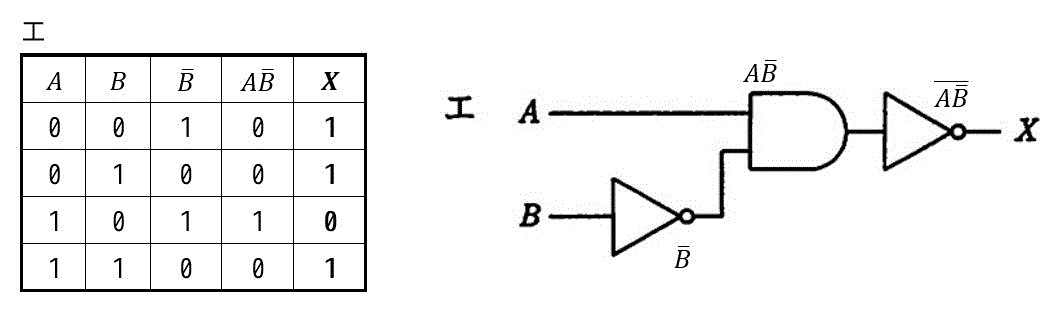
解答4

解答：ウ

７．さいごに

今回は論理回路の基本についてのまとめをしました。

論理回路を論理式や真理値表に落とし込めるようになりましょう。

 

次回は論理回路を簡単化するために使うカルノー図について説明します。