スポンサードリンク
こんにちは、ももやまです。
今回は順序回路であるフリップフロップについての説明をしたいとおもいます。
論理回路の基礎であるAND回路・OR回路が登場してくるので、基本的なAND・OR回路などの理解がまだできてない人はこちらの記事で復習をしましょう！
目次
スポンサードリンク
１．クロック
まずはフリップフロップに出てくるクロックについて説明したいと思います。
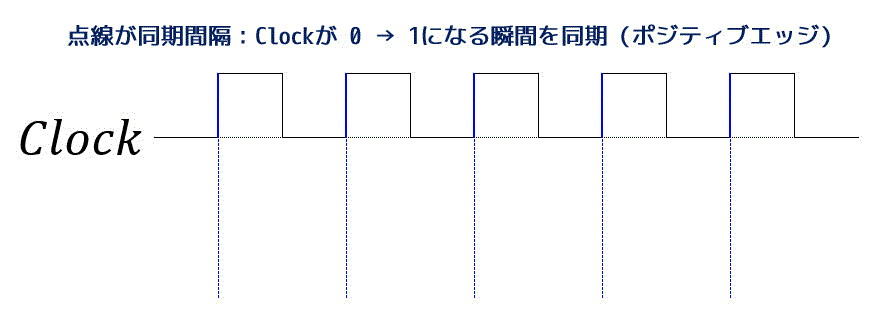
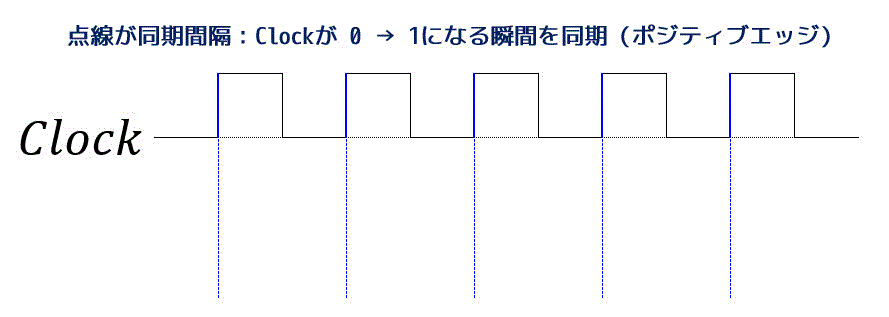
一定間隔で0, 1が周期的に変わるよう信号をクロックと呼びます。
クロックは、回路のタイミングをあわせる（同期を取る）ために使われます。
クロックが0→1になるときに同期を取るものをポジティブエッジといい、1→0になるときに同期を取るものをネガティブエッジといいます。
今回のフリップフロップの説明では、0→1になるときに同期を取るポジティブエッジで説明していきたいと思います。
また、1秒間に何回クロックが発振するか（同期するか）を表したものをクロック周波数と呼び、単位をヘルツ（Hz）で表します。例えば、1秒間に1,000回発振すればクロック周波数は 1,000 [Hz] = 1 [kHz] です。
例題1
50 [MHz] で同期するフリップフロップがある。
このフリップフロップの周期（同期間隔）を答えなさい。
解答1
50 [MHz] は、\( 50 \times 10^6 \) を表す。\[ \frac{1}{50 \times 10^6} = 2.0 \times 10^{-8} \]となる。
よって、\( 2.0 \times 10^{-8} \) [s] となり、単位を変えると 20 [ns] となる。
スポンサードリンク
２．フリップフロップ
フリップフロップは順序回路の1つで1ビットの情報を記録することができる回路です。
順序回路なので、出力が入力だけでなく、現在の状態によって変わります。
主に４種類のフリップフロップがあるので、今回は４種類を順番に説明していきましょう。
(1) RSフリップフロップ
まずは、最も基本的な回路であるRSフリップフロップについて説明します。
RSフリップフロップのRはResetを表し、SはSetを表します。
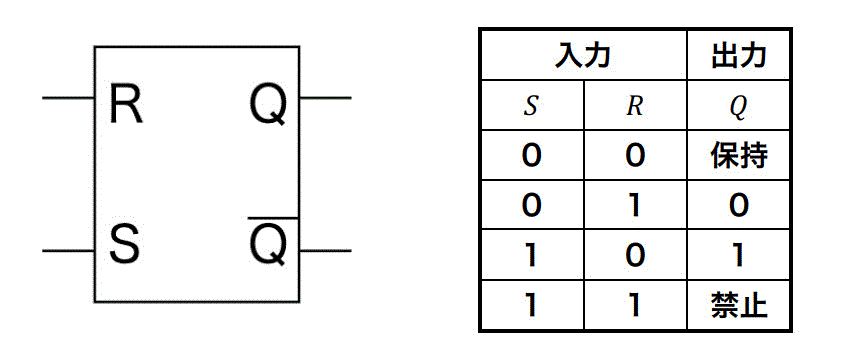
RSフリップフロップは、以下のような回路で示すことができます。
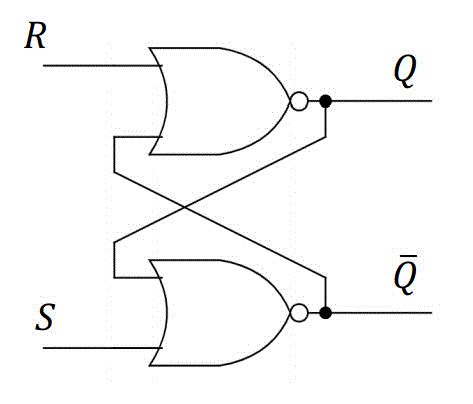
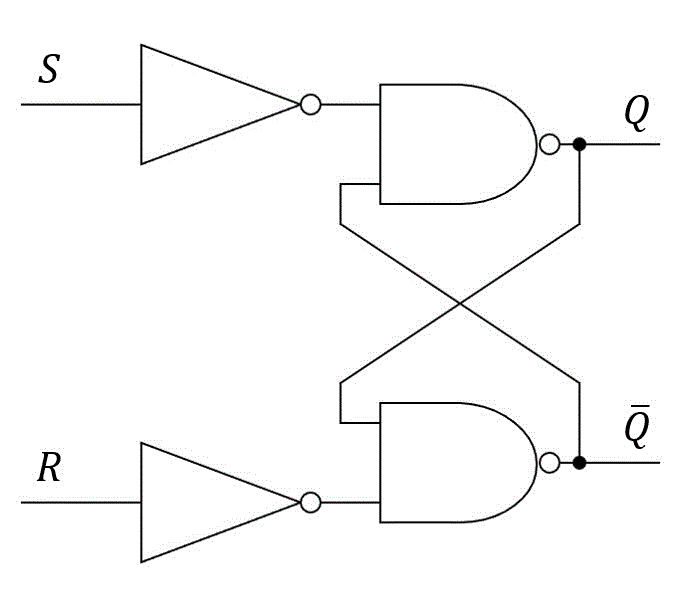
この回路の動きを1つずつ追っていきましょう。
(a) S = 0, R = 1 の場合
S = 0, R = 1 なので Resetに該当する操作です。
この場合は、上側のNOR回路の出力が0となります。
つまり、\( Q = 0 \) が確定します。
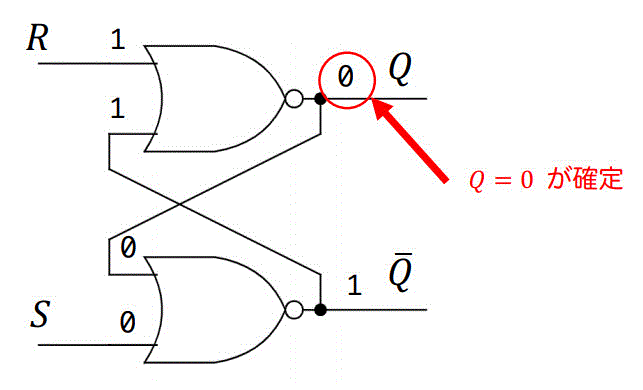
あとは残りの回路をたどると、\( \bar{Q} = 1 \) も確定します。
(b) S = 1, R = 0 の場合
S = 1, R = 0 なので Setに該当する操作です。
この場合は、下側のNOR回路の出力が0となります。
つまり、\( \bar{Q} = 0 \) が確定します。
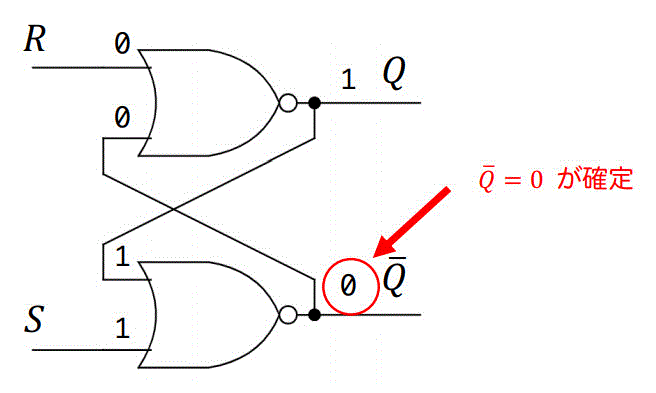
あとは残りの回路をたどると、\( Q = 1 \) も確定します。
(c) S = 0, R = 0 の場合
S = 0, R = 0 なのでSetでもResetでもない状態です。
この場合は、上側、下側のNOR回路の出力がともにわかりません。
なので、1つ前の状態の \( Q, \bar{Q} \) の状態を確認する必要があります。
(i) \( Q = 0 \), \( \bar{Q} = 1 \) のとき
まず、\( Q = 0 \), \( \bar{Q} = 1 \) の状態を考えます。
このときは、\( \bar{Q} \) が1なので、上側のNORゲートの入力に1が来るため、出力が0になります。よって、\( Q \) の値は変わらず0となります。
同様に \( Q \) が0なので下側のNORゲート入力はともに0となり、出力が1になります。よって、\( \bar{Q} \) の値も変わらず1となります。
(ii) \( Q = 1 \), \( \bar{Q} = 0 \) のとき
つぎに(i)の逆、つまり \( Q = 1 \), \( \bar{Q} = 0 \) の状態を考えます。
このときは、\( \bar{Q} \) が0なので、上側のNORゲートの入力はともに0となり、出力が1になります。よって、\( Q \) の値は変わらず1となります。
同様に \( Q \) が1なので下側のNORゲート入力に1が来るため、出力が0になります。よって、\( \bar{Q} \) の値も変わらず0となります。
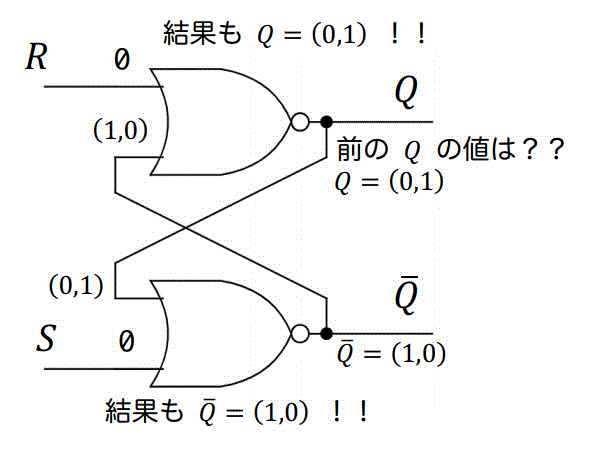
(i), (ii) の2つより、S, Rがともに0のときは前の状態と変わらないことがわかりますね。
(d) S = 1, R = 1 の場合
S = 1, R = 1 なのでSetでもResetの状態です。
この場合だと、両側のNORゲートの入力に1が入るため、出力がともに0となります。
なので、\( Q \), \( \bar{Q} \) ともに0になります。
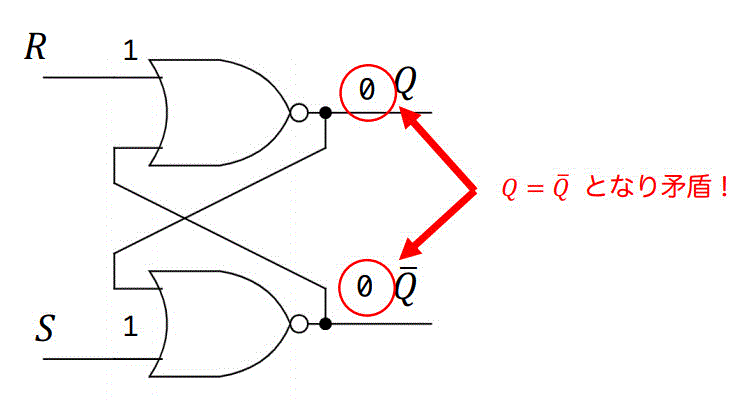
この状態は明らかにおかしく、予期せぬ動作をすることがあるため、S, Rがともに1のときは禁止入力として扱います。
これを踏まえると、RSフリップフロップの動作は以下のような真理値表で表すことができます。
(2) JKフリップフロップ
RSフリップフロップでは、RとSがともに1のときは予期せぬ動作をするので禁止入力でしたね。
RとSがともに1のときにも予期せぬ動作をしないように改良したのがJKフリップフロップとなります。
JKフリップフロップの真理値表は、下のように示すことができます。
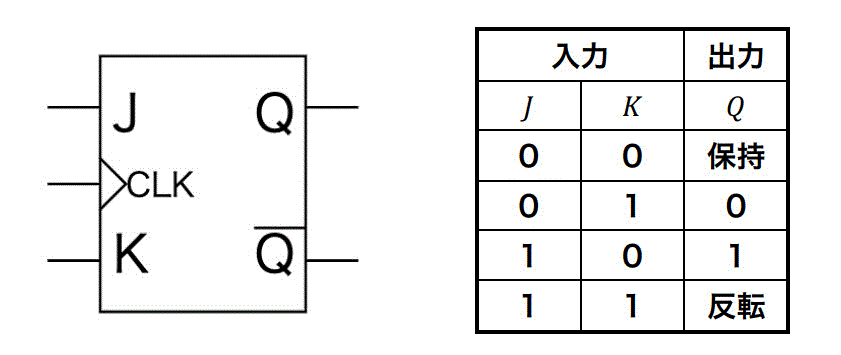
RSフリップフロップのSの部分がJ、Rの部分がKとおぼえておくといいと思います。
ちなみにJKフリップフロップの名前の由来は不明です。トランプの Jack, Kingから取っているとか、作成者のJack Kilby氏から取ってるとか……。決して女子高生のJKではないですよ()
(3) Dフリップフロップ
多くの場面で使われるフリップフロップです。
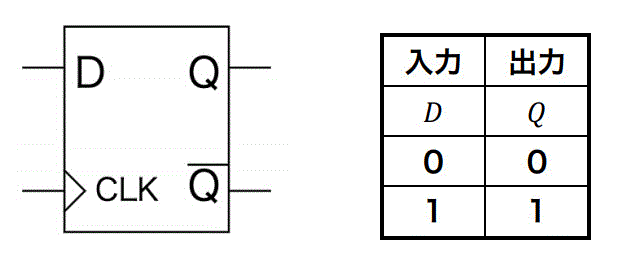
Dフリップフロップは、同期時の入力の値をそのまま出力するフリップフロップとなります。
真理値表は、下のようになります。
(4) Tフリップフロップ
カウンタ、トグルフリップフロップとも呼ばれます。
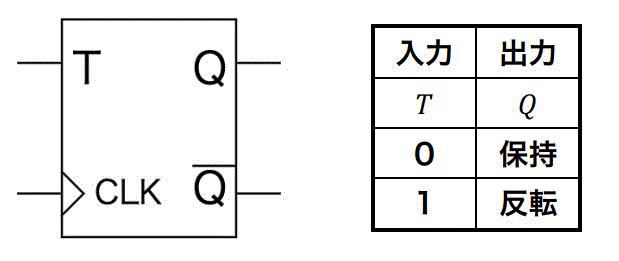
Tフリップフロップは、同期時に入力Tが0のときは出力はそのまま、入力Tが1のときは出力を反転させる回路です。
真理値表は下のようになります。
スポンサードリンク
３．タイミングチャート
実際に先程紹介した4つのフリップフロップの動きをタイミングチャートを記すことにより確認しましょう。
※先ほど説明した順番と異なる順番で確認していきます。
※問題を解く前に注意
入力が同期タイミングと同時に変化する場合、同期タイミングの直前の値・直後の値のどちらを取るかがわかりませんね。
なので、今回の問題の場合は、同期タイミングと同時に入力が変化する場合は、同期タイミングの直前の値を取るものとします。
（本当は同期と同時に入力を変化させると、出力0,1が曖昧になってしまうメタステーブル状態が起こることがあるので対策が必要である。）
例題2 Dフリップフロップのタイミングチャート
Dフリップフロップの回路において、入力Dが以下のようなタイミングチャートで表されたときの出力Qの波形を書きなさい。
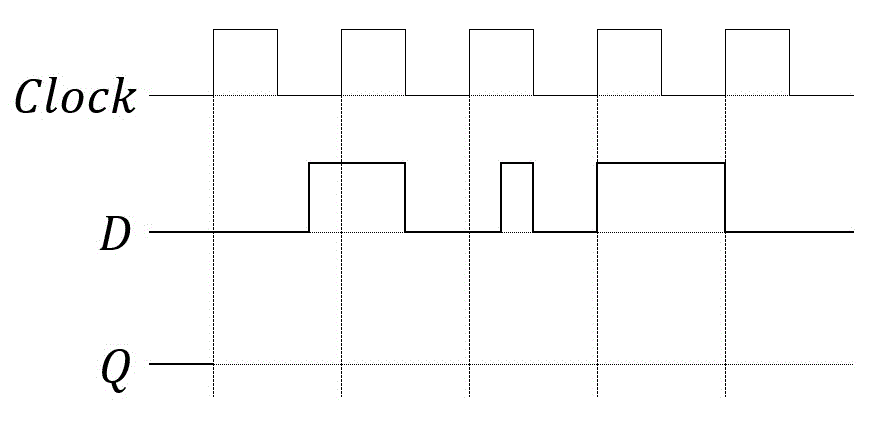
解説2
クロックが0→1になる瞬間を確認し、Dが0ならQは0、Dが1ならQは1とします。
また、クロックの間（同期と同期の間）はDの値がいくら変わろうとQの値が変わらないことに注意してください。
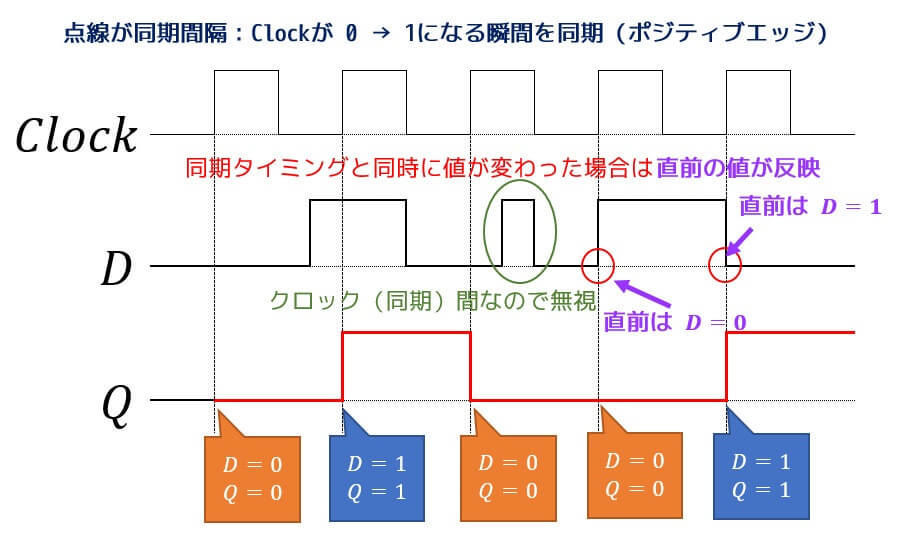
※今回は同時に値が変わった場合は直前の値を反映させてください。
例題3 Tフリップフロップのタイミングチャート
Tフリップフロップの回路において、入力Tが以下のようなタイミングチャートで表されたときの出力Qの波形を書きなさい。
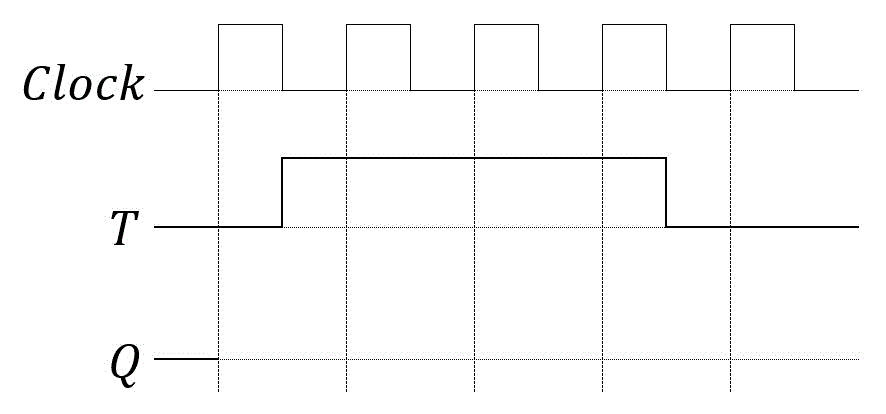
解説3
同期タイミングのときにTが1のときはQの値を入れ替え（0と1をチェンジ）、Tが0のときはQの値をそのままとなる。
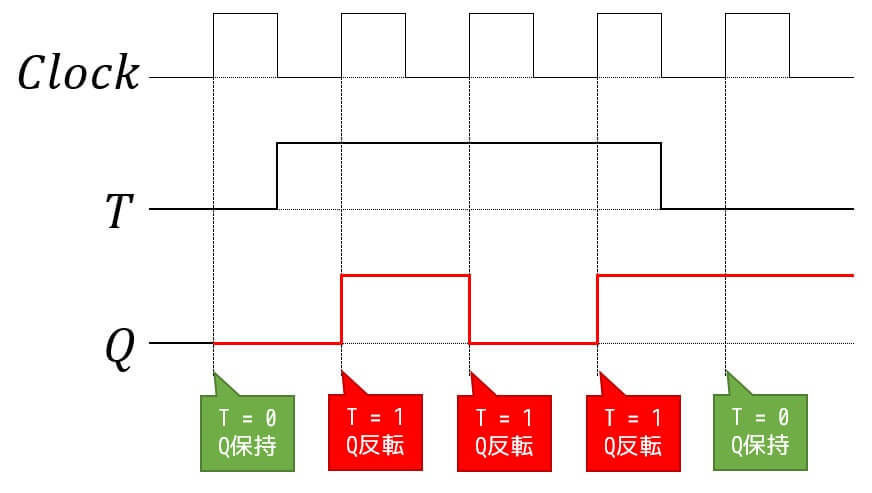
例題4 RSフリップフロップのタイミングチャート
RSフリップフロップの回路において、入力S、入力Rが以下のようなタイミングチャートで表されたときの出力Qの波形を書きなさい。
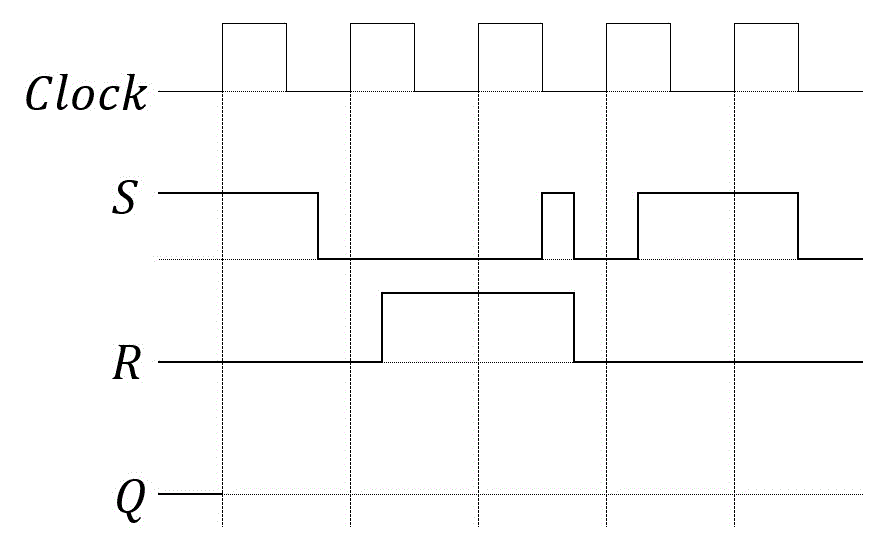
解説4
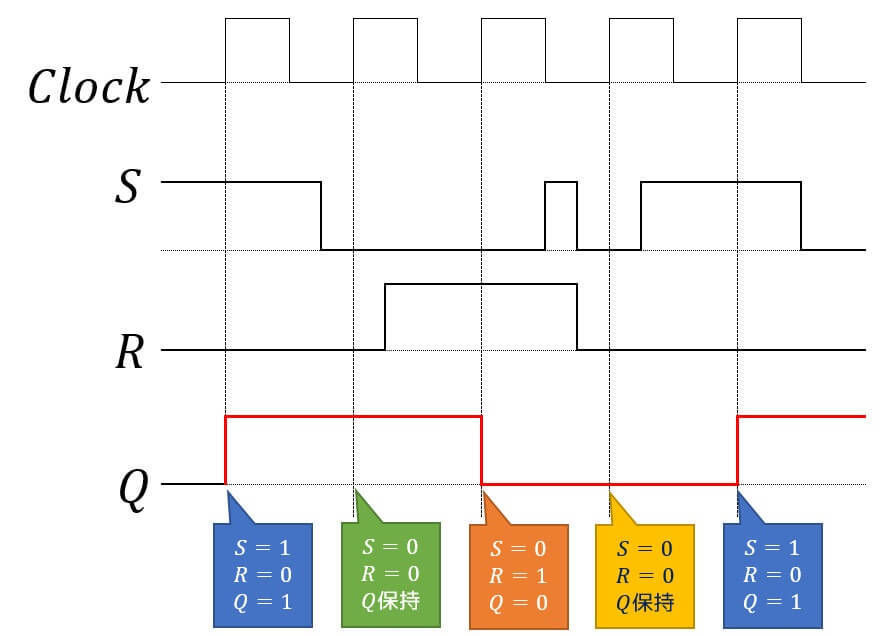
RSフリップフロップは、Sが1、Rが0ならQは1、Sが0、Rが1ならQは0、ともに0ならQの値はそのままにするフリップフロップである。
例題2、例題3と同様に同期タイミングだけをチェックすること。
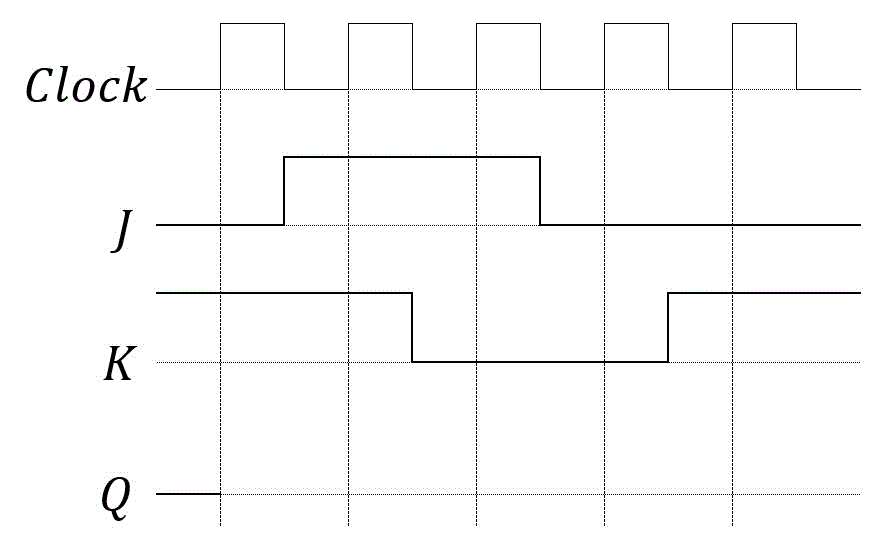
例題5 JKフリップフロップのタイミングチャート
JKフリップフロップの回路において、入力J、入力Kが以下のようなタイミングチャートで表されたときの出力Qの波形を書きなさい。
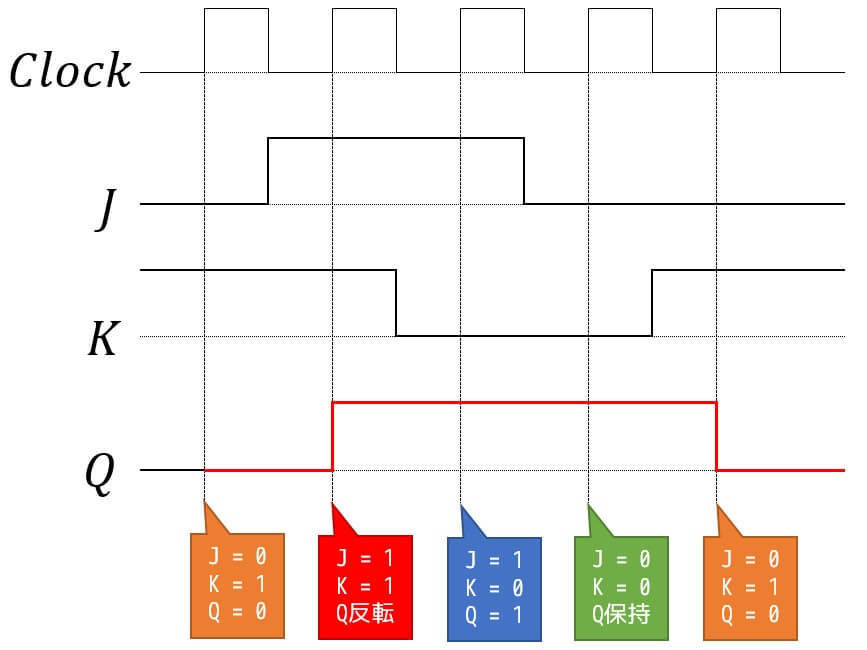
解説5
JKフリップフロップはRSフリップフロップの進化版。
JがSに相当し、KがRに相当する。
同期時に両者が1のときは、Qの値を反転させる。
４．練習問題
では、実際に練習していきましょう。
今回は、タイミングチャートを読む問題です。
練習1
つぎの(1)〜(4)の各フリップフロップの入力が、タイミングチャートで表されたときのそれぞれの出力Qの波形を示しなさい。
(1) Dフリップフロップ
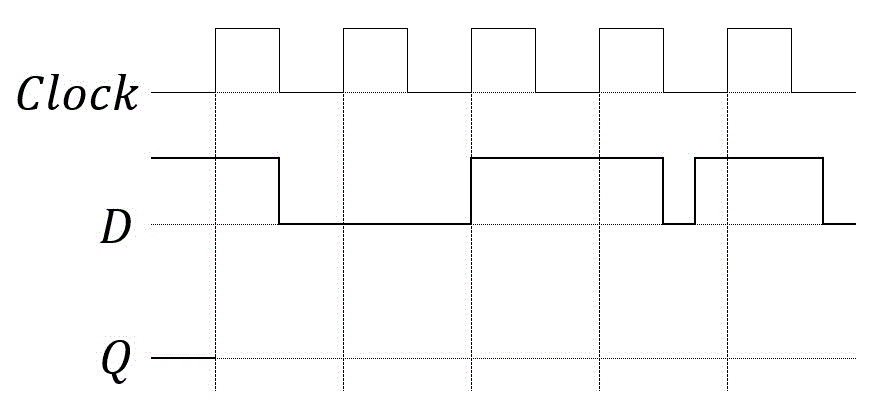
(2) Tフリップフロップ
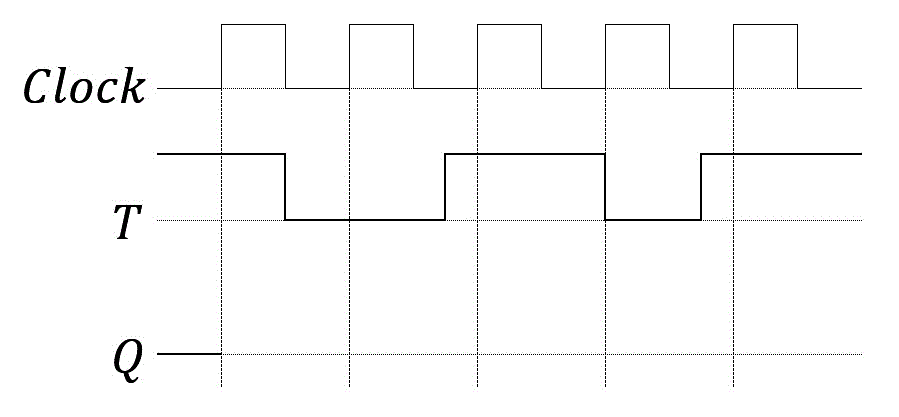
(3) RSフリップフロップ
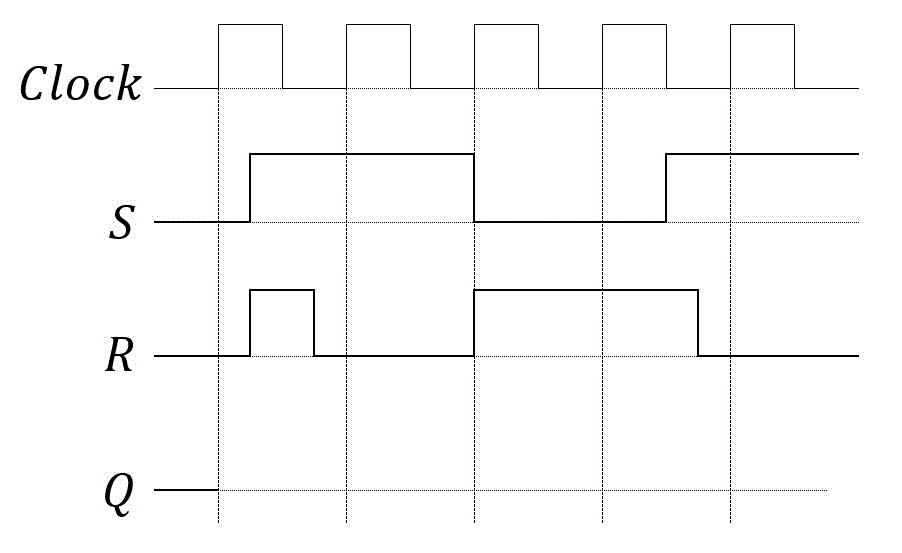
(4) JKフリップフロップ
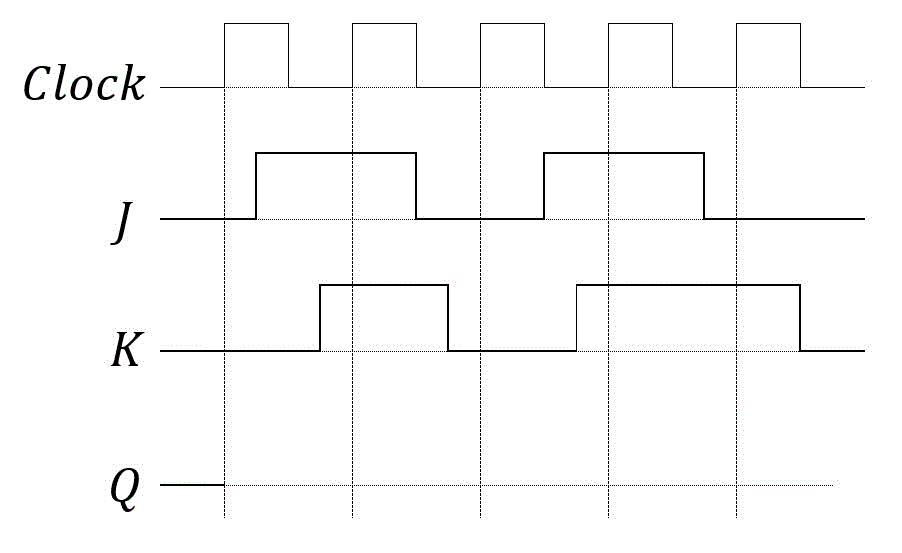
練習2
つぎの(1), (2)の回路に対し、入力 \( a \) が示す入力がタイミングチャートで表されたときの空いているタイミングチャートを書きなさい。
(1)
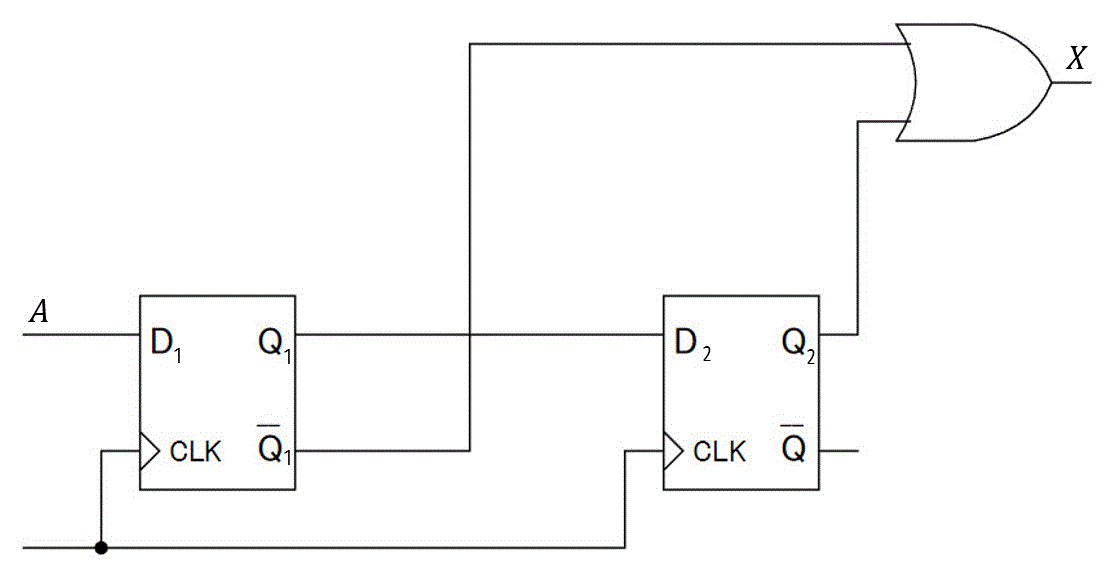
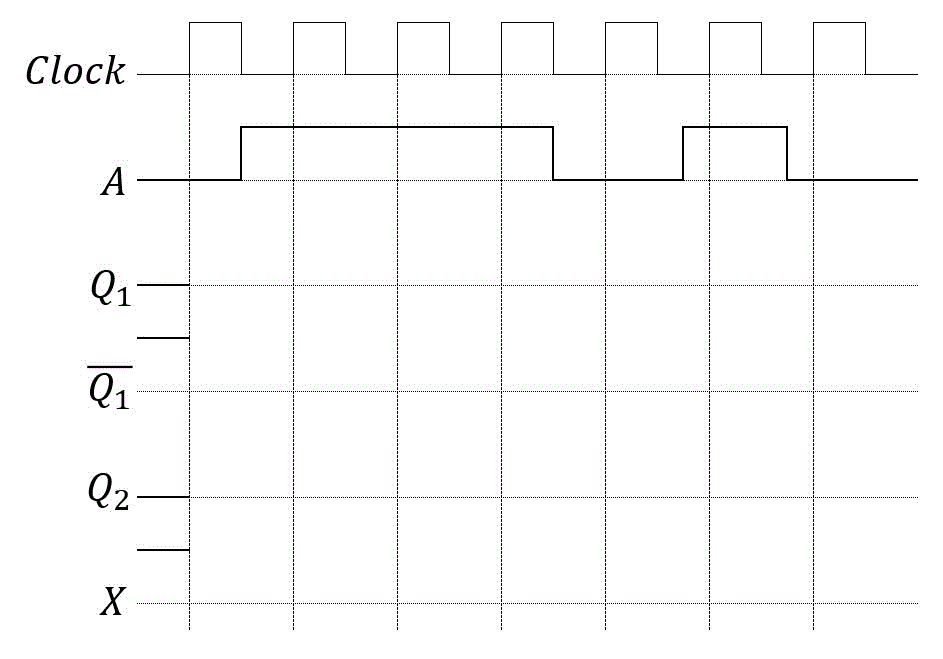
(2)
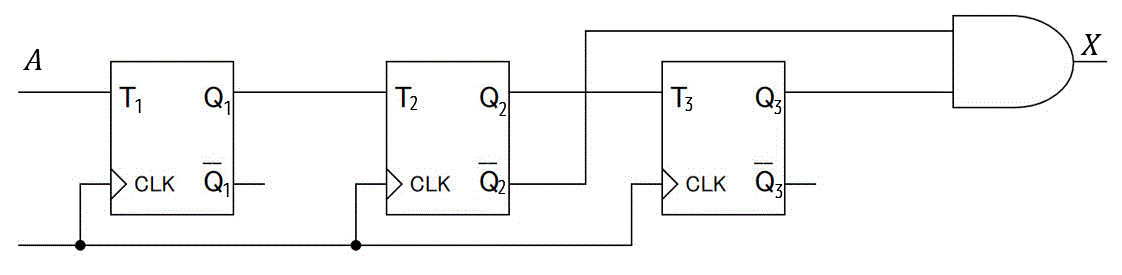
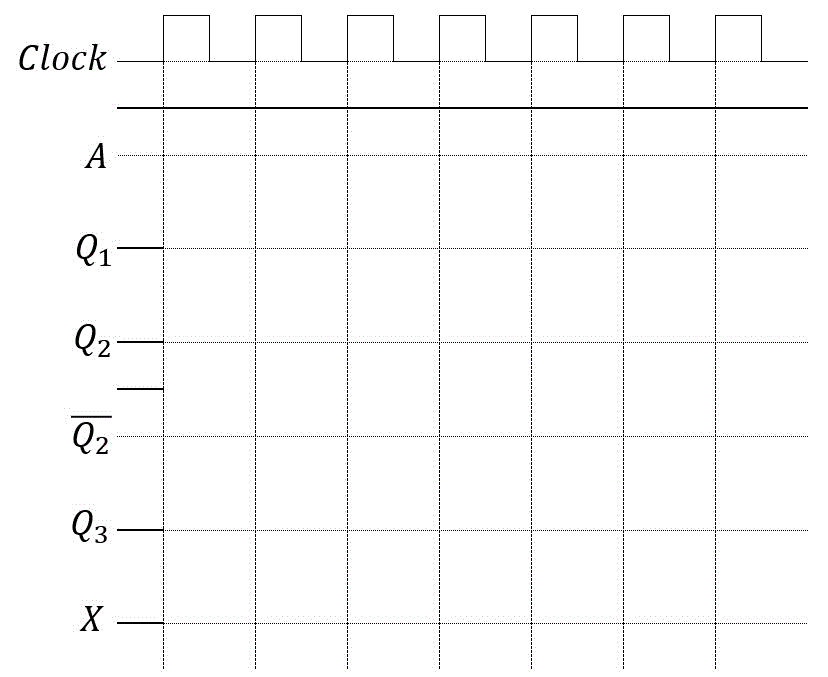
５．練習問題の解答
練習1
例題と同じように同期時のみをチェックしていくこと。
(1) Dフリップフロップ
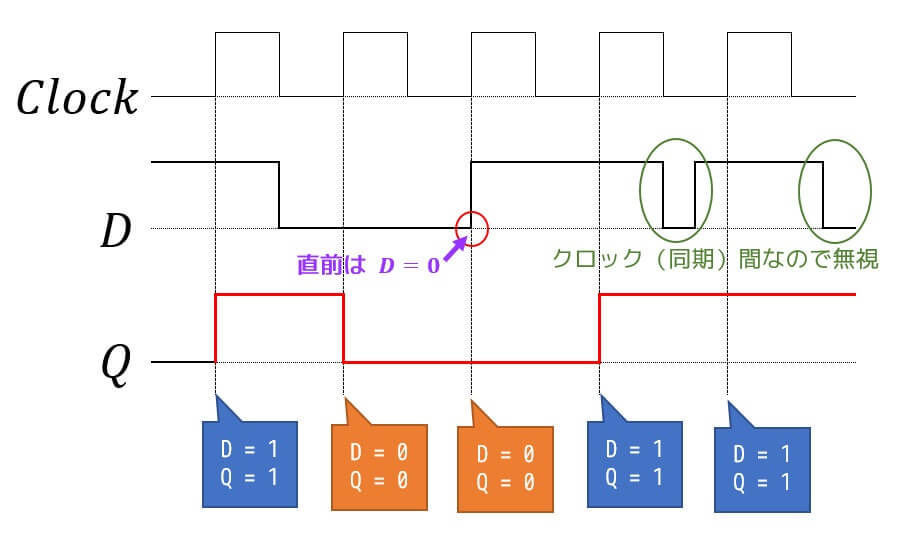
(2) Tフリップフロップ
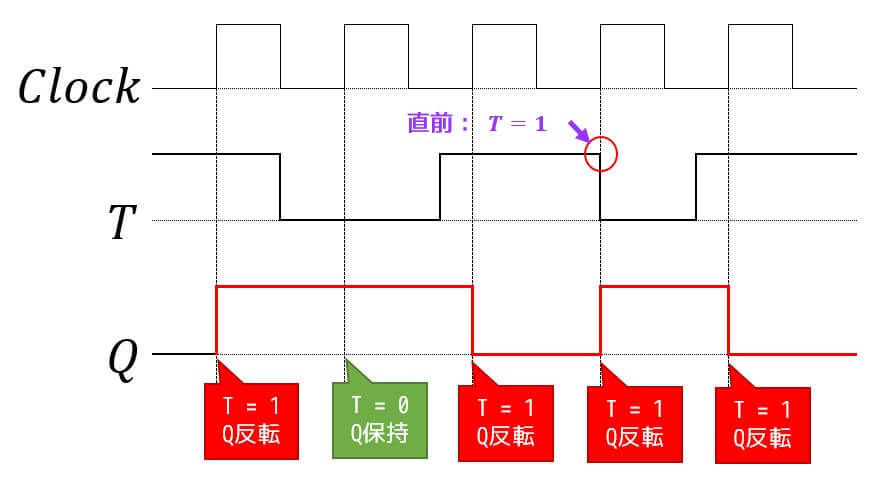
(3) RSフリップフロップ
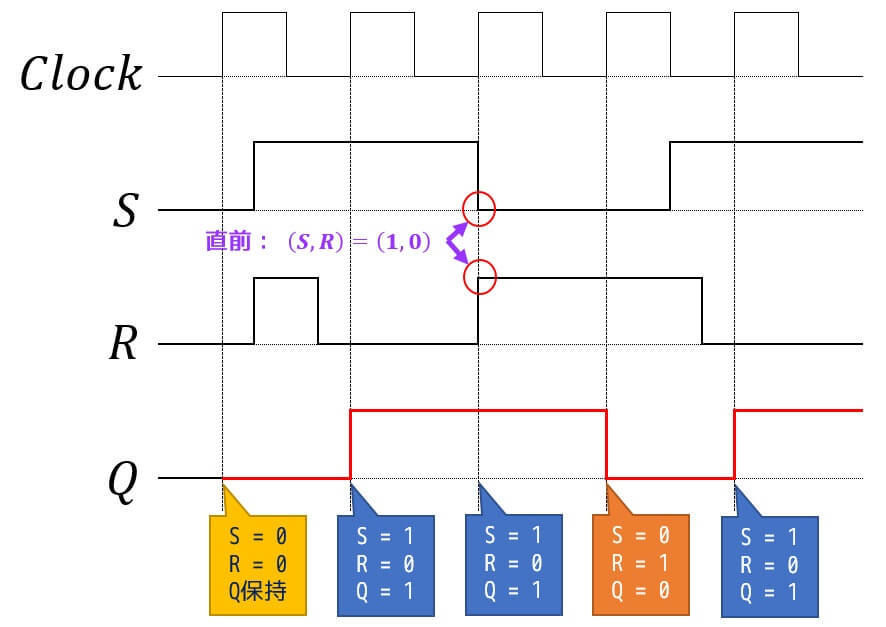
(4) JKフリップフロップ
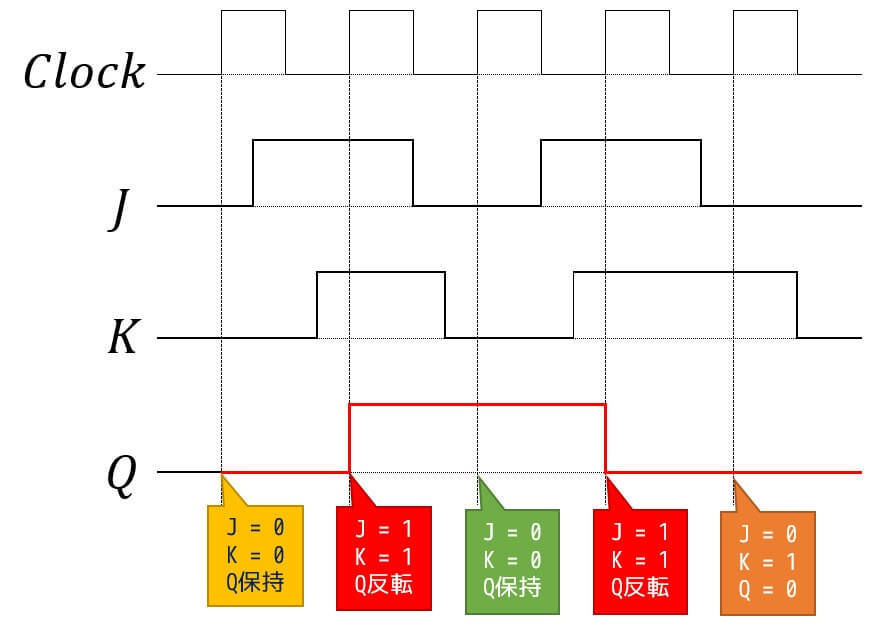
練習2
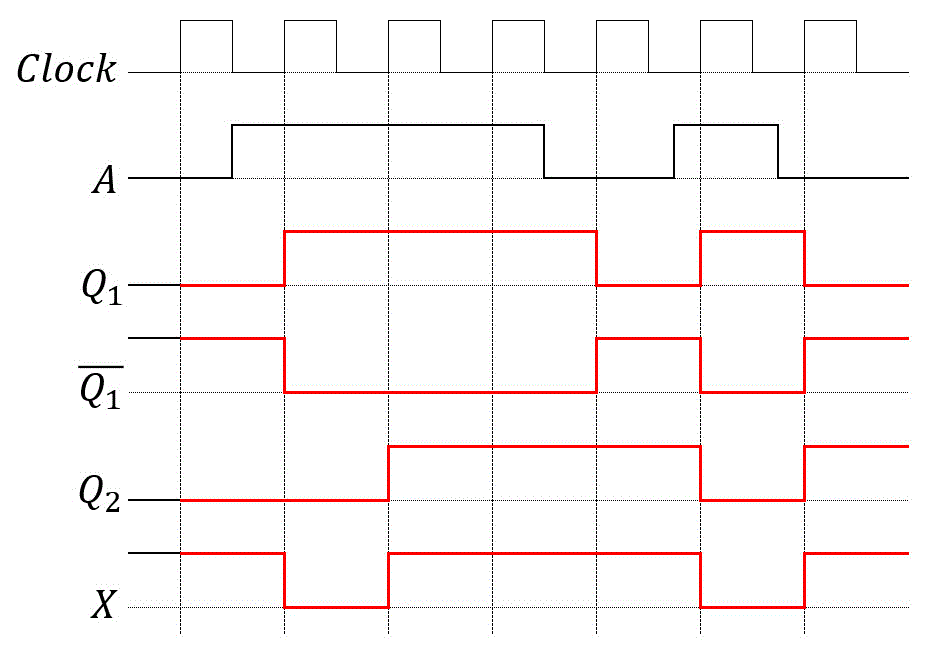
(1)
それぞれの入力がどうなるのかを確認。
入力 \( T_1 \) ：\( A \)
入力 \( T_2 \) ：\( T_1 \)
入力 \( T_3 \) ：\( T_2 \)
出力 \( X \) ：\( \bar{Q_1} + Q_2 \)
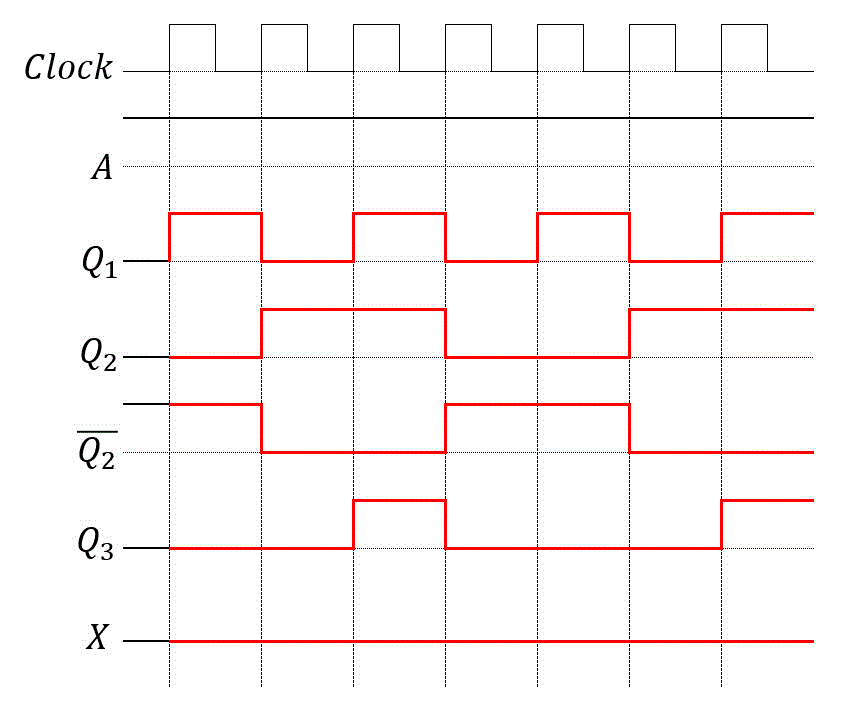
(2)
入力 \( D_1 \) ：\( A \)
入力 \( D_2 \) ：\( Q_1 \)
出力 \( X \) ：\( \bar{Q_2} Q_3 \)
６．さいごに
今回はフリップフロップについてのまとめを行いました。
実際に論理回路を設計する際には、組み合わせ回路だけではなく、フリップフロップのような順序回路も必要なので、フリップフロップのことは頭にいれておきましょう。
今回の例題、練習問題のようなタイミングチャートが書ければフリップフロップの動きは理解できたと言えるでしょう！
関連広告・スポンサードリンク
