スポンサードリンク
こんにちは、ももやまです。
今回から前編、後編の2回にわけてMIPSの命令について紹介していきます。
前編では、
- MIPSのレジスタ構成
- MIPSの命令形式・命令長
- 加算・減算命令
- 即値加算命令
- 乗算・除算命令
- 論理演算命令
- 即値論理演算命令
- シフト命令
の8つについて説明していきたいと思います。
以下の5つの項目は理解できていますか?
- 2進数・10進数・16進数の相互変換
- 2の補数を用いた負の数の表現
- ビットごとのAND / OR / XOR 演算
- 論理シフト・算術シフトの違い
- 符号拡張・ゼロ拡張の違い
もし、1つでもわかっていない項目があれば、下にある記事(アセンブラを学ぶ前に必ず知っておくべき9つの知識)を読んでから下の内容を読むことを強くおすすめします。
目次
スポンサードリンク
1.MIPSのレジスタ構成
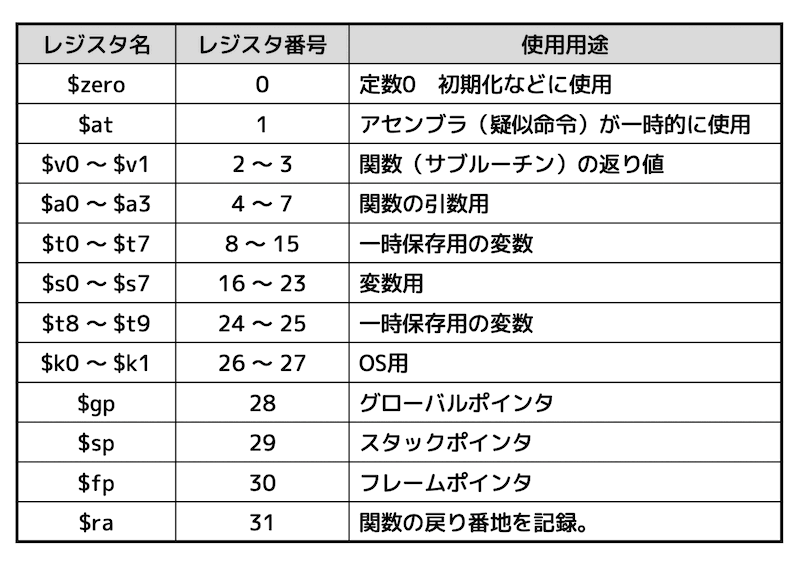
MIPSには、32ビットのレジスタが32本ついており、それぞれのレジスタに番号と名前がついています。
それぞれのレジスタの使用用途を下に示しています。
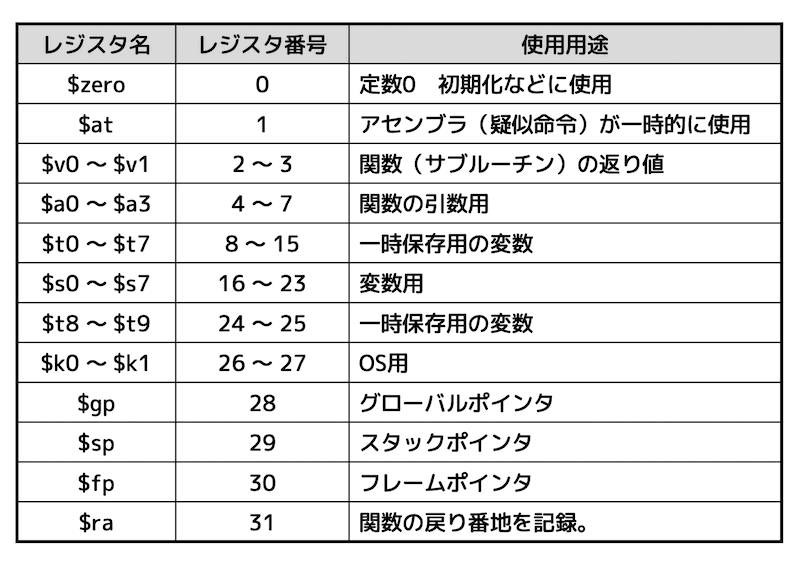
「こんなレジスタがあるんだな〜」て思っていただけたらOKです。
「それぞれのレジスタの使用例」は、命令を紹介する際に合わせて紹介したいと思います。
なお、レジスタ $zero と $ra 以外は汎用レジスタとなっています*1。
スポンサードリンク
2.MIPSの命令長・命令形式
命令は命令内容を示すオペコードと、命令の対象を示すオペランドから成っています。
(MIPSアーキテクチャに限りません)
MIPSの命令はすべて32ビット固定長です。
(つまりどんな命令もオペコード、オペランド合わせて32ビット、32桁の2進数で示されています)
32ビットに統一を行い、設計を単純化することで、動作の高速性を重視しています。
しかし、32ビットに統一したことにより命令形式を1つに抑えることが難しくなったため、MIPSではオペランドによって命令形式がR形式、I形式、J形式の3つに分けられています。
3つの形式の判定は、オペコードと呼ばれる最初の6ビットで判定されます。
(1) R形式
R形式は、主にレジスア同士の演算を対象にした形式です。
32ビットを下のようなフィールドに分割しています。
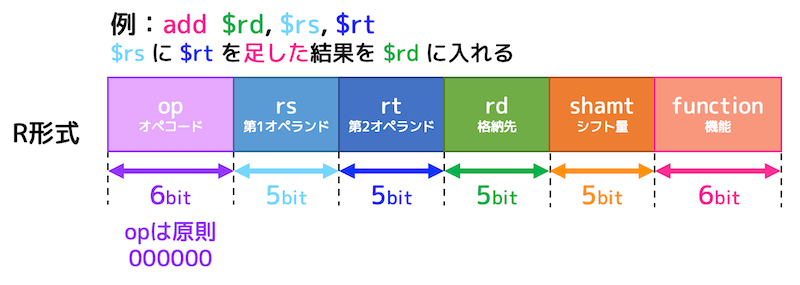
op(オペコード)[6ビット]
R形式の場合、0b000000が入っています。
ですが、このままでは命令内容がわからないため、function(機能)の6ビットで具体的な命令内容を判別します。
rs(第1オペランド)[5ビット]
result = source1 + source2の source1 に相当する部分です。
計算対象の元となるレジスタ番号が2進数(絶対値)で入ります。
例えば、$s0 を指定する場合、$s0 の番号は16番なので、16を2進数にした 0b10000 が入ります。
なお、MIPSを記述する場合、レジスタ番号表記である $16 、名前付けされた $s0 どちらで書いてもOKです。
(分かりやすさ重視のため、原則 $s0 のようなレジスタ名で書かれます。)
なお、第1オペランドを使わない命令の場合、0b00000(オール0)が入ります。
rt(第2オペランド)[5ビット]
result = source1 + source2の source2 に相当する部分です。
計算対象の先となるレジスタ番号が2進数(絶対値)で入ります。
例えば、$s1 を指定する場合、$s1 の番号は17番なので、17を2進数にした 0b10001 が入ります。
なお、第2オペランドを使わない命令の場合、0b00000(オール0)が入ります。
(第1オペランドと同じ)
rd(格納先・デスティネーションレジスタ)[5ビット]
result = source1 + source2の result に相当する部分です。
計算結果を代入するレジスタをレジスタ番号が2進数(絶対値)で指定します。
(格納先を指定しない命令の場合、0が入ります。)
例えば、$t0 を指定する場合、$t0 の番号は8番なので、8を2進数にした 0b01000 が入ります。
shamt(シフト量)[5ビット]
シフト命令でのみ使います。
どれくらいシフトするかを2進数絶対値で入れます。
例えば、3桁シフトさせる場合、shamtには3を2進数にした 0b00011 が入ります。
なお、シフト命令以外ではshamtを使わないので、0b00000が入ります。
function(機能)[6ビット]
result = source1 + source2の + に相当する部分です。
R形式の場合、最初のop部分(6ビット)だけでは命令内容を特定できません。
そのため、最後の6ビット部分でどんな命令なのかを判定します。
例えば足し算 + の命令の場合、0b100000 が入ります。
(それぞれの命令におけるコードは後ほど紹介したいと思います。)
(2) I形式
I形式は、主に即値(定数)やデータ転送用に使われる形式です。
I形式では32ビットを下のようなフィールドに分割しています。
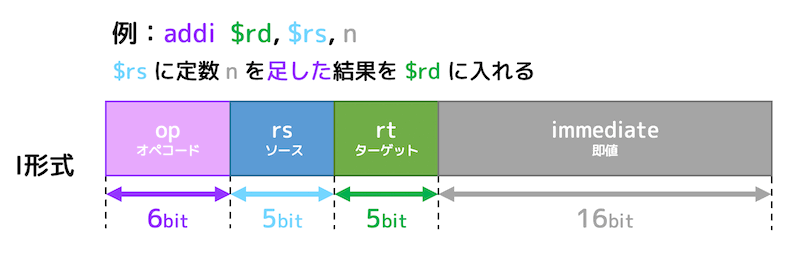
op(オペコード)[6ビット]
命令形式、および命令内容を特定します。
例えばI形式の即値を足す命令の場合、0b001000 が入ります。
(それぞれの命令におけるコードは後ほど紹介したいと思います。)
rs(ソース)[5ビット]
result = source + 5 の source に相当する部分です。
計算対象の元となるレジスタ番号が2進数(絶対値)で入ります。
例えばレジスタ番号17の s1 を指定すると、0b10001(2進数で17)が入ります。
rt(ターゲット)[5ビット]
result = source + 5 の result に相当する部分です。
計算結果を入れるレジスタの番号が2進数(絶対値)で入ります。
例えばレジスタ番号9の t1 を指定すると、0b01001(2進数で9)が入ります。
immediate(即値)[16ビット]
result = source + 5 の 5 に相当する部分です。
即値を指定します。10進数もしくは16進数で指定することができ、10進数の場合はそのまま数字を、16進数の場合は、数字の前に 0x を指定することで入れられます。
例1:10進数で12を指定 → 12
例2:10進数で-5を指定 → -5
例3:16進数で50(10進数に直すと80)を指定 → 0x50
指定された数字を2進数(2の補数表現)で変換されたものが immediate の16ビットに入ります*2。
例1:12を指定 → 0b0000000000001100 が入る
例2:-5を指定 →0b1111111111111011 が入る
復習問題1
I形式の16ビット即値で表現できる数の範囲を「符号なし整数」の場合と「符号付き整数(2の補数表現)」の場合に分けて答えなさい。
必要ならば \( 2^{16} = 65536 \) を使うこと。
復習問題1の解答
符号なし整数:0 〜 65535
符号つき整数:-32768 〜 32767
n ビットで表現できる数の範囲を必ず確認しておきましょう。
(2) J形式
J形式は、ジャンプ命令で使われます。
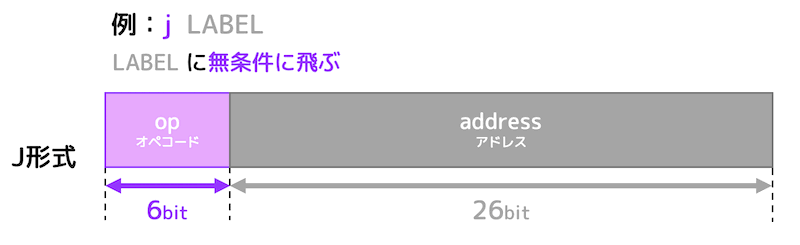
op(オペコード)[6ビット]
命令形式、および命令内容を特定します。
address(即値)[26ビット]
移動先を26ビットで指定します。
詳しくは後編で説明したいと思います。
スポンサードリンク
3.命令紹介1 加算・減算命令
では、ここからは実際にMIPSの命令を紹介していきたいと思います。
まずは、加算や減算命令から紹介していきます。
(1) 加算命令 add
add は足し算のR形式命令です。
add $rd, $rs, $rt は、2つのレジスタ $rd, $rs の和を $rt に格納する命令を表します。
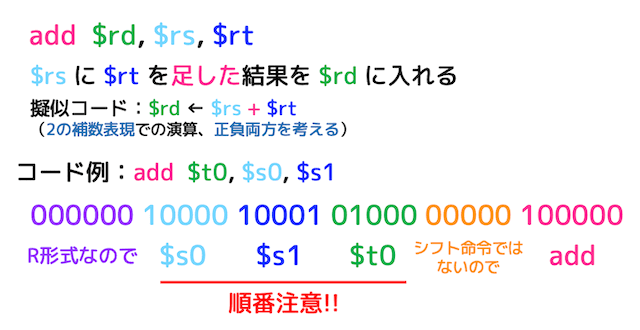
例えば上の命令の $s0 に 0x00000004 (10進数で4)、$s1 に 0x00000007 (10進数で7) が入っていれば、$t0 は 0x0000000B (10進数で11) となります。
(2) 絶対値加算命令 addu [add unsigned]
add に u を付けて addu とすることで、符号なし整数の加算命令となります*3。R形式命令です。
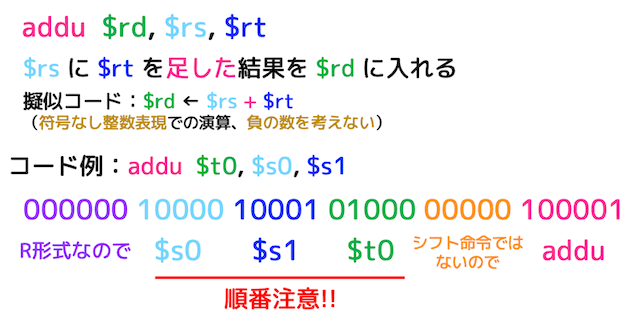
符号なし整数を使わないと問題が発生するとき以外は先程説明した add を使うことをおすすめします。
(3) 減算命令 sub [subtract]
sub は引き算ののR形式命令です。
sub $rd, $rs, $rt は、2つのレジスタ $rd から $rs を引いた結果を $rt に格納する命令となります。
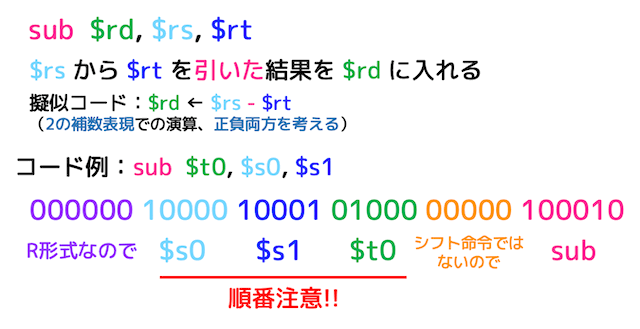
例えば上の命令の $s0 に 0x00000002 (10進数で2)、$s1 に 0x00000003 (10進数で3) が入っていれば、$t0 は 0xFFFFFFFF (10進数で-1) となります。
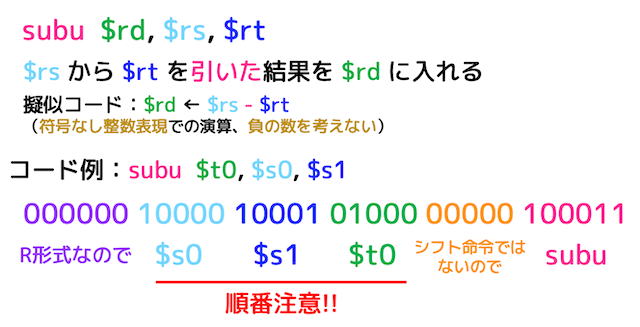
(4) 絶対値減算命令 subu [subtract unsigned]
sub に u を付けて subu とすることで、符号なし整数の(負の数が使えない)減算命令となります。R形式の命令です。
4.命令紹介2 即値加算命令
(1) 即値加算命令 addi [add immediate]
足し算命令の即値Verです。 I形式の命令です。
addi $r, $s, n は、レジスタ $s に n を足した結果を $rt に格納する命令を表します。

例えば上の命令の $s0 に 0x0000000D (10進数で13)、n が11なら、$t0 は 0x00000018 (10進数で24) となります。
(2) 即値絶対値加算命令 addiu [add immediate unsigned]
addi に u を付けて addiu とすることで、符号なし整数の(負を考えない)加算命令となります。こちらもI形式命令です。

即値減算命令は??
実は、即値加算命令 addi, addiu はあっても即値減算命令 subi, subiu はありません。
実は subi に相当する命令は、n に負の数を入れることで代用できるため、mipsではわざわざ用意されていません。

例えば上の命令の $s0 に 0x00000050 (10進数で80)、n が -24 なら、$t0 は 0x00000018 (10進数で56) となります。
絶対値命令addiu であっても、即値部分 n に負の値を指定することができるため、安心して即値減算処理が行えます[1]addiu の場合でも、n には2の補数表現が使われます。。
5.命令紹介3 乗算・除算命令
掛け算や割り算を行う命令も紹介していきます。
MIPSでは掛け算や割り算命令の演算は足し算や引き算と違い、専用レジスタ HI, LO の2つにわけて格納されます。
なお、掛け算や割り算命令はあまり使わないので、参考程度に理解していただけたらOKです。
重要なのは、「加減算演算命令」と「論理演算命令」を組み合わせて「乗算・除算命令」をどうやったら表現できるかです。
(1) 乗算命令 mult [multiply]
mult は掛け算を行うR形式の命令です。
2つの計算元のレジスタを指定し、結果の上位32ビットをレジスタ HI に、下位32ビットをレジスタ LO に格納します*4。
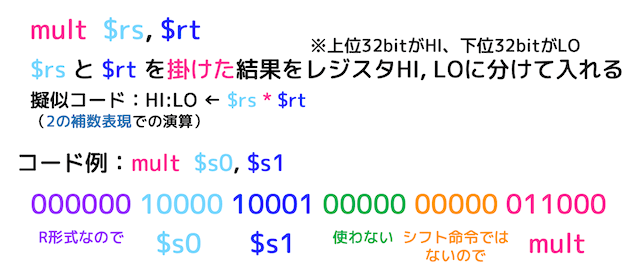
例えば上の命令の $s0 に 0x00000015 (10進数で2)、$s1 に 0x00000003 (10進数で3) が入っていれば、計算結果(64ビット、16進数16桁)は、0x0000000000000006 となります。
なので、レジスタ HI は上位32ビットである 0x00000000、レジスタ LO は下位32ビットである 0x00000006 が入ります。
なお、mult に u multu とすることで、符号なし整数の(負を考えない)乗算命令となります。
(2) 除算命令 div [divide]
div は割り算を行うR形式の命令です。
2つの計算元のレジスタを指定し、結果の商をレジスタ HI に、あまりをレジスタ LO に格納します*5。

例えば上の命令の $s0 に 0x00000015 (10進数で21)、$s1 に 0x00000004 (10進数で4) が入っているとします。
21÷4の商は5、あまりは1となりますね。
なので、レジスタ LO は商である 0x00000005 、レジスタ HI はあまりである 0x00000001 が入ります。
なお、div に u divu とすることで、符号なし整数の(負を考えない)除算命令となります。
(3) HIレジスタの値をレジスタに格納 mfhi [move from hi]
乗算命令や除算命令で使った HI レジスタを汎用レジスタに入れます。R形式の命令です。
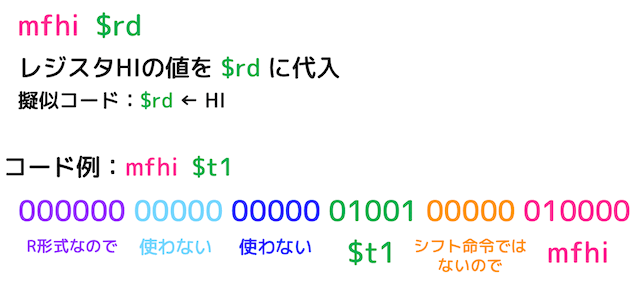
例えば、mfhi $t1 とするとレジスタ HI の値を $t1 に格納します。
(4) LOレジスタの値をレジスタに格納 mflo [move from lo]
乗算命令や除算命令で使った LO レジスタを汎用レジスタに入れます。R形式の命令です。
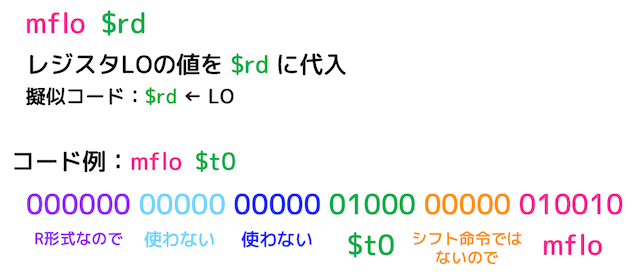
例えば、mfhi $t1 とするとレジスタ HI の値を $t1 に格納します。
6.命令紹介4 論理演算命令
MIPSではビットごとの論理演算命令も行うことができます。具体的には、
- 論理積(and)
- 論理和(or)
- 排他的論理和(xor)
- 否定論理和(nor)
の4つの計算が可能です。
(1) 論理積演算 and
and は論理積演算のR形式の命令です。
and $rd, $rs, $rt は、2つのレジスタ $rd, $rs のビットごとの論理積を $rt に格納します。
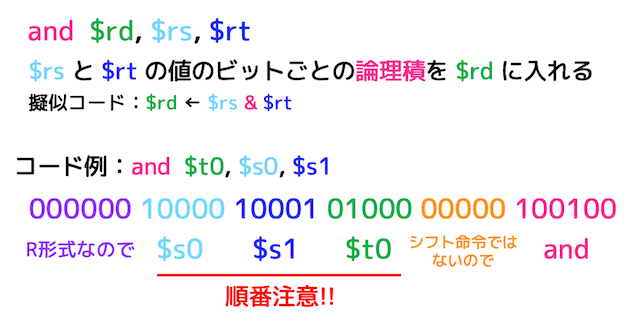
例えば上の命令の $s0 に 0x0600FFFF 、$s1 に 0x03FFFF08 が入っていれば、$t0 は 0x0100FF08 となります。
★計算過程★
$t0 = $s0 & $s1 # $t0 は $ s0 と $s1 のビットごとの論理積 $s0 = 0b 0000 0110 0000 0000 1111 1111 1111 1111 $s1 = 0b 0000 0011 1111 1111 1111 1111 0000 1000 $t0 = 0b 0000 0010 0000 0000 1111 1111 0000 1000
$s0 と $s1 の各ビットの値がともに1なら1、それ以外なら0が入ります。
(2) 論理和演算 or
or は論理和演算のR形式命令です。
or $rd, $rs, $rt は、2つのレジスタ $rd, $rs のビットごとの論理和を $rt に格納します。
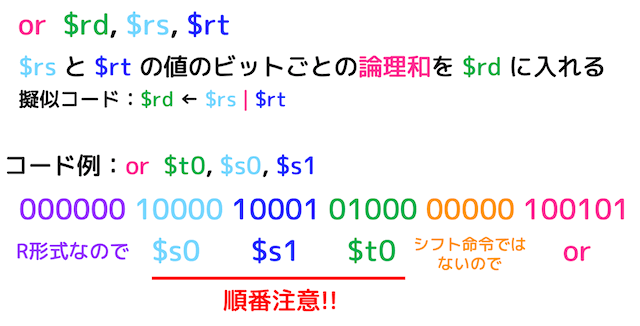
例えば上の命令の $s0 に 0x0600FFFF 、$s1 に 0x03FFFF08 が入っていれば、$t0 は 0x07FFFFFF となります。
★計算過程★
$t0 = $s0 | $s1 # $t0 は $ s0 と $s1 のビットごとの論理和 $s0 = 0b 0000 0110 0000 0000 1111 1111 1111 1111 $s1 = 0b 0000 0011 1111 1111 1111 1111 0000 1000 $t0 = 0b 0000 0111 1111 1111 1111 1111 1111 1111
各ビットごとに $s0 と $s1 のどちらかが1なら1、それ以外なら0が入ります。
(3) 排他的論理和演算 xor
xor は排他的論理和演算のR形式命令です。
xor $rd, $rs, $rt は、2つのレジスタ $rd, $rs のビットごとの排他的論理和を $rt に格納します。

例えば上の命令の $s0 に 0x0600FFFF 、$s1 に 0x03FFFF08 が入っていれば、$t0 は 0x05FF00F7 となります。
★計算過程★
$t0 = $s0 | $s1 # $t0 は $ s0 と $s1 のビットごとの排他的論理和 $s0 = 0b 0000 0110 0000 0000 1111 1111 1111 1111 $s1 = 0b 0000 0011 1111 1111 1111 1111 0000 1000 $t0 = 0b 0000 0101 1111 1111 0000 0000 1111 0111
各ビットごとに $s0 と $s1 のビットが異なっていれば1、それ以外なら0が入ります。
(4) 否定論理和演算 nor [not or]
nor $rd, $rs, $rt は、2つのレジスタ $rd, $rs のビットごとの否定論理和を $rt に格納します。R形式の命令です。

例えば上の命令の $s0 に 0x0600FFFF 、$s1 に 0x03FFFF08 が入っていれば、$t0 は 0xF8000000 となります。
★計算過程★
$t0 = $s0 | $s1 # $t0 は $ s0 と $s1 のビットごとの論理和 $s0 = 0b 0000 0110 0000 0000 1111 1111 1111 1111 $s1 = 0b 0000 0011 1111 1111 1111 1111 0000 1000 $t0 = 0b 1111 1000 0000 0000 0000 0000 0000 0000
各ビットごとに $s0 と $s1 のビットがともに0であれば1、それ以外なら0が入ります。
否定論理和norを用いた否定の表現
MIPSでは否定演算子 not (ビットの0, 1を入れ替える)操作が存在しません。
その代わり、nor 演算子とゼロレジスタ $zero を用いて否定演算子 not に相当する操作ができます。
nor演算子は、両方のビットが0のときだけ1になる演算子ですね。なので片方のビットを0に固定させると、もう片方のビットが1であれば0、0であれば1となりますね。
なので、片方のレジスタを $zero に固定させることで片方のビットがすべて0に固定されるので、もう1つのレジスタの各ビットが1のときに0、0のときに1にすることができ、not 演算子と同じ操作が実現できます。
否定を取りたいレジスタ(計算元)を $s0、結果(計算先)を $t0 とすると、
nor $t0, $s0, $zero
で否定の操作をすることができます。
★計算過程★
$t0 = $s0 | $zero # $t0 は $ s0 と $zero のビットごとの論理和 $s0 = 0b 0000 0110 0000 0000 1111 1111 1111 1111 $zero = 0b 0000 0000 0000 0000 0000 0000 0000 0000 $t0 = 0b 1111 1001 1111 1111 0000 0000 0000 0000
排他的論理和xorを用いた否定の表現
少し操作が多くなりますが(2操作)、排他的論理和を用いても否定を求めることができます。
すべてのビットが1のレジスタ $t1(10進数で-1)を作り、反転させたいもとのビット $s0 と排他的論理和を取ることで計算ができます。
addi $t1, $zero, -1 # t1 = -1 (0xFFFFFFFF) xor $t0, $s0, $t1
※ #以降はコメントを表します。メモなどを書けます。
xor演算子は、両方のビットが異なるときに1になる演算子ですね。なので、片方のビットを1に固定させると、もう片方のビットが1であれば0、0であれば1となりますね。
なので、片方のレジスタの値を 0xFFFFFFFF(10進数で-1) に固定させることで、もう1つのレジスタの各ビットが1のときに0、0のときに1にすることができ、not 演算子と同じ操作が実現できます。
7.命令紹介5 即値論理演算命令
- 論理積(and)
- 論理和(or)
- 排他的論理和(xor)
の3つに対して、即値論理演算が行えます。すべてI形式の命令となります。
(1) 即値論理積演算 andi [and immediate]
論理積命令の即値Verです。 命令はI形式です。
andi $t, $s, n は、レジスタ $s と即値 n のビットごとの論理積をとった結果を $t に格納する命令です。

例えば上の命令の $s0 に 0x00000AED (10進数で2797)、n が1なら、$t0 は 0x00000001 (10進数で1) となります。
★計算過程★
$t0 = $s0 & $n # $t0 は $ s0 と即値 n のビットごとの論理積 $s0 = 0b 0000 0000 0000 0000 0000 1010 1110 1101 n = 1 = 0b 0000 0000 0000 0000 0000 0000 0000 0001 $t0 = 0b 0000 0000 0000 0000 0000 0000 0000 0001
andi は、レジスタから下位の何ビットかを抽出する際によく使われます*6。
andi $t0, $s0, 1 # 1 = 0b 0000 …… 0001
下位1ビットを抽出(上位31ビットをマスク)
レジスタ s0 の値を10進数としたとき、2で割ったあまりが t0 に入る
andi $t0, $s0, 3 # 3 = 0b 0000 …… 0011
下位2ビットを抽出(上位30ビットをマスク)
レジスタ s0 の値を10進数としたとき、4で割ったあまりが t0 に入る
andi $t0, $s0, 7 # 7 = 0b 0000 …… 0111
下位3ビットを抽出(上位29ビットをマスク)
レジスタ s0 の値を10進数としたとき、8で割ったあまりが t0 に入る
andi $t0, $s0,15 # 15 = 0b 0000 …… 1111
下位4ビットを抽出(上位28ビットをマスク)
レジスタ s0 の値を10進数としたとき、16で割ったあまりが t0 に入る
(2) 即値論理和演算 ori [or immediate]
論理和命令の即値Verです。 命令はI形式です。
ori $t, $s, n は、レジスタ $s と即値 n のビットごとの論理和をとった結果を $t に格納する命令です。

例えば上の命令の $s0 に 0x00000005 、n が 0x0030 (10進数で48)なら、$t0 は 0x00000035 (10進数で53) となります。
$t0 = $s0 | $n # $t0 は $ s0 と即値 n のビットごとの論理和 $s0 = 0b 0000 0000 0000 0000 0000 0000 0000 0101 n = 0b 0000 0000 0000 0000 0000 0000 0011 0000 $t0 = 0b 0000 0000 0000 0000 0000 0000 0011 0101
ori の実用例として、数字をASCIIコードの文字に変換するときに使えます。
ASCIIコードだと、数字の文字列は 0x30 〜 0x39 が
(3) 即値排他的論理和演算 xori [xor immediate]
排他的論理和命令の即値Verです。 命令はI形式です。
xori $t, $s, n は、レジスタ $s と即値 n のビットごとの排他的論理和をとった結果を $t に格納する命令です。

例えば上の命令の $s0 に 0x00000005 、n が 0xFFFF (10進数で-1)なら、$t0 は 0x00000035 (10進数で53) となります。
xori の実用例として、数字をASCIIコードの文字に変換するときに使います。
7.命令紹介5 シフト命令
MIPSではシフト命令を行うことができます。
右シフトの場合、「符号つき整数」を扱う場合と「符号なし整数」を扱う場合で命令が異なるので注意しましょう。
もし、算術シフトと論理シフトの違いがわからない人は、こちらの記事で必ず確認してください!! 超重要です。
(1) 左シフト(論理・算術共通) sll [shift left logical]
sll は左シフトを行うR形式の命令です。
sll $rd, $rt, n は、レジスタ $rt を n ビット左にシフトさせたものをレジスタ $rd に格納します。
左シフトさせたときにあふれた桁は消え、空いた桁には0が補填されます。
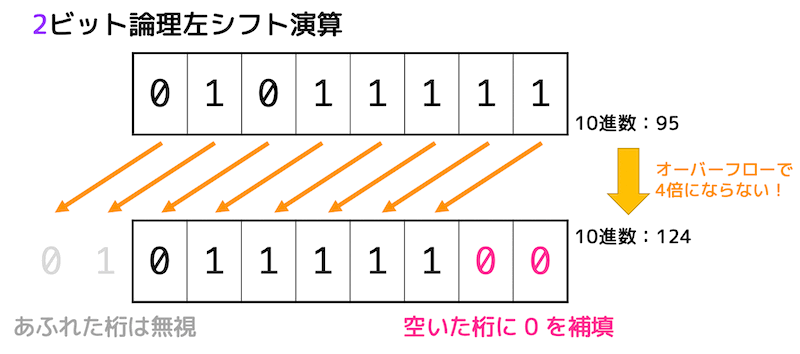
つまり、この命令は、$rt の値を \( 2^{n} \) 倍したものを $rd に格納する命令となります。

例えば上の命令の $s0 に 0b00…0001011 (10進数で11) 、n が 0b00010 (10進数で2)なら、$t0 は 0b00…0101100 (10進数で44) となります。
なお、左シフトの場合は「論理シフト」と「算術シフト」に関わらず処理内容が同じなので、算術左シフト専用の命令(sla 命令)は存在しません。
なので、論理・算術シフトに関わらず sll を使います。
つぎに紹介する右シフトでは、「論理シフト」用の命令と「算術シフト」の命令がわけられています。
(2) 論理右シフト srl [shift right logical]
sll は論理右シフトを行うR形式の命令です。
sll $rd, $rt, n は、レジスタ $rt を n ビット右にシフトさせたものをレジスタ $rd に格納します。
※なお、論理シフト右シフトさせたときにあふれた桁は消え、空いた桁には0が補填されます。
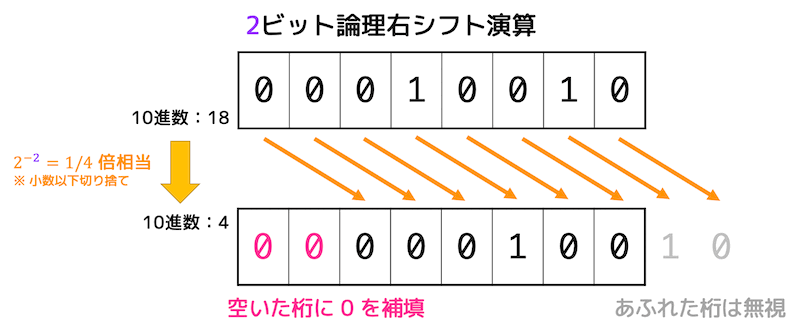
つまり、この命令は、$rt の値を \( 1/ 2^{n} \) 倍したものを $rd に格納する命令となります。

例えば上の命令の $s0 に 0b00…0110101 (10進数で53) 、n が 0b00001 (10進数で1)なら、$t0 は 0b00…0011010 (10進数で26) となります。
srl は、論理シフトの命令のため、負の数が考慮されていません。
負の数になりうるレジスタをシフトさせる場合は、srl ではなく、次に紹介する sra を使いましょう。
(3) 算術右シフト sra [shift right arithmetic]
sra は算術右シフトを行うR形式の命令です。
算術右シフトは、符号あり整数(負の数を考える整数)をシフトさせるときに使います。
sra $rd, $rt, n は、レジスタ $rt を n ビット右に算術シフトさせたものをレジスタ $rd に格納します。
※算術右シフトさせたときにあふれた桁は消え、空いた桁には元の符号ビット(つまり元の値の最上位ビット)が補填されます。
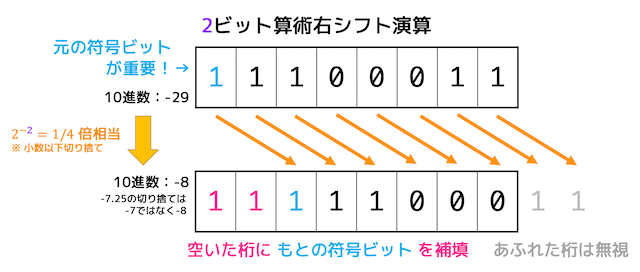
この命令は、$rt の値を \( 1/ 2^{n} \) 倍したものを $rd に格納する命令となります。
(このとき、小数点以下は切り捨てられます*7。)

例えば上の命令の $s0 に 0b11…1100011 (10進数で-29) 、n が 0b00001 (10進数で1)なら、$t0 は 0b11…1110001 (10進数で-15) となります。
右シフトでどっちを使うか迷った場合、よほど大きな数を使うとき以外は論理シフトの srl ではなく、算術シフトができる sra を使いましょう。
8.MIPSで書かれたコードの読み方
ある程度命令を紹介したので、実際に下のようなMIPSで書かれたコードの読み方について簡単にですが説明したいと思います。
LABEL1: add $t0, $s1, $s2 # $s1+$s2の計算 sub $t1, $s1, $s2 # $s1-$s2の計算 LABEL2: addi $s1, $s1, -1 sra $s2, $s2, 1 # $s2 /= 2;
(1) 処理される命令の順番
MIPSなどのアセンブリ言語では、原則上にある命令から1行ずつ順番に実行されます。
ここはC言語, Java, Pythonなどの高級言語と一緒ですね。
(2) アセンブリ言語における4つの欄
MIPSなどのアセンブリ言語では、ラベル欄、命令欄、オペランド欄、コメント欄の4つの欄でプログラムが構成されています。
先程のプログラムを4つの欄にわけると、下のようになります。

[1] ラベル欄(ふせん)
行ごとの操作内容に好きな名前をつけることができます。
付箋みたいなものです。
上の例の場合、1行目の命令に LABEL1、3行目の命令に LABEL2 という名前がつけられています。
名前をつけることで、(次回紹介する)分岐命令で「操作内容に付けた名前」を用いて分岐先を設定できるようになりますす。
ただし、3つの条件を満たす必要があります。
- 使える文字はアルファベット大文字と数字のみ
- 1文字目は必ずアルファベット大文字
- 8文字以内
[2] 命令欄
処理の内容を書く欄です。
加算 add、減算 sub、論理演算 and、即値を用いた演算、分岐など様々な命令があります。
[3] オペランド欄
処理の対象(オペランド)を書く欄です。
命令によってオペランドの数が異なります。
MIPSでは最大で3つのオペランドを指定され、順番に第1オペランド、第2オペランド、第3オペランドと呼びます。
例えば1行目の $t0, $s1, $s2 の第1オペランドは $t0、第2オペランドは $s1、第3オペランドは $s2 となります。
オペランドは、レジスタ以外にも定数を指定したり、メモリの番地を指定することができます。
このようなオペランドの指定の方法のことをアドレシングモードと呼びます。
(アドレシングモードについては次回の記事で説明します。)
[4] コメント欄
メモなどを書く欄です。(CやJavaのコメントと同じです)
コメント欄の内容は無視されるので、日本語などを書いてメモしてもOKです。
MIPSでは # 以降はコメントとなります。
9.さいごに
今回はMIPSの命令の前編について説明していきました。
後編は、
- データ転送の流れ
- データ転送命令
- 条件分岐命令
- アドレシングモード
などを説明しているのでもしよければご覧ください!
*1:コーティング規約で使うレジスタが決められています。
*2:念の為補足すると、プログラムで指定する際には10進数 or 16進数を使い、実際に機械語のコードになるときは2進数で格納されます。
*3:符号なし整数では負の数を使うことができない一方、符号ビットも値を入れるのに使えるため、符号あり(通常バージョン)整数に比べて2倍の値を表現することができます。
*4:掛け算は計算結果が大きくなることを想定して64ビットまで計算できるようになっています。
*5:割り算は計算結果が大きくならないので32ビットしか想定されていませんが、商とあまりをわけて格納することで2つのレジスタをうまく使っています。
*6:上位ビットを0にするため、「上位ビットのマスク」と呼ぶこともあります。
例:下位2ビットの抽出 → 上位30ビットのマスク
*7:負の数の切り捨てには注意してください。例えば、-7.25 の場合、-7ではなく-8となります。
(元の数より小さい数の中で最も大きい整数になると思ってください。)
注釈
| ↑1 | addiu の場合でも、n には2の補数表現が使われます。 |
|---|
関連広告・スポンサードリンク