スポンサードリンク
こんにちは、ももやまです。
今回は前回、前々回の2回で学んだMIPSアーキテクチャについて、10問の練習問題で理解できているかを確かめていきましょう。
MIPSアーキテクチャの基本・命令一覧をまとめた記事はこちら!
(自信がない人などはまずはこちらでお勉強しましょう!)
前編
後編
なお、こちらのMIPSアーキテクチャの仕様書を見ながら解いてもOKです。
(基本的にアセンブリの問題を解く場合はMIPSに限らず、それぞれの命令の仕様が書かれた仕様書は試験中でも見れます。)
スポンサードリンク
練習1
つぎのMIPSアーキテクチャの16進数で表された機械語をアセンブリに直したものはどれですか。
機械語内容:0x02329824
選択肢
1. and $s1, $s2, $s3 2. and $s3, $s1, $s2 3. or $s1, $s2, $s3 4. or $s3, $s1, $s2 5. andi $s1, $s2, 38948 6. andi $s2, $s1, 38948 7. ori $s1, $s2, 38948 8. ori $s2, $s1, 38948
スポンサードリンク
練習2
次のMIPSアーキテクチャの命令 lw $s2 -12($fp) について(1)〜(3)の問に答えなさい。
(1) 上の命令を16進数の機械語に直しなさい。
(2) 第1オペランド、第2オペランドのアドレシングモードとして正しいものを1〜5の中からそれぞれ選びなさい。
- レジスタアドレシング
- 即値アドレシング
- ベースアドレシング
- 疑似直接アドレシング
- PC相対アドレシング
(3) $fp の値が 0x0000000A のときのオペランド -12($fp) の実効アドレスを答えなさい。
スポンサードリンク
練習3
つぎの(1)〜(5)の命令を1行で書きなさい。ただし、乗算命令および除算命令を使ってはならない。
(1) レジスタ $s0 の値を1減らす命令
(2) レジスタ $s0 の値が偶数であれば0、奇数であれば1をレジスタ $t0 に入れる
(3) レジスタ $s0 の値を8倍する命令
(4) レジスタ $s0 の各ビットを反転させたものを $t0 に入れる命令
(5) レジスタ $s0 が0であればラベル DETONATE に飛ぶ
練習4
プロセッサにおけるパイプライン処理方式を説明したものはどれか。
[基本情報技術者平成21年春期 午前問11]ア:単一の命令を基に,複数のデータに対して複数のプロセッサが同期をとりながら並列にそれぞれのデータを処理する方式
イ:一つのプロセッサにおいて,単一の命令に対する実行時間をできるだけ短くする方式
ウ:一つのプロセッサにおいて,複数の命令を少しずつ段階をずらしながら同時実行する方式
エ:複数のプロセッサが,それぞれ独自の命令を基に複数のデータを処理する方式
練習5
つぎのC言語で書かれたプログラムの一部がある。
int x, y; y = x * 5;
上のプログラムと同じになるようにMIPSプログラムの空欄を埋められるものとして正しいものを1〜8の中から記号で答えなさい。
lw $s0, 0($fp) # xの値読み込み [ ] add $s1, $s1, $s0 sw $s1, 4($fp) # yの値書き込み
選択肢
1. addi $s1, $s0, 2 2. addi $s1, $s0, 3 3. andi $s1, $s0, 2 4. andi $s1, $s0, 3 5. sll $s1, $s0, 2 6. sll $s1, $s0, 3 7. sra $s1, $s0, 2 8. sra $s1, $s0, 3
練習6
つぎのC言語で書かれたプログラムの一部がある。
int main() { int i, k, s; s = 0; i = 1; while(i < k) { s += i; i += 1; } return 0; }
上のプログラムと同じになるようにMIPSプログラムの空欄1, 2を埋められるものとして正しいものを1〜8の中から記号で答えなさい。
addi $s0, $zero, 1 # i = 1; lw $s1, 4($fp) # kの値読み込み addi $s2, $zero, 0 # s = 0; L1: slt $t0, $s0, $s1 [ 1 ] nop [ 2 ] addi $s0, $s0, 2 j L1 L2: sw $s2, 8($fp) # sの値書き込み
選択肢
1. beq $s0, $zero, L2 2. beq $t0, $zero, L2 3. bne $s0, $zero, L2 4. bne $t0, $zero, L2 5. and $s0, $s0, $s2 6. and $s2, $s2, $s0 7. add $s0, $s0, $s2 8. add $s2, $s2, $s0
練習7
つぎのMIPSプログラムの $s0 の初期値を自分の誕生月、 $s1 の初期値を自分の誕生日としたとき、実行したときにメモリに格納される $s2 の値はなにかを示す値となります。さて、どんな値になるでしょうか?
addi $s0, $zero, 4 # 自分の誕生月(例:4月なら4) addi $s1, $zero, 7 # 自分の誕生日(例:7日なら7) addi $s2, $zero, 0 sll $s2, $s0, 2 addi $s2, $s2, 9 sll $t0, $s2, 4 add $t2, $s2, $t0 sll $t1, $s2, 3 add $s2, $t2, $t1 add $s2, $s2, $s1 addi $s2, $s2, -225 sw $s2, 0($fp) # $s2の値はどうなる…?
練習8
つぎのMIPSプログラムについて、(1)〜(3)の問いに答えなさい。
addi $s0, $zero, 7 addi $s1, $zero, 5 addi $s2, $zero, 0 L1: beq $s1, $zero, L2 # (1) add $s2, $s2, $s0 addi $s1, $s1, -1 j L1 L2: sw $s2, -8($fp) # (2) `$s2 = ??`
(1) 4行目のコード beq $s1, $zero, L2 を機械語に直し、16進数で答えなさい。
(2) 8行目の $s2, -8($fp) でメモリに格納される $s2 の値を10進数で答えなさい。
(3) このプログラムの初期値 $s0, $s1 とメモリに格納される $s2 にはどのような関係がありますか。
練習9
つぎのMIPSプログラムについて、(1)〜(4)の問いに答えなさい。
addi $s0, $zero, 14 addi $s1, $zero, 11 addi $s2, $zero, 0 L1: beq $s1, $zero, L3 # (1) andi $t0, $s1, 1 beq $t0, $zero, L2 add $s2, $s2, $s0 # (2) L2: sll $s0, $s0, 1 sra $s1, $s1, 1 j L1 L3: sw $s2, -12($fp)
(1) 4行目の命令 beq $s1, $zero, L3 は何回実行されますか?
(2) 7行目の命令 add $s2, $s2, $s0 は何回実行されますか?
(3) 11行目の $s2, -12($fp) でメモリに格納される $s2 の値を10進数で答えなさい。
(4) このプログラムの初期値 $s0, $s1 とメモリに格納される $s2 にはどのような関係がありますか。
練習10
つぎのMIPSプログラムについて、(1)〜(4)の問いに答えなさい。
addi $s0, $zero, 7 [ ] # (1) $s1に$s0の値をコピー addi $s2, $zero, 0 L1: beq $s1, $zero, L2 # (2) add $s2, $s2, $s1 addi $s1, $s1, -1 j L1 L2: sll $s2, $s2, 1 sub $s2, $s2, $s0 sw $s2, 8($fp)
(1) 2行目に「$s1 に $s0 の値をコピーする」命令を書きなさい
(2) 4行目の命令 beq $s1, $zero, L2 は何回実行されますか?
(3) 10行目の $s2, 8($fp) でメモリに格納される $s2 の値を10進数で答えなさい。
(4) このプログラムの初期値 $s0 とメモリに格納される $s2 にはどのような関係がありますか。
解答1
解答:2
2進数に直すと、
0b 000000 10001 10010 10011 00000 100100
となる。
上位6ビットが0のため、R形式の命令とわかる。
よって5〜8の選択肢が消える。
つぎにR形式なので、最後の下6桁で命令を把握する。
すると、100100 なので and 命令であることがわかる。
すると1, 2が残る。あとはオペランドの順番を考えればよい。
よって答えは2となる。
解答2
★解答★
(1) 0x8FD2FFF4
(2) 第1オペランド:1 第2オペランド:3
(3) 0xFFFFFFFE
(1)
lw $s2 -12($fp) を2進数のコードに直すと、
0b 100011 11110 10010 1111111111110100
となる。これを16進数にすると、0x8FD2FFF4 となる。
(2)
第1オペランドは $s2、第2オペランドは -12($fp) である。
よって第1オペランドがレジスタを指定するレジスタアドレシング、第2オペランドがレジスタと偏位から求められたアドレスを指定するベースアドレシングとなる。
(3)
0x0000000A(10進数で10) の値と -12(16進数:0xFFFFFFF4)を足せばよい。
厳密に計算するのであれば、0x0000000A と 0xFFFFFFF4 の足し算を行う。結果は 0xFFFFFFFE となり、実効アドレスは 0xFFFFFFFE となる。
あまりおすすめしないが、10進数で 10 - 12 をして16進数に戻しても一応正しい結果が得られる。
解答3
解答
(1) addi $s0, $s0, -1 (2) andi $t0 $s0 1 (3) sll $s0, $s0, 3 (4) nor $t0, $s0, $zero (5) beq $s0, $zero, DETONATE
(1)
即値を1減らす命令は addi の即値部分を -1 にすればよい。
よって addi $s0, $s0, -1 が答え。
(2)
偶数か奇数かは下位1ビットが0であれば偶数、1であれば奇数なので、下位1ビット以外をすべて and 命令で消せば良い。
よって、andi $t0 $s0 1 が答え
(3)
レジスタの値を8倍するためには、3ビット左シフトさせてレジスタの値を \( 2^{3} \) 倍すればよい。
よって答えは sll $s0, $s0, 3 となる。
(4)
ビットの値を判定させるためには、nor 命令と $zero を使う。
するともう片方のビットが1であれば0、0であれば1になるため題意を満たす。
よって答えは nor $t0, $s0, $zero となる。
(なお $s0 と $zero の順番は順不同)
(5)
0であればラベルにジャンプするので等号の分岐命令 beq とゼロレジスタ $zero を使う。
よって答えは beq $s0, $zero, DETONATE となる。
解答4
解答:ウ
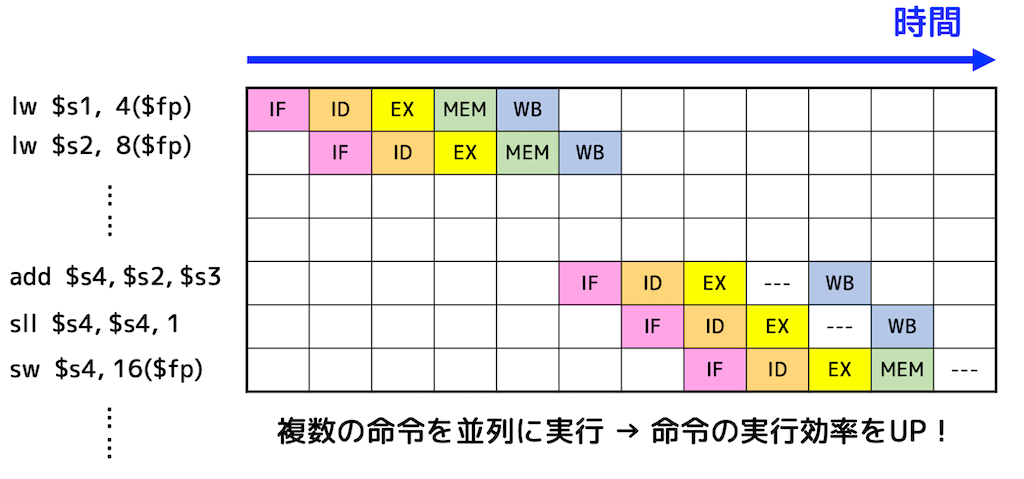
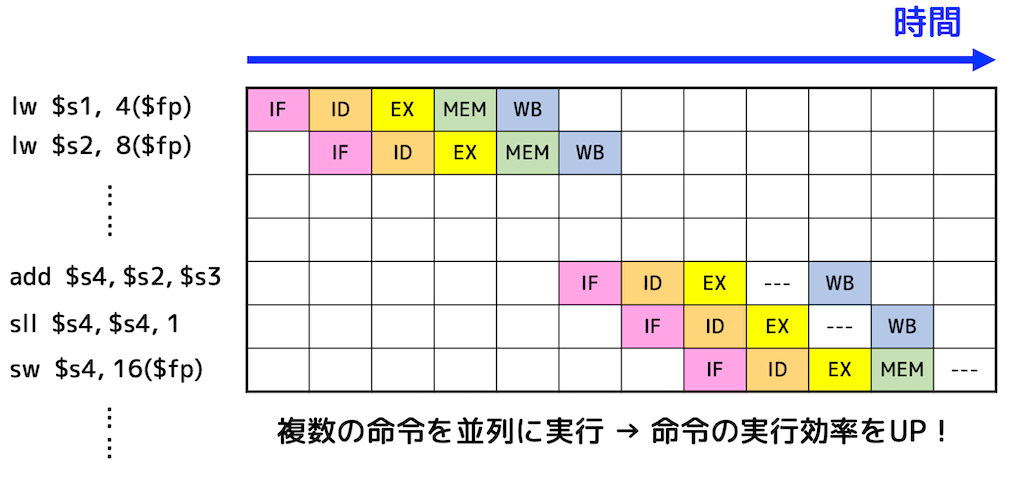
下の図のようにそれぞれの命令を少しずつずらし、並列的に処理することで処理効率を上げるのがパイプライン処理。
解答5
解答:5
lw $s0, 0($fp) # xの値読み込み [ ] # add $s1, $s1, $s0 # $s0 の値を sw $s1, 4($fp) # ここで $s1 = $s0 * 5 になっていればOK
3行目で $s0 の値を $s1 に足しているため、2行目で $s0 に4倍したものを足すことで、$s1 = $s0 * 4 + $s0 = $s0 * 5 にすることができます。
よってカッコには $s0 を4倍にしたものを $s1 に入れる処理である sll $s1, $s0, 2 となり、選択肢としては5が正解となります。
解答6
解答:[1] 2 [2] 8
プログラムの行数が多くなってきたときは下のようにメモをとっていくことをおすすめします。
(メモをとることで処理内容や分岐先がわかりやすくなります。)

i < k、つまり $s0 < $s2 かどうかの判定結果を使ってループを抜けるかどうかを判定してあげるような命令が入ります。(
$s0 < $s2 であれば $t0 には1、$s0 < $s2 でなければ0がはいります。)
さらに、ループを抜けるためには j L1 の下にある L2 にジャンプする必要があります。
よって、while の条件となる $s0 < $s2 を満たさなくなったら L2 にジャンプする beq $t0, $zero, L2 が答えとなり、選択肢は2となります。
($s0 < $s2 を満たさない時、slt 命令により $t0 には0が入る。)
while の条件内では、s += i と i += 1 の2つの処理が実行される必要があります。そのうちの i += 1 の処理は addi $s0, $s0, 1 の部分で行われているため、[2] の部分には s += i の処理をMIPSで表現したものがあてはまります。よって[2] には add $s2, $s2, $s0 となり、答えは8となります。
解答7
解答:$s2 に誕生月と誕生日が現れます。
例:4月7日 → 407、6月30日→ 630、10月24日 → 1024
実行結果をたどるような問題では、下のように変数の変化を1行ずつ書いていくことをつよくおすすめします。

また、$s2 と $s0, $s1 の関係性を考える際には、何個か適当な値で試してみることをおすすめします。
(6月30日、つまり $s0 = 6, $s1 = 30 のときは下のようになります。)

解答8
★解答★
(1) 0x12200003
(2) 35
(3) $s0 と $s1 を掛けたものが $s2 になっている。
(1)
命令を2進数に直すと、
0b 000100 10001 00000 0000000000000011
となるので、これを16進数に直せば良い。
(2)
下のように変数の変化の様子をメモしていきましょう。
ループにより、複数回同じ命令が繰り返される場合、「何回目のループ」かがわかるようにメモしましょう。

答えは 35 となります。
(3)
関係性を考えるために $s0, $s1 の値を少し変えてから変数の変化を調べていきます。

すると、「$s0 と $s1 を掛けたものが $s2 になっている」ことがわかってくるはずです!
なお、このプログラムで積(掛け算)を行う原理としては、\[
7 \times 5 = 7 + 7 + 7 + 7 + 7 \
6 \times 3 = 6 + 6 + 6
\]のように掛けられる回数だけ足し算をすることで積を求めています。
解答9
★解答★
(1) 6回
(2) 4回
(3) 154
(4) $s0 と $s1 を掛けたものが $s2 になる。
(練習8と同じ)
今までの練習と同じように変数の変化をメモしていきましょう。

メモを取ることで、(1)が6回、(2)が4回になることが可視化されます。
また、(3)が154になることもわかります。
(頭の中で回数を数えるのは絶対にやめましょう。ミスの原因となります。)
最後の(4)は、今までの練習と同じように $s0, $s1 の値の関係を調べるために $s0, $s1 の値を変えてから実験してみましょう。

すると、$s0 と $s1 の積が $s2 になることがわかります。
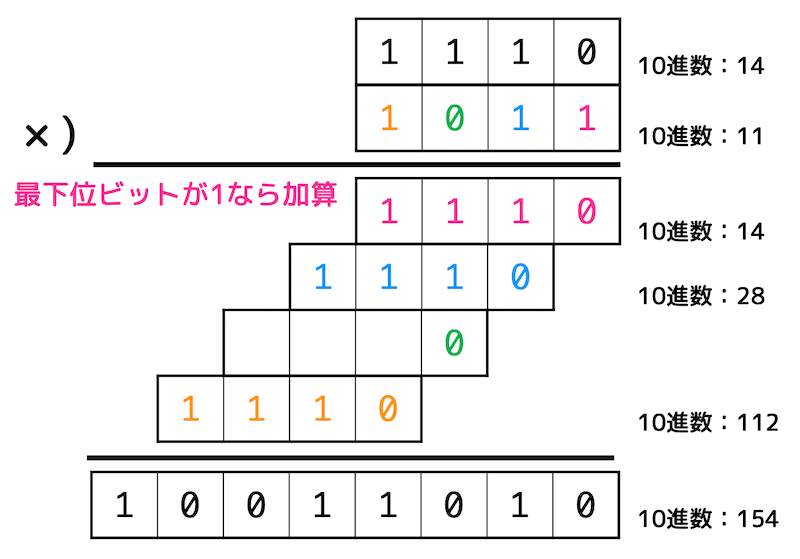
なお、このプログラムで積を求める原理は、2進数の掛け算を下のような筆算で求めるのと全く同じ原理となっています。
各ビットが1であるか判定するのに and 命令を使ったり、それぞれのビットで調べるためにシフト演算を利用しています。
解答10
(1) add $s1, $s0, $zero もしくは addi $s1, $s0, 0
(2) 8回
(3) 49
(4) $s0 を2乗したもの($s0 と $s0 の積)が $s2 になる。
(1)
レジスタの値をコピーする命令がないので、add 命令と $zero レジスタを用いて代用します。
add $s1, $s0, $zero addi $s1, $s0, 0
のどちらかで $s0 の値を $s1 にコピーすることができます。
(2), (3) はいつものように変数の動きをメモしておきましょう。
ここまで来ると慣れてくる(はず)です。

(4)も今までの練習のように他の $s0 の値で試せば法則がつかめるはずです!

ちなみに2乗を求める仕組みですが、まずは1から $s2 までの総和を求めます。 $s2 の数が n のときの総和は、\[
\frac{1}{2} n (n+1) = \frac{1}{2} n^{2} + \frac{1}{2} n
\]で求められます。
つぎに、先程求めた値を2倍し、$s2 を引くことで、\[
2 \times \left( \frac{1}{2} n^{2} + \frac{1}{2} n \right) - n = n^{2}
\]となり、2乗が求められます。
さいごに
今回は、前編と後編の2回にわけて説明したMIPSアーキテクチャについての演習問題と、その解き方についてまとめていきました。
仕様書だけを見て練習問題を解くことができればアセンブリの基礎は理解できと思ってOKです。
全23回にわたり、計算機システムの記事をご覧いただきありがとうございました!
なにかおかしい点などがあればコメントなどでお知らせください。
関連広告・スポンサードリンク