スポンサードリンク
こんにちは、ももやまです。
今日はUnixのファイルシステムであるブロック数の数え方、考え方についてまとめてみました。
目次
スポンサードリンク
1.ブロック数とは
Unixでは、データをブロック、つまり箱で表現します。
1つあたりのブロック、つまり1つの箱に入るサイズのことをブロックサイズといいます。
例えば1つあたりのブロックサイズ(箱のサイズ)を4[KB]としましょう。
このとき、15[KB]のファイルは4つのブロックが必要なことがわかります。
4つブロックを食うので、ファイルの保存には15[KB]ではなく16[KB]の領域が必要となります。
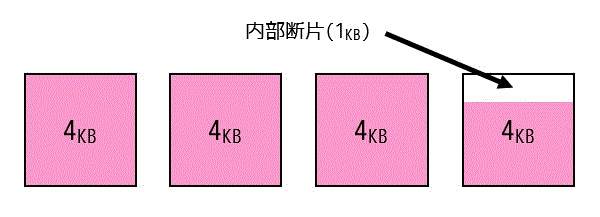
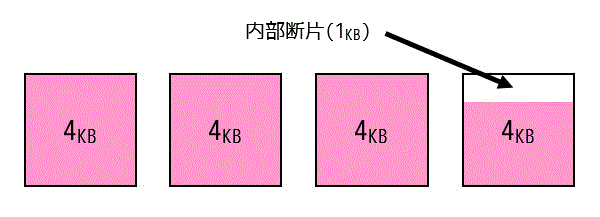
4つ目のブロックは箱のサイズが4[KB]なのに実際に入っているデータは3[KB]で、1[KB]分余っていますね。
このように箱に詰め込んで行ったときの余っている部分(今回は1[KB])を内部断片といいます。
Unixでは、ファイルを管理するためにiノード*1を用いて行います。
iノードのデータブロック用の配列は全部で15個あります。そのうちの12個を直接参照用、残りの3個をそれぞれ単一間接参照、2重間接参照、3重間接参照用として使います。

余談ですが、初代のプレステのゲームを遊んだ人はいますか?
初代のプレステのメモリーカードはUnixと同じようにブロックで管理されていました。ゲームの箱に「このゲームの保存には3ブロック領域を使います」など書いてあったはずです*2。
プレステのメモリーカードの場合、1ブロック8[KB]で15ブロック*3までデータを保存することができます。
ここからは、直接参照、間接参照について説明していきたいと思います。
スポンサードリンク
2.直接参照
直接参照できる配列は12個あるので、12ブロックまで直接参照することができます。
スポンサードリンク
3.間接参照
13ブロック以上は直接参照することができません。
そのため、13ブロック以上を保存する場合には、12ブロック分を直接保存し、残りの部分を間接ブロックを使ってデータブロックを間接参照する必要があります。
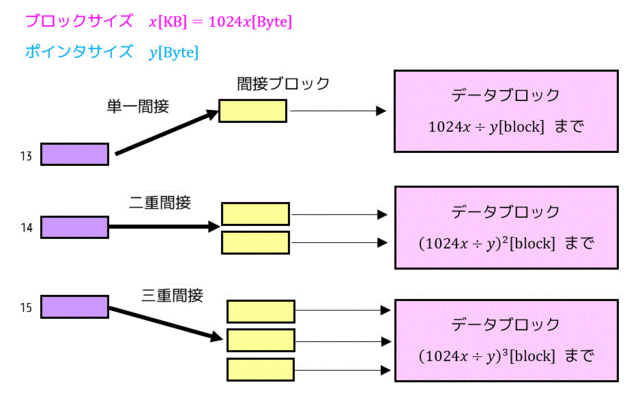
単一間接の場合
まずは、データブロックを1つ使う場合です。
単一間接で扱えるブロック数は、ブロックサイズを \( x \) [KB](\( 1024x \) [byte])、Iノードの大きさを \( y \) [byte] とすると、\( 1024x \div 4 \) ブロックまで扱うことができます*4。
例えば、ブロックサイズが 4[KB] (4096[byte]),iノードの大きさが32bit、つまり4[byte]の場合、単一間接で扱うことができるブロック数は \( 1024 \times 4\div 4 = 1024 \) ブロックまで扱うことができます。
二重間接の場合
単一間接の保存部分が一杯になった場合、残りの部分をデータブロックを2つ使った二重間接で保存を行います。
間接ブロックを2つ使うと、それぞれの間接ブロックで \( 1024x \div 4 \) 通りのブロックを管理できるので、二重間接で扱うことのできるブロック数は \( (1024x \div 4)^{2} \) 個までとなります。
例えば、ブロックサイズが 4KB,iノードの大きさが32bit、つまり4[byte]の場合、単一間接で扱うことができるブロック数は \( (1024 \times 4\div 4)^{2} = 2^{20} \) ブロック(4[GB])まで扱うことができます。
三重間接の場合
二重間接の保存部分が一杯になった場合、残りの部分をデータブロックを3つ使った三重間接で保存します。
間接ブロックを3つ使うと、それぞれの間接ブロックで \( 1024x \div 4 \) 通りのブロックを管理できるので、三重間接で扱うことのできるブロック数は \( (1024x \div 4)^{3} \) 個までとなります。
例えば、ブロックサイズが 4KB,iノードの大きさが32bit、つまり4[byte]の場合、単一間接で扱うことができるブロック数は \( (1024 \times 4\div 4)^{2} = 2^{30} \) ブロック(4[TB])まで扱うことができます。

4.ブロックサイズの大小における長所
(1) ブロックサイズが小さい場合
ブロックサイズが小さい場合の長所としては、内部断片が少なくなり、ディスク内で消費する容量を抑えることができます。
例えば、9[KB]のファイルを保存するとします。
ブロックサイズが8[KB/block]の場合、2ブロック必要で、残りの1ブロックの7[KB]は内部断片ですね。ディスク上では、合計16[KB]の領域を食います。
ここでブロックサイズを2[KB/block]にすると、5ブロック必要ですが、残りの1ブロックの内部断片は1[KB]ですね。ディスク上では、合計10[KB]の領域を食います。
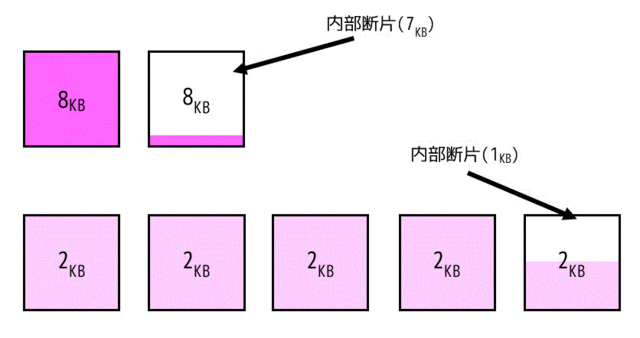
このように、ブロックサイズを小さくした場合は余分な部分(内部断片)が少なくなり、ディスク内の消費容量を抑えることができます。
(2)ブロックサイズが大きい場合
長所1 ファイルの領域が管理しやすい
ブロックサイズが大きくなると、ファイルを構成するブロック数は減りますよね。
例えば、40[KB]のファイルの場合、ブロックサイズが4[KB/block]の場合は10ブロックですが、8[KB/block]にすると5ブロックになりますね。
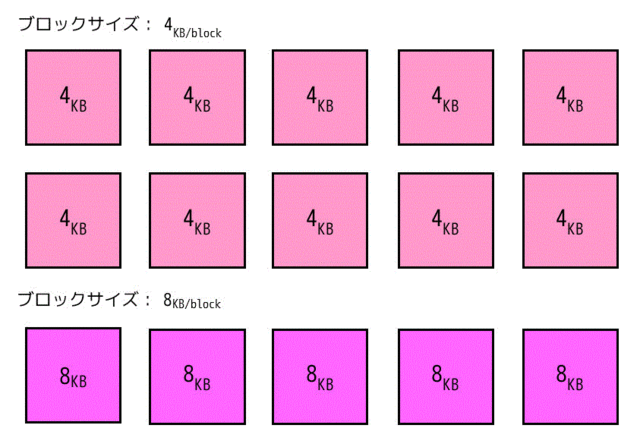
ブロック数が減るということは管理する箱の数が減るということなので、ファイルの領域は管理しやすくなります。
長所2 アクセス速度が上がる
ブロックサイズを増やすとブロック数が減るので、ディスクにアクセスする回数も減少します。ディスクのアクセス回数が減少すると、アクセスしなくなった回数分だけアクセス速度が向上します*5。
4.練習問題
では、1問練習問題を解いてみましょう。
問題
ブロックサイズが8[KB]、iノード(ブロックを指すポインタ)の大きさを4バイトとしたとき、以下の問いに答えなさい。
[1] SSD*6に1919[KB]のデータ naranara.png を格納したい。
(1) データブロックはいくつ必要ですか。
(2) データブロック中の内部断片の大きさを答えなさい。
(3) 間接ブロックはいくつ必要ですか。
(4) naranara.png を格納するために必要なSSD上の領域の大きさを答えなさい。
ponque.mp4 を格納したい。(1) 間接ブロックも含めて必要なデータブロックの数を答えなさい。
(2) 二重間接までを用いて保存できる最大のファイルの大きさは何GBですか。
(3) 三重間接までを用いて保存できる最大のファイルの大きさは何TBですか。
(ただし(2),(3)は小数以下四捨五入)
解説
ブロックサイズが 8[KB]、iノードサイズが4バイトなので、1つの間接ブロックには2048ブロック = \( 2^{11} \) ブロック分を指すことができる。
- 直接表せるのは12ブロック、つまり96[KB]まで。
- 単一間接で表せるのは \( 2^{11} \) ブロック、つまり 16 [MB] まで。
- 二重間接で表せるのは \( 2^{22} \) ブロック、 つまり 32 [GB] まで。
- 三重間接で表せるのは \( 2^{33} \) ブロック、つまり 64 [TB] まで。
(2) 240×8-1919=1より内部断片の大きさは1[KB]。
(3) 単一間接で保存が可能なので必要な間接ブロックの数は1つ。
(4) 240 + 1 = 241ブロックを食っているので必要な領域は 241×8 = 1928[KB] [2] (1)
必要なデータブロックの数は5,120ブロック。
直接保存できるのが12ブロック (残り5,108ブロック)
単一間接で保存できるのが2,048ブロック(残り3,060ブロック)
残りを二重間接で保存できる。
間接ブロックは、単一間接で1つ、二重間接で2つ必要なので合計3つ必要。
よって、必要なブロックの数は5,120 + 3 = 5,123ブロックとなる。
(2) 二重間接で表せるのは32[GB]まで。*7
(3) 三重間接で表せるのは64[TB]まで。*8
5.さいごに
今回はUnixにおけるデータブロックの概念、ブロック数の計算方法、保存されるデータが単一間接、二重間接、三重間接になるための条件についてまとめました。
*1:iノードに管理されている情報としては、ファイルの大きさ、ファイルの最終アクセス時間、ファイルを最後に閲覧した時間、ファイルの保護情報、所有者情報、グループ情報などがあります。
*2:たまに1つのゲームで15ブロックすべて保存領域を使うゲームとかあって大変だった……。
*3:プレステ用のメモリーカードはデータブロック用の配列15個すべてを保存領域に使っている。
*4:それぞれのiノードで \( y \) バイトを食う。これを \( x \) [KB]分まで保存できるから。
*5:本当は内部断片の大きさを考慮する必要があるが、ディスクのアクセス速度にデータの大きさはほどんど影響がないので無視しても構わない。
*6:簡単に言うとハードディスクの進化バージョン
*7:本来は単一間接、直接分も足す必要があるが、あまりにも小さいので無視した。
*8:本来は二重間接、単一間接、直接分も足す必要があるが、あまりにも小さいので無視した。
関連広告・スポンサードリンク