スポンサードリンク
こんにちは、ももやまです。
今回は、高校数学(数A)、数検、基本情報、SPIなどで出てくる「確率」分野の基礎を1時間でマスターできるような記事を作りました!
具体的には、確率で重要な
- 場合の数と確率
- 確率の基本的な4つの性質
- 確率における積の性質(独立性を利用)
- 確率における和の性質
- 条件付き確率
の5つについて、うさぎでも1時間でもマスターできるようわかりやすく書きました!
まだ確率を習ったことがない人も、確率を習った人もぜひご覧ください!
※もし、「場合の数(特に順列と組み合わせの違い)がわからないなぁ」と思う人は、下の記事で復習することを強くお勧めします。
目次
スポンサードリンク
1.場合の数と確率
事象A*1が起こる確率とは、「全体の場合の数」の中から「ある事象Aが起こる場合の数」がどれくらいあるかを表したものです。
具体例1 サイコロ
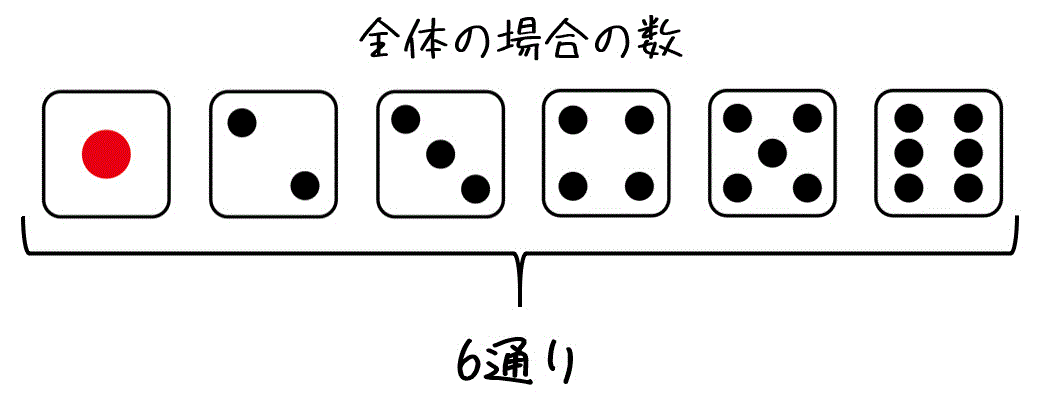
試しに、サイコロで4の目が出る確率を考えてみましょう。
まず、全体の場合の数は、サイコロの目1, 2, 3, 4, 5, 6に相当する6通りがあります。
この6通りの中から、「4が出る場合」は1通りありますね。
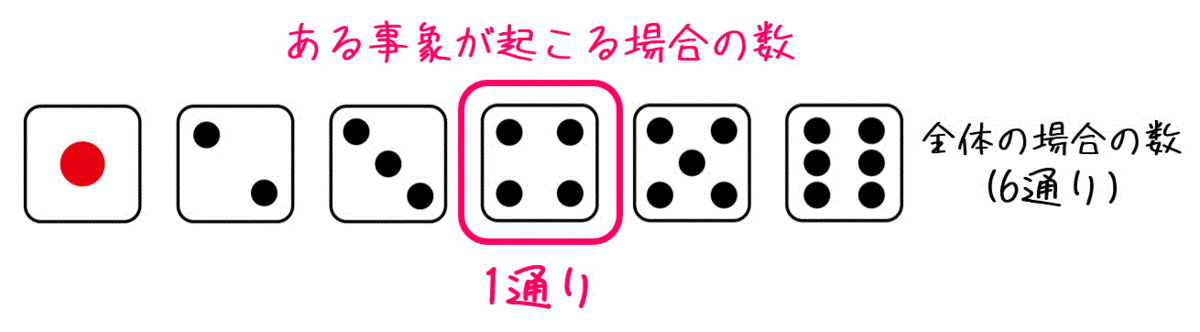
なので、確率は下のように計算することができます。

具体例2 玉の取り出し
もう1つ例を考えてみましょう。
「赤玉3個、白玉2個」入った箱の中から2つ玉を取り出したとき、「赤玉と白玉が1つずつ取り出せる確率」を求めてみましょう。

場合の数を数えるときの注意点
確率を求める際の「場合の数」の計算で1つだけ注意することがあります。
それは、同じ赤玉・白玉であっても区別して場合の数を計算する点です。
もし、区別せずに計算した場合、赤玉の数と白玉の数が何個だろうが確率が同じになってしまいます。
- 「赤玉3個・白玉2個」から赤玉・白玉を1つずつ取り出す確率
- 「赤玉100個・白玉2個」から赤玉・白玉を1つずつ取り出す確率
この2つの確率はどう考えても同じなわけありませんよね。
なので、確率を計算するときは、それぞれの赤玉・白玉を区別して場合の数を計算していく必要があります。
実際に計算していこう
では、実際に場合の数を求めて計算していきましょう。
まず、全体の確率、つまり5個の中から2個を取り出すパターンの数を考えましょう。
取り出すだけなので順序は関係ありませんね。なので、\[\begin{align*}
{}_5 \mathrm{C} _2 & = \frac{5 \cdot 4}{1 \cdot 2} \\ & = 10
\end{align*}\]で計算でき、10通り求められます。
次に、赤玉1個・白玉1個を取り出すパターン数を求めましょう。
パターン数は、「赤玉3個の中から1つ取り出すパターン数」それぞれに「白玉2個の中から1つ取り出すパターン数」だけ存在するので、\[\begin{align*}
{}_3 \mathrm{C} _1 \cdot {}_2 \mathrm{C} _1 = 6
\end{align*}\]で計算でき、6通りと求められます。
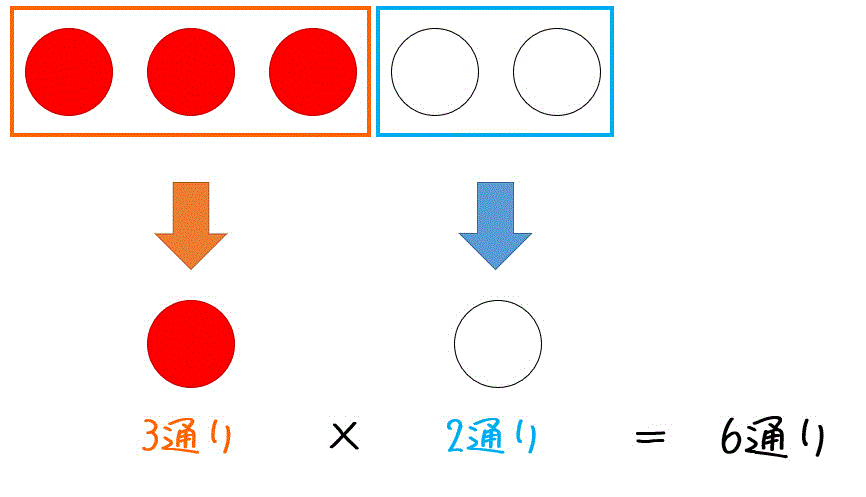
よって、確率は

と求められます。
補足:確率を表す記号 P(A), P(B)
問題によっては、事象にA, Bのような名前が付けられ、それらの確率を \( P(A) \), \( P(B) \) のように表すこともあります。
スポンサードリンク
2.確率の基本的な4つの性質
基本的な4つの性質を見ていきましょう。
「どれも当たり前じゃん」と思うかもしれませんが…
1つ目 絶対に起こる事象の確率は1
絶対に起こる事象の確率は1(100%)です。当たり前ですね。
例えば、1つのサイコロを振ったときに1, 2, 3, 4, 5, 6のどれかが出る確率は1ですね。
2つ目 絶対に起こらない事象の確率は0
絶対に起こらない事象の確率は0(0%)です。これも当たり前。
例えば、1つのサイコロを振ったときに7の目が出る確率は0です。
(サイコロに7の目はない)
3つ目 確率は必ず0以上1以下になる
確率は、必ず0以上1以下(0%以上100%以下)の値を取ります。
当たりくじがある確率が-0.2 (-20%) とか 150% (1.5) とか言われてもわけがわかりませんよね。
4つ目 ある事象が起こらない確率は「1 - 起こる確率」
ある事象が起こらない確率というのは、「全体(1)」から、「事象が起こる確率」を引くことで求めることができます。
例えば、サイコロで6の目が出る確率は1/6ですね*2。
なので、6の目が出ない確率は下のように求めることができます。
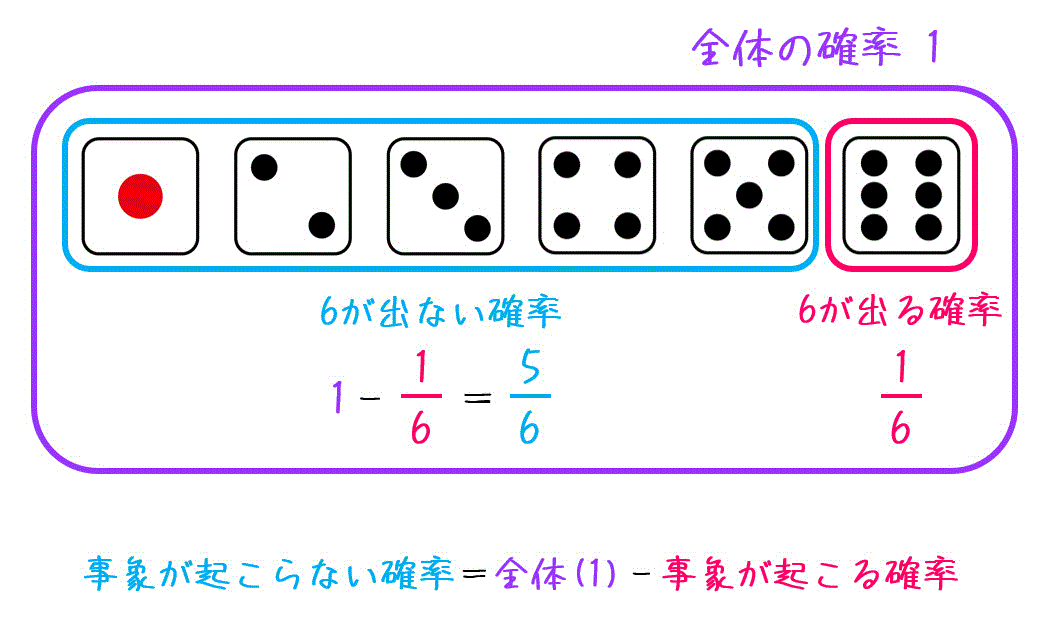
この公式は、「サイコロを2つ投げたとき、少なくとも1つは6の目が出る確率」のような「少なくとも1つは~」のような問題で使います。
この問題の場合、「全体」から「1つも6の目が出ない確率」を引くことで求めることができます*3。
スポンサードリンク
3.確率における積の法則
ある2つの事象A, Bがあるとします。
それぞれの事象A, Bが互いの確率に全く影響しない(独立な)とき、2つの事象A, Bが両方起こる確率 \( P( A \cap B ) \) は、
- 事象Aが起こる確率 \( P( A) \)
- 事象Bが起こる確率 \( P( B) \)
の積で求めることができます。
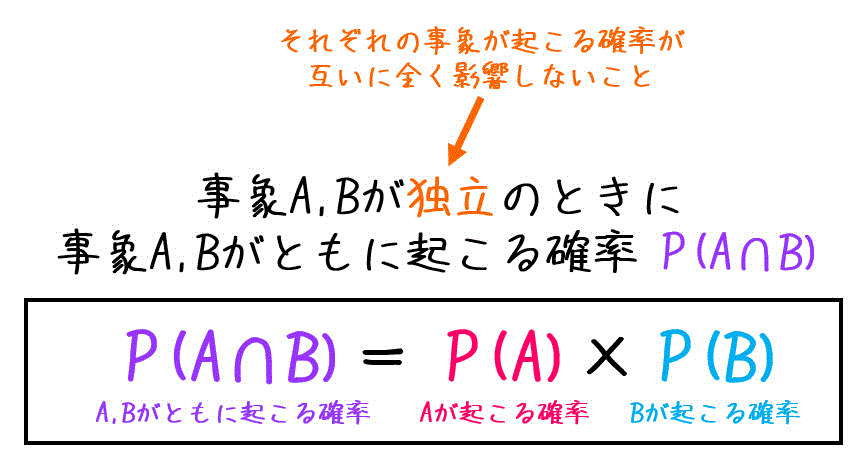
(集合記号を用いた表記にも慣れておきましょう。)
例えば2つのサイコロA, Bを同時に振ったときに「サイコロAが偶数」かつ「サイコロBが奇数」になることを考えましょう。
まず、「サイコロAが奇数」、「サイコロBが偶数」になる確率は下のように求めることができますね。
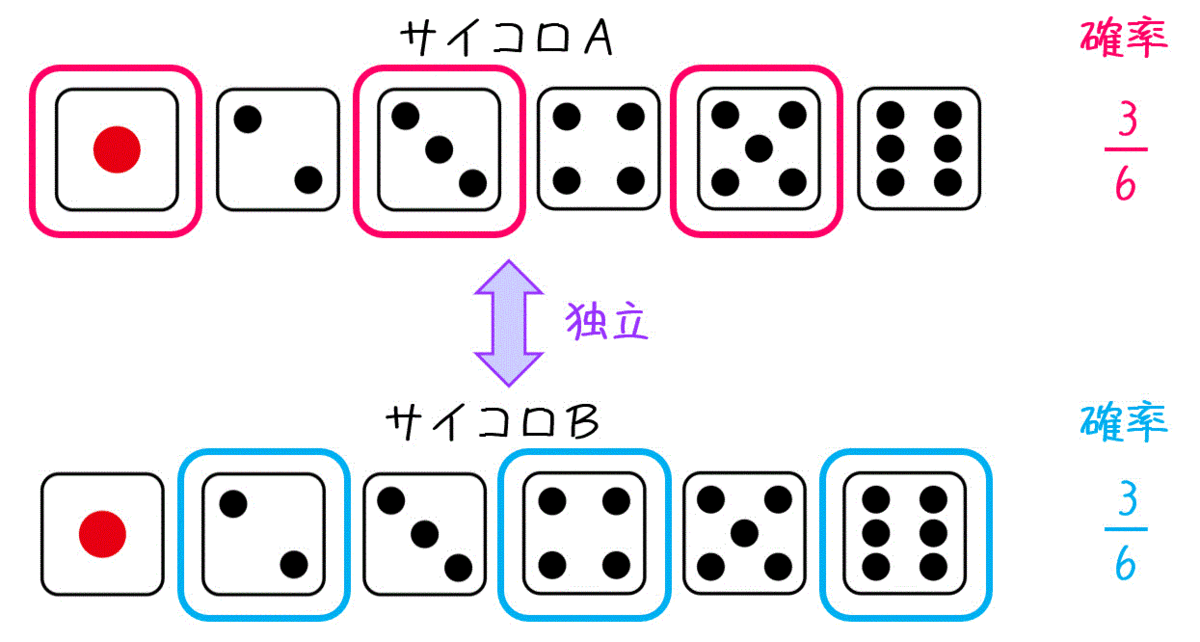
ここで、サイコロAの出目が何だろうがサイコロBの出目に一切関係はありませんね。
(もちろんサイコロBの出目が何だろうがサイコロAの出目に一切関係はない。)
なので、「サイコロAが奇数」になる事象と「サイコロBが偶数」になる事象は独立といえます。
よって、「サイコロAが奇数」かつ「サイコロBが偶数」になる確率 \( P( A \cap B ) \) は、\[\begin{align*}
P( A \cap B ) & = \frac{3}{6} \times \frac{3}{6} \\ & = \frac{9}{36} \\ & = \frac{1}{4}
\end{align*}\]と求めることができます。
念のため、実際に36通りパターンを書いて確率を計算してみましょう。
36通り中、事象Aと事象Bの両方が起こるのは9通りとなるので、\[\begin{align*}
P( A \cap B ) & = \frac{9}{36} \\ & = \frac{1}{4}
\end{align*}\]と同じ答えになりますね!
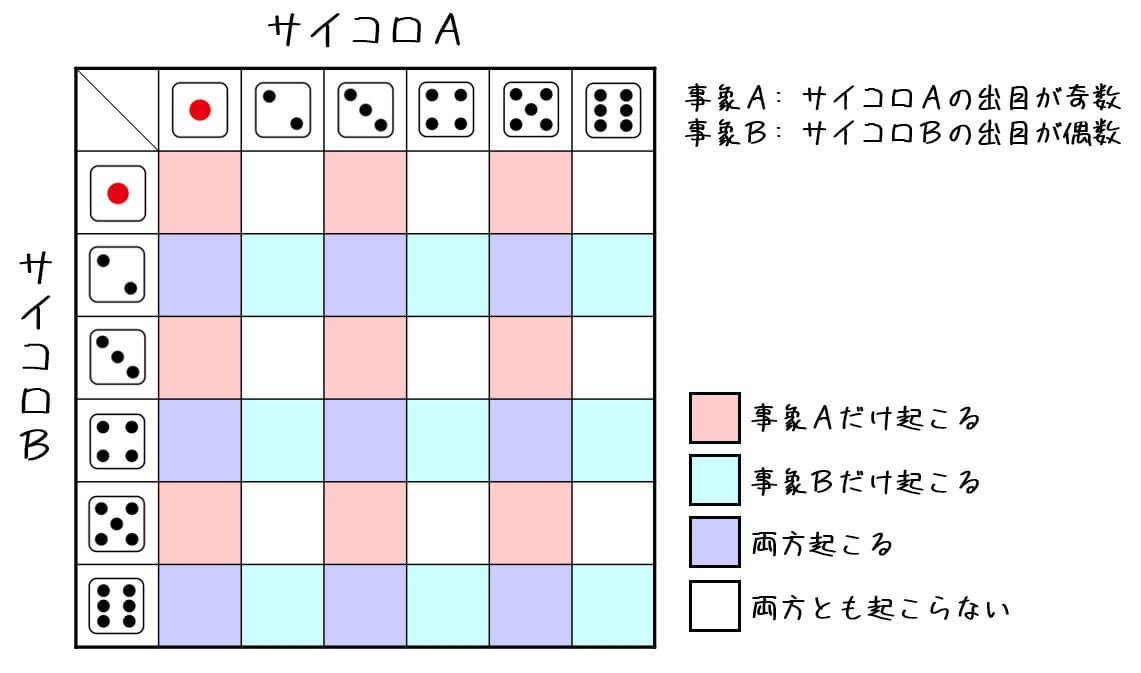
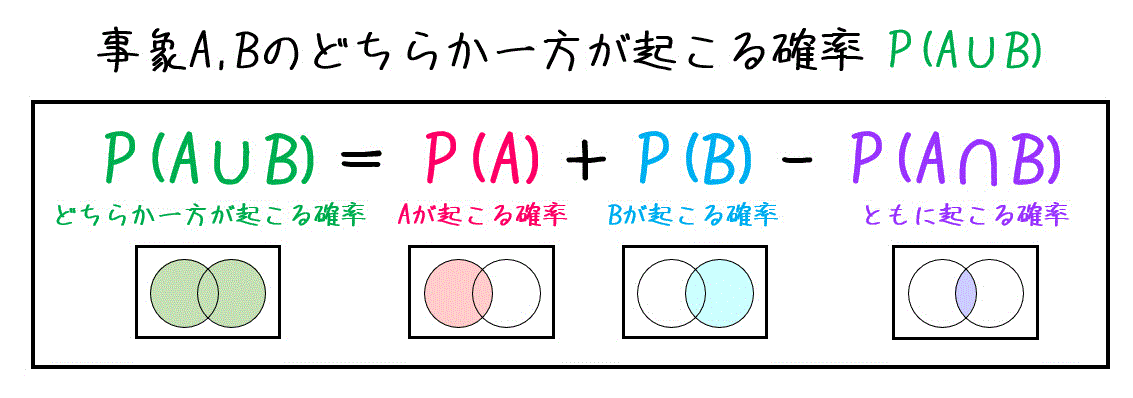
4.確率における和の法則
ある2つの事象A, Bがあるとします。
このとき、2つの事象A, Bが両方起こる確率 \( P( A \cup B ) \) 「事象Aが起こる確率 \( P( A) \) と事象Bが起こる確率 \( P( B) \) の和」から「両方の事象が起こる確率 \( P( A \cap B) \) を引いたものとなります。
例えば1つのサイコロ振ったときに出た目が「2の倍数」もしくは「3の倍数」になる確率を考えましょう。
まずは、サイコロを振ったときに出た目が「2の倍数」か「3の倍数」になる確率を求めます。

しかし、上の図でみればわかる通り6の目を2回カウントしていますね。
なので、ダブルカウントしている「2の倍数」かつ「3の倍数」の部分を引いてあげましょう。
2の倍数かつ3の倍数(つまり6の倍数)になる確率は、下のように求めることができます。

よって、出た目が「2の倍数」もしくは「3の倍数」になる確率は\[\begin{align*}
P( A \cup B ) & = \frac{3}{6} + \frac{2}{6} - \frac{1}{6} \\ & = \frac{4}{6} \\ & = \frac{2}{3}
\end{align*}\]と求めることができます。
2つの事象が同時に起こらないとき
ある事象A, Bが同時に起こりえないとき、つまり \( P( A \cap B ) = 0 \) のときは、どちらか一方(あるいは両方)が求まる確率を以下のように求めることができます。

例えば、サイコロを振ったときに「1」もしくは「5」が出る確率を求めてみましょう。
1、5が出る確率はそれぞれ \( \frac{1}{6} \) と求まります。
ここで、1個のサイコロを振ったとき、1の目と5の目が同時に出ることなんてありえませんよね。
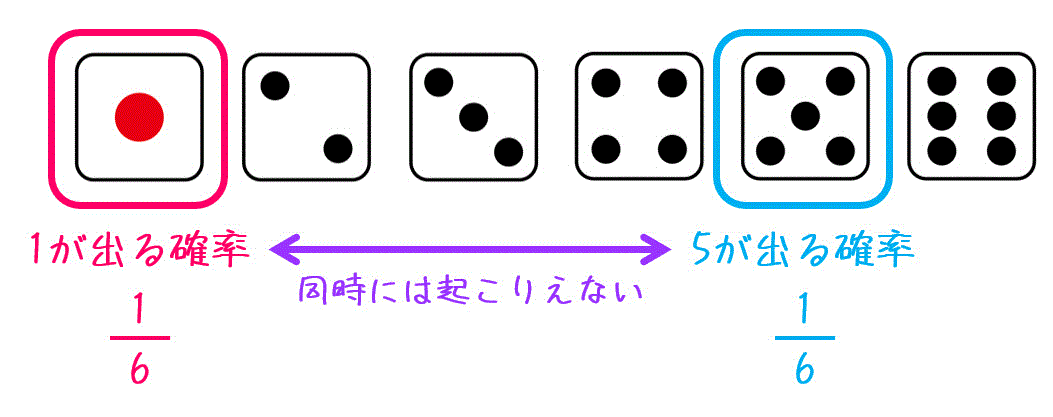
なので、1の目と5の目のどちらかが出る確率は\[
\frac{1}{6} + \frac{1}{6} = \frac{1}{3}
\]と求めることができます。
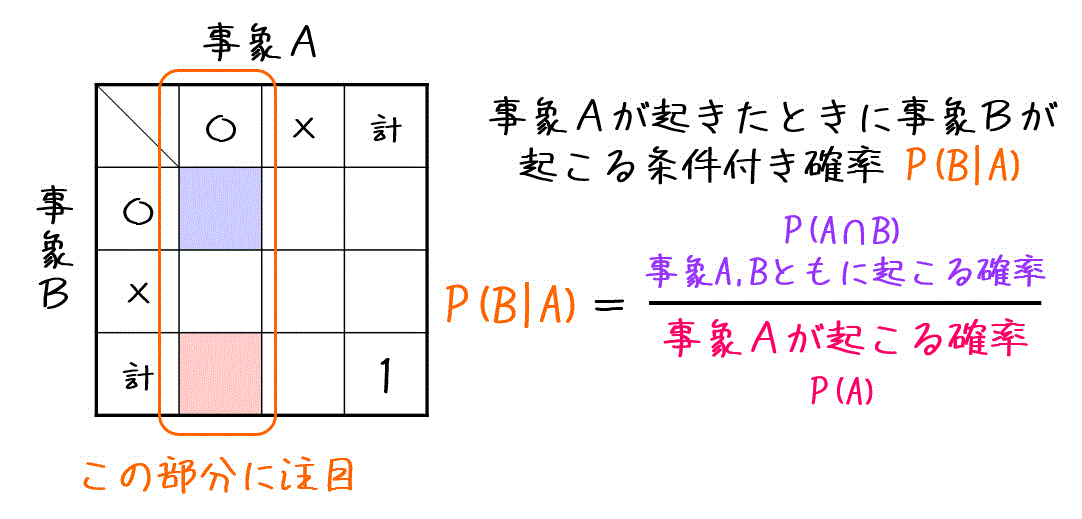
5.条件付き確率
最後は条件付き確率です。
条件付き確率とは、とある事象Aが起こるとき(起こることが分かったとき)、目的の事象Bが起こる確率のことを表し、\( P( B | A) \) と表されます。
つまり、ある事象Aが起こると分かったとき、どれくらいの確率で目的の事象Bが発生するかを示したもの条件付き確率なのです。
(記号表記の順番に注意*4。 P( 求めたい事象の条件付き確率 | 分かったと仮定する事象 ) と頭にいれておきましょう。)
条件付き確率は表で考えよう!
条件付き確率を求める際には、下のような表を用いて考えていくことを強くおすすめします。
(事象A, Bの起こる確率・起こらない確率(場合の数)を表に記述していく。)
例えば、事象Aが起きたときの事象Bが起こる条件付き確率 \( P( B | A) \) は、下の式で求めることができます。
表を書くことにより、どこの確率(場合の数)を使って求めることができるかが一目瞭然となるのでおススメです。
(※公式部分の確率は、場合の数と考えて\[
\frac{ \color{purple}{事象A, Bともに起こる場合の数}}{\color{magenta}{事象Aが起こる場合の数}}
\]と考えてもOKです。むしろこっちのほうが分数計算が減るので間違えにくいと思います。)
同じように、事象Bが起きたときの事象Aが起こる条件付き確率 \( P( A | B) \) は、下の式で求めることができます。
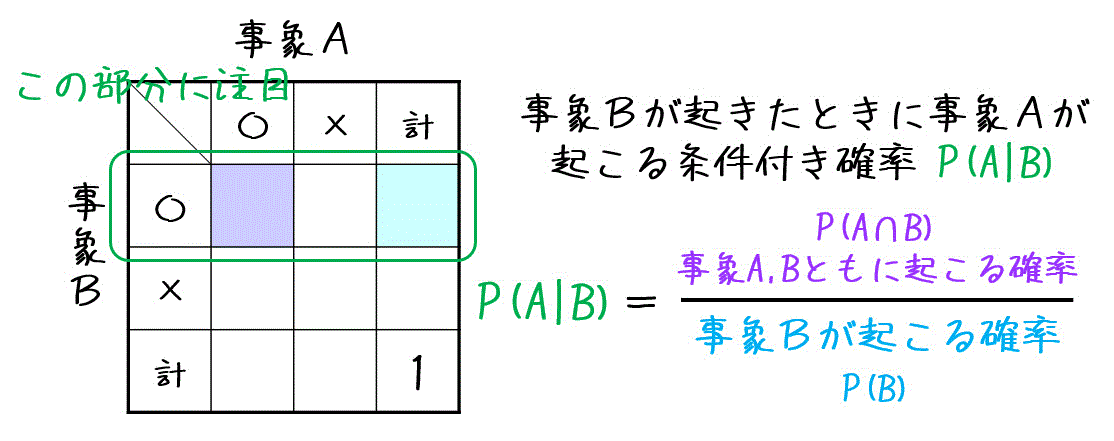
(※公式部分の確率は、場合の数と考えて\[
\frac{ \color{purple}{事象A, Bともに起こる場合の数}}{\color{skyblue}{事象Bが起こる場合の数}}
\]と考えてもOKです。むしろこっちのほうが分数計算が減るので間違えにくいと思います。)
条件付き確率の例題
具体的に1問条件付き確率に関する例題を解いてみましょう。
今まで出てきた確率法則の復習もかねています。
[解説]
(1)
出た目の和が9以上になるパターンをすべて書いていくのがおすすめ。
和が9:「3-6, 4-5, 5-4, 6-3」の4通り
和が10:「4-6, 5-5, 6-4」の3通り
和が11:「5-6, 6-5」の2通り
和が12:「6-6」の1通り
なので、「出た目が9以上になる」確率 \( P(A) \) は\[
P(A) = \frac{10}{36} = \frac{5}{18}
\]となる。
また、サイコロBの出目が5以上(5か6)になる確率 \( P(B) \) は\[
P(B) = \frac{2}{6} = \frac{1}{3}
\]となる。
(2)
サイコロの出た目の和は、サイコロBの出た目に依存していないとは言えない。
(サイコロBの出目を変えると、出た目の和は変わってしまう。)
そのため、「出た目の和が9以上になる」と「サイコロBの出目が5以上になる」の事象は独立とはいえず、積の公式が使えない。
なので、出た目の和が9以上になるパターンの中から、出目が5となるパターンを数える。
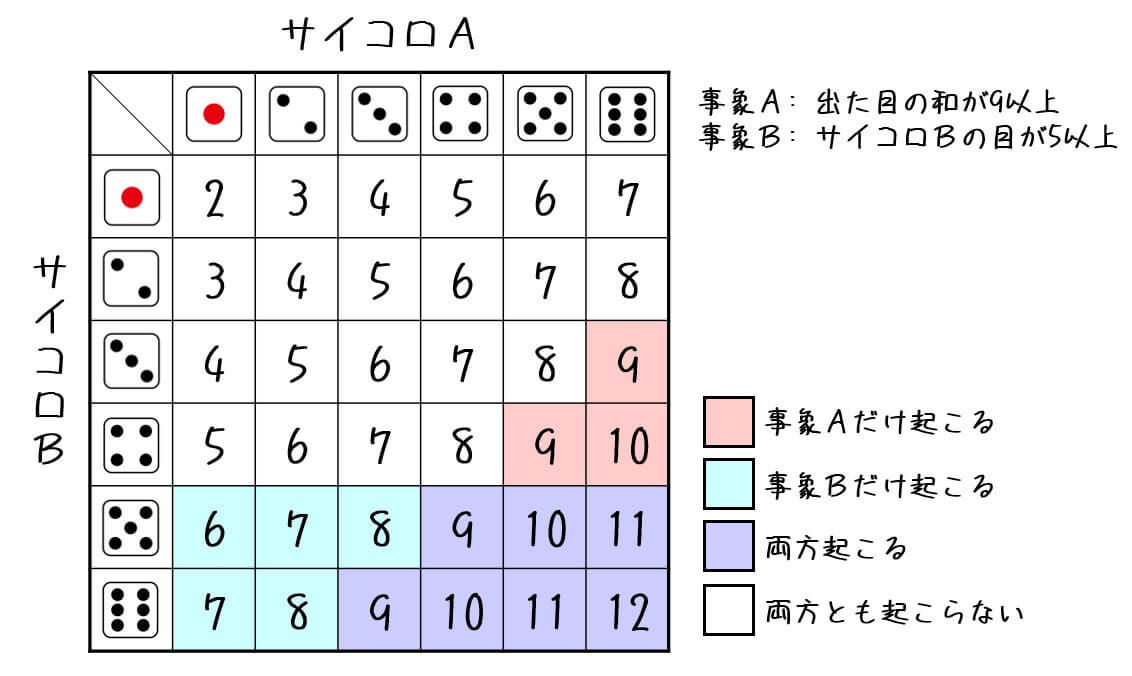
すると、7パターンあることがわかるので確率 \( P(A \cap B) \) は\[
P(A \cap B) = \frac{7}{36}
\]となる。
(3)
(2)で書いた36通りから、それぞれの事象A, Bが発生する場合の数(確率でももちろんOK)を表にしてみましょう。
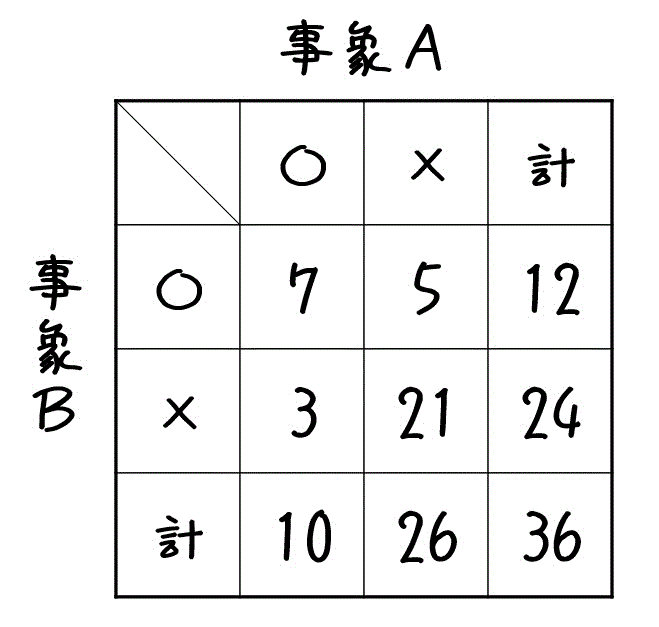
表より、事象A(和が9以上)が起きたときの事象B(サイコロBの出目が5以上)が起こる条件付き確率 \( P( B | A ) \) は、以下のように求めることができます。
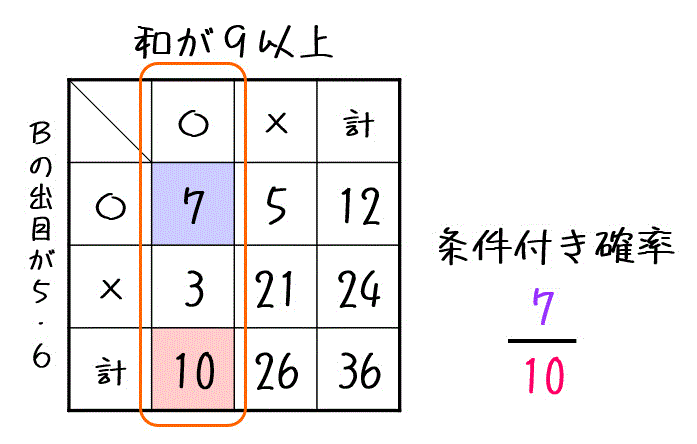
もちろん、\[\begin{align*}
P( B | A ) & = \frac{ P( A \cap B ) }{ P(A) }
\\ & = \frac{ \frac{7}{36} }{ \frac{5}{18} }
\\ & = \frac{7}{10}
\end{align*}\]と確率から求めてもOKです。
同じように事象B(サイコロBの出目が5以上)が起きたときの事象A(和が9以上)が起きるの条件付き確率 \( P( A | B ) \) は、以下のように求めることができます。
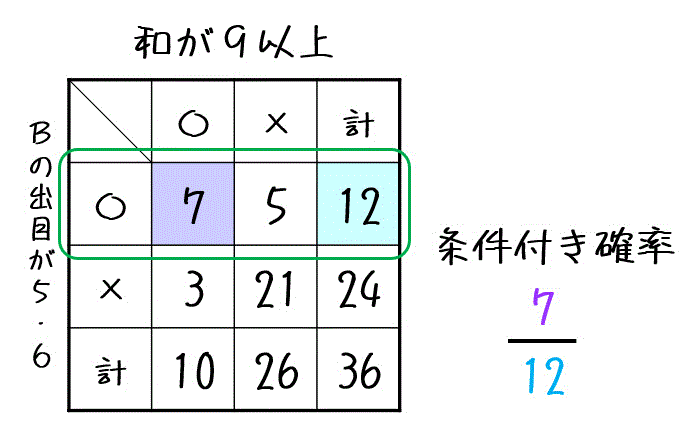
もちろん、\[\begin{align*}
P( A | B ) & = \frac{ P( A \cap B ) }{ P(B) }
\\ & = \frac{ \frac{7}{36} }{ \frac{1}{3} }
\\ & = \frac{7}{12}
\end{align*}\]と確率から求めてもOKです。
おまけ:ベイズの定理
高校数学の範囲を外れてしまいますが、条件付き確率を応用したものに「ベイズの定理」というものがあります。
数学が好きで興味がある人 or 大学で「ベイズの定理」を習った人はもしよかったらご覧ください。
6.練習問題
では、重要な5つの法則を復習するために練習問題にチャレンジしてみましょう。
練習1
5本のくじがあり、そのうち2本が当たりである。
くじを同時に2本引いたとき、2本とも当たりとなる確率はいくらか。
[基本情報技術者平成20年秋期 午前問8]練習2
コインを4回投げたときに、少なくとも表が1回出る確率はいくらか。
練習3
「赤玉4個、白玉2個」入った箱の中から同時に玉を3つ取り出す。
このとき、赤玉が2個以上含まれる確率を求めなさい。
練習4
袋の中に重心の偏った2つのサイコロA、Bが入っている。Aは1の目が3/10の確率で、Bは1の目が3/5の確率が出る。
袋の中からサイコロを一つ取り出し、振ってみたら1の目が出たという条件の下で、取り出したサイコロがAである条件付き確率は幾らか。
[ソフトウェア開発技術者平成18年秋期 午前問2]
7.練習問題の答え
解答1
全体の場合の数(5本から2本引いたときのパターン数)は\[\begin{align*}
{}_5 \mathrm{C} _2 & = \frac{5 \cdot 4}{1 \cdot 2} \\ & = 10
\end{align*}\]と求められる。
(引く順番は関係ないので順列ではない)
また、2本中2本あたりを引くパターンは\[\begin{align*}
{}_2 \mathrm{C} _2 & = 1
\end{align*}\]となる。
よって、2本とも当たりになる確率は\[\begin{align*}
\frac{{}_2 \mathrm{C} _2 }{{}_5 \mathrm{C} _2 } = \frac{1}{10}
\end{align*}\]となる。
解答2
「少なくとも表が1回出る確率」は、「全体」から表が1回も出ない確率を引けばよい。
(少なくとも~という問題の多くは「全体」から引いたほうが答えが圧倒的に早く出せる)
4回の試行で表が出る確率は、他の試行に一切影響がない(独立)なので、\[
\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{16}
\]と求められる。
よって、「少なくとも表が1回出る確率」は、\[
1 - \frac{1}{16} = \frac{15}{16}
\]となる。
解答3
6個中3個とりだすパターン(全体)は、\[\begin{align*}
{}_6 \mathrm{C} _3 & = \frac{6 \cdot 5 \cdot 4}{1 \cdot 2 \cdot 3}
\\ & = 20
\end{align*}\]となり、20通りと求められる。
ここで、3個中が赤玉2個以上含まれる確率は、
- 赤玉が2つ含まれる確率
- 赤玉が3つ含まれる確率
の2つの和で計算できる。
(「赤玉2つ含まれること」と「赤玉3つ含まれることは」は同時には起こらないため)
[赤玉が2つ含まれる確率]
赤玉が2つ含まれる(白玉が1つとなる)パターン数は\[\begin{align*}
{}_4 \mathrm{C} _2 \cdot {}_2 \mathrm{C} _1 & = 6 \cdot 2
\\ & = 12
\end{align*}\]となり、12通りとなる。
よって、赤玉が2つ含まれる確率は\[
\frac{12}{20} = \frac{3}{5}
\]となる。
[赤玉が3つ含まれる確率]
赤玉が3つ含まれるパターン数は\[\begin{align*}
{}_4 \mathrm{C} _3 = \frac{ 4 \cdot 3 \cdot 2}{ 1 \cdot 2 \cdot 3}
\end{align*}\]となり、4通りとなる。
よって、赤玉が3つ含まれる確率は\[
\frac{4}{20} = \frac{1}{5}
\]となる。
よって、赤玉が2個以上出る確率は\[
\frac{3}{5} + \frac{1}{5} = \frac{4}{5}
\]と求められる。
(12通りと4通りを足して、16通り/20通りから4/5を出してもOKです。)
解答4
問題文をもう少し詳しく書くと、
- 袋からAを選んだ条件の下で1の目が出る確率は 3/10
- 袋からBを選んだ条件の下で1の目が出る確率は 3/5
となる。
また、2つの袋のうち、Aを選ぶ確率・Bを選ぶ確率はそれぞれ1/2である。
ここで、「袋Aを選び」かつ「1の目」が出る確率は\[
\frac{1}{2} \times \frac{3}{10} = \frac{3}{20}
\]となる。
同様に「袋Bを選び」かつ「1の目」が出る確率は\[
\frac{1}{2} \times \frac{3}{5} = \frac{3}{10}
\]となる。
よって、1の目が出る確率は\[
\frac{3}{20} + \frac{3}{10} = \frac{9}{20}
\]と計算できる。
(下のように「Aを取り出す事象」と「1の目が出る」事象に注目しながら表を埋めながら計算していくことをおすすめします。)
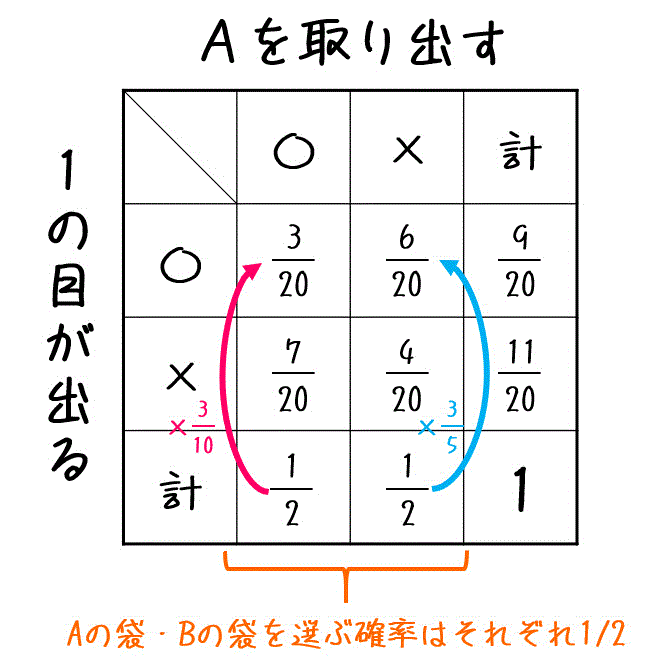
よって、1の目が出たという条件の下で、取り出したサイコロがAである条件付き確率は以下のように求めることができる。
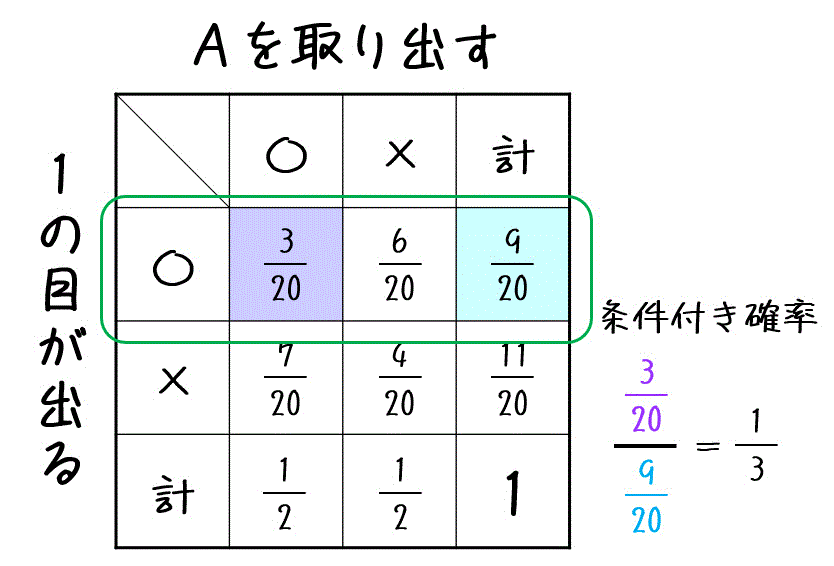
よって、答えは\[
\frac{1}{3}
\]となる。
8.さいごに
今回は、数Aの「確率」で出てくる中で特に重要な
- 場合の数と確率
- 確率の基本的な4つの性質
- 確率における積の性質(独立性を利用)
- 確率における和の性質
- 条件付き確率
の5つの法則・公式について説明していきました。
確率で使う性質、法則は基本的に上の5つのみなので、あとは練習問題を解くなどで慣れていきましょう。
*1:事象というと少し難しい言葉に聞こえますが「ある出来事が~」くらいに思っていただけたらOKです。
*2:出目が6通りある中で、6の目が出る場合の数は1通りなので。
*3:後ろのほうに出てくる「積の法則」を使うと、1つも6の目が出ない確率(2回とも1, 2, 3, 4, 5の目が出る確率)は\[
\frac{5}{6} \times \frac{5}{6} = \frac{25}{36}
\]で求めることができるので、少なくとも1つは6の目が出る確率は\[
1 - \frac{25}{36} = \frac{11}{36}
\]と求まります。
*4:英語だとAが起こると分かったときのBが起こる条件付き確率のことを「B given A」というため、記号表記の順番がややこしくなっています。
関連広告・スポンサードリンク