スポンサードリンク
確率分布と統計的な推測について解説をしているサイト、本はそこまで多くはないと思います。
ということで今回は、2021年共通テストの「確率分布と統計的な推測」部分の解説をうさぎでもわかるようにわかりやすく説明しちゃいます!
![]()
(余談:2021年からなぜか「確率分布」の問題が第5問から第3問に移動していましたね…。誤マーク要注意…)
※「確率分布と統計的な推測」取ろうかなと思っている人は、1週間で勉強できるまとめをこちらに用意しているのでぜひお勉強しましょう…!
順番に見ていきましょう。
目次
スポンサードリンク
(1) 母比率といえば何分布?
全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本のうちで全く読書をしなかった生徒の数を表す確率変数を \( X \) とすると、\( X \) は [ ア ] に従う。また、\( X \) の平均(期待値)は イウ 、標準偏差は エ である。
[ ア ] については、最も適当なものを、次の⓪~⑤の中から1つ選べ。
⓪ 正規分布 \( N ( 0, 1) \) ① 二項分布 \( B ( 0, 1) \)
② 正規分布 \( N ( 100, 0.5) \) ③ 二項分布 \( B ( 100, 0.5) \)
④ 正規分布 \( N ( 100, 36) \) ⑤ 二項分布 \( B ( 100, 36) \)
まずは、全く読書をしなかった生徒の数を表す確率変数 \( X \) が何に従うかを見ていきましょう。
ここで、それぞれの(Q高校の)生徒は、「まったく読書をしないか」、「読書をするのか」の2つのどちらかに属しますよね。
2つのどちらかとくれば、二項分布で決まりです。
さらに、二項分布 \( B ( n,p) \) の \( n \) は繰り返す回数、\( p \) は確率を表しますね。
今回の場合は、生徒100人それぞれに対して、「読書をしないか」、「読書をするのか」を調査しているので、
- 繰り返す回数 → \( n = 100 \)
(生徒の数100人に相当) - 確率 → \( p = 0.5 \)
母比率(全体の中で読書をしない生徒の割合)に相当
となりますね。
なので、[ ア ] の答えは③の二項分布 \( B ( 100, 0.5) \) となりますね。
[余談]
消去法で解いてもいいでしょう。
例えば、二項分布 \( B(n,p) \) の \( p \) は確率なので、必ず \( p \) の値は0以上1以下ですね。
なので、選択肢⑤は \( p = 36 \) となるので論外です。また、①も \( p = 1 \) と一応ありえますが、確率が1のものをわざわざ推定するような問題は基本的に出ないのでこちらも抹消できます。
つぎに、\( X \) の平均と標準偏差を求めていきましょう。
\( X \) が二項分布 \( B(100, 0.5) \) に従うとわかってしまえば楽勝です。
平均は、\[
100 \cdot 0.5 = 50
\]と求まります。(イウ … 50)
標準偏差は、\[
\sqrt{ 50 \cdot 0.5 } = 5
\]とあっという間に求められます。(エ … 5)
ちなみに今回の(1)の問題で解いている内容は下の問題とほぼ同じ。
スポンサードリンク
(2) 二項分布と正規分布表
標本の大きさ 100 は十分に大きいので、100人のうちまったく読書をしなかった生徒の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を 0.5 とするとき、全く読書をしなかった生徒が 36 人以下となる確率を \( p_ 5 \) とおく。\( p_5 \) の近似値を求めると \( p_5 = [\underline{ \ \ \ オ \ \ \ }] \) である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった生徒が36人以下となる確率を \( p_4 \) とおくと [ カ ] となる。
[ オ ] については、最も適当なものを、次の⓪~⑤の中から1つ選べ。
⓪ 0.001 ① 0.003 ② 0.026
③ 0.050 ④ 0.133 ⑤ 0.497
[ カ ] の解答群
⓪ \( p_4 < p_5 \) ① \( p_4 = p_5 \) ② \( p_4 > p_5 \)
(1)で確率分布 \( X \) の平均は50、標準偏差は5と求めましたね。
このとき、「\( X \) が36以下になる」というのを、「標準偏差何個分ずれているかを表す確率変数 \( Z \) として」考えましょう。
36以下というのは、\[
\frac{36 - 50}{5} = - 2.8
\]となる。
つまり、標準偏差-2.8個分以下となる確率 \( P ( Z \leqq -2.8 ) \) を求めればOK。
標準偏差-2.8個分以下となる確率は、下の計算をすればOK。
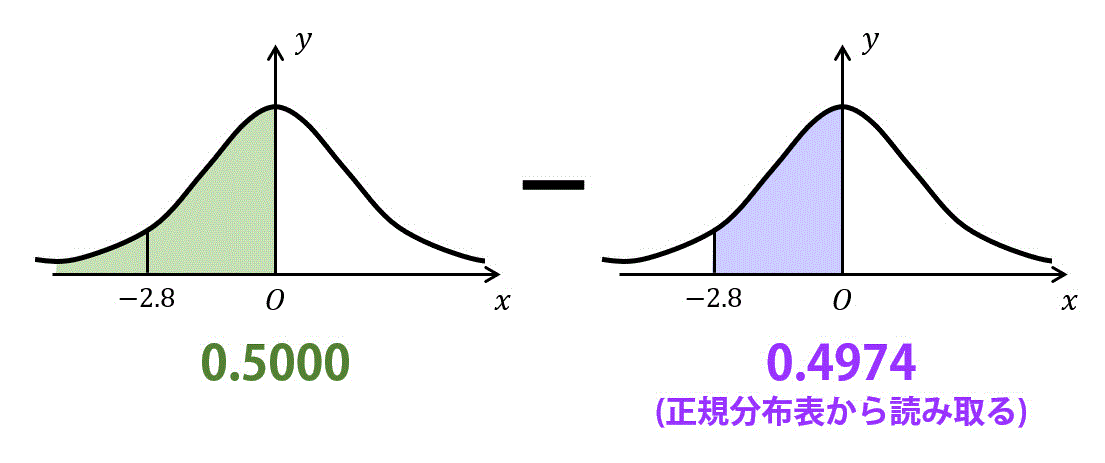
正規分布表は、この部分を読み取る。
よって、標準偏差-2.8個分以下となる確率は、\[\begin{align*}
P ( Z \leqq -2.8 ) & = P ( Z \geqq 2.8 )
\\ & = P ( Z \geqq 0 ) - P ( Z \geqq 2.8 )
\\ & = 0.5 - 0.4974
\\ & = 0.0026
\\ & \fallingdotseq 0.003
\end{align*}\]で求めることができるので、[ オ ] の答えは1。
(焦って②の0.026を選ばないように要注意!!)
つぎに、[ カ ] を求めるために \( p_4 \) を求める必要があるが、\( p_5 \) との大小を比べるので \( p_4 \) の値を厳密に出す必要はない。
母比率が0.4のときの平均 \( m \)と標準偏差 \( \sigma \) は\[
m = 100 \cdot 40 = 40 \\
\sigma = \sqrt{40 \cdot 0.6} = \sqrt{24} > 4
\]となる。
母比率が0.4(まったく読書をしなかった生徒が)36人以下となる確率というのは、標準偏差を4としたときに標準偏差-1個分となる確率 \( P ( Z \leqq -1 ) \) 以上である。
(実際の標準偏差は4ではなく、4よりも大きい値なので、本当の確率 \( p_4 \) は \( P ( Z \leqq -1) \) よりは大きな値となる。)
ここで、
- 標準偏差-2.8個分以下となる確率 \( p_5 \)
- 標準偏差-1個分以下となる確率
を比べると、標準偏差-1個分以下となる確率のほうが明らかに高い。
さらに、 \( p_4 \) は「標準偏差-1個分以下となる確率」よりも大きな確率となる。
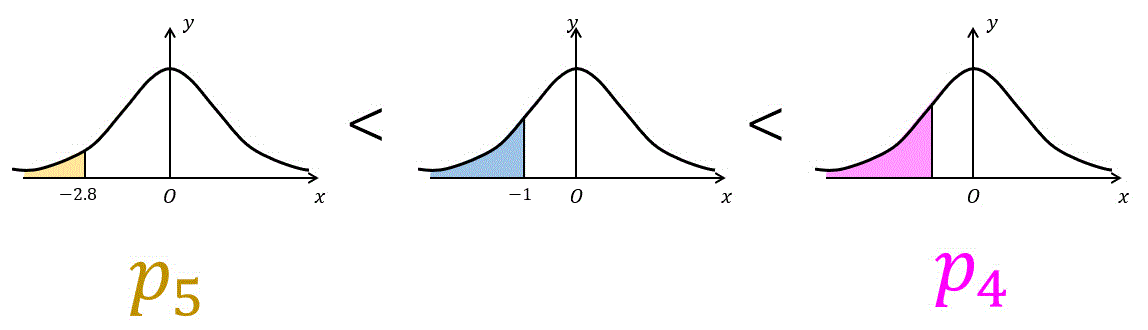
よって、答えは \( p_4 > p_5 \) となり、[ カ ] の答えは2。
スポンサードリンク
(3) 信頼区間って何か理解してる?
1週間の読書時間の母平均 \( m \) に対する信頼度 95 %の信頼区間を \( C_1 \leqq m \leqq C_2 \) とする。標本の大きさ100は十分大きいことと、1週間の読書時間の標本平均が204、母標準偏差が150であることを用いると、\( C_1 + C_2 = \) キクケ 、\( C_2 - C_1 = \) コサ . シ であることがわかる。
また、母平均 \( m \) と \( C_1, C_2 \) については [ ス ]。
[ ス ] の解答群
⓪ \( C_1 \leqq m \leqq C_2 \) が必ず成り立つ
① \( m \leqq C_2 \) は必ず成り立つが、\( C_1 \leqq m \) が成り立つとは限らない
② \( C_1 \leqq m \) は必ず成り立つが、\( m \leqq C_2 \) が成り立つとは限らない
③ \( C_1 \leqq m \) も \( m \leqq C_2 \) も成り立つとは限らない
信頼区間は、\[
\overline{X} - \frac{ z_0 \sigma}{ \sqrt{n} } \leqq m \leqq \overline{X} + \frac{ z_0 \sigma}{ \sqrt{n} }
\]で求められるのでしたね。
(ここで、\( \overline{X} \) は標本平均、\( \sigma \) は母標準偏差、\( z_0 \) は標準正規分布の灰色部分の面積が0.95になるような \( z_0 \) である。)
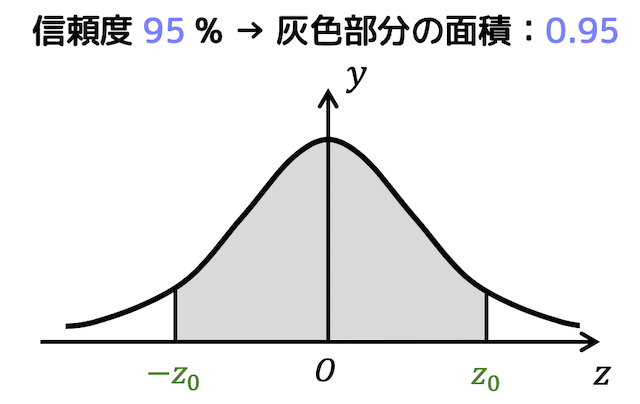
\( z_0 \) の値は、灰色面積の半分( \( 0 \) から \( z_0 \) の部分)が0.475になる確率を正規分布表から読み取ることで求められる。
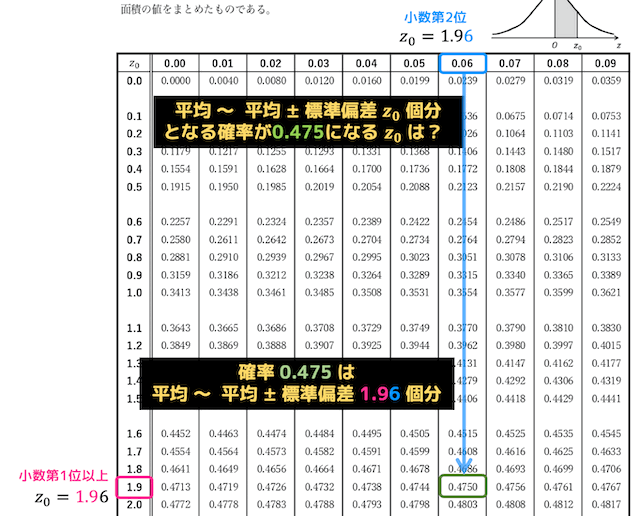
すると、\( z_0 = 1.96 \)(標準偏差1.96個分)と求められる。
よって、\[\begin{align*}
C_1 + C_2 & = \overline{X} - \frac{ z_0 \sigma}{ \sqrt{n} } + \overline{X} + \frac{ z_0 \sigma}{ \sqrt{n} }
\\ & = 2 \overline{X}
\\ & = 2 \cdot 204
\\ & = 408
\end{align*}\]と計算できる。(キクケ … 408)
また、\[\begin{align*}
C_1 - C_2 & = \overline{X} - \frac{ z_0 \sigma}{ \sqrt{n} } - \left( \overline{X} + \frac{ z_0 \sigma}{ \sqrt{n} } \right)
\\ & = 2 \cdot \frac{ z_0 \sigma}{ \sqrt{n} }
\\ & = 2 \cdot \frac{ 1.96 \cdot 150}{ \sqrt{100} }
\\ & = 2 \cdot 1.96 \cdot 15
\\ & = 58.8
\end{align*}\]と計算できる。(コサ . シ … 58.8)
[ ス ] は、
信頼区間 \( C_1 \leqq m \leqq C_2 \) というのは標本平均 \( \overline{X} \) の値によって決まりますね。
標本平均というのは、どのように標本を取ったかによってきまるので、必ずしも母平均 \( m \) は信頼区間 \( C_1 \leqq m \leqq C_2 \) に収まるとは限りません。
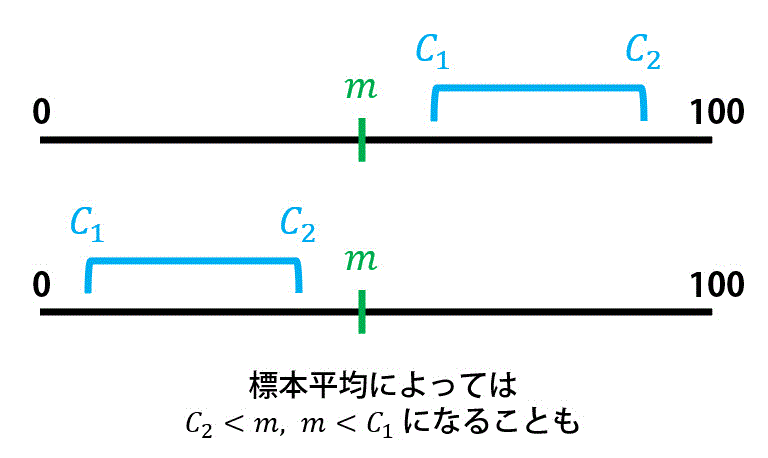
なので、[ ス ] の答えは3となります。
よくわかんないなぁという人は下のような極端な例で考えてみるといいかもしれません。
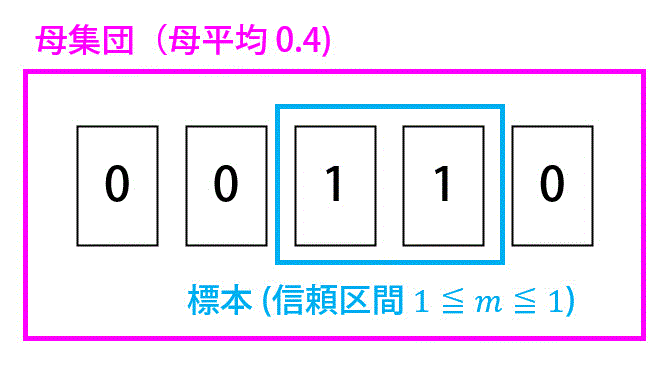
上の例の場合、母集団は0, 0, 1, 1, 0なので、母平均 \( m\) は0.4ですね。
標本として 1, 1を選べば信頼区間は \( 1 \leqq m \leqq 1 \) となり \( m < C_1 \) となりますね。
同様に 0, 0を選べば信頼区間は \( 0 \leqq m \leqq 0 \) となり \( C_2 < m \) となりますね。
困ったら極端な例を考えてみよう!!
(4) 標本の選び方を変えると調査結果はどうなる?
Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が調査をしていることを知らずに、図書委員会として校長先生と同様の調査を独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、対象をQ高校の生徒全員として 100 人の生徒を無作為に抽出した。その調査における、全く読書をしなかった生徒の数を \( n \) とする。
校長先生の調査結果によると全く読書をしなかった生徒は 36 人であり、[ セ ]。
[ ス ] の解答群
⓪ \( n \) は必ず 36 に等しい
① \( n \) は必ず 36 未満である
② \( n \) は必ず 36 より大きい
③ \( n \) と 36 との大小はわからない
この問題は、標本調査ってわかっていますか?? という問題です。
計算など一切必要ありません。
今回の問題で行くと、無作為に抽出する100人を変えると、当然「全く読書をしなかった生徒の数(結果)」も変わりますよね。
なので、答えは3「 \( n \) と 36 との大小はわからない」です。
よくわからないなぁって人のために、1つ実例で試してみましょう。
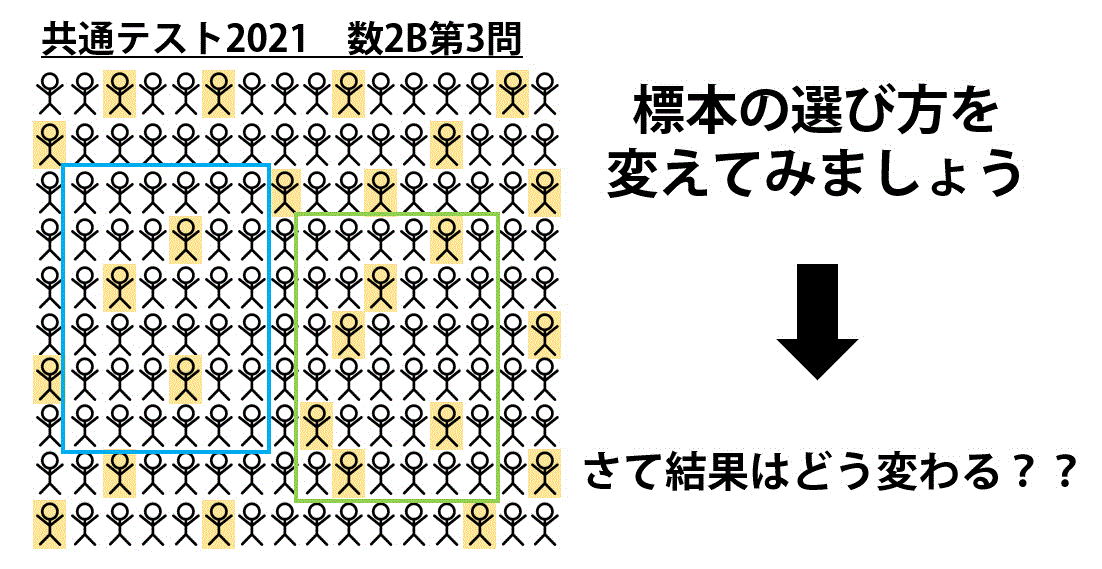
下の図の棒人形の中から、
- 適当に20人抜きだしてグループA
- 適当に20人抜きだしてグループB
と、20人ごとのグループを2つ作ってみましょう。

つぎに、選んだグループの中に「青色の棒人形」が20人中何人いるか数えてみてください。
するとどうでしょう。
グループの選び方によって、「青色の棒人形」の人数は変わることが実感できると思います。
例えば下の例であれば、
- 水色のグループ(A) … 3人
- 緑色のグループ(B) … 5人
と、確かに異なっていますね。

20人の選び方によって青色の棒人形の人数が変わるというのは、今回の問題でいう「無作為に抽出する人を変えると、全く読書をしなかった生徒の数も変わる」というのを表しています。
(5) 標本の選び方を変えると信頼区間はどうなる?
(4)の図書委員会が行った調査結果による母平均 \( m \) に対する信頼度 95 %の信頼区間を \( D_1 \leqq m \leqq D_2 \)、校長先生が行った調査結果による母平均 \( m \) に対する信頼度 95 %の信頼区間を (3) の \( C_1 \leqq m \leqq C_2 \) とする。ただし、母平均は同一であり、1週間の読書時間の母標準偏差は150とする。
このとき、つぎの⓪~⑤のうち、正しいもの [ ソ ] と [ タ ] はである。
[ ソ ]・[ タ ] の解答群(解答の順序は問わない)
⓪ \( C_1 = D_1 \) と \( C_2 = D_2 \) が必ず成り立つ
① \( C_1 < D_2 \) または \( D_1 < C_2 \) のどちらか一方のみが必ず成り立つ
② \( D_2 < C_1 \) または \( C_2 < D_1 \) となる場合もある
③ \( C_2- C_1 > D_2 - D_1 \) が必ず成り立つ
④ \( C_2- C_1 = D_2 - D_1 \) が必ず成り立つ
⑤ \( C_2- C_1 < D_2 - D_1 \) が必ず成り立つ
「標本調査の方法を変えると、信頼区間ってどう変わるの?」という問題です。
信頼区間を求める式は、\[
\overline{X} - \frac{ z_0 \sigma}{ \sqrt{n} } \leqq m \leqq \overline{X} + \frac{ z_0 \sigma}{ \sqrt{n} }
\]でしたね。(ここで \( n \) は標本のサイズ、つまり100人を表す)
今回は、2つの信頼区間ともに信頼度 95 %による推定なので、\( z_0 \) は変化しませんね。
また、2つの信頼区間ともに母標準偏差 \( \sigma \) も同じなので、\( \sigma \) も変化しません。
よって、信頼区間は標本平均 \( \overline{X} \) にのみ依存しますね。
[選択肢 ⓪ - ② について]
まずは、選択肢⓪~②についてみてみましょう。
標本平均 \( \overline{X} \) が変化すると、必ず信頼区間は変化しますね。
なので、⓪はありえません。ばいばーい。
つぎに①と②を見てみましょう。信頼区間\[
\overline{X} - \frac{ z_0 \sigma}{ \sqrt{n} } \leqq m \leqq \overline{X} + \frac{ z_0 \sigma}{ \sqrt{n} }
\]の \( \overline {X} \) を \( 2 \frac{ z_0 \sigma}{ \sqrt{n} } \) より大きく増減させると、信頼区間は下の図のように \( D_2 < C_1 \) または \( C_2 < D_1 \) となりますね。
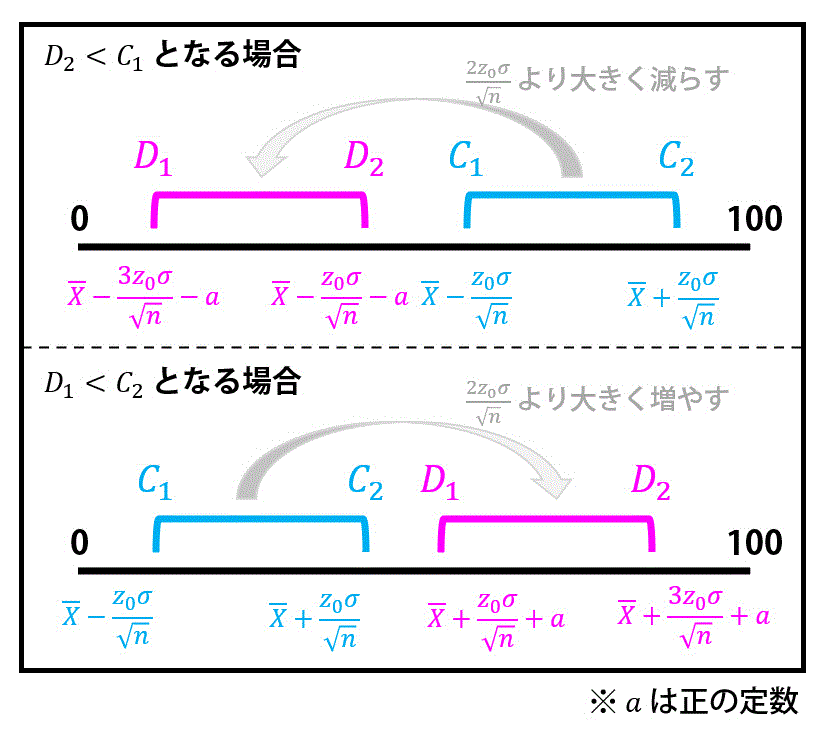
なので、1つ目の答えは②となります。
[選択肢 ③ - ⑤ について]
選択肢③~⑤についてもみてみましょう。
信頼区間の差 \( C_2 - C_1 \) は、\[
C_2 - C_1 = 2 \cdot \frac{ z_0 \sigma}{ \sqrt{n} }
\]で求めるのでしたね。
ここで、母標準偏差 \( \sigma = 150 \)、標本のサイズ \( n = 100 \)、\( z_0 \) が集団によらずに一定であるという点に注目します。
すると、標本集団がどうなろうが、信頼区間の差 \( D_2 - D_1 \) は \( C_2 - C_1 \) と等しくなることがわかりますね。
よって、答えは4となります。
(ソ・タの答えは 2・4、順不同)
さいごに
今回は、2021年共通テストの確率分布と統計的な推測の簡単な解説、コメントを書いてみました。
ほかの数学の問題にも共通するかもしれませんが、共通テストの「確率分布と統計的な推測」では、
- 計算力はそこまで求められない
- なぜそのような計算で求まるのか
のように、ただただごり押しで計算する力よりも、推定などの仕組みを理解しているかなどを問われることが多い気がします。
これから共通テストを受ける人は、
- 公式を丸暗記せず、どうしてその式になるのかを理解する
- 困ったら極端な例で考えてみる
というのを意識すると、確率分布と統計的な推測で高得点が取れる気がします。
そこまで計算力はいらないので、文系の人におすすめかも…?
関連広告・スポンサードリンク