スポンサードリンク
こんにちは、ももうさです。
前回までの統計的推測では、区間推定(母平均、母比率)について勉強していきました。
今回からは、統計的な推測の最終テーマ「仮説検定」について3回に分けて学習していきましょう!
例題、練習問題を解く際にお使いください。
目次
スポンサードリンク
1. 仮説検定とは
まず、初めに「そもそも仮説検定とはなにか?」から説明していきます。
例えば、あなたが友達とコイントス勝負をしたとしましょう。
- 友達がコインを投げます。
- 表が出ると、あなたは友達にご飯を奢らなければなりません。
- 裏が出ると、友達があなたにご飯を奢ってくれます。
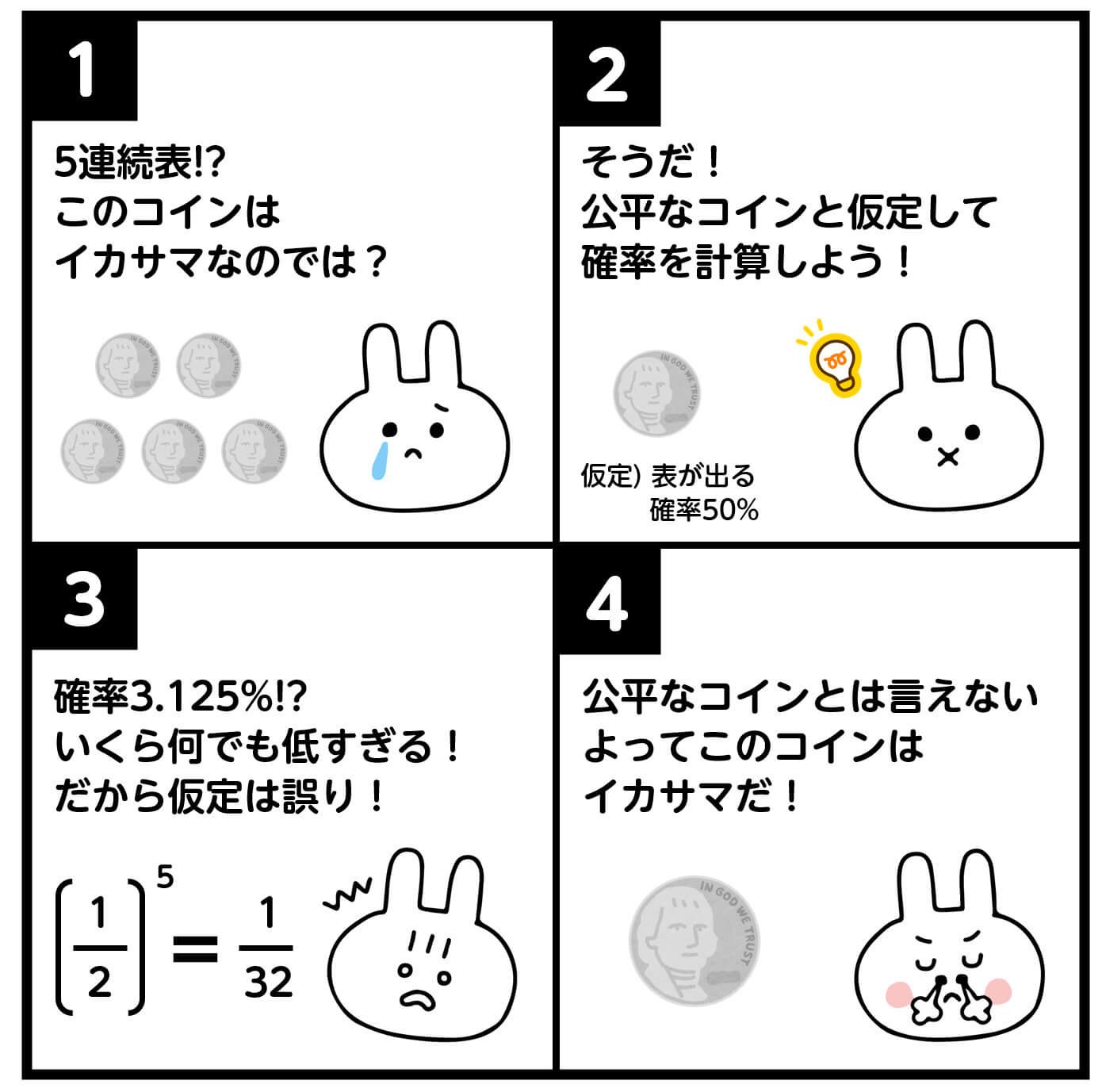
この勝負で5回連続で表が出たとします。
すると、「このコインは表が出やすいイカサマコインなのではないか?」と疑いたくなりますよね。
しかし、何も根拠がないのに「イカサマだ!」と言うのは良くないです。単なる偶然の可能性もありえるからです。
そこで、登場するのが仮説検定です。
仮説検定では、まるで背理法のような方法で、表が出やすいイカサマコインであることを、示します。

スポンサードリンク
2. 仮説検定で使う用語紹介
では、ここからは仮説検定で使う用語を見ていきましょう。
(1) 帰無仮説
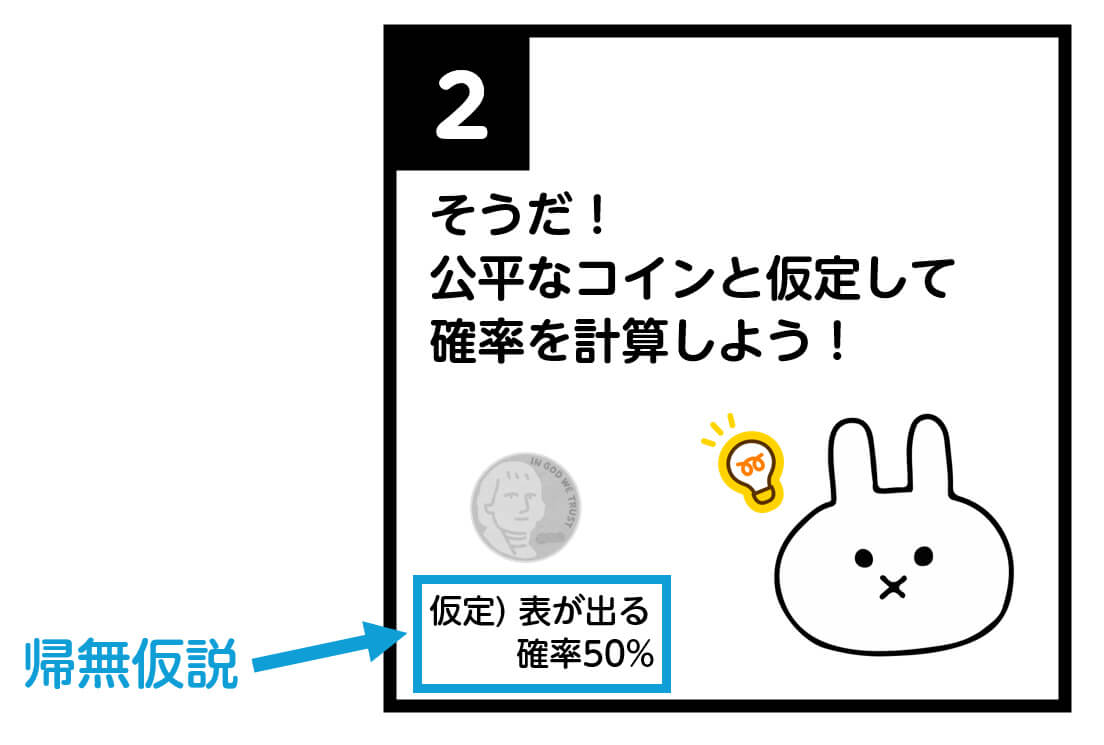
帰無仮説は、仮説検定において最初に設定する仮説です。記号で \( H_0 \) と書くこともあります。
これは、背理法における仮定を立てる部分に相当します。
例えば、「このコインは表が出やすいイカサマコインなのではないか?」という疑問を調べるためには、まず「コインは公平である(表と裏が出る確率は等しい)」という仮説を立てます。
(2) 対立仮説
対立仮説は、帰無仮説と反する主張です。記号で \( H_1 \) と書くこともあります。
この主張は、帰無仮説が誤りと判定されたときに示したいものを表します。
例えば、「表が出やすいイカサマコインかどうか」を検定したい場合は、対立仮説は「表が出る確率が50%よりも大きいコインである」と設定します。
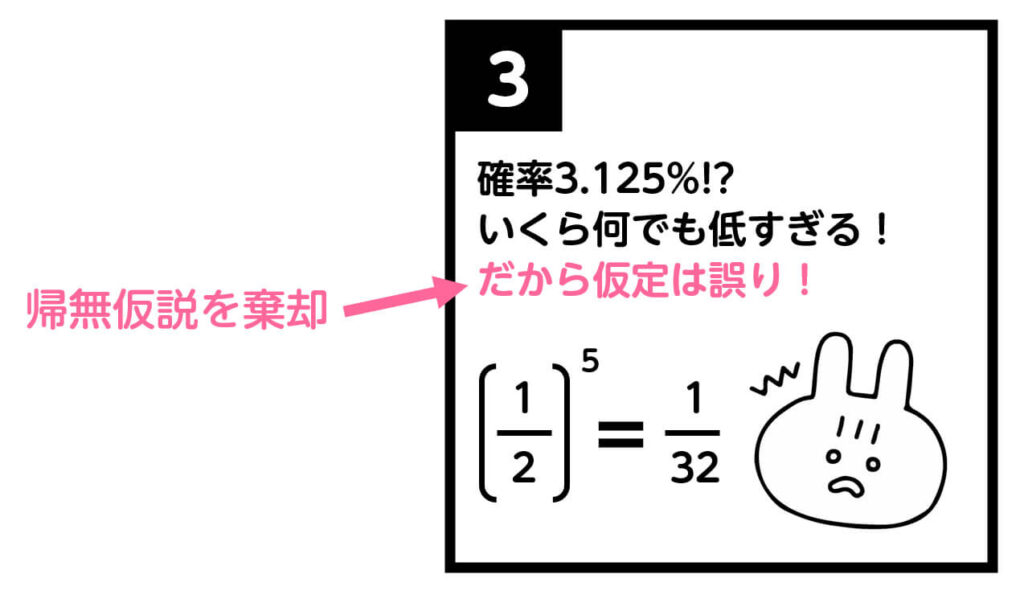
(3) 棄却
帰無仮説が誤りであること、帰無仮説を棄却すると言います。
帰無仮説が誤りでないと明確には言えない場合、「帰無仮説を採択する」と表現されることがあります。ここでの「採択」は、帰無仮説が正しいとするのではなく、現時点ではそれを棄却するだけの十分な証拠がないという意味です。これは誤りとは言えないが、真であるとも証明されていない状態を示します。
(4) p値
帰無仮説が正しいと仮定したときに、その事象が起こる確率を表します。
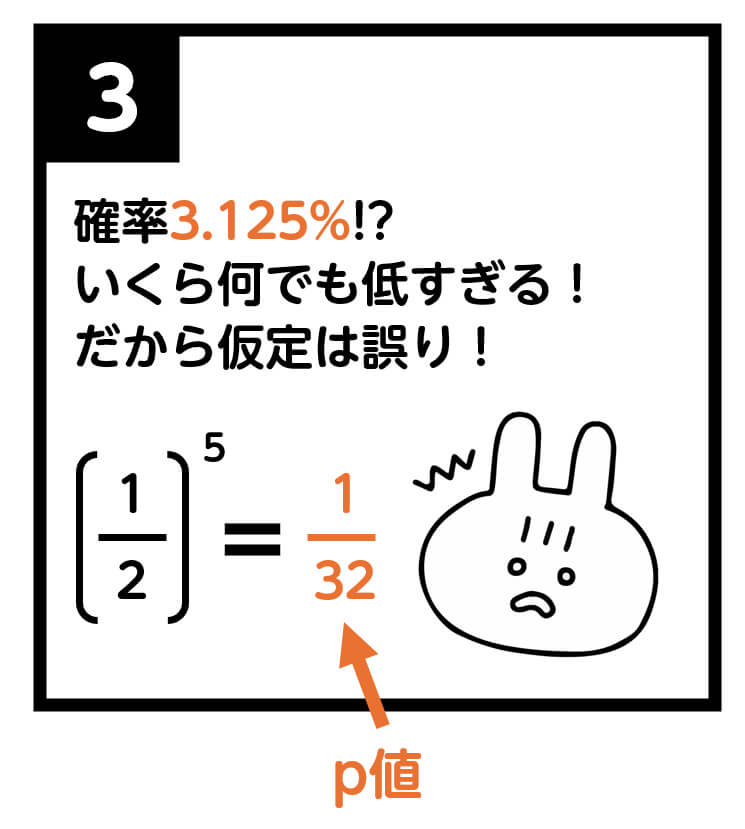
例えば、「5連続表が出たときに、表が出やすいかを検定すること」を考えてみましょう。
帰無仮説で表が出る確率が \( \frac{1}{2} \) であると仮定したとき、5連続で表が出る確率は \( \left( \frac{1}{2} \right)^5 = \frac{1}{32} \) と求められます。
この \( \frac{1}{32} \) がこの検定のp値となります。
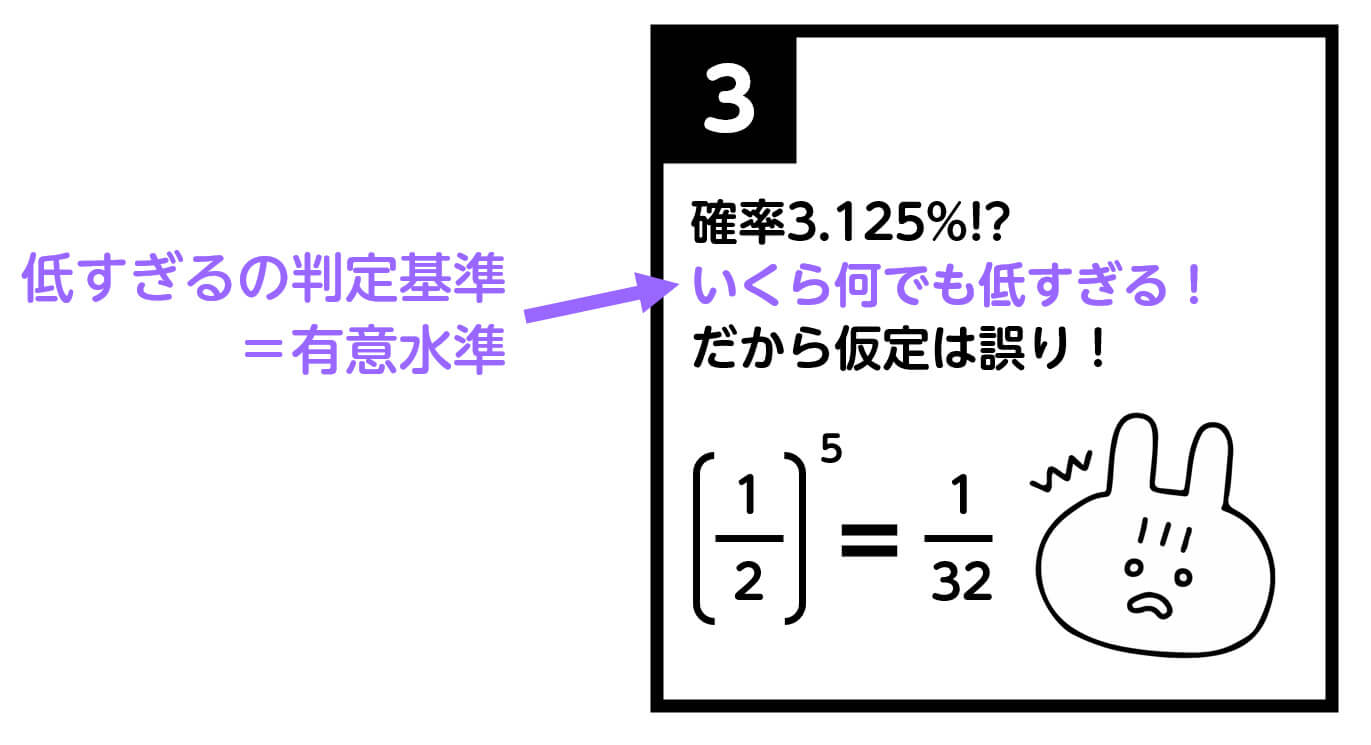
(5) 有意水準
有意水準は、帰無仮説が正しいとしたときに、観測された値が得られる確率がどの程度以下であれば、帰無仮説を棄却するかを示す基準です。一般的には5%(0.05)や1%(0.01)が用いられます。
例えば、有意水準を5%に設定した場合、帰無仮説が正しいと仮定したときに、観察されたデータが得られる確率が5%未満となった場合、帰無仮説を棄却します。
(6) 棄却域
仮説検定において帰無仮説を棄却するための基準となる範囲です。この範囲にデータが入ると、帰無仮説が誤りであると判断されます。
スポンサードリンク
3. 仮説検定の流れ
ここからは、実際に例題を通じて仮説検定の流れを確認していきましょう。
ある硬貨を投げたときに、表が出やすいかどうか仮説検定により確認したい。
(1) 帰無仮説と対立仮説を述べなさい。
(2) コインを4回投げたところ、4回とも表が出た。この結果をもとに、有意水準5%で仮説検定をし、結論を示しなさい。
(3) コインを5回投げたところ、5回とも表が出た。この結果をもとに、有意水準5%で仮説検定をし、結論を示しなさい。
解説1
Step1. 帰無仮説・対立仮説の設定
仮説検定を行う際、最初にすることは「帰無仮説」と「対立仮説」の設定です。
帰無仮説 \( H_0 \)
帰無仮説は、仮説検定を行うための基準となる仮定を立てます。
この問題では、硬貨が公平であると仮定します。つまり、表が出る確率は裏が出る確率と等しいとします。
そのため、いったん表と裏が出る確率が等しいコインであると仮定をします。
そのため、帰無仮説は「硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である」となります。
対立仮説 \( H_1 \)
対立仮説では、帰無仮説が誤りと判定されたときに示したいものを表すのでしたね。
ここで、今回の目標は表が出やすいコインかどうかを確認することです。
そのため、対立仮説は「硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より大きい」となります。
帰無仮説 \( H_0 \)
硬貨を投げたときに、表が出る確率が \( \frac{1}{2} \) である。
対立仮説 \( H_1 \)
硬貨を投げたときに、表が出る確率が \( \frac{1}{2} \) より大きい。
Step2. 帰無仮説が正しいと仮定したときの確率の計算
つぎに、帰無仮説「硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である」が正しいと仮定したときの確率の計算をします。
(2) 硬貨を4回投げて、4回とも表が出る確率
\[
\left( \frac{1}{2} \right)^4 = \frac{1}{16}
\]
(3) 硬貨を5回投げて、5回とも表が出る確率
\[
\left( \frac{1}{2} \right)^5 = \frac{1}{32}
\]
Step3. 結果の判定
Step2で求めた確率と、有意水準を比べて仮説検定の結論を出します。
(2) 硬貨を4回投げて、4回とも表が出た場合
求めた確率 \( \frac{1}{16} \) を、有意水準5%と比較します。\[
\frac{1}{16} > \frac{1}{20} = 5 \%
\]
このため、帰無仮説を棄却することはできません。(仮説が誤りであるとは言えない。)
硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より大きいとは言えない。
理由: 硬貨を4回投げて、4回とも表が出る確率は \( \frac{1}{16} \) と、5% ( \( \frac{1}{2} \) ) よりも大きいため。
(3) 硬貨を5回投げて、5回とも表が出た場合
(2)と同様に、求めた確率 \( \frac{1}{32} \) を、有意水準5%と比較します。\[
\frac{1}{32} < \frac{1}{20} = 5 \%
\]
このため、帰無仮説を棄却することができます。(仮説が誤りであると言える。)
硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より大きい言える。
理由: 硬貨を4回投げて、4回とも表が出る確率は \( \frac{1}{16} \) と、5% ( \( \frac{1}{2} \) ) より小さいため。
仮説検定の手順まとめ
ここで、仮説検定の手順について振り返りましょう。
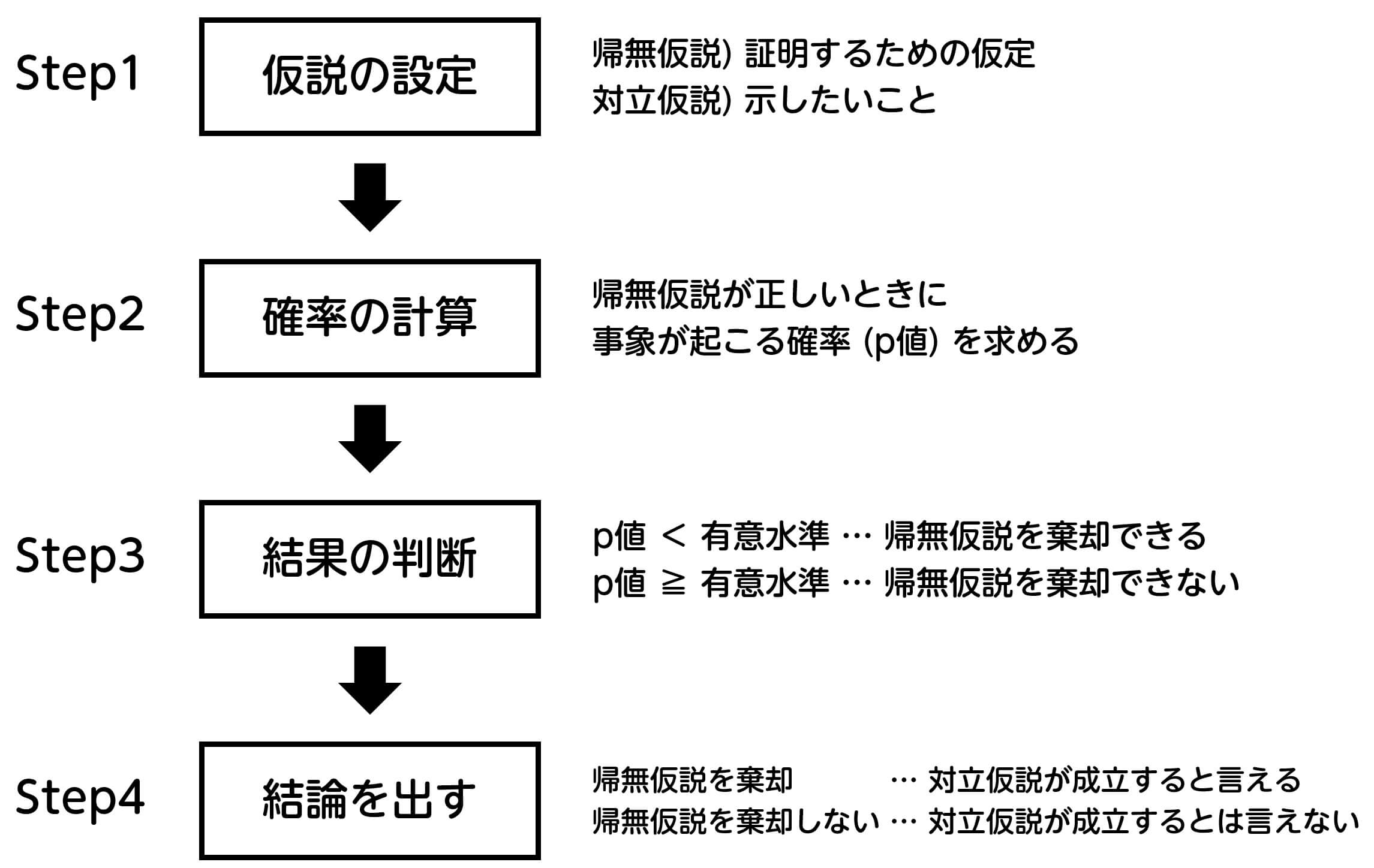
先ほどの例題(硬貨投げの仮説検定)の場合、仮説検定の手順は以下の通りとなります。
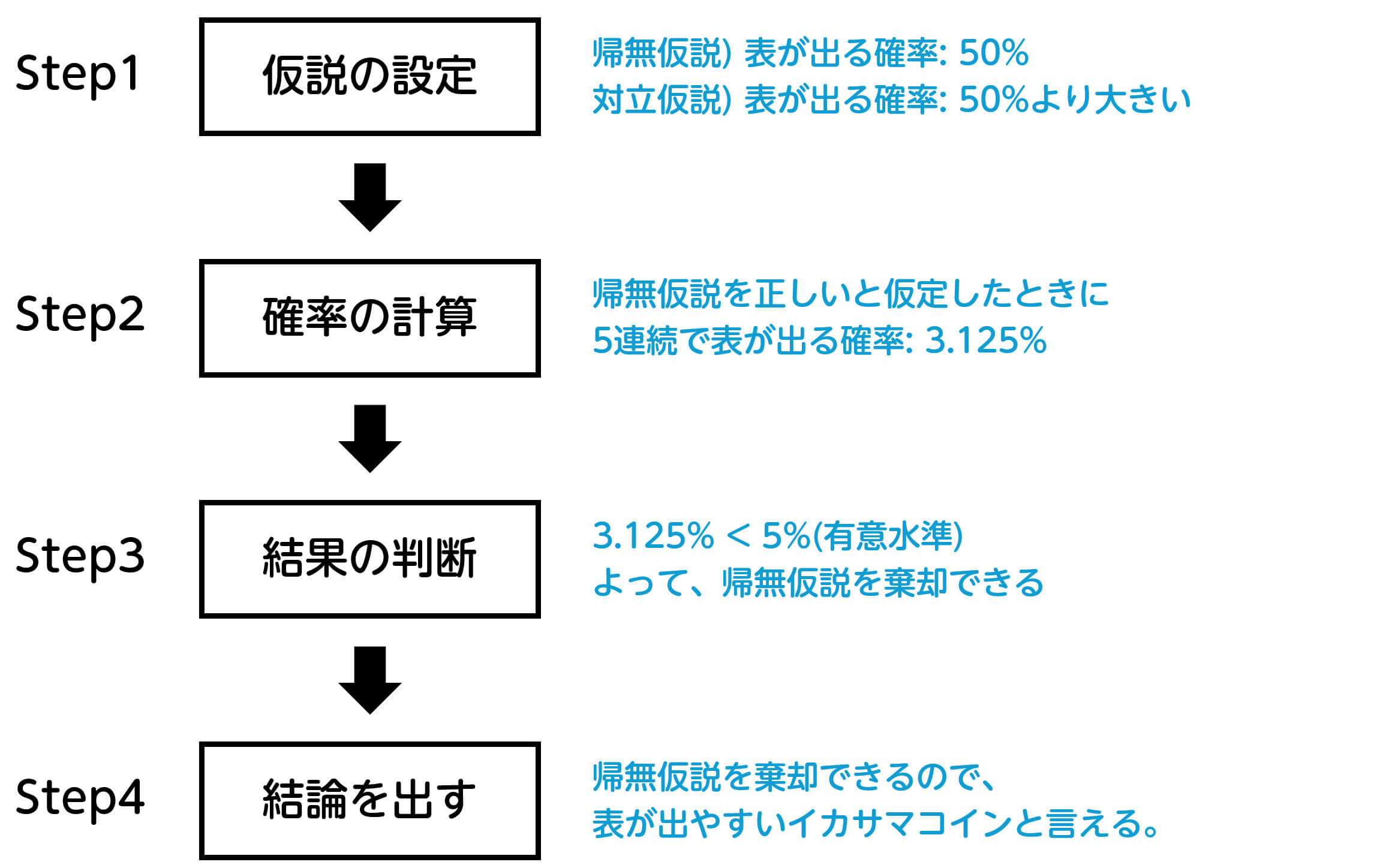
仮説検定の手順を、背理法と比較してみましょう。
| 仮説検定の手順 | 仮説検定 | 対応する背理法の手順 |
|---|---|---|
| 帰無仮説の設定 (仮説検定をするための仮定) | 公平なコインである (表が出る確率: 50%) | \( \sqrt{3} \) は有理数 |
| 対立仮説の設定 (問題で示したいもの) | 表が出やすいコイン (表が出る確率: 50%) | \( \sqrt{3} \) は無理数 |
| 仮定が正しいとしたときの 確率の計算 | 確率 3.125% | 仮定が正しいとしたときに 矛盾を示す |
| 結果の判断 | 3.125%が有意水準(5%)より 小さいので仮定を棄却 | 矛盾が発生しているため 仮定は誤り |
| 結論 | 表が出やすいコイン | \( \sqrt{3} \) は無理数 |
4. 片側検定と両側検定
仮説検定には、片側検定と両側検定の2つがあります。どちらの検定をするかによって、対立仮説の決め方が変わってきます。
この章では、それぞれの検定方法の違いについて学習していきましょう。
(1) 片側検定
両側検定は、「表が出やすいとき」や「裏が出やすいとき」のように、期待値から特定の方向に逸脱しているかどうかを検証する方法です。
ある硬貨を投げたときに、表が出やすいかどうか仮説検定により確認したい。
- 帰無仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である
対立仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より大きい
→ この仮説検定では、表が出やすい場合のみに着目します。表が出にくい場合は考慮しません。
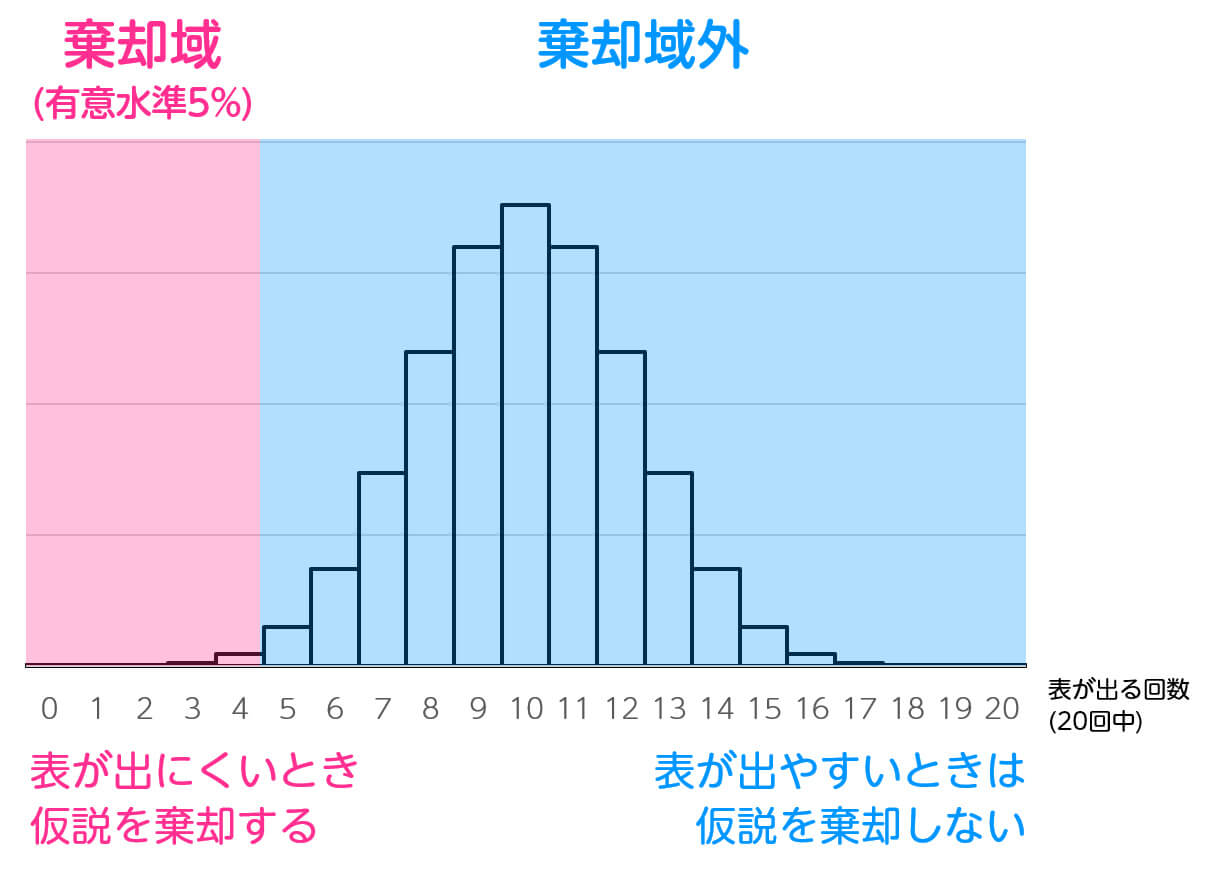
ある硬貨を投げたときに、表が出にくいかどうか仮説検定により確認したい。
帰無仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である
対立仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より小さい
→ この仮説検定では、表が出にくい場合のみに着目します。表が出やすい場合は考慮しません。
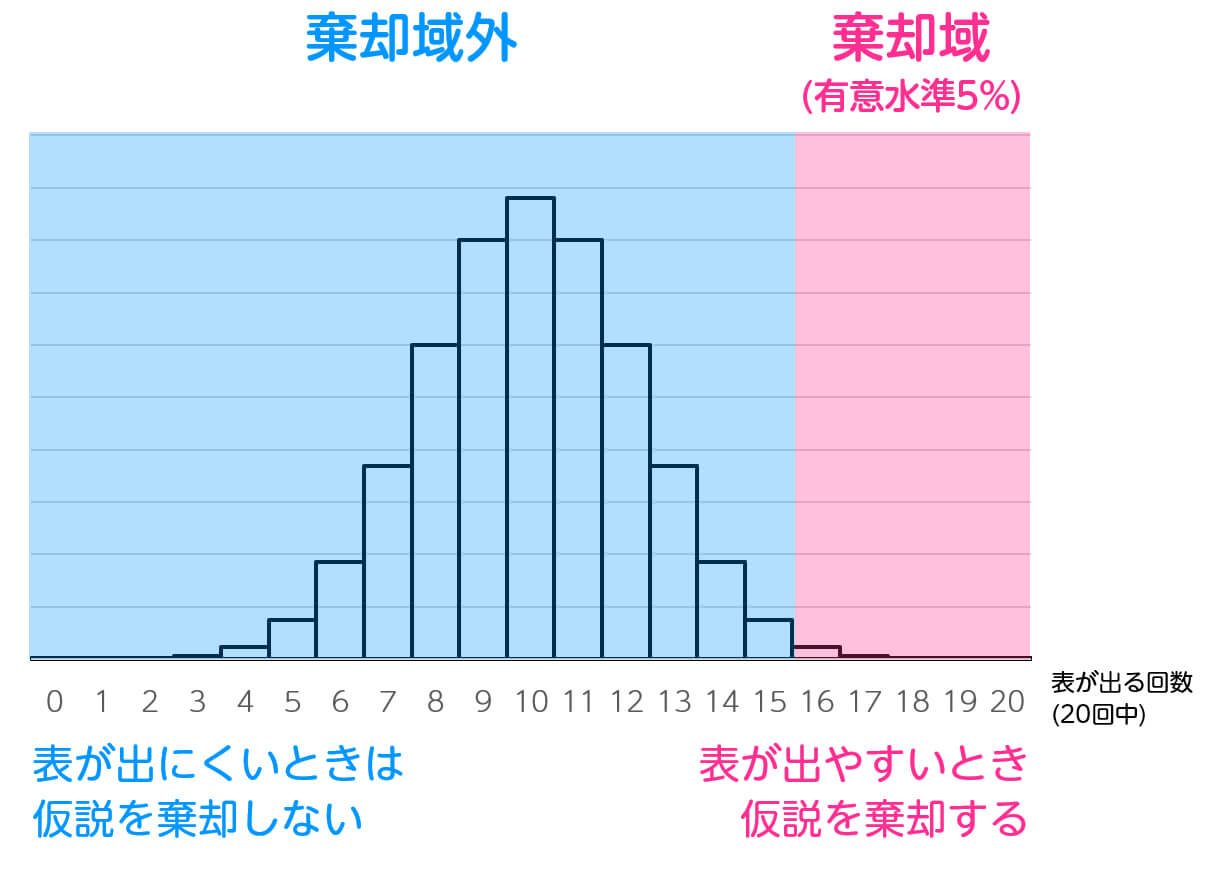
片側検定の場合、帰無仮説を仮定して事象が起こる確率を計算し、その確率が有意水準より小さければ仮説を棄却します。
(2) 両側検定
両側検定は、「コインが公平(表と裏が出る確率が異なる)」のように、データが期待値からどちらの方向にも逸脱しているかどうかを検証する方法です。
ある硬貨が公平(表と裏が出る確率が異なる)ではないかどうかを検証したい。
帰無仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である
対立仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) ではない
→ この仮説検定では、表が出にくいとき、表が出やすいときの両方に着目します。
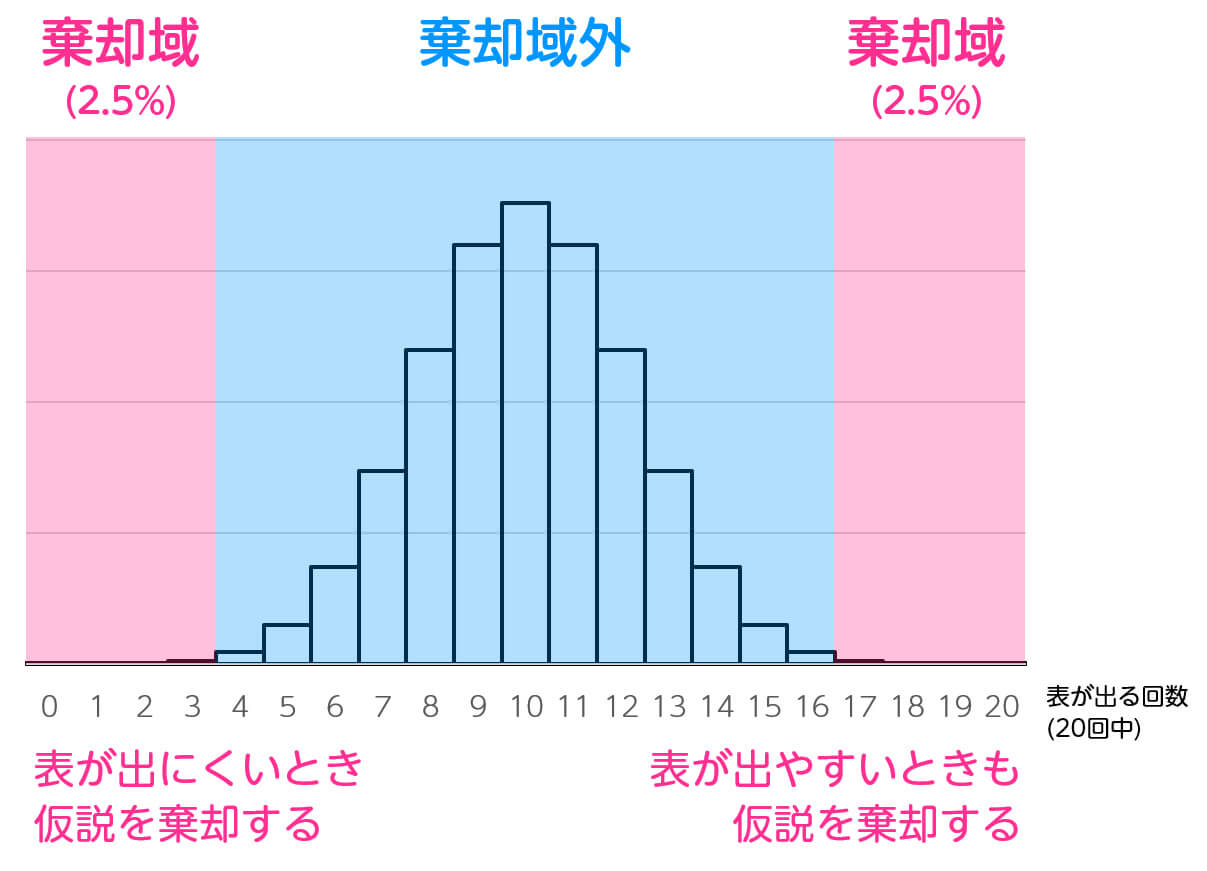
両側検定では、有意水準を2つの側に半分ずつ分けます。たとえば、全体の有意水準を5%に設定した場合、各側の有意水準は2.5%(0.025)となります。
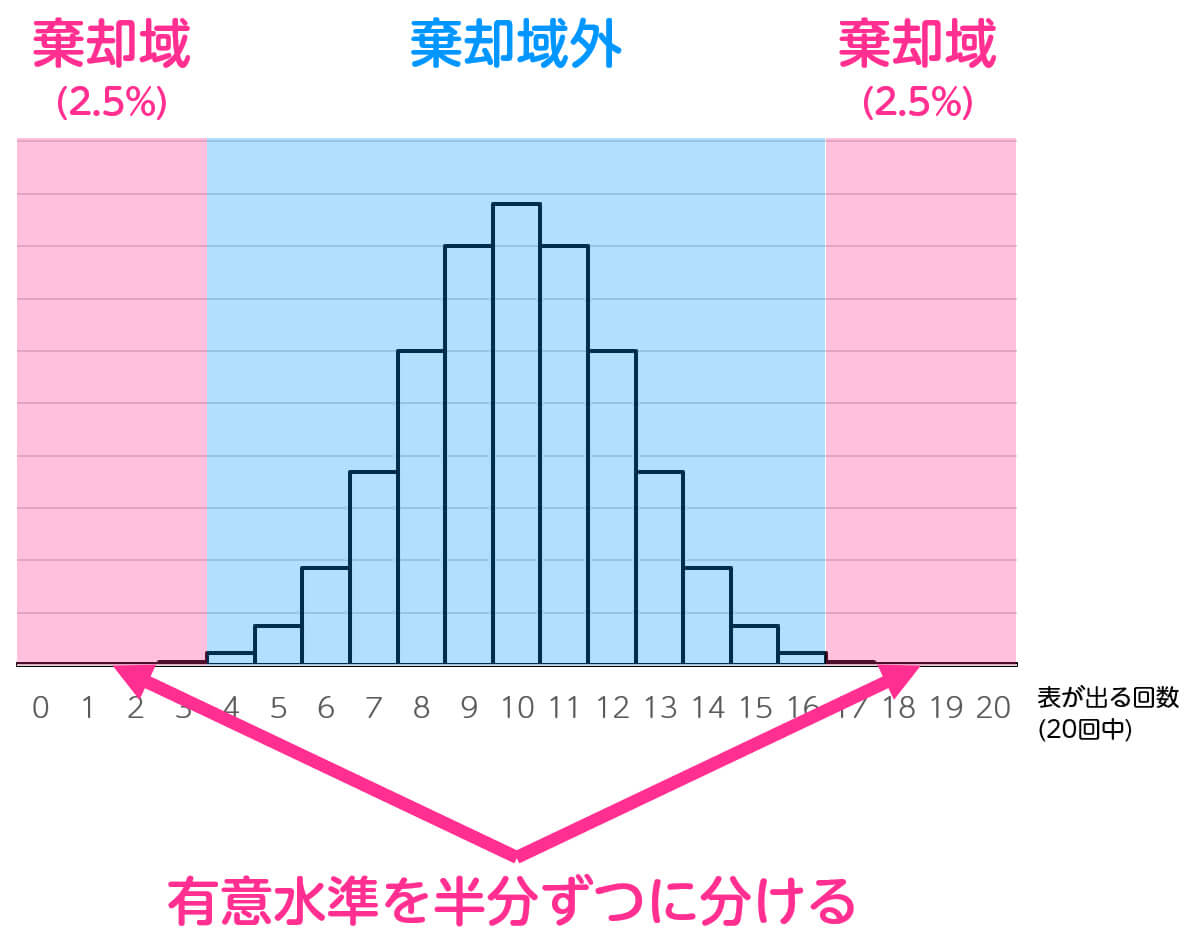
(3) 例題で確認!
実際に、片側検定と両側検定でどのように検定方法が変わるか、例題で確認しましょう。
ある硬貨を5回投げたところ、5回とも表が出た。
(1) 表が出やすい硬貨と言えるか、有意水準5%で検定しなさい。
(2) 公平でない硬貨と言えるか、有意水準5%で検定しなさい。
解説2
(1) 片側検定の場合
Step1. 帰無仮説・対立仮説の設定
帰無仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である
対立仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より大きい
Step2. 帰無仮説が正しいと仮定したときの確率の計算
硬貨を5回投げたときに、5回とも表が出る確率は次の通りです。
\[
\left( \frac{1}{2} \right)^5 = \frac{1}{32}
\]
Step3. 結果の判定
確率 \( \frac{1}{32} \) を、有意水準5%と比較します。\[
\frac{1}{32} < \frac{1}{20} = 5\%
\]
このため、帰無仮説は棄却されます。(5回とも表が出る確率が、5%よりも小さいため)
したがって、「表が出やすい硬貨である」と結論づけられます。
(2) 両側検定の場合
Step1. 帰無仮説・対立仮説の設定
帰無仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である
対立仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) ではない
Step2. 帰無仮説が正しいと仮定したときの確率の計算
ある硬貨を5回投げたところ、5回とも表が出る確率は、次の通り求められます。
\[
\left( \frac{1}{2} \right)^5 = \frac{1}{32}
\]
Step3. 結果の判定
両側検定では、有意水準を2つの側に分けます。
5%の有意水準の場合、各側の有意水準は2.5%(0.025)になります。
確率 \( \frac{1}{32} \) を、2.5%と比較します。\[
\frac{1}{32} > \frac{1}{40} = 2.5\%
\]
このため、帰無仮説は棄却されません。(5回とも表が出る確率が、2.5%よりも大きい)
したがって、「公平でない硬貨であるとは言えない」と結論づけられます。
4. 二項分布と仮説検定
二項分布の知識を組み合わせて仮説検定を実施する問題は、テストに頻出です。
実際に例題で解き方を確認しましょう。
例題を解いてみよう
ある硬貨を100回投げたところ、59回表が出た。
表が出やすい硬貨と言えるか、有意水準5%で検定しなさい。
解説3
Step1. 帰無仮説・対立仮説の設定
帰無仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) である
対立仮説: ある硬貨を投げたときに表が出る確率が \( \frac{1}{2} \) より大きい
Step2. 帰無仮説が正しいと仮定したときの確率の計算
59回以上表が出る確率を、下の式にように直接計算するのは難しいです。
\[
{}_{100} \mathrm{C} _{59} \times \left( \frac{1}{2} \right)^{59} \times \left( 1 - \frac{1}{2} \right)^{41} + {}_{100} \mathrm{C} _{60} \times \left( \frac{1}{2} \right)^{60} \times \left(1 - \frac{1}{2} \right)^{40} + \cdots
\]
そこで、二項分布を用いて確率を計算します。
まず、100回の硬貨投げにおける表が出る回数を \( X \) としましょう。
すると、\( X \) の平均 \( E(X) \)、分散 \( V(X) \)、標準偏差 \( \sigma (X) \) は次のように計算ができます。
\[\begin{align*}
E(X) & = 100 \times \frac{1}{2}
\\ & = 50
\end{align*}\]
\[\begin{align*}
V(X) & = 100 \times \frac{1}{2} \times \left( 1 - \frac{1}{2} \right)
\\ & = 100 \times \frac{1}{2} \times \frac{1}{2}
\\ & = 25
\end{align*}\]
\[\begin{align*}
\sigma(X) & = \sqrt{ V(X) }
\\ & = \sqrt{25}
\\ & = 5
\end{align*}\]
よって、表が出る回数 \( X \) は平均50、標準偏差5の二項分布に従うことが分かります。
ここで、硬貨投げの試行回数が100と大きいため、二項分布を正規分布で近似することができます。
つぎに、59回以上表が出る確率を標準正規分布(平均0、標準偏差1の正規分布)に変換します。
ここで、\( X \) は平均50、標準偏差5ということは、つぎの式で標準正規分布に変換が出来ます。\[
Z = \frac{X - 50}{5}
\]
ここで、\( X = 59 \) に対応する \( Z \) の値は \( Z = 1.8 \) となります。\[\begin{align*}
Z & = \frac{59 - 50}{5}
\\ & = 1.8
\end{align*}\]
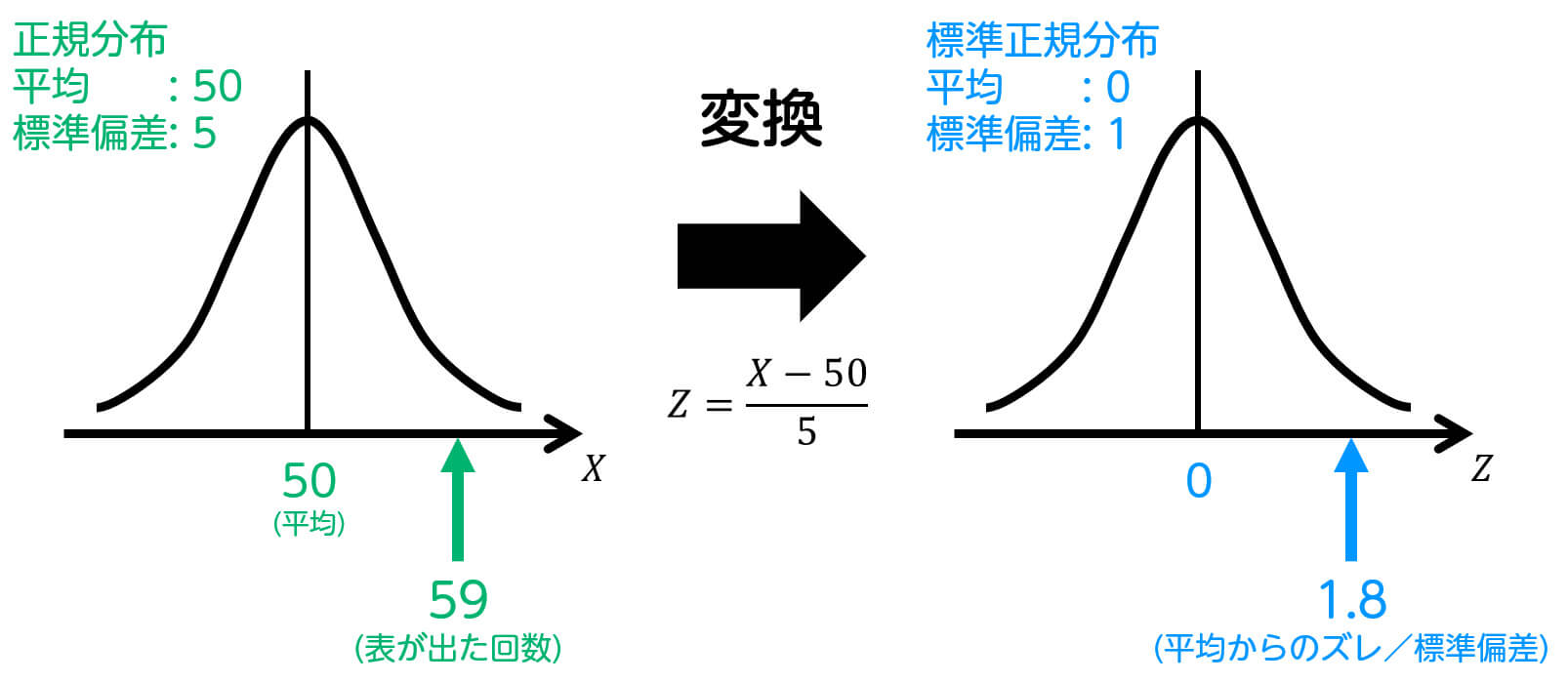
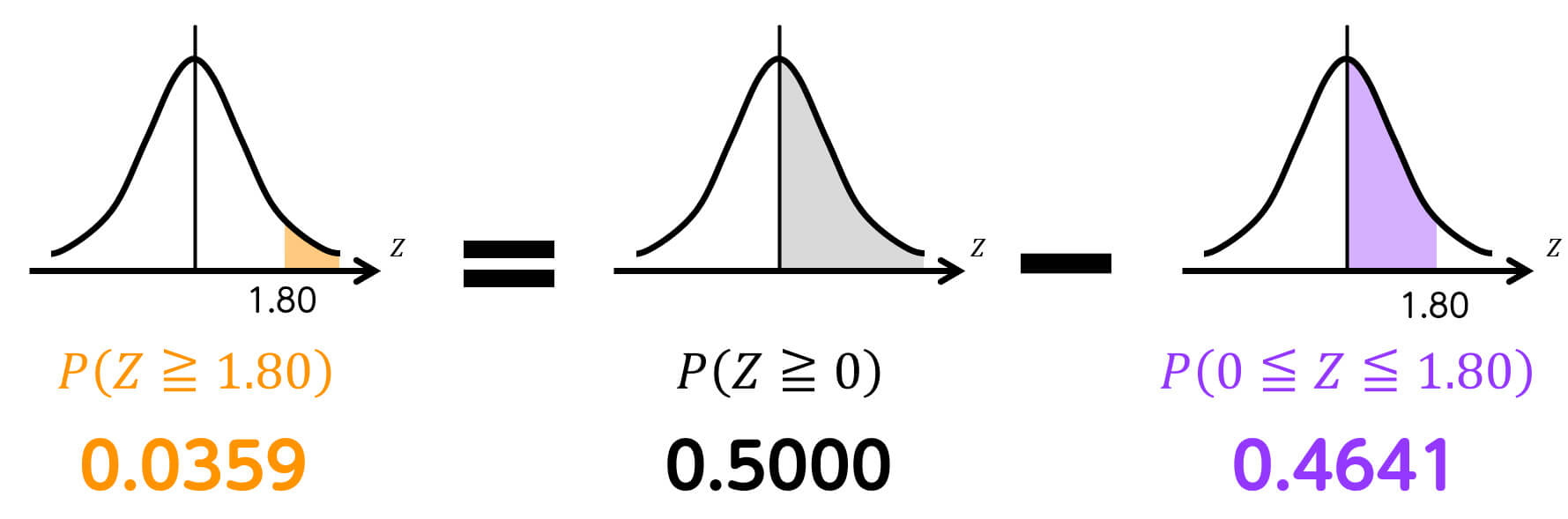
59回以上表が出る確率 \( P(X \geqq 59) \) は、標準偏差1.8個分以上大きくなる確率 \( P(Z \geqq 1.8) \) と等しいです。\[
P(X \geqq 59) = P(Z \geqq 1.8)
\]
この確率 \( P(Z \geqq 1.8) \) は、つぎの計算により求めることが出来ます。
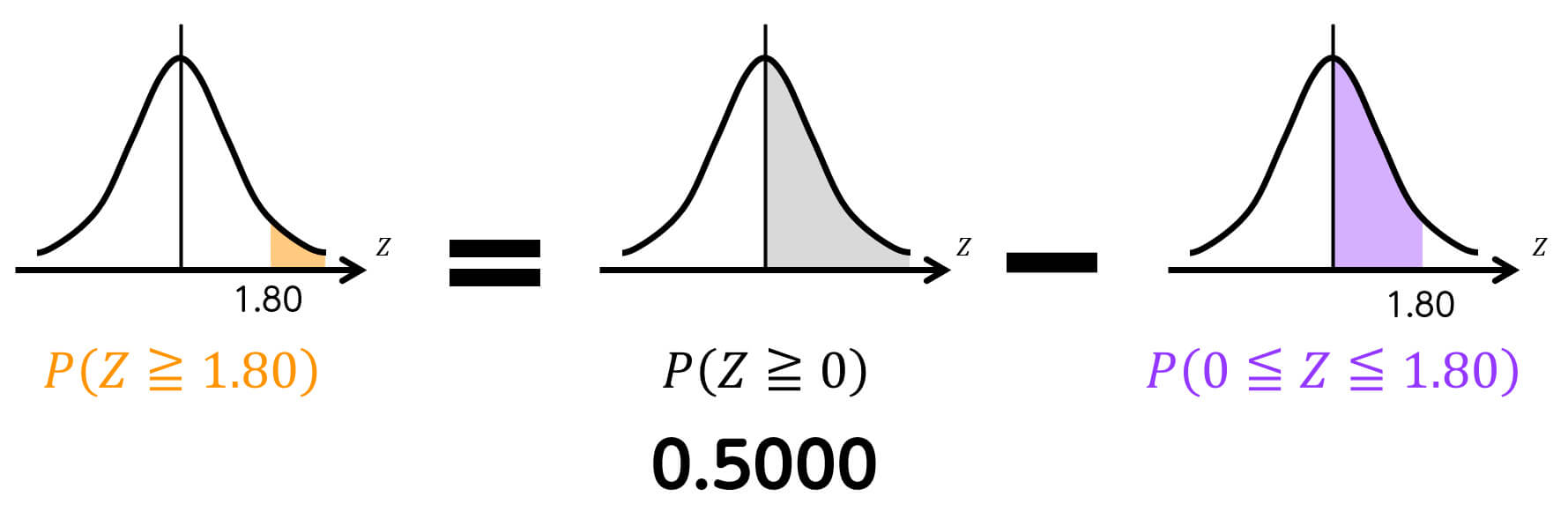
また、確率 \( P(0 \leqq Z \leqq 1.8) \) は正規分布表から 0.4641 と求められます。
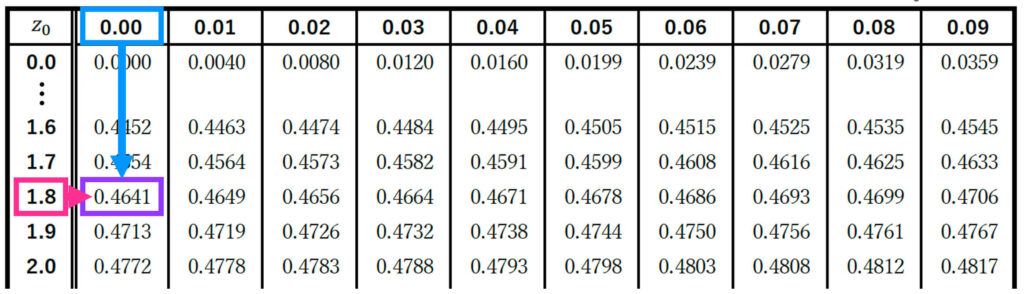
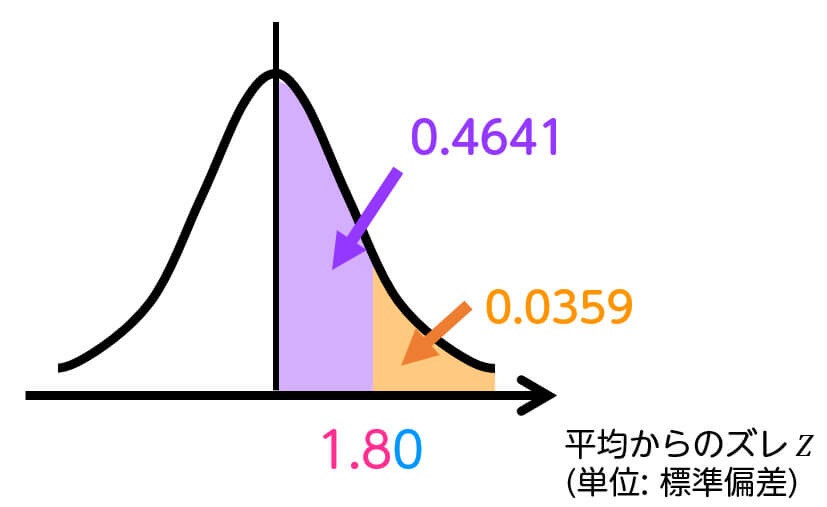
よって、59回以上表が出る確率は 0.0359 と求められます。
Step3. 結果の判定
確率 0.0359 は、有意水準5% (0.05) よりも小さいです。
このため、帰無仮説は棄却されます。(59回以上表が出る確率が5%よりも小さいため)
したがって、「表が出やすい硬貨である」と結論づけられます。
別解:\( Z \) で結果の判定をする方法
まず、表が出る回数59回に対応する \( Z \) の値を \( z \) とします。\[\begin{align*}
Z & = \frac{59 - 50}{5}
\\ & = 1.8
\end{align*}\]
つぎに、有意水準5%に対応する \( z_0 \) の値を求めます。ここで、\( z_0 \) とは、\( P( Z \geqq z_0 ) = 0.05 \) を満たす点です。
つぎに、\( z_0 \) の値を求めるために、次の変形を実施します。
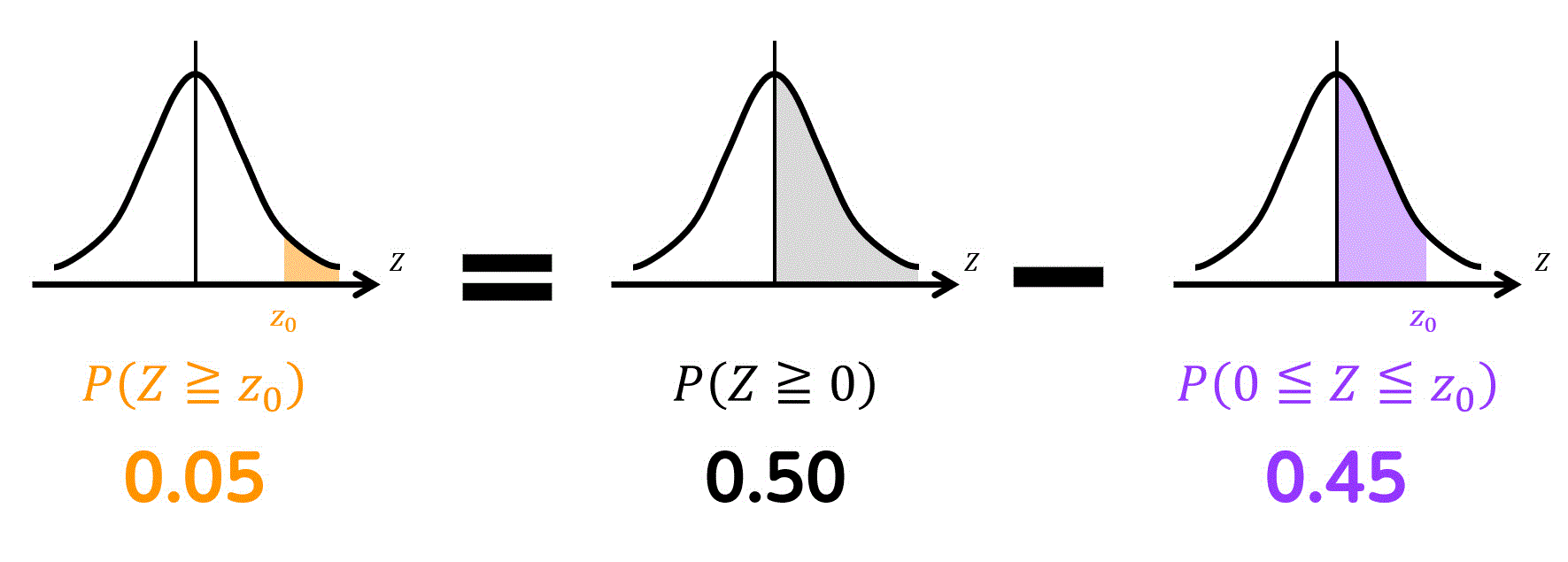
ここで、\( P( 0 \leqq Z \leqq z_0 ) = 0.45 \) を満たす点を正規分布表から探すと、\( z_0 = 1.64 \) と分かります。
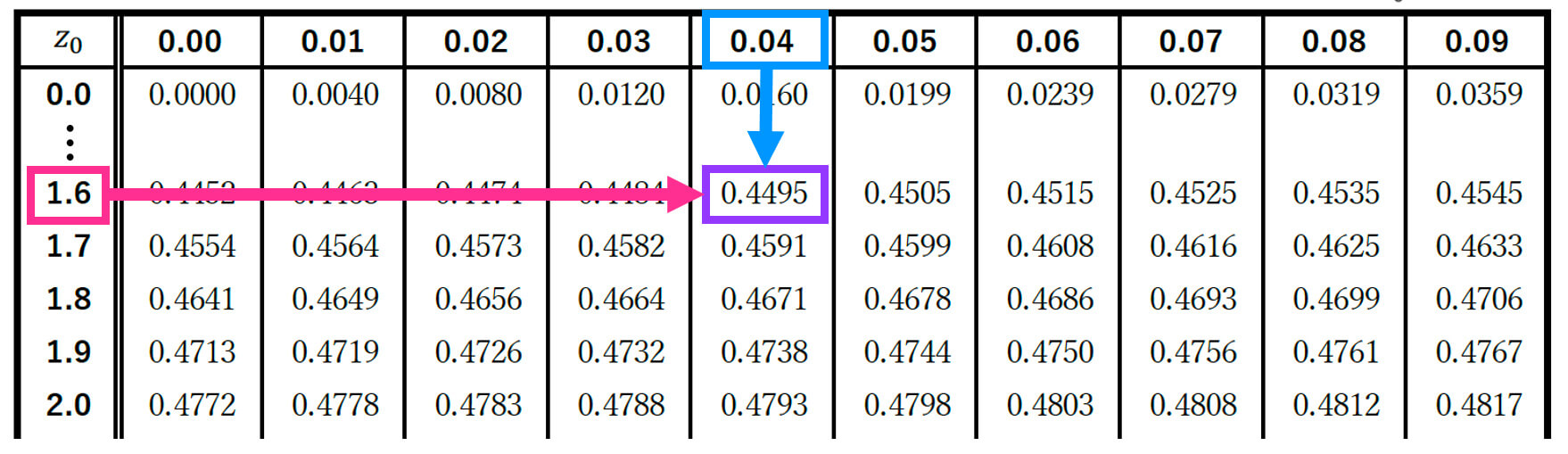
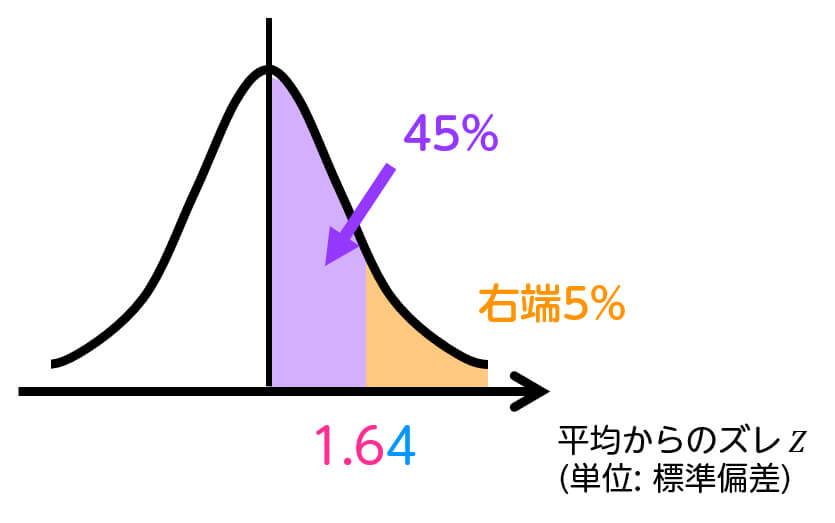
つまり、\( z \) の値が \( z_0 = 1.64 \) より大きければ仮説を棄却します。
ここで、\( z \) と \( z_0 \) の値を比較しましょう。\[
Z = 1.8 > 1.64 = z_0
\]
このため、帰無仮説は棄却されます。
したがって、「表が出やすい硬貨である」と結論づけられます。
5. 練習問題にチャレンジ
最後に、仮説検定について練習問題を解いてみましょう。共通テスト形式としています。
1の目が出やすいと言われているサイコロがある。
このサイコロに対して、1の目が出やすいか有意水準5%で仮説検定を実施する。
(1)
帰無仮説と対立仮説を設定する。すると、以下のようになる。
- 帰無仮説: 1の目が出る確率は [[ ア ]]
- 対立仮説: 1の目が出る確率は [[ イ ]]
※ 同じ選択肢を2度以上選んでもよい。
⓪ \( \frac{1}{6} \) である。
① \( \frac{1}{6} \) でない。
② \( \frac{1}{6} \) より大きい。
③ \( \frac{1}{6} \) より小さい。
(2)
サイコロを3回振ったところ、1の目が2回出た。
ここで、1の目が出る回数を \( X \) とする。帰無仮説が正しいと仮定したとき、つぎのように確率が計算できる。\[ P(X = 2) = \frac{ [ \ \ \ \text{ウ} \ \ \ ] }{ [ \ \ \ \text{エオ} \ \ \ ] } \]\[ P(X = 3) = \frac{ [ \ \ \ \text{カ} \ \ \ ] }{ [ \ \ \ \text{キクケ} \ \ \ ] } \]\[ P(X \geqq 2) = \frac{ [ \ \ \ \text{コ} \ \ \ ] }{ [ \ \ \ \text{サシ} \ \ \ ] } \]
よって、\( P(X \geqq 2) \) は [[ ス ]] なので、1の目が [[ セ ]]。
(3)
サイコロを720回振ったところ、1の目が137回出た。
1の目が出る回数を \( Y \) とする。帰無仮説が正しいと仮定したとき、\( Y \) は平均 [ ソタチ ]、標準偏差 [ ツテ ] の 二項分布に従う。
ここで、720回は十分に大きいと考えて良いので、\( Y \) は正規分布に近似的に従う。さらに、\( Z \) を次のようにおく。\[
Z = \frac{ Y - [ \ \ \ \text{ソタチ} \ \ \ ] }{ [ \ \ \ \text{ツテ} \ \ \ ] }
\]
すると、以下の式が成立する。\[\begin{align*}
P( X \geqq 127 ) & = P( Z \geqq [ \ \ \ \text{ト} \ \ \ ]. [ \ \ \ \text{ナニ} \ \ \ ] )
\\ & = 0.[ \ \ \ \text{ヌネノ} \ \ \ ]
\end{align*}\]
よって、\( P(X \geqq 3) \) は [[ ハ ]] なので、1の目が [[ ヒ ]]。
※ 同じ選択肢を2度以上選んでもよい。
⓪ \( \frac{1}{6} \) で出ると言える
① \( \frac{1}{6} \) で出るとは言えない
② 出やすいと言える
③ 出やすいとは言えない
④ 出にくいと言える
⑤ 出にくいと言えない
6. 練習問題の答え
(1) 帰無仮説と対立仮説の設定
★ 解答
ア: 0 ( \( \frac{1}{6} \) である。)
イ: 4 ( \( \frac{1}{6} \) より大きい。)
★ 解説
帰無仮説 \( H_0 \)
仮説検定をするために、1の目が他の目と同じ確率で出ることを仮定します。
対立仮説 \( H_1 \)
今回は「1の目が出やすいことを」を確認したいので、対立仮説は「\( \frac{1}{6} \) より大きい。」となります。(片側検定)
(2) 試行回数が少ないとき
★ 解答
ウ, エオ: 5, 72 ( \frac{5}{72} )
カ, キクケ: 1, 216 ( \frac{1}{216} )
コ, サシ: 2, 27 ( \frac{2}{27} )
ス: 0 (5%より大きい)
セ: 3 (出やすいとは言えない)
★ 解説
\[\begin{align*}
P(X=2) & = {}_3 \mathrm{C} _2 \times \left( \frac{1}{6} \right)^{2} \times \left( 1- \frac{1}{6} \right)^{1}
\\ & = 3 \times \frac{1}{36} \times \frac{5}{6}
\\ & = \frac{15}{216}
\\ & = \frac{5}{72}
\end{align*}\] (ウ … 5、エオ … 72)
\[\begin{align*}
P(X=3) & = {}_3 \mathrm{C} _3 \times \left( \frac{1}{6} \right)^{3} \times \left( 1- \frac{1}{6} \right)^{0}
\\ & = \left( \frac{1}{6} \right)^{3}
\\ & = \frac{1}{216}
\end{align*}\] (カ … 1、キクケ … 216)
\[\begin{align*}
P(X \geqq 2) & = P(X=2) + P(X=3)
\\ & = \frac{5}{72} + \frac{1}{216}
\\ & = \frac{16}{216}
\\ & = \frac{2}{27}
\end{align*}\] (コ … 2、サシ … 27)
片側検定なので、\( P( X \geqq 2 ) \) が有意水準5%よりも大きいか小さいか確認します[1]もし両側検定(1の目が出る確率が偏っているかどうかを調べたい場合)をする場合は、有意水準2.5%よりも大きいか小さいかを確認します。。\[
P(X \geqq 2) = \frac{2}{27} > \frac{1.35}{27} = 5\%
\](ス … 0)
よって、確率 \( P(X \geqq 2) \) は、「ス. ⓪ 5%より大きい」です。
このため、帰無仮説は棄却されません。(2回以上表が出る確率が、5%よりも小さいため)
したがって、1の目が「③ 出やすいとは言えない」と結論づけられます。
(3) 試行回数が多いとき
★ 解答
ソタチ: 120
ツテ: 10
ト.ナニ: 1.70
ヌネノ: 045
ハ: 1 (5%より小さい)
ヒ: 4 (出やすいと言える)
★ 解説
サイコロを720回振ったとき、1の目が出る回数を \( Y \) とすると、\( Y \) は二項分布に従います。
ここで、帰無仮説が正しいと仮定したとき、\( Y \) の平均 \( E(Y) \) 、分散 \( V(Y) \)、標準偏差 \( \sigma (Y) \) は次のように計算できます。\[\begin{align*}
E(Y) & = 720 \times \frac{1}{6}
\\ & = 120
\end{align*}\](ソタチ … 120)
\[\begin{align*}
V(Y) & = 720 \times \frac{1}{6} \times \left( 1 - \frac{1}{6} \right)
\\ & = 720 \times \frac{1}{6} \times \frac{5}{6}
\\ & = 100
\end{align*}\]
\[\begin{align*}
\sigma (Y) & = \sqrt{V(Y)}
\\ & = \sqrt{100}
\\ & = 10
\end{align*}\](ツテ … 10)
つぎに、以下の式の通り \( Z \) をおきます。\[
Z = \frac{X - 120}{10}
\]
ここで、\( X = 137 \) に対応する \( Z \) の値は、\[\begin{align*}
Z & = \frac{137 - 120}{10}
\\ & = 1.7
\end{align*}\]となります。
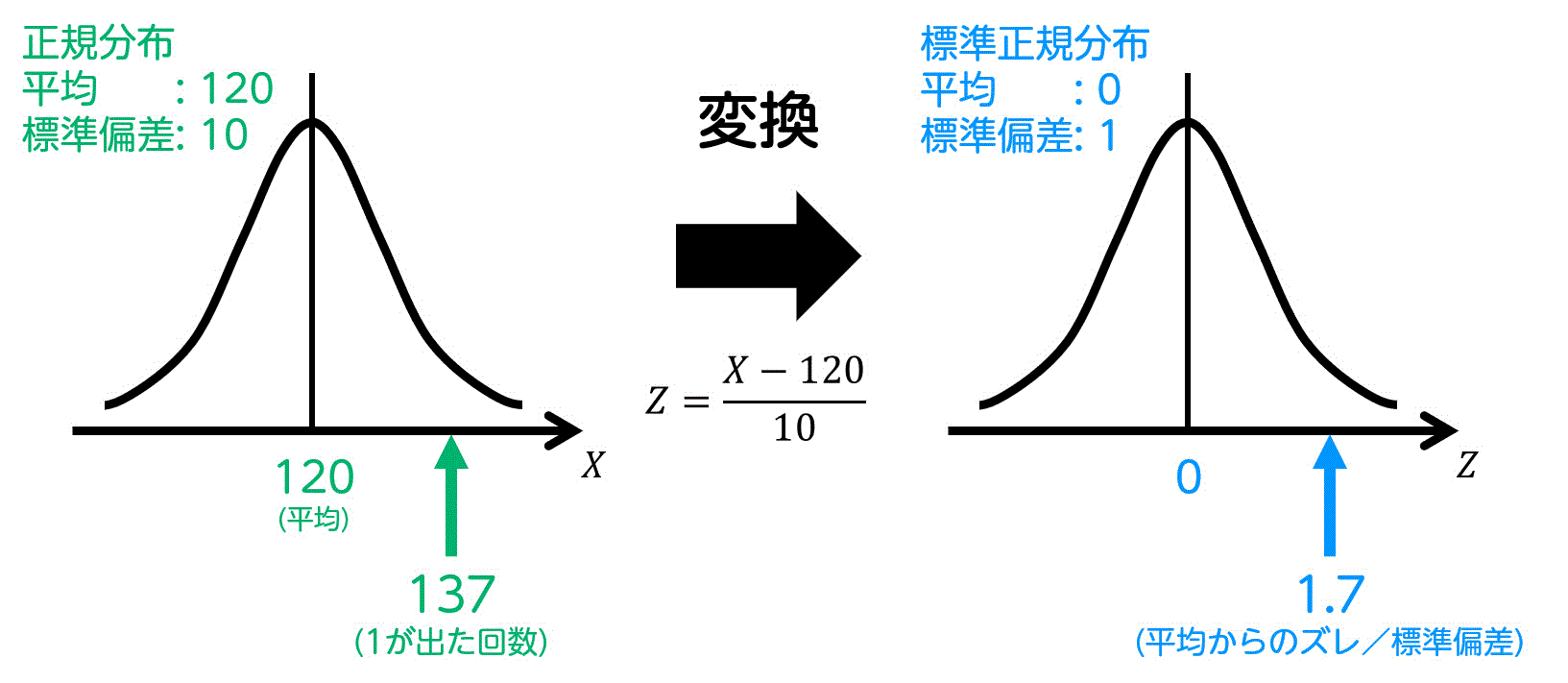
よって、サイコロで137回以上1の目が出る確率 \( P( X \geqq 137) \) は、標準偏差1.7個分以上大きくなる確率 \( P(Z \geqq 1.70) \) と等しくなります。\[
P( X \geqq 137) = P(Z \geqq 1.70)
\](トナニ … 170)
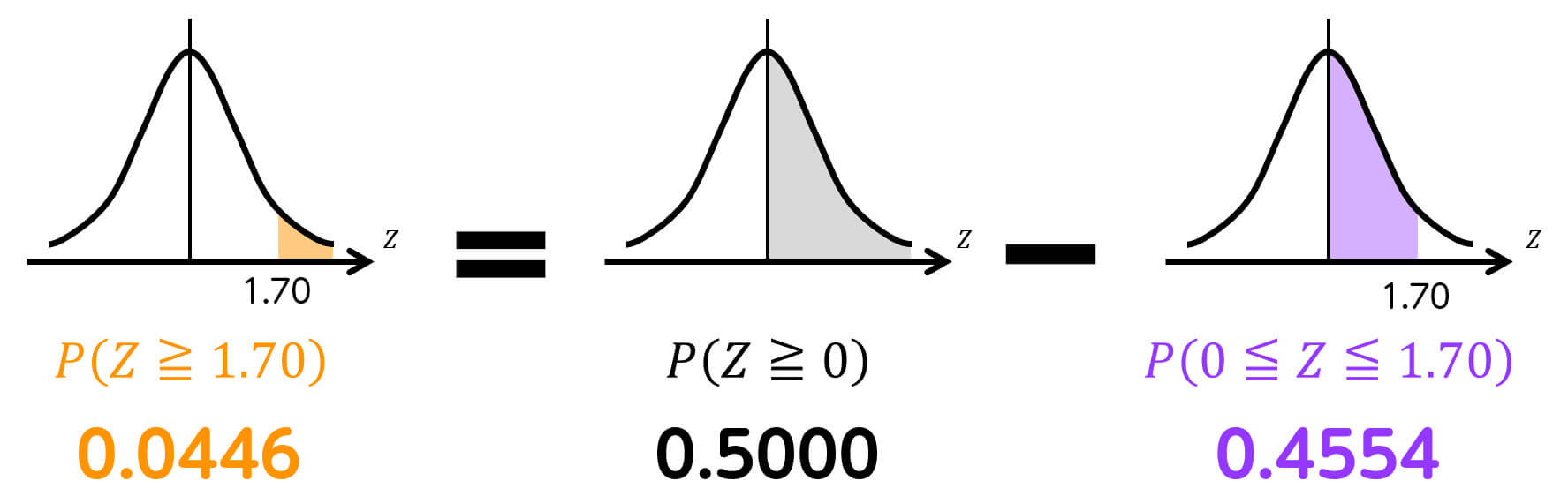
この確率 \( P(Z \geqq 1.70) は、つぎの計算により求めることが出来ます。
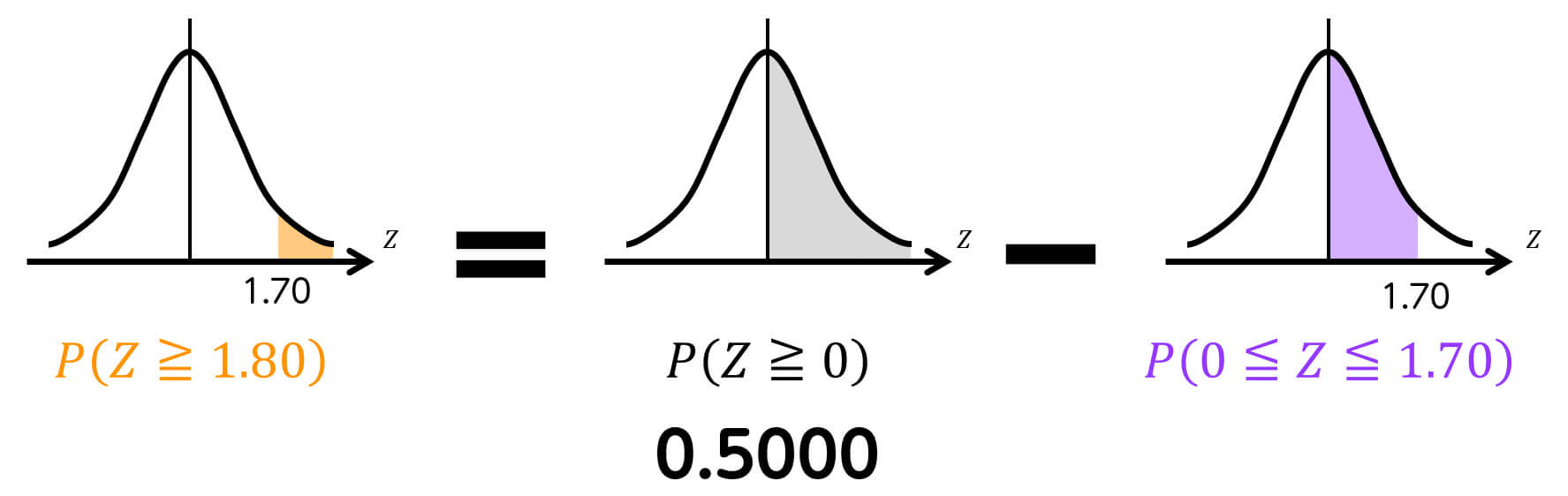
ここで、確率 \( P(0 \leqq Z \leqq 1.70) \) は正規分布表から 0.4554 と求められます。
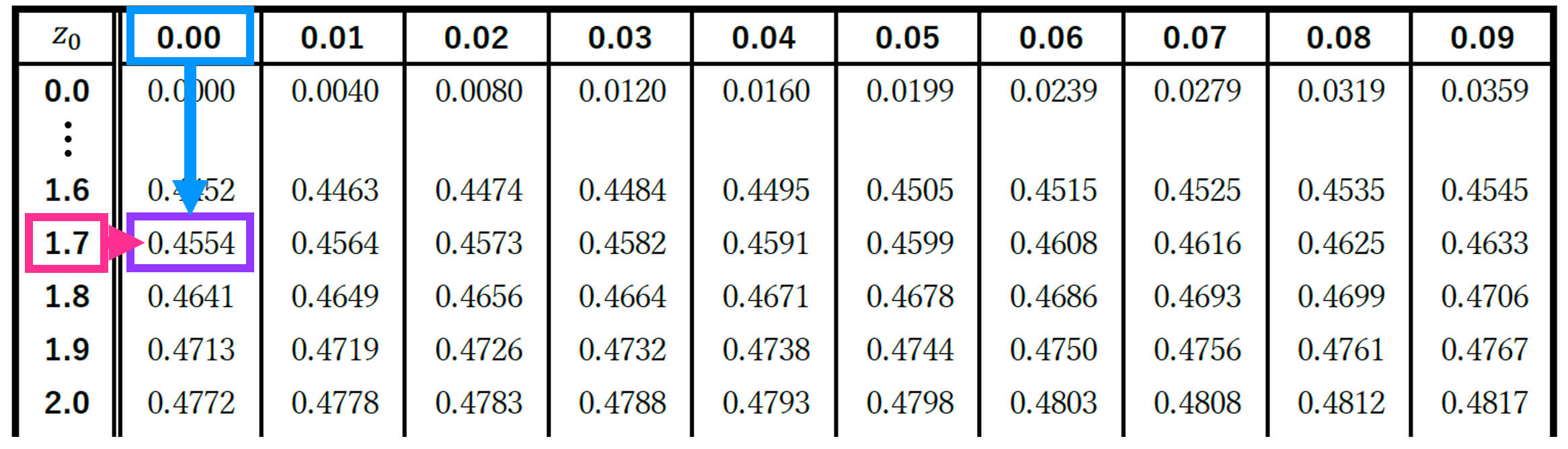
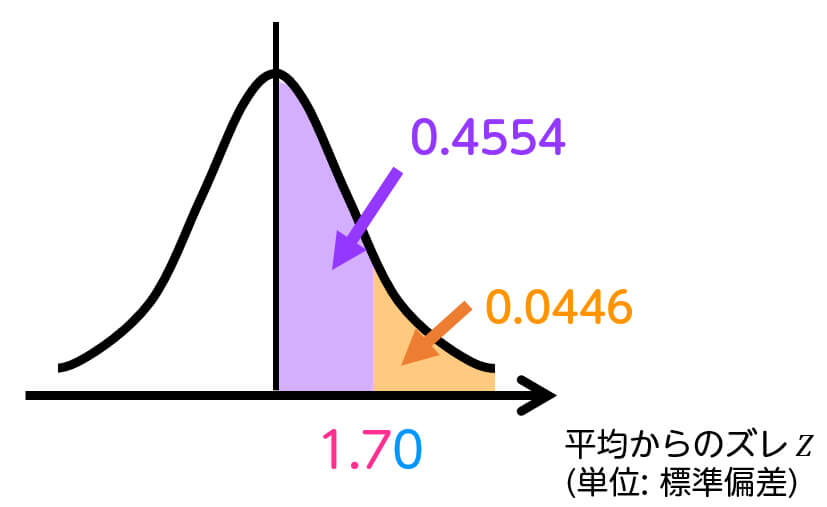
よって、137回以上表が出る確率は 0.045 と求められます。(ヌネノ … 045)
Step3. 結果の判定
確率 \( P( X \geqq 137) = 0.0446 \) は、有意水準「① 5%より小さい」です。
このため、帰無仮説は棄却されます。(137回以上表が出る確率が5%よりも小さいため)
したがって、1の目が「② 出やすいと言える」と結論づけられます。
注釈
| ↑1 | もし両側検定(1の目が出る確率が偏っているかどうかを調べたい場合)をする場合は、有意水準2.5%よりも大きいか小さいかを確認します。 |
|---|
関連広告・スポンサードリンク