スポンサードリンク
こんにちは、ももやまです。
今回から3回に分けて双曲線関数についてみていきましょう。
双曲線関数の初回となる今回は、下の赤い部分について解説をしていきます。
- 双曲線関数ってなに?
- 双曲線関数のグラフ
- 双曲線関数の基本変形公式
- 双曲線関数の加法定理
- 双曲線関数の2倍角・3倍角公式
- 双曲線関数の積和公式
- 双曲線関数の微分
- 双曲線関数の積分
- 双曲線関数のマクローリン展開
- 双曲線関数の逆関数
目次
スポンサードリンク
1. 双曲線関数ってなに??
(1) 双曲線関数が出てくるまで
[復習] 三角関数の定義
三角関数の \( \cos \theta \), \( \sin \theta \) は、下のように単位円 \( x^2 + y^2 = 1 \) 上のある点 \( (x,y) \) を \( (x,y) = ( \cos \theta , \sin \theta ) \) と定義することができます。
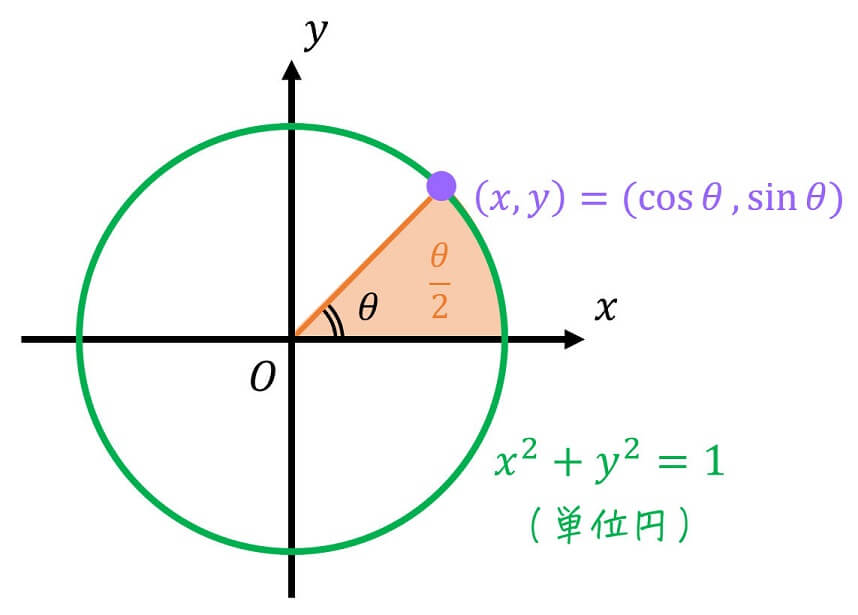
(オレンジ色部分の面積は \( \theta / 2 \) となる)
ここで、\( \theta \) は「\( x \) 軸」と「原点から \( (x,y) \) への線分」がなす角度に対応しています。さらに、「\( x \) 軸」、「原点から \( (x,y) \) への線分」、および「単位円の円周」に囲まれる部分の面積(オレンジ色部分)が \( \frac{ \theta }{2} \) になるのも特徴です。
また、\( \cos \theta \), \( \sin \theta \) から \( \tan \theta \) を\[
\tan \theta = \frac{ \sin \theta }{ \cos \theta }
\]とすることができます。
双曲線関数の定義
ここからが大学数学で出てくる新たな概念、双曲線関数の定義の説明に入ります。
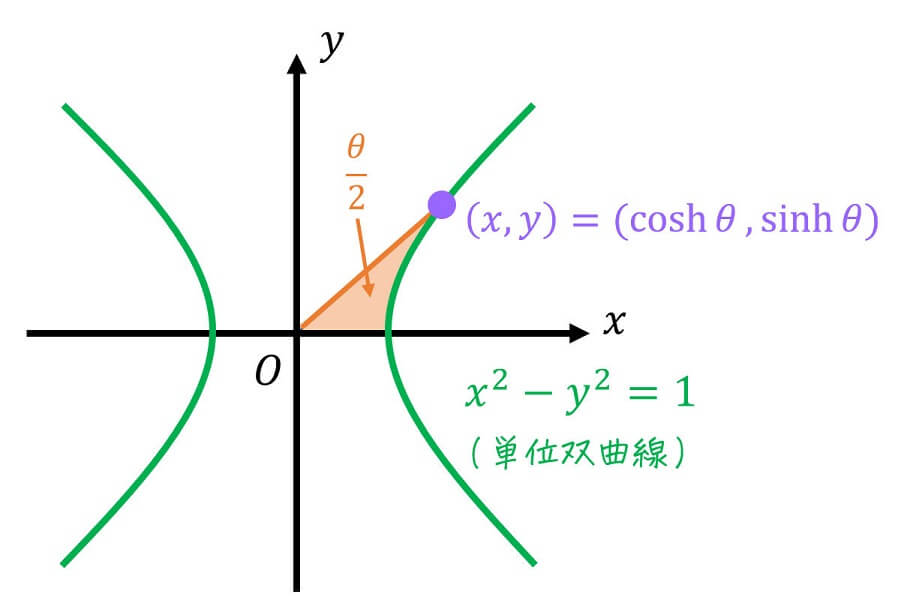
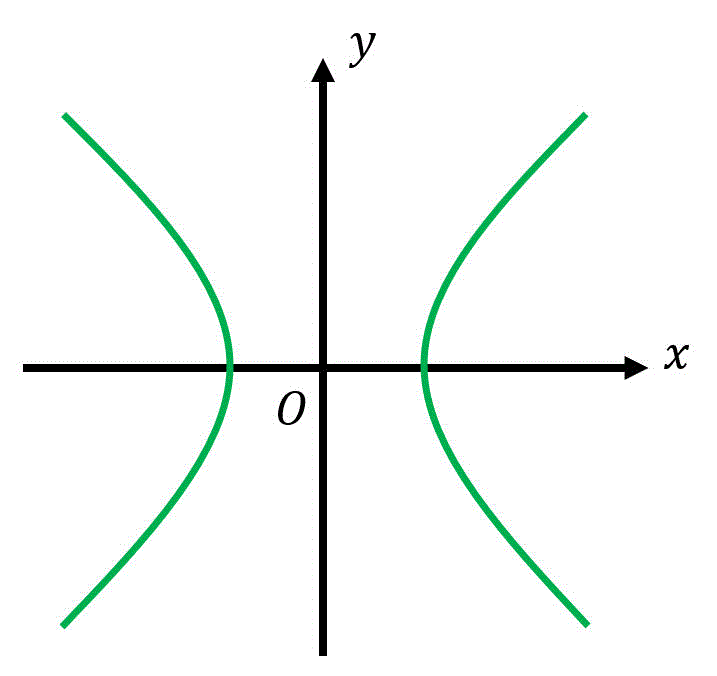
まず、双曲線の中でも最も基本的な形 \( x^2 - y^2 = 1 \) を考えます。この双曲線のことを単位双曲線と名付けましょうか。
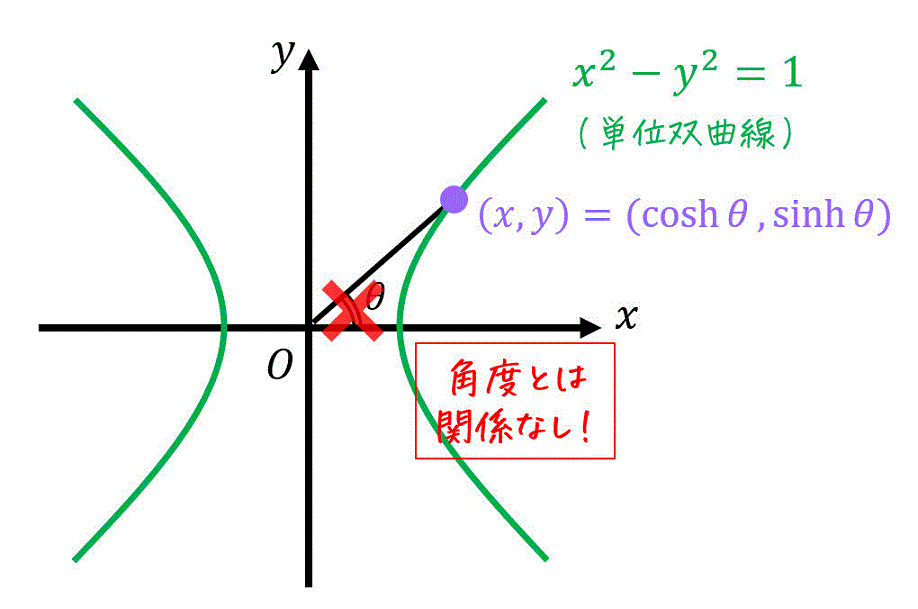
この単位双曲線上のある点 \( (x,y) \) を1つの変数 \( \theta \) で\[
(x,y) = ( \cosh \theta , \sinh \theta )
\]と対応づけるような関数 \( \cosh \theta \), \( \sinh \theta \) のことを双曲線関数と呼びます。

さらにこの \( \theta \) ですが、\( x \) 軸、原点と \( (x,y) \) のなす線分、双曲線 \( x^2 - y^2 = 1 \) が囲まれる部分が \( \frac{ \theta }{2} \) になる特徴があります。
ただし、三角関数のように \( \theta \) が角度に対応しているわけではないことに要注意です。
また、双曲線関数には \( \sinh \theta \), \( \cosh \theta \) のほかに \( \tanh \theta \) もあり、\[
\tanh \theta = \frac{ \sinh \theta }{ \cosh \theta }
\]で定義されます。
三角関数の公式\[
\tan \theta = \frac{ \sin \theta }{ \cos \theta }
\]にそっくりですね。
単位双曲線 \( x^2 - y^2 = 1 \) に対して、\( (x,y) = ( \cosh \theta , \sinh \theta ) \) と1つの変数 \( \theta \) を用いて対応づけることを考える。
このときに出てくる \( \cosh \theta \), \( \sinh \theta \) のことを双曲線関数と呼ぶ。
※ 定義より、必ず \( \cosh^2 \theta - \sinh^2 \theta = 1 \) が成立する[1]三角関数の \( \cos^2 \theta + \sin^2 \theta = 1 \) に近い形。。
また、双曲線関数には \( \tanh \theta \) もあり、\[
\tanh \theta= \frac{ \sinh \theta }{ \cosh \theta }
\]で定義される。
※ これ以降双曲線関数は \( \theta \) ではなく、\( x \) を用いて書くことにします。つまり、\( \cosh \theta \), \( \sinh \theta \) ではなく \( \sinh x \), \( \cosh x \) で書きます。
(2) 定義式の書き変え(この形で覚えよう)
\( \cosh^2 x - \sinh^2 x = 1 \) を満たすように \( \sinh x \), \( \cosh x \) を定義する、と言われても少し難しいですよね。
そこで、双曲線関数 \( \sinh x \), \( \cosh x \) ネイピア数 \( e \) を使うことで、次のように定義することもできます。
\[\begin{align*}
\sinh x & = \frac{ e^{x} - e^{-x} }{2} \\
\cosh x & = \frac{ e^{x} + e^{-x} }{2}
\end{align*}\]
さらに、\[
\tanh x = \frac{ \sinh x }{ \cosh x }
\]であることを利用して、\( \tanh x \) はつぎのように定義されます。
\[\begin{align*}
\tanh x & = \frac{ \sinh x}{ \cosh x } \ \left( \mathrm{これで頭に入れる!} \right)
\\ & = \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} } \ \left( \mathrm{基本形} \right)
\\ & = \frac{e^{2x} - 1}{ e^{2x} + 1} \ \left( \mathrm{基本形の分子分母に} \ e^{x} \ を掛けた形 \right)
\\ & = \frac{1 - e^{-2x}}{1 + e^{-2x}} \ \left( \mathrm{基本形の分子分母に} \ e^{-x} \ を掛けた形 \right)
\end{align*}\]
※ 一番上の形で覚えてから、残り3つは都度導出することをお勧めします。
(3) 練習問題にチャレンジ
ここで、双曲線関数に関する練習問題を1問解いてみましょう。
\( \sinh 1 \), \( \cosh 1 \), \( \tanh 1 \) の値を小数第2位まで求めなさい。ただし、 \( e = 2.72 \), \( e^{-1} = 0.37 \) とする。
[解説1]
定義式\[\begin{align*}
\sinh x & = \frac{ e^{x} - e^{-x} }{2} \\
\cosh x & = \frac{ e^{x} + e^{-x} }{2} \\
\tanh x & = \frac{ e^{x} - e^{-x} }{e^x + e^{-x}}
\end{align*}\]に \( x = 1 \) を代入してひたすら計算するだけ。
\[\begin{align*}
\sinh 1 & = \frac{ e^1 - e^{-1} }{2}
\\ & = \frac{ 2.72 - 0.37 }{2}
\\ & = \frac{ 2.35}{2}
\\ & = 1.175
\\ & \fallingdotseq 1.18
\end{align*}\]
\[\begin{align*}
\cosh 1 & = \frac{ e^1 + e^{-1} }{2}
\\ & = \frac{ 2.72 + 0.37 }{2}
\\ & = \frac{ 3.09 }{2}
\\ & = 1.545
\\ & \fallingdotseq 1.55
\end{align*}\]
\[\begin{align*}
\tanh 1 & = \frac{ e^1 - e^{-1} }{e^1 + e^{-1}}
\\ & = \frac{1.175}{1.545}
\\ & \fallingdotseq 0.76
\end{align*}\]
スポンサードリンク
2. 双曲線関数のグラフ
次に、双曲線関数 \( \sinh x \), \( \cosh x \), \( \tanh x \) がどのような値を取るかを見てみましょう。
赤色 → \( y = \sinh x \) のグラフ(奇関数)
青色 → \( y = \cosh x \) のグラフ(偶関数)
緑色 → \( y = \tanh x \) のグラフ(奇関数)
※ 偶関数は、\( y \) 軸対称のグラフで、\( f(x) = f(-x) \) が成立する関数。
奇関数は、原点対称のグラフで、\( f(x) =- f(-x) \) が成立する関数。
グラフの形の導出方法
微分をし、増減表を書くことで \( \sinh x \), \( \cosh x \), \( \tanh x \) のグラフを導出してみましょう。
sinh x のグラフ
\( f(x) = \sinh x \) とする。
[極限計算]\[\begin{align*}
f(x) & = \sinh x
\\ & = \frac{1}{2} (e^x - e^{-x} )
\end{align*}\]である。よって、\[\begin{align*}
\lim_{x \to - \infty} \frac{1}{2} ( \underbrace{ e^x }_{0} - \underbrace{ e^{-x} }_{ \infty } ) & = - \infty \\
\lim_{x \to \infty} \frac{1}{2} ( \underbrace{ e^x }_{ \infty } - \underbrace{ e^{-x} }_{ 0 } ) & = \infty
\end{align*}\]となるので、\( x \to - \infty \) では \( f(x) \) は負の無限大、\( x \to \infty \) では \( f(x) \) は正の無限大を取る。
\[
f(x) = \frac{1}{2} ( e^x - e^{-x} )
\]を微分する。
\[\begin{align*}
f'(x) = \frac{1}{2} ( e^x + e^{-x} )
\end{align*}\]となるので、常に \( f'(x) > 0 \)。よって、このグラフは単調増加。
\( f'(x) \) をさらにもう1回微分する。
\[\begin{align*}
f''(x) = \frac{1}{2} ( e^x - e^{-x} )
\end{align*}\]となる。ここで、両辺を \( 2 e^{x} \) 倍、つまり\[
2e^{x} f''(x) = e^{2x} -1
\]としても \( f''(x) \) の正負は変わらないため、\( e^{2x} - 1 \) の正負からグラフの凹凸を求める。
すると、
- \( e^{2x} - 1 = 0 \) を満たすような \( x \) は、\( x = 0 \) となる。よって、\( x = 0 \) は変曲点。
- \( x > 0 \) のとき、\( e^{2x} - 1 > 0 \) を満たす。よって、\( f''(x) > 0 \) も満たすため、下に凸となる。
- \( x < 0 \) のとき、\( e^{2x} - 1 < 0 \) を満たす。よって、\( f''(x) < 0 \) も満たすため、上に凸となる。
となる。
また、\( x = 0 \) のとき、\[\begin{align*}
f(0) & = \sinh 0
\\ & = \frac{1}{2} ( e^0 - e^0 )
\\ & = 0
\end{align*}\]となる。
よって、増減表は下のようになる。
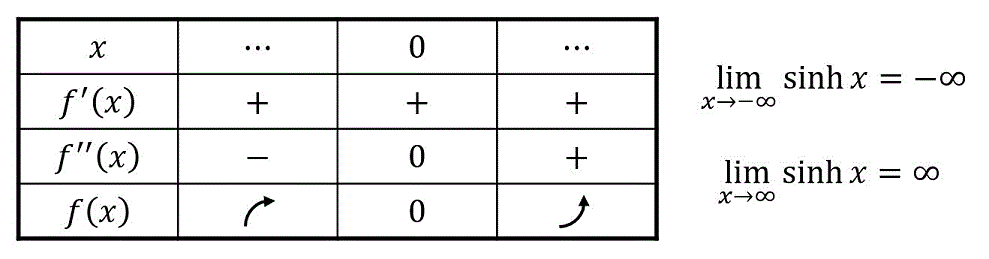
増減表より、\( \sinh x \) のグラフを下のように導出ができる。
cosh x のグラフ
\( f(x) = \cosh x \) とする。
[極限計算]\[\begin{align*}
f(x) & = \cosh x
\\ & = \frac{1}{2} (e^x + e^{-x} )
\end{align*}\]である。よって、\[\begin{align*}
\lim_{x \to \infty} \frac{1}{2} ( \underbrace{ e^x }_{0} + \underbrace{ e^{-x} }_{ \infty } ) & = \infty \\
\lim_{x \to \infty} \frac{1}{2} ( \underbrace{ e^x }_{ \infty } - \underbrace{ e^{-x} }_{ 0 } ) & = \infty
\end{align*}\]となるので、\( x \to - \infty \) では \( f(x) \) は正の無限大、\( x \to \infty \) でも \( f(x) \) は正の無限大を取る。
\[
f(x) = \frac{1}{2} ( e^x + e^{-x} )
\]を微分する。
\[\begin{align*}
f'(x) = \frac{1}{2} ( e^x - e^{-x} )
\end{align*}\]となる。ここで、両辺を \( 2 e^{x} \) 倍、つまり\[
2e^{x} f'(x) = e^{2x} -1
\]としても \( f'(x) \) の正負は変わらないため、\( e^{2x} - 1 \) の正負からグラフの傾きを求める。
すると、
- \( e^{2x} - 1 = 0 \) を満たすような \( x \) は、\( x = 0 \) となる。よって、\( x = 0 \) は極値。
- \( x > 0 \) のとき、\( e^{2x} - 1 > 0 \) を満たす。よって、\( f'(x) > 0 \) も満たすため、この部分では単調増加。
- \( x < 0 \) のとき、\( e^{2x} - 1 < 0 \) を満たす。よって、\( f'(x) < 0 \) も満たすため、この部分では単調減少。
となる。
[\( f'’(x) \) を計算し、グラフの凹凸を求める]\[\begin{align*}
f''(x) = \frac{1}{2} ( e^x + e^{-x} )
\end{align*}\]となるので、常に \( f''(x) > 0 \)。よって、このグラフは常に下に凸。
また、\( x = 0 \) のとき、\[\begin{align*}
f(0) & = \cosh 0
\\ & = \frac{1}{2} ( e^0 + e^0 )
\\ & = 1
\end{align*}\]となる。
よって、増減表は下のようになる。
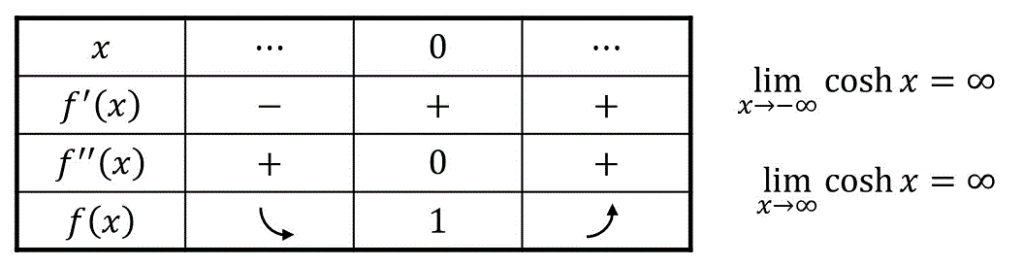
増減表より、\( \cosh x \) のグラフを下のように導出ができる。
tanh x のグラフ
\( f(x) = \tanh x \) とする。
ここで、\[\begin{align*}
f(x) & = \frac{ \sinh x}{ \cosh x }
\\ & = \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\\ & = \frac{e^{2x} - 1}{ e^{2x} + 1}
\\ & = \frac{1 - e^{-2x}}{1 + e^{-2x}}
\end{align*}\]と4パターンの式に変形できることを思い出す。
\[\begin{align*}
\lim_{x \to - \infty} f(x) & = \lim_{x \to - \infty} \frac{\textcolor{magenta}{e^{2x}} - 1}{ \textcolor{magenta}{e^{2x}} + 1}
\\ & = \frac{\textcolor{magenta}{0} - 1}{ \textcolor{magenta}{0} + 1}
\\ & = -1
\end{align*}\]
\[\begin{align*}
\lim_{x \to \infty} f(x) & = \lim_{x \to \infty} \frac{1 - \textcolor{magenta}{e^{-2x}} }{ 1 + \textcolor{magenta}{e^{-2x}} }
\\ & = \frac{1 - \textcolor{magenta}{0} }{ 1 + \textcolor{magenta}{0} }
\\ & = 1
\end{align*}\]
となるので、\( x \to - \infty \) では \( f(x) \) は-1、\( x \to \infty \) では \( f(x) \) は1を取る。
[\( f'(x) \) を計算し、グラフの傾きを求める]\[
f(x) = \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\]を微分する。
\[\begin{align*}
f'(x) & = \frac{ (e^{x} - e^{-x})' \cdot ( e^{x} + e^{-x} ) - (e^{x} - e^{-x}) \cdot ( e^{x} + e^{-x} )' }{ ( e^{x} + e^{-x} )^2 }
\\ & = \frac{ (e^x + e^{-x})^2 - (e^x - e^{-x})^2 }{ ( e^{x} + e^{-x} )^2 }
\\ & = \frac{ (e^{2x} + 2 + e^{-2x}) - (e^{2x} - 2 + e^{-2x}) }{ ( e^{x} + e^{-x} )^2 }
\\ & = \frac{ 4 }{ ( e^{x} + e^{-x} )^2 }
\end{align*}\]となる。
ここで、\( x \) の値にかかわらず、常に \( ( e^{x} + e^{-x} )^2 > 0 \) なので、\( f'(x) \) も常に \( f'(x) > 0 \) となる。よって、このグラフは単調増加である。
[\( f'’(x) \) を計算し、グラフの凹凸を求める]\( f'(x) \) をさらにもう1回微分する。
\[\begin{align*}
f''(x) & = \frac{ (4)' \cdot ( e^{x} + e^{-x} )^2 - 4 \cdot \left( (e^x + e^{-x})^2 \right)' }{ ( e^{x} + e^{-x} )^4 }
\\ & = \frac{ - 8 \cdot (e^x - e^{-x}) (e^x + e^{-x}) }{ ( e^{x} + e^{-x} )^4 }
\\ & = \frac{ - 8 (e^x - e^{-x}) }{ ( e^{x} + e^{-x} )^3 }
\end{align*}\]となる。
ここで、\( x \) の値にかかわらず、常に \( ( e^{x} + e^{-x} )^3 > 0 \) なので[2]\( e^x + e^{-x} > 0 \) となるため。、\( f''(x) \) の正負を判定するためには \( - 8 (e^x - e^{-x}) \) の正負を考えればよい。
- \( - 8 (e^x - e^{-x}) = 0 \) を満たすような \( x \) は、両辺を \( -\frac{1}{8} e^{x} \) 倍し、\( e^{2x} - 1 = 0 \) とすることで \( x = 0 \) と求められる。よって、\( x = 0 \) は変曲点。
- \( x > 0 \) のとき、\( e^x - e^{-x} > 0 \) となるので \( - 8 (e^x - e^{-x}) < 0 \) を満たす。よって、\( f'(x) < 0 \) となるため、この部分では上に凸。
- \( x < 0 \) のとき、\( e^x - e^{-x} < 0 \) となるので \( - 8 (e^x - e^{-x}) > 0 \) を満たす。よって、\( f'(x) > 0 \) となるため、この部分では下に凸。
また、\( x = 0 \) のとき、\[\begin{align*}
f(0) & = \tanh 0
\\ & = \frac{e^0 - e^0}{e^0 + e^0}
\\ & = 0
\end{align*}\]となる。
よって、増減表は下のようになる。
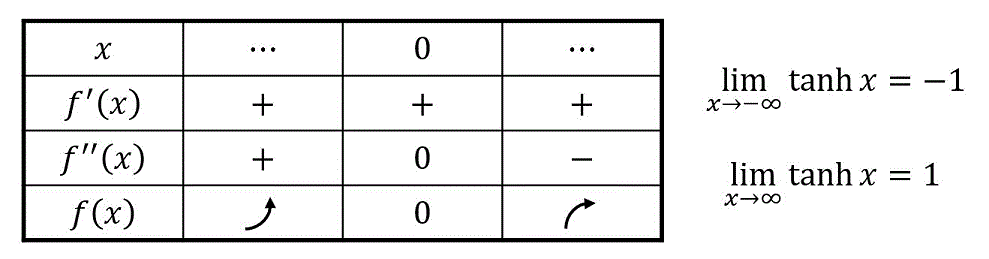
増減表より、\( \tanh x \) のグラフを下のように導出ができる。
スポンサードリンク
3. 双曲線関数の基本変形公式
ここでは、双曲線関数 \( \sinh x \), \( \cosh x \), \( \tanh x \) の変形公式を三角関数の公式と比較していきながら見ていきましょう。
\[
\cosh^2 x \textcolor{red}{-} \sinh^2 x = 1
\]\[
\tanh x = \frac{\sinh x }{\cosh x}
\]\[
1 \textcolor{red}{-} \tanh^2 x = \frac{1}{ \cosh^2 x }
\]
\[
\cos^2 x \textcolor{red}{+} \sin^2 x = 1
\]\[
\tan x = \frac{\sin x }{\cos x}
\]\[
1 \textcolor{red}{+} \tan^2 x = \frac{1}{ \cos^2 x }
\]
※ 色がついている部分が三角関数と微妙に違う部分です。
3番目の公式のみ、導出方法を載せておきます。
\[\begin{align*}
1 - \tanh^2 x & = 1 - \left( \frac{ \sinh x }{ \cosh x } \right)^2
\\ & = 1 - \frac{ \sinh^2 x }{ \cosh^2 x }
\\ & = \frac{ \cosh^2 - \sinh^2 x }{ \cosh^2 x }
\\ & = \frac{ 1 }{ \cosh^2 x }
\end{align*}\]
練習問題にチャレンジ
ここで、双曲線関数の基本変形についての練習問題を解いてみましょう。
次の(1), (2) の問いに答えなさい。
(1) \( \sinh x = 3 \) とする。このときの \( \cosh x \), \( \tanh x \) の値を求めなさい。
(2) \( \tanh x = \frac{1}{2} \) とする。このときの \( \cosh x \), \( \sinh x \) の値を求めなさい。
[解答]
(1)
基本公式 \( \cosh^2 x - \sinh^2 x = 1 \) を変形すると、\( \cosh^2 x = 1 + \sinh^2 x \) となる。
この式に \( \sinh x = 3 \) を代入すればOK。
よって、\[\begin{align*}
\cosh^2 x & = 1 + \sinh^2 x
\\ & = 1 + 3^2
\\ & = 10
\end{align*}\]
ここで、\( \cosh x > 0 \) なので、\( \cosh x = \sqrt{10} \) となる。
また、\[\begin{align*}
\tanh x & = \frac{ \sinh x }{ \cosh x }
\\ & = \frac{ 3 }{ \sqrt{10} }
\\ & = \frac{ 3 \sqrt{10} }{10}
\end{align*}\]と求められる。
(2)
基本公式 \( 1 - \tanh^2 x = \frac{1}{ \cosh^2 x } \) を変形すると、\[
\cosh^2 x = \frac{1}{1 - \tanh^2 x}
\]となる。
よって、\[\begin{align*}
\cosh^2 x & = \frac{1}{1 - \tanh^2 x}
\\ & = \frac{1}{1 - \left( \frac{1}{2} \right)^2 }
\\ & = \frac{1}{1 - \frac{1}{4} }
\\ & = \frac{1}{ \frac{3}{4} }
\\ & = \frac{4}{3}
\end{align*}が成立。
ここで、\( \cosh x > 0 \) なので、\[\begin{align*}
\cosh & = \frac{2}{ \sqrt{3} }
\\ & = \frac{ 2 \sqrt{3} }{3}
\end{align*}\]と求められる。
さらに、基本公式 \( \cosh^2 x - \sinh^2 x = 1 \) を変形すると、\( \sinh^2 x = \cosh^2 x - 1 \) となる。よって、\[\begin{align*}
\sinh^2 x & =\frac{4}{3} - 1
\\ & = \frac{1}{3}
\end{align*}\]となる。
ここで、\( \tanh x > 0 \) なので、\( \sinh x > 0 \) となる[3]\( \sinh x \) は \( \cosh x \) と異なり、\( x \) の値によっては負の値を取ることもある。そのため、\( \tanh x \) の正負(グラフより \( \tanh x \) と \( \sinh x … Continue reading。よって、\[\begin{align*}
\sinh x & = \frac{1}{ \sqrt{3} }
\\ & = \frac{ \sqrt{3} }{3}
\end{align*}\]となる。
4. 双曲線関数の加法定理
続いて加法定理を見ていきましょう。
加法定理は、この後の公式(2倍角、3倍角、半角)などのベースとなる公式の上に、導出がめんどくさいので覚えてしまいましょう。
ただし、三角関数と基本的には似ていますが一部符号が異なる部分があるので注意です。
\[\begin{align*}
\sinh ( \alpha + \beta ) & = \sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta \\
\sinh ( \alpha - \beta ) & = \sinh \alpha \cosh \beta - \cosh \alpha \sinh \beta \\
\cosh ( \alpha + \beta ) & = \cosh \alpha \cosh \beta \textcolor{red}{+} \sinh \alpha \sinh \beta \\
\cosh ( \alpha - \beta ) & = \cosh \alpha \cosh \beta \textcolor{red}{-} \sinh \alpha \sinh \beta \\
\tanh ( \alpha + \beta ) & = \frac{ \tanh \alpha + \tanh \beta }{ 1 \textcolor{red}{+} \tanh \alpha \tanh \beta } \\
\tanh ( \alpha - \beta ) & = \frac{ \tanh \alpha - \tanh \beta }{ 1 \textcolor{red}{-} \tanh \alpha \tanh \beta }
\end{align*}\]
\[\begin{align*}
\sin ( \alpha + \beta ) & = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\sin ( \alpha - \beta ) & = \sin \alpha \cos \beta - \cos \alpha \sin \beta \\
\cos ( \alpha + \beta ) & = \cos \alpha \cos \beta \textcolor{red}{-} \sin \alpha \sin \beta \\
\cos ( \alpha - \beta ) & = \cos \alpha \cos \beta \textcolor{red}{+} \sin \alpha \sin \beta \\
\tan ( \alpha + \beta ) & = \frac{ \tan \alpha + \tan \beta }{ 1 \textcolor{red}{-} \tan \alpha \tan \beta } \\
\tan ( \alpha - \beta ) & = \frac{ \tan \alpha - \tan \beta }{ 1 \textcolor{red}{+} \tan \alpha \tan \beta }
\end{align*}\]
[証明]
[1] \( \sinh ( \alpha + \beta ) = \sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta \) の証明\[\begin{align*}
\mathrm{ (左辺) } & = \frac{ e^{\alpha + \beta} - e^{- \alpha - \beta } }{2}
\end{align*}\]
\[\begin{align*}
\mathrm{ (右辺) } & = \left( \frac{ e^{\alpha} - e^{- \alpha} }{2} \right) \left( \frac{ e^{\beta} + e^{- \beta} }{2} \right) + \left( \frac{ e^{\alpha} + e^{- \alpha} }{2} \right) \left( \frac{ e^{\beta} - e^{- \beta} }{2} \right)
\\ & = \frac{1}{4} ( e^{\alpha + \beta} + e^{\alpha - \beta} - e^{- \alpha + \beta} - e^{- \alpha - \beta}) + \frac{1}{4} ( e^{\alpha + \beta} - e^{\alpha - \beta} + e^{- \alpha + \beta} - e^{- \alpha - \beta})
\\ & = \frac{2}{4} (e^{\alpha + \beta} - e^{- \alpha - \beta} )
\\ & = \frac{ e^{\alpha + \beta} - e^{- \alpha - \beta} }{2}
\\ & = \mathrm{(左辺)}
\end{align*}\]
\[\begin{align*}
\mathrm{ (左辺) } & = \frac{ e^{\alpha - \beta} - e^{- \alpha + \beta } }{2}
\end{align*}\]
\[\begin{align*}
\mathrm{ (右辺) } & = \left( \frac{ e^{\alpha} - e^{- \alpha} }{2} \right) \left( \frac{ e^{\beta} + e^{- \beta} }{2} \right) + \left( \frac{ e^{\alpha} + e^{- \alpha} }{2} \right) \left( \frac{ e^{\beta} - e^{- \beta} }{2} \right)
\\ & = \frac{1}{4} ( e^{\alpha + \beta} + e^{\alpha - \beta} - e^{- \alpha + \beta} - e^{- \alpha - \beta}) - \frac{1}{4} ( e^{\alpha + \beta} - e^{\alpha - \beta} + e^{- \alpha + \beta} - e^{- \alpha - \beta})
\\ & = \frac{2}{4} (e^{\alpha - \beta} - e^{- \alpha + \beta} )
\\ & = \frac{ e^{\alpha - \beta} - e^{- \alpha + \beta } }{2}
\\ & = \mathrm{(左辺)}
\end{align*}\]
\[\begin{align*}
\mathrm{ (左辺) } & = \frac{ e^{\alpha + \beta} + e^{- \alpha - \beta } }{2}
\end{align*}\]
\[\begin{align*}
\mathrm{ (右辺) } & = \left( \frac{ e^{\alpha} + e^{- \alpha} }{2} \right) \left( \frac{ e^{\beta} + e^{- \beta} }{2} \right) + \left( \frac{e^{\alpha} - e^{- \alpha} }{2} \right) \left( \frac{e^{\beta} - e^{- \beta} }{2} \right)
\\ & = \frac{1}{4} ( e^{\alpha + \beta} + e^{\alpha - \beta} + e^{- \alpha + \beta} + e^{- \alpha - \beta}) + \frac{1}{4} ( e^{\alpha + \beta} - e^{\alpha - \beta} - e^{- \alpha + \beta} + e^{- \alpha - \beta})
\\ & = \frac{2}{4} (e^{\alpha + \beta} + e^{- \alpha - \beta} )
\\ & = \frac{ e^{\alpha + \beta} + e^{- \alpha - \beta} }{2}
\\ & = \mathrm{(左辺)}
\end{align*}\]
\[\begin{align*}
\mathrm{ (左辺) } & = \frac{ e^{\alpha - \beta} + e^{- \alpha + \beta } }{2}
\end{align*}\]
\[\begin{align*}
\mathrm{ (右辺) } & = \left( \frac{ e^{\alpha} + e^{- \alpha} }{2} \right) \left( \frac{ e^{\beta} + e^{- \beta} }{2} \right) + \left( \frac{e^{\alpha} - e^{- \alpha} }{2} \right) \left( \frac{e^{\beta} - e^{- \beta} }{2} \right)
\\ & = \frac{1}{4} ( e^{\alpha + \beta} + e^{\alpha - \beta} + e^{- \alpha + \beta} + e^{- \alpha - \beta}) - \frac{1}{4} ( e^{\alpha + \beta} - e^{\alpha - \beta} - e^{- \alpha + \beta} + e^{- \alpha - \beta})
\\ & = \frac{2}{4} (e^{\alpha - \beta} + e^{- \alpha + \beta} )
\\ & = \frac{ e^{\alpha - \beta} + e^{- \alpha + \beta } }{2}
\\ & = \mathrm{(左辺)}
\end{align*}\]
\tanh ( \alpha + \beta ) = \frac{ \tanh \alpha + \tanh \beta }{ 1 \textcolor{red}{+} \tanh \alpha \tanh \beta }
\]の証明
\[\begin{align*}
\mathrm{ (左辺) } & = \tanh ( \alpha + \beta )
\\ & = \frac{ \sinh ( \alpha + \beta ) }{ \cosh ( \alpha + \beta ) }
\\ & = \frac{ \sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta }{ \cosh \alpha \cosh \beta + \sinh \alpha \sinh \beta }
\\ & = \frac{ (\sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta) \cdot \frac{1}{ \cosh \alpha \cosh \beta } }{ (\cosh \alpha \cosh \beta + \sinh \alpha \sinh \beta) \cdot \frac{1}{ \cosh \alpha \cosh \beta } }
\\ & = \frac{ \frac{\sinh \alpha}{\cosh \alpha} + \frac{\sinh \beta}{\cosh \beta} }{ 1 + \frac{\sinh \alpha}{\cosh \alpha} \cdot \frac{\sinh \beta}{\cosh \beta} }
\\ & = \frac{ \tanh \alpha + \tanh \beta }{ 1 + \tanh \alpha \tanh \beta }
\\ & = \mathrm{(右辺)}
\end{align*}\]
手順としては、
- \( \tanh x = \frac{\sinh x }{ \cosh x } \) の公式を適用
- 加法定理で \( \sinh ( \alpha + \beta ) \), \( \cosh ( \alpha + \beta ) \) を分解する
- 分子分母 \( \cosh \alpha \cosh \beta \) で割る
で証明が可能です。
[6] \[\tanh ( \alpha - \beta ) = \frac{ \tanh \alpha - \tanh \beta }{ 1 \textcolor{red}{-} \tanh \alpha \tanh \beta }
\]の証明
\[\begin{align*}
\mathrm{ (左辺) } & = \tanh ( \alpha - \beta )
\\ & = \frac{ \sinh ( \alpha - \beta ) }{ \cosh ( \alpha - \beta ) }
\\ & = \frac{ \sinh \alpha \cosh \beta - \cosh \alpha \sinh \beta }{ \cosh \alpha \cosh \beta - \sinh \alpha \sinh \beta }
\\ & = \frac{ (\sinh \alpha \cosh \beta - \cosh \alpha \sinh \beta) \cdot \frac{1}{ \cosh \alpha \cosh \beta } }{ (\cosh \alpha \cosh \beta - \sinh \alpha \sinh \beta) \cdot \frac{1}{ \cosh \alpha \cosh \beta } }
\\ & = \frac{ \frac{\sinh \alpha}{\cosh \alpha} - \frac{\sinh \beta}{\cosh \beta} }{ 1 - \frac{\sinh \alpha}{\cosh \alpha} \cdot \frac{\sinh \beta}{\cosh \beta} }
\\ & = \frac{ \tanh \alpha - \tanh \beta }{ 1 - \tanh \alpha \tanh \beta }
\\ & = \mathrm{(右辺)}
\end{align*}\]※ 符号が変わる以外は \( \tanh ( \alpha + \beta ) \) のときと証明過程は全く同じです。
5. 双曲線関数の2倍角公式
加法定理から簡単に導けるので覚える必要はありません。聞かれたら加法定理からその場で導出しましょう。
\[\begin{align*}
\sinh 2x & = 2 \sinh x \cosh x \\
\cosh 2x & = \cosh^2 x \textcolor{red}{+} \sinh^2 x
\\ & = 2 \cosh^2 x - 1
\\ & = 1 \textcolor{red}{+} 2 \sinh^2 x \\
\tanh 2x & = \frac{ 2 \tanh x }{1 \textcolor{red}{+} \tanh^2 x}
\end{align*}\]
\[\begin{align*}
\sin 2x & = 2 \sin x \cos x \\
\cos 2x & = \cos^2 x \textcolor{red}{-} \sin^2 x
\\ & = 2 \cos^2 x - 1
\\ & = 1 \textcolor{red}{-} 2 \sin^2 x \\
\tan 2x & = \frac{ 2 \tan x }{1\textcolor{red}{-} \tan^2 x }
\end{align*}\]
加法定理\[
\sinh ( \alpha + \beta ) = \sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta
\]に、\( \alpha = x \), \( \beta = x \) を代入。
すると、\[\begin{align*}
\sinh 2x & = \sinh (x+x)
\\ & = \sinh x \cosh x + \cosh x \sinh x
\\ & = 2 \sinh x \cosh x
\end{align*}\]と導出できる。
加法定理\[
\cosh ( \alpha + \beta ) = \cosh \alpha \cosh \beta + \sinh \alpha \sinh \beta
\]に、\( \alpha = x \), \( \beta = x \) を代入。
すると、\[\begin{align*}
\cosh 2x & = \cosh (x+x)
\\ & = \cosh x \cosh x + \sinh x \sinh x
\\ & = \cosh^2 x + \sinh^2 x
\end{align*}\]と導出できる。
さらに、\( \cosh^2 x - \sinh^2 x = 1 \) を使うことで、残り2種類の公式も導出可能。
\[\begin{align*}
\cosh 2x & = \cosh^2 x + \sinh^2 x
\\ & = \cosh^2 x + \sinh^2 x - 1 + (\cosh^2 x - \sinh^2 x )
\\ & = 2 \cosh^2 x - 1
\end{align*}\]
\[\begin{align*}
\cosh 2x & = \cosh^2 x + \sinh^2 x
\\ & = \cosh^2 x + \sinh^2 x + 1 - (\cosh^2 x - \sinh^2 x )
\\ & = 1 + 2 \sinh^2 x
\end{align*}\]
加法定理\[
\tanh ( \alpha + \beta ) = \frac{ \tanh \alpha + \tanh \beta }{ 1 \textcolor{red}{+} \tanh \alpha \tanh \beta }
\]に、\( \alpha = x \), \( \beta = x \) を代入。
\[\begin{align*}
\tanh 2x & = \tanh (x+x)
\\ & = \frac{ \tanh x + \tanh x }{ 1 + \tanh x \tanh x }
\\ & = \frac{ 2 \tanh x }{ 1 + \tanh^2 x }
\end{align*}\]
6. 双曲線関数の3倍角公式
加法定理と2倍角の公式から導ける上に出てくる頻度がめったにないので覚える必要はありません。聞かれたら加法定理からその場で導出しましょう。
\[\begin{align*}
\sinh 3x & = 3 \sinh x \textcolor{red}{+} 4 \sinh^3 x \\
\cosh 3x & = 4 \cosh^3 x - 3 \cosh x \\
\tanh 3x & = \frac{ 3 \tanh x \textcolor{red}{+} \tanh^3 x }{1 \textcolor{red}{+} 3 \tanh^2 x}
\end{align*}\]
\[\begin{align*}
\sin 3x & = 3 \sin x \textcolor{red}{-} 4 \sin^3 x \\
\cos 3x & = 4 \cos^3 x - 3 \cos x \\
\tan 3x & = \frac{3 \tan x \textcolor{red}{-} \tan^3 x}{1 \textcolor{red}{-} 3 \tan^2 x}
\end{align*}\]
※ \( \tan 3x \) の加法定理は高校でも習っている人は少ないと思います。
加法定理\[
\sinh ( \alpha + \beta ) = \sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta
\]に、\( \alpha =2x \), \( \beta = x \) を代入。
さらに、倍角の公式、双曲線関数の基本変形公式\[\begin{align*}
\sinh 2x & = 2 \sinh x \cosh x \\
\cosh 2x & = 1 \textcolor{red}{+} 2 \sinh^2 x \\
\cosh^2 x & = 1 + \sinh^2 x \ \ \ (\because \cosh^2 x - \sinh^2 x = 1)
\end{align*}\]を利用。
すると、\[\begin{align*}
\sinh 3x & = \sinh (2x+x)
\\ & = \sinh 2x \cosh x + \cosh2x \sinh x
\\ & = ( 2 \sinh x \cosh x ) \cosh x + (1 + 2 \sinh^2 x) \sinh x
\\ & = 2 \sinh x \cosh^2 x + \sinh x + 2 \sinh^3 x
\\ & = 2 \sinh x (1 + \sinh^2 x) + \sinh x + 2 \sinh^3 x
\\ & = 2 \sinh x + 2 \sinh^3 x + \sinh x + 2 \sinh^3 x
\\ & = 3 \sinh x + 4 \sinh^3 x
\end{align*}\]と導出できる。
加法定理\[
\cosh ( \alpha + \beta ) = \cosh \alpha \cosh \beta + \sinh \alpha \sinh \beta
\]に、\( \alpha =2x \), \( \beta = x \) を代入。
さらに、倍角の公式、双曲線関数の基本変形公式\[\begin{align*}
\sinh 2x & = 2 \sinh x \cosh x \\
\cosh 2x & = 2 \cosh^2 x - 1 \\
\sinh^2 x & = \cosh^2 x - 1 \ \ \ (\because \cosh^2 x - \sinh^2 x = 1)
\end{align*}\]を利用。
すると、\[\begin{align*}
\cosh 3x & = \cosh (2x+x)
\\ & = \cosh 2x \cosh x + \sinh 2x \sinh x
\\ & = \cosh 2x \cosh x + \sinh 2x \sinh x
\\ & = (2 \cosh^2 x - 1) \cosh x + (2 \sinh x \cosh x) \sinh x
\\ & = 2 \cosh^3 x - \cosh x + 2 \sinh^2 x \cosh x
\\ & = 2 \cosh^3 x - \cosh x + 2 (\cosh^2 x - 1) \cosh x
\\ & = 2 \cosh^3 x - \cosh x + 2 \cosh^3 x - 2 \cosh x
\\ & = 4 \cosh^3 - 3 \cosh x
\end{align*}\]と導出できる。
加法定理\[
\tanh ( \alpha + \beta ) = \frac{ \tanh \alpha + \tanh \beta }{ 1 \textcolor{red}{+} \tanh \alpha \tanh \beta }
\]に、\( \alpha =2x \), \( \beta = x \) を代入。
さらに、倍角の公式\[\begin{align*}
\tanh 2x = \frac{ 2 \tanh x }{1 + \tanh^2 x}
\end{align*}\]を利用。
すると、\[\begin{align*}
\tanh 3x & = \tanh (2x+x)
\\ & = \frac{ \tanh 2x + \tan x }{ 1 + \tanh 2x \tanh x }
\\ & = \frac{ \frac{ 2 \tanh x }{1 + \tanh^2 x} + \tanh x }{ 1 + \frac{ 2 \tanh x }{1 + \tanh^2 x} \cdot \tanh x }
\\ & = \frac{ \frac{ 2 \tanh x + \tanh x (1 + \tanh^2 x) }{1 + \tanh^2 x} }{ \frac{ 1 + \tanh^2 x + 2 \tanh^2 x }{1 + \tanh^2 x} }
\\ & = \frac{ 2 \tanh x + \tanh x (1 + \tanh^2 x) }{ 1 + \tanh^2 x + 2 \tanh^2 x }
\\ & = \frac{ 2 \tanh x + \tanh + \tanh^3 x }{ 1 + 3 \tanh^2 x }
\\ & = \frac{ 3 \tanh x + \tanh^3 x }{ 1 + 3 \tanh^2 x }
\end{align*}\]と導出できる。
7. 双曲線関数の積和公式
積分をするときにもしかしたら使うかもしれない公式ですが、加法定理から導出できるので導出方法だけ確認しておきましょう。
\[\begin{align*}
\sinh \alpha \cosh \beta & = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) + \sinh ( \alpha - \beta ) \right\} \\
\cosh \alpha \sinh \beta & = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) - \sinh ( \alpha - \beta ) \right\} \\
\cosh \alpha \cosh \beta & = \frac{1}{2} \left\{ \cosh ( \alpha + \beta ) + \cosh ( \alpha - \beta ) \right\} \\
\sinh \alpha \sinh \beta & = \frac{1}{2} \left\{ \cosh ( \alpha + \beta ) - \cosh ( \alpha - \beta ) \right\}
\end{align*}\]
※ 4番目の公式のみ、三角関数の積和公式と符号が微妙に異なるため要注意。
\[\begin{align*}
\sin \alpha \cos \beta & = \frac{1}{2} \left\{ \sin ( \alpha + \beta ) + \sin ( \alpha - \beta ) \right\} \\
\cos \alpha \sin \beta & = \frac{1}{2} \left\{ \sin ( \alpha + \beta ) - \sin ( \alpha - \beta ) \right\} \\
\cos \alpha \cos \beta & = \frac{1}{2} \left\{ \cos ( \alpha + \beta ) + \cos ( \alpha - \beta ) \right\} \\
\sin \alpha \sin \beta & = \textcolor{red}{-} \frac{1}{2} \left\{ \cos ( \alpha + \beta ) - \cos ( \alpha - \beta ) \right\}
\end{align*}\]
※ \( tan 3x \) の加法定理は高校でも習っている人は少ないと思います。
\sinh \alpha \cosh \beta = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) + \sinh ( \alpha - \beta ) \right\}
\]の導出
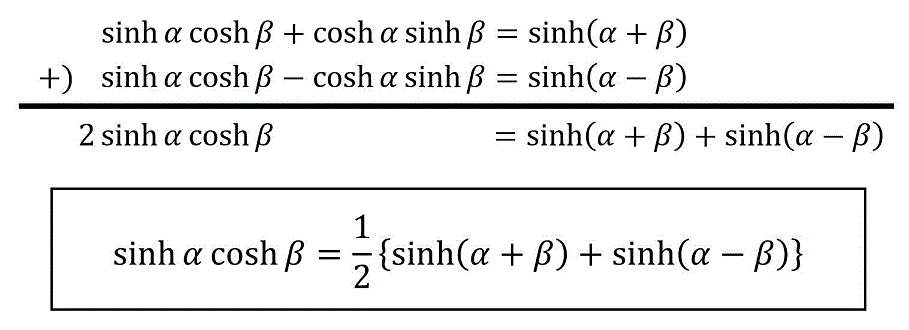
\cosh \alpha \sinh \beta = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) - \sinh ( \alpha - \beta ) \right\}
\]の導出
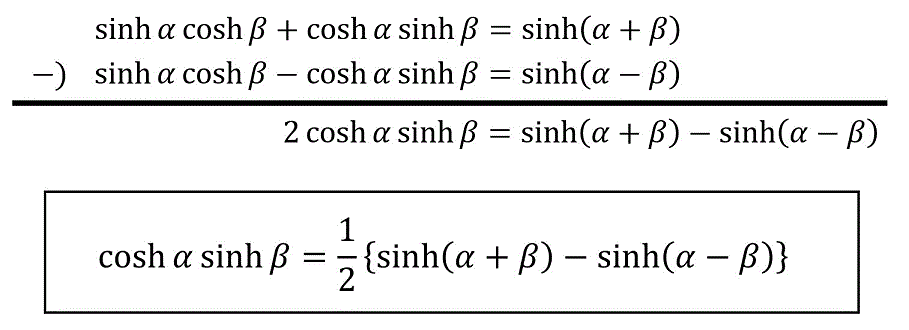
\cosh \alpha \cosh \beta = \frac{1}{2} \left\{ \cosh ( \alpha + \beta ) + \cosh ( \alpha - \beta ) \right\}
\]の導出
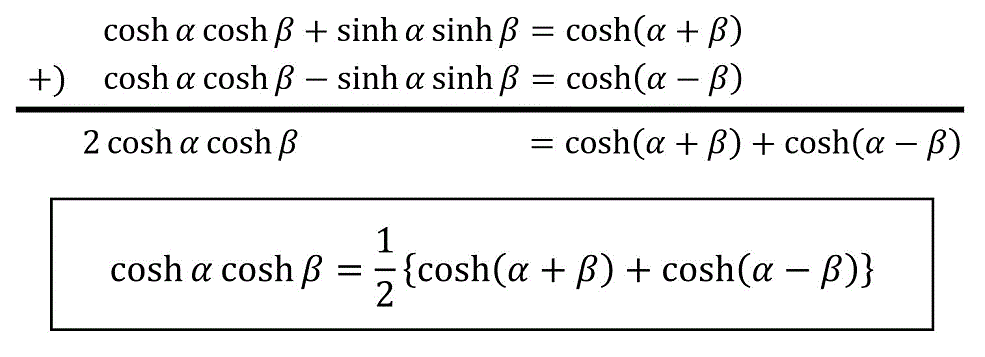
\sinh \alpha \sinh \beta = \frac{1}{2} \left\{ \cosh ( \alpha + \beta ) - \cosh ( \alpha - \beta ) \right\}
\]の導出
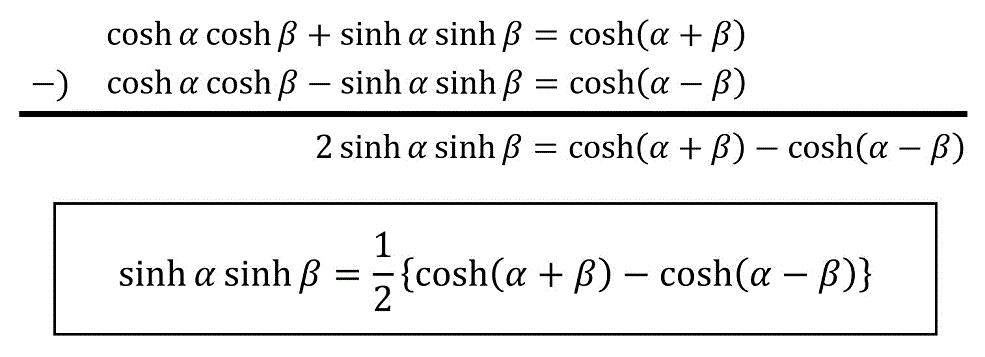
※ 練習問題は、補充編1-2(双曲線関数の微分積分編)で積分と共に出したいと思います。
8. さいごに
今回は、双曲線関数の中でも定義や基本的な公式を中心に解説をしていきました。
色々と説明しましたが、特に覚えていてほしいのは、
- 双曲線関数の定義式(\( e \) を用いた形)
- 双曲線関数のグラフの概形
- 双曲線関数の基本公式
- 双曲線関数の加法定理
の4つです。
この4種類の式は下にまとめているので、テスト前に見返す際などにご利用ください。
[定義式]
\[\begin{align*}
\sinh x & = \frac{ e^{x} - e^{-x} }{2} \\
\cosh x & = \frac{ e^{x} + e^{-x} }{2} \\
\tanh x & = \frac{ \sinh x }{ \cosh x }
\end{align*}\]
[グラフの概形]
赤色 → \( y = \sinh x \) のグラフ(奇関数)
青色 → \( y = \cosh x \) のグラフ(偶関数)
緑色 → \( y = \tanh x \) のグラフ(奇関数)
[基本公式]
\[
\cosh^2 x \textcolor{red}{-} \sinh^2 x = 1
\]\[
\tanh x = \frac{\sinh x }{\cosh x}
\]\[
1 \textcolor{red}{-} \tanh^2 x = \frac{1}{ \cosh^2 x }
\]
[加法公式]
\[\begin{align*}
\sinh ( \alpha + \beta ) & = \sinh \alpha \cosh \beta + \cosh \alpha \sinh \beta \\
\sinh ( \alpha - \beta ) & = \sinh \alpha \cosh \beta - \cosh \alpha \sinh \beta \\
\cosh ( \alpha + \beta ) & = \cosh \alpha \cosh \beta \textcolor{red}{+} \sinh \alpha \sinh \beta \\
\cosh ( \alpha - \beta ) & = \cosh \alpha \cosh \beta \textcolor{red}{-} \sinh \alpha \sinh \beta \\
\tanh ( \alpha + \beta ) & = \frac{ \tanh \alpha + \tanh \beta }{ 1 \textcolor{red}{+} \tanh \alpha \tanh \beta } \\
\tanh ( \alpha - \beta ) & = \frac{ \tanh \alpha - \tanh \beta }{ 1 \textcolor{red}{-} \tanh \alpha \tanh \beta }
\end{align*}\]
次回(補充編1-2)では、双曲線関数の微分、積分、マクローリン展開について解説をしていきたいと思います。それではまた次回。
注釈
| ↑1 | 三角関数の \( \cos^2 \theta + \sin^2 \theta = 1 \) に近い形。 |
|---|---|
| ↑2 | \( e^x + e^{-x} > 0 \) となるため。 |
| ↑3 | \( \sinh x \) は \( \cosh x \) と異なり、\( x \) の値によっては負の値を取ることもある。そのため、\( \tanh x \) の正負(グラフより \( \tanh x \) と \( \sinh x \) の正負は一致する)を確認するか、\[ \tanh x = \frac{ \sinh x }{ \cosh x} \]を計算することで \( \sinh x \) の正負を確認する必要がある。もちろん、上の式を変形して \( \sinh x = \tanh x \cosh x \) から \( \sinh x \) を計算してもOK。 |
関連広告・スポンサードリンク