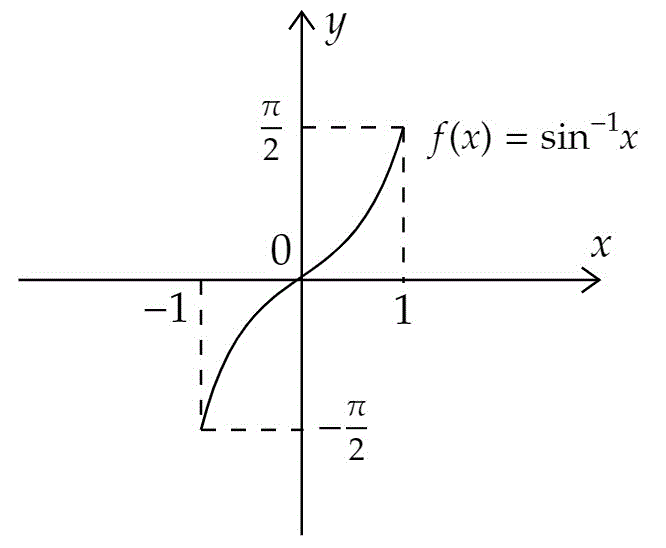
スポンサードリンク
こんにちは、ももやまです。
今回は解析の前半で習う逆三角関数についてまとめました。
前回のロピタルの定理と同様、演習問題が若干多めです。
前回のロピタルの定理はこちらから↓
目次 [hide]
スポンサードリンク
1.逆三角関数とは
たとえば、
同様に
逆三角関数の -1 表記は、-1乗という意味ではありません。
これらの逆関数の
| 定義域 | 値域 | |
| すべての実数 |
定義域や値域に注意が必要です。
逆三角関数の定義域は、もともとの三角関数
(例えば
また、値域も限定されています。
例えば、
このとき、
逆三角関数の値域が存在しなかった場合、逆三角関数の答えが無限に考えられてしまうため、上のように値域を限定しているのです(なるべく便利なように値域を設定するため、
また、つぎのように逆三角関数を表記する人もいます。
成り立つ関係
逆三角関数には次の関係が成り立ちます。
まずほぼ自明ですが、
ここからは、逆三角関数に成り立つ関係を示していきながら紹介しましょう。
まずは、
同様の方法で
つぎに、
例題1
解説1
順番に解いていきましょう。
同様に、
例題2
(1)
(2)
解説2
(1)
(2) (1)の結果を使って示すのがおすすめ。
スポンサードリンク
2.逆三角関数のグラフ
それぞれの逆三角関数をグラフにすると、つぎのようになります。
(1) 逆正弦関数
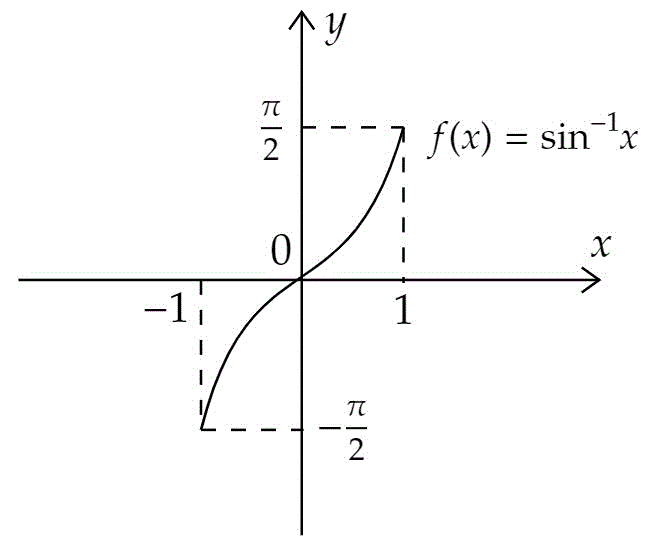
(2) 逆余弦関数
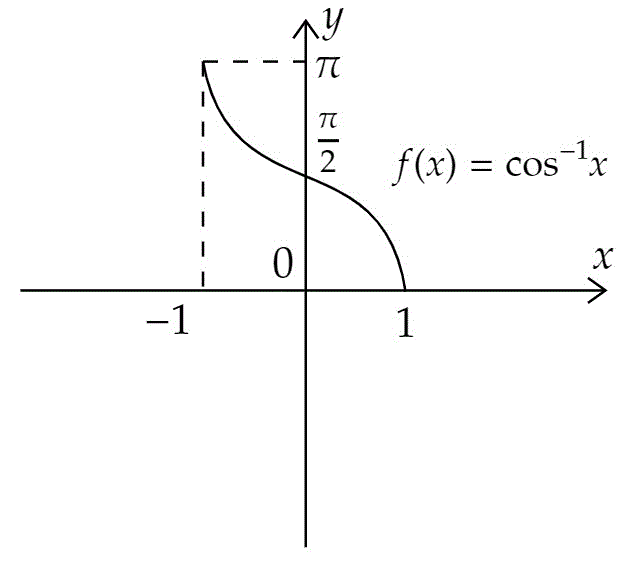
(3) 逆正接関数
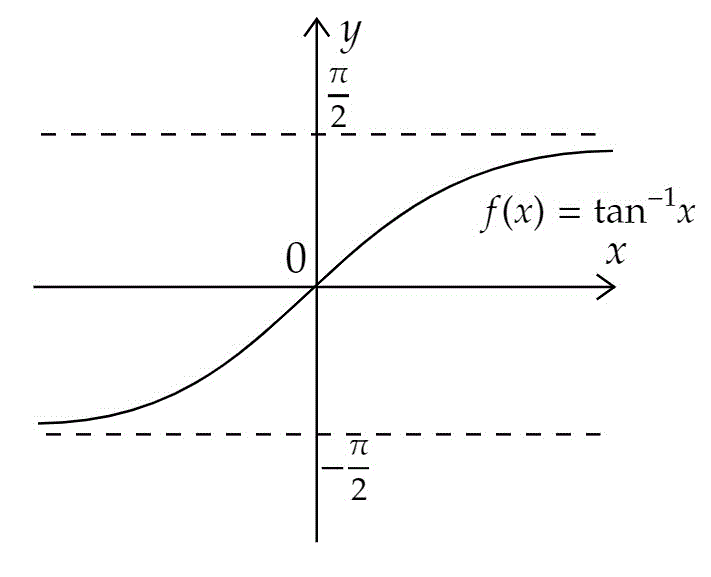
逆正接関数
また、グラフから、
スポンサードリンク
3.逆三角関数の微分
それぞれの逆三角関数の導関数を、逆関数の微分公式を使って求めることができます。
微分公式の導出
(1) 逆正弦関数の微分公式の導出
あとは、逆関数の微分公式を使えば、
(2) 逆余弦関数の微分公式の導出
(1)と同様にして微分公式を導出することができます。
あとは、逆関数の微分公式を使えば、
(3) 逆正接関数の微分公式の導出
逆三角関数の微分公式
では1問例題を解いてみましょう。
例題3
解説3
合成関数の微分を使う。
すると、
つぎのような定数
定数
例題4
関数
ただし、
(1)
(2) 導関数
(3) 関数
解説4
(1)
(2)
(3) (2)より、
となる。
4.逆三角関数の積分公式
上の微分公式から、積分公式も得ることができます。
逆三角関数の積分公式
皆さんは数学3で、
高校までは、
しかし、これも上の積分公式を使うことですぐに答えを出すことができるようになります。
逆三角関数を使った場合
おまけ(数3でのやり方)
よって、
5.練習問題
では、実際に何問か解いてみましょう。
練習1
次の(1)~(3)の計算結果を答えなさい。
(1)
(2)
(3)
練習2
次の(1)~(3)の導関数をもとめなさい。
(1)
練習3
次の(1)~(3)の定積分、不定積分をもとめなさい。
(1)
6.練習問題の解答
解答1
次の(1)~(3)の計算結果を答えなさい。
(1)
(2)
(3)
ここで、加法定理を用いると、
解答2
(1)
すると、
(2)
(3)
すると、
解答3
(1) (逆三角関数の積分を利用)
(2)
と求められる。あとは上の式を計算するだけ、
(3) 部分積分を行う。積分定数を
7.さいごに
今回は逆三角関数についてのまとめを行いました。
逆三角関数を用いると、高校までやっていた
期末試験や数検1級では、逆三角関数の性質だけでなく、微分や積分が頻出するので、逆三角関数の微分積分にも慣れましょう。
*1:一応念のために確認。
関連広告・スポンサードリンク