うさぎでもわかる解析（高校数学・数3）　Part10　特殊な積分 sqrt(x^2+a^2) が含まれたタイプ

こんにちは、ももやまです。
今回も特殊な置換積分についてまとめました。

今回は \( \sqrt{x^2 + a^2} \) が含まれた積分についてまとめたいと思います。

スポンサードリンク

１．t = x + sqrt(x^2 + a^2) と置換する積分

今回はいきなり例題から入ります。

例題1

\[ \int \frac{1}{\sqrt{x^2 + 1}} \ dx \]について、つぎの問いに答えなさい。

(1) \( x + \sqrt{x^2 + 1} \) の導関数を求めなさい。
(2) \( t = x + \sqrt{x^2 + 1} \) と置くことで、不定積分を計算しなさい。

解説1

(1)

これは普通に微分すればOK。\[ \frac{d}{dx} \left(  x + \sqrt{x^2 + 1} \right) = 1 + \frac{x}{\sqrt{x^2+1}} \]となる。

(2)

(1) より、\[\begin{align*} dt & = 1 + \frac{x}{\sqrt{x^2+1}} \ dx \\ & = \frac{x + \sqrt{x^2 + 1}}{\sqrt{x^2+1}} \ dx \\ & = \frac{t}{\sqrt{x^2 + 1}}  \ dx
\end{align*} \] となります。よって、\[ dx = \frac{\sqrt{x^2 + 1}}{t} \ dt \]が導出でき、\[\begin{align*} \int \frac{1}{\sqrt{x^2 + 1}} \ dx  & =
\int \frac{1}{\sqrt{x^2 + 1}} \cdot \frac{\sqrt{x^2 + 1}}{t} \ dt
\\ & = \int \frac{1}{t} \ dt
\\ & = \log \left( t \right) + C
\\ & = \log \left( x + \sqrt{x^2 + 1} \right) + C
\end{align*} \]と求めることができます。

例題1の積分の結果\[ \int \frac{1}{\sqrt{x^2 + 1}} \ dx \]を使うことで、つぎの積分も解くことができます。

例題2

例題1の結果を踏まえて、\[ \int \sqrt{x^2 + 1}\ dx \]を求めなさい。

解説2

部分積分を行います。

左側に1があると思いこむパターンです。

\[\begin{align*}  & \int \sqrt{x^2 + 1}\ dx
\\ = & x \sqrt{x^2 + 1} - \int x \cdot \frac{x}{\sqrt{x^2+1}} \ dx
\\ = & x \sqrt{x^2 + 1} - \int \frac{(x^2+1) - 1}{\sqrt{x^2+1}} \ dx
\\ = & x \sqrt{x^2 + 1} - \int \left( \frac{x^2+1}{\sqrt{x^2+1}} - \frac{1}{\sqrt{x^2+1}} \right) \ dx
\\ = & x \sqrt{x^2 + 1} - \int \frac{x^2+1}{\sqrt{x^2+1}} \ dx + \int \frac{1}{\sqrt{x^2+1}} \ dx
\\ = & x \sqrt{x^2 + 1} - \int \sqrt{x^2+1} \ dx + \int \frac{1}{\sqrt{x^2+1}} \ dx
\end{align*} \]

と計算することで、元の部分積分の式が出てくるので、\[
2 \int \sqrt{x^2 + 1} \ dx = \left( x \sqrt{x^2 + 1}  + \int \frac{1}{\sqrt{x^2+1}} \right)
\]を解けばよい。

ここで例題1を使うと、\[
\int \sqrt{x^2 + 1}\ dx = \frac{1}{2} \left( x \sqrt{x^2 + 1}  + \log \left( x + \sqrt{x^2 + 1} \right) \right) + C
\]と計算することができます。

これらの計算を踏まえ、\( \sqrt{x^2 + a^2} \) が含まれたタイプの積分の公式を示して置きます。

1回導出をしてから暗記をすると覚えやすいのではないかと思います。

ついでに \( \sqrt{x^2 - a^2} \) のパターンの公式も書いておきましょう。

練習ではこの負のパターンの問題を用意しています。

スポンサードリンク

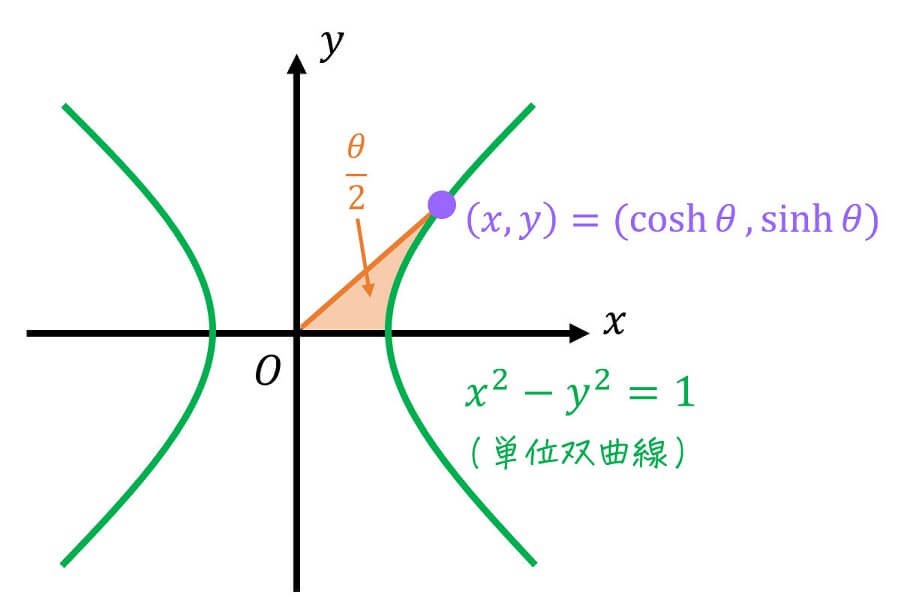
２．x = (e^t + e^(-t))/2 と置換する方法（双曲線関数）

例題1の積分は双曲線関数の形\[ x = \frac{e^t + e^{-t}}{2} \]を使うことで解くこともできます。

ここで、双曲線関数とは、\[ \sinh x = \frac{e^x +e^{-x}}{2} , \ \ \  \cosh x = \frac{e^x - e^{-x}}{2} \]と表されるような関数のことです（大学で習います）。

双曲線関数については、こちらの3つの記事にまとめているので、もし興味があればご覧ください。

[双曲線関数1: 双曲線関数のいろは] [双曲線関数2: 双曲線関数の微分・積分] [双曲線関数3: 逆双曲線関数（双曲線関数の逆関数）] （※ 今回説明している積分は、この逆双曲線関数を用いて表記することもできます、もし逆双曲線関数を用いた導出や公式が気になる人はこちらもご覧ください）

今回は、双曲線関数の表記を使わずに\[ x = \frac{e^t + e^{-t}}{2}\]とおいて解いてみましょう。

\[ dx = \frac{e^t - e^{-t}}{2} \ dt  \]となるので、\[ \begin{align*} &
\int \frac{1}{\sqrt{x^2 + 1}} \ dx
\\ = & \frac{1}{ \sqrt{ \left(\frac{e^t + e^{-t}}{2} \right)^2 + 1} } \cdot  \frac{e^t - e^{-t} }{2} \ dt
\\ = & \frac{1}{ \sqrt{ \frac{e^{2t} - 2 + e^{-2t} + 4}{4}} } \cdot  \frac{e^t - e^{-t} }{2} \ dt
\\ = & \frac{1}{ \sqrt{ \frac{e^{2t} + 2 + e^{-2t} }{4}} } \cdot  \frac{e^t - e^{-t} }{2} \ dt
\\ = & \frac{1}{ \sqrt{ \frac{\left( e^t + e^{-t} \right)^2 }{2^2}} } \cdot  \frac{e^t - e^{-t} }{2} \ dt
\\ = & \frac{1}{ \frac{ e^t + e^{-t} }{2}} \cdot  \frac{e^t - e^{-t} }{2} \ dt
\\ = & 1 \ dt
\\ = & t + C
\\ = &  \log \left( x + \sqrt{x^2 + 1} \right) + C
\end{align*} \]

と計算できます。

最後の \( t \) から、\( x \) に戻す際の計算は、\( e^t = s , \ (s \gt 0) \) とおくと、\[ x = \frac{1}{2} \left( s + \frac{1}{s} \right) \]より、\[ s^2 - 2xs + 1 = 0 \]が計算できるので、\[ s = x \pm \sqrt{x^2 - 1 }\]と計算ができます。さらに \( s \gt 0 \) のため、\[ s = e^t = x + \sqrt{x^2 + 1 } \]\[ t = \log \left| x + \sqrt{x^2 + 1} \right| \]となるためです。

（双曲線関数 \( \sinh x \) の逆関数に相当します。）

スポンサードリンク

３．練習問題

1問だけですが、練習してみましょう。

練習

次の(1)～(3)の問いに答えなさい。

(1) \( x + \sqrt{x^2 - 4} \) の導関数を求めなさい。
(2) 不定積分\[ \int \frac{1}{\sqrt{x^2 - 4}} \ dx \]を求めなさい。
(3) 不定積分\[ \int \sqrt{x^2 - 4} \ dx \]を求めなさい。

４．練習問題の解答

(1) \[ \frac{d}{dx} \left(  x + \sqrt{x^2 - 4} \right) = 1 + \frac{x}{\sqrt{x^2 - 4}} \]となる。

(2)

(1) より、\[\begin{align*} dt & = 1 + \frac{x}{\sqrt{x^2-4}} \ dx \\ & = \frac{x + \sqrt{x^2 -  4}}{\sqrt{x^2- 4}} \ dx \\ & = \frac{t}{\sqrt{x^2 - 4}}  \ dx
\end{align*} \] となる。

よって、\[ dx = \frac{\sqrt{x^2 - 4}}{t} \ dt \]が導出でき、\[\begin{align*} \int \frac{1}{\sqrt{x^2 -  4}} \ dx  & =
\int \frac{1}{\sqrt{x^2 -  4}} \cdot \frac{\sqrt{x^2 - 4}}{t} \ dt
\\ & = \int \frac{1}{t} \ dt
\\ & = \log \left| t \right| + C
\\ & = \log \left| x + \sqrt{x^2 - 4} \right| + C
\end{align*} \]と求めることができます。

(3)

(2)より、\[\begin{align*} dt & \int \sqrt{x^2 - 4}\ dx
\\ = & x \sqrt{x^2 - 4} - \int x \cdot \frac{x}{\sqrt{x^2 - 4}} \ dx
\\ = & x \sqrt{x^2 - 4} - \int \frac{(x^2- 4) + 4}{\sqrt{x^2- 4}} \ dx
\\ = & x \sqrt{x^2 - 4} - \int \left( \frac{x^2 - 4}{\sqrt{x^2 - 4}} + \frac{4}{\sqrt{x^2 - 4}} \right) \ dx
\\ = & x \sqrt{x^2 - 4} - \int \frac{x^2 - 4}{\sqrt{x^2 - 4}} \ dx - \int \frac{4}{\sqrt{x^2 - 4}} \ dx
\\ = & x \sqrt{x^2- 4} - \int \sqrt{x^2 - 4} \ dx - 4  \int \frac{1}{\sqrt{x^2 - 4}} \ dx
\end{align*} \]

と計算することで、元の部分積分の式が出てくるので、\[
2 \int \sqrt{x^2 - 4} \ dx = \left( x \sqrt{x^2 - 4}  - 4 \int \frac{1}{\sqrt{x^2-4}} \ dx \right)
\]を解けばよい。

ここで(2)を使うと、\[
\int \sqrt{x^2 - 4}\ dx = \frac{1}{2} \left( x \sqrt{x^2 - 4}  - 4 \log \left| x + \sqrt{x^2 - 4} \right| \right) + C
\]と計算できる。

５．さいごに

今回は特殊な積分の中でもかなり難易度が高い \( \sqrt{x^2 + a^2} \) が含まれているタイプについてまとめを行いました。

このタイプの積分を見かけたら、1番のやり方の置換を行いましょう。

双曲線関数については余裕があればまとめます。