うさぎでもわかる解析　Part24　変数変換を用いた2重積分の求め方・ヤコビアン

こんにちは、ももやまです。

今回は置換積分の2重積分バージョンに進化したものを紹介していきたいと思います。

前回の記事（Part23　2重積分の基礎・積分範囲の交換）はこちら！

www.momoyama-usagi.com

（2重積分がうーんな人は上の記事で復習してからこちらの記事を読むことをおすすめします。）

スポンサードリンク

１．ヤコビアンとは

領域 $D$ が$$D=\{(x,y)\mid a\leqq x\leqq b,c\leqq y\leqq d\}$$の形になっていない場合、2重積分の値を求めることができません。

このような場合、$$D^{\prime }=\{(p,q)\mid a^{\prime }\leqq p\leqq b^{\prime },c^{\prime }\leqq q\leqq d^{\prime }\}$$の形に置き換えることで2重積分の値を求めていきます。

（置換積分の2重積分バージョンだと思ってくれればOK！）

具体的に1題練習してみましょう。

例題

つぎの重積分$${\iint }_D(x-2y)e^{x+y}dxdy$$$$D=\{(x,y)\mid 1\leqq x-2y\leqq 3,0\leqq x+y\leqq 1\}$$を計算しなさい。

解説

範囲の形を変えるため、$x-2y=p$, $x+y=q$ とおきます。

ここで1変数関数の置換積分を思い出してください。1変数関数のときは、$$dx=adt$$のような $dx$, $dt$ の関係式を微分することにより求めていましたね。

2変数関数も同様に $dxdy$ と $dpdq$ の関係式を求めなければなりません。

2変数関数の積分範囲は領域（平面）で表されていましたね。この積分領域の面積の変化率が $dxdy$ と $dpdq$ の関係式になります。

変換における面積変化の具合$$dxdy=adpdq$$の関係式を求めるために $x$, $y$ が $p$, $q$ を用いてどう表されるかを計算します。$$\begin{array}{rl}p+2q& =(x-2y)+2(x+y)=3x\\ -p+q& =-(x-2y)+(x+y)=3y\end{array}$$となるので、$$\{\begin{array}{l}x=\frac{1}{3}p+\frac{2}{3}q\\ y=-\frac{1}{3}p+\frac{1}{3}q\end{array}$$と変換できます。

ここで線形代数を思い出してみましょう。

2次の行列式は面積のイメージでしたね。なのでそれぞれの変数を偏微分し、行列式で計算してあげれば $dxdy$ と $dpdq$ の変化率が求められそうですね。

これをヤコビアン、もしくはヤコビ行列式といい、下のような数式で表されます。

ヤコビアンは領域 $D^{\prime }$ を $D$ に戻した場合の面積の変化率を表しています*1。そのため、必ず正となることに注意してください。

行列式についてもし分からないことがあればこちらの記事をご覧ください！

www.momoyama-usagi.com

（2次のサラスの公式は覚えていてほしいです…）

例題の場合のヤコビアン $J$ は$$\begin{array}{rl}J=& \left|\begin{array}{cc}\frac{\partial x}{\partial p}& \frac{\partial x}{\partial q}\\ \frac{\partial y}{\partial p}& \frac{\partial y}{\partial q}\end{array}\right|\\ =& \left|\begin{array}{cc}\frac{1}{3}& \frac{2}{3}\\ -\frac{1}{3}& \frac{1}{3}\end{array}\right|\\ =& \frac{1}{9}\left|\begin{array}{cc}1& 2\\ -1& 1\end{array}\right|\\ =& \frac{1}{3}\end{array}$$と求められるので、$$\begin{gathered} dxdy=\frac{1}{3}dpdq, \\ {D}^{\prime }=\{(p,q)\mid 1\leqq p\leqq 3,0\leqq q\leqq 1\} \end{gathered}$$となる。

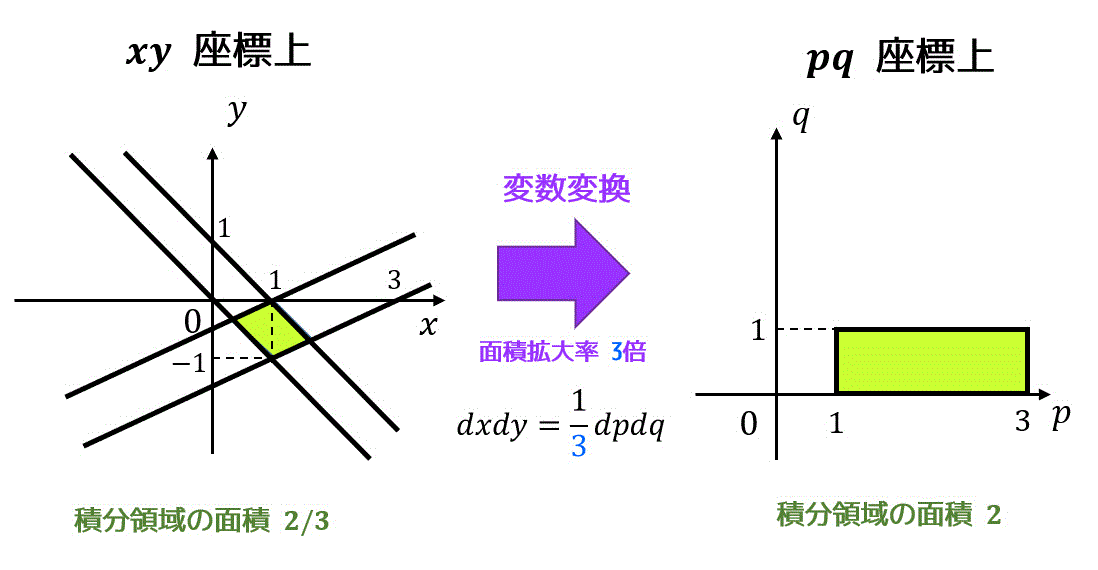
変換前の領域 $D$ と変換後の領域 $D^{\prime }$ を図示すると下のようになります。

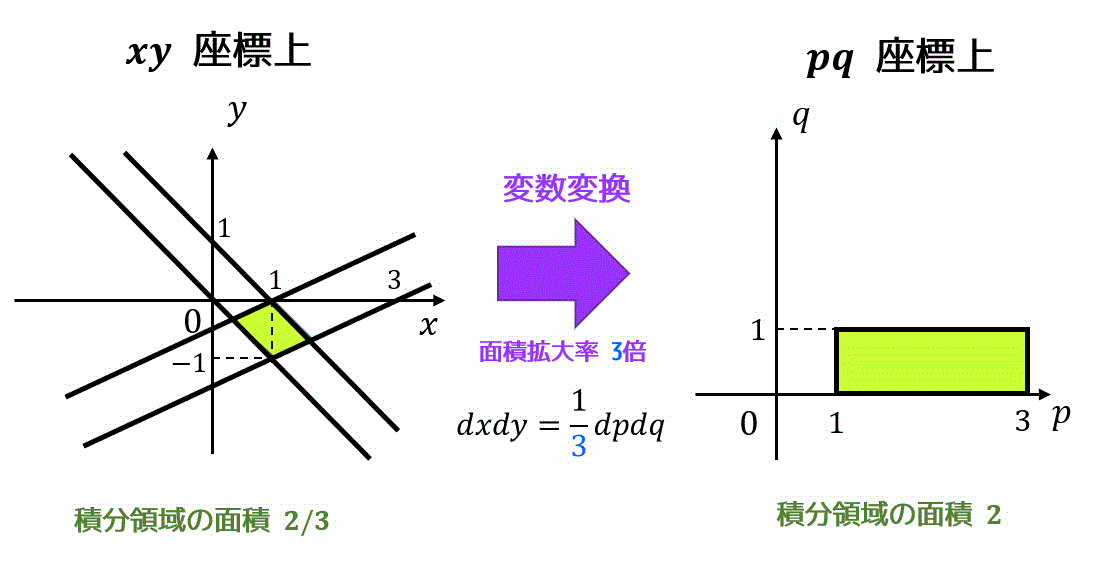
※変換前 $D$ と変換後 $D^{\prime }$ では領域の面積が変わってしまいますね（今回は3倍）、なので拡大率の逆数を積分結果に掛ける*2（今回は1/3倍）することで積分計算結果を変わらないようにしていると頭の中では思ってください。

あとは前回の2重積分と同じように計算するだけ。$$\begin{array}{rl}& {\iint }_D(x-2y)e^{x+y}dxdy\\ =& {\iint }_{D^{\prime }}\frac{1}{3}u{e}^{v}dpdq\\ =& \frac{1}{3}\cdot {\int }_1^{3}pdp\cdot {\int }_0^1{e}^{q}dq\end{array}$$を計算すればよい。

それぞれの積分の値は$$\begin{array}{rl}{\int }_1^{3}pdp=& {\left[\frac{1}{2}{p}^2\right]}_1^3\\ =& \frac{1}{2}(3^2-1^2)\\ =& 4\end{array}$$$$\begin{array}{rl}{\int }_0^1{e}^{q}dq=& {\left[e^q\right]}_0^1\\ =& e-1\end{array}$$となるので、$$\begin{array}{rl}& {\iint }_D(x-2y)e^{x+y}dxdy\\ =& \frac{1}{3}\cdot 4\cdot (e-1)\\ =& \frac{4}{3}(e-1)\end{array}$$となる。

スポンサードリンク

２．練習問題

では1問だけですが練習してみましょう。

練習1

つぎの重積分$${\iint }_D{x}^{2}dxdy$$$$D=\{(x,y)\mid 0\leqq x+y\leqq 1,0\leqq x-y\leqq 1\}$$を計算しなさい。

スポンサードリンク

３．練習問題の答え

解答1

$x+y=p$, $x-y=q$ とおく。すると、$$\begin{gathered} 2x=(x+y)+(x-y)=p+q \\ 2y=(x+y)-(x-y)=p-q \end{gathered}$$となるので$$\{\begin{array}{l}x=\frac{1}{2}p+\frac{1}{2}q\\ y=\frac{1}{2}p-\frac{1}{2}q\end{array}$$ヤコビアン $J$ は$$\begin{array}{rl}J& =\left|\begin{array}{cc}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& -\frac{1}{2}\end{array}\right|\\ & =\frac{1}{4}\left|\begin{array}{cc}1& 1\\ 1& -1\end{array}\right|\\ & =-\frac{1}{2}\end{array}$$の絶対値となる。よって変数変換は$$\begin{gathered} dxdy=\frac{1}{2}dpdq, \\ {D}^{\prime }=\{(p,q)\mid 0\leqq p\leqq 1,0\leqq q\leqq 1\} \end{gathered}$$となる。（絶対値忘れに要注意！）

よって$$\begin{array}{rl}& {\iint }_D{x}^{2}dxdy\\ =& {\iint }_{D^{\prime }}\frac{1}{2}(\frac{1}{2}p+\frac{1}{2}q{)}^{2}dpdq\\ =& \frac{1}{8}{\int }_0^1({\int }_0^1(p+q{)}^{2}dp)dq\end{array}$$を計算すればよい。

$$\begin{array}{rl}{\int }_0^1(p+q{)}^{2}dp& ={[\frac{1}{3}(p+q{)}^3]}_0^1\\ & =\frac{1}{3}(q+1{)}^3-\frac{1}{3}{q}^3\\ & =q^2+q+\frac{1}{3}\end{array}$$より、$$\begin{array}{rl}& \frac{1}{8}{\int }_0^1({\int }_0^1(p+q{)}^{2}dp)dq\\ =& \frac{1}{8}{\int }_0^1{q}^2+q+\frac{1}{3}dq\\ =& \frac{1}{8}{[\frac{1}{3}{q}^3+\frac{1}{2}{q}^2+\frac{1}{3}q]}_0^1\\ =& \frac{1}{8}(\frac{1}{3}+\frac{1}{2}+\frac{1}{3})\\ =& \frac{1}{8}\cdot \frac{7}{6}\\ =& \frac{7}{48}\end{array}$$となる。

４．さいごに

今回は2重積分における置換積分（変数変換を用いて2重積分を解く）方法についてまとめました。

ヤコビアンは置換後の領域 $D^{\prime }$ から置換前の領域 $D$ における面積の変化率と頭の片隅にいれておきましょう。

また、この分野は数検1級でも頻出するので数検取りたい人もこの積分法はマスターしましょう！

次回は変数変換の中でも特別な極座標を用いた変数変換についてまとめていきたいと思います。