うさぎでもわかる線形代数　補充3　平面の方程式

こんにちは、ももやまです。

前回の補充2では平面、空間上にある直線の方程式を求める方法について説明しました。

 

今回は、平面の方程式を求める方法について説明していきたいと思います。

 

 

スポンサードリンク

１．媒介変数を用いた平面の方程式の表し方

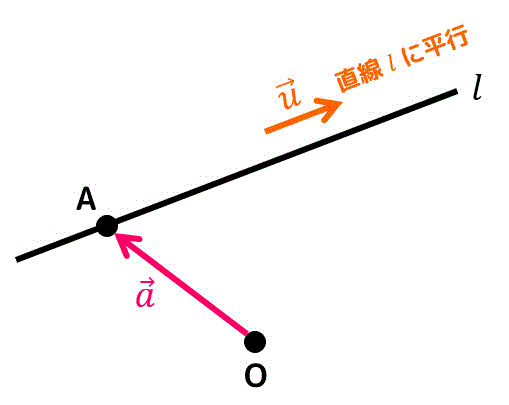
前回の補充2で、直線をベクトルで表すためには

• 直線を通るある1点
  （無数の直線から1つを特定するために必要）
• 直線 \( l \) に平行なベクトル1本
  （ベクトル1本で直線を表現できる）

の2つが必要なことを説明しました。

同じように平面をベクトルで表すためには

• 平面を通るある1点 [直線の場合と同じ]（無数の平面から1つを特定するために必要）
• 平面に平行なベクトル2本 [1本だと直線しか表現できない]（ベクトル2本で平面を表現できる、ただし条件に注意）

が必要となります。

 

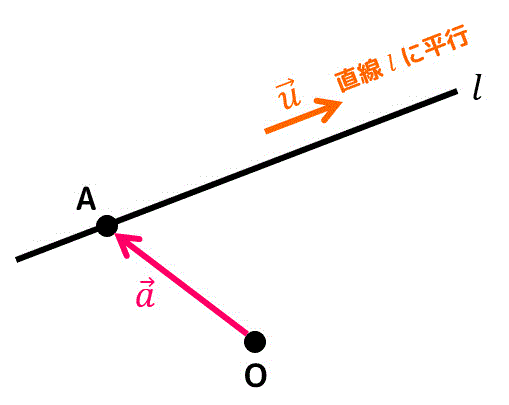
まずは、平面を表現するために必要なベクトル2本について考えましょう。

 

平面を通るある2点A, Pを考えます。

すると、ある平面における2点間のベクトル \( \overrightarrow{AP} \) を平面に平行な2つのベクトル \( \vec{u} \), \( \vec{v} \) と実数 \( s \), \( t \) を用いて\[
\overrightarrow{AP} = s \vec{u} + t \vec{v}
\]と表すことができますね。

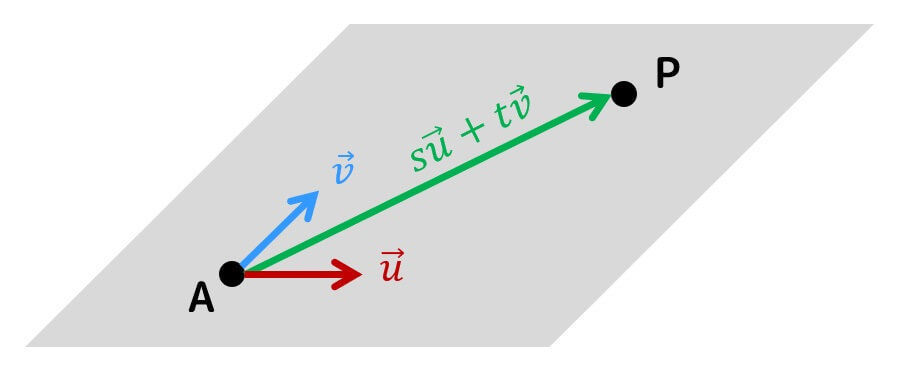
（ただし、\( \vec{u} \not = \vec{0} \), \( \vec{v} \not = 0 \) であり、\( \vec{u} \) と \( \vec{v} \) が平行ではないのが条件です*1。

 

よって、平面を通るある点Aの座標さえわかれば、平面上にあるあらゆる点（点P）をベクトルを用いて表すことができますね。

 

点Aの位置ベクトルを \( \vec{a} \) とすると、平面上のある点Pの位置ベクトル \( \vec{p} \) は\[\begin{align*}
\vec{p} & = \overrightarrow{OP} 
\\ & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \vec{a} + s \vec{u} + t \vec{v}
\end{align*}\]と表すことができ、平面をベクトルで表現することができましたね。

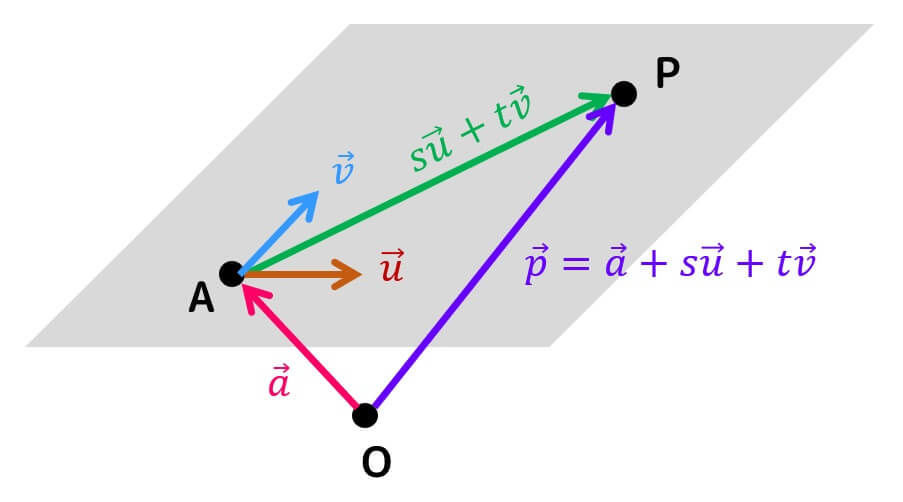
なお、この \( \vec{p} \) の式を、平面のベクトル方程式と呼びます。

あとは点Pの座標を \( (x,y,z) \) で平面の方程式を媒介変数表示で求めることができます。

ここで例題を1問解いておきましょう。

 例題1 

ある点A (1,3,2) を通り、\[
\vec{u} = \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right), \ \ \ 
\vec{v} = \left( \begin{array}{ccc} 3 \\ -1 \\ -1 \end{array} \right)
\]に平行な平面を考える。

 

このとき、平面の方程式を媒介変数 \( s \), \( t \) を用いて表しなさい。

 

解答1

点Pを平面 \( l \) 上におく（位置ベクトル \( \vec{p} \)）。

すると、\(  \overrightarrow{OP} \) は、媒介変数 \( s \), \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) + s \vec{u} + t \vec{v}
\\ & =\left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) + s \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right) + t \left( \begin{array}{ccc} 3 \\ -1 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} s+3t+1 \\ -2s-t+3 \\ s-t+2 \end{array} \right)
\end{align*}\]と求められる。

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} s+3t+1 \\ -2s-t+3 \\ s-t+2 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( s \), \( t \) を用いて\[
\left\{ \begin{array}{l} x = s + 3t + 1 \\ y = -2s - t + 3 \\ z = s - t + 2 \end{array}\right.
\]となる。

 

スポンサードリンク

２．法線ベクトルと平面の方程式

(1) 法線ベクトルから平面の方程式を求める方法

媒介変数 \( s \), \( t \) を変形すれば、\( ax+by+cz+d = 0 \) のように \( s \), \( t \) を使わずに平面の方程式を表すことができますね。

しかし、1変数ならまだしも、2変数を削除するのは少しめんどくさいですよね。

 

そこで、平面の法線ベクトル \( \vec{n} \) から平面の方程式を出す方法を考えてみましょう。

 

法線ベクトル \( \vec{n} \) とは平面と垂直なベクトルのことでしたね。

図にすると、下のようになります。

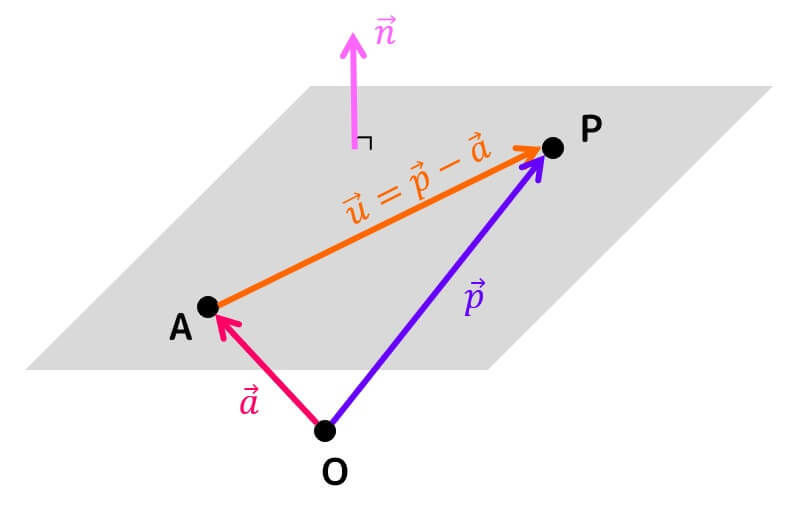
ここで、平行なベクトル \( \vec{u} \) として、\(  \overrightarrow{AP} \) を考えます。

すると、\( \vec{u} \) と \( \vec{n} \) は直交するので、\[
\vec{u} \cdot \vec{n} = 0 \\
( \vec{p} - \vec{a} ) \cdot \vec{n} = 0
\]の関係式が成り立ちますね。

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[
\vec{p} = \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) 
\]となります。さらに、\[
\vec{a} = \left( \begin{array}{ccc} x_0 \\ y_0 \\ z_0 \end{array} \right) , \ \ \ 
\vec{n} =  \left( \begin{array}{ccc} p \\ q \\ r \end{array} \right) 
\]とすると、\[\begin{align*}
( \vec{p} - \vec{a} ) \cdot \vec{n} & =  0 \\
\left( \begin{array}{ccc} x - x_0 \\ y - y_0 \\ z - z_0 \end{array} \right)  \cdot \left( \begin{array}{ccc} p \\ q \end{array} \right) & = 0 
\end{align*}\]となるので、\[
p (x - x_0) + q (y - y_0) + r (z - z_0) = 0
\]の関係式が成り立ちますね。

 

 

 

また、上の公式から \( ax + by + cz + d = 0 \) の係数がわかれば法線ベクトル \( \vec{n} \) も下のようにあっという間に求められます。

 

(2) 法線ベクトルと外積

いくら法線ベクトルから方程式が求められたとしても、法線ベクトル自体を求められなければ方程式を求めることができません。

 

ということで、平面に平行な2本のベクトル \( \vec{u} \), \( \vec{v} \) から法線ベクトル、つまり平面に垂直なベクトル \( \vec{n} \) を求める方法を考えましょう。

 

ここで、ベクトル \( \vec{u} \) と \( \vec{v} \) は両方とも \( \vec{n} \) と直交していますね。

（実際に図を書くと直交しているのがわかりやすいと思います）

 

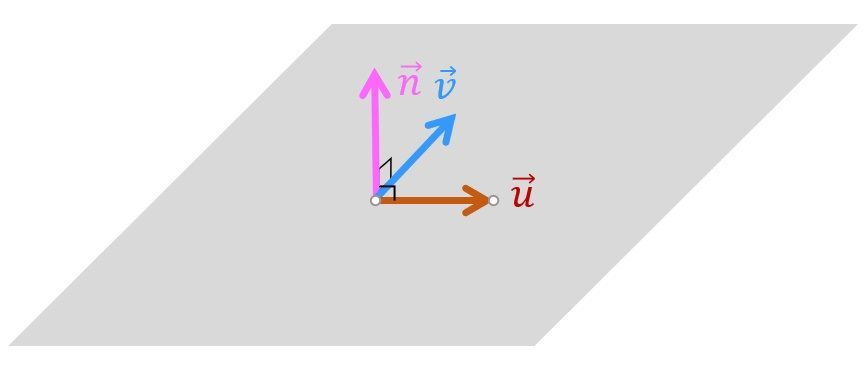
2つのベクトル \( \vec{u} \), \( \vec{v} \) に直交するベクトルと聞いてなにか思い浮かびませんか…？

 

ここで、大学の線形代数で習った外積が役に立つのです！（補充1）

外積 \( \vec{u} \times \vec{v} \) は2つのベクトル \( \vec{u} \), \( \vec{v} \) に直交するベクトルでしたよね。

なので、\[
\vec{n} = \vec{u} \times \vec{v}
\]を計算することで法線ベクトルを求めることができるのです！

（ちなみに \( \vec{u} \) と \( \vec{v} \) の計算順序を逆にすると向きが反対になります。しかし、向きが反対でも法線ベクトルに変わりはないので、法線ベクトルを計算する際には外積の計算順序を考慮する必要はありません。）

 

もし、外積がわからない or よく思い出せないという人は下の記事で復習しましょう。

www.momoyama-usagi.com

 

ここで、実際に例題を解いて流れを確認しましょう。

 例題2 

ある点A (1,3,2) を通り、\[
\vec{u} = \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right), \ \ \ 
\vec{v} = \left( \begin{array}{ccc} 3 \\ -1 \\ -1 \end{array} \right)
\]に平行な平面を考える。

 

(1) 外積 \( \vec{u} \times \vec{v} \) を計算しなさい。

(2) 平面の方程式を \( ax+by+cz+d=0 \) の形で表しなさい。

 

解答2

(1)

外積 \( \vec{u} \times \vec{v} \) は\[\begin{align*}
\vec{u} \times \vec{v} & = \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right) \times \left( \begin{array}{ccc} 3 \\ -1 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2-(-1) \\ 3-(-1) \\ -1-(-6) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 \\ 4 \\ 5 \end{array} \right)
\end{align*}\]と計算できる。

 

(2)

外積 \( \vec{u} \times \vec{v} \) は平面に平行なベクトルと直交するため、法線ベクトル \( \vec{n} \) となる。

 

ここで、平面上にある点Pをおく。すると、\(  \overrightarrow{AP} \) と \( \vec{n} \) は直交するので、\[
\overrightarrow{AP} \cdot \vec{n} = 0 
\]の関係式が成り立つ。

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[\begin{align*}
\overrightarrow{AP} & = \overrightarrow{OP} - \overrightarrow{OA}
\\ & = \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) - \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} x-1 \\ y-3 \\ z-2 \end{array} \right)
\end{align*}\]となるので、\[\begin{align*}
\vec{AP} \cdot \vec{n} & = 0 \\
 \left( \begin{array}{ccc} x-1 \\ y-3 \\ z-2 \end{array} \right) \cdot \left( \begin{array}{ccc} 3 \\ 4 \\ 5 \end{array} \right)
\end{align*}\]となるので、\[
3(x-1)+4(y-3)+5(z-2)=0
\]の関係式が成り立ちますね。

あとは \( ax+by+cz+d=0 \) の形に直すと、\[
3x+4y+5z-25=0
\]となります。

 

[もっと早く答えを出す方法]

実は上の内積の変形を使わなくても、法線ベクトルさえ求めれれば、係数の \( a \), \( b \), \( c \) は決定するので、適当な点を1点選んで\[
ax + by + cz + d = 0
\]の方程式が成り立つような \( d \) を求めるだけでOK。

今回の場合、法線ベクトル \( \vec{n} \) は、\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{3} \\ \color{blue}{4} \\ \color{green}{5} \end{array} \right)
\]となるので、方程式\[
\color{red}{3}x + \color{blue}{4} y+ \color{green}{5} z + d = 0
\]にある1点（\( (x,y,z) = (1,3,2) \) など）を代入し、\( d = -25 \) を得てから\[
3x + 4y + 5z - 25 = 0
\]とした方が圧倒的に早い。

スポンサードリンク

３．平面内の3点から求める方法

最後に、平面内の3点から平面の方程式を求めてみましょう。

(1) 外積を用いて解く方法

 例題3 

点A (1,-2,2), B(-1,-2,1), C(1,-1,1) の3点を通る平面の方程式を \( ax + by + cz + d = 0 \) の形で表しなさい。

 

解説3

まずは、平面に平行なベクトルとして \(  \overrightarrow{AB} \), \(  \overrightarrow{AC} \) を取ります。

それぞれの成分は\[\begin{align*}
\overrightarrow{AB} & = \overrightarrow{OB} - \overrightarrow{OA}
\\ & =  \left( \begin{array}{ccc} -1 \\ -2 \\ 1 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ -2 \\ 2 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} -2 \\ 0 \\ -1 \end{array} \right)
\end{align*}\]\[\begin{align*}
\overrightarrow{AC} & = \overrightarrow{OC} - \overrightarrow{OA}
\\ & =  \left( \begin{array}{ccc} 1 \\ -1 \\ 1 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ -2 \\ 2 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} 0 \\ 1 \\ -1 \end{array} \right)
\end{align*}\]となる。

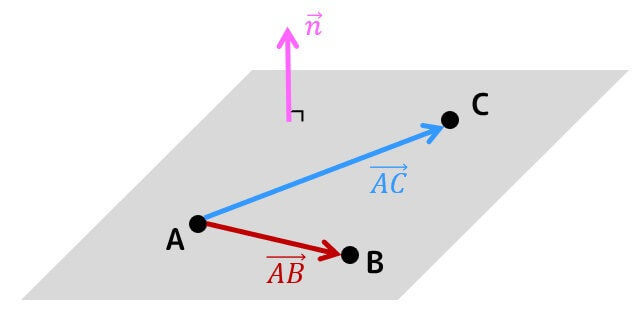
ここで、法線ベクトル \( \vec{n} \) は \(  \overrightarrow{AB} \), \(  \overrightarrow{AC} \) の外積 \( \overrightarrow{AB} \times \overrightarrow{AC} \) で求められる。\[\begin{align*}
\vec{n} & = \overrightarrow{AB} \times \overrightarrow{AC}
\\ & = \left( \begin{array}{ccc} -2 \\ 0 \\ -1 \end{array} \right) \times \left( \begin{array}{ccc} 0 \\ 1 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ -2 \\ -2 \end{array} \right)
\end{align*}\]と計算でき、法線ベクトルとなる。

 

ここで、平面上にある点Pをおく。すると、\(  \overrightarrow{AP} \) と \( \vec{n} \) は直交するので、\[
\overrightarrow{AP} \cdot \vec{n} = 0 
\]の関係式が成り立つ。

（\(  \overrightarrow{BP} \) や \( \overrightarrow{CP} \) を使ってもOK）

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[\begin{align*}
\overrightarrow{AP} & = \overrightarrow{OP} - \overrightarrow{OA}
\\ & = \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) - \left( \begin{array}{ccc} 1 \\ -2 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} x-1 \\ y+2 \\ z-2 \end{array} \right)
\end{align*}\]となるので、\[\begin{align*}
\vec{AP} \cdot \vec{n} & = 0 \\
 \left( \begin{array}{ccc} x-1 \\ y+2 \\ z-2 \end{array} \right) \cdot \left( \begin{array}{ccc} 1 \\ -2 \\ -2 \end{array} \right)
\end{align*}\]となるので、\[
1(x-1)-2(y+2)-2(z-2)=0
\]の関係式が成立。

あとは \( ax+by+cz+d=0 \) の形に直すと、\[
x-2y-2z-1=0
\]と答えを出せる。

 

[もっと早く答えを出す方法]

法線ベクトル \( \vec{n} \) が\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{1} \\ \color{blue}{-2} \\ \color{green}{-2} \end{array} \right)
\]となるので、方程式\[
\color{red}{1}x \color{blue}{-2} y \color{green}{-2} z + d = 0
\]にある1点（\( (x,y,z) = (1,-2,2) \) など）を代入し、\( d = -1 \) を得てから\[
x-2y-2z-1=0
\]とした方が圧倒的に早い。

（他の2点の座標を実際に代入し、合っているかどうかを検算しましょう）

(2) 連立方程式を解く方法

外積は大学数学レベルなので、少し難しいなと思った人がいるかもしれません。

そこで、中学生レベルで平面の方程式を求める方法を考えてみましょう。

 例題4 

点A (1,-2,2), B(-1,-2,1), C(1,-1,1) の3点を通る平面の方程式を外積を使わずに \( ax + by + cz + d = 0 \) の形で表しなさい。

（例題3と同じ問題）

 

解説4

点A, B, Cは平面 \( ax + by + cz + d = 0 \) を満たすので、\[
\left\{ \begin{array}{l} a - 2b + 2c + d = 0 \\ -a - 2b + c + d = 0 \\ a - b + c + d = 0 \end{array}\right.
\]の連立方程式を満たしますね。

しかし、未知数が4つに対し、式が3つしかないのでこのままだと式を解くことができません。

 

そこで、\( d = 1 \) と仮定します。

（もちろん1以外と仮定してももちろんOK。）

 

すると、\[
\left\{ \begin{array}{l} a - 2b + 2c + 1 = 0 \\ -a - 2b + c + 1 = 0 \\ a - b + c + 1 = 0 \end{array}\right.
\]となるので、\[
\left\{ \begin{array}{l} a - 2b + 2c = -1 \\ -a - 2b + 2c = -1 \\ a - b + c = -1 \end{array}\right.
\qquad \therefore \quad \left\{\begin{array}{l} \displaystyle a = -1 \\ \displaystyle b =  2 \\  \displaystyle c = 2 \end{array}\right.
\]と連立方程式を解くことができますね。

 

よって平面の方程式を\[
-x + 2y + 2z + 1 = 0
\]と求めることができます。

（最初にマイナスが来て気持ち悪いなと思った人は両辺を-1倍して\[
x - 2y - 2z - 1 = 0
\]とすればOK。これなら例題3と同じ形だね！）

 

４．練習問題

では、何問か練習してみましょう。

数問ですが、応用問題を入れております。

練習1　平面の方程式と外積

点A (1,2,-1), B(-3,-2,5), C(-1,3,3) の3点を通る平面の方程式を求めたい。

つぎの(1), (2)の問いに答えなさい。

 

(1) 外積 \( \overrightarrow{AB} \times \overrightarrow{AC} \) を求めなさい。

(2) 平面の方程式を \( ax + by + cz + d = 0 \) の形で表しなさい。

練習2　平面に垂直な直線の方程式

点A (1,2,-1) を通り、平面 \( 2x-2y+3z-1=0 \) に垂直な直線の方程式を求めなさい。

練習3　平面に平行な平面の方程式

点A (1,2,-1) を通り、平面 \( 2x-2y+3z-1=0 \) に平行な平面の方程式を求めなさい。

 

 

５．練習問題の答え

解答1

(1)

\( \overrightarrow{AB} \), \( \overrightarrow{AC} \) は\[\begin{align*}
\overrightarrow{AB} & = \overrightarrow{OB} - \overrightarrow{OA}
\\ & =  \left( \begin{array}{ccc} -3 \\ -2 \\ 5 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ 2 \\ -1 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} -4 \\ -4 \\ 6 \end{array} \right)
\end{align*}\]\[\begin{align*}
\overrightarrow{AC} & = \overrightarrow{OC} - \overrightarrow{OA}
\\ & =  \left( \begin{array}{ccc} -1 \\ 3 \\ 3 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ 2 \\ -1 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} -2 \\ 1 \\ 4 \end{array} \right)
\end{align*}\]となる。

 

よって、外積 \( \overrightarrow{AB} \times \overrightarrow{AC} \) は、\[\begin{align*}
\overrightarrow{AB} \times \overrightarrow{AC}
& = \left( \begin{array}{ccc} -4 \\ 0 \\ 6 \end{array} \right) \times \left( \begin{array}{ccc} -2 \\ 5 \\ 4 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -16-6 \\ -12+16 \\ -12 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -22 \\ 4 \\ -12 \end{array} \right)
\\ & = -2 \left( \begin{array}{ccc} 11 \\ -2 \\ 6 \end{array} \right)
\end{align*}\]と計算でき、法線ベクトルとなる。

 

(2)

外積 \( \vec{AB} \times \vec{AC} \) と同じ向きのベクトルは法線ベクトル \( \vec{n} \) となるので、法線ベクトルは\[
\vec{n} = \left( \begin{array}{ccc} 11 \\ -2 \\ 6 \end{array} \right)
\]となる。

（もちろん\[
\vec{n} = \left( \begin{array}{ccc} -22 \\ 4 \\ -12 \end{array} \right)
\]でもOK。でも長さを -1/2 倍にしたほうが後々計算が楽になる）

 

法線ベクトル \( \vec{n} \) が\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{11} \\ \color{blue}{-2} \\ \color{green}{6} \end{array} \right)
\]となるので、方程式\[
\color{red}{11}x \color{blue}{-2} y+ \color{green}{6} z + d = 0
\]にある1点（\( (x,y,z) = (1,2,-1) \) など）を代入すると、\( d = -1 \) となる。

 

よって、平面の方程式は\[
11x-2y+6z-1=0
\]となる。

（他の2点の座標を実際に代入し、合っているかどうかを検算しましょう）

 

解答2

平面 \( 2x-2y+3z-1=0 \) に垂直な直線ということは、平面の法線ベクトル \( \vec{n} \) に平行な直線の方程式を求めればよい。

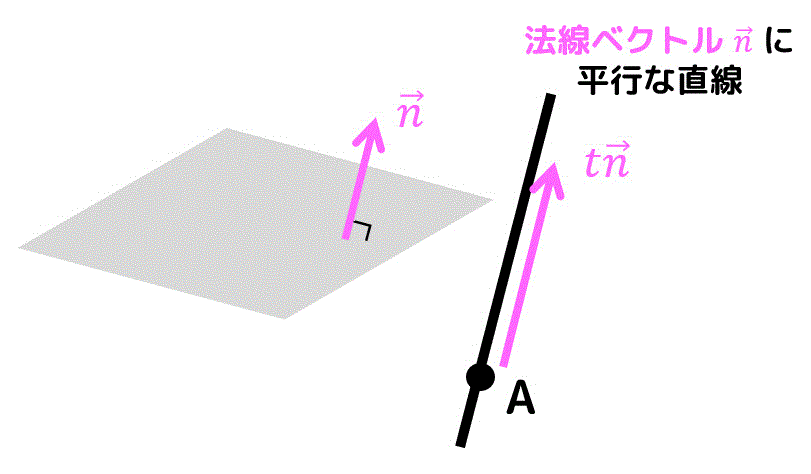
ここで、平面\[
\color{red}{2}x \color{blue}{-2} y+ \color{green}{3} z - 1 = 0
\]の法線ベクトル \( \vec{n} \) は、\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{2} \\ \color{blue}{-2} \\ \color{green}{3} \end{array} \right)
\]となるので、\( \vec{n} \) に平行かつ点A (1,2,-1)を通るような直線を求めればよい。

 

 

このような直線の方程式は\[
\frac{x-1}{2} = \frac{y-2}{-2} = \frac{z-1}{3}
\]となる。（公式より）

 

解答3

平面 \( 2x-2y+3z-1=0 \) に平行な平面では、平面の法線ベクトル \( \vec{n} \) も平行となる。

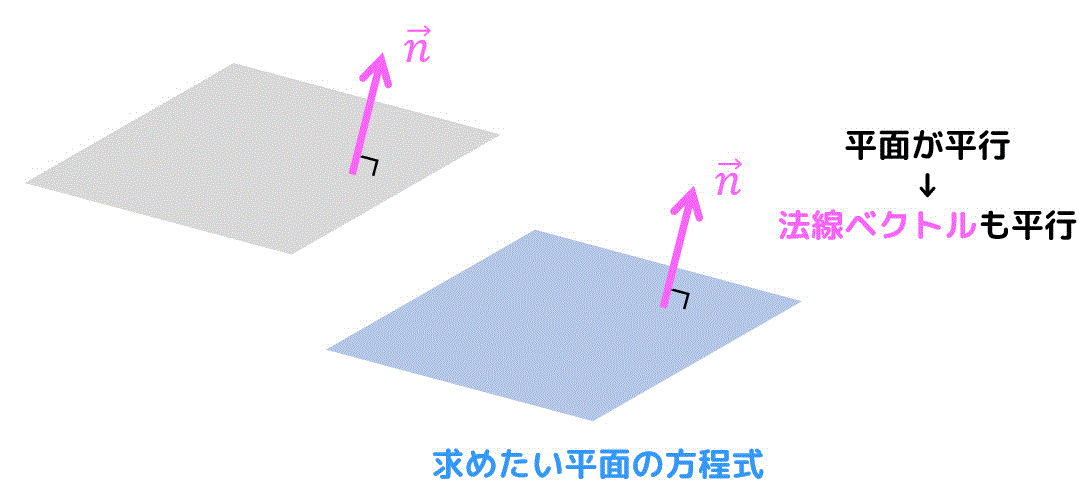
ここで、平面\[
\color{red}{2}x \color{blue}{-2} y+ \color{green}{3} z - 1 = 0
\]の法線ベクトル \( \vec{n} \) は、\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{2} \\ \color{blue}{-2} \\ \color{green}{3} \end{array} \right)
\]となるので、求めたい平面の法線ベクトルも同じく\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{2} \\ \color{blue}{-2} \\ \color{green}{3} \end{array} \right)
\]となる。

 

方程式\[
\color{red}{2}x \color{blue}{-2} y+ \color{green}{3} z + d = 0
\]にある1点（\( (x,y,z) = (1,2,-1) \) など）を代入すると、\( d = 5 \) となる。

 

よって、平面の方程式は\[
2x-2y+3z+5=0
\]と求められる。

 

 

６．さいごに

今回は、平面の方程式を求める方法について説明しました。

特に、

• 外積を用いた法線ベクトルの求め方
• 平面上の3点から方程式を求める方法

は重要なので、必ず理解しましょう！