スポンサードリンク
こんにちは、ももやまです。
うさぎでもわかる線形代数第20羽では、行列の固有値から2次形式の定値性(行列の定値性)を学習しました。
今回は、固有値を求めずに正定値・半正定値を確認できるシルベスターの判定法についてみていきましょう。
目次
スポンサードリンク
[復習] 行列の固有値と定値性
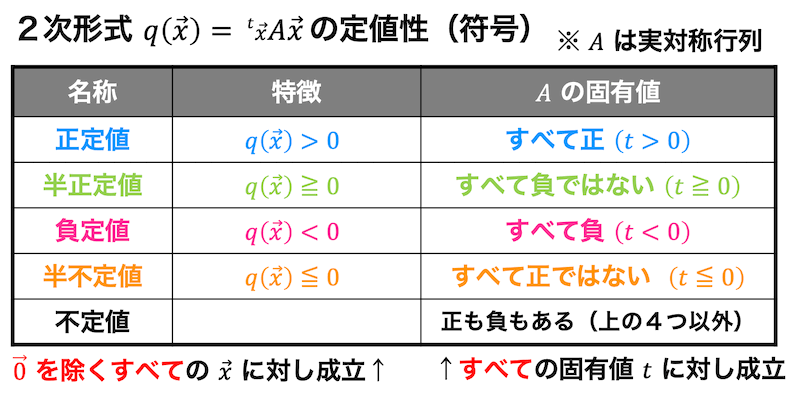
2次形式 \( q ( \vec{x} ) = \vec{x}^{\top} A \vec{x} \) の定値性には次の5つがあります。
- 正定値(\( A \) は正定値行列と呼ばれる)
- 半正定値(\( A \) は半正定値行列と呼ばれる)
- 負定値(\( A \) は負行列と呼ばれる)
- 半負定値(\( A \) は半正定値行列と呼ばれる)
- 不定値(\( A \) は不定値行列と呼ばれる)
定値性の判別方法には様々な方法がありますが、1年生の線形代数でも習う一番メジャー(?)な方法は2次形式 \( q( \vec{x} ) = \vec{x}^{\top} A \vec{x} \) をなす行列 \( A \) の固有値を計算して判定する方法です。
ここで、行列 \( A \) の固有値と定値性(正定値、半正定値、負定値、半負定値、不定値のどれになるか)には下のような関係があります。
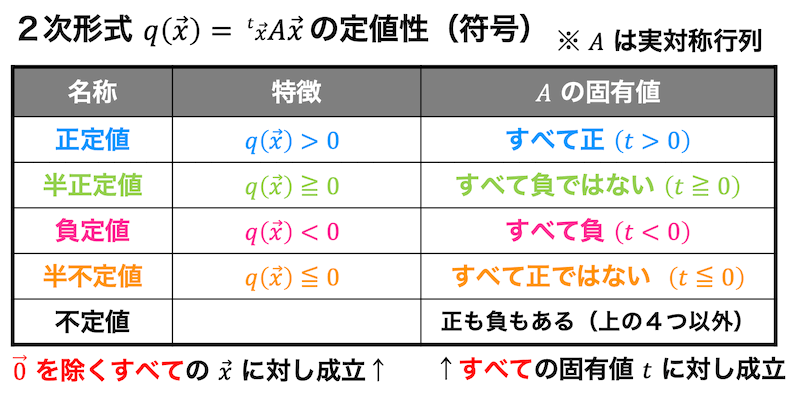
※ \( ^t \! A \), \( A^{\top} \) は行列 \( A \) の転置を表します。
試しに1問例題で確認しましょう。
次の行列\[
A = \left( \begin{array}{ccc} 3 & 4 \\ 2 & 5 \end{array} \right)
\]は、(半)正定値行列、、(半)負定値行列、不定値行列のいずれか。
行列 \( A \) の固有値 \( t \) とし、素直に計算しましょう。\[\begin{align*}
| A - tE | & = \left| \begin{array}{ccc} 3-t & 4 \\ 2 & 5-t \end{array} \right|
\\ & = (3-t)(5-t) - 8
\\ & = t^2 - 8t + 15 - 8
\\ & = t^2 - 8t + 7
\\ & = (t-7)(t-1)
\\ & = 0
\end{align*}\]となるので、固有値は1, 6となる。
ここで、\( A \) の固有値はすべて正なため、行列 \( A \) は正定値行列である[1] … Continue reading
固有値の計算
2×2の行列であれば比較的簡単に固有値を出すことができますね。
しかし、固有値の計算は3×3、4×4、5×5、…となるにつれて計算量が急激に増えてしますし、例題のように答えが全部整数になるとは限りません(整数だと計算がらく)。
例えばこんな行列の固有値なんてとても手計算したくありませんね。\[
\left( \begin{array}{ccc} 6 & -4 & 1 & -5 & 1 \\ -4 & 10 & 2 & 4 & 2 \\ 1 & 2 & 9 & -2 & -6 \\ -5 & 4 & -2 & 7 & 1 \\ 1 & 2 & -6 & 1 & 9 \end{array} \right)
\]
そこで、今回は固有値の計算なしに定値性を判定する方法、シルベスターの判定法を紹介します!
[注意] この先、(半)正定値行列・(半)負定値行列、不定値行列のことをそれぞれ(半)正定値、(半)負定値、不定値と省略して書いている箇所があります。スポンサードリンク
1. シルベスターの判定法の適用手順
Step1. 行列の対角成分を確認し、定値性の候補を絞る
まずは、2次形式を成す行列の対角成分を確認しましょう。\[
\left( \begin{array}{ccc} \textcolor{magenta}{8} & 1 & -5 & 0 \\ 1 & \textcolor{magenta}{8} & 3 & -7 \\ -5 & 3 & \textcolor{magenta}{9} & -2 \\ 0 & -7 & -2 & \textcolor{magenta}{7} \end{array} \right)
\]
2次形式を成す行列 \( A \) の対角成分から、定値性を絞りこむことができる。
(1) 行列 \( A \) の対角成分がすべて正の場合
→ 正定値、半正定値、不定値のいずれか
→ Step2-1に飛ぶ\[
\left( \begin{array}{ccc} \textcolor{red}{9} & 3 & -2 \\ 3 & \textcolor{red}{4} & 2 \\ -2 & 2 & \textcolor{red}{3} \end{array} \right)
\]
(2) 行列 \( A \) の対角成分がすべて0以上かつ、対角成分に0が含まれる場合。
→ 半正定値、不定値のいずれか
→ Step3-1に飛ぶ\[
\left( \begin{array}{ccc} \textcolor{orange}{0} & -1 & 4 \\ -1 & \textcolor{red}{3} & 5 \\ 4 & 5 & \textcolor{red}{2} \end{array} \right)
\]
(3) 行列 \( A \) の対角成分がすべて負の場合。
→ 負定値、半負定値、不定値のいずれか
→ Step2-2に飛ぶ\[
\left( \begin{array}{ccc} \textcolor{blue}{-4} & -3 & 1 \\ -3 & \textcolor{blue}{-3} & -1 \\ 1 & -1 & \textcolor{blue}{-5} \end{array} \right)
\]
(4) 行列 \( A \) の対角成分がすべて0以下かつ、対角成分に0が含まれる場合
→ 半負定値、不定値のいずれか
→ Step3-2に飛ぶ\[
\left( \begin{array}{ccc} \textcolor{blue}{-2} & 4 & 0 \\ 4 & \textcolor{deepskyblue}{0} & -3 \\ 0 & -3 & \textcolor{blue}{-7} \end{array} \right)
\]
(5) 行列 \( A \) の対角成分に正も負も含まれる場合。
→ 不定値である
→ おしまい。\[
\left( \begin{array}{ccc} \textcolor{red}{6} & -6 & -10 \\ 3 & \textcolor{blue}{-1} & 1 \\ -4 & -3 & \textcolor{blue}{-4} \end{array} \right)
\]
定値性の絞り込む方法を図にすると、このようになります。
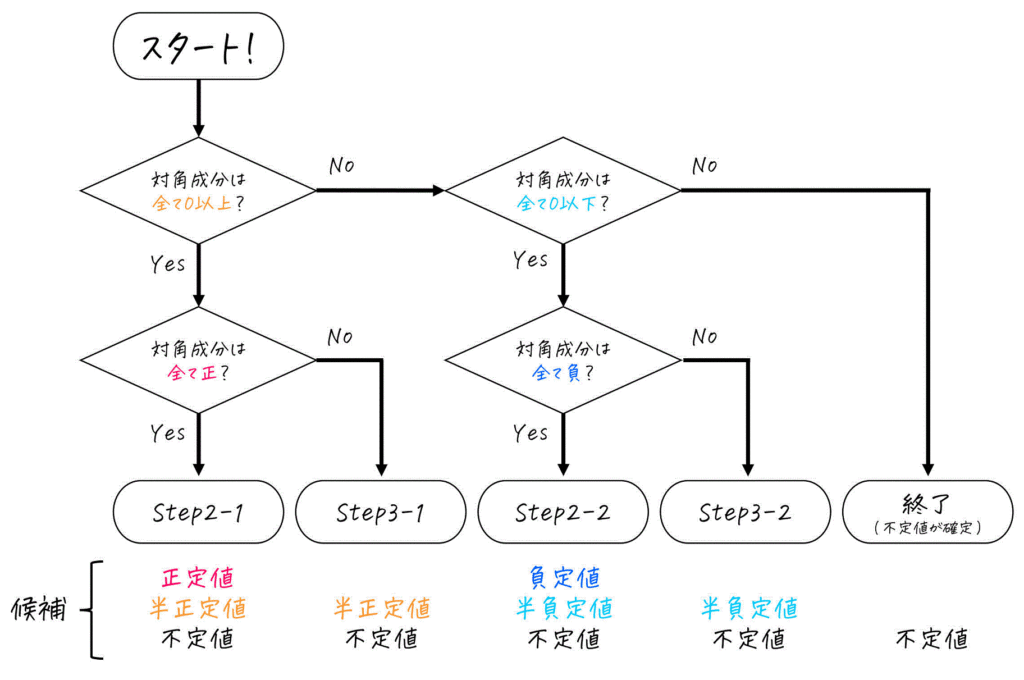
対角成分から定値性が絞れる理由
正定値、半正定値、負定値、半負定値というためには、すべてのベクトル \( \vec{x} \) に対して2次形式 \( \vec{x}^{\top} A \vec{x} \) が一定の条件を満たす必要があります。
つまり、ある1つのベクトル \( \vec{x} \) に対しても、条件を満たさければ、正定値、半正定値、負定値、半負定値とは言えません。
ここでベクトル \( \vec{x} \) ある1つ(\( k \) 番目としましょう)の成分が1、それ以外が0の全ての単位ベクトル \( \vec{x} \) を考えていきます。例えば3次のベクトルであれば、以下の3つが考えられます。\[
\left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) , \ \ \ \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right), \ \ \ \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\]
このとき、2次形式 \( \vec{x}^{\top} A \vec{x} \) の値は、対角成分の中の \( (k,k) \) 成分 \( a_{kk} \) の値と一致します。例えば、3次正方行列であれば\[
\left( \begin{array}{ccc} \textcolor{red}{1} & 0 & 0 \end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{a_{11}} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{1} \\ 0 \\ 0 \end{array} \right) = \textcolor{red}{a_{11}}
\]\[
\left( \begin{array}{ccc} 0 & \textcolor{red}{1} & 0 \end{array} \right) \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & \textcolor{red}{a_{22}} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right) \left( \begin{array}{ccc} 0 \\ \textcolor{red}{1} \\ 0 \end{array} \right) = \textcolor{red}{a_{22}}
\]\[
\left( \begin{array}{ccc} 0 & 0 & \textcolor{red}{1} \end{array} \right) \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & \textcolor{red}{a_{33}} \end{array} \right) \left( \begin{array}{ccc} 0 \\ 0 \\ \textcolor{red}{1} \end{array} \right) = \textcolor{red}{a_{33}}
\]となります。
すべての \( \vec{x} \) に対して(正定値、半正定値、負定値、半負定値の)条件が成立する必要があるということは、当然 \( k \) 番目の成分が1、それ以外が0の全ての単位ベクトル \( \vec{x} \) に対しても成立する必要がありますね。
そのため、行列の対角成分を確認するだけで正定値、半正定値、負定値、半負定値のうちどれが成り立たないかを瞬時に確認することができるのです!
Step2. 正定値 or 負定値の判定
- 行列のすべての対角成分が正(0より大きい)
→ Step2-1. 正定値の判定法へ - 行列のすべての対角成分が負(0より大きい)
→ Step2-2. 負定値の判定法へ
Step2-1. 正定値の判定
まず、元の行列 \( A \) の左上から順に1×1、2×2、3×3と元のサイズになるまで正方行列を取り出せるだけ取り出していきます。

例えば、5次正方行列であれば、取り出す行列は1×1、2×2、3×3、4×4、5×5の5つになります。
※ この取り出した正方行列のことを主座小行列と呼びます。ちなみに、\( n \) 次正方行列にある主座小行列の数は全部で \( n \) 個なので、頭の片隅に入れておくと列挙のし忘れを防げます。
次に、取り出したすべての行列(主座小行列)の行列式を計算します。
(1×1については、対角成分の確認の際に確認済みなので、省略してもOKです)
この行列式の計算結果がすべて正であれば元の行列 \( A \) は正定値行列であるということができます。
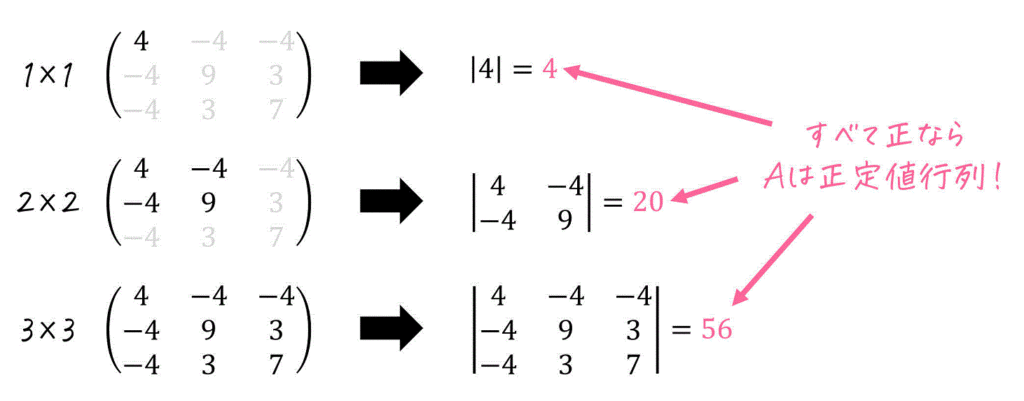
逆に、1つでも計算結果(主座小行列の行列式)が正でない(0以下)の場合があった場合、その行列は正定値行列でないことが確定します。
さらに言うと、1つでも計算結果(どれか1つの主座小行列の行列式)が負になった場合、不定値行列であることが確定します[2] … Continue reading。
ただし、(主座小行列の行列式の)計算結果が負になることはなかったものの、0となるものがあった場合は、半正定値行列か不定値行列のどちらかがわからないため、Step3に移る必要があります。
- 行列 \( A \) の主座小行列を、左上から順に1×1、2×2、3×3、…と取り出すことで求める。(\( n \) 次正方行列の場合、主座小行列は全部で \( n \) 個ある)
- 取り出した行列の行列式を求めていく。
- 1つでも行列式が負になった場合、不定値確定。
- すべての行列式が正になった場合、正定値確定。
- 負になる行列式はなかったが、主座小行列の行列式が0になるものがあった場合、Step3で半正定値かどうかを調べる。
(言い換えると、すべての行列式が0以上の場合はStep3へ移動)
Step2-2. 負定値の判定
どのような \( \vec{x} \) に対しても、\( \vec{x}^{\top} A \vec{x} < 0 \) を満たすとき、2次形式のことを負定値、行列 \( A \) のことを負定値行列(以下、負定値)と呼ぶのでしたね。
ここで \( \vec{x}^{\top} A \vec{x} < 0 \) が成立する場合、\( - \vec{x}^{\top} A \vec{x} > 0 \) も必ず成立しますよね。
さらに、この式は \( \vec{x}^{\top} (-A) \vec{x} > 0 \) と変形することができますね。
そのため、\( A \) が負定値である条件は、「どのような \( \vec{x} \) に対しても \( \vec{x}^{\top} (-A) \vec{x} > 0 \) を満たす」、つまり \( -A \) が正定値であると言い換えることができるのです!

例えば、行列\[
A = \left( \begin{array}{ccc} -4 & 3 & -4 \\ 3 & -4 & 2 \\ -4 & 2 & -5 \end{array} \right)
\]が負定値であることを確認するためには、\[
- A = \left( \begin{array}{ccc} 4 & -3 & 4 \\ -3 & 4 & -2 \\ 4 & -2 & 5 \end{array} \right)
\]が正定値であることを、下のように1×1、2×2、3×3と左上から順に行列(主座小行列)を作ればOKです。
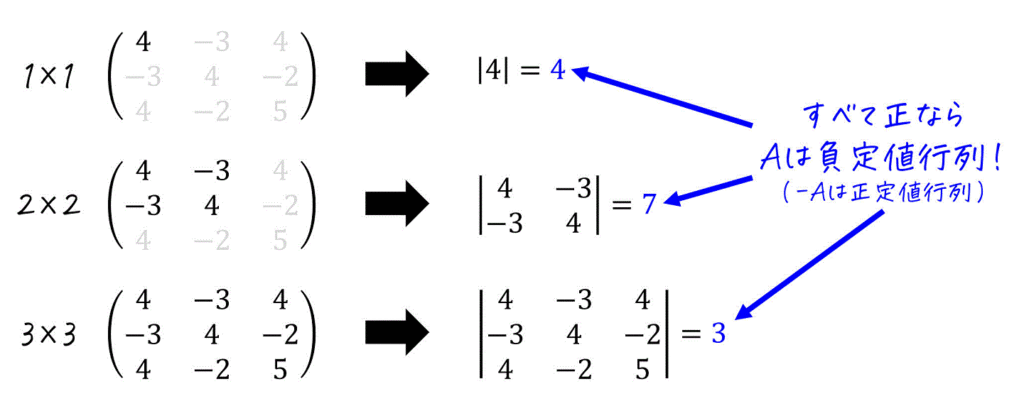
- 行列 \( -A \) の、主座小行列を左上から順に1×1、2×2、3×3、…と取り出すことで求める。
- 取り出した行列の行列式を求めていく。
- 1つでも行列式が負になった場合、不定値確定。
- すべての行列式が正になった場合、負定値確定。
- 負になる行列式はなかったが、主座小行列の行列式が0になるものがあった場合、Step3-2で半負定値かどうかを調べる。
(言い換えると、すべての行列式が0以上の場合はStep3-2へ移動)
Step3. 半正定値 or 半負定値の判定
Step3-1. 半正定値の判定
まず、下のように元の行列 \( A \) に対して、同じ番号の行・列を取り除いてできる正方行列を全通り考えます。(このような行列のことを主小行列と呼びます)
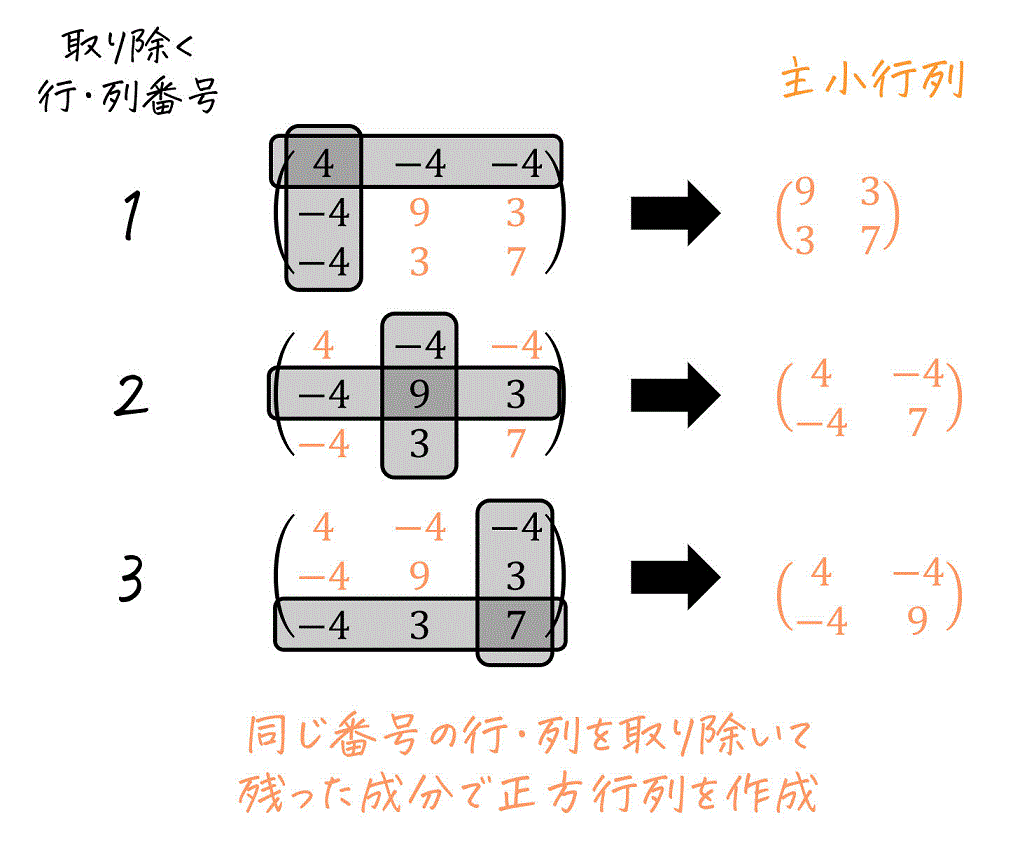
主小行列は、下のように2つ以上の同じ番号の行・列を取り除いた場合や、全く取り除かなかった場合も含まれますので要注意です。
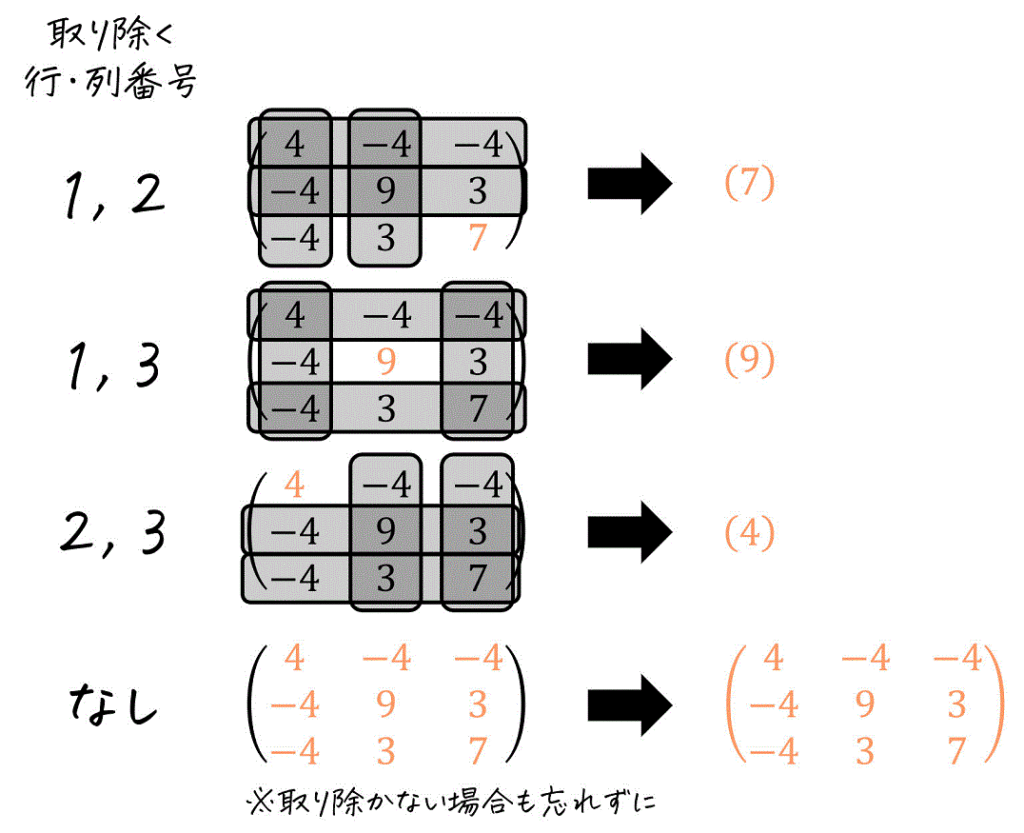
\( n \) 次正方行列の主小行列は全部で \( 2^{n} - 1 \) 個[3]( n ) 次正方行列で主小行列を作るばあい、\( n \) … Continue readingあると頭の片隅に入れておくと安心です。今回の場合は、3次正方行列 ( \( n = 3 \) ) なので、確かに \( 2^3 - 1 = 7 \) 個あることが確認できますね。
つぎに、取り出したすべての主小行列の行列式を求めます。
すべて0以上であれば、\( A \) は半正定値(行列)であることが確定します。
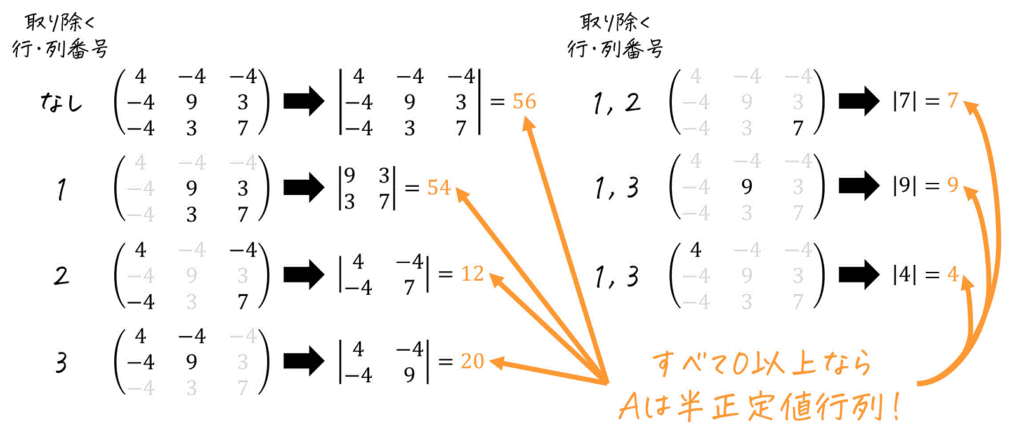
一方、1つでも負(0未満)であった場合、\( A \) は不定値(行列)となります。
- 行列 \( A \) の主小行列を、同じ番号行・列を削除してできるような行列をすべて列挙することで求める。(\( n \) 次正方行列の場合、主小行列は全部で \( 2^{n-1} \) 個ある)
- 取り出した行列の行列式を求めていく。
- 1つでも行列式が負になった場合、不定値確定。
- すべての行列式が0以上になった場合、半正定値確定。
[おまけ] もう1つの主小行列の求め方
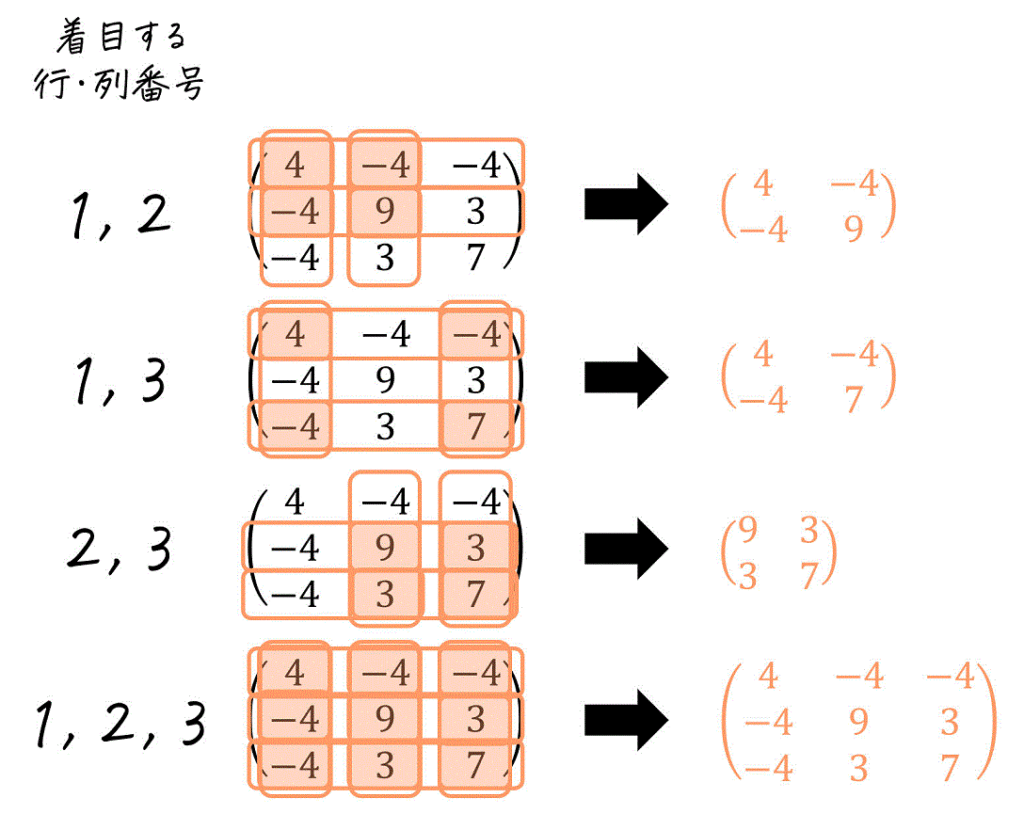
主小行列を求めるもう1つの方法として、同じ番号の行・列に着目し、重なった部分の成分を取り出して方法があります。
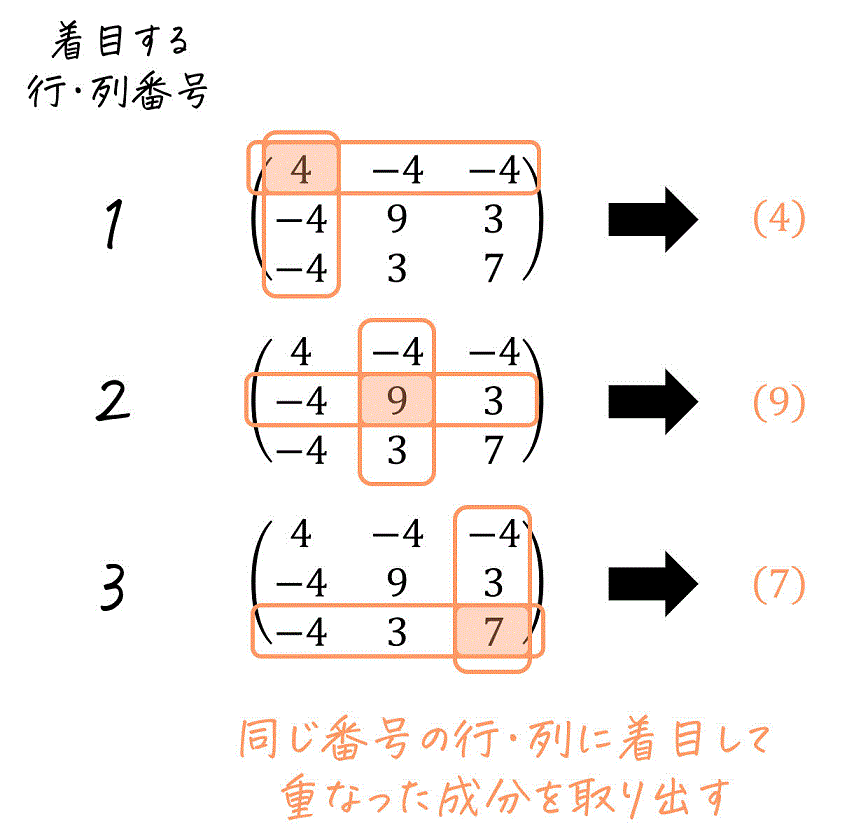
この方法で主小行列を求める場合も、(1つ目のやり方のとき)同じように「複数の行・列に着目した場合、すべての行・列に着目した場合」も考慮してください。
Step3-2. 半負定値の判定
どのような \( \vec{x} \) に対しても、\( \vec{x}^{\top} A \vec{x} \leqq 0 \) を満たすとき、2次形式のことを負定値、行列 \( A \) のことを半負定値行列(以下、負定値)と呼ぶのでしたね。
ここで、\( \vec{x}^{\top} A \vec{x} \leqq 0 \) が成立する場合、\( - \vec{x}^{\top} A \vec{x} \geqq 0 \) も必ず成立しますよね。
さらに、この式は \( \vec{x}^{\top} (-A) \vec{x} \geqq 0 \) と変形できますね。
よって、\( A \) が半負定値である条件は、「どのような \( \vec{x} \) に対しても \( \vec{x}^{\top} (-A) \vec{x} \geqq 0 \) を満たす」、つまり \( -A \) が半正定値であると言い換えられます。

例えば、行列\[
A = \left( \begin{array}{ccc} -5 & 0 & 1 \\ 0 & -5 & -2 \\ 1 & -2 & -1 \end{array} \right)
\]が半負定値であることを確認するためには、\[
- A = \left( \begin{array}{ccc} 5 & 0 & -1 \\ 0 & 5 & 2 \\ -1 & 2 & 1 \end{array} \right)
\]が半正定値であることを、下のように様々な行・列を取り除き、全パターンの主小行列を作ることで確認すればOKです。
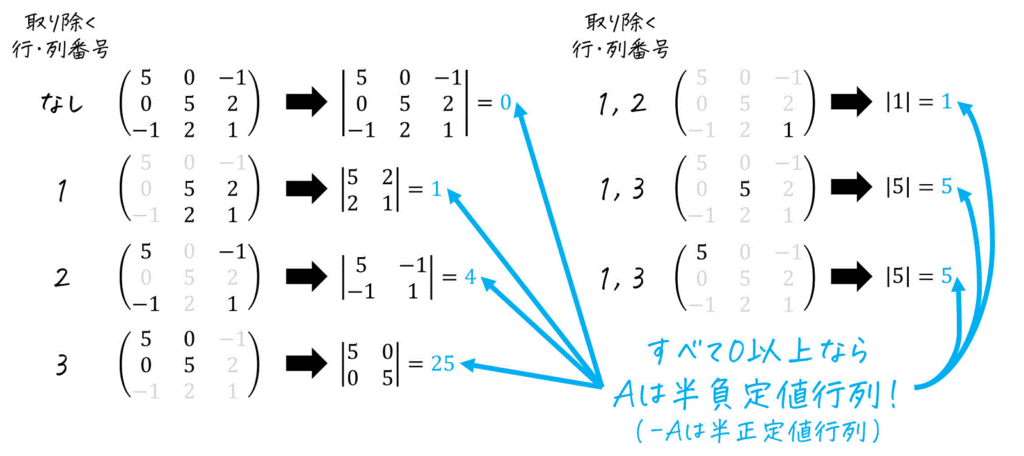
- 行列 \( -A \) の主小行列を、同じ番号行・列を削除してできるような行列をすべて列挙することで求める。
- 取り出した行列の行列式を求めていく。
- 1つでも行列式が負になった場合、不定値確定。
- すべての行列式が0以上になった場合、半負定値確定。
スポンサードリンク
2. 練習問題
それでは、実際に定値性の判定について、5問ほど解いてみましょう。
※ 解説は5/11の23時に更新する予定です
次の行列(1)~(5)の定値性として正しいものを、下の選択肢から1つ選びなさい。
(1)\[
\left( \begin{array}{ccc} 4 & -2 & -4 \\ -2 & 6 & -3 \\ -4 & -3 & 9 \end{array} \right)
\]
(2)\[
\left( \begin{array}{ccc} -7 & 0 & 1 \\ 0 & -8 & 6 \\ 1 & 6 & -10 \end{array} \right)
\]
(3)\[
\left( \begin{array}{ccc} 5 & 5 & 3 \\ 5 & 4 & -5 \\ 3 & -5 & 0 \end{array} \right)
\]
(4)\[
\left( \begin{array}{ccc} -8 & 0 & 4 \\ 0 & -5 & 5 \\ 4 & 5 & -7 \end{array} \right)
\]
(5)\[
\left( \begin{array}{ccc} 4 & 0 & -2 & -2 \\ 0 & 2 & -3 & 3 \\ -2 & -3 & 9 & -1 \\ -2 & 3 & -1 & 10 \end{array} \right)
\]
[選択肢]
ア:正定値である
イ:正定値ではないが、半正定値である
ウ:負定値である
エ:負定値ではないが、半負定値である
オ:不定値である(半正定値でも半負定値でもない)
3. 練習問題の解説
(1)
解答: イ
対角成分がすべて正なため、Step2-1(正定値の判定)を行う。\[
\left( \begin{array}{ccc} \textcolor{red}{4} & -2 & -4 \\ -2 & \textcolor{red}{6} & -3 \\ -4 & -3 & \textcolor{red}{9} \end{array} \right)
\]具体的には、すべての主座小行列(1×1、2×2、3×3)が正であることを確認すればOK。
(次回の判定以降は、対角成分1つからなる主座小行列の行列式は省略する。すでに対角成分がすべて正であることを確認済みなので。) [2×2] → OK\[
\left| \begin{array}{ccc} 4 & -2 \\ -2 & 6 \end{array} \right| = 20
\] [3×3] → △(行列式が0)\[\begin{align*}
\left| \begin{array}{ccc} 4 & -2 & -4 \\ -2 & 6 & -3 \\ -4 & -3 & 9 \end{array} \right| & =
\left| \begin{array}{ccc} 0 & 10 & -10 \\ -2 & 6 & -3 \\ 0 & -15 & 15 \end{array} \right|
\\ & = \left| \begin{array}{ccc} 0 & 1 & -1 \\ -2 & 6 & -3 \\ 0 & 0 & 0 \end{array} \right| \\ & = 0
\end{align*}\]
ここで、主座小行列の行列式が負になることはなかったが、0となるものがあった。
そのため、次に半正定値性を確認するために主小行列の行列式を(行列のサイズが小さい順に)確認していく。
[2つの行を削除した場合] → 対角成分1つしか残らない。対角成分は正であることが確認済みなので、確認省略可。OK。 [1行・1列を削除] → OK\[
\left| \begin{array}{ccc} 6 & -3 \\ -3 & 9 \end{array} \right| = 45 > 0
\]
[2行・2列を削除] → OK
\[
\left| \begin{array}{ccc} 4 & -4 \\ -4 & 9 \end{array} \right| = 30 > 0
\]
[3行・3列を削除] → 2×2の主座小行列と同じ → OK\[
\left| \begin{array}{ccc} 4 & -2 \\ -2 & 6 \end{array} \right| = 20
\]
[削除なし] → 3×3の主座小行列と同じ、行列式は0以上。
よって、すべての主小行列の行列式が0以上なため、(1)の行列は半正定値(行列)である。
主座小行列、主小行列の行列式を用いて判定する際には、サイズが小さいもの(1×1、2×2、3×3…)から行うことをおすすめします。(行列式が負になった瞬間に不定値が確定し、計算を終了できるため、サイズが大きな行列の行列式を計算せずに済む可能性があるため。)
(2)
解答: ウ
対角成分がすべて負なため、Step2-2(負定値の判定)を行う。\[
\left( \begin{array}{ccc} \textcolor{blue}{-7} & 0 & 1 \\ 0 & \textcolor{blue}{-8} & 6 \\ 1 & 6 & \textcolor{blue}{-10} \end{array} \right)
\]
負定値を判定する際には\[
- \left( \begin{array}{ccc} -7 & 0 & 1 \\ 0 & -8 & 6 \\ 1 & 6 & -10 \end{array} \right) = \left( \begin{array}{ccc} 7 & 0 & -1 \\ 0 & 8 & -6 \\ -1 & -6 & 10 \end{array} \right)
\]の主座小行列の行列式が正になるかどうかを確認すればOK。
\left| \begin{array}{ccc} 7 & 0 \\ 0 & 8 \end{array} \right| = 56 > 0
\] [3×3] → OK\[\begin{align*}
\left| \begin{array}{ccc} 7 & 0 & -1 \\ 0 & 8 & -6 \\ -1 & -6 & 10 \end{array} \right| & =
560 + 0 + 0 - (8+0+252)
\\ & = 300 > 0
\end{align*}\]より、(2)の行列は負定値(行列)である。
(3)
解答:オ
対角成分に0が含まれるが、すべて0以上なので、Step3-1の半正定値の確認を行う。\[
\left( \begin{array}{ccc} \textcolor{orange}{5} & 5 & 3 \\ 5 & \textcolor{orange}{4} & -5 \\ 3 & -5 & \textcolor{orange}{0} \end{array} \right)
\]
[2つの行を削除した場合] → 対角成分1つしか残らない。対角成分は正であることが確認済みなので、確認省略可。OK。
\[
\left| \begin{array}{ccc} 4 & -5 \\ -5 & 0 \end{array} \right| = -25 < 0
\]
主小行列の行列式が負になるパターンが発見されたため、(3)の行列は不定値である。
(4)
解答: エ
対角成分がすべて負なため、Step2-2(負定値の判定)を行う。\[
\left( \begin{array}{ccc} \textcolor{blue}{-8} & 0 & 4 \\ 0 & \textcolor{blue}{-5} & 5 \\ 4 & 5 & \textcolor{blue}{-7} \end{array} \right)
\]
負定値を判定する際には\[
- \left( \begin{array}{ccc} -8 & 0 & 4 \\ 0 & -5 & 5 \\ 4 & 5 & -7 \end{array} \right) = \left( \begin{array}{ccc} 8 & 0 & -4 \\ 0 & 5 & -5 \\ -4 & -5 & 7 \end{array} \right) = -A
\]の主座小行列の行列式が正になるかどうかを確認すればOK。
\left| \begin{array}{ccc} 8 & 0 \\ 0 & 5 \end{array} \right| = 40 > 0
\] [3×3] → △(行列式が0)\[\begin{align*}
\left| \begin{array}{ccc} -8 & 0 & 4 \\ 0 & -5 & 5 \\ 4 & 5 & -7 \end{array} \right|& =
280 + 0 + 0 - (80 + 200)
\\ & = 0
\end{align*}\]
ここで、\( - A \) の主座小行列の行列式が負になることはなかったが、0となるものがあった。
そのため、次に半負定値性を確認するため、\( -A \) の主小行列の行列式を(行列のサイズが小さい順に)確認していく。
[2つの行を削除した場合] → 対角成分1つしか残らない。対角成分は正であることが確認済みなので、確認省略可。OK。 [1行・1列を削除] → OK\[
\left| \begin{array}{ccc} 5 & -5 \\ -5 & 7 \end{array} \right| = 10 > 0
\]
[2行・2列を削除] → OK
\[
\left| \begin{array}{ccc} 8 & -4 \\ -4 & 7 \end{array} \right| = 40 > 0
\]
[3行・3列を削除] → 2×2の主座小行列と同じ、行列式は0以上、OK。
よって、\( -A \) の主小行列の行列式が0以上なため、(4)の行列は半負定値(行列)である。
(5)
解答: ア
対角成分がすべて正なため、Step2-1(正定値の判定)を行う。\[
\left( \begin{array}{ccc} \textcolor{red}{4} & 0 & -2 & -2 \\ 0 & \textcolor{red}{2} & -3 & 3 \\ -2 & -3 & \textcolor{red}{9} & -1 \\ -2 & 3 & -1 & \textcolor{red}{10} \end{array} \right)
\]具体的には、すべての主座小行列(1×1、2×2、3×3、4×4)が正であることを確認すればOK。
\left| \begin{array}{ccc} 4 & 0 \\ 0 & 2 \end{array} \right| = 8 > 0
\] [3×3] → OK\[\begin{align*}
\left| \begin{array}{ccc} 4 & 0 & -2 \\ 0 & 2 & -3 \\ -2 & -3 & 9 \end{array} \right| & =
72 + 0 + 0 - (8 +36)
\\ & = 28 > 0
\end{align*}\] [4×4] → OK\[\begin{align*}
\left| \begin{array}{ccc} 4 & 0 & -2 & -2 \\ 0 & 2 & -3 & 3 \\ -2 & -3 & 9 & -1 \\ -2 & 3 & -1 & 10 \end{array} \right|
& = \left| \begin{array}{ccc} 0 & 6 & -4 & 18 \\ 0 & 2 & -3 & 3 \\ 0 & -6 & 10 & -11 \\ -2 & 3 & -1 & 10 \end{array} \right|
\\ & = 2 \left| \begin{array}{ccc} 6 & -4 & 18 \\ 2 & -3 & 3 \\ -6 & 10 & -11 \end{array} \right|
\\ & = 2 \left| \begin{array}{ccc} 0 & 5 & 9 \\ 2 & -3 & 3 \\ 0 & 1 & -2 \end{array} \right|
\\ & = 2 \cdot (-2) \left| \begin{array}{ccc} 5 & 9 \\ 1 & -2 \end{array} \right|
\\ & = -4(-10 - 9)
\\ & = 76 > 0
\end{align*}\]
よって、すべての主座小行列の行列式が0以上なため、(1)の行列は正定値(行列)である。
4. さいごに
今回は、固有値を求めずに行列(2次形式)が正定値、半正定値、負定値、半負定値、不定値のどれに属するかを、行列の対角成分の着目+シルベスターの判定法を用いて求める方法について説明しました。
次回からは、いよいよ行列の対角化、直交行列による対角化を進化させた「特異値分解」について取り上げていきたいと思います。
注釈
| ↑1 | 固有値が正であるということは、固有値は0以上なので半正定値行列ですが、期末試験などでは「正定値行列ではないが、半正定値行列となる条件(すべての固有値が0以上)を満たしている行列」のみ、半正定値行列と答えるようにしましょう。半負定値行列に関しても同じ(負定値行列ではないが、半負定値行列の条件を満たすときのみ、半負定値行列と答える)です。 |
|---|---|
| ↑2 | Step3で説明しますが、主座小行列は主小行列の特殊なパターンです。そのため、主座小行列の行列式が1つでも負になる場合、主小行列の行列式も同じく負になるパターンが1つ以上あるといえます。そのため、半正定値の条件も満たさず、不定値であることが確定します。 |
| ↑3 | ( n ) 次正方行列で主小行列を作るばあい、\( n \) 個それぞれの行(と列)ごとに「削除する」か「削除しない」かの2通りの選び方がありますね。なので、\( 2^n \) 個、と言いたいですが全部取り除く場合(1通り)を取り除く必要があるので、\( n \) 次正方行列に存在する主小行列の数は全部で \( 2^n - 1 \) 個となります。 |
関連広告・スポンサードリンク