うさぎでもわかる線形代数　応用編第9羽　行列を使って最小2乗法を解いてみよう！

2022年5月25日 2022年6月29日 63分19秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

前回の第08羽では、逆行列 \( A^{-1} \) を持たない行列に対して、無理やり逆行列っぽいもの（擬似逆行列）について求めてから掃き出し計算なしに解を計算する方法について説明しました。

今回の第09羽では、そもそも解をもたないような連立方程式 \( A \vec{x} = \vec{b} \) に対して、最もそれっぽい解 \( \vec{x} \) を計算する方法である最小2乗法について説明していきます。

この最小2乗法は、実験のデータ解析や、研究分野など様々な分野で応用が利くので、是非マスターしていきましょう！

行列と連立方程式 [復習]
1. 擬似逆行列（一般化逆行列）]
- (1) 擬似逆行列とは
- (2) 解をもたない場合
2. 最もそれらしい解とは - 最小2乗法の始まり
3. 擬似逆行列で最小2乗法が計算できる仕組み
4. 例題で最小2乗法の計算方法を確認しよう
5. 実験と最小2乗法（回帰直線）
6. 練習問題
7. 練習問題の答え
8. さいごに

スポンサードリンク

行列と連立方程式 [復習]

うさぎでもわかる線形代数　第02羽では、行列を用いて連立方程式を解く方法について説明しました。

本題の最小2乗法に入る前に、まずは今回使う知識「行列と連立方程式」について軽く復習しましょう。

皆さんは、下のように\( m \) 個の式、\( n \) 個の未知数がある連立方程式\[
\left\{ \begin{align*} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n & = b_1 \\
a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n & = b_2 \\
& \vdots \\
a_{m1} x_1 + a_{m2} x_2 + \cdots + a_{mn} x_n & = b_m \\
\end{align*} \right.
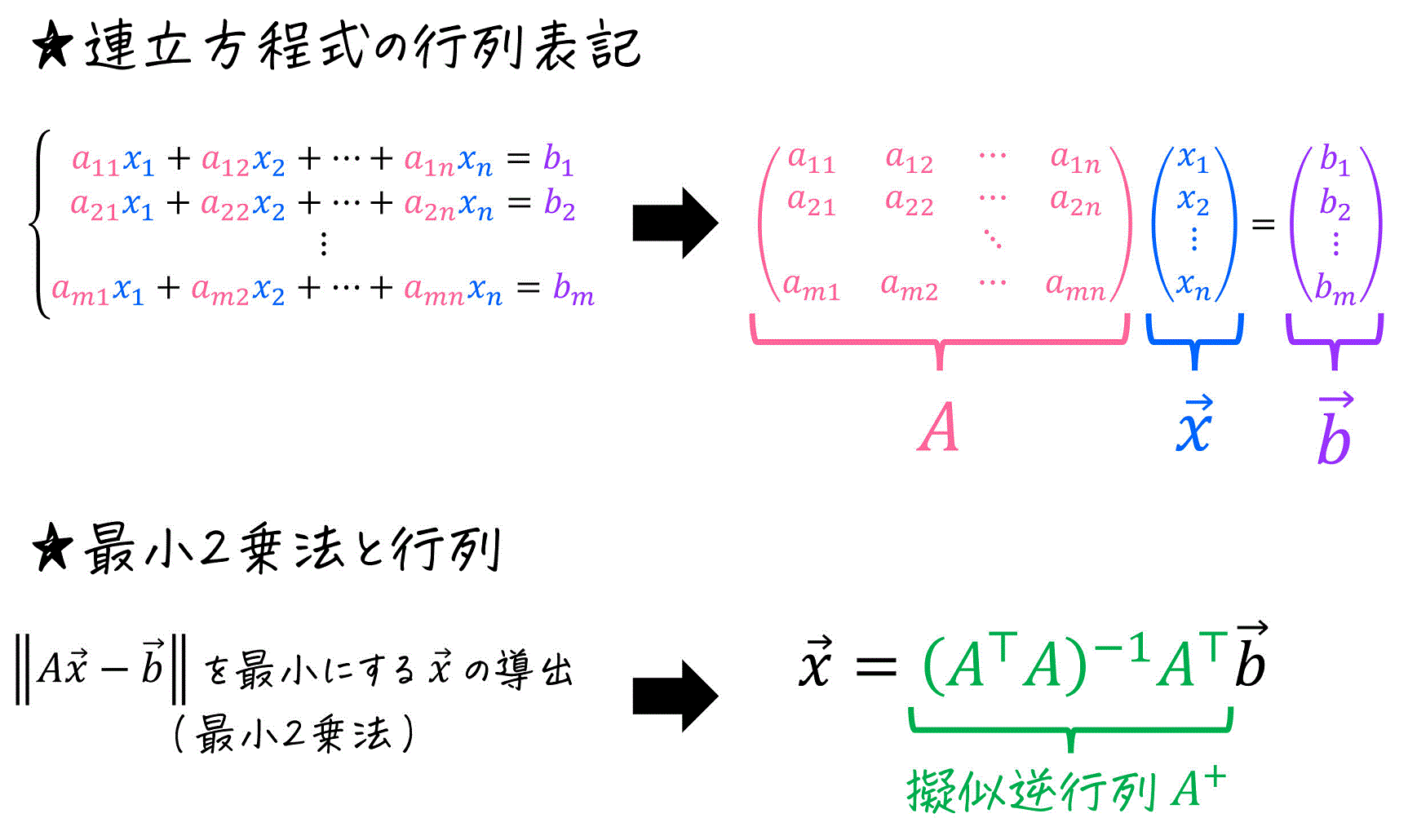
\]を下のように係数行列 \( A \)、解ベクトル \( \vec{x} \)、右辺を集めたベクトル \( \vec{b} \) で表すことを勉強しました。

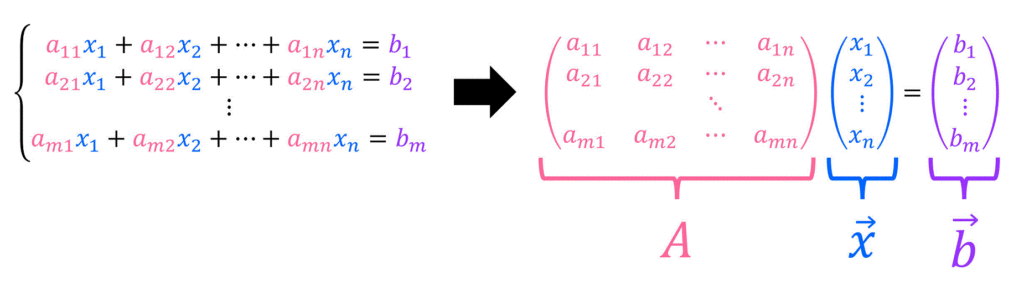
この連立方程式が解をもつかどうかは \( m \) 行 \( n \) 列の行列 \( A \) と拡大係数行列 \( B = (A| \vec{b}) \) を比べることでわかるのでしたね。

具体的には、

\( \mathrm{Rank} \ A < \mathrm{Rank} \ B \) のときは解なし
\( \mathrm{Rank} \ A = \mathrm{Rank} \ B \) のときはさらに場合分け
- \( \mathrm{Rank} \ A = n \) のときはただ1つの解をもつ
- \( \mathrm{Rank} \ A < n \) のときは無数の解をもつ。
  （どのような解をもつかは \( n - \mathrm{Rank} \ A \) 個の任意定数で表現可）

でしたね。

今回「行列を用いた最小2乗法」では、

解なしのとき
ただ1つの解をもつとき

の2つに着目していきたいと思います。

スポンサードリンク

1. 擬似逆行列（一般化逆行列）]

前回の第08羽で擬似逆行列について勉強しましたが、もう1度擬似逆行列について復習をしてから本題の最小2乗法に入りましょう。

(1) 擬似逆行列とは

たとえ、係数行列 \( A \) がただ1つの解をもつとしても、\( A \) が正方行列ではない場合、逆行列 \( A^{-1} \) を計算できないため、連立方程式 \( A \vec{x} = \vec{b} \) を \( \vec{x} = A^{-1} \vec{b} \) と計算することができません。

そこで、両辺に \( \textcolor{red}{A^{\top}} \) を掛けて、\[\begin{align*}
A \vec{x} & = \vec{b} \\
\textcolor{red}{A^{\top}} A \vec{x} & = \textcolor{red}{A^{\top}} \vec{b} \\
(A^{\top} A)^{-1} (A^{\top} A) \vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b} \\
\vec{x} & = \underbrace{ (A^{\top} A)^{-1} A^{\top} }_{A^+} \vec{b}
\end{align*}\]と変形することで、解 \( \vec{x} \) を計算することができます。

このときに出てくる \( (A^{\top} A)^{-1} A^{\top} \) を \( A^+ \) としたものが擬似逆行列です。
（疑似逆行列・一般化逆行列・一般逆行列と呼ばれることもあります）

擬似逆行列とは

連立方程式 \( A \vec{x} = \vec{b} \) の係数行列 \( A \) が正方行列ではなかった場合でも、\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]とおくことで、掃き出し法を計算せずに解 \( \vec{x} \) を計算できる。このときの \( A^+ \) を擬似逆行列と呼ぶ。

(2) 解をもたない場合

擬似逆行列は、\( n \) 次正方行列 \( A^{\top} A \) が正則^[1]\( A^{\top} A \) の逆行列を計算するため、\( A^{\top} A \) が正則でないとダメ。でないと計算できません。

この条件は、行列 \( A \) が正則、つまり \( \mathrm{Rank} \ A = n \) と言い換えることができます。

しかし、\( \mathrm{Rank} \ A = n \) だったとしても、\( \mathrm{Rank} (A| \vec{b}) > n \) だった場合、\( \mathrm{Rank} \ A < \mathrm{Rank} \ \vec{b} \) となり、解をもちません。

一方、擬似逆行列が計算できる条件は \( \mathrm{Rank} \ A = n \) なので、擬似逆行列 \( A^+ \) が計算できてしまいます。擬似逆行列が計算できるいうことは、解 \( \vec{x} = A^+ \vec{b} \) も計算できてしまいます。本当は解がないはずなのに。あら不思議。

実は解がない連立方程式 \( A \vec{x} = \vec{b} \) の中に対しては、擬似逆行列で出てくる解 \( \vec{x} \) は必ず最も連立方程式の左辺 \( A \vec{x} \) と右辺 \( \vec{b} \) が近くなるような解（それっぽい解）となるのです！

なぜそんなことができるのかは、3章にて詳しく説明します。

スポンサードリンク

2. 最もそれらしい解とは - 最小2乗法の始まり

最もそれらしい解と言われても、人によって「それらしい」の解釈が変わってきます。そこで、「それらしい解かどうかの基準」を明確に設定しましょう。

まず、連立方程式 \( A \vec{x} = \vec{b} \) を変形すると、\( A \vec{x} - \vec{b} = \vec{0} \) とできます。

ここで、左辺 \( A \vec{x} - \vec{b} \) がどれだけ右辺 \( \vec{b} \) に近くなるかでそれらしい解かどうかを判断しましょう。とはいっても、ベクトルの大小はそのままでは比べることができません。

そこで登場するのがノルム（長さ・大きさ）です。

まず、右辺 \( \vec{0} \) のノルムは当然0です。なので左辺 \( A \vec{x} - \vec{b} \) はどれだけ右辺のノルム（0に近いのか）で最もそれらしい解かどうかを判断することを考えましょう。

ここで、ノルムは必ず0以上となるのでしたね。つまり、\( \| A \vec{x} - \vec{b} \| \geqq 0 \)　も成り立ちますね。

そのため、 \( \| A \vec{x} - \vec{b} \| \) が最も小さくなるような \( \vec{x} \) が最もそれらしい解であると言い換えることができますね^[2]今までの記事では、ベクトルのノルムを \( | \vec{x} | \) のように絶対値っぽく表してきましたが、本記事ではベクトルのノルム（長さ）を \( \| \vec{x} … Continue reading。

また、 \( \| A \vec{x} - \vec{b} \| \) は、連立方程式 \( A \vec{x} = \vec{b} \) の左辺 \( A \vec{x} \)が右辺 \( \vec{b} \) とどの程度ずれているかを表す誤差の指標にもなります。

この「それっぽい解 \( \vec{x} \)」を求める方法、より数学的に言うと誤差 \( \| A \vec{x} - \vec{b} \| \) を最も小さくなるような \( \vec{x} \) を求める方法のことを、最小2乗法と呼びます。

3. 擬似逆行列で最小2乗法が計算できる仕組み

ここからは、連立方程式 \( A \vec{x} = \vec{b} \) に対し、\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]と擬似逆行列 \( A^+ \) を使うだけで、誤差 \( \| A \vec{x} - \vec{b} \| \) を最小にする最小2乗法が実現できる仕組みを説明していきます。

(1) 前提知識 - ベクトルの偏微分

(i) ベクトルの偏微分とは？

皆さんは、高校の数2、数3、大学の解析学の前半で微分を、解析学の後半では偏微分を習いましたね。これらの微分は、\[
\frac{\partial}{\partial x} x^5 y^4 = 5x^4 y^4
\]のように、スカラーをある1つのスカラー変数で微分するのでしたね。

最小2乗法では、下のようにこの偏微分の概念を拡張した「スカラーをある1つのベクトルで偏微分する」ということをします。\[\begin{align*}
\frac{\partial f}{\partial x} = \left( \begin{array}{cc} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{array} \right)
\end{align*}\]

とは言っても、いまいち実感がわかないと思うので、まずは計算例を見てみましょう。

例題1

ベクトル \( \vec{x} \)、および \( f( \vec{x} ) \) を\[
\vec{x} = \left( \begin{array}{cc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\]\[ f( \vec{x} ) = f( x_1, x_2, x_3) = 5x_1^2 + 3 x_2^4 - x_3^3 \]とする。このとき、\[
\frac{ \partial f}{ \partial \vec{x} }
\]を計算しなさい。

[解説1]

\[\begin{align*}
\frac{ \partial f}{ \partial \vec{x} } & = \left( \begin{array}{cc} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \frac{\partial f}{\partial x_3} \end{array} \right)
\\ & = \left( \begin{array}{cc} 10 x_1 \\ 12x_2^3 \\ - 3 x_3^2 \end{array} \right)
\end{align*}\]

(ii) 最小2乗法で使うベクトルの偏微分の導出

最小2乗法の公式を計算する際には、\( n \) 次実対称行列 \( A \)、および \( n \) 次のベクトル \( \vec{b} \) および解ベクトル \( \vec{x} \) を

\( \vec{x}^{\top} A \vec{x} \)　※ \( A \) は実対称行列
\( \vec{x}^{\top} \vec{b} \)

を微分する場面が出てきます。

この2式の微分を導出してみましょう。

[1] \( \vec{x}^{\top} A \vec{x} \) の偏微分

\( n \) 次のときを導出すると計算量がえげつなさすぎるので、\( n = 2 \) のときで確かめることにします。

まず、\( n = 2 \) なので、\[
A = \left( \begin{array}{cc} u & p \\ p & v \end{array} \right), \ \ \ \vec{x} = \left( \begin{array}{cc} x_1 \\ x_2 \end{array} \right), \ \ \ \vec{b} = \left( \begin{array}{cc} b_1 \\ b_2 \end{array} \right)
\]とします。

すると、\[\begin{align*}
\vec{x}^{\top} A \vec{x} & = \left( \begin{array}{cc} x_1 & x_2 \end{array} \right) \left( \begin{array}{cc} u & p \\ p & v \end{array} \right) \left( \begin{array}{cc} x_1 \\ x_2 \end{array} \right)
\\ & = \left( \begin{array}{cc} x_1 & x_2 \end{array} \right) \left( \begin{array}{cc} u x_1 + p x_2 \\ p x_1 + v x_2 \end{array} \right)
\\ & = x_1 (u x_1 + p x_2 ) + x_2 (p x_1 + v x_2)
\\ & = u x_1^2 +2p x_1 x_2 + v x_2^2
\end{align*}\]と計算できます。

この式を \( \vec{x} \) で偏微分すると、\[\begin{align*}
\frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} A \vec{x} & = \frac{ \partial }{ \partial \vec{x} } u x_1^2 +2p x_1 x_2 + v x_2^2
\\ & = \left( \begin{array}{cc} \frac{\partial }{\partial x_1} u x_1^2 +2p x_1 x_2 + v x_2^2 \\ \frac{\partial}{\partial x_2} u x_1^2 +2p x_1 x_2 + v x_2^2 \end{array} \right)
\\ & = \left( \begin{array}{cc} 2 u x_1 +2p x_2 \\ +2p x_1 + 2 v x_2 \end{array} \right)
\\ & = 2 \left( \begin{array}{cc} u & p \\ p & v \end{array} \right) \left( \begin{array}{cc} x_1 \\ x_2 \end{array} \right)
\\ & = 2 A \vec{x}
\end{align*}\]となります。

よって、\( \vec{x}^{\top} A \vec{x} \) を \( \vec{x} \) 偏微分すると\[
\frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} A \vec{x} = 2 A \vec{x}
\]と導出ができます。

※ \( n = 3 \) 以上のときも同様の手順で導出できます。計算がしんどいですが…

[2] \( \vec{x}^{\top} \vec{b} \) の偏微分

こちらは、\( n \) 次の場合でも計算量が大したことないので、\( n \) 次のままで導出します。つまり、\[
\vec{x} = \left( \begin{array}{cc} x_1 \\ x_2 \\ \cdots \\ x_n \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{cc} b_1 \\ b_2 \\ \cdots \\ b_n \end{array} \right)
\]です。まずは、\( \vec{x}^{\top} \vec{b} \) を展開します。

\[\begin{align*}
\vec{x}^{\top} \vec{b} & = \left( \begin{array}{cc} x_1, x_2, \cdots, x_n \end{array} \right) \left( \begin{array}{cc} b_1 \\ b_2 \\ \cdots \end{array} \right)
\\ & = x_1 b_1 + x_2 b_2 + \cdots + x_n b_n
\\ & = b_1 x_1 + b_2 x_2 + \cdots + b_n x_n
\end{align*}\]

さらに微分すると、\[\begin{align*}
\frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} \vec{b} & = \left( \begin{array}{cc} \frac{\partial }{\partial x_1} ( b_1 x_1 + b_2 x_2 + \cdots + b_n x_n) \\ \frac{\partial }{\partial x_2} (b_1 x_1 + b_2 x_2 + \cdots + b_n x_n) \\ \vdots \\ \frac{\partial}{\partial x_n} (b_1 x_1 + b_2 x_2 + \cdots + b_n x_n) \end{array} \right)
\\ & = \left( \begin{array}{cc} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right)
\\ & = \vec{b}
\end{align*}\]と計算できるため、\( \vec{x}^{\top} \vec{b} \) を \( \vec{x} \) で偏微分した結果を\[
\frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} \vec{b} = \vec{b}
\]と導出ができます。

(2) 勾配と最小値

皆さんは、数2・数3で、「スカラーな変数（\( x \) など）を微分し、増減表を書くことで極大値・極小値（最大値・最小値）を求めるような経験」をしましたね。

例えば、2次関数 \( f(x) = (x - a)^2 = x^2 - 2ax + a^2 \) の極小値であれば、\[
f'(x) = 2x - 2a
\]と微分し、傾き \( f'(x) = 2x - 2a = 0 \) となる \( x \)、つまり \( x = a \) が極小値になりますね。

また、増減表やグラフを書くことで、グラフ \( f(x) = (x-a)^2 \) が下に凸になることがわかりますね。

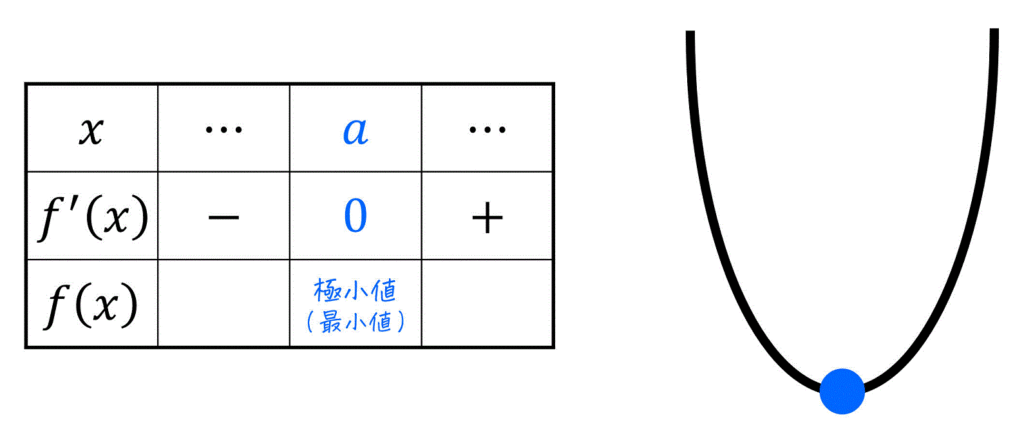
よって、極小値 \( x = a \) が最小値になることが確認できます。

ベクトルの場合も同じように、「ベクトル \( \vec{x} \) を微分することで、極大値や極小値を求める」ことがスカラー変数と同じように実現できるのです！

スカラー変数の場合は、傾き \( f'(x) = 0 \) となる点が極値（最大値・最小値の候補）となるように、ベクトルの場合も勾配 \( f'( \vec{x} ) = 0 \) となる点が極値（最大値・最小値の候補）となるのです。ただし、\[
f' ( \vec{x} ) = \frac{ \partial f}{\partial \vec{x} }
\]とします（勾配ベクトル）。

ここで、最小2乗法で求めたい式\[
f( \vec{x} ) = \| A \vec{x} - \vec{b} \|
\]において、最小にする \( \vec{x} \) を求めることを考えましょう。

まず、極値は勾配 \( f'( \vec{x} ) = 0 \) を計算することで求められますね。

次に、極値が最小値を取るかどうかの確認ですが、\( \| A \vec{x} - \vec{b} \| \) は「まるでスカラー変数 \( x \) で表される2次関数 \( g(x) = (ax - b)^2 = a^2 x^2 - 2ab + b^2 \) のような形」になっていますね。

ここで、\( g(x) \) は、\( a^2 \geqq 0 \) となるので、グラフの形は \( a \not = 0 \) のときを除き、下のような形（下に凸）になりますね。

この形の場合、極値 \( g'(x) = 0 \) となる \( x \) は最小値となることがわかりますね。

ベクトル関数 \( f（\vec{x} ) = \| A \vec{x} - \vec{b} \| \) もスカラーの場合と同じように、勾配 \( f'( \vec{x} ) = 0 \) となる \( \vec{x} \) を計算すれば最小値が求まりそうですね。

(3) 最小2乗法の導出

ここからは、実際に \( f'( \vec{x} ) = 0 \) となる \( \vec{x} \) を計算することで、\( \| A \vec{x} - \vec{b} \| \) を最小にする \( \vec{x} \) を求めていきます。

まず、\( \| A \vec{x} - \vec{b} \| \geqq 0 \) なので、2乗して \( \| A \vec{x} - \vec{b} \|^2 \) としても最小値をとる \( \vec{x} \) は変わりませんよね。

なので、\( \| A \vec{x} - \vec{b} \|^2 \) を最小にする \( \vec{x} \) を導出していきましょう。

まず、\( \| \vec{x} \|^2 = \vec{x}^{\top} \vec{x} \) ですね。よって、\[\begin{align*}
\| A \vec{x} - \vec{b} \|^2 = (A \vec{x} - \vec{b})^{\top} (A \vec{x} - \vec{b})
\end{align*}\]が成り立ちますね。

さらに、この式を展開することで、\[\begin{align*}
\| A \vec{x} - \vec{b} \|^2 & = (A \vec{x} - \vec{b})^{\top} (A \vec{x} - \vec{b})
\\ & = \left\{ (A \vec{x})^{\top} - \vec{b}^{\top} \right\} (A \vec{x} - \vec{b})
\\ & = ( \vec{x}^{\top} A^{\top} - \vec{b}^{\top} ) ( A \vec{x} - \vec{b} )
\\ & = \vec{x}^{\top} A^{\top} A \vec{x} - \vec{x}^{\top} A^{\top} \vec{b} - \vec{b}^{\top} A \vec{x} - \vec{b}^{\top} \vec{b}
\end{align*}\]となりますね。

ここで、\( \vec{b}^{\top} A \vec{x} \) はスカラー値（1×1の行列）となるため、転置しても値はそのままですね。よって、\[\begin{align*}
(\vec{b}^{\top} A \vec{x} )^{\top} & = \vec{x}^{\top} A^{\top} (\vec{b}^{\top})^{\top}
\\ & = \vec{x}^{\top} A^{\top} \vec{b}
\end{align*}\]と変形できます。

また、\( \vec{b}^{\top} \vec{b} = \| \vec{b} \|^2 \) ですね。

したがって、\( \| A \vec{x} - \vec{b} \|^2 \) は、\[\begin{align*}
\| A \vec{x} - \vec{b} \|^2 & = \vec{x}^{\top} A^{\top} A \vec{x} - \vec{x}^{\top} A^{\top} \vec{b} - \vec{b}^{\top} A \vec{x} - \vec{b}^{\top} \vec{b}
\\ & = \vec{x}^{\top} A^{\top} A \vec{x} - \vec{x}^{\top} A^{\top} \vec{b} - \vec{x}^{\top} A^{\top} \vec{b} - \vec{b}^{\top} \vec{b}
\\ & = \vec{x}^{\top} A^{\top} A \vec{x} - 2 \vec{x}^{\top} A^{\top} \vec{b} + \| \vec{b} \|^2
\end{align*}\]と変形できますね。

ここからは、上の式を \( \vec{x} \) で偏微分していきます。ここで、(1)の\[
\frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} \textcolor{red}{A} \vec{x} = 2 \textcolor{red}{A} \vec{x} \ \ \ \left( \textcolor{red}{A} \ \mathrm{は実対称行列} \right)
\]\[
\frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} \textcolor{blue}{\vec{b}} = \textcolor{blue}{ \vec{b} }
\]を使います。すると、\[\begin{align*}
\frac{\partial }{ \partial \vec{x} } \| A \vec{x} - \vec{b} \|^2 & = \frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} \textcolor{red}{A^{\top} A} \vec{x} - 2 \frac{ \partial }{ \partial \vec{x} } \vec{x}^{\top} \textcolor{blue}{A^{\top} \vec{b}} + \underbrace{ \frac{ \partial }{ \partial \vec{x} } \| \vec{b} \|^2 }_{ 0 }
\\ & = 2 \textcolor{red}{A^{\top} A} \vec{x} - 2 \textcolor{blue}{A^{\top} \vec{b}}
\end{align*}\]

となりますね^[3]\( A^{\top} A \) は必ず実対称行列となる。また、転置の公式 \( (ABC)^{\top} = C^{\top} B^{\top} A^{\top} \) … Continue reading。

よって、勾配が0となる \( \vec{x} \) は、\[\begin{align*}
2 A^{\top} A \vec{x} - 2 A^{\top} \vec{b} & = \vec{0} \\
2 A^{\top} A \vec{x} & = 2 A^{\top} \vec{b} \\
(A^{\top} A) \vec{x} & = A^{\top} \vec{b} \\
(A^{\top} A)^{-1} (A^{\top} A) \vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b} \\
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\end{align*}\]と求められますね。

この形、まさに擬似逆行列から \( \vec{x} \) を計算する式\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]と同じですね！　よって、擬似逆行列 \( A^+ \) を計算し、\( \vec{x} = A^+ \vec{b} \) とすることで最小2乗法、つまり \( \| A \vec{x} - \vec{b} \| \) を最小にすることができますね。

最小2乗法擬似逆行列とは

連立方程式 \( A \vec{x} = \vec{b} \) の誤差を \( \| A \vec{x} - \vec{b} \| \) で定義する。

この誤差を最小にするような \( \vec{x} \) を求める手法を最小2乗法と呼び、\( \vec{x} \) のことを最小2乗解と呼ぶ。

最小2乗解 \( \vec{x} \)は擬似逆行列 \( A^+ \) を用いて\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]で計算できる。

4. 例題で最小2乗法の計算方法を確認しよう

では、例題を見てみましょう。

例題1

つぎの解をもたない連立方程式\[
\left\{ \begin{align*} \ \ 2 x - 2y & = -2 \\ -4 x + 3y & = \ \ \ 2 \\ -2x + \ \ y & = \ \ \ 0 \\ -5x + 4y & = \ \ \ 1 \end{align*} \right.
\]がある。この連立方程式に対して、最小2乗法を適用したい。

ここで、行列 \( A \)、ベクトル \( \vec{b} \)、解ベクトル \( \vec{x} \) を\[
A = \left( \begin{array}{cc} 2 & -2 \\ -4 & 3 \\ -2 & 1 \\ -5 & 4 \end{array} \right), \ \ \ \vec{b} = \left( \begin{array}{cc} -2 \\ 2 \\ 0 \\ 1 \end{array} \right) , \ \ \ \vec{x} = \left( \begin{array}{cc} x \\ y \end{array} \right)
\]とすることで、連立方程式を \( A \vec{x} = \vec{x} \) と表現する。次の(1), (2)の問いに答えなさい。

(1) 擬似逆行列 \( A^+ \) を計算しなさい。
(2) (1)の誤差 \( \| A \vec{x} - \vec{b} \| \) が最も小さくなるような最小2乗解 \( \vec{x} \) を計算することで、最小2乗法を適用しなさい。

[解説1]

(1) 擬似逆行列 \( A^+ = (A^{\top} A)^{-1} A^{\top} \) を

\( A^{\top} A \) の計算
\( (A^{\top} A)^{-1} \) の計算
\( (A^{\top} A)^{-1} A^{\top} \) の計算

の3ステップにわけて計算する。

[Step1] \( A^{\top} A \) の計算

\[\begin{align*}
A^{\top} A & = \left( \begin{array}{cc} 2 & -4 & -2 & -5 \\ -2 & 3 & 1 & 4 \end{array} \right) \left( \begin{array}{cc} 2 & -2 \\ -4 & 3 \\ -2 & 1 \\ -5 & 4 \end{array} \right)
\\ & = \left( \begin{array}{cc} 4 + 16 + 4 + 25 & -4 - 12 - 2 - 20 \\ -4 - 12 - 2 - 20 & 4 + 9 + 1 + 16 \end{array} \right)
\\ & = \left( \begin{array}{cc} 49 & -38 \\ -38 & 30 \end{array} \right)
\end{align*}\]

[Step2] \( (A^{\top} A)^{-1} \) の計算

\[\begin{align*}
(A ^{\top} A)^{-1} & = \frac{1}{ |A^{\top} A| } \left( \begin{array}{cc} 30 & 38 \\ 38 & 49 \end{array} \right)
\\ & = \frac{1}{1470-1444} \left( \begin{array}{cc} 30 & 38 \\ 38 & 49 \end{array} \right)
\\ & = \frac{1}{26} \left( \begin{array}{cc} 30 & 38 \\ 38 & 49 \end{array} \right)
\end{align*}\]

[Step3] 擬似逆行列 \( A^+ = (A^{\top} A)^{-1} A^{\top} \) の計算

\[\begin{align*}
A^+ & = (A^{\top} A)^{-1} A^{\top}
\\ & = \frac{1}{26} \left( \begin{array}{cc} 30 & 38 \\ 38 & 49 \end{array} \right) \left( \begin{array}{cc} 2 & -4 & -2 & -5 \\ -2 & 3 & 1 & 4 \end{array} \right)
\\ & = \frac{1}{26} \left( \begin{array}{cc} 60-76 & -120+114 & -60+38 & -150+152 \\ 76-98 & -152+147 & -76+49 & -190+196 \end{array} \right)
\\ & = \frac{1}{26} \left( \begin{array}{cc} -16 & -6 & -22 & 2 \\ -22 & -5 & -27 & 6 \end{array} \right)
\end{align*}\]

(2)

最小2乗解 \( \vec{x} \) は、擬似逆行列 \( A^+ \) から\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]で計算できる。

よって、( \vec{x} \) は\[\begin{align*}
\vec{x} & = A^+ \vec{b}
\\ & = \frac{1}{26} \left( \begin{array}{cc} -16 & -6 & -22 & 2 \\ -22 & -5 & -27 & 6 \end{array} \right) \left( \begin{array}{cc} -2 \\ 2 \\ 0 \\ 1 \end{array} \right)
\\ & = \frac{1}{26} \left( \begin{array}{cc} 32 - 12 + 0 + 2 \\ 44 - 10 + 0 + 6 \end{array} \right)
\\ & = \frac{1}{26} \left( \begin{array}{cc} 22 \\ 40 \end{array} \right)
\\ & = \frac{1}{13} \left( \begin{array}{cc} 11 \\ 20 \end{array} \right)
\end{align*}\]と計算できるため、最小2乗解 \( \vec{x} \) は\[
\vec{x} = \left( \begin{array}{cc} x \\ y \end{array} \right) = \frac{1}{13} \left( \begin{array}{cc} 11 \\ 20 \end{array} \right)
\]となる。

※ 行列に使わずに書くと、最小2乗解は\[
x = \frac{11}{13} , \ \ \ y = \frac{20}{13}
\]となる。

5. 実験と最小2乗法（回帰直線）

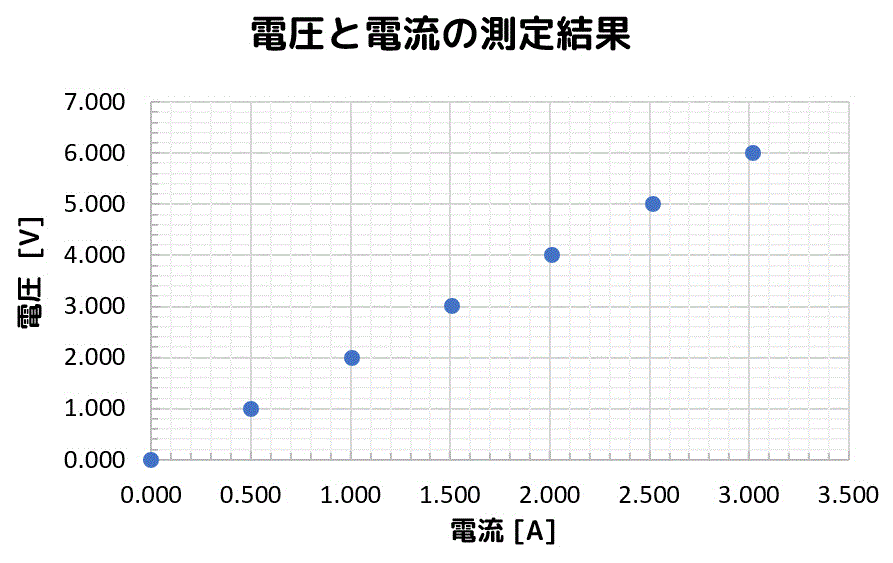
（大学の）物理実験では、「条件を変えて得られた2つのデータの組 \( (x,y) = (x_k,y_k) \) を直線 \( y = px + q \) に当てはめていき、最もそれっぽい \( p \), \( q \) を求める」ということをします。これが実験でよく使う最小2乗法です。

1つ最小2乗法を使う物理実験の例を出してみましょう。皆さんは、オームの法則を中学校や高校で習いましたね。これは、電圧 \( V \)、電流 \( I \)、抵抗 \( R \) に対して \( V = RI \) が成り立つという法則でしたね。

しかし、実世界ではこれに加えて初期の起電力 \( V_0 \) を考えて、\( V = RI + V_0 \) とする必要があります。

そこで、抵抗値 \( R \) が未知の抵抗に対して、ある電流値 \( x = I \) を与えたときの観測される電圧 \( y = V \) を調べていきます。

すると、式 ( y = \textcolor{magenta}{p} x + \textcolor{deepskyblue}{q} \)（つまり \( V = \textcolor{magenta}{R} I + \textcolor{deepskyblue}{V_0} \)）が大量に出てきますね。この導出された式から、最も適した \( \textcolor{magenta}{p = R} \) , \( \textcolor{deepskyblue}{q = V_0} \) を計算していきます。

通常であれば、共分散 \( s_{xy} \), データ \( x_i \) の分散 \( s_x^2 \)、データ \( x \), \( y \) のそれぞれの平均 \( \bar{x} \), \( \bar{y} \) を用いて\[\begin{align*}
p & = \frac{ s_{xy} }{ s_x^2 } \\
q & = \bar{y} - a \bar{x}
\end{align*}\]と計算できるのですが、今回はこれを行列の力で解いてみます。

※ もし、実験で使う最小2乗法の仕組みについて詳しく勉強してみたいよという人は、こちらの記事もぜひご覧ください。

(1) 行列を用いた形 \( A \vec{x} = \vec{b} \) への変換

まず、2つのデータの組 \( x,y = I_k, V_k \) を下のように得られたとします。

電流 \( I \) [A]	電圧 \( V \) [V]
0.000	0.000
0.502	1.000
1.005	2.000
1.508	3.000
2.012	4.001
2.516	5.001
3.019	6.001

すると、得られたデータの組から、連立方程式\[
\left\{ \begin{align*} 0.000 & = 0.000p + q \\ 1.000 & = 0.502p +q \\ 2.000 & = 1.005 p + q \\ 3.000 & = 1.508 p + q \\ 4.001 & = 2.012p + q \\ 5.001 & = 2.516 p + q \\ 6.001 & = 3.019 p + q \end{align*} \right.
\]が得られますね。

ここで、\[
A = \left( \begin{array}{cc} 0.000 & 1 \\ 0.502 & 1 \\ 1.005 & 1 \\ 1.508 & 1 \\ 2.012 & 1 \\ 2.516 & 1 \\ 3.019 & 1 \end{array} \right) , \ \ \ \vec{x} = \left( \begin{array}{cc} p \\ q \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{cc} 0.000 \\ 1.000 \\ 2.000 \\ 3.000 \\ 4.001 \\ 5.001 \\ 6.001 \end{array} \right)
\]とすることで、行列を用いた連立方程式の形 \( \vec{b} = A \vec{x} \)、つまり \( A \vec{x} = \vec{b} \) に変形できるので、あとは、\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]を計算することで最小2乗解 \( \vec{x} \) を求められます。

(2) Python, MATLABで計算

さすがに手計算で \( A^+ \) やら \( \vec{x} = A^+ \vec{b} \) を計算するのはさすがに少ししんどいので、今回はPythonとMATLABを使って計算したいと思います。

Pythonで計算する場合（プログラム）

import numpy as np # numpyを用いた行列計算に必要

## プロットデータ(x_k,y_k)から、回帰直線 y = px + q を擬似逆行列 np.linalg.pinv(A) で計算
def find_kaiki_line(x_data,y_data):
    n = len(x_data) # 連立方程式の数
    A = np.zeros( (n,2) ) # 係数行列のサイズ: n×2

    ## Ax = b の形に変更
    A[:,0] = x_data[:,0]
    A[:,1] = 1
    b      = y_data

    ## 擬似逆行列を用いて最小2乗解を計算
    x = np.matmul(np.linalg.pinv(A),b)
    
    return x

## 処理データをここに書く
ampere  =  np.array([[-0.001],[0.502],[1.005],[1.508],[2.012],[2.516],[3.019]]) # 電流Iの観測結果
voltage =  np.array([[ 0.000],[1.000],[2.000],[3.000],[4.001],[5.001],[6.001]]) # 電圧Vの観測結果

## 結果
result = find_kaiki_line(ampere,voltage)
print('回帰直線: y = {p:0.4f}x {q:0=+0.4f}'.format(p = result[0,0],q = result[1,0]))

MATLABで計算する場合（プログラム）

%% 処理データをここに書く
voltage = [ 0.000; 1.000; 2.000; 3.000; 4.001; 5.001; 6.001];
ampere  = [-0.001; 0.502; 1.005; 1.508; 2.012; 2.516; 3.019];

%% 結果
result = find_kaiki_line(ampere,voltage);
disp(strcat("回帰直線: y = ",sprintf("%0.4f",result(1)),"x ",sprintf("%+0.4f",result(2))))


%% プロットデータ(x_k,y_k) から、回帰直線 y = px + q を擬似逆行列　pinv(A) で計算
function [x] = find_kaiki_line(x_data,y_data)
    n = numel(x_data); % 連立方程式の数
    A = zeros(n,2);    % 係数行列のサイズ(n×2)

    %% Ax = b の形に変更
    A(:,1) = x_data;
    A(:,2) = 1;
    b = y_data;
    
    %% 擬似逆行列を用いて最小2乗解を計算
    x = pinv(A) * b; % p = x(1), q = x(2)
end

実行結果（Python, MATLAB共通）

回帰直線: y = 1.9869x +0.0027

実行結果から、抵抗 \( R = p = 1.9869 \) [Ω]、起電力\( V_0 = q = 0.0027 \) と推定できました。

(3) 計算結果があっているかExcelで確認

Excelの近似機能を使って、本当に最小2乗法の計算が正しくできているかを \( y = px + q \) の \( p \), \( q \) の値で確認しましょう。

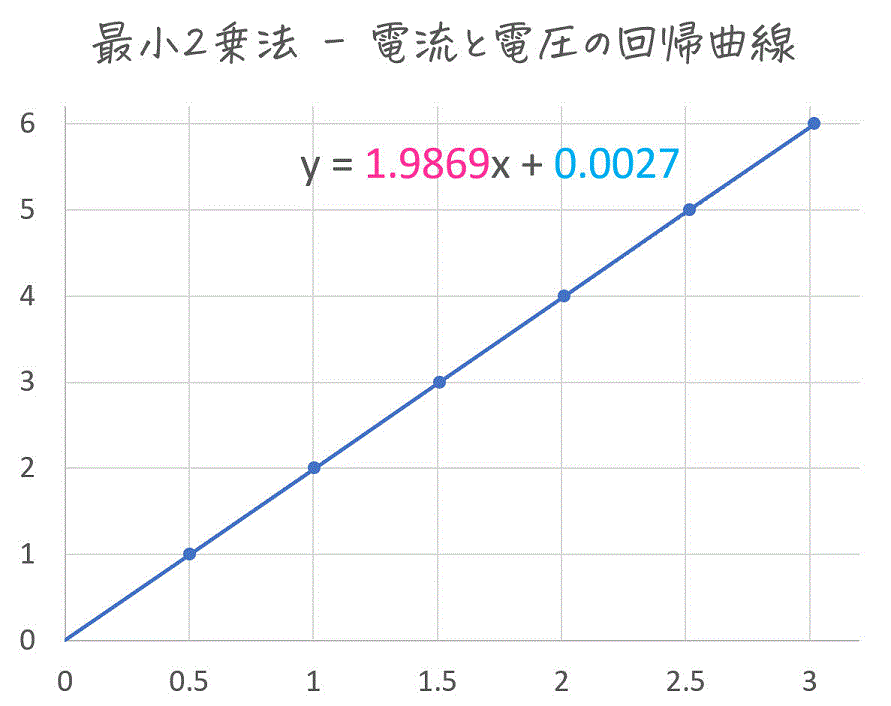
確かに行列で最小2乗法を計算した場合と一致していますね！

回帰直線と最小2乗法

結果が \( y = px + q \) に比例するデータが \( (x,y) = (x_1,y_1), (x_2, y_2), \cdots, (x_n,y_n) \) とある。

このとき、\[
A = \left( \begin{array}{cc} x_1 & 1 \\ x_2 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{array} \right), \ \ \ \vec{x} = \left( \begin{array}{cc} p \\ q \end{array} \right), \ \ \ \vec{b} = \left( \begin{array}{cc} y_1 \\ y_2 \\ \cdots \\ y_n \end{array} \right)
\]おくことで、連立方程式 \( A \vec{x} = \vec{b} \) の形に持ち込める。

さらに、\( A \) の擬似逆行列 \( A^+ \) を求めることで \( p \), \( q \) を下のように求めることができる。\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\\ & = \left( \begin{array}{cc} p \\ q \end{array} \right)
\end{align*}\]

6. 練習問題

それでは、もう1問「行列を用いた最小2乗法の計算練習」をしましょう。

練習問題

つぎの解をもたない連立方程式\[
\left\{ \begin{align*} \ \ \ \ x - \ \ y & = -2 \\ \ \ 4 x - 2y & = \ \ \ 2 \\ -3x + 2 y & = \ \ \ 0 \\ \ \ 5x - 3y & = \ \ \ 0 \\ -4 x + 3y & = \ \ \ 4 \end{align*} \right.
\]がある。この連立方程式に対して、最小2乗法を適用したい。

ここで、行列 \( A \)、ベクトル \( \vec{b} \)、解ベクトル \( \vec{x} \) を\[
A = \left( \begin{array}{cc} 1 & -1 \\ 4 & -2 \\ -3 & 2 \\ 5 & -3 \\ -4 & 3 \end{array} \right), \ \ \ \vec{b} = \left( \begin{array}{cc} -2 \\ 2 \\ 0 \\ 0 \\ 4 \end{array} \right) , \ \ \ \vec{x} = \left( \begin{array}{cc} x \\ y \end{array} \right)
\]とすることで、連立方程式を \( A \vec{x} = \vec{b} \) と表現する。

\( A \) の擬似逆行列 \( A^+ \) を求めなさい。さらに、連立方程式の計算誤差 \( \| A \vec{x} - \vec{b} \| \) が最も小さくなるような最小2乗解 \( \vec{x} \) を \( A^+ \) を用いて計算し、最小2乗法を適用しなさい。

7. 練習問題の答え

最小2乗解 \( \vec{x} \) を擬似逆行列 \( A^+ \) を用いて、\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]となるので、これを計算すればOK。

まずは3ステップで擬似逆行列 \( A^+ \) を計算する。

[Step1] \( A^{\top} A \) の計算

\[\begin{align*}
A^{\top} A & = \left( \begin{array}{cc} 1 & 4 & -3 & 5 & -4 \\ -1 & -2 & 2 & -3 & 3 \end{array} \right) \left( \begin{array}{cc} 1 & -1 \\ 4 & -2 \\ -3 & 2 \\ 5 & -3 \\ -4 & 3 \end{array} \right)
\\ & = \left( \begin{array}{cc} 1 + 16 + 9 + 25 + 16 & -1 - 8 - 6 - 15 - 12 \\ -1 - 8 - 6 - 15 - 12 & 1 + 4 + 4 + 9 + 9 \end{array} \right)
\\ & = \left( \begin{array}{cc} 67 & -42 \\ -42 & 27 \end{array} \right)
\end{align*}\]

[Step2] \( (A^{\top} A)^{-1} \) の計算

\[\begin{align*}
(A ^{\top} A)^{-1} & = \frac{1}{ |A^{\top} A| } \left( \begin{array}{cc} 67 & -42 \\ -42 & 27 \end{array} \right)
\\ & = \frac{1}{1809-1764} \left( \begin{array}{cc} 27 & 42 \\ 42 & 67 \end{array} \right)
\\ & = \frac{1}{45} \left( \begin{array}{cc} 27 & 42 \\ 42 & 67 \end{array} \right)
\end{align*}\]

[Step3] 擬似逆行列 \( A^+ = (A^{\top} A)^{-1} A^{\top} \) の計算

\[\begin{align*}
A^+ & = (A^{\top} A)^{-1} A^{\top}
\\ & = \frac{1}{45} \left( \begin{array}{cc} 27 & 42 \\ 42 & 67 \end{array} \right) \left( \begin{array}{cc} 1 & 4 & -3 & 5 & -4 \\ -1 & -2 & 2 & -3 & 3 \end{array} \right)
\\ & = \frac{1}{45} \left( \begin{array}{cc} 27-42 & 108-84 & -81+84 & 135-126 & -108+126 \\ 42-67 & 168-134 & -126+134 & 210-201 & -168+201 \end{array} \right)
\\ & = \frac{1}{45} \left( \begin{array}{cc} -25 & 24 & 3 & 9 & 18 \\ -15 & 34 & 8 & 9 & 33 \end{array} \right)
\end{align*}\]

[Step4] 解ベクトル \( \vec{b} \) の計算

\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\\ & = \frac{1}{45} \left( \begin{array}{cc} -25 & 24 & 3 & 9 & 18 \\ -15 & 34 & 8 & 9 & 33 \end{array} \right) \left( \begin{array}{cc} -2 \\ 2 \\ 0 \\ 0 \\ 4 \end{array} \right)
\\ & = \frac{1}{45} \left( \begin{array}{cc} 50 + 48 + 0 + 0 + 72 \\ 30 + 68 + 0 + 0 + 132 \end{array} \right)
\\ & = \frac{1}{45} \left( \begin{array}{cc} 170 \\ 230 \end{array} \right)
\\ & = \frac{1}{9} \left( \begin{array}{cc} 34 \\ 46 \end{array} \right)
\end{align*}\]

よって、最小2乗解 \( \vec{x} \) は\[
\vec{x} = \left( \begin{array}{cc} x \\ y \end{array} \right) = \frac{1}{9} \left( \begin{array}{cc} 34 \\ 46 \end{array} \right)
\]となる。

※ ベクトル表記をしない場合は、\[
x = \frac{34}{9} , \ \ \ y = \frac{46}{9}
\]となる。

8. さいごに

今回は、行列（擬似逆行列）を使った最小2乗法について説明しました。

まずは、1枚の画像で最小2乗法の計算方法について振り返りましょう。

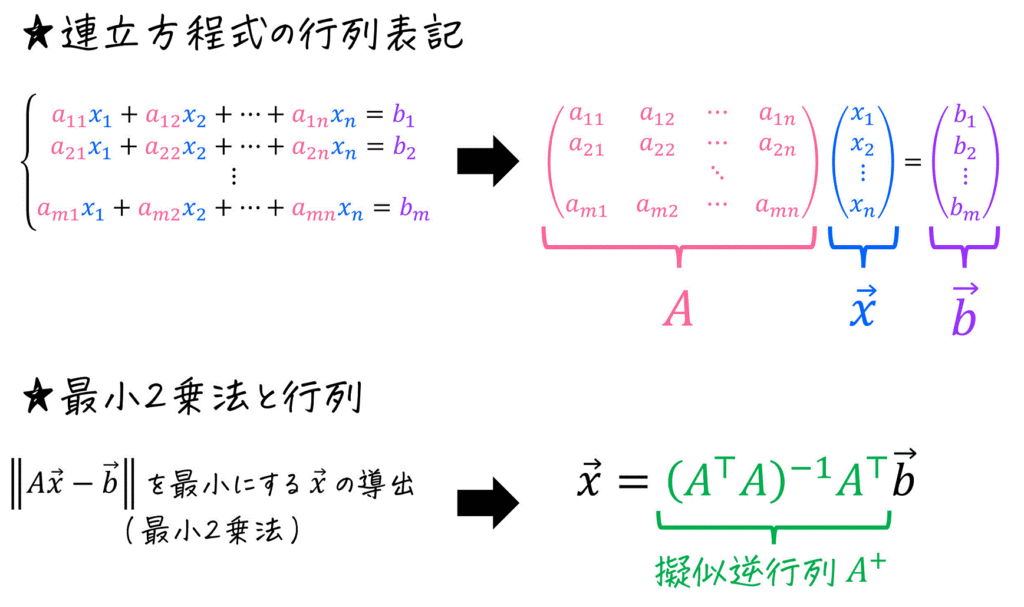
最小2乗法は、単なる計算だけでなく、実験データの解析や研究など様々な分野で使えるので、是非理系の皆さんは使いこなせるようになりましょう！

それでは、また次の記事で。

注釈[+]

注釈
↑1	\( A^{\top} A \) の逆行列を計算するため、\( A^{\top} A \) が正則でないとダメ。
↑2	今までの記事では、ベクトルのノルムを \( \| \vec{x} \| \) のように絶対値っぽく表してきましたが、本記事ではベクトルのノルム（長さ）を \( \\| \vec{x} \\| \) のように2重線で表現します。なお、念のため説明しますが、今回出てくるベクトルのノルムはすべて2ノルム（ユークリッドノルム）です。
↑3	\( A^{\top} A \) は必ず実対称行列となる。また、転置の公式 \( (ABC)^{\top} = C^{\top} B^{\top} A^{\top} \) を多用している（転置をバラバラにすると、積の順番が逆になる。）