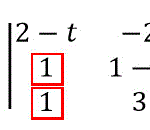スポンサードリンク
ここでは、線形代数の分野の1つ「逆行列」の問題演習をひたすらすることができます。
問題PDFも用意したので、チャレンジしたい方はまずはPDFをダウンロードし、問題を解いてください。
もっと逆行列計算(掃き出し法・余因子)の基本的なところから知りたい人は、まずは下の解説記事からご覧ください!
掃き出し法編
余因子編
目次 [hide]
スポンサードリンク
要点チェック
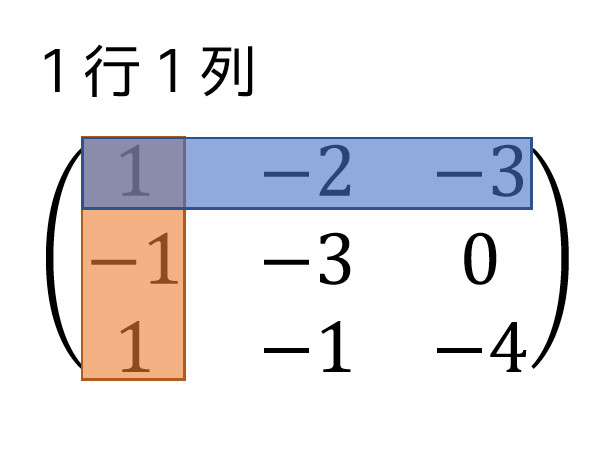
1. 行列
ア:
イ:
ウ:
エ:
2.
ア:
イ:
ウ:
エ:
3.
ア:
イ:
ウ:
エ:
4.
ア:
イ:
5.
ア:
イ:
[解答]
- ウ
- イ
- エ
- イ
- ア
- 連立方程式
- 逆行列の分解公式(積・定数倍)
- 逆行列と転置の入れ替えが可能:
- 逆行列の行列式は元の(行列の)行列式の逆数
スポンサードリンク
計算例題.掃き出し法による逆行列の計算
[誘導]
よって、逆行列は
[解答]
No.01: 5
No.02: 1
No.03: -3
No.04: -4
No.05: 7
No.06: -3
No.07: 5
行列
※ 列基本変形をしてもよいが、行基本変形と列基本変形を混合して使用するのはNG
[具体的な計算手順]- ある1列に着目し、1つの成分以外をすべて0にする。
- 1(ある1列に着目し、1つの成分以外をすべて0にすること)を、他すべての列にも適用すればOK。
- 行基本変形の最中に分数を出さないこと! → 問1(3)で練習可能
(分数が出る計算は、行基本変形の最後にまとめてすること)
[解説]
※ 計算後には、定義式
スポンサードリンク
レベル1. 基本レベル [単位取りたい人~優(A)狙いの人向け]
問1. 逆行列の基本的な計算
次の(1)~(3)の行列に対して、逆行列を計算しなさい。
(1)
(2)
(3)
例題では、掃き出し法による逆行列の計算方法を学びましたが、掃き出し法以外の逆行列計算方法もここで確認しておきましょう。
特に2次正方行列の逆行列は、公式で計算できるようになっておくことを強くおすすめします。
(計算速度がかなり変わるため)
3次以上の正方行列の逆行列は、余因子と呼ばれるものを使って計算をします。
3次以上の正方行列の場合、掃き出し法を使わずに逆行列を計算するためには余因子の計算が必要になってくる。
[余因子]ある行列から、特定の行(
ただし、行番号
例えば、行列
※
ある行列
さらに逆行列
掃き出し法と(余因子)公式、どちらを使うかは皆さんの慣れ具合などで変わってくるかと思いますが、参考までに私が
- 2次正方行列の逆行列:公式
- 3次正方行列の逆行列:掃き出し法と方式どっちでもOK(慣れている方で)
- 4次以上の正方行列の逆行列:掃き出し法
(ただし、本記事の問4のように逆行列のある1つの成分のみを計算で求められいる場合は掃き出し法)
[解説1]
(1)
[掃き出し法で解く場合](2)
[掃き出し法で解く場合]となるので、
まずは、それぞれの成分の余因子を計算しましょう。
次に行列式を計算しましょう。
よって、逆行列は、
(3)
[掃き出し法で解く場合]となるので、
まずは、それぞれの成分の余因子を計算しましょう。
次に行列式を計算しましょう。
よって、逆行列は、
問2. 逆行列が存在するかの確認
次の①~④の行列の中で、逆行列を持つ行列は何個あるか答えなさい。
①
②
③
④
解答: 2個
なので、より簡単に計算できる
①
②
③
④ そもそも正方行列ではないので、逆行列を持たない。
よって、逆行列を持つのは2個。
問3. 逆行列と連立方程式
逆行列を用いて、次の連立方程式を計算しなさい。
(1)
(2)
連立方程式
係数行列
この連立方程式の解
(1)
まずは、行列を用いた連立方程式の形式
次に、行列
2次正方行列なので逆行列の公式
よって、
(2)
(1)と同じように行列を用いた連立方程式の形式
次に、逆行列を求めればOK。3次なので掃き出し法、余因子どちらを使ってもOKだが、今回は掃き出し法で計算をする。
よって、
レベル2. 応用レベル [秀(A+)取りたい人向け]
問4. 逆行列を持つ条件
次の行列
[解説]
逆行列を持たないという条件は
問5. 行列の変形
次の行列
[例2]
(1)
(2)
(3)
(4)
[解説]
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
(5)
問6. 余因子を用いた逆行列計算
次の [ ★ ] に当てはまる数字を答えなさい。ただし、[ ★ ] 以外の成分は求めなくてよい。
今回は、
なので、掃き出し法ではなく、余因子を使って求める。
ここで、
また、
レベル3. 発展レベル [線形代数で満点を取りたい人向け]
問7. 4次正方行列の逆行列
次の行列の逆行列を計算しなさい。
①
[解説]
4次正方行列の逆行列は、掃き出し法で計算するのがおすすめ。
(余因子で求めると、3次正方行列の行列式を16回計算する必要があるため)
となるので、逆行列は以下の通りになる。
問8. 擬似逆行列の計算(応用)
※ 擬似逆行列を知らなくても計算できるように誘導がついています。
正方行列でない係数行列
このとき、連立方程式
順番に素直に計算していればOK。
[Step1]
[Step2]
あとは地味に計算するだけ
[余談]
今回計算した、
もし、擬似逆行列について詳しく知りたい人は、下の記事をご覧ください!
(1年生の線形代数の期末試験には基本的に出ないので、単位がとりたいだけであればスルーしてOKです)
関連広告・スポンサードリンク