スポンサードリンク
こんにちは、ももやまです。
理系大学や高専で線形代数という科目を習っている人は多いと思います。昔は高校数学でも理系は数Cで行列について習っていたのですが今は「複素数平面」に代わってしまいましたね…。
線形代数では主に「行列」について習っていくのですが、初めて「行列」を習う人にとって線形代数はかなり難しい科目だと思ってしまうかもしれません。
ということで、何回かにわけて線形代数をわかりやすく説明していこうと思います。
本記事では、主に計算方法についてまとめていることが多いので定義とかはあまり丁寧に説明していません。定義とかをしっかりと知りたいという人は別のサイトをご覧ください……。
今回は初回なので、行列についての基礎知識について、
- 行列とはなにか
- 行列の等号確認、四則演算の仕方
- 行列の用語(一部のみ)
をまとめていきたいと思います。
目次
スポンサードリンク
1.行列とは
行列とは、\[ \left( \begin{array}{ccc} 4 & 3 & -5 \\ 2 & -1 & 0 \\ -2 & 0 & 1 \end{array} \right) \\
\left[ \begin{array}{ccc} 1 & 4 & 3 \\ 2 & -1 & 0 \end{array} \right] \] のように、縦と横に数値を並べて、( ) や [ ] で閉じたものを表します。
この記事では ( ) で閉じていこうとおもいます。
行列を使うことで2次元以上のデータを一括で管理できます。
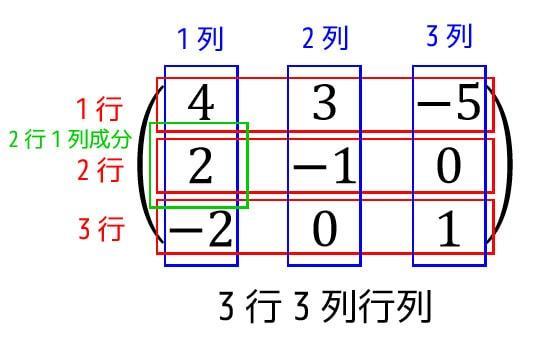
また、横方向の並びを行といい、縦方向の並びを列といいます。
どの行や列か表すために行の場合は上から順番に1行、2行…、列の場合は左から順番に1列、2列…と表していきます。
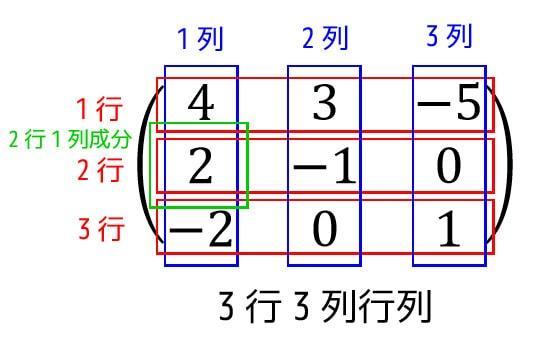
この行列の行は3行まで、列も3列までありますね。なので、この行列は3行3列の行列ですね。3×3の行列と言うこともあります。
このように行列のサイズは \( i \) 行 \( j \) 列、\( i \times j \) 行列のように表現します。もちろん行と列の数が異なる(例えば3行4列)行列もあります。
さらに行列の特定の要素のことを成分と言います。
例えば、2行1列の成分は2となります。文字を使って \( a_{21} \) と表すこともあります。
文字を使うときは、行列の成分が何行何列にあるかによって\[ \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right) \]と表します。
スポンサードリンク
2.行列の四則演算
ではまずは行列の四則演算について説明します。
(1) 行列の等号
行列が等しいというのは、
- 行列のサイズが等しい
- 行列のそれぞれの成分がすべて等しい
この2つ両方満たしている状態を表します。
例えば、\[
A = \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) \ \ \
B = \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{array} \right)
\]の場合、行列のサイズが違うので等しいとは言えません ( \( A \not = B \) )。
また、\[
A = \left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) \ \ \
B = \left( \begin{array}{ccc} 1 & 2 \\ -2 & 4 \end{array} \right)
\]の場合、2行1列の成分が違うので等しいと言えません ( \( A \not = B \) )。
\[ \left( \begin{array}{ccc} 2 & 1 \\ -2 & 4 \end{array} \right) =
\left( \begin{array}{ccc} 2 & 1 \\ -2 & 4 \end{array} \right) \]のようにサイズもそれぞれの成分もすべて等しいときに行列が等しいということができます。
(2) 行列の定数倍
行列を \( k \) 倍すると、もとの行列のすべての要素が \( k \) 倍されます。
スカラー倍ともいいます。
例えば、\( 2A \) 、つまり行列 \( A \) を2倍したものとします。これは、行列 \( A \) のすべての成分を2倍にしたものと同じです。つまり、\[ 2A = \left( \begin{array}{ccc} 6 & 2 \\ 10 & -4 \end{array} \right) \] となります。もちろん\[ \frac{1}{2}A = \left( \begin{array}{ccc} \frac{3}{2} & \frac{1}{2} \\ \frac{5}{2} & -1 \end{array} \right) \]のように1/2倍(2で割る)のような分数を指定することもできます。
ですが分数の場合はできる限り行列のそとに分数を出して行列内に分数を残さない形、例えばこのような形で書くことをおすすめします。 \[ \frac{1}{2}\left( \begin{array}{ccc} 3 & 1 \\ 5 & -2 \end{array} \right) \]
(3) 行列の足し算・引き算
行列の足し算はそれぞれの行と列の成分同士を足します。
また、行列の引き算はそれぞれの行と列の成分同士を引きます。(足し算と同じ)
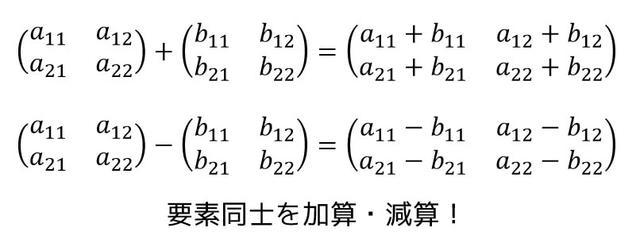
足し算と引き算の計算例を見てみましょう。\[ \begin{align*} & \left( \begin{array}{ccc} 1 & 2 \\ 1 & -3 \end{array} \right) + \left( \begin{array}{ccc} -2 & 0 \\ 1 & 2 \end{array} \right) \\ = \ & \left(\begin{array}{ccc} 1+(-2) & 2+0 \\ 1+1 & -3+2 \end{array} \right)
\end{align*} \] \[
\begin{align*} & \left( \begin{array}{ccc} 2 & 0 \\ -1 & 4 \end{array} \right) - \left( \begin{array}{ccc} -2 & 1 \\ 4 & 3 \end{array} \right) \\ = \ & \left(\begin{array}{ccc} 2-(-2) & 0-1 \\ -1-4 & 4-3 \end{array} \right)
\\ = \ & \left(\begin{array}{ccc} 4 & -1 \\ -5 & 1 \end{array} \right)
\end{align*}
\]
それぞれの行と列の成分同士を足したり引いたりするので、次のような、2つの行列の形が違った行列の足し算と引き算をすることはできません。

(4) 行列の掛け算
行列の掛け算は少ししんどいです。試しに2×2同士の掛け算をやってみましょう。
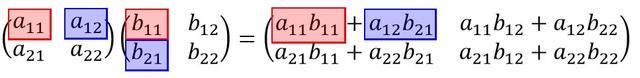
掛ける場所がわかりにくいので1行1列のところだけ色をつけてみました。
1行1列を計算するときに、(1行目の列)と(1列目の行)の同じ順番の数同士を掛けたものをすべて足していますよね。上の行列の場合だと、
- 1行1列:1行1列×1行1列 + 1行2列×2行1列
- 1行2列:1行1列×1行2列 + 1行2列×2行2列
- 2行1列:2行1列×1行1列 + 2行2列×2行1列
- 2行2列:2行1列×1行2列 + 2行2列×2行2列
で計算されていますね。どの行列の成分を見ても確かに対応する行と対応する列を最初に選んでから、対応する行の列番号と対応する列の行番号を掛け合わせてそれをすべて足した値になっています。
3×3行列同士の掛け算も見てみましょう。
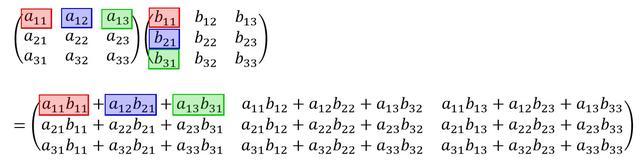
- 1行1列:1行1列×1行1列 + 1行2列×2行1列 + 1行3列×3行1列
- 1行2列:1行1列×1行2列 + 1行2列×2行2列 + 1行3列×3行2列
- 1行3列:1行1列×1行3列 + 1行2列×2行3列 + 1行3列×3行3列
- 2行1列:2行1列×1行1列 + 2行2列×2行1列 + 2行3列×3行1列
- 2行2列:2行1列×1行2列 + 2行2列×2行2列 + 2行3列×3行2列
- 2行3列:2行1列×1行3列 + 2行2列×2行3列 + 2行3列×3行3列
- 3行1列:3行1列×1行1列 + 3行2列×2行1列 + 3行3列×3行1列
- 3行2列:3行1列×1行2列 + 3行2列×2行2列 + 3行3列×3行2列
- 3行3列:3行1列×1行3列 + 3行2列×2行3列 + 3行3列×3行3列
で計算できますね。
さらに行列の積は、次のような行列のサイズが異なる場合でも計算できることができます。
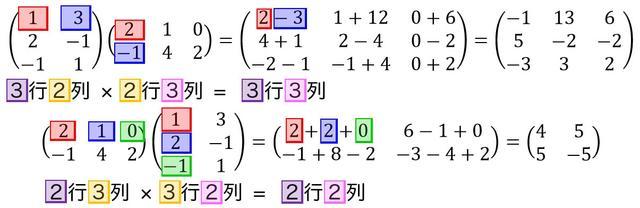
その条件は、左の列数と右の行列が等しいことです。
また計算結果の行列のサイズは、左の行数×右の列数になります。
例
- 3行4列行列×4行5列行列=3行5列行列
- 2行3列行列×2行3列行列=計算できない
- 5行3列行列×3行2列行列=5行2列行列
- 3行3列行列×3行1列行列=3行1列行列(横ベクトル)
ところで気づいた人もいるかもしれませんが、行列の掛け算は順番が大事です。
順番によって計算結果がかわります。正方行列同士の掛け算以外に至っては行列の形まで変わってしまいます。(上のやつが例)
試しに行数と列数が等しい行列(正方行列)においても掛け算の順番によって結果が変わることを2次正方行列(2×2行列)で試してみましょう。\[
\begin{align*} & \left( \begin{array}{ccc} 1 & 2 \\ 1 & -3 \end{array} \right) \left( \begin{array}{ccc} -2 & 0 \\ 1 & 2 \end{array} \right) \\ = \ & \left(\begin{array}{ccc} -2+2 & 0+4 \\ -2-3 & 0 - 6 \end{array} \right)
= \left(\begin{array}{ccc} 0 & 4 \\ -5 & -6 \end{array} \right)
\end{align*}
\] \[\begin{align*} & \left( \begin{array}{ccc} -2 & 0 \\ 1 & 2 \end{array} \right) \left( \begin{array}{ccc} 1 & 2 \\ 1 & -3 \end{array} \right) \\ = \ & \left(\begin{array}{ccc} -2+0 & -4+0 \\ 1+2 & 2-6 \end{array} \right)
= \left(\begin{array}{ccc} -2 & -4 \\ 3 & -4 \end{array} \right)
\end{align*}
\]確かに結果が変わりますね。よって、\[ AB \not= BA \]と言うことができます。
ちなみに3つ以上の積、例えば \( ABC \) の場合は、先に \( AB \) の計算をしてから \( (AB)C \) を求めるか、先に \( BC \) の計算をしてから \( A(BC) \) の計算をします。このように3つ以上の積の場合は、順番さえ変えなければどこから計算しても計算結果は変わりません。
また、\( A(B+C) = AB +AC \) のように順番さえ変えなければ展開をして計算をすることもできます。
(5) 行列の割り算(逆行列)
行列の割り算は簡単には計算できません。
しかし、逆行列というものを求めることで、行列の割り算みたいなことをすることができます。
逆行列についてはこちらでまとめているので逆行列について知りたい人はこちらをみてください。
スポンサードリンク
3.行列で出てくる用語まとめ(前編)
ここでは、行列について習っていたら出てくる用語をまとめてみました。
今回は全部で7つほど紹介します。
(1) 正方行列
\[ A =\left( \begin{array}{ccc} 1 & 2 \\ 3 & 4 \end{array} \right) \\
B = \left( \begin{array}{ccc} 1 & 4 & 2 \\ 2 & -1 & 3 \\ 0 & 2 & -1 \end{array} \right) \]
のような、行数と列数の等しい行列のことを正方行列と呼びます。
\( A \) のような2行2列の行列は2次正方行列、\( B \) のような3行3列行列は3次正方行列と呼ばれます。
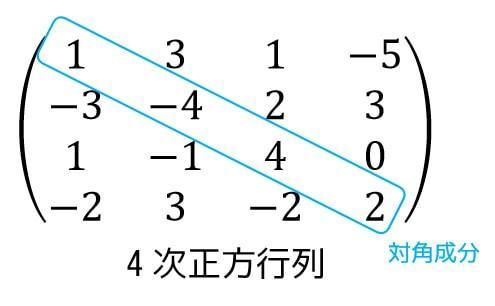
また、下の図のような行数と列数が等しい成分のことを対角成分と言います。
この場合は1行1列成分の1、2行2列成分の-4、3行3列成分の4、4行4列の2がそれぞれ対角成分ですね。(ちなみにこの行列は4×4行列、4次正方行列です)
(2) 対角行列
正方行列の中で、
\[ A =\left( \begin{array}{ccc} 1 & 0 \\ 0 & 2 \end{array} \right) \\
B = \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 2 \end{array} \right) \]
のような、対角成分以外の成分が0である行列を対角行列と言います。
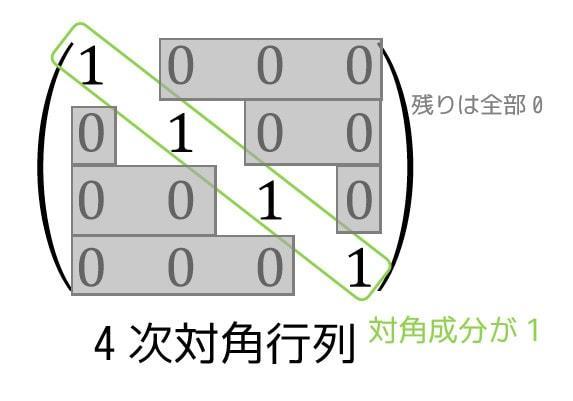
図は4×4の対角行列なので4次対角行列と呼びます。
対角行列を \( n \) 回掛けた行列の成分は、それぞれの元の行列の成分の \( n \) 乗になります。
例えば、\[ B^n = \left( \begin{array}{ccc} 3^n & 0 & 0 \\ 0 & (-1)^n & 0 \\ 0 & 0 & 2^n \end{array} \right) \]です。
(3) 単位行列
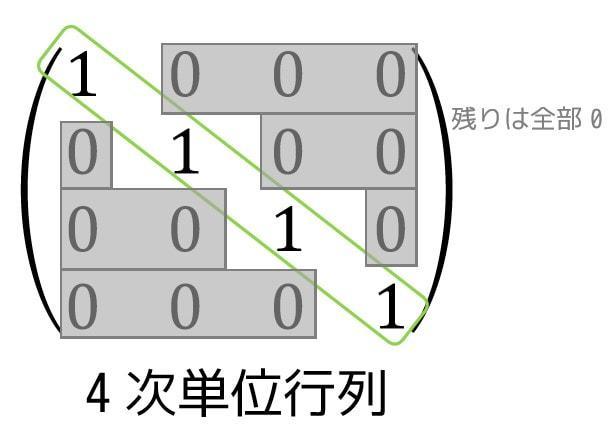
正方行列の中で、
\[ \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) \\
\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \]
のような、対角成分以外の成分が0である行列、対角成分が1の行列を対角行列と言います。
対角成分のことを記号で \( I \) や \( E \) と表します。
(4) 転置行列
行列の行と列を入れ替えた行列を転置行列といい、記号で \( {}^t\!A \) や \( A^T \) と表します。
なお、\( A \) のような正方行列ではない場合は行列の形が変わるので注意が必要です。
例えば、2×3の行列は3×2になります。
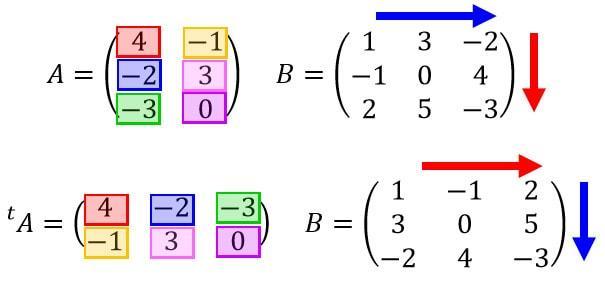
例えば1行2列の成分は2行1列に、2行2列の行列の成分はそのまま2行2列ですね。
転置行列には次の法則が成り立つので暇な人は実際に計算して確認してみてください。\[ {}^t\!(AB) = {}^t\!B {}^t\!A \]
(5) 対称行列
正方行列の中で、次のような、もとの行列も転置行列も等しい行列、つまり \( A = {}^t\!A \) を満たす行列を対称行列といいます。
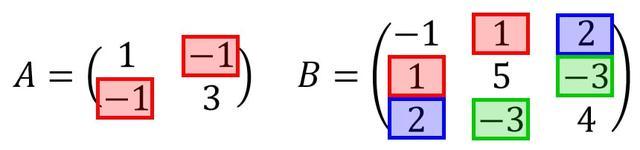
よく見ると対角成分を基準に対称的に数字が並んでいますね。
また、すべての成分が実数の対称行列のことを実対称行列と言います。
(6) 階段行列
次のような、下にいけばいくほど0の数が増えていき、0の隣が1になっているような行列のことを階段行列といいます。*1
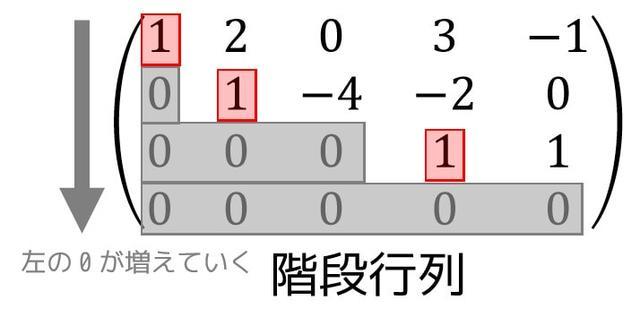
階段行列や行列の階数についてはこのページにまとめているのでこちらをご覧ください。
(7) 行列式
行列式は、簡単にいうと行列の面積や体積が何倍になるか(拡大率)を表します。正方行列な行列でしか行列式は計算できません。*2
正方行列の場合のみ、行列の行列式を出すことができます。
なお、2×2の場合は次の簡単な式で求めることができます。
(1) 2×2行列の行列式 \[
\left| \begin{array}{cc} a & b \\ c & d \end{array} \right| = ad - bc
\]
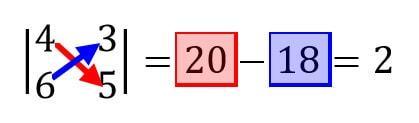
こんな感じに2×2の場合はたすき掛けをすることですぐに計算ができますね。
2×2以外の行列式の求め方についてはまた後日まとめたいと思います。
(8) 正則行列
正方行列の中で、逆行列が存在する行列、つまり行列の割り算ができる行列のことを正則行列と呼びます。
ある n次正方行列 \( A \) が正則行列のとき、以下の文章はすべて同値です。
(言い換えると、下に書かれているものをどれか1つを満たせば、残りもすべて満たすことを示せます。)
- 行列 \( A \) は正則行列である
- 行列 \( A \) の階数は \( n \) となる。(第01羽)
- 連立方程式 \( A \vec{x} = \vec{0} \) が自明な解(\( \vec{x} = \vec{0} \) )のみを持つ(第02羽)
- 行列 \( A \) は逆行列 \( A^{-1} \) を持つ(第03羽)
- 行列式 \( |A| \) が0ではない。(第05羽)
- 行列 \( A \) を\[ A = \left( \vec{a}_1, \vec{a}_2, \cdots, \vec{a}_n \right) \] としたとき、\( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) は1次独立となる(第06羽)
- 行列 \( A \) の固有値に0は含まれない(第15羽)
が挙げられます。とくに、上5つはすべて重要なので1つ漏らさず頭にいれておきましょう。
4.行列とベクトルの関係
この記事では、ベクトルは特に指示のない限り列ベクトルを表すことにします。
ベクトルの中でも、\[ \left( \begin{array}{ccc} 3 & 1 & 4 \end{array} \right) \]のように横方向に並べたベクトルを行ベクトルと言います。1行3列の行列と考えることもできます。
また、\[ \left( \begin{array}{ccc} 1 \\ 2 \\ -3 \end{array} \right) \]のように横方向に並べたベクトルを列ベクトルと言います。3行1列の行列と考えることもできます。
ベクトルを3行1列と考えることで行列とベクトルを掛け算することができます。例えば、\[ A = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 0 & -1 & 1 \\ 2 & -1 & 1 \end{array} \right) \ \
\vec{b} = \left( \begin{array}{ccc} 1 \\ 2 \\ 4 \end{array} \right) \] とすると、
\[\begin{align*} A \vec{b} = & \left( \begin{array}{ccc} 1 & 2 & 3 \\ 0 & -1 & 1 \\ 2 & -1 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 \\ 2 \\ 4 \end{array} \right) \\ = & \left( \begin{array}{ccc} 1+4+12 \\ 0-2+4 \\ 2-2+4 \end{array} \right) = \left( \begin{array}{ccc} 17 \\ 2 \\ 4 \end{array} \right)
\end{align*} \]と計算できる。(3行3列×3行1列=3行1列)
また、行列はベクトルが何個か並んだものと考えることもできます。
例えば、\[ \vec{a_1} = \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right) \ \ \ \vec{a_2} = \left( \begin{array}{ccc} 2 \\ 5 \\ 1 \end{array} \right) \ \ \ \vec{a_3} = \left( \begin{array}{ccc} 0 \\ 1 \\ 4 \end{array} \right) \]とします。
すると、行列 \( A \) は3つのベクトルを使って、\[\begin{align*} A = & \left( \begin{array}{ccc} \vec{a_1} & \vec{a_2} & \vec{a_3} \end{array} \right) \\ = & \left( \begin{array}{ccc} 1 & 2 & 0 \\ 2 & 5 & 1 \\ 3 & 1 & 4 \end{array} \right)
\end{align*}
\]と書けます。
5.さいごに
今回は行列の四則演算と基本的な用語についてまとめていきました。
行列の四則演算の練習問題を最後に貼ろうと思ったのですが、記事が長くなるので次回練習問題だけを別の記事にしようと思います。
練習編はこちら!
行列の四則演算は、これから出てくる線形代数の単元で確実に使っていくものばかりなので確実に計算をできるようにしましょう。
また、行列の用語もこれから使っていくことが多い用語ばかりなので覚えていきましょう!
ではまた次回。
Next:行基本変形と階数の出し方
関連広告・スポンサードリンク