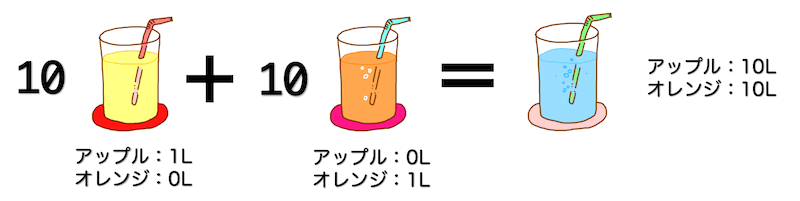
スポンサードリンク
こんにちは、ももやまです。
今回は線形代数に出てくる基底についてです!
でも、基底って概念は最初はなかなか理解しにくいですよね。
私も最初は全く理解できませんでした。
なので、今回は基底をジュースにたとえてわかりやすく説明をしてみました!
また、後半部分では基底の交換についてのまとめをしているのでこちらもご覧ください!
前回の線形代数のまとめ(1次独立、1次従属)はこちらから!
(1次独立、1次従属は今回かなり出てくるのでまだ理解できてない人はこちらから復習をすることをおすすめします)
目次
スポンサードリンク
1.基底をジュースで考えてみよう!
まずは基底という概念について説明をしましょう。
ですが、いきなりベクトルを使って説明するのは少し難しいと思うので、まずはジュースを使って説明をしたいと思います。
アップルジュースが10L、オレンジジュースが10L入った合計20Lのミックスジュースを想像してください。
このジュースを「1Lアップルジュース」、「1Lオレンジジュース」の2つで作りたいと思います。
このとき、「1Lアップル」が10セット、「1Lオレンジ」が10セットずつあればアップル、オレンジがそれぞれ10Lずつ入ったミックスジュースが作れますね。
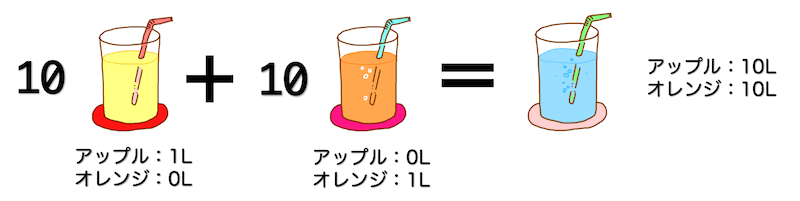
さて、今度は別のジュースのセットで先程と同じ20Lのミックスジュースを作ってみましょう。
例えば、「アップル3L、オレンジ1Lのミックスジュース(セット1)」と「アップル1L、オレンジ2Lのミックスジュース(セット2)」の2つのセットだとそれぞれ何セット必要でしょうか。
連立方程式を解くと、セット1が2セット、セット2が4セットあれば先程と同じミックスジュースが20Lつくれますね。
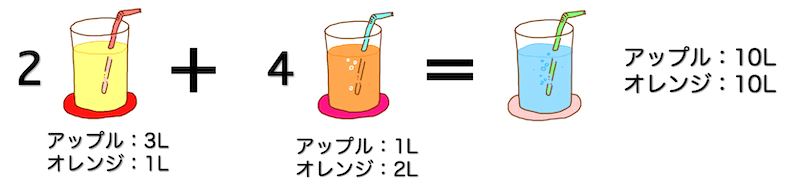
このように、それぞれのセットごとのジュースの量を変えると、それぞれのセットの必要数ももちろん変化します。

基底というのは、目標のミックスジュースを作るために必要なセットを表します。
英語だと基底は base と呼ばれるので、ミックスジュースを作るためのベースになるものと頭に入れておくとわかりやすいと思います。
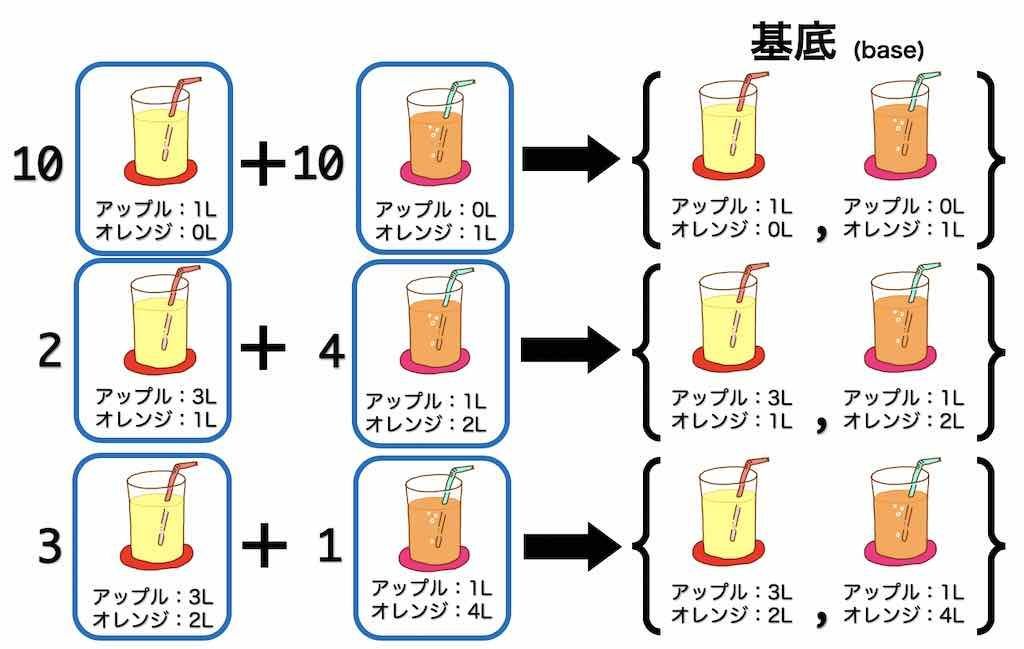
ただし、基底になるためには2つの条件を満たさなければなりません。
- 目標のミックスジュースを表現できること
- 基底の中身のジュースは全く別物であること(1次独立であること)
条件1は意外と忘れがちなので注意しましょう。
例えば、「アップル1L入りジュース」だけの基底を考えましょう。

「アップル1L入りジュース」だけだとオレンジジュース入りミックスジュースを表現することができません。なので基底*1ということはできません。
問題は条件2です。
まずは条件2を満たしている例を2つあげます。
例えば「アップル1L入りジュース」、「オレンジ1L入りジュース」はもちろん全く別物ですよね。アップルジュースからオレンジジュースを作り出すことなんて無理ですね。なので、当然基底となります。また、このようにそれぞれのジュースを1単位ずつ(今回は1単位=1L)集めて基底にしたものを標準基底と呼びます。
また、「アップル3L・オレンジ1Lセット」、「アップル1L・オレンジ2Lセット」も全く別物なので基底となります。
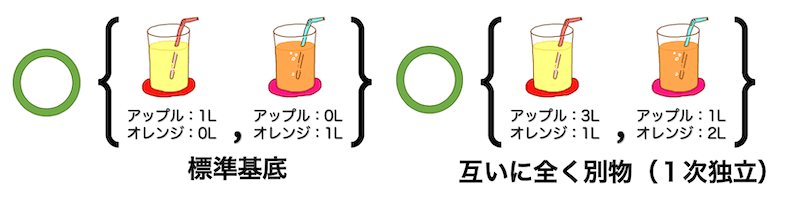
次に条件2を満たしていないものを挙げていきます。
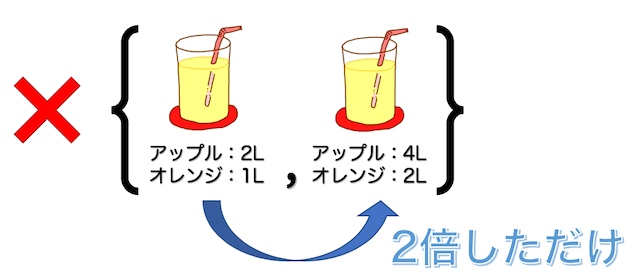
例えば「アップル4L・オレンジ2Lセット」は「アップル2L・オレンジ1Lセット」が2つ分入っているだけですよね。
このように、他のセットを何倍かしただけのものを同じ基底に入れることはできません。
また、このようにグループ内のセットを他のセットで表すことができる場合も基底と呼ぶことはできません。
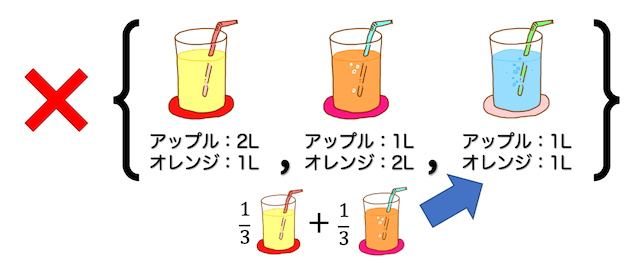
では、ここからは実際にベクトルで基底を考えていきましょう。
スポンサードリンク
2.基底とは?(正式に)
では、ベクトルを使って正式に基底の説明をしたいと思います。
先程のジュースの部分をベクトルに置き換えるとほとんど説明ができます。
ベクトル空間 \( V \) 内のベクトルの組 \( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) に対し、次の2つの条件を満たすとき、\( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) は \( V \) の基底であるといい、\[
V = \left\{ \vec{a_1}, \vec{a_2} , \cdots , \vec{a_n} \right\}
\]で表される。
条件1:\( V \) のすべてのベクトルが \( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) の1次結合、つまり\[
c_1 \vec{a_1} + c_2 \vec{a_2} + \cdots + c_n \vec{a_n}
\]で書き表される。
条件2:\( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) が1次独立
つまり、基底というのは、表したいベクトルをすべて満たすために必要な1次独立なベクトルの組を表します。
1次独立なベクトルであっても表したいベクトルをすべて表現できなければそれは基底とは呼べないので注意してください。
\( \mathbb{R}^n \)(\( n \) 次元)のベクトルの各軸方向の単位ベクトルを組み合わせてできた基底を標準基底と呼び、\( \vec{e_1} \), \( \vec{e_2} \), … \( \vec{e_n} \) で表す。
例1:2次元の場合\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) \ \ \ \vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \\ V = \left\{ \vec{e_1}, \vec{e_2} \right\} \]
例2:3次元の場合\[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) \ \ \ \vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) \ \ \ \vec{e_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \\ V = \left\{ \vec{e_1}, \vec{e_2}, \vec{e_3} \right\} \]
また、基底の次元についての定義も書いておきます。
ベクトル空間 \( V \) 内の基底に含まれるベクトルの数を次元と呼び、\( \dim V \) で表す。
例えば、\[ V = \left\{ \vec{a_1}, \vec{a_2} \right\} \ \ \ \ \dim V = 2 \]である。
その他基底について知っておいたら便利なことをまとめてみました。
\( \mathbb{R}^n \)(\( n \) 次元)のベクトル \( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) を並べた行列を\[ A = \left( \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \right) \]とするとき、行列 \( A \) の階数が \( n \) であれば \( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) は \( \mathbb{R}^n \) の基底である。
つまり、 本の \( \mathbb{R}^n \) のベクトルが基底であることを示すためには、行列 \( A \) が1次独立であることを示せばよい。
\( \mathbb{R}^m \)(\( m \) 次元)のベクトル空間 \( V \) の基底の数の上限は \( m \) 個までである。つまり、\[
\dim V \leqq m
\]である*2。
また、ベクトル空間 \( V \) に1次独立な \( r \) 本の1次独立なベクトルにさらに \( m - r \) 本のベクトルを追加し、基底を作ることができる。
では、例題にチャレンジしてみましょう。
例題1
次の3次元ベクトル空間内の3つのベクトル\[
\vec{a_1} = \left( \begin{array}{ccc} 2 \\ 2 \\ -3 \end{array} \right) \ \ \
\vec{a_2} = \left( \begin{array}{ccc} 3 \\ 4 \\ -4 \end{array} \right) \ \ \
\vec{a_3} = \left( \begin{array}{ccc} -1 \\ -2 \\ 2 \end{array} \right)
\]は \( \mathbb{R}^3 \) の基底か?
解説1
3つのベクトルを並べた行列 \( A \) が1次独立かどうかを判定する。\[
\begin{align*} |A| = &
\left| \begin{array}{ccc} 2 & 3 & -1 \\ 2 & 4 & -2 \\ -3 & -4 & 2 \end{array} \right|
\\ = & 16 + 18 + 8 - (12 +12 +16)
\\ = & 42 - 40
\\ = & 2 \not = 0
\end{align*} \]なので1次独立である。
(もちろん行列の階数が3であることを確認し1次独立であることを示してもOK)
よって \( \mathbb{R}^3 \) の3本のベクトルが1次独立なので \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) は \( \mathbb{R}^3 \) の基底である。
スポンサードリンク
3.基底の取り替え
※ここからはあまりジュースが出てきません。必要であれば適宜脳内でジュースに変換してお読みください。
ジュースの場合でも、セットに入っているジュースの量が変われば、必要なセットの数はもちろん変化しますよね。
ベクトルでも同じように、基底によってかかる係数、座標は変わってきます。
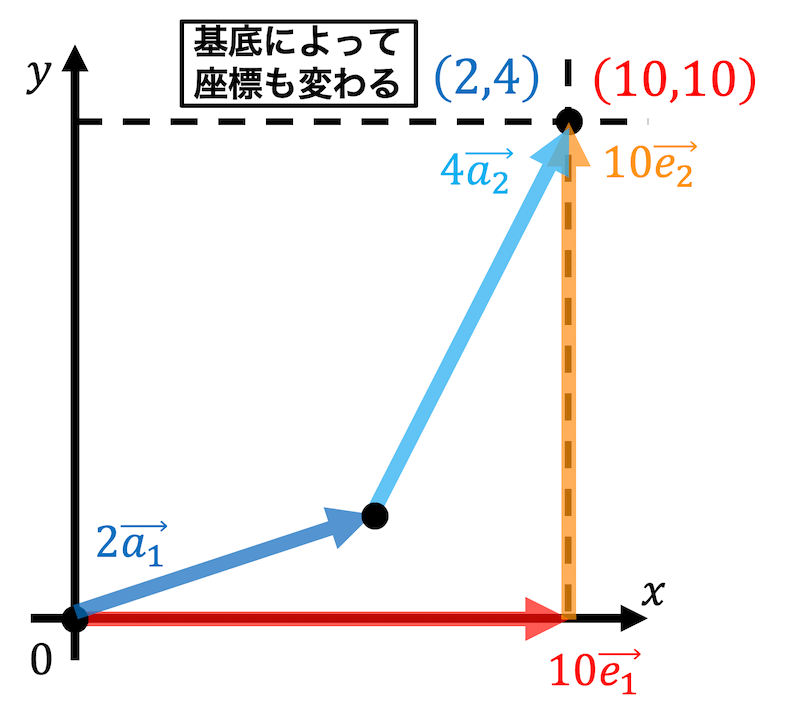
例えば、\[ \vec{x} = \left( \begin{array}{ccc} 10 \\ 10 \end{array} \right) \]を標準基底\[ \vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) \ \ \ \vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \]で表すと、\[ \left( \begin{array}{ccc} 10 \\ 10 \end{array} \right) = 10 \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) + 10 \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \\ \vec{x} = 10 \vec{e_1} + 10 \vec{e_2} \]となり、座標は \( (10,10) \) となります。
基底を\[ \vec{a_1} = \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right) \ \ \ \vec{a_2} = \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) \]で表すと\[ \left( \begin{array}{ccc} 10 \\ 10 \end{array} \right) = 2 \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right) + 4 \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) \\ \vec{x} = 2 \vec{a_1} + 4 \vec{a_2} \]となります。
さらに別の基底を\[ \vec{b_1} = \left( \begin{array}{ccc} 3 \\ 2 \end{array} \right) \ \ \ \vec{b_2} = \left( \begin{array}{ccc} 1 \\ 4 \end{array} \right) \]で表すと\[ \left( \begin{array}{ccc} 10 \\ 10 \end{array} \right) = 3 \left( \begin{array}{ccc} 3 \\ 2 \end{array} \right) + \left( \begin{array}{ccc} 1 \\ 4 \end{array} \right) \\ \vec{x} = 3 \vec{b_1} + \vec{b_2} \]となります。
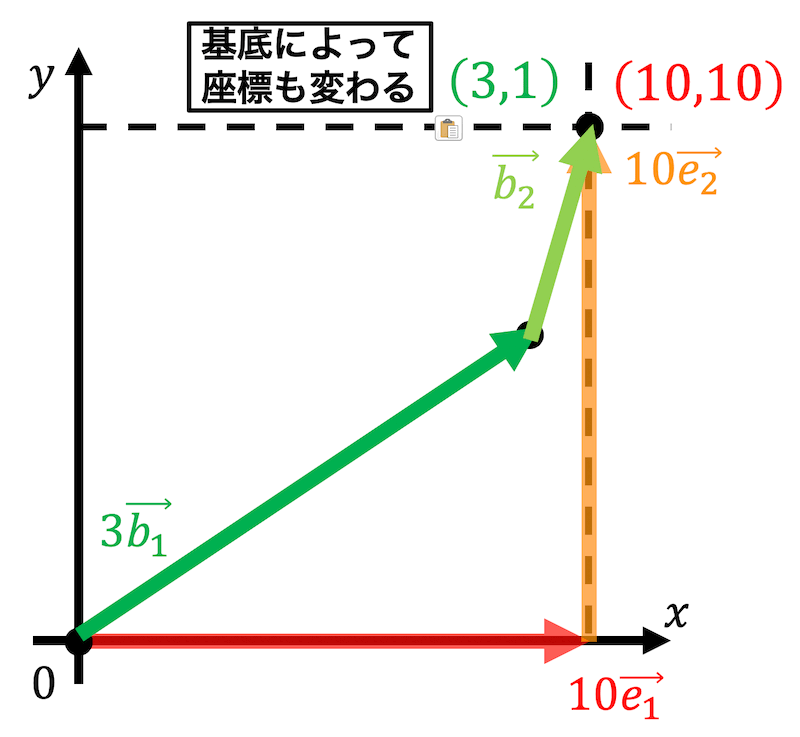
このように基底によって座標は変わってしまいます。
そのため、基底を変えるときには座標を新しい基底に対応させるために変換を行う必要があります。この変換を行う行列を取り替え行列などと呼びます。
では、今回は旧基底 \( \vec{a_1} \), \( \vec{a_2} \) で表された座標を新基底 \( \vec{b_1} \), \( \vec{b_2} \) で表された座標に変換するために変換するための変換行列を考えてみましょう。
まずは、\( \vec{b_1} \), \( \vec{b_2} \) を \( \vec{a_1} \), \( \vec{a_2} \) の1次結合で表しましょう。\[
\vec{b_1} = \frac{4}{5} \vec{a_1} + \frac{3}{5} \vec{a_2} \\
\vec{b_2} = - \frac{2}{5} \vec{a_1} + \frac{11}{5} \vec{a_2}
\]となります。
ここで、ベクトル \( \vec{b_1} \), \( \vec{b_2} \) を \( \vec{a_1} \), \( \vec{a_2} \) で表すための行列 \( P \) を考えてみましょう。\[ P = \frac{1}{5} \left( \begin{array}{ccc} 4 & -2 \\ 3 & 11 \end{array} \right) \]とすると、\[\begin{align*} \left( \vec{b_1}, \vec{b_2} \right)
= & \frac{1}{5} \left( 4 \vec{a_1} + 3 \vec{a_2} , - 2 \vec{a_1} + 11 \vec{a_2} \right)
\\ = & \frac{1}{5} \left( \vec{a_1}, \vec{a_2} \right)
\left( \begin{array}{ccc} 4 & -2 \\ 3 & 11 \end{array} \right)
\\ = & \left( \vec{a_1}, \vec{a_2} \right) P
\end{align*} \]と変形できます。
(実際に変換行列 \( P \) を求めるときは下に示す逆行列を使って計算を行ったほうが早いので逆行列で変換を行います。)
つぎに、変換行列 \( P \) を使って旧座標から新座標に変換しましょう。
旧基底を \( \left( x_1,x_2 \right) \)、新基底を \( \left( y_1, y_2 \right) \) とすると、
\[
\begin{align*} y_1 \vec{b_1} + y_2 \vec{b_2} & = \left( \vec{b_1}, \vec{b_2} \right) \left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) \\ & = \left( \vec{a_1}, \vec{a_2} \right) P \left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right)
\end{align*} \]と変形でき、さらに \[
\begin{align*}
\left( \vec{a_1}, \vec{a_2} \right) P \left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) = & \left( \vec{a_1}, \vec{a_2} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) \\ = & x_1 \vec{a_1} + x_2 \vec{a_2}
\end{align*} \]が成立するので、旧座標と新座標には\[
P \left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) = \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\]の関係があります。
実際に新座標と旧座標の関係が成り立つか計算して確認しましょう。 \[
\begin{align*}
P \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right) & =
\frac{1}{5} \left( \begin{array}{ccc} 4 & -2 \\ 3 & 11 \end{array} \right) \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right) \\ & =
\frac{1}{5} \left( \begin{array}{ccc} 10 \\ 20 \end{array} \right) \\ & =
\left( \begin{array}{ccc} 2 \\ 4 \end{array} \right)
\end{align*}
\]となり、たしかに関係が成り立ってますね。
交換元の基底 \( \vec{a_1} \), \( \vec{a_2} \), …, \( \vec{a_n} \) からなる行列を \( A \)、交換先の基底 \( \vec{b_1} \), \( \vec{b_2} \), …, \( \vec{b_n} \) からなる行列を \( B \) としたとき、基底の変換行列 \( P \)は、\[
B = AP \\ P = A^{-1} B \]と表せる。
また、基底の変換行列 \( P \) を用いると、交換元の座標 \( x_1 \)〜 \( x_n \) から交換先の座標 \( y_1 \) 〜 \( y_n \) は、\[
P \left( \begin{array}{ccc} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right) =
\left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)
\\
\left( \begin{array}{ccc} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right) =
P^{-1} \left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)
\]と座標変換ができる。
少しむずかしいことを書いてあるかもしれませんが、実は\[
x_1 \vec{a_1} + x_2 \vec{a_2} = y_1 \vec{b_1} + \vec{b_2}
\]を使って計算しているだけなのです。
4.変換行列を用いない座標変換
しかし、変換行列 \( P \) を用いた座標変換では \[
P = A^{-1} B \\
\vec{y} =
P^{-1} \vec{x}
\]と2回逆行列の計算が必要なので少しめんどくさいですよね*3。
なので、変換行列 \( P \) を使わずに一気に座標変換をする方法を考えましょう。
変換前の座標を示すベクトルを \( \vec{x} \)、変換後の座標を示すベクトルを \( \vec{y} \) とすると、\[
\begin{align*}
\vec{y} & = P^{-1} \vec{x}
\\ & = (A^{-1} B)^{-1} \vec{x} \\ & = B^{-1} A\vec{x}
\end{align*}
\]
となる。
交換元の基底 \( \vec{a_1} \), \( \vec{a_2} \), …, \( \vec{a_n} \) からなる行列を \( A \)、交換先の基底 \( \vec{b_1} \), \( \vec{b_2} \), …, \( \vec{b_n} \) からなる行列を \( B \) としたとき、交換元の座標 \( x_1 \)〜 \( x_n \) から交換先の座標 \( y_1 \) 〜 \( y_n \) は、\[
\left( \begin{array}{ccc} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right) = B^{-1} A \left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)
\]と表される。
この座標変換の意味を考えてみましょう。
まず、交換元の基底を標準基底に変換する計算をしています。
この計算は、\[
\vec{t} = A \vec{x}
\]で表せます。
つぎに標準基底に変換したものを交換先の基底に変換する計算をします。
この計算は、\[
\vec{y} = B^{-1} \vec{t}
\]で表せます。
2つの計算をあわせると、\[
\vec{y} = B^{-1} \vec{t} = B^{-1} A \vec{x}
\]と変換することができます。
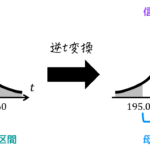
基底 \( \vec{a_1} \), \( \vec{a_2} \), …, \( \vec{a_n} \) から基底 \( \vec{b_1} \), \( \vec{b_2} \), …, \( \vec{b_n} \) への変換(と逆変換)を図示すると以下のようになります。
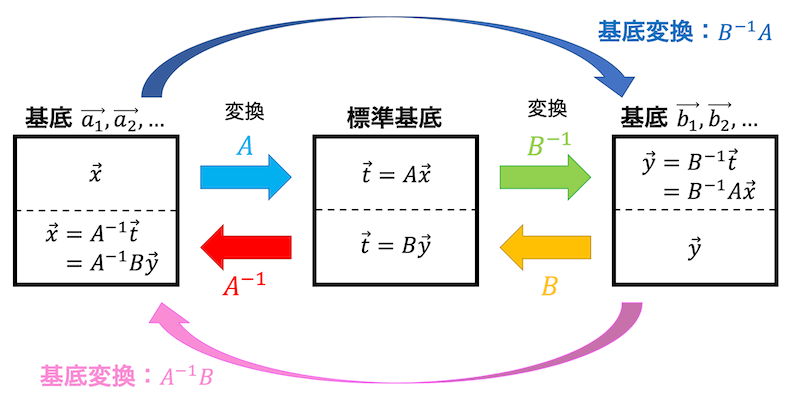
※行列 \( A \) は基底 \( \vec{a_1} \), \( \vec{a_2} \), …, \( \vec{a_n} \) からなる行列、行列 \( B \) は基底 \( \vec{b_1} \), \( \vec{b_2} \), …, \( \vec{b_n} \) からなる行列です*4。
例題2
2次元ベクトル \( \mathbb{R}^2 \) の変換元基底 \( \vec{a_1} \), \( \vec{a_2} \) および変換先基底 \( \vec{b_1} \), \( \vec{b_2} \) がつぎのように与えられている。 \[
\vec{a_1} =\left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) \ \ \ \vec{a_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) , \ \ \ \ \ \vec{b_1} =\left( \begin{array}{ccc} 3 \\ 5 \end{array} \right) \ \ \ \vec{b_2} =\left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) \]
(1) 変換元基底 \( \vec{a_1} \), \( \vec{a_2} \) から 変換先基底 \( \vec{b_1} \), \( \vec{b_2} \) への変換行列 \( P \) を求めなさい。
(2) 変換元基底上で \[ \left( \begin{array}{ccc} 4 \\ 5 \end{array} \right) \]と表示されるベクトルは変換先基底上ではどのように表示されますか*5。
解説2
逆行列を使うので、もし逆行列の求め方を忘れてしまった人はこちらで復習をしましょう!
(1)
変換元基底からできる基底行列を \( A \), 変換先基底からできる基底行列を \( B \) とすると、\[
A = \left( \vec{a_1} , \vec{a_2} \right) = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) \\ B = \left( \vec{b_1} , \vec{b_2} \right) = \left( \begin{array}{ccc} 3 & 1 \\ 5 & 2 \end{array} \right)
\]となる。
変換行列は\[ P = A^{-1} B = E^{-1} B = EB = \left( \begin{array}{ccc} 3 & 1 \\ 5 & 2 \end{array} \right) \]と求められる。
(2)
まずは変換行列の逆行列を求める。\[
P^{-1} = \left( \begin{array}{ccc} 2 & -1 \\ -5 & 3 \end{array} \right)
\]となるので、
\[ \begin{align*}
P^{-1} \left( \begin{array}{ccc} 4 \\ 5 \end{array} \right) = &
\left( \begin{array}{ccc} 2 & -1 \\ -5 & 3 \end{array} \right) \left( \begin{array}{ccc} 4 \\ 5 \end{array} \right)
\\ = & \left( \begin{array}{ccc} 3 \\ -5 \end{array} \right)
\end{align*} \]と求められる。
座標が〜って書いてあって少し難しいかもしれませんが、実際には、\[
4 \vec{a_1} + 5 \vec{a_2} = s \vec{b_1} + t \vec{b_2}
\]となる \( s \), \( t \) を求めているだけです。
では実際に練習をしていきましょう!
4.練習問題
では2問練習をしましょう。
練習1
次の3次元ベクトル空間内の3つのベクトル\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) \ \ \
\vec{a_2} = \left( \begin{array}{ccc} 4 \\ 7 \\ 7 \end{array} \right) \ \ \
\vec{a_3} = \left( \begin{array}{ccc} x \\ -4 \\ -5 \end{array} \right)
\]は \( \mathbb{R}^3 \) の基底となるための \( x \) の条件を求めなさい。
練習2
2次元ベクトル \( \mathbb{R}^2 \) の変換元基底 \( \vec{a_1} \), \( \vec{a_2} \) および変換先基底 \( \vec{b_1} \), \( \vec{b_2} \) がつぎのように与えられている。 \[
\vec{a_1} =\left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) \ \ \ \vec{a_2} = \left( \begin{array}{ccc} 3 \\ 5 \end{array} \right) , \ \ \ \ \ \vec{b_1} =\left( \begin{array}{ccc} 3 \\ 1 \end{array} \right) \ \ \ \vec{b_2} =\left( \begin{array}{ccc} -1 \\ 2 \end{array} \right) \]
(1) 変換元基底 \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) から 変換先基底 \( \vec{b_1} \), \( \vec{b_2} \), \( \vec{b_3} \) への変換行列 \( P \) を求めなさい。
(2) 変換元基底上で \[ \left( \begin{array}{ccc} 5 \\ 2 \end{array} \right) \]と表示されるベクトルは変換先基底上ではどのように表示されますか。
(3) 変換先基底上で \[ \left( \begin{array}{ccc} 3 \\ 4 \end{array} \right) \]と表示されるベクトルは変換元基底上ではどのように表示されますか。
5.練習問題の答え
解答1
3つのベクトルを並べた行列 \( A \) が1次独立であればよい。\[
\begin{align*} |A| = &
\left| \begin{array}{ccc} 1 & 4 & x \\ 3 & 7 & -4 \\ 2 & 7 & -5 \end{array} \right|
\\ = & -35 - 32 + 21x - (14x - 60 - 28)
\\ = & 7x - 67 + 88
\\ = & 7x + 21
\\ = & 7 (x+3)
\not = 0
\end{align*} \]を満たすような \( x \) が基底となるための条件となる。
よって、\( x \not = - 3 \) のとき、3つのベクトルは \( \mathbb{R}^3 \) の基底となる。
解答2
(1)
変換元基底からできる基底行列を \( A \), 変換先基底からできる基底行列を \( B \) とすると、\[
A = \left( \vec{a_1} , \vec{a_2} \right) = \left( \begin{array}{ccc} 1 & 3 \\ 2 & 5 \end{array} \right) \\ B = \left( \vec{b_1} , \vec{b_2} \right) = \left( \begin{array}{ccc} 3 & -1 \\ 1 & 2 \end{array} \right)
\]となる。
ここで、行列 \( A \) の逆行列 \( A^{-1} \) は、\[
A^{-1} = \left( \begin{array}{ccc} -5 & 3 \\ 2 & -1 \end{array} \right)
\]と求められるので、
変換行列は\[ P = A^{-1} B = \left( \begin{array}{ccc} -12 & 11 \\ 5 & -4 \end{array} \right) \]と求められる。
掃き出し法で求める場合のコツ
普段掃き出し法を使う際には、\[
(A|E) \to (AA^{-1}| EA{-1}) \to (E|A^{-1})
\]と求めると思いますが、\[ (A|B) \to (AA^{-1}| EA{-1} B) \to (E|A^{-1} B) \]とすると、一度に行列 \( A^{-1} B \) を求められてスピードアップに繋がります。
今回の場合だと、\[ \begin{align*} &
\left( \begin{array}{cc|cc} 1 & 3 & 3 & -1 \\ 2_{-2} & 5_{-6} & 1_{-6} & 2_{+2} \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 1 & 3_{-3} & 3_{-15} & -1_{+12} \\ 0_{\times (-1)} & -1_{\times (-1)} & -5_{\times (-1)} & 4_{\times (-1)} \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 1 & 0 & -12 & 11 \\ 0 & 1 & 5 & -4 \end{array} \right)
\end{align*} \]と求めると \( A^{-1} B \) が一度に求まります*6。
特に3×3行列以上になったときに計算速度が上がるのでぜひお試しください!
(2)
まずは変換行列の逆行列を求める。\[
P^{-1} = \frac{1}{7} \left( \begin{array}{ccc} 4 & 11 \\ 5 & 12 \end{array} \right)
\]となるので、変換先の座標は、\[ \begin{align*}
P^{-1} \left( \begin{array}{ccc} 4 \\ 5 \end{array} \right) & = \frac{1}{7}
\left( \begin{array}{ccc} 4 & 11 \\ 5 & 12 \end{array} \right) \left( \begin{array}{ccc} 5 \\ 2 \end{array} \right)
\\ & = \frac{1}{7} \left( \begin{array}{ccc} 42 \\ 49 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 6 \\ 7 \end{array} \right)
\end{align*} \]と求められる。
変換行列を(1)で求めているため、変換行列から求めているが、直接座標を求めるのであれば、\[
5 \vec{a_1} + 2 \vec{a_2} = s \vec{b_1} + t \vec{b_2}
\]を計算する手もある。この場合、\[
\left( \begin{array}{ccc} 11 \\ 20 \end{array} \right) = s \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right) + t \left( \begin{array}{ccc} -1 \\ 2 \end{array} \right)
\]となる \( s,t \) を求めればOK。
(3)
先程の逆パターンの問題。
変換元の座標は、 \[ \begin{align*}
P \left( \begin{array}{ccc} 3 \\ 4 \end{array} \right) & =
\left( \begin{array}{ccc} -12 & 11 \\ 5 & -4 \end{array} \right) \left( \begin{array}{ccc} 3 \\ 4 \end{array} \right)
\\ & = \frac{1}{7} \left( \begin{array}{ccc} 8 \\ -1 \end{array} \right)
\end{align*} \]と求められます。
同じく直接座標を求めるのであれば、\[
3 \vec{b_1} + 4 \vec{b_2} = s \vec{a_1} + t \vec{a_2}
\]を計算する手もある。この場合、\[
\left( \begin{array}{ccc} 5 \\ 11 \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) + t \left( \begin{array}{ccc} 3 \\ 5 \end{array} \right)
\]となる \( s,t \) を求めればOK。
6.さいごに
今回は、線形代数における基底についてジュースを用いたわかりやすい説明と、基底の変換についてのまとめを行いました。
基底とは、作りたいジュースを作れるそれぞれ別物なセットのまとまり、つまり表現したいすべてのベクトルを1次独立なベクトルのまとまり(集合)で表したものであることを頭にいれておきましょう。
また、基底の変換や座標変換は難しいことをやっているように見えるかもしれませんが、実はただの1次結合の計算をしているだけなので、やり方さえわかれば簡単に変換することができます。
でも逆行列は使うので逆行列がわからないって人は復習をしておきましょう!
*1:アップルジュースだけしか入らないジュースはミックスとは言えませんよね……。
*2:\( m \) 次元ベクトルを \( n \) 本並べた行列を考えると、\( m \lt n \) のとき、ベクトルの要素に関わらず行列の階数が \( m \) 以下となり、\( n \) にはならないため、どうがんばっても1次従属になり、基底とはならないから。
*3:ベクトル \( \vec{x} \), \( \vec{y} \) は交換元の座標 \( x_1 \)〜 \( x_n \) から交換先の座標 \( y_1 \) 〜 \( y_n \) を用いて\[ \vec{x} =\left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right) \ \ \ \vec{y} = \left( \begin{array}{ccc} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right) \]であることを表している。
*4:具体的には、\[ A = \left( \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \right) \\ B = \left( \vec{b_1}, \vec{b_2}, \cdots , \vec{b_n} \right) \]としています。
*5:わからなければジュースに例えましょう。『アップルジュース4L、オレンジジュース5Lは、「アップル3L、オレンジ5Lセット」、「アップル1L、オレンジ2Lセット」をそれぞれ何セット使いますか?』などと脳内変換して解いてみましょう。
*6:検算する際には \( A \) と \( A^{-1} B \) の積が \( B \) になることを確かめましょう。
関連広告・スポンサードリンク