うさぎでもわかる微分方程式　Part06　定数係数線形微分方程式（同次式編）

こんにちは、ももやまです。

今回から2階以上の線形微分方程式（基本は2階）の解き方について説明していきたいと思います。

まずは、2階以上の線形微分方程式の中でも、

• 定数係数
• 同次式

の解き方について説明していきたいと思います。

前回の微分方程式の記事はこちら！

www.momoyama-usagi.com

2階線形微分方程式ってどんなのだっけ、基本解ってなんだっけとなった人は必ず上にある前回の記事で復習しておきましょう。

スポンサードリンク

１．定数係数2階線形微分方程式とは

定数係数2階線形微分方程式とは、2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]の \( P(x) \), \( Q(x) \) の部分が定数になっている微分方程式、つまり\[
\frac{d^2 y}{dx^2} + a \frac{dy}{dx} + b y = R(x)
\]となっている微分方程式のことを表します。（\( a \), \( b \) は定数）

さらに、\( R(x) = 0 \) のとき、つまり\[
\frac{d^2 y}{dx^2} + a \frac{dy}{dx} + b y = 0
\]の形の場合、同次式の2階線形微分方程式となります。

今回はこの同次式の定数係数2階線形微分方程式について解いていきたいと思います。

スポンサードリンク

２．同次式定数係数2階線形微分方程式の一般解

(1) まずは同次式定数係数1階微分方程式の一般解から

まずは、復習として、同次式の定数係数1階微分方程式\[
\frac{dy}{dx} + a y = 0
\]の一般解を出してみましょう。

この微分方程式は、両辺を \( y \) で割り、\[
\frac{1}{y} \frac{dy}{dx} = -a
\]と変数分離形にできるので、任意定数 \( C_1 \) を用いて\[
\int \frac{1}{y} \ dy =  \int -a \ dx \]\[
\log |y| = -ax + C_1 \]\[
\log |y| = \log e^{-ax} + \log e^{C_1} \]\[
|y| = e^{-ax} e^{C_1} \]\[
y = \pm e^{C_1} e^{-ax}
\]と一般解を求めることができます。さらに、\( C = e^{C_1} \) とすることで、一般解を\[
y = C e^{-ax}
\]の形にすることができます。

(2) 定数係数2階線形微分方程式の基本解

1階の同次式の定数係数1階微分方程式\[
\frac{dy}{dx} + a y = 0
\]の一般解は \( y = Ce^{-ax} \) と、\( e^{kx} \) の形になりましたね。

なので、2階の同次の定数係数微分方程式も \( y = e^{kx} \) の形になりそうですよね！

実際に \( y = e^{kx} \) と仮定して、同次式の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + a \frac{dy}{dx} + b y = 0
\]に代入してみましょう。\[
\frac{dy}{dx} = k e^{kx}, \ \ \ \frac{d^2 y}{dx^2} = k^2 e^{kx}
\]なので、\[\begin{align*}
k^2 e^{kx} + ak e^{kx} + b e^{kx}  & = 0 \\
\textcolor{red}{\left( k^2 + ak + b \right)} e^{kx} & = 0
\end{align*} \]となりますね。

なので、赤色部分 \( k^2 + ak + b \) が0となるような \( k \)、つまり\[
k^2 + ak + b = 0 \tag{1}
\]を満たすような \( k \) のとき、\( y = e^{kx} \) は解になるといえますね。

この方程式 \( k^2 + ak + b = 0 \) のことを特性方程式と呼びます。

特性方程式 \( k^2 + ak + b = 0 \) は2次の方程式なので、方程式を満たす \( k \) は重解のときを除いて必ず2つありますね。なので、解の数も2つ存在します。

このように、特性方程式から導き出せる1次独立な解のことを基本解と呼びます。

（基本解がもしわからない人 or 忘れた人はこちらの記事で復習しましょう。）

1つ例として、微分方程式\[
\frac{d^2 y}{dx^2} - 5 \frac{dy}{dx} + 6 y = 0
\]を満たすような基本解を特性方程式から求めてみましょう。

特性方程式は、\[\begin{align*}
k^2 - 5k + 6 = 0
\end{align*} \]となるので、\[
(k-2)(k-3) = 0
\]より、特性方程式の解は \( k = 2,3 \) となるので、\( y = e^{2x} \), \( y = e^{3x} \) の2つが基本解となります。

スポンサードリンク

３．3つの解パターン

同次式定数係数2階線形微分方程式\[
\frac{d^2 y}{dx^2} + a \frac{dy}{dx} + b y = 0
\]の一般解の形は、特性方程式\[
k^2 + ak + b = 0
\]解の形（判別式）によって、3パターンに分けられます。具体的には、

1. 特性方程式が異なる2つの実数解をもつとき
2. 特性方程式が重解をもつとき
3. 特性方程式が異なる2つの虚数解をもつとき

の3つに分けられます。

先に、解のパターンがどうなるかを書きましょう。

1つずつ見ていきましょう。

(1) 特性方程式が異なる2つの実数解をもつとき

最も基本的なパターンです。

特性方程式\[
k^2 + ak + b = 0
\]が異なる2つの実数解 \( k_1 \), \( k_2 \) をもつとき、つまり判別式 \( D \) が\[
D = a^2 - 4b > 0
\]となるときの基本解は \( e^{k_1x} \), \( e^{k_2 x} \) となります。

また、一般解は2つの任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 e^{k_1 x} + C_2 e^{k_2 x}
\]と表すことができます。

例題1

微分方程式\[
\frac{d^2 y}{dx^2} - 3 \frac{dy}{dx} - 10 y = 0
\]の基本解と一般解を求めなさい。

解説1

特性方程式は、\[
k^2 - 3k - 10 = 0
\]となるので、\[
(k-5)(k + 2) = 0
\]とすることで特性方程式の解は \( k = 5, -2 \) となる。

よって、基本解は \( y = e^{5x} \), \( y = e^{-2x} \) となる。

また、それぞれの基本解を定数倍したものの和も解となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 e^{5x} + C_2 e^{-2x}
\]となる。

(2) 特性方程式が重解となるとき

特性方程式\[
m^2 + am + b = 0
\]は、2次方程式なので、基本的には2つの解を持ちます。しかし、判別式\[
D = a^2 - 4b = 0
\]となるときは重解となるので、解は1つしか持ちませんね。

（この重解を \( k \) としましょう。）

すると、基本解は \( e^{k x} \) となります。

(1)と同じようにすると、一般解は、\[
y = C_1 e^{k x} + C_2 e^{k x}
\]となりますが、この形は1つにまとめられて\[
y = C e^{k x}
\]となってしまいます。

あれ、2階の微分方程式なので、任意定数は2つ出てくるはずなのに1つになっちゃいました。

ということで \( e^{kx} \) になるべく近い形（微分しても \( e^{kx} \) の形を保つような関数）かつ \( e^{kx} \) の定数倍ではないもう1つの基本解を探してみましょう。

ここで、\( y = e^{k x} \) を \( x \) 倍した \( y = x e^{k x} \) を考えてみましょう。

すると、\[\begin{align*}
\frac{dy}{dx} & = e^{k x} + k_1 x e^{k x}
\\ & = (k x + 1) e^{k x} \end{align*} \] \[\begin{align*} \frac{d^2 y}{dx^2} & =k e^{k} +k e^{k x} + k^2 x e^{k x}
\\ & = 2 k e^{k} + k_1^2 x e^{k}
\\ & = (k^2 x + 2k)e^{k}
\end{align*} \]となるので、\[
\frac{d^2 y}{dx^2} + a \frac{dy}{dx} + b y = 0
\]に代入すると、\[
(k^2 x + 2k) e^{k} + a (k x + 1) e^{k x} + b x e^{k x}= 0 \]\[
\left( (k^2 + a k + b) x + (2k + a) \right) e^{k x} = 0
\]と変形できます。

ここで、\(  e^{kx} \gt 0 \) なので、\( y = x e^{k x} \) が解を持つためには\[
(k^2 + a k + b ) x + (2k + a) = 0
\]を満たす必要があります。

\( e^{k x} \) が基本解のとき、\[
k^2 + a k + b = 0
\]は必ず満たすため（特性方程式）、\( e^{k x} \) が基本解のとき、\( x e^{k x} \) が基本解になるかどうかは\[
2k + a = 0
\]、つまり \( a = -2k \) を満たすかどうか確認すればOKです。

特性方程式\[
m^2 + a m + b = 0
\]が重解をもつとき、判別式\[
D = a^2 - 4b = 0
\]の関係 \( b = \frac{1}{4} a^2 \) が成立するので、\( a = -2k \) を代入すると、\[\begin{align*}
b & = \frac{1}{4} \left( -2k \right)^2
\\ & = \frac{1}{4} \cdot 4 k^2
\\ & = k^2
\end{align*} \]となるので、\[\begin{align*}
m^2 + a m + b & = m^2 - 2km + k^2
\\ & = (m-k)^2
\\ & = 0
\end{align*}\]となり、特性方程式が重解をもつときだけ、\( e^{kx} \) が解であれば \( x e^{kx} \) も解となることが示せましたね。

例題2

微分方程式\[
\frac{d^2 y}{dx^2} - 4 \frac{dy}{dx} + 4 y = 0
\]の基本解と一般解を求めなさい。

解説2

微分方程式の特性方程式は、\[
k^2 -4k + 4 = 0
\]となるので、\[
(k-2)^2 = 0
\]とすることで特性方程式の解は \( k = 2 \)（2重解）となる。

よって、基本解は \( y = e^{2x} \), \( y = xe^{2x} \) となる。

また、それぞれの基本解を定数倍したものの和も解となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 e^{2x} + C_2 x e^{2x}
\]となる。

(3) 特性方程式が虚数解となるとき

特性方程式\[
m^2 + am + b = 0
\]の判別式が負になるとき、つまり\[
D = a^2 - 4b < 0
\]となるときは虚数解となりますよね。

このときの特性方程式の解は、\[
\frac{-a \pm \sqrt{D} }{2} = - \frac{a}{2} + \frac{\sqrt{-D}}{2} i
\]と実部と虚部で表すことができますね。

ここで、特性方程式の解を \( k_1 = \alpha + \beta i \), \( k_2 = \alpha - \beta i \) と実部と虚部で分けて表現します。

すると、微分方程式の基本解は \( y = e^{(\alpha + \beta i)x} \), \( y = e^{(\alpha + \beta i)x} \)となり、一般解は\[
y = A_1 e^{(\alpha + \beta i)x} + A_2 e^{(\alpha + \beta i)x}
\]となります。

でも、微分方程式の一般解に虚数解があるのはちょっと…と思いますよね。

なんとか実数だけで表現することはできないでしょうか。

ということで、虚数で表された一般解をなんとか実数範囲だけで表すことを考えてみましょう。

ここで、オイラーの公式\[
e^{i \theta} = \cos \theta + i \sin \theta
\]を思い出してみましょう。

（オイラーの公式についてはこちらの記事をご覧ください。）

すると、\[
e^{i \beta x} = \cos \beta x + i \sin \beta x
\]となるので、一般解は\[\begin{align*}
y & = A_1 e^{(\alpha + \beta i)x} + A_2 e^{(\alpha - \beta i)x}
\\ & = A_1 e^{\alpha x} e^{i \beta x} + A_2 e^{\alpha x} e^{- i \beta x}
\\ & = A_1 e^{\alpha x} \left( \cos \beta x + i \sin \beta x \right) +  A_2 e^{\alpha x} \left\{ \cos ( - \beta x ) + i \sin (- \beta x) \right\}
\\ & = A_1 e^{\alpha x} \left( \cos \beta x + i \sin \beta x \right) +  A_2 e^{\alpha x} \left( \cos \beta x - i \sin \beta x \right)
\\ & = e^{\alpha x} \left\{ ( A_1 + A_2 ) \cos \beta x + i (A_1 - A_2) \sin \beta x \right\}
\end{align*} \]と表すことができる。

さらに、任意定数を改めて \( C_1 = A_1 + A_2 \), \( C_2 = i(A_1 - A_2) \) とすると、一般解を\[
e^{\alpha x} \left( C_1 \cos \beta x + C_2 \sin \beta x \right)
\]と虚数 \( i \) を使わずに表現することができます！

（基本解は \( e^{ax} \cos \beta x \), \( e^{ax} \sin \beta x \) となる。）

例題3

微分方程式\[
\frac{d^2 y}{dx^2} + y = 0
\]の基本解と一般解を求めなさい。

解説3

微分方程式の特性方程式は、\[
k^2 + 1 = 0
\]となるので、\[
k^2 = -1
\]とすることで特性方程式の解は \( k = \pm i \)（2重解）となる。

よって、基本解は \( y = e^0 \cos x = \cos x \), \( y = e^0 \sin x = \sin x \) となる。

また、それぞれの基本解を定数倍したものの和も解となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 \cos x + C_2 \sin x
\]となる。

４．ばね振り子の単振動（応用）

実際に同次式の定数係数2階線形微分方程式の応用して、ばね振り子の単振動について少しだけですが見ていきましょう。

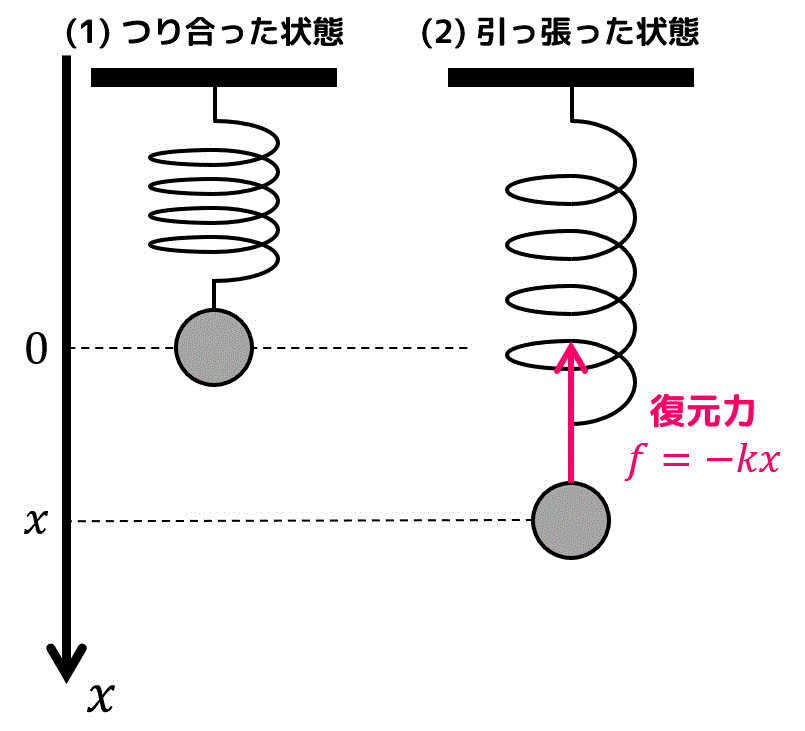
下の図に示すような軽い（質量を無視できる）ばねに重さ \( m \) のおもりを付け合うと、左側のようにある地点でつりあいます。

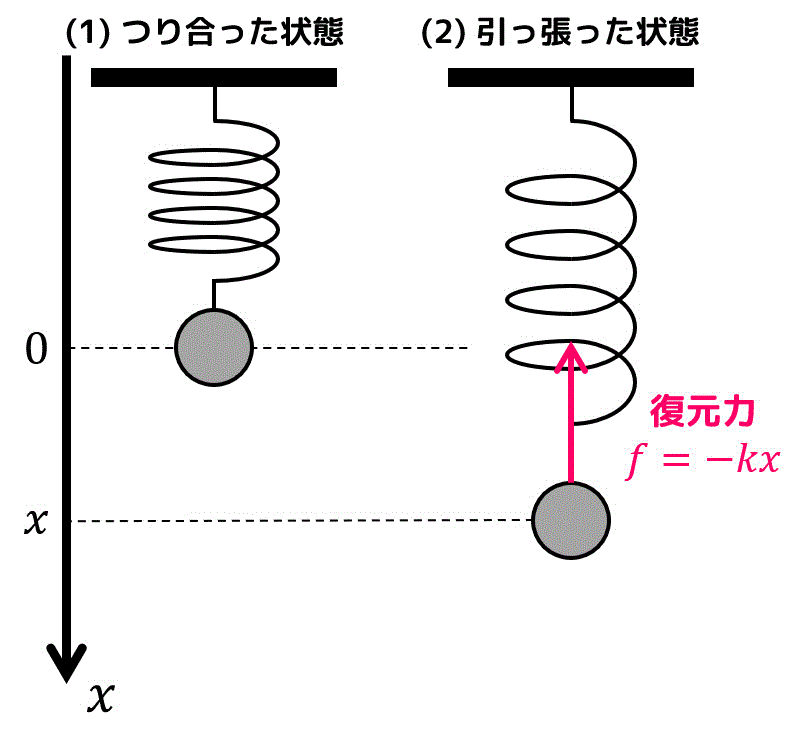
このつり合った点を0として、\( x \) だけ引っ張った状態を考えましょう。

すると、つりあった点に戻ろうとする力（復元力）が働きますね。この力 \( f \) は、ばね定数 \( k \)、引っ張った距離 \( x \) を用いて\[
f = - kx
\]と表すことができます。（変位とは逆向きなのでマイナスが必要なことに注意！）

すると、運動方程式は加速度 \( \frac{d^2 x}{dt^2} \) を用いて\[
m \frac{d^2 x}{d t^2} = - kx
\]となりますね。早速この時刻 \( t \) に対する微分方程式を解いていくことで、ある時間 \( t \) に対するおもりがいる場所（変位） \( x \) を求めてみましょう。

まず、両辺を \( m \) で割り、さらに移項させて\[
\frac{d^2 x}{d t^2} + \frac{k}{m} x = 0
\]とし、さらに\[
\omega^2 = \frac{k}{m}
\]とすると、\[
\frac{d^2 x}{d t^2} + \omega^2 x = 0
\]となります。

すると、特性方程式は、\[
k^2 + \omega^2 = 0
\]となるので、\( k = \pm i \omega \) となりますね。

ここで、特性方程式の解が \( k = \alpha \pm \beta i \) となるときの基本解は \( e^{at} \cos \beta t \), \( e^{at} \sin \beta t \) 、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
x = e^{\alpha t} \left( C_1 \cos \beta t + C_2 \sin \beta t \right)
\]となるのでしたね。

なので、微分方程式の基本解は \( \cos \omega t \), \( \sin \omega t \) となり、一般解は\[\begin{align*}
x & = e^0 C_1 \cos \omega t + e^0 C_2 \sin \omega t
\\ & = C_1 \cos \omega t + C_2 \sin \omega t
\end{align*} \]と求めることができます。

（角速度が \( \omega \) となるので、単振動の周期 \( T \) は\[
T = \frac{ 2\pi}{\omega} = 2 \pi \sqrt{ \frac{m}{k} }
\]となります。）

さらに、\[
C = \sqrt{C_1^2 + C_2^2}
\]とし、\[
C_1 = A \sin \alpha, \ \ \ C_2 = A \cos \alpha
\]と任意定数を \( C \), \( \alpha \) におきかえることで、\[\begin{align*}
x & = A \sin \alpha \cos \omega t + A \cos \alpha \sin \omega t
\\ & = A \left( \sin \alpha \cos \omega t + \cos \alpha \sin \omega t  \right)
\\ & = A \sin \left( \alpha + \omega t \right)
\\ & = A \sin \left( \omega t + \alpha \right)
\end{align*} \]と表現することもできます。

（ちなみに任意定数のつけかたを変えて、一般解を\[
x = A \cos \left( \omega t + \alpha \right)
\]としてもOKです*1。

実際の力学の問題では、一般解に加え、2つの初期条件が加わります。

初期条件の例としては、

• 距離4だけ引っ張った状態でスタート（\( t = 0 \) のとき \( x = 4 \)）
• 静かにおもりを離した（初速度は0、\( \frac{dx}{dt} = 0 \) ）

のようなものがあります。

実際に \( \omega = 2 \) としたときの上の初期条件を満たすような特解を求めてみましょう。

まず、\( x(0) = 4 \) より、\[
x = C_1 \cos 0 + C_2 \sin 0 = C_1 = 4
\]が成立し、さらに\[
\frac{dx}{dt} = - 2 C_1 \sin 0 + 2 C_2 \cos 0 = 0
\]となるので、\( C_2 = 0 \) となるので、特解を\[
x = 4 \cos 2t
\]と求めることができます。

５．高階定数係数微分方程式（応用）

同次式の定数係数2階線形微分方程式の解の形は、特性方程式の解の形によって求められると説明しました。

3階以上の同次式高階定数係数微分方程式の解の形も、特性方程式を解くことで一般解を求めることができます。

基本解の組み合わせは、下の4パターンに分けることができます。

3問ほど例題で練習してみましょう。

例題4（重解ではない実数解になる場合）

微分方程式\[
\frac{d^3 y}{dx^3} - 6 \frac{d^2 y}{dx^2} + 11 \frac{dy}{dx} - 6 y = 0
\]の基本解と一般解を求めなさい。

解説4

特性方程式は、\[
k^3 - 6k + 11k - 6 = 0
\]となるので、\[
(k-1)(k^2-5k+6) = 0 \]\[
(k-1)(k-2)(k-3) = 0
\]とすることで特性方程式の解は \( k = 1, 2, 3 \) となる。

よって、基本解は \( e^{x} \), \( e^{2x} \), \( e^{3x} \) となる。

また、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[
y = C_1 e^{x} + C_2 e^{2x} + C_3 e^{3x}
\]となる。

例題5（重解の実数解が含まれる場合）

微分方程式\[
\frac{d^3 y}{dx^3} - \frac{d^2 y}{dx^2} - 8 \frac{dy}{dx} + 12 y = 0
\]の基本解と一般解を求めなさい。

解説5

特性方程式は、\[
k^3 - k^2 - 8k + 12 = 0
\]となるので、\[
(k-2)(k^2+k-6) = 0 \]\[
(k-2)^2 (k+3) = 0
\]とすることで特性方程式の解は \( k = -3 \) と、\( k = 2 \) の2重解となる。

よって、基本解は \( e^{-3x} \) と \( e^{2x} \), \( xe^{2x} \) となる。

また、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[\begin{align*}
y  &= C_1 e^{-3x} + C_2 e^{2x} + C_3 x e^{2x}
\\ & = C_1 e^{-3x} + \left( C_2 + C_3 x \right) e^{2x}
\end{align*} \]となる。

例題6（虚数解が出てくる場合）

微分方程式\[
\frac{d^3 y}{dx^3} + \frac{d^2 y}{dx^2} + 4 \frac{dy}{dx} + 4 y = 0
\]の基本解と一般解を求めなさい。

解説6

特性方程式は、\[
k^3 + k^2 + 4k + 4 = 0
\]となるので、\[
(k+1)(k^2 + 4) = 0 \]\[
(k+1)(k+2i)(k-2i)= 0
\]とすることで特性方程式の解は \( k = -1 \) と、\( k = 2i \), \( k = -2i \) の2重解となる。

よって、基本解は \( e^{-x} \), \( \cos 2x \), \( \sin 2x \) となる。

また、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[\begin{align*}
y  = C_1 e^{-x} + C_2 \cos 2x + C_3 \sin 2x
\end{align*} \]となる。

６．練習問題

では、定数係数線形微分方程式の基本解と一般解を実際に求める練習をしましょう。

全部で10問用意しています。後ろのほうほど階数が増えていきます。

練習1

微分方程式\[
\frac{dy}{dx} - 10 y = 0
\]の基本解と一般解を求めなさい。

練習2

微分方程式\[
\frac{d^2 y}{dx^2} - 3 \frac{d y}{dx}  = 0
\]の基本解と一般解を求めなさい。

練習3

微分方程式\[
\frac{d^2 y}{dx^2} - 2 \frac{d y}{dx} - 8y = 0
\]の基本解と一般解を求めなさい。

練習4

微分方程式\[
\frac{d^2 y}{dx^2} + 8 \frac{d y}{dx} + 16y = 0
\]の基本解と一般解を求めなさい。

練習5

微分方程式\[
\frac{d^2 y}{dx^2} -4 \frac{d y}{dx} + 13y = 0
\]の基本解と一般解を求めなさい。

練習6

微分方程式\[
\frac{d^3 y}{dx^3} - 2 \frac{d^2 y}{dx^2} - \frac{d^3 y}{dx^3} + 2y = 0
\]の基本解と一般解を求めなさい。

練習7

微分方程式\[
\frac{d^3 y}{dx^3} + 2 \frac{d^2 y}{dx^2} - 15 \frac{dy}{dx} - 36y = 0
\]の基本解と一般解を求めなさい。

練習8

微分方程式\[
\frac{d^3 y}{dx^3} - 9 \frac{d^2 y}{dx^2} + 27 \frac{d^3 y}{dx^3} - 27y = 0
\]の基本解と一般解を求めなさい。

練習9

微分方程式\[
\frac{d^4y}{dx^4} - 2 \frac{d^3 y}{dx^3} + 5 \frac{d^2 y}{dx^2} = 0
\]の基本解と一般解を求めなさい。

練習10

微分方程式\[
\frac{d^4y}{dx^4} + 2 \frac{d^2 y}{dx^2} + y = 0
\]の一般解を求めなさい。

７．練習問題の答え

解答1

特性方程式は、\[
k - 10 = 0
\]となるので、特性方程式の解は \( k = 10 \) となる。

よって、基本解は \( e^{10x} \)となる。

さらに、一般解は任意定数 \( C \) を用いて\[\begin{align*}
y = C_1 e^{10x}
\end{align*} \]となる。

同次式の定数係数の1階線形微分方程式は、特性方程式で一気に求めましょう！

解答2

特性方程式は、\[
k^2 - 3k = 0
\]となるので、\[\begin{align*}
k(k-3) = 0
\end{align*}\]とすることで特性方程式の解は \( k = 0 \), \( k = 3 \) となる。

よって、基本解は \( e^{0} = 1 \), \( e^{3x} \)となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[\begin{align*}
y = C_1 + C_2 e^{3x}
\end{align*} \]となる。

解答3

特性方程式は、\[
k^2 - 2k - 8 = 0
\]となるので、\[\begin{align*}
(k-4)(k+2) = 0
\end{align*}\]とすることで特性方程式の解は \( k = 4 \), \( k = -2 \) となる。

よって、基本解は \( e^{4x} \), \( e^{-2x} \)となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[\begin{align*}
y = C_1 e^{4x} + C_2 e^{-2x}
\end{align*} \]となる。

解答4

特性方程式は、\[
k^2 + 8k + 16 = 0
\]となるので、\[\begin{align*}
(k+4)^2 = 0
\end{align*}\]とすることで特性方程式の解は \( k = -4 \) の2重解となる。

よって、基本解は \( e^{-4x} \), \( xe^{-4x} \)となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[\begin{align*}
y & = C_1 e^{-4x} + C_2 xe^{-4x}
\\ & = (C_1 + C_2 x) e^{-4x}
\end{align*} \]となる。

解答5

特性方程式は、\[
k^2 - 4k + 13 = 0
\]となるので、\[\begin{align*}
k & = \frac{4 \pm \sqrt{16-52}}{2}
\\ & = \frac{4 \pm \sqrt{-36}}{2}
\\ & = \frac{4 \pm 6i}{2}
\\ & = 2 \pm 3i
\end{align*}\]とすることで特性方程式の解は \( k = 2 \pm 3i \) となる。

よって、基本解は \( e^{2x} \cos 3x \), \( e^{2x} \sin 3x \) となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[\begin{align*}
y = C_1 e^{2x} \cos 3x + C_2 e^{2x} \sin 3x
\end{align*} \]となる。

解答6

特性方程式は、\[
k^3 - 2k^2 - k + 2 = 0
\]となるので、\[
(k-1)(k^2 - k - 2) = 0 \]\[
(k-1)(k+1)(k-2) = 0
\]とすることで特性方程式の解は \( k = 1 \), \( k = -1 \), \( k = 2 \) となる。

よって、基本解は \( e^x \), \( e^{-x} \), \( e^{2x} \) となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[\begin{align*}
y = C_1 e^x + C_2 e^{-x} + C_3 e^{2x}
\end{align*} \]となる。

解答7

特性方程式は、\[
k^2 + 2k - 15k - 36 = 0
\]となるので、\[
(t+3)(t^2 - t - 12) = 0 \]\[
(t-4)(t+3)^2 = 0
\]とすることで特性方程式の解は \( k = -3 \) と \( k = 4 \) の2重解となる。

よって、基本解は \( e^{-3x} \), \( e^{4x} \), \( xe^{4x} \) となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[\begin{align*}
y & = C_1 e^{-3x} + C_2 e^{4x} + C_3 x e^{4x}
\\ & = C_1 e^{-3x} + ( C_2 + C_3 x ) e^{4x}
\end{align*} \]となる。

解答8

特性方程式は、\[
k^3 - 9k^2 + 27k - 27 = 0
\]となるので、\[
(k-3)(k^2 - 6k + 9) = 0 \]\[
(k-3)^3 = 0
\]とすることで特性方程式の解は \( k = 3 \) の3重解となる。

よって、基本解は \( e^{3x} \), \( xe^{3x} \), \( x^2 e^{3x} \) となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[\begin{align*}
y & = C_1 e^{3x} + C_2 x e^{3x} + C_3 x^2 e^{3x}
\\ & = (C_1 + C_2 x + C_3 x^2) e^{3x}
\end{align*} \]となる。

解答9

特性方程式は、\[
k^4 - 2k^3 + 5k^2 = 0
\]となるので、\[
k^2 (k^2 - 2k + 5) = 0
\]とすることで特性方程式の解は \( k = 0 \) （2重解）と、\( k = 1 \pm 2i \) となる。

よって、基本解は \( e^0 = 1 \), \( xe^0 = x \), \( e^x \cos 2x \), \( e^x \sin 2x \) となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \), \( C_4 \) を用いて\[\begin{align*}
y & = C_1 + x C_2 + C_3 e^x \cos 2x + C_4 e^x \sin 2x
\\ & = C_1 + x C_2 + e^x ( C_3 \cos 2x + C_4 \sin 2x )
\end{align*} \]となる。

解答10

特性方程式は、\[
k^4 + 2k^2 + 1 = 0
\]となるので、\( t = k^2 \) とすると、\[
t^2 + 2t + 1 = 0
\]となるので、\[
(t+1)^2 = 0
\]となり、\( t = -1 \) の2重解となる。

さらに、\( k^2 = -1 \) を解くと、\( k = \pm i \) となるので、特性方程式の解は \( k = \pm -i \) の2重解となる。

よって、基本解は \( \cos x \), \( \sin x \), \( x \cos x \), \( x \sin x \)となる。

さらに、一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \), \( C_4 \) を用いて\[\begin{align*}
y & = C_1 \cos x + C_2 x \cos x + C_3 \sin x + C_4 x \sin x
\\ & = (C_1 + C_2 x) \cos x + (C_3 + C_4 x) \sin x
\end{align*} \]となる。

８．さいごに

今回は、

• 2階を中心とした同次式の定数係数線形微分方程式の解き方
• 基本解とロンスキアン

について解説していきました。

次回は、少し特殊な形をした同次式の「2階オイラー微分方程式」を定数係数微分方程式の形に持ち込んで解く方法について説明したいと思います。