スポンサードリンク
こんにちは、ももやまです。
今回から何回かにわけて連立微分方程式について書いていきたいと思います。
前回の微分方程式の記事はこちら!
定数変化法を用いて2階の微分方程式を求める方法についてです。
目次
スポンサードリンク
1.連立微分方程式とは
連立微分方程式とは、\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y \\ \frac{dy}{dt} = 2x + y \end{array}\right.
\]のように未知数(今回は \( x \), \( y \))が連立方程式の式の数だけ与えられている微分方程式のことを表します。
連立微分方程式の解き方には、主に
- 高階(2階以上)微分方程式に変換する方法
- 行列の対角化・指数行列を用いる方法
- 微分演算子を用いる方法
- ラプラス変換を用いる方法(初期値が与えられているとき限定)
の4パターンがありますが、今回は「高階微分方程式に変換する方法」についてやっていきたいと思います。
スポンサードリンク
2.高階微分方程式に変形して解く方法
(1) まずは同次の連立微分方程式を解いてみよう!
\( n \) 個の式がある連立微分方程式は、変形を行うことにより \( n \) 階の微分方程式に変形することができます。
まずは同次の連立微分方程式の解き方を、早速例題で確認してみてみましょう。
(※連立微分方程式内に
例題1
連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y \\ \frac{dy}{dt} = 2x + y \end{array}\right.
\]を高階微分方程式に変形することで解いてみましょう。
解説1
1番目の式より、\[
y = \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x \tag{1}
\]が成り立ちますね。さらにこの式の両辺を \( t \) で微分すると、\[
\frac{dy}{dt} = \frac{1}{2} \frac{d^2 x}{dt^2} - \frac{1}{2} \frac{dx}{dt} \tag{2}
\]となるので、(1), (2)を2番目の式に代入すると、\[
\frac{1}{2} \frac{d^2 x}{dt^2} - \frac{1}{2} \frac{dx}{dt} = 2x + \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x \]\[
\frac{1}{2} \frac{d^2 x}{dt^2} - \frac{dx}{dt} - \frac{3}{2} x = 0 \]\[
\frac{d^2 x}{dt^2} - 2 \frac{dx}{dt} - 3 x = 0
\]となり、2階の微分方程式\[
\frac{d^2 x}{dt^2} - 2 \frac{dx}{dt} - 3x = 0
\]が導出できます。
ここで、特性方程式\[
k^2 -2k - 3 = (k-3)(k+1) = 0
\]より、\( k = 3 \), \( k = -1 \) となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
x = C_1 e^{3t} + C_2 e^{-t}
\]と求められます。
あとは、(1)式\[
y = \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x \tag{1}
\]に代入するだけで一般解を求められます。
ここで、\( x \) の両辺を \( t \) で微分すると\[
\frac{dx}{dt} = 3 C_1 e^{3t} - C_2 e^{-t}
\]となるので、\[\begin{align*}
y & = \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x
\\ & = \frac{1}{2} \left( 3 C_1 e^{3t} - C_2 e^{-t} \right) - \frac{1}{2} \left( C_1 e^{3t} + C_2 e^{-t} \right)
\\ & = C_1 e^{3t} - C_2 e^{-t}
\end{align*}\]となります。
よって、\( x \), \( y \) の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
\left\{ \begin{array}{l} x = C_1 e^{3t} + C_2 e^{-t} \\ y = C_1 e^{3t} - C_2 e^{-t} \end{array}\right.
\]と表せます。
公式化
2元の定数係数の連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = ax + by \\ \frac{dy}{dt} = cx + dy \end{array}\right.
\]を2階の微分方程式に直す方法を確認しておきましょう。
1番目の式より、\[
by = \frac{dx}{dt} - ax \]\[
y = \frac{1}{b} \frac{dx}{dt} - \frac{a}{b} x \tag{1}
\]が成り立つ。さらに両辺を \( x \) で微分すると、\[
\frac{dy}{dt} = \frac{1}{b} \frac{d^2 x}{dt^2} - \frac{a}{b} \frac{dx}{dt} \tag{2}
\]となる。
(1), (2)を2番目の式に代入すると、\[
\frac{1}{b} \frac{d^2 x}{dt^2} - \frac{a}{b} \frac{dx}{dt} = cx + d \left( \frac{1}{b} \frac{dx}{dt} - \frac{a}{b} x \right)
\]\[
\frac{1}{b} \frac{d^2 x}{dt^2} - \frac{a}{b} \frac{dx}{dt} = cx + \frac{d}{b} \frac{dx}{dt} - \frac{ad}{b} x \]\[
\frac{d^2 x}{dt^2} - a \frac{dx}{dt} = bc x + d \frac{dx}{dt} - ad x \]\[
\frac{d^2 x}{dt^2} - (a+d) \frac{dx}{dt} + (ad-bc) x = 0
\]となり、2階の微分方程式\[
\frac{d^2 x}{dt^2} - (a+d) \frac{dx}{dt} + (ad-bc) x = 0
\]が導出できます。
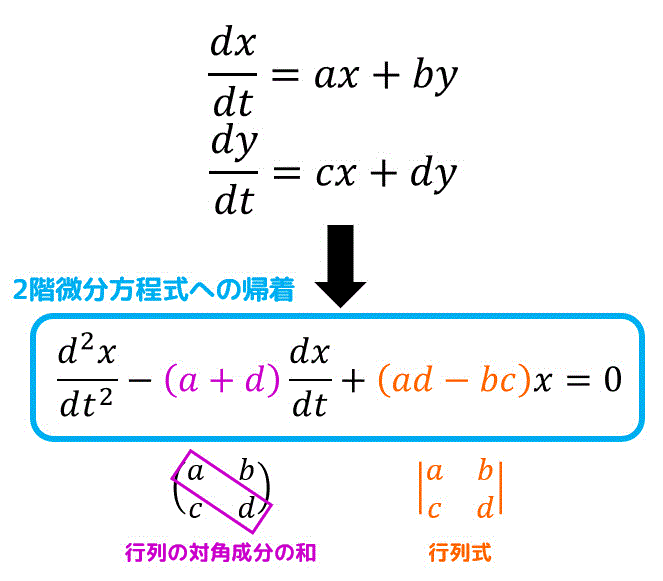
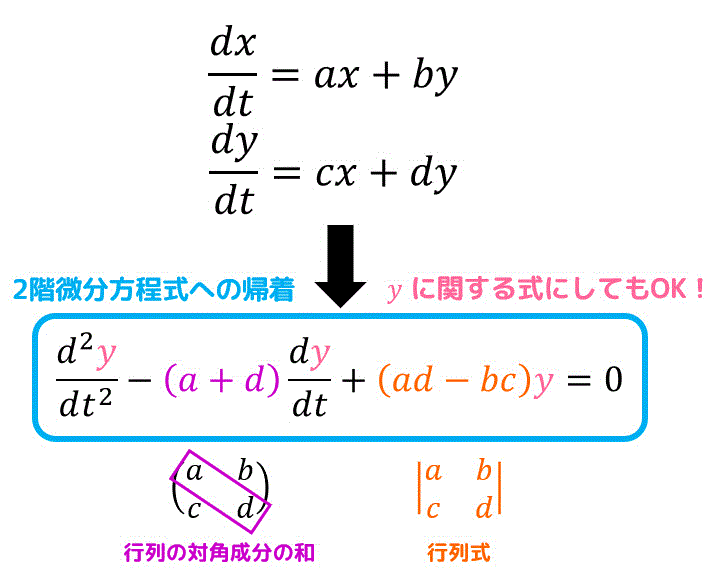
上のように、\( a + d \) は行列の対角成分の和、\( ad - bc \) は行列式(サラスの公式)と考えると頭にいれやすいかと思います。
ケーリーハミルトンの定理に似たような形ですよね。
未知変数が \( x \), \( y \) の2元連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = ax + by \\ \frac{dy}{dt} = cx + dy \end{array}\right.
\]は、2階の定数係数同次微分方程式\[
\frac{d^2 x}{dt^2} - (a+d) \frac{dx}{dt} + (ad-bc) x = 0
\]に変形できる。
あとは、
- 特性方程式を解き、\( x \) の一般解を求める
- 求めた \( x \) を微分し、\( \frac{dx}{dt} \) を求める
- \( x \), \( \frac{dx}{dt} \) を\[
y = \frac{1}{b} \left( \frac{dx}{dt} - a x \right)
\]に代入する。
ことで \( x \), \( y \) の一般解を求めることができる。
なお、2番目の式を\[
x = \frac{1}{c} \left( \frac{dy}{dt} - dy \right)
\]と変形し、さらに両辺を \( x \) で微分し、\[
\frac{dx}{dt} = \frac{1}{c} \left( \frac{d^2y}{dt^2} - d \frac{dy}{dx} \right)
\]とすることで1番目の式に代入し、\[
\frac{1}{c} \left( \frac{d^2y}{dt^2} - d \frac{dy}{dx} \right) = \frac{a}{c} \left( \frac{dy}{dt} - dy \right) + by \]\[
\frac{d^2 y}{dt^2} - (a+d) \frac{dy}{dt} + (ad-bc) y = 0
\]とすることで、\( y \) に関する2階微分方程式としてから解いてももちろんOKです。
(なお、この場合は、求めた \( y \) の一般解と \( \frac{dy}{dx} \) を\[
x = \frac{1}{c} \left( \frac{dy}{dt} - dy \right)
\]に代入することで \( x \) の一般解を求められます。)
なお、練習3では \( y \) に関する2階微分方程式として解いているので、\( y \) から変形したい人はぜひご覧ください。
(2) 非同次の連立微分方程式も解いてみよう
非同次の2元連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = ax + by + f(t) \\ \frac{dy}{dt} = cx + dy + g(t) \end{array}\right.
\]も変形を行うことで、非同次の2階微分方程式に変形をすることができます。
(\( x \), \( y \) に関係ない項(\( f(t) \), \( g(t) \))があるので非同次の連立微分方程式です。)
例題2
連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = x + 2y + e^{2t} \\ \frac{dy}{dt} = 2x + y + 2e^{2t} \end{array}\right.
\]を高階微分方程式に変形することで解いてみましょう。
解説2
例題1の連立微分方程式に \( e^t \) という関係ない項を入れただけの問題です。
ですが、\( x \), \( y \) に関係ない項があっても基本的にはやり方は同じです。
1番目の式より、\[
y = \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x - \frac{1}{2} e^{2t} \tag{1}
\]が成り立ちますね。さらにこの式の両辺を \( t \) で微分すると、\[
\frac{dy}{dt} = \frac{1}{2} \frac{d^2 x}{dt^2} - \frac{1}{2} \frac{dx}{dt} - e^{2t} \tag{2}
\]となるので、(1), (2)を2番目の式に代入すると、\[
\frac{1}{2} \frac{d^2 x}{dt^2} - \frac{1}{2} \frac{dx}{dt} - e^{2t} = 2x + \left( \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x - \frac{1}{2} e^{2t} \right) + 2 e^{2t} \]\[
\frac{1}{2} \frac{d^2 x}{dt^2} - \frac{dx}{dt} - \frac{3}{2} x = \frac{5}{2} e^{2t}\]\[
\frac{d^2 x}{dt^2} - 2 \frac{dx}{dt} - 3 x = 5 e^{2t}
\]となり、2階の微分方程式\[
\frac{d^2 x}{dt^2} - 2 \frac{dx}{dt} - 3x = 5 e^{2t}
\]が導出できます。
ここからは、2階の定数係数非同次線形微分方程式の解き方の復習です。
まずは、同次方程式\[
\frac{d^2 x}{dt^2} - 2 \frac{dx}{dt} - 3x = 0
\]の一般解を求めましょう。
特性方程式\[
k^2 -2k - 3 = (k-3)(k+1) = 0
\]より、\( k = 3 \), \( k = -1 \) となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
x = C_1 e^{3t} + C_2 e^{-t}
\]と求められます。
特殊解が \( e^{2t} \) の形と予想できるので未定係数法で解いちゃいましょう。
ここで、特殊解を\[
x = a e^{2t}
\]とおくと、\[
\frac{dx}{dt} = 2a e^{2t}, \ \ \ \frac{d^2 x}{dt^2} = 4a e^{2t}
\]なので、\[\begin{align*}
& \frac{d^2 x}{dt^2} - 2 \frac{dx}{dt} - 3x
\\ = \ & 4a e^{2t} - 4a e^{2t} - 3a e^{2t}
\\ = \ & 5a e^{2t}
\end{align*}\]となるので、\( a = - 5/3 \) となり、特殊解の1つが\[
y = - \frac{5}{3} e^{2t}
\]となるので、\( x \) に関する一般解が\[
x = C_1 e^{3t} + C_2 e^{-t} - \frac{5}{3} e^{2t}
\]と求まります。
あとは、(1)式\[
y = \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x - \frac{1}{2} e^{2t} \tag{1}
\]に代入するだけで一般解を求められます。
ここで、\( x \) の両辺を \( t \) で微分すると\[
\frac{dx}{dt} = 3 C_1 e^{3t} - C_2 e^{-t} - \frac{10}{3} e^{2t}
\]となるので、\[\begin{align*}
y & = \frac{1}{2} \frac{dx}{dt} - \frac{1}{2} x - \frac{1}{2} e^{2t}
\\ & = \frac{1}{2} \left( 3 C_1 e^{3t} - C_2 e^{-t} - \frac{10}{3} e^{2t} \right) - \frac{1}{2} \left( C_1 e^{3t} + C_2 e^{-t} - \frac{5}{3} e^{2t} \right) - \frac{1}{2} e^{2t}
\\ & = C_1 e^{3t} - C_2 e^{-t} - \frac{4}{3} e^{2t}
\end{align*}\]となります。
よって、\( x \), \( y \) の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
\left\{ \begin{array}{l} \frac{dx}{dt} = C_1 e^{3t} + C_2 e^{-t} - \frac{5}{3} e^{2t} \\ \frac{dy}{dt} = C_1 e^{3t} - C_2 e^{-t} - \frac{4}{3}e^{2t} \end{array}\right.
\]と表せます。
公式化
2元の定数係数の連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = ax + by + f(t) \\ \frac{dy}{dt} = cx + dy + g(t) \end{array}\right.
\]を2階の微分方程式に直す方法を確認しておきましょう。
1番目の式より、\[
by = \frac{dx}{dt} - ax \]\[
y = \frac{1}{b} \frac{dx}{dt} - \frac{a}{b} x - \frac{1}{b} f(t) \tag{1}
\]が成り立つ。さらに両辺を \( x \) で微分すると、\[
\frac{dy}{dt} = \frac{1}{b} \frac{d^2 x}{dt^2} - \frac{a}{b} \frac{dx}{dt} - \frac{1}{b} f'(t) \tag{2}
\]となる。
(1), (2)を2番目の式に代入すると、\[
\frac{1}{b} \frac{d^2 x}{dt^2} - \frac{a}{b} \frac{dx}{dt} - \frac{1}{b} f'(t) = cx + d \left( \frac{1}{b} \frac{dx}{dt} - \frac{a}{b} x - \frac{1}{b} f(t) \right) + g(t)
\]\[
\frac{1}{b} \frac{d^2 x}{dt^2} - \frac{a}{b} \frac{dx}{dt} - \frac{1}{b} f'(t) = cx + \frac{d}{b} \frac{dx}{dt} - \frac{ad}{b} x - \frac{d}{b} f(t) + g(t) \]\[
\frac{d^2 x}{dt^2} - a \frac{dx}{dt} - f'(t) = bc x + d \frac{dx}{dt} - ad x - d \ f(t) + b \ g(t) \]\[
\frac{d^2 x}{dt^2} - (a+d) \frac{dx}{dt} + (ad-bc) x = f'(t) - d \ f(t) + b \ g(t)
\]となり、2階の微分方程式\[
\frac{d^2 x}{dt^2} - (a+d) \frac{dx}{dt} + (ad-bc) x = f'(t) - d \ f(t) + b \ g(t)
\]が導出できます。

公式とはいっても、同次2階微分方程式の公式の右辺側の 0 が \( f'(t) - d \ f(t) + b \ g(t) \) に変わるだけです。
未知変数が \( x \), \( y \) の非同次2元連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = ax + by + f(t) \\ \frac{dy}{dt} = cx + dy +g(t) \end{array}\right.
\]は、2階の定数係数同次微分方程式\[
\frac{d^2 x}{dt^2} - (a+d) \frac{dx}{dt} + (ad-bc) x = f'(t) - d \ f(t) + b \ g(t)
\]に変形できる。
あとは、
- 特性方程式を解き、\( x \) の一般解を求める
- 求めた \( x \) を微分し、\( \frac{dx}{dt} \) を求める
- \( x \), \( \frac{dx}{dt} \) を\[
y = \frac{1}{b} \left( \frac{dx}{dt} - ax - f(t) \right)
\]に代入する
ことで \( x \), \( y \) の一般解を求めることができる。
なお、2番目の式を\[
x = \frac{1}{c} \left( \frac{dy}{dt} - dy - g(t) \right)
\]と変形し、さらに両辺を \( x \) で微分し、\[
\frac{dx}{dt} = \frac{1}{c} \left( \frac{d^2y}{dt^2} - d \frac{dy}{dx} - g' (t) \right)
\]とすることで1番目の式に代入し、\[
\frac{1}{c} \left( \frac{d^2y}{dt^2} - d \frac{dy}{dx} - g' (t) \right) = \frac{a}{c} \left( \frac{dy}{dt} - dy - g(t) \right) + by + f(t) \]\[
\frac{d^2 y}{dt^2} - (a+d) \frac{dy}{dt} + (ad-bc) y = g'(t) - a \ g(t) + c \ f(t)
\]とすることで、\( y \) に関する2階微分方程式としてから解いてももちろんOKです。
(この場合は、求めた \( y \) の一般解と \( \frac{dy}{dx} \) を\[
x = \frac{1}{c} \left( \frac{dy}{dt} - dy - g(t) \right)
\]に代入することで \( x \) の一般解を求められます。)

同次の場合は、\( x \) から変形しても \( y \) から変形しても公式自体は大きく変わらないのですが、非同次になると右辺部分がかなり変化するので気を付けましょう。
スポンサードリンク
3.練習問題
では、4問ほど練習してみましょう。
3問が同次の連立微分方程式、1問が非同次の連立微分方程式です。
練習1
つぎの連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = 8x+2y \\ \frac{dy}{dt} = -6x+y \end{array}\right.
\]の一般解を求めなさい。
練習2
つぎの連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = 5x - 2y \\ \frac{dy}{dt} = 2x + y \end{array}\right.
\]の一般解を求めなさい。
練習3
つぎの非同次の連立微分方程式\[
\left\{ \begin{array}{l} \frac{dx}{dt} = -3x+2y+2t+1 \\ \frac{dy}{dt} = -4x+3y+5t \end{array}\right.
\]の一般解を求めなさい。
4.練習問題の答え
解答1
1番目の式より、\[
y = \frac{1}{2} \frac{dx}{dt} - 4 x \tag{1}
\]が成立する。
さらにこの式の両辺を \( t \) で微分すると、\[
\frac{dy}{dt} = \frac{1}{2} \frac{d^2 x}{dt^2} - 4 \frac{dx}{dt} \tag{2}
\]となるので、(1), (2)を2番目の式に代入すると、\[
\frac{1}{2} \frac{d^2 x}{dt^2} - 4 \frac{dx}{dt} = -6x + \left( \frac{1}{2} \frac{dx}{dt} - 4 x \right) \]\[
\frac{1}{2} \frac{d^2 x}{dt^2} - \frac{9}{2} \frac{dx}{dt} - 10x = 0 \]\[
\frac{d^2 x}{dt^2} - 9 \frac{dx}{dt} + 20 x = 0
\]となり、2階の微分方程式\[
\frac{d^2 x}{dt^2} - 9 \frac{dx}{dt} + 20x = 0
\]が導出できる。
ここで、特性方程式\[
k^2 -9k +20 = (k-4)(k-5) = 0
\]より、\( k = 4 \), \( k = 5 \) となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
x = C_1 e^{4t} + C_2 e^{5t}
\]と求められる。
あとは、(1)式\[
y = \frac{1}{2} \frac{dx}{dt} - 4 x \tag{1}
\]に代入するだけでOK。
ここで、\( x \) の両辺を \( t \) で微分すると\[
\frac{dx}{dt} = 4 C_1 e^{4t} + 5 C_2 e^{5t}
\]となるので、\[\begin{align*}
y & = \frac{1}{2} \frac{dx}{dt} - 4 x
\\ & = \frac{1}{2} \left( 4 C_1 e^{4t} + 5 C_2 e^{5t} \right) - 4 \left( C_1 e^{4t} + C_2 e^{5t} \right)
\\ & = - 2 C_1 e^{4t} - \frac{3}{2} C_2 e^{5t}
\end{align*}\]となる。
よって、\( x \), \( y \) の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
\left\{ \begin{array}{l} x = C_1 e^{4t} + C_2 e^{5t} \\ y = -2 C_1 e^{4t} - \frac{3}{2} C_2 e^{5t} \end{array}\right.
\]と表せ、これが答えとなる。
解答2
1番目の式より、\[
y = - \frac{1}{2} \frac{dx}{dt} + \frac{5}{2} x \tag{1}
\]が成立する。
さらにこの式の両辺を \( t \) で微分すると、\[
\frac{dy}{dt} = - \frac{1}{2} \frac{d^2 x}{dt^2} + \frac{5}{2} \frac{dx}{dt} \tag{2}
\]となるので、(1), (2)を2番目の式に代入すると、\[
- \frac{1}{2} \frac{d^2 x}{dt^2} + \frac{5}{2} \frac{dx}{dt} = 2x + \left( - \frac{1}{2} \frac{dx}{dt} + \frac{5}{2} x \right) \]\[
- \frac{1}{2} \frac{d^2 x}{dt^2} + 3 \frac{dx}{dt} - \frac{9}{2} x = 0 \]\[
\frac{d^2 x}{dt^2} - 6 \frac{dx}{dt} + 9 x = 0
\]となり、2階の微分方程式\[
\frac{d^2 x}{dt^2} - 6 \frac{dx}{dt} + 9x = 0
\]が導出できる。
ここで、特性方程式\[
k^2 -6k + 9 = (k-3)^2 = 0
\]より、\( k = 3 \) の2重解となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
x = C_1 e^{3t} + C_2 t e^{3t}
\]と求められる。
あとは、(1)式\[
y = - \frac{1}{2} \frac{dx}{dt} + \frac{5}{2} x \tag{1}
\]に代入するだけでOK。
ここで、\( x \) の両辺を \( t \) で微分すると\[
\frac{dx}{dt} = 3 C_1 e^{3t} + C_2 e^{3t} + 3 C_2 te^{3t}
\]となるので、\[\begin{align*}
y & = - \frac{1}{2} \frac{dx}{dt} + \frac{5}{2} x
\\ & = - \frac{1}{2} \left( 3 C_1 e^{3t} + C_2 e^{3t} + 3 C_2 te^{3t} \right) + \frac{5}{2} \left( C_1 e^{3t} + C_2 t e^{3t} \right)
\\ & = C_1 e^{3t} - \frac{1}{2} C_2 e^{3t} + C_2 t e^{3t}
\end{align*}\]となる。
よって、\( x \), \( y \) の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
\left\{ \begin{array}{l} x = C_1 e^{3t} + C_2 t e^{3t} \\ y = C_1 e^{3t} - \frac{1}{2} C_2 e^{3t} + C_2 t e^{3t} \end{array}\right.
\]と表せ、これが答えとなる。
解答3
1番目の式より、\[
y = \frac{1}{2} \frac{dx}{dt} + \frac{3}{2} x - t - \frac{1}{2} \tag{1}
\]が成立する。
さらにこの式の両辺を \( t \) で微分すると、\[
\frac{dy}{dt} = \frac{1}{2} \frac{d^2 x}{dt^2} + \frac{3}{2} \frac{dx}{dt} - 1 \tag{2}
\]となるので、(1), (2)を2番目の式に代入すると、\[
\frac{1}{2} \frac{d^2 x}{dt^2} + \frac{3}{2} \frac{dx}{dt} - 1 = -4x + 3 \left( \frac{1}{2} \frac{dx}{dt} + \frac{3}{2} x - t - \frac{1}{2} \right) + 5t \]\[
\frac{1}{2} \frac{d^2 x}{dt^2} - \frac{1}{2} x = 2t + \frac{1}{2}
\frac{d^2 x}{dt^2} - x = 4t - 1
\]となり、2階の非同次微分方程式\[
\frac{d^2 x}{dt^2} - x = 4t - 1
\]が導出できる。
一般解を出すためにまずは同次方程式\[
\frac{d^2 x}{dt^2} - x = 0
\]の一般解を求める。
ここで、特性方程式\[
k^2 - 1 = 0
\]より、\( k = 1 \), \( k = -1 \) となるので、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
x = C_1 e^{t} + C_2 e^{-t}
\]と求められる。
右辺が \( 4t - 1 \) なので、特殊解を\[
x = at + b
\]とおくと、\[
\frac{dx}{dt} = a, \ \ \ \frac{d^2 x}{dt^2} = 0
\]なので、\[\begin{align*}
& \frac{d^2 x}{dt^2} - x
\\ = \ & - (at + b)
\\ = \ & -at - b
\\ = \ & 4t - 1
\end{align*}\]となるので、\[
\left\{\begin{array}{l} -a = 4 \\[4px] -b = -1 \end{array}\right.
\qquad \therefore \quad \left\{\begin{array}{l} \displaystyle a = -4 \\ \displaystyle b = 1 \end{array}\right.
\]となり、特殊解の1つが\[
y = -4t + 1
\]となるので、\( x \) に関する一般解が\[
x = C_1 e^{t} + C_2 e^{-t} - 4t + 1
\]と求まります。
あとは、(1)式\[
y = \frac{1}{2} \frac{dx}{dt} + \frac{3}{2} x - t - \frac{1}{2} \tag{1}
\]に代入するだけでOK。
ここで、\( x \) の両辺を \( t \) で微分すると\[
\frac{dx}{dt} = C_1 e^{t} - C_2 e^{-t} -4
\]となるので、\[\begin{align*}
y & = \frac{1}{2} \frac{dx}{dt} + \frac{3}{2} x - t - \frac{1}{2}
\\ & = \frac{1}{2} \left( C_1 e^{t} - C_2 e^{-t} -4 \right) + \frac{3}{2} \left( C_1 e^{t} + C_2 e^{-t} - 4t + 1 \right) - t - \frac{1}{2}
\\ & = 2 C_1 e^{3t} + C_2 e^{3t} - 7t - 1
\end{align*}\]となる。
よって、\( x \), \( y \) の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
\left\{ \begin{array}{l} x = C_1 e^{t} - C_2 e^{-t} -4 \\ y = 2 C_1 e^{3t} + C_2 e^{3t} - 7t - 1 \end{array}\right.
\]と表せ、これが答えとなる。
5.さいごに
今回は、2元の連立微分方程式を2階の連立微分方程式に解く方法について説明しました。
次回は、行列の対角化を用いて連立微分方程式を解く方法についてまとめていきたいと思います。
関連広告・スポンサードリンク