うさぎでもわかる離散数学　第5羽　順序関係とハッセ図・重要な8つの性質

こんにちは、ももうさです。

今回は、順序関係とハッセ図についてお勉強していきましょう！

今回学ぶのは、これ！

• 順序関係
• ハッセ図
• 順序関係の重要な性質
  • 上界
  • 下界
  • 最大元
  • 最小元
  • 極大元
  • 極小元
  • 上限（最小上界）
  • 下限（最大下界）

※ 2025/5/28　大幅リニューアルしました！

1. 全順序集合　全順序って何？

離散数学で登場する「全順序」と「半順序」という概念。

難しそうな名前ですが、実は身の回りにたくさんの例があり、私たちの日常感覚とも密接に結びついています。

この章では、まず直感的にわかりやすい「全順序」から説明し、一般的な「半順序」について解説していきます。

(1) 簡単にいうと…。

全順序集合とは、「すべての要素を一列に並べられる」という性質を持った集合のことです。

つまり、集合の中からどんな2つの要素を選んでも、必ず「どちらが先か後か」「どちらが大きいか小さいか」が明確に決まります。

例えば、3, 2, 11, 5, 7 という数字の集合を考えてみましょう。これらを小さい順に並べると、下のように一直線上に並べることができます。

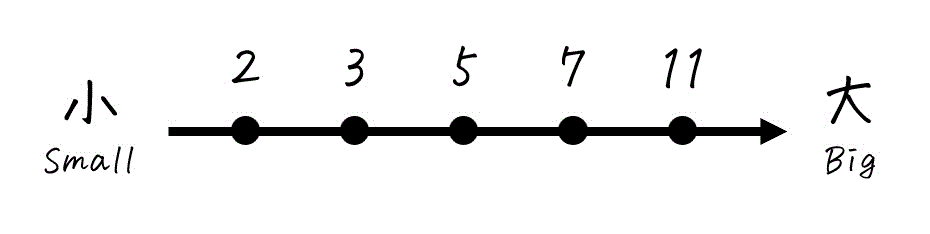
2 → 3 → 5 → 7 → 11

この数列中のどの2つの数字を取り上げても、必ずどちらが大きいか判断できますね。例えば：

• 5と3 → 5が大きい
• 7と11 → 11が大きい

このように、集合内のどの2つの要素も比較可能で、順序関係が明確に決まる集合を「全順序集合」と呼びます。

また、全順序集合で成り立つ関係（どの2つの要素も比較可能で、順序関係が明確に決まる関係）を「全順序」または「全順序関係」と呼びます。

身近な例としては：

• クラスの出席番号
• 身長の高さ
• テストの点数
• 年齢

これらはすべて、「どちらが大きい／小さい」が明確に決まる全順序の例です。

(2) 全順序集合の数学的定義

ただ、いきなり定義だけを見ても腑に落ちるのは難しいと思います。

これらの性質について、もう少し詳しく見ていきましょう。

反射性．

反射性とは、「どの要素も自分自身と比較したとき、必ず自分は自分以上である」という性質です。

数学的に書くと、「どの要素も自分自身 \( x \) と比較したとき、\( x \leqq x \) が成立する」となります。

反射性は、次に説明する反対称性と合わせて「自分自身と比べる関係を定義するため」 に使われます。

反対称性．

反対称性とは、「2つの要素が互いに順序関係を持つなら、それらは同じものである」という性質です。

数学的に書くと「もし \( x \leqq y \) かつ \( y \leqq x \) ならば、必ず \( x = y \) である」となります。

言い換えると、同じ2つの要素が順序関係で

• \( x \) の値は \( y \) 以上である
• \( y \) の値は \( x \) 以上である

と同時に言えるのは、それらが同じものであるときだけだということです。

全順序関係では、この反対称性を使って「ある2つの要素が『小さい』かつ『大きい』とき」に、その2つの順序が完全に等しいことを定義しています。

言い換えると、異なる要素同士が「同じ値である」ということは許されず、必ず大小関係が定義されると言えます。

表．\( x \leqq y \) と \( y \leqq x \) の成立／不成立とその関係

◯ … 成立する
× … 成立しない

推移性．

推移性とは、「順序関係が三段論法的に連鎖する」という性質です。

数学的に書くと、「\( x \leqq y \) かつ \( y \leqq z \) が成り立つとき、必ず \( x \leqq z \) が成立する」となります。

例えば、Aさんの身長がBさんより高く、BさんがCさんより高ければ、必然的にAさんはCさんより高くなります。もし、この性質がないと順序関係に矛盾が生じてしまいます^[1]もし、Aさんの身長がBさんより高く、BさんがCさんより高いのに、AさんはCさんより身長が低いとなると、順序関係がおかしなことになりますよね。。

完全性．

完全性は全順序関係の最も重要な特徴で、「どんな2つの要素も必ず比較可能である」という性質です。

数学的に書くと「（集合内の）どの2つの要素に対しても、\( x \leqq y \)、\( y \leqq x \) のどちらか一方、あるいは両方が成り立つ」という性質です。

これこそが全順序の本質で、集合内のすべての要素が一列に並べられることを保証します。

言い換えると、集合の中のどんな2つの要素を取ってきても、必ずどちらが「小さい」、「大きい」、あるいは「等しい」と結論を下すことができるのです。

表．\( x \leqq y \) と \( y \leqq x \) の成立／不成立とその関係

◯ … 成立する
× … 成立しない

2. 半順序集合　半順序って何？

(1) 簡単にいうと…。

半順序は、「すべての要素に順番をつけるわけではなく、一部の要素の間だけ順序が決まっている」というイメージの順序関係です。

全順序集合では、「どんな2つの要素を選んでも、必ず順序が決まる（比較できる）」という性質がありましたね。

それに対して、半順序集合では「順序が決まる要素同士もあれば、順序が決まらない要素同士もある」という特徴があります。

つまり、集合の中から2つの要素を選んだとき、必ずしも「どちらが先か後か」「どちらが大きいか小さいか」が決まるとは限らないというのが、全順序との大きな違いです。

実際に、例を挙げて考えてみましょう。

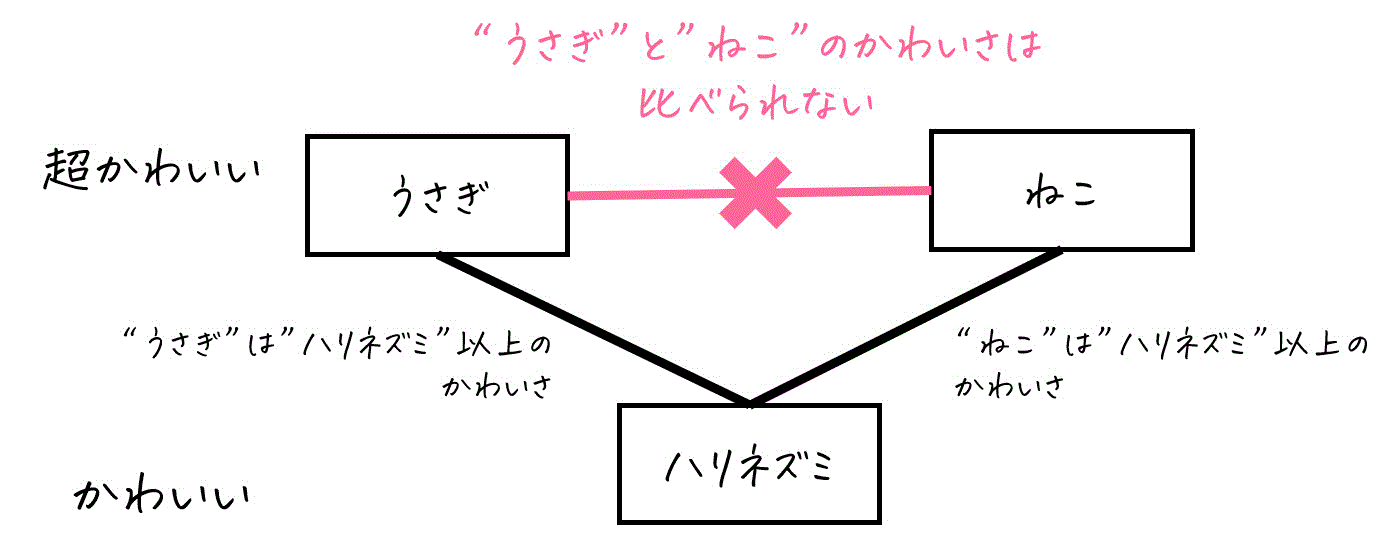
たとえば、「うさぎ、ねこ、ハリネズミ」という3匹の動物について、「かわいさ（ももうさの独断と偏見による）」という基準で順序関係を考えてみます。

• 「うさぎ」は「ハリネズミ」以上のかわいさ
• 「ねこ」は「ハリネズミ」以上のかわいさ

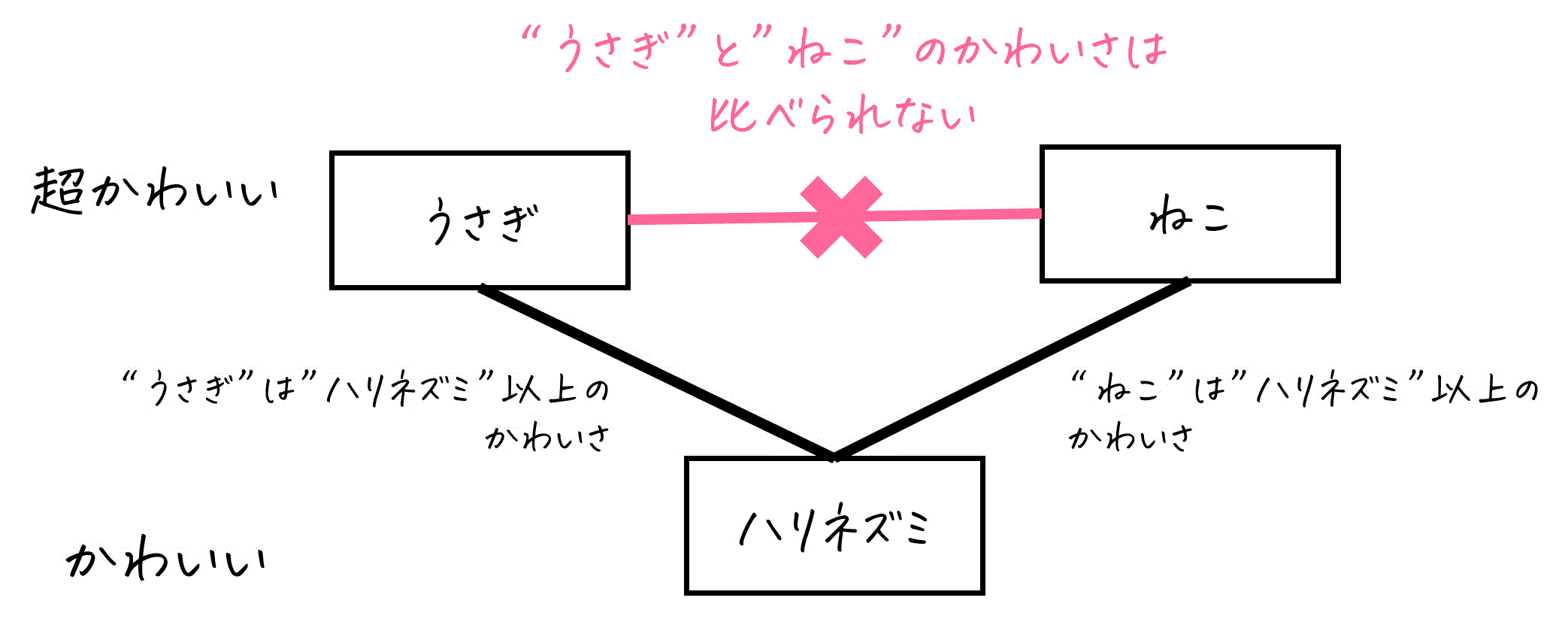
この場合、うさぎとねこを比べる情報がないので、どちらがよりかわいいかは決められません。つまり、「うさぎとねこ」は比較できない関係にあります。

このように、すべての要素同士を比較できるわけではないけれど、一部の要素同士については順序関係が成り立つという場合、これを「半順序」と呼びます。

(2) 半順序集合の数学的定義

全順序との違いは、「完全性が成り立たなくてもOK」ということです。つまり、下の表の青色部分の関係を許すのが半順序となります。

表．\( x \leqq y \) と \( y \leqq x \) の成立／不成立とその関係

◯ … 成立する
× … 成立しない

3. ハッセ図

(1) ハッセ図とは

ハッセ図は、半順序集合の構造を視覚的にわかりやすく表した図のことです。

半順序では、すべての要素が順序づけられているとは限らないため、一直線上で関係を表現することはできません。

かといって、下のように文字だけで順序関係を書くのもわかりにくいですよね。

【私がかわいいと思う動物のかわいさ比較（ももうさの偏見）】

• 「いぬ」は「しろくま」よりかわいい
• 「ぺんぎん」は「いぬ」よりかわいい
• 「あざらし」は「いぬ」よりかわいい
• 「ハリネズミ」は「ぺんぎん」よりかわいい
• 「ハリネズミ」は「あざらし」よりかわいい
• 「うさぎ」は「ハリネズミ」よりかわいい
• 「ねこ」は「ハリネズミ」よりかわいい

そこで、どの要素がどれより上（あるいは下）にあるかを図で示すことで、構造を直感的に理解しやすくするのがハッセ図の役割です。

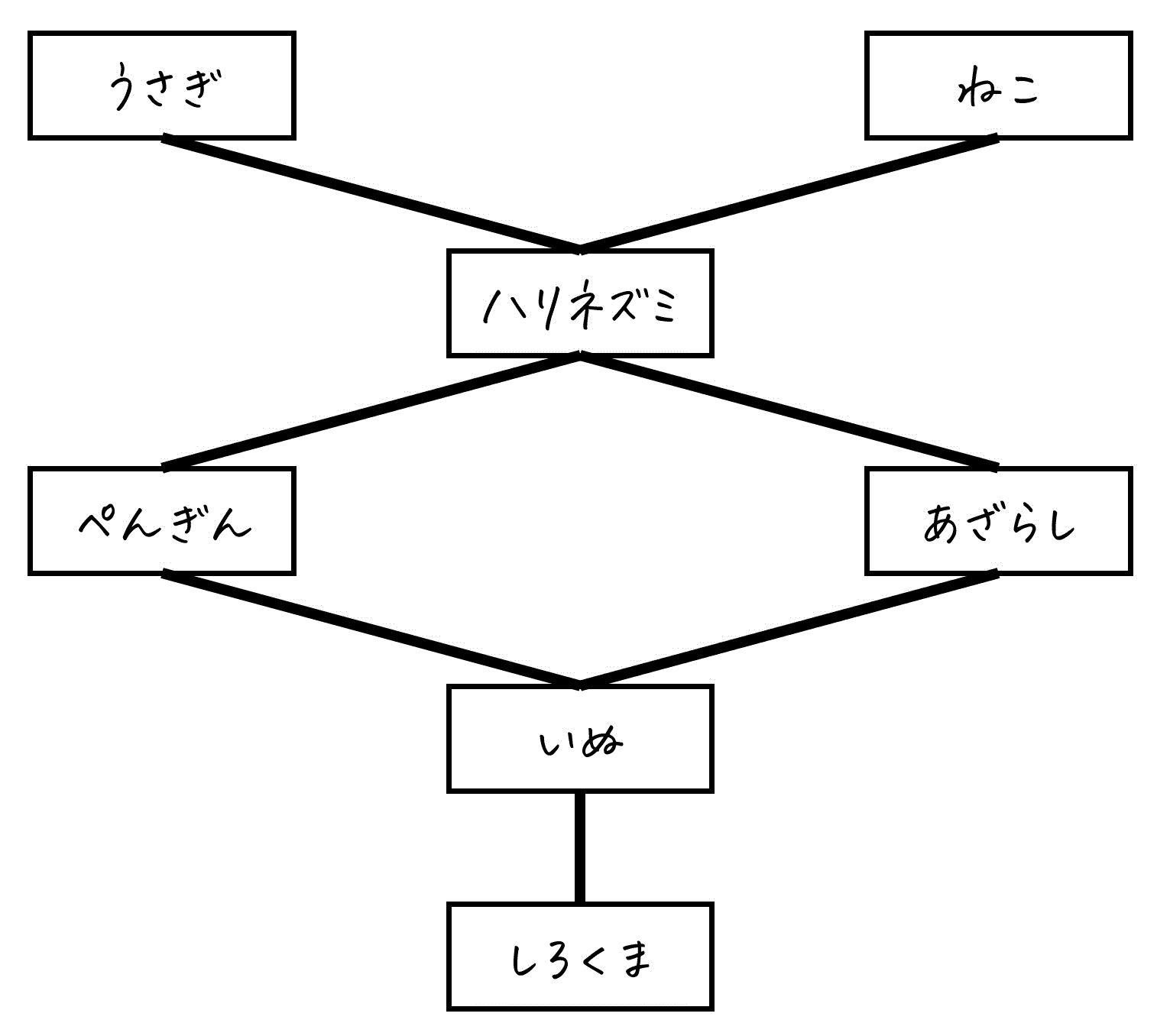
(2) ハッセ図の読み方

ルール1．要素と順序関係

点（ノード）：集合の要素を表します
線（エッジ）：要素間の直接的な順序関係を表します

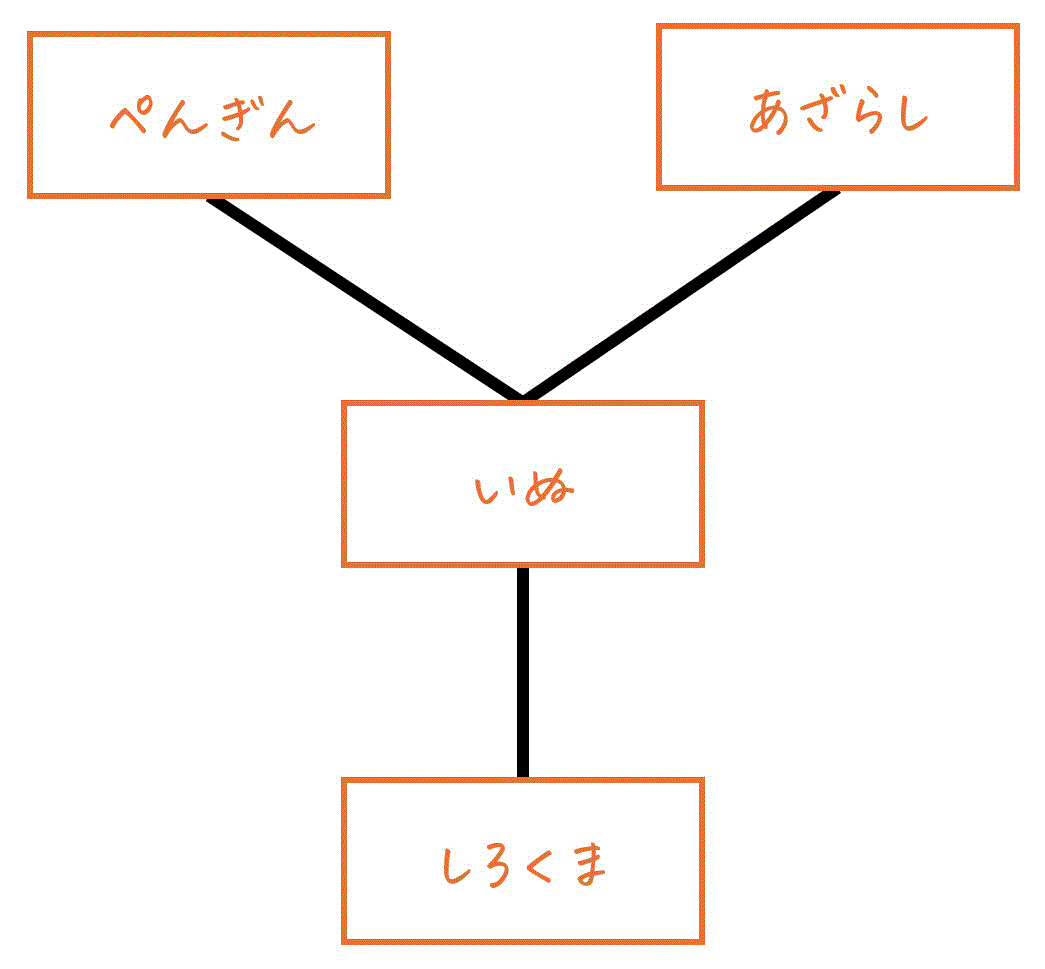
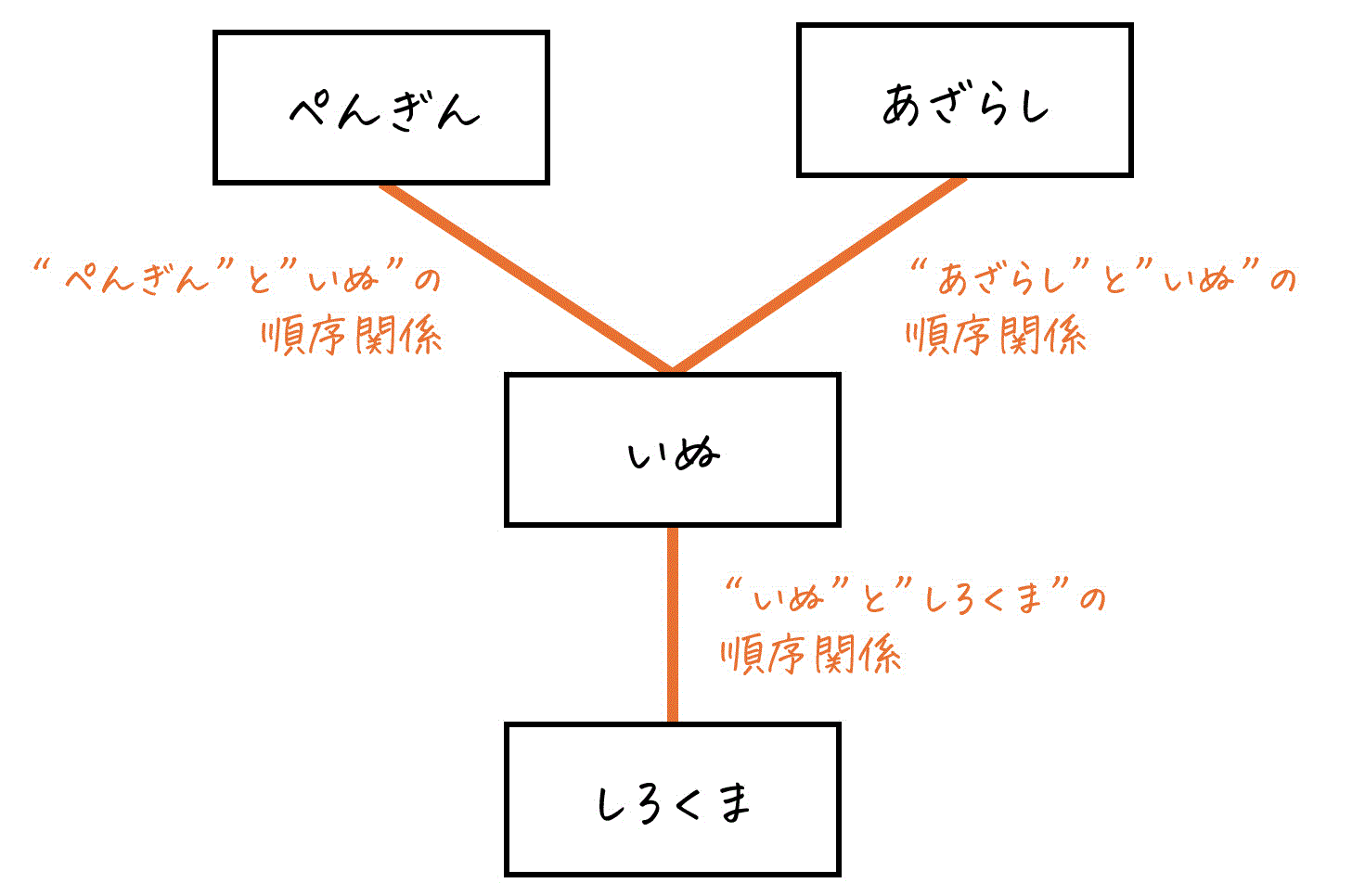
例えば、次の図では「ぺんぎん」「あざらし」「いぬ」「しろくま」の4つの要素があることが示されています。

この図では、以下の4つの要素があります： -

• ぺんぎん
• いぬ
• あざらし
• しろくま

また、線に着目すると次の要素同士で順序関係があることがわかります。

• 「ぺんぎん」と「いぬ」
• 「あざらし」と「いぬ」
• 「いぬ」と「しろくま」

ルール2．上下関係で順序を読む

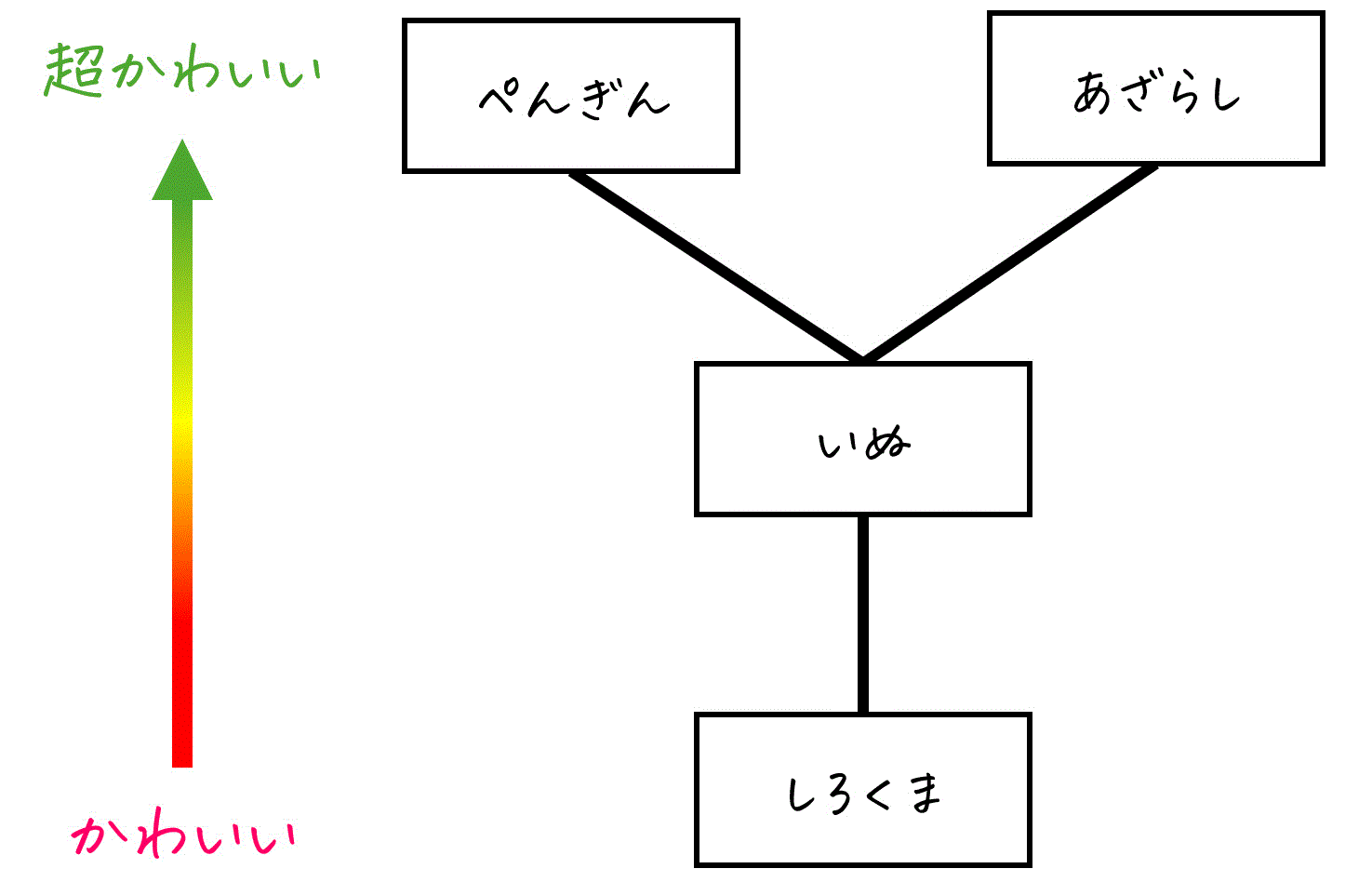
ハッセ図では、下から上に向かって順序関係を読みます。

• 下にある要素
  → より「小さい」（この例では「かわいさが低い」）
• 上にある要素
  → より「大きい」（この例では「かわいさが高い」）
• 線で直接つながった要素同士に順序関係がある

(1) 直接的な関係の読み取り

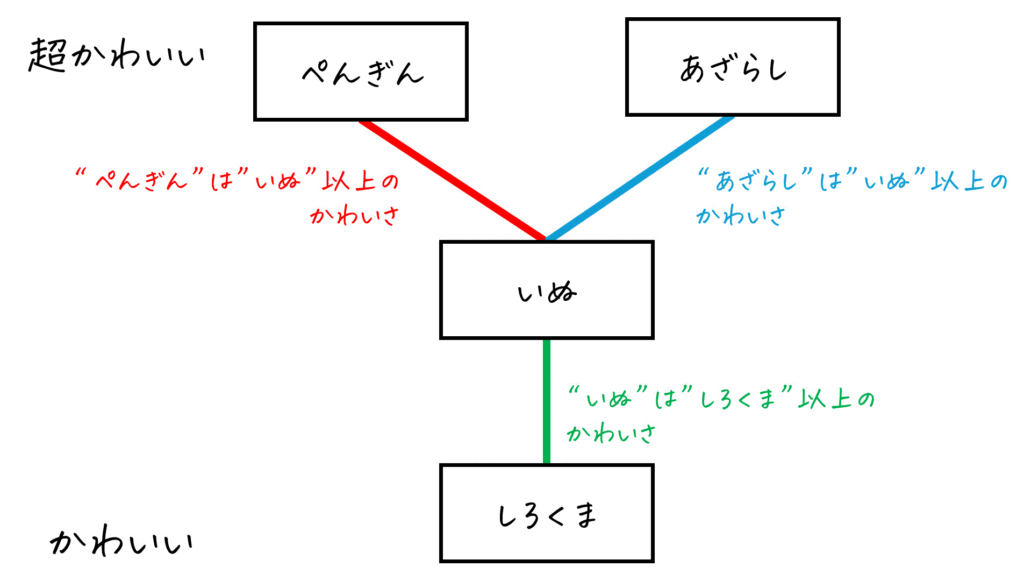
線で直接つながっている要素を見てみましょう。

• 「ぺんぎん」と「いぬ」の線
  → ぺんぎん \( \sqsubseteq \) いぬ、「いぬ」のかわいさは「ぺんぎん」以上
• 「あざらし」と「いぬ」の線
  → あざらし \( \sqsubseteq \) いぬ、「いぬ」のかわいさは「あざらし」以上
• 「いぬ」と「しろくま」の線
  → しろくま \( \sqsubseteq \) いぬ、「しろくま」のかわいさは「いぬ」以上

たとえば、以下の、図の「いぬ」と「しろくま」に着目すると、この2つは線で直接つながっていて、「いぬ」が「しろくま」より上にありますね。

このとき、「しろくま \( \sqsubseteq \) いぬ」、つまり「いぬのかわいさはしろくま」という関係を読み取ることができます。

また、「しろくま」と「ぺんぎん」は、直接つながっていませんが、「しろくま」 → 「いぬ」 → 「ぺんぎん」 のように上方向にたどれることができます。

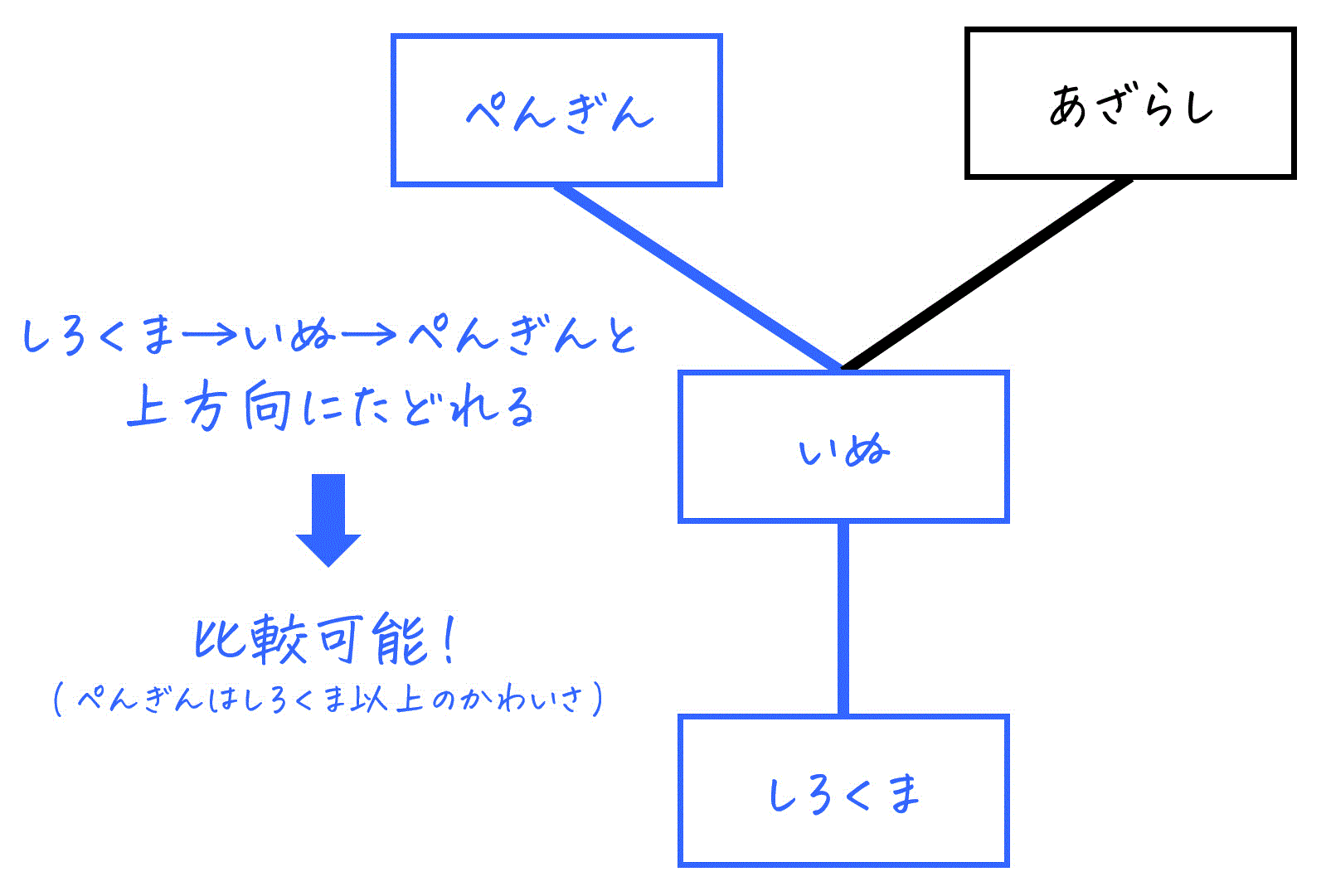
この場合、2つの要素間に推移的な順序関係があるとみなします。

つまり、「しろくま \( \sqsubseteq \) ぺんぎん」、言い換えると「あざらしは、いぬよりもかわいい」という関係を読み取ることができます。

一方で、「ぺんぎん」と「あざらし」のように、上方向にも下方向にも一方通行で辿れない要素同士は、順序関係が定まっていない（比較できない）ことを意味します。

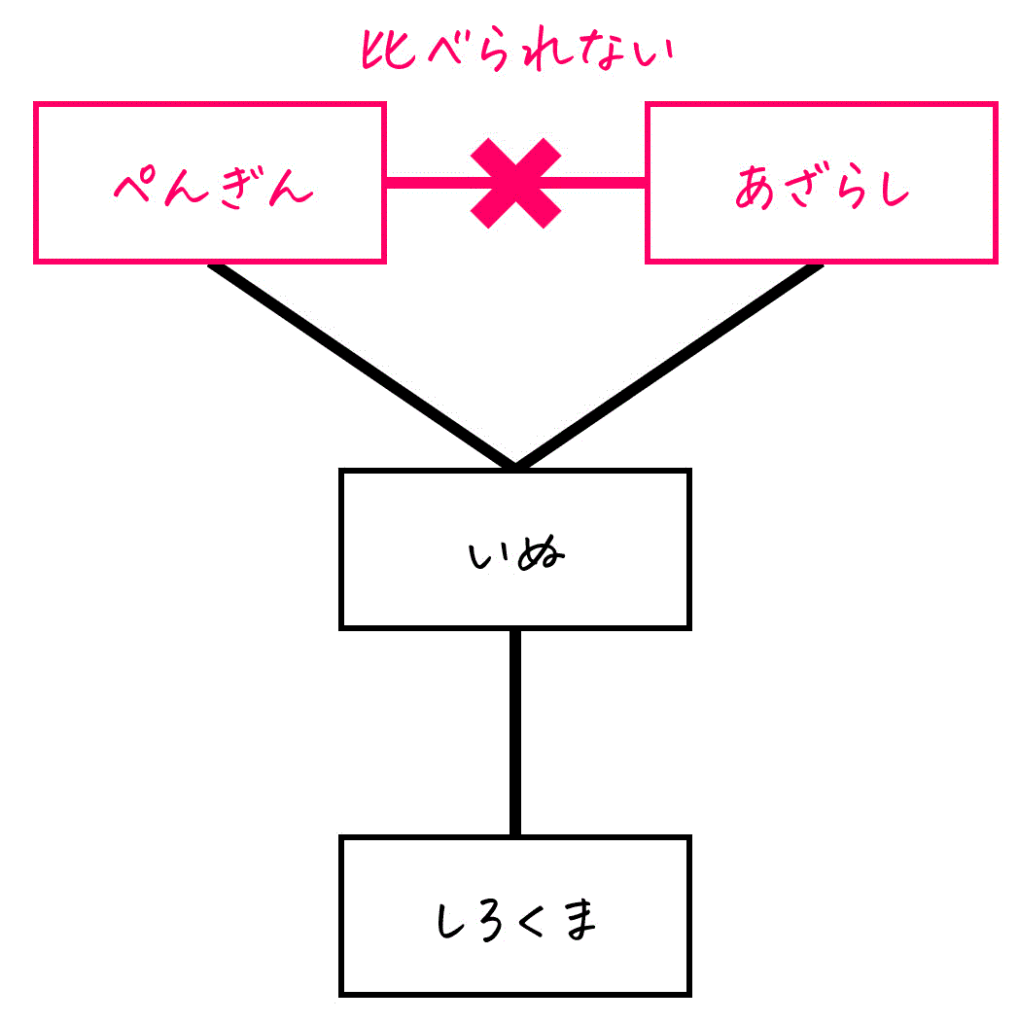
このようなペアは、「どちらが大きいか（かわいいか）」を判断できないため、順序が存在しないとみなします。

(3) 例題で確認

では、実際にハッセ図の読み取りについて、例題で確認していきましょう。

例題1

以下のハッセ図は、筆者ももうさ（私）が「かわいい！」と思う動物7種について、独断と偏見でかわいさの順序関係を定めたものです。図には、それぞれの動物の「かわいさの比較結果」が反映されています。

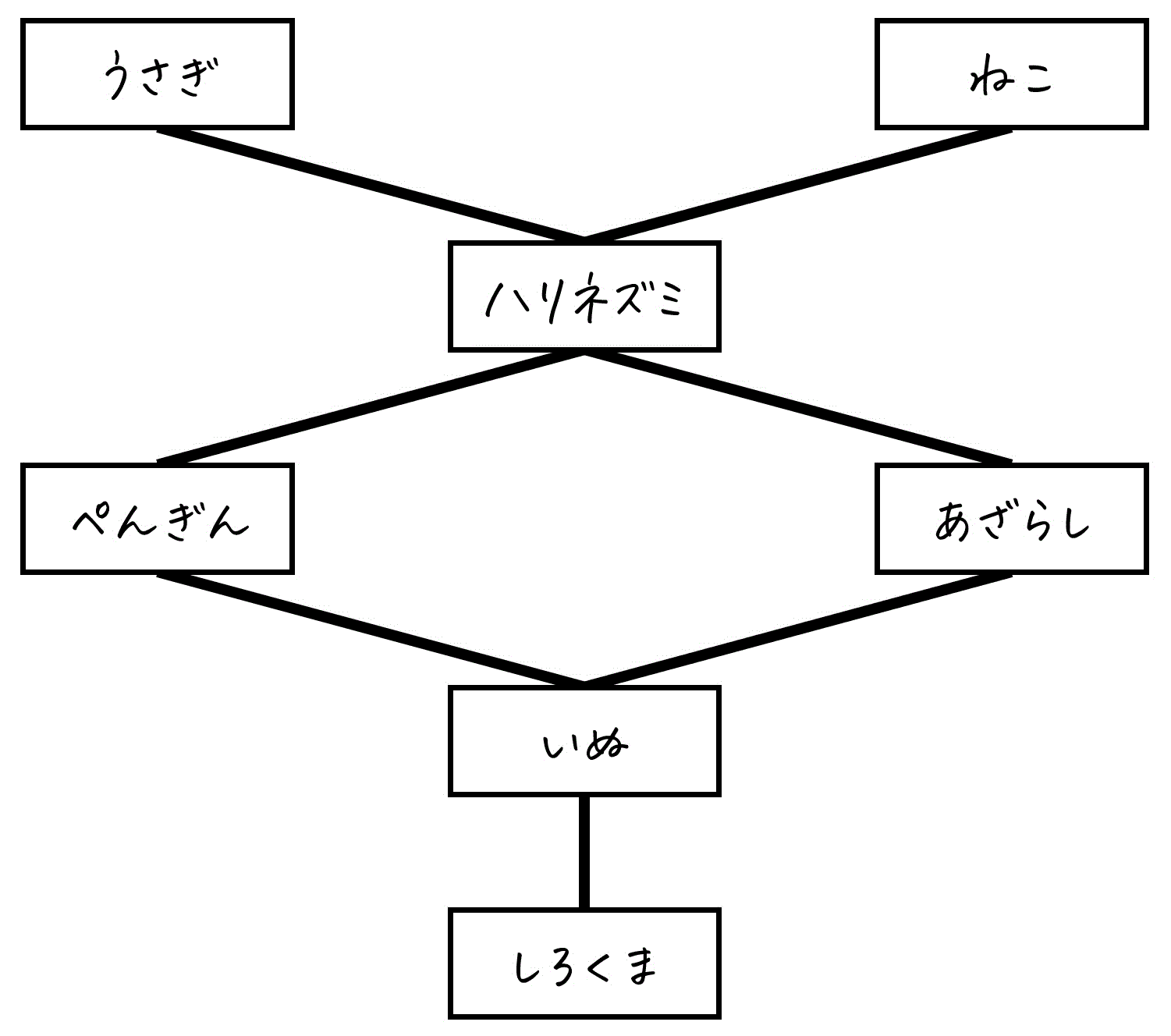
次のペアについて、ハッセ図に順序関係（かわいさの比較）があれば「◯」を、なければ「×」を答えなさい。

(1) 「うさぎ」と「ぺんぎん」
(2) 「うさぎ」と「ねこ」

解説1

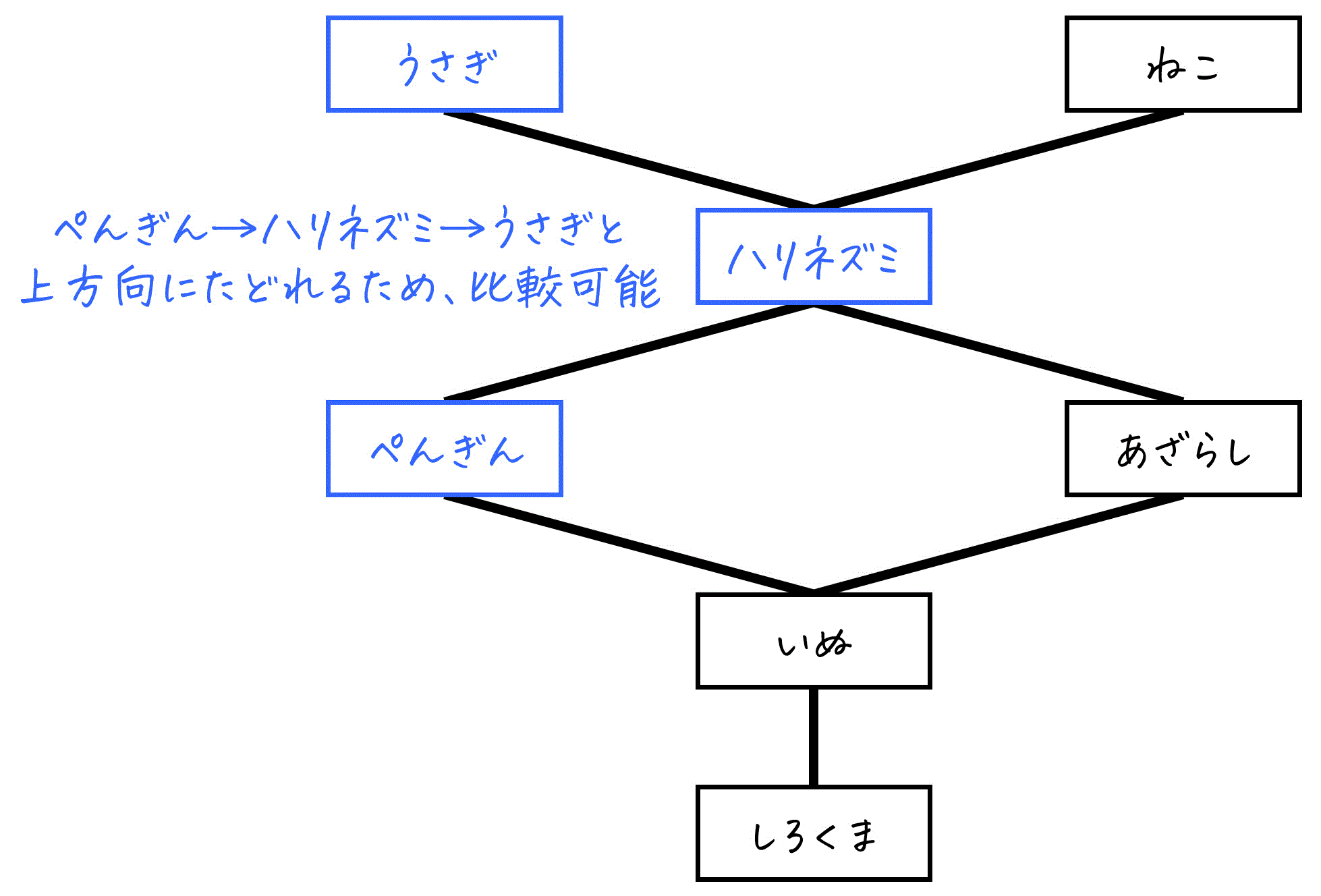
(1)

ぺんぎん→ハリネズミ→うさぎ、と上方向にたどることが出来るため、比較可能です。

解答：〇

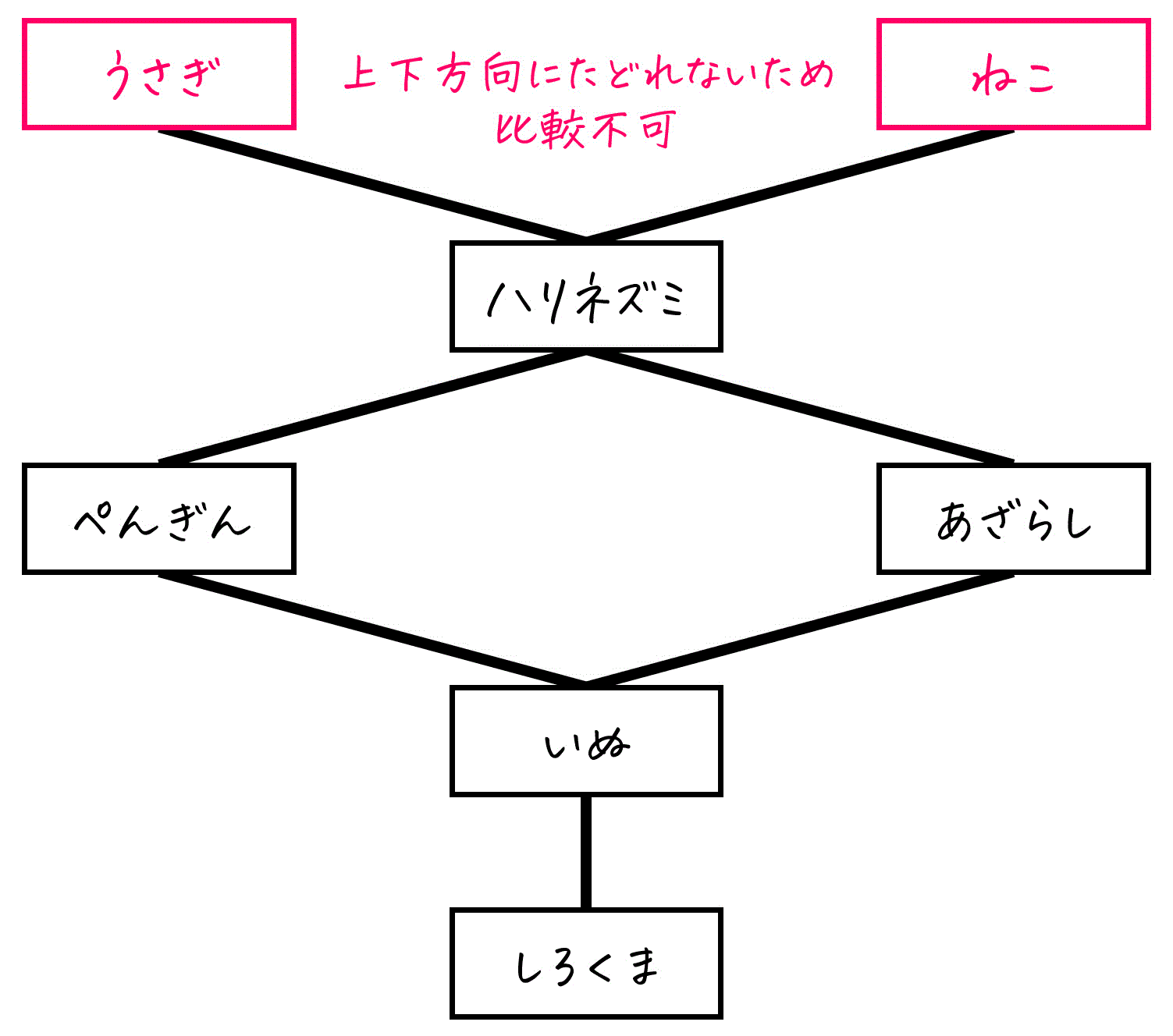
(2)

うさぎ→ねこ、ねこ→うさぎは、どう頑張っても上方向、下方向にたどることが出来ません。

よって、比較不可能です。

解答：×

(4) 練習問題

少し難しめの練習問題も用意しました。

練習問題の解説．

まずは、部分集合をすべて列挙する

べき集合とは、その集合から作れるすべての部分集合を集めた集合のことでしたね。

まずは、\( X = \{a,b,c\} \) にどんな部分集合があるか、全部書き出してみましょう。

要素の数（要素数）ごとに分けて書くとわかりやすいですよ。

• 要素数0: \( \phi \) [空集合]
• 要素数1: \( \{ a \} \), \( \{ b \} \), \( \{ c \} \)
• 要素数2: \( \{ a,b \} \), \( \{ a,c \} \), \( \{ b,c \} \)
• 要素数3: \( \{ a,b,c \} \)

すると、全部で 8個 の部分集合があることがわかります。これらの部分集合をすべて要素としたものがべき集合です。

復習．部分集合とは

部分集合は、元の集合の要素をいくつか（0個でも全部でもOK！）選んで作る集合のことです。

【成立する例】

• \( \phi \subseteq \{ a \} \)
• \( \{ a \} \subseteq \{ a,b \} \)

【成立しない例】

• \( \{ a,b \} \subseteq \{ a \} \)
• \( \{ c \} \subseteq \{ a,b \} \)

ハッセ図を書いていこう！

ハッセ図は、その部分集合同士の包含関係（どっちがどっちに含まれているか）をスッキリ見やすく図にしたものです。

では、いよいよ作図です！

各部分集合を点で表して、包含関係を線で結んでいくよ。

では、つぎの3つのポイントを意識しながら、ハッセ図をかいて行きましょう。

• 一番下に、空集合 \( \phi \) を書く。
• 要素が少ない順番に、下から順に書いていく
• 線は、1つ要素が多い部分集合とだけ結ぶ（推移的な関係は書かない）

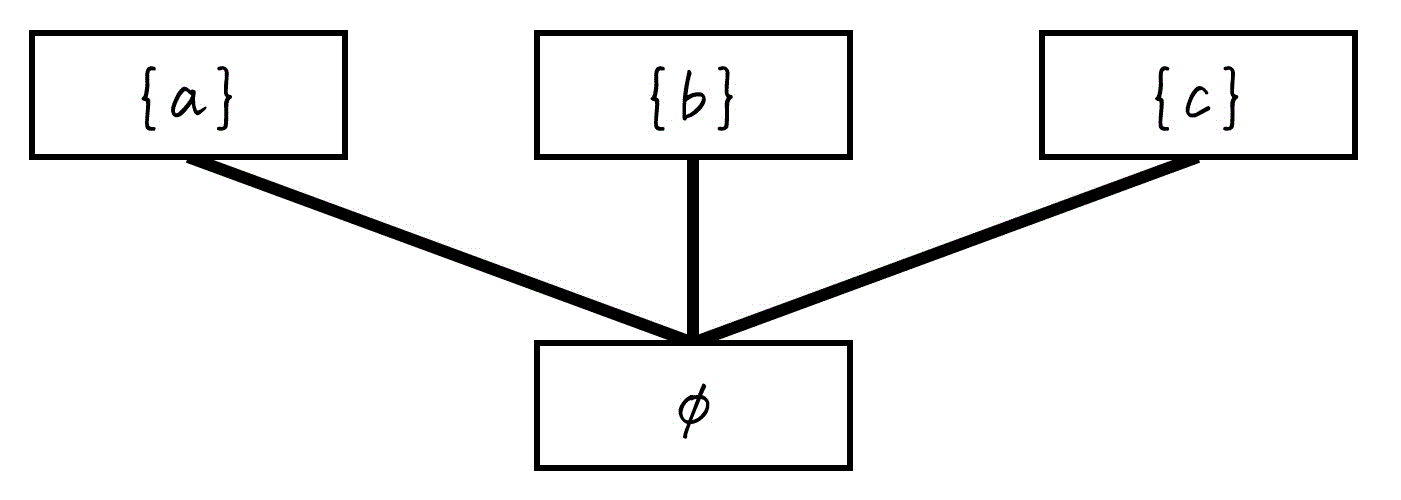
Step1. 要素数0 → 要素数1

空集合 \( \phi \) は、 \( \{ a \} \), \( \{ b \} \), \( \{ c \} \) の部分集合です。なので、線を引きましょう。

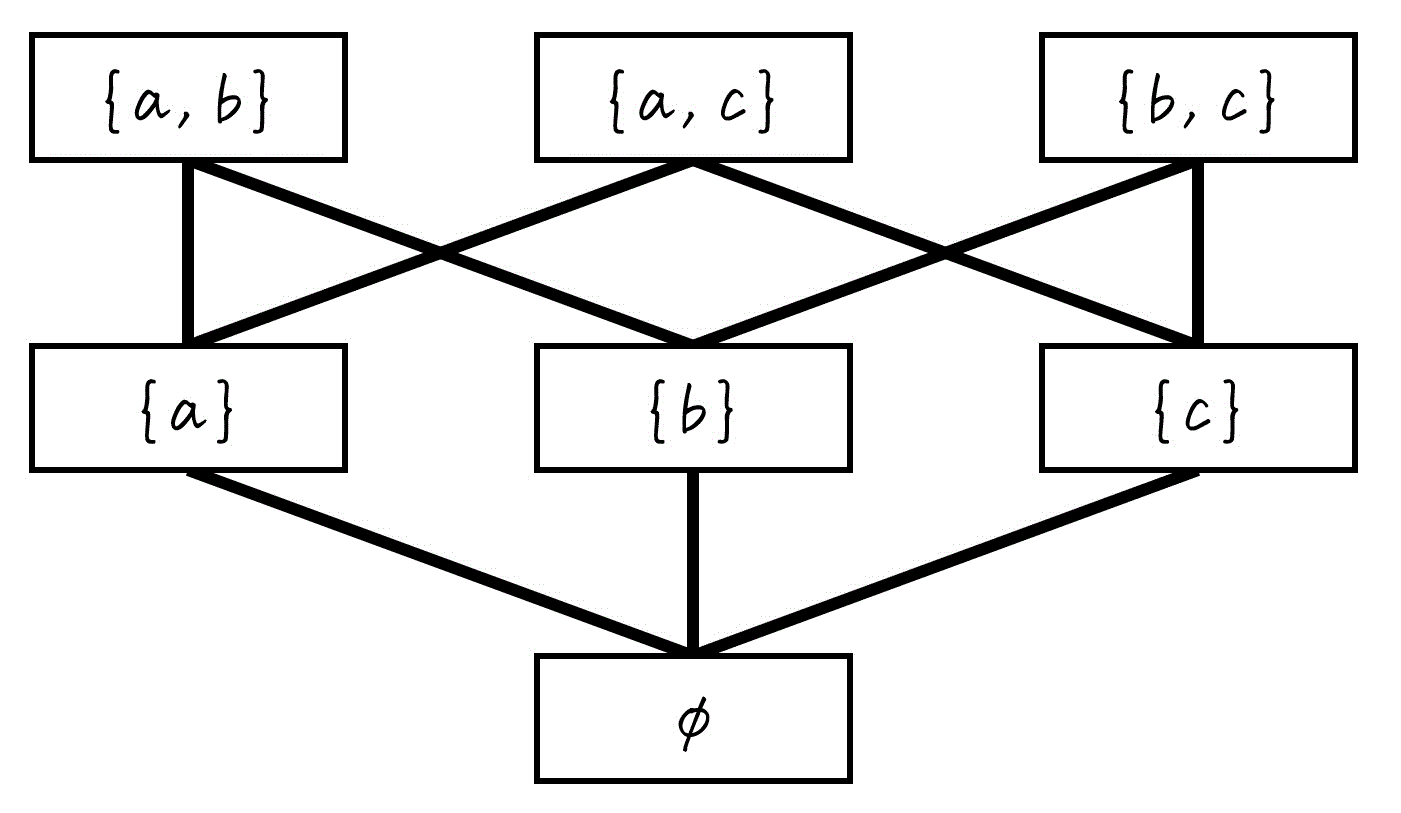
Step2. 要素数1 → 要素数2

• \( \{ a \} \) は、\( \{ a,b \} \), \( \{ a,c \} \) の部分集合
• \( \{ b \} \) は、\( \{ a,b \} \), \( \{ b,c \} \) の部分集合
• \( \{ c \} \) は、\( \{ a,c \} \), \( \{ b,c \} \) の部分集合

これらの対応する部分集合関係を、線で結びましょう。

Step3. 要素数2 → 要素数3

• \( \{ a,b \} \) は、\( \{ a,b,c \} \) の部分集合
• \( \{ b,c \} \) は、\( \{ a,b,c \} \) の部分集合
• \( \{ b,c \} \) は、\( \{ a,b,c \} \) の部分集合

これらの対応する部分集合関係を、線で結びましょう。

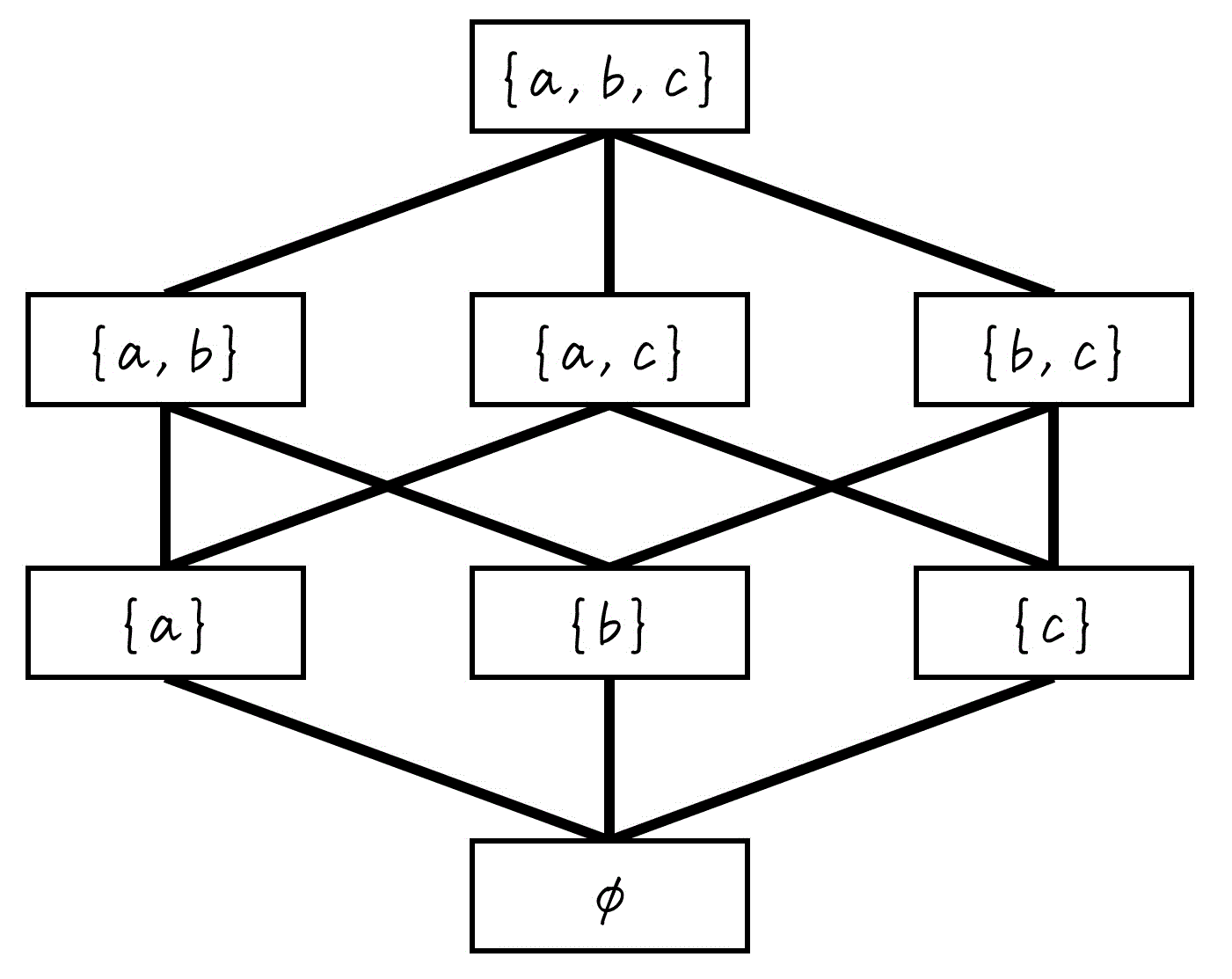
これで、ハッセ図の完成です！

4. ハッセ図と述語論理

ここからは、ハッセ図の読み取りでよく出題される「述語論理」の式の読み解き方について解説していきます。

一見難しそうな数式も、図のイメージと結びつければ決して難しくありません。

図の中の要素がどのようなルールでつながっているのか、記号の意味を一つずつ確認していきましょう。

(1) 図のつながりを定義する4つの記号

まずは、基本となる半順序の記号 \( \sqsubseteq \) 以外によく登場する、4つの重要な記号を見てみましょう。

① 等しい =

半順序関係の \( = \) は、つぎのように定義されます。\[
x = y \Leftrightarrow (x \sqsubseteq y) \land (y \sqsubseteq x)
\]

これは、「相手が自分より上（または同じ）にいて、かつ、自分も相手より上（または同じ）にいる」という状態を指します。

お互いがお互いを見上げている……なんてことは物理的にありえませんよね。つまり、2つの要素は「完全に同じ位置で重なっている」しかありえません。

つまりハッセ図においては、場所が完全に一致している（同じ要素である）ということを意味します。

成立する例　ハリネズミ ＝ ハリネズミ

② 等しくない ≠

半順序関係の \( \not = \) は、つぎのように定義されます。\[\begin{align*}
x \not = y & \Leftrightarrow \lnot ( (x \sqsubseteq y) \land (y \sqsubseteq x) )
\\ & \Leftrightarrow \lnot (x = y)
\end{align*}\]

数式は少し複雑に見えますが、要するに先ほどの「等しい（ $x = y$ ）」という状態を、$\lnot$（否定）を使って真っ向から否定した形です。

つまり、「完全に同じ要素ではない」というごく当たり前のことを表しています。

ハッセ図で見れば、場所が完全に一致していない（違う名前がついている、あるいは違う位置にある）要素同士であれば、この関係が成り立ちます。

成立する例　ハリネズミ ≠ ぺんぎん

③ 比較不能 #

半順序関係の \( \# \) は、つぎのように定義されます。\[
x \ \# \ y \iff \neg ( (x \sqsubseteq y) \lor (y \sqsubseteq x) )
\]

「相手が自分より上にいる」わけでもなく、逆に「自分が相手より上にいる」わけでもない、という状態です。

日常の感覚だと「じゃあ同じ（イコール）なの？」と思うかもしれませんが、そうではありません。

ハッセ図においては、「決めたルール（条件）が、この2つの間ではどちらの方向にも全く当てはまらないため、そもそも比べることができない」という意味で「比較不能」**と呼びます。枝分かれして、全く別のルートにいる要素同士の関係ですね。

成立する例

例： ぺんぎん $\#$ あざらし

どちらも「いぬ」より上にはいますが、ぺんぎんとあざらしの間には直接の上下関係がありません。そのため、「ぺんぎん $\#$ あざらし 」が成立します。

成立しない例

例1: ハリネズミ $\#$ いぬ

途中の要素（ぺんぎん or あざらし）を経由して上下にパス（線）が繋がっており、すでに「比較可能」な関係であるため、この例は成り立ちません。

例2: いぬ $\#$ いぬ

理由: 同じ要素同士は常に等しい（比較可能である）ため、「比較不能」にはなりません。そのため、この例も成り立ちません。

④ 狭義順序 \( \sqsubset \)

狭義順序の \( \sqsubset \) は、つぎのように定義されます。\[\begin{align*}
x \sqsubset = y & \Leftrightarrow (x \sqsubseteq y) \land ( \lnot (y \sqsubseteq x) )
\\ & \Leftrightarrow (x \sqsubseteq y) \land ( \lnot (x = y) )
\end{align*}\]

「相手は自分より上にいるが、自分自身（完全に同じ位置）は除外する」というルールです。

直感的には、「確実に自分より上にいる」という関係です。

成立する例

例1： いぬ \( \sqsubset \) ぺんぎん

「いぬ」から「ぺんぎん」へ向けて、下から上へとパス（線）をたどることができます。そのため、「いぬ \( \sqsubset \) ぺんぎん」が成立します。

例2： いぬ \( \sqsubset \) ハリネズミ

途中の要素（ぺんぎんやあざらし）を挟んでいても、下から上へとパス（線）が繋がっていれば、ハリネズミは「いぬ」より明らかに上であるとわかります。そのため、「いぬ \( \sqsubset \) ハリネズミ」が成立します。

ハッセ図において直接の線が引かれていなくても、このように下から上へたどっていける関係であれば、狭義の半順序 $ \sqsubset $ も、半順序 $ \sqsubseteq $ と同様に成立するのです。

成立しない例

例1： いぬ \( \sqsubset \) いぬ

狭義の半順序 $\sqsubset$ は「自分自身（完全に同じ要素）」を含みません。そのため、「いぬ $\sqsubset$ いぬ」のように自分自身と比べるのはNGとなります。

例2： ぺんぎん \( \sqsubset \) あざらし

ぺんぎんとあざらしは枝分かれした別々の要素（比較不能）です。そのため、どちらが上かを比べることができません。

⑤ 狭義順序 \( \lessdot \)

狭義順序の \( \lessdot \) は、つぎのように定義されます。\[\begin{align*}
x \lessdot = y \Leftrightarrow (x \sqsubset y) \land \textcolor{red}{\neg(\exists z ( (x \sqsubset z) \land (z \sqsubset y) ) )}
\end{align*}\]

式が少し長くなりましたが、言っていることはシンプルです。

「自分と、上にいる相手 $y$ との間に、他の要素 $z$ が入り込む隙間がない」、つまり「間に誰も挟まず、直接の線でつながっている『すぐ上』の関係」を指します。ハッセ図で、間に別の点（要素）を挟まずに一本の線で結ばれているかどうかがポイントです。

成立する例

例1： いぬ \( \lessdot \) ぺんぎん

「いぬ」から「ぺんぎん」へ向けて、下から上へとパス（線）をたどることができます。かつこの2つの間に他の要素（中間の要素）が存在しませんね。

なので、「いぬ \( \lessdot \) ぺんぎん」と書くことができます。

成立しない例

例1： いぬ \( \lessdot \) ハリネズミ

「いぬ」と「ハリネズミ」の間に、「ぺんぎん」や「あざらし」といった中間の要素が存在している場合は、被覆は成り立ちません。よって、この例は成立しません。

例2： いぬ \( \lessdot \) いぬ

被覆を表す記号 $\lessdot$ は、「自分の『1つすぐ上（または下）』の要素であること」を示します。自分自身が自分の「1つすぐ上」になることは物理的にあり得ないため、自分自身との関係（例：いぬ $\lessdot$ いぬ）はNGとなります。

(2) 例題で確認

では、実際にハッセ図と命題について、それぞれの真偽（真か偽か）を判定してみましょう。

例題2

半順序 \( \sqsubseteq \) が定義された、つぎのハッセ図 \( P_1 \), \( P_2 \) で与えられる半順序集合を考える。(1), (2)の問いに答えなさい。

さらに、記号 \( \sqsubset \), \( \# \), \( \lessdot \) を次のように定義する。\[
\begin{align*}
x \sqsubset y & \Leftrightarrow (x \sqsubseteq y) \land (x \neq y) \\
x \mathrel{\#} y & \Leftrightarrow \lnot(x \sqsubseteq y) \land \lnot(y \sqsubseteq x) \\x \lessdot y & \Leftrightarrow (x \sqsubset y) \land \neg(\exists z ( (x \sqsubset z) \land (z \sqsubset y) ) )
\end{align*}
\]

(1) ハッセ図 \( P_1 \) に対して、[i], [ii] の論理式が真になる場合を〇、偽になる場合は×と答えなさい。

• [i]\[
  \forall x \forall y ( (x \sqsubset y) \rightarrow (x \lessdot y) )
  \]
• [ii]\[
  \forall x \forall y ( (x \ \# \ y) \rightarrow \exists z ( (z \sqsubset x) \land (z \sqsubset y) ) )
  \]

(2)

ハッセ図 \( P_2 \) に対して、つぎの論理式が真になる場合を〇、偽になる場合は×と答えなさい。\[
\forall x \forall y ( (x \ \# \ y) \rightarrow \exists z ( (z \sqsubset x) \land (z \sqsubset y)) )
\]

例題2の解説

(1) [i]\[
\forall x \forall y ( (x \sqsubset y) \rightarrow (x \lessdot y) )
\]

式の意味: どんな \( x \), \( y \) でも、\( y \) が \( x \) より大きければ（上ならば）、必ず直接つながっていなければならない。

全称記号 \( \forall \) は、「反例（ダメな例）」を1つ探します。コツは、一番離れたペアを見ることです。

例えば、「\( x \) を一番下の水色」、「\( y \) を左上のピンク色」とします。

すると、\( P_1 \) では間にオレンジ色の要素が挟まってしまいます。

よって、ルールを破る例が見つかったので、答えは × です。

(1) [ii]\[
\textcolor{orange}{\forall x \forall y} ( \textcolor{deepskyblue}{(x \ \# \ y)} \rightarrow \textcolor{magenta}{\exists z ( (z \sqsubset x) \land (z \sqsubset y) )} )
\]

式の意味: 「比較不能（横並び）な2つの要素には、必ず共通の『下の要素』がある」

存在記号（\( \exists \) ）は、条件を満たす要素 \( z \) が「1つでもあればOK」です。

\( P_1 \) では、比較不能なのは「紫色のペア」だけです。この2つの下をたどると、分岐点となる中央の「ピンクの点」で合流します。共通の下の要素が見つかったので、答えは 〇 です。

(2)

式は、(1) [ii] と同じです。

ただし、\( P_2 \) は一本道なので、そもそも「比較不能（横並び）なペア」が1つも存在しません。

論理学では、\[
\mathrm{(前提条件)} \to \mathrm{(結論)}
\]の「(前提条件)、もし～ならば」の前提がそもそも成り立たない場合、命題全体を 真（True） と判定します（空虚な真）。

反例（ルールを破る対象）が存在しないため、この論理式は真となります。

答えは 〇 です。

5. 順序関係における8つの重要な性質

ここからは、順序関係に出てくる上界、下界、最大元、最小元、極大元、極小元、上限、下限についてどんな性質かを見ていきましょう。

テストによく出るので必見ですよ！

(1) 上界 (じょうかい)

直感的理解

全体（半順序集合） \( X \) の中の、あるグループ（部分集合 \( S \) ）を考えます。

このグループ \( S \) のメンバー全員よりも大きい or 等しいような \( X \) の要素があれば、それを \( S \) の上界と呼びます。

かわいさで例えると、グループ \( S \) の動物たちみんなよりもかわいいか、同じくらいかわいい動物（ただし全体 \( X \) の中で）が上界ですね！

数学的な定義

数式的な表記：
\( \forall s \in S \), \( s \sqsubseteq x \) を満たす \( x \in X \)
→ どの \( s \in S \) に対しても、\( s \sqsubseteq x \) となるような \( x \in X \)

言葉での表記：

\( X \) の部分集合 \( S \) 内のどの要素 \( s \) を持ってきても、それより大きい or 等しい \( x \) が、\( S \) の上界となります。

具体例で確認

先ほど出した、このカワイイ動物たちのかわいさを図示したハッセ図を使ってみましょう！

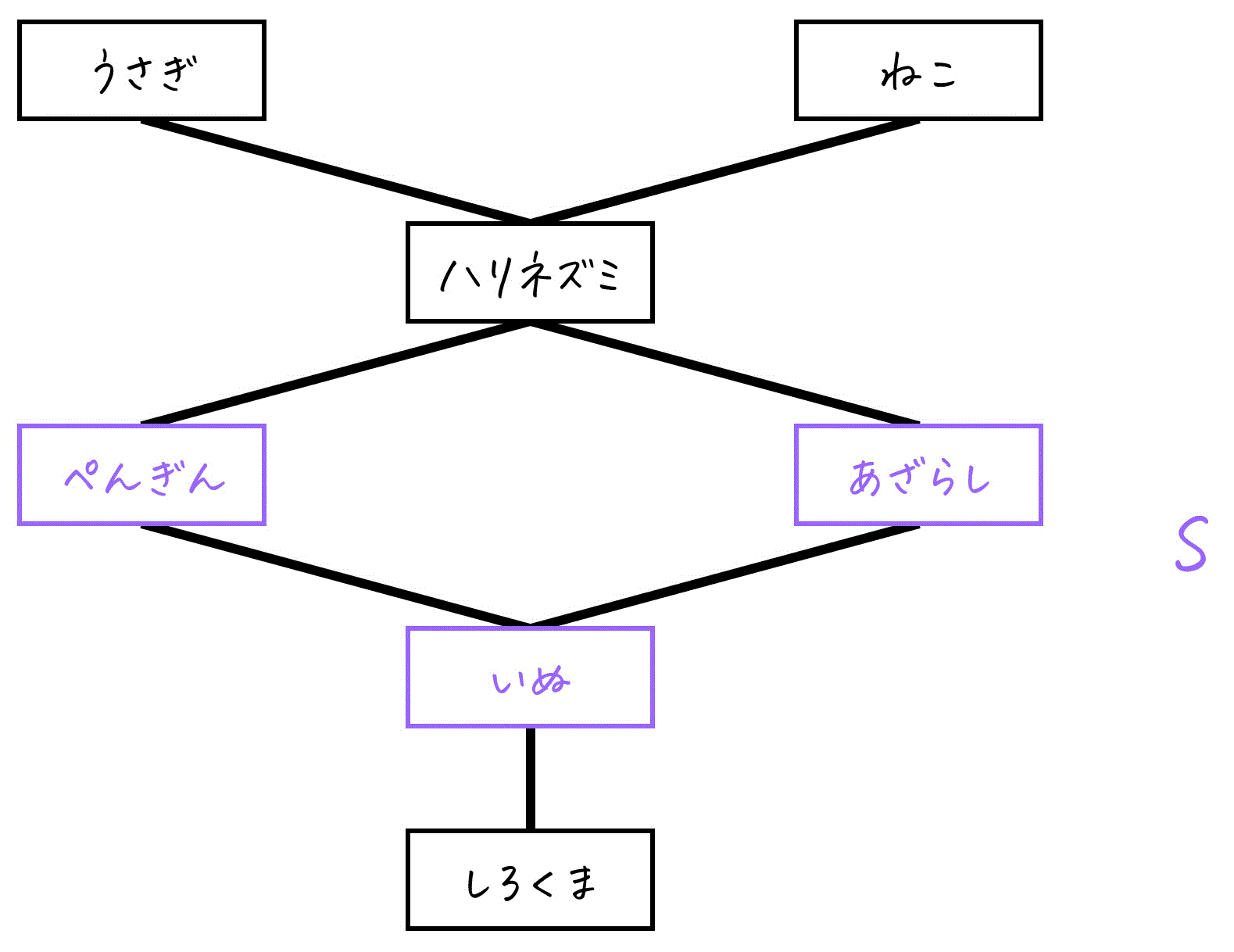
ここで、集合 X = {しろくま, いぬ, ぺんぎん, あざらし, ハリネズミ, うさぎ, ねこ} としましょう。

早速、S = {ぺんぎん, あざらし, いぬ} の上界、つまりこれら3匹全員以上にかわいい動物を求めていきましょう。

まずは、Sの各要素ごとに、それ以上にかわいいものを求めていきましょう。

• ぺんぎん以上にかわいい動物：ぺんぎん、ハリネズミ、うさぎ、ねこ
• あざらし以上にかわいい動物：あざらし、ハリネズミ、うさぎ、ねこ
• いぬ以上にかわいい動物：ぺんぎん、あざらし、ハリネズミ、うさぎ、ねこ

この3つに共通するものは、ハリネズミ、うさぎ、ねこですね。

よって、Sの上界は「ハリネズミ、うさぎ、ねこ」となります。

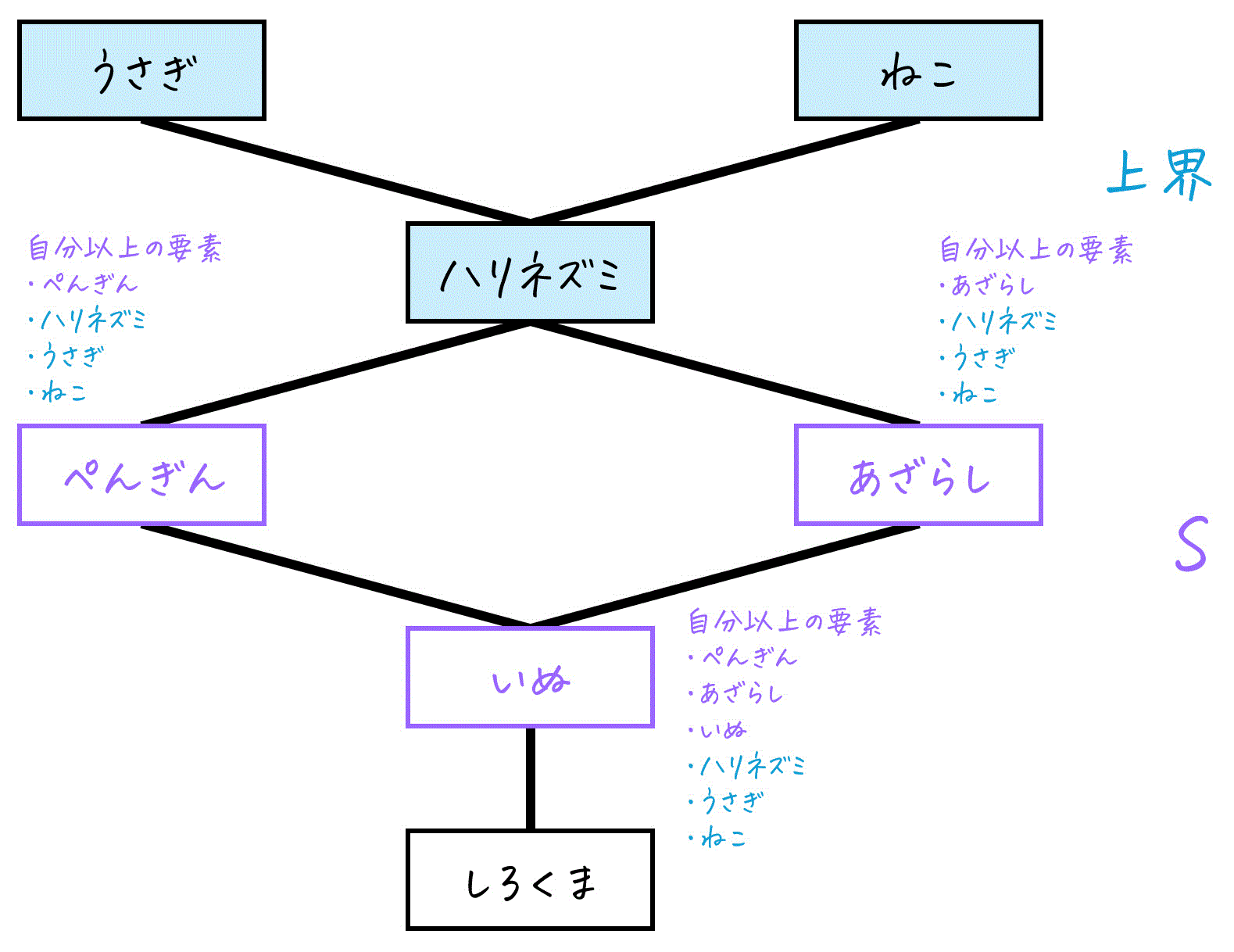
言い換えると、この3匹の動物は常に「ぺんぎん, あざらし, いぬ (S)」以上にかわいいと言えるわけだ。

テストでの注意ポイント！

• 上界は、考えている部分集合 S の外側にあることが多いけど、S の中の要素が上界になることもあります。
  例えば、先ほどのハッセ図に対して、S = {ハリネズミ、ぺんぎん} とすると、上界は「ハリネズミ、うさぎ、ねこ」になって、Sの中にあるハリネズミを含みます^[2] … Continue reading。
• 上界は、1つとは限りません。複数存在することがあります。
• 上界が存在しないこともあります。例えば、S = {うさぎ, ねこ} とすると、うさぎ以上にかわいい動物はうさぎ、ねこ以上にかわいい動物はねこで、共通して当てはまる動物がいなくなりますね。

(2) 下界 (かかい)

直感的理解

全体（半順序集合） \( X \) の中の、あるグループ（部分集合 \( S \) ）を考えます。

このグループ \( S \) のメンバー全員よりも小さい or 等しいような \( X \) の要素があれば、それを \( S \) の下界と呼びます。

かわいさで例えると、グループ S の動物たちみんなよりもかわいくないか、同じくらいかわいくない（つまり、序列が下か同じ）動物が下界です。

数学的な定義

数式的な表記：
\( \forall s \in S \), \( x \sqsubseteq s \) を満たす \( x \in X \)（どの \( s \in S \) に対しても、\( x \sqsubseteq s \) となるような \( x \in X \)

言葉での表記：

\( X \) の部分集合 \( S \) 内のどの要素 \( s \) を持ってきても、それより小さい or 等しい \( x \) が、\( S \) の下界となります。

具体例で確認

同じように、このカワイイ動物たちのかわいさを図示したハッセ図を使ってみましょう！

集合 X = {しろくま, いぬ, ぺんぎん, あざらし, ハリネズミ, うさぎ, ねこ} でしたね。

早速、S = {ぺんぎん, あざらし, いぬ} の下界、つまりこれら3匹全員よりもかわいくない or かわいさが同じ動物を求めていきましょう。

まずは、Sの各要素ごとに、それ以下にかわいいものを求めていきましょう。

• ぺんぎん以下にかわいい動物：ぺんぎん、いぬ、しろくま
• あざらし以下にかわいい動物：あざらし、いぬ、しろくま
• いぬ以下にかわいい動物：いぬ、しろくま

この3つに共通するものは、いぬ、しろくまですね。

よって、Sの下界は「いぬ、しろくま」となります。

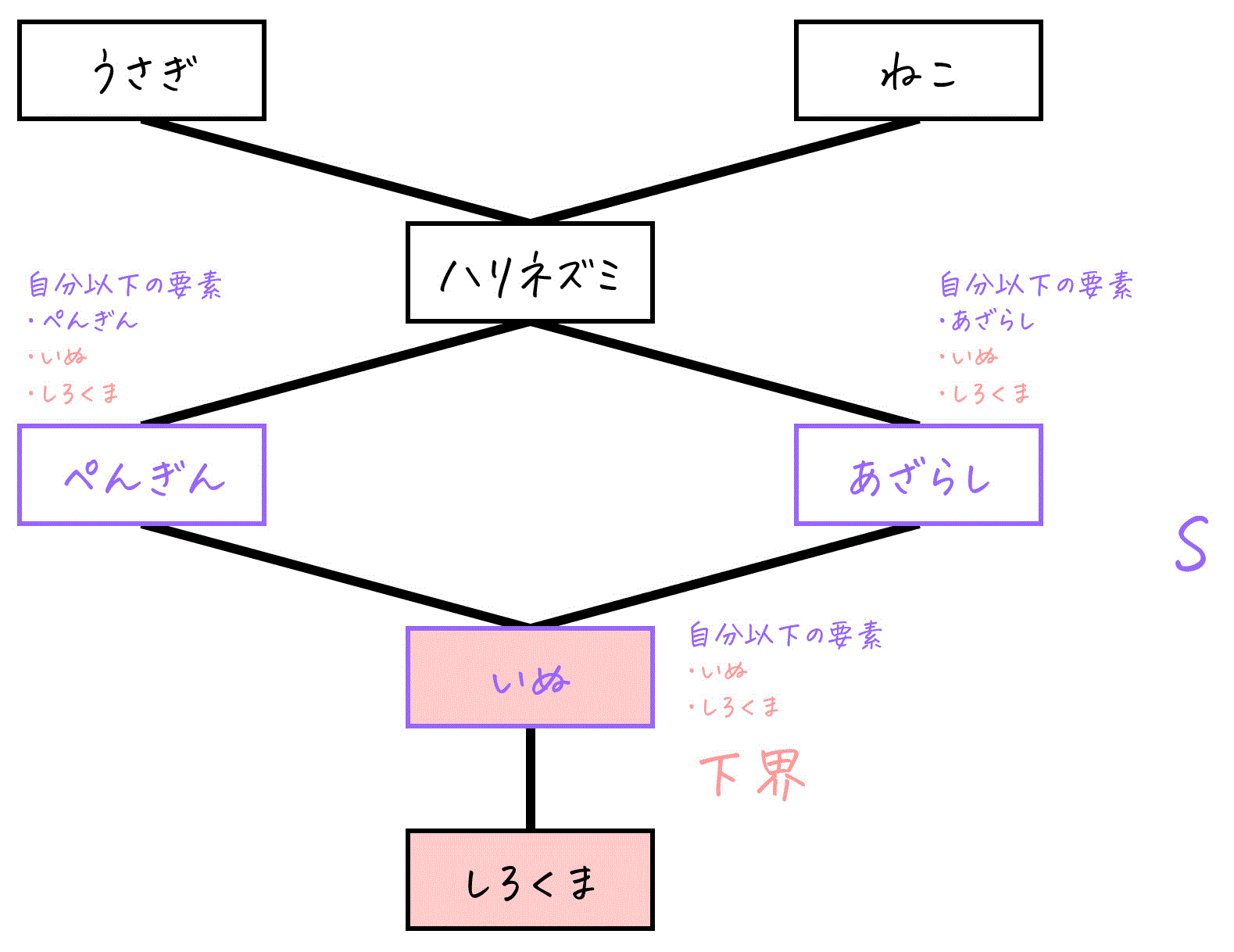
言い換えると、この3匹の動物は常に「ぺんぎん, あざらし, いぬ (Sの部分集合)」以下にかわいいと言えるわけだ。

テストでの注意ポイント！

下界は、上界と定義の不等号の向きが反対なだけで、考え方は同じです！

• 下界も、部分集合 S の中の要素が下界になることがあるし、外側の要素がなることもある。
• 下界も1つとは限らない。存在しないこともある。

(3) 最大元 (さいだいげん)

ここからは、「集合 \( S \) の一番」を決める概念、(3)最大元と (4)最小元を見ていきましょう。

直感的理解

あるグループ（部分集合 \( S \) ）の中で、「最も大きい」と言える要素のこと。

かわいさで言うと、グループ \( S \) 内の他のどの動物と比べても、それ以上（または同等）にかわいい、グループ内ナンバーワンの動物がいれば、それが「\( S \) の最大元」です。

数学的な定義

数式的な表記：
\( \forall s \in S \), \( s \sqsubseteq m \) を満たす \( m \in S \)
→ どの \( s \in S \) に対しても、\( s \sqsubseteq x \) となるような \( x \in S \)

言葉での表記：
\( S \) 内のどの要素 \( s \) を持ってきても、それより大きい or 等しい自身 \( m \) が、\( S \) の最大元となります。

具体例で確認

このハッセ図で、S = {ぺんぎん, あざらし, いぬ} の最大元を考えてみましょう。

• いぬ → ぺんぎん、あざらしにかわいさで負けるため、最大元とは言えない。
• ぺんぎん → あざらしとかわいさが比較できないため、最大元とは言えない。
• あざらし → ぺんぎんかわいさが比較できないため、最大元とは言えない。

したがって、S の最大元は存在しません。

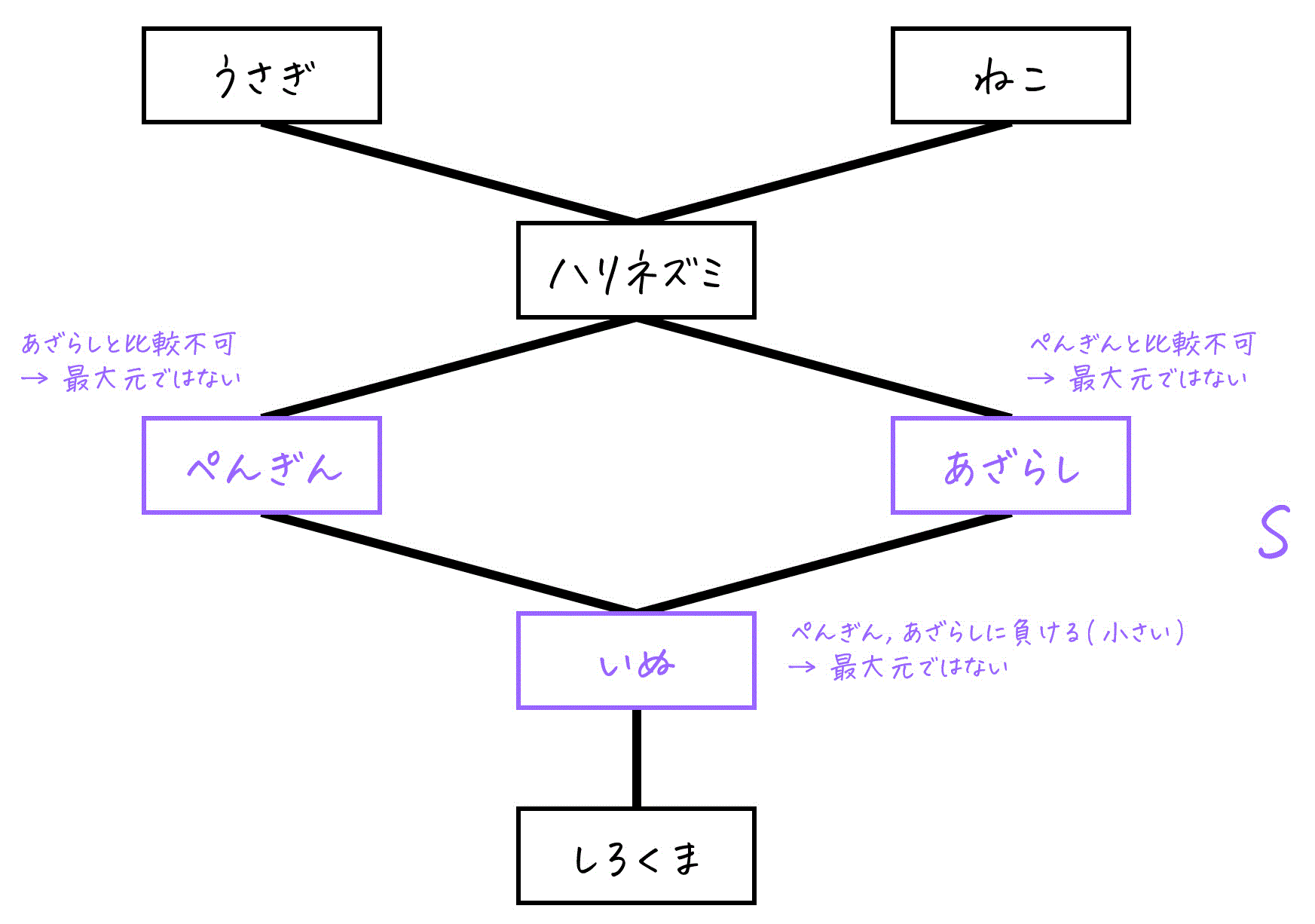
テストでの注意ポイント！

• 最大元は、存在する場合「必ず唯一」に決まります。
• 最大元は、存在するとは限らない。
• 極大元（後で説明します）と混合しないこと！

(4) 最小元 (さいしょうげん)

直感的理解

あるグループ（部分集合 S）の中で、「最も小さい」と言える要素です。

そのグループ内の他のどの動物と比べても、それ以下（または同等）にかわいくない、グループ内最下位の動物がいれば、それが「S の最小元」だよ。

数学的な定義

数式的な表記：
\( \forall s \in S \), \( m \sqsubseteq s \) を満たす \( m \in S \)
（どの \( s \in S \) に対しても、\( m \sqsubseteq s \) となるような \( m \in S \)

言葉での表記：
\( S \) 内のどの要素 \( s \) を持ってきても、それより小さい or 等しい \( m \) が、\( S \) の最小元となります。

具体例で確認

このハッセ図で、S = {ぺんぎん, あざらし, いぬ} の最小元を考えてみましょう。

• ぺんぎん → いぬにかわいさで勝ってしまうため、最小元とは言えない。
• あざらし → いぬにかわいさで勝ってしまうため、最小元とは言えない。
• いぬ → ぺんぎん、あざらしにかわいさで負ける。よって最小元と言える。

したがって、S の最小元は「いぬ」です。

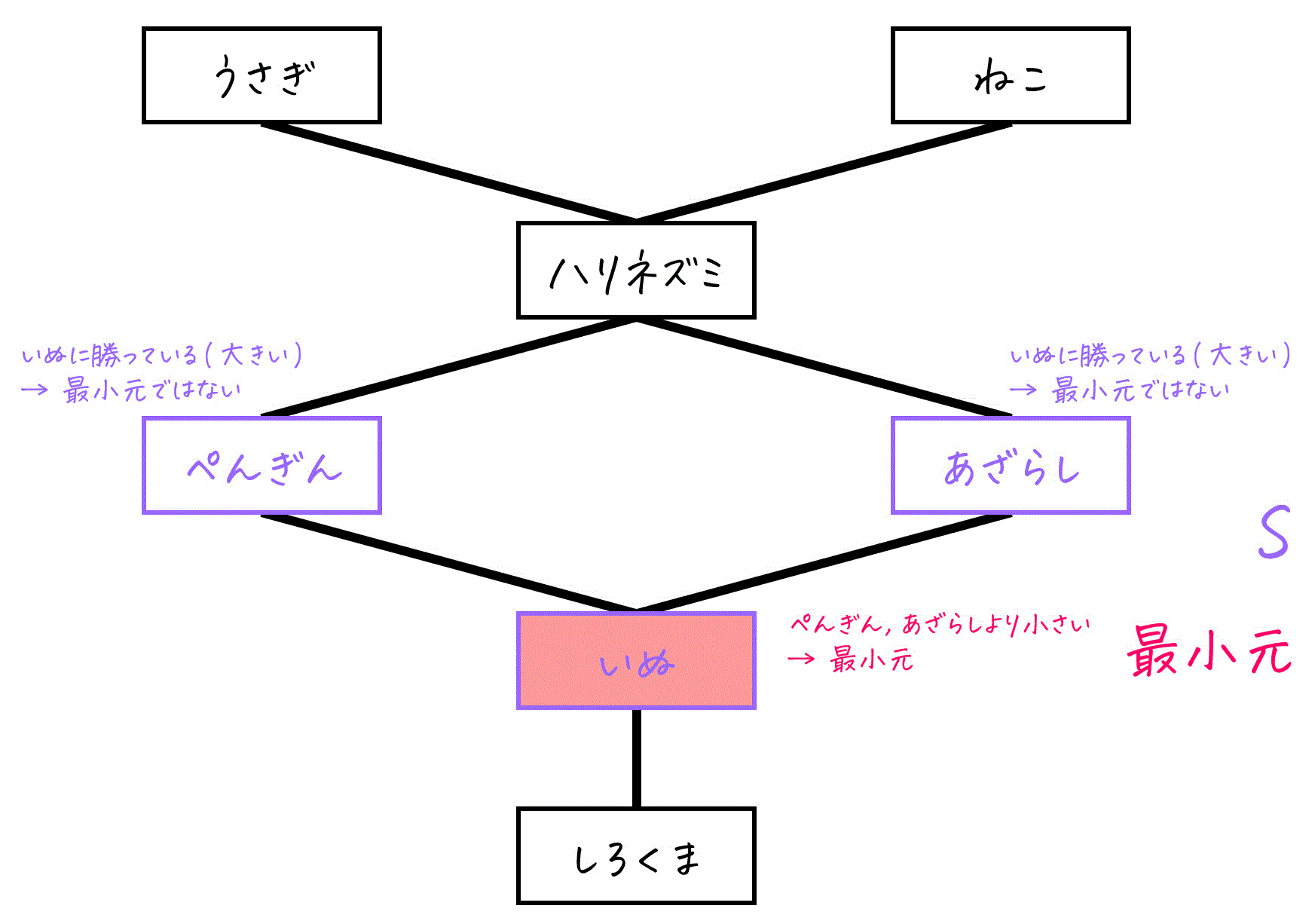
テストでの注意ポイント！

最小元は、最大元と定義の不等号の向きが反対なだけで、考え方は同じです！

• 最小元も、最大元と同じく存在する場合「必ず唯一」に決まります。
• 最小元は、最大元と同じく存在するとは限らない。
• 極小元（後で説明します）と混合しないこと！

(5) 極大元 (きょくだいげん)

直感的理解

あるグループ（部分集合 S）の中で、「自分より大きい要素が \( S \) 内にない」と言える要素のこと。

かわいさで言うと、グループ S 内のどの動物とも比較したとき、「自分よりかわいい」動物が S 内に存在しない要素が「S の極大元」です。

数学的な定義

数式的な表記：
\( \forall s \in S \), \( a \sqsubseteq s \to s = a \) を満たす \( a \in S \)
→ どの \( s \in S \) に対しても、もし \( a \sqsubseteq s \) であれば \( s = a \) である。

言葉での表記：
\( S \) の要素 \( a \) について、自身 \( a \) より大きい \( S \) 内の要素は \( S \) 内に存在しない。

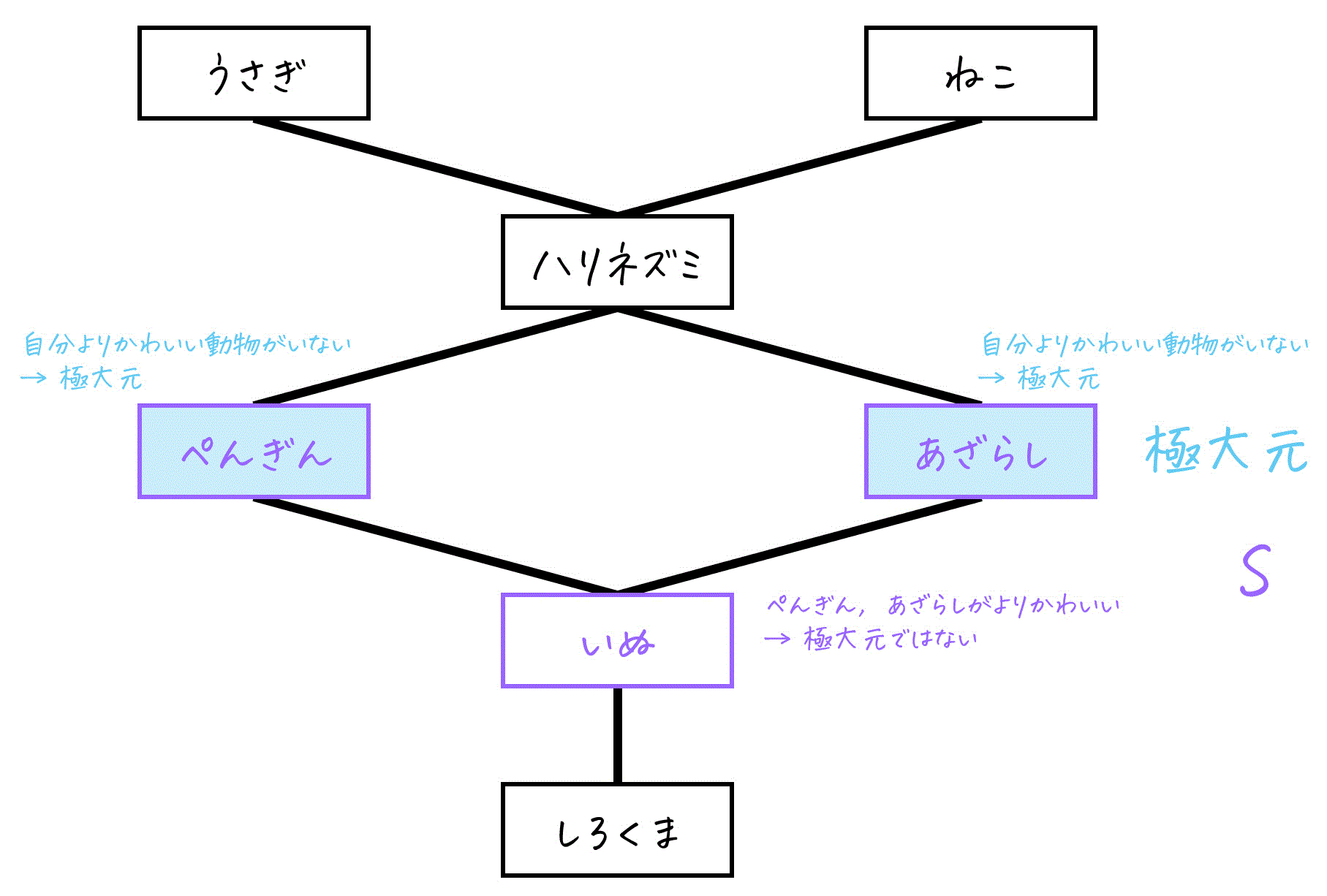
具体例で確認

先ほどと同じハッセ図で、S = {ぺんぎん, あざらし, いぬ} の極大元を考えてみましょう。

• ぺんぎん → S内でこれよりかわいい動物がいないため、極大元です。
• あざらし → S内でこれよりかわいい動物がいないため、極大元です。
• いぬ → ぺんぎんとあざらしがS内でよりかわいいため、極大元ではありません。

したがって、S = {ぺんぎん, あざらし, いぬ} の極大元は「ぺんぎん」と「あざらし」です。

テストでの注意ポイント！

• 極大元は複数存在することがあります（この例では2つ）。
  ※ 最大元は存在する場合は必ず1つ！
• 最大元とは異なり、互いに比較できない要素が極大元になることがあります。
• 極大元が1つだけ存在する場合、最大元と必ず等しくなります。

(6) 極小元 (きょくしょうげん)

直感的理解

あるグループ（部分集合 S）の中で、「これより下の要素が \( S \) 内にない」と言える要素のこと。

かわいさで言うと、グループ S 内のどの動物とも比較したとき、「自分よりかわいくない」動物が S 内に存在しない要素が「S の極小元」です。

数学的な定義

数式的な表記：
\( \forall s \in S \), \( s \sqsubseteq a \to s = a \) を満たす \( a \in S \)
→ どの \( s \in S \) に対しても、もし \( s \sqsubseteq a \) であれば \( s = a \) である。

言葉での表記：
\( S \) の要素 \( a \) について、自身 \( a \) より小さい \( S \) 内の要素は \( S \) 内に存在しない。

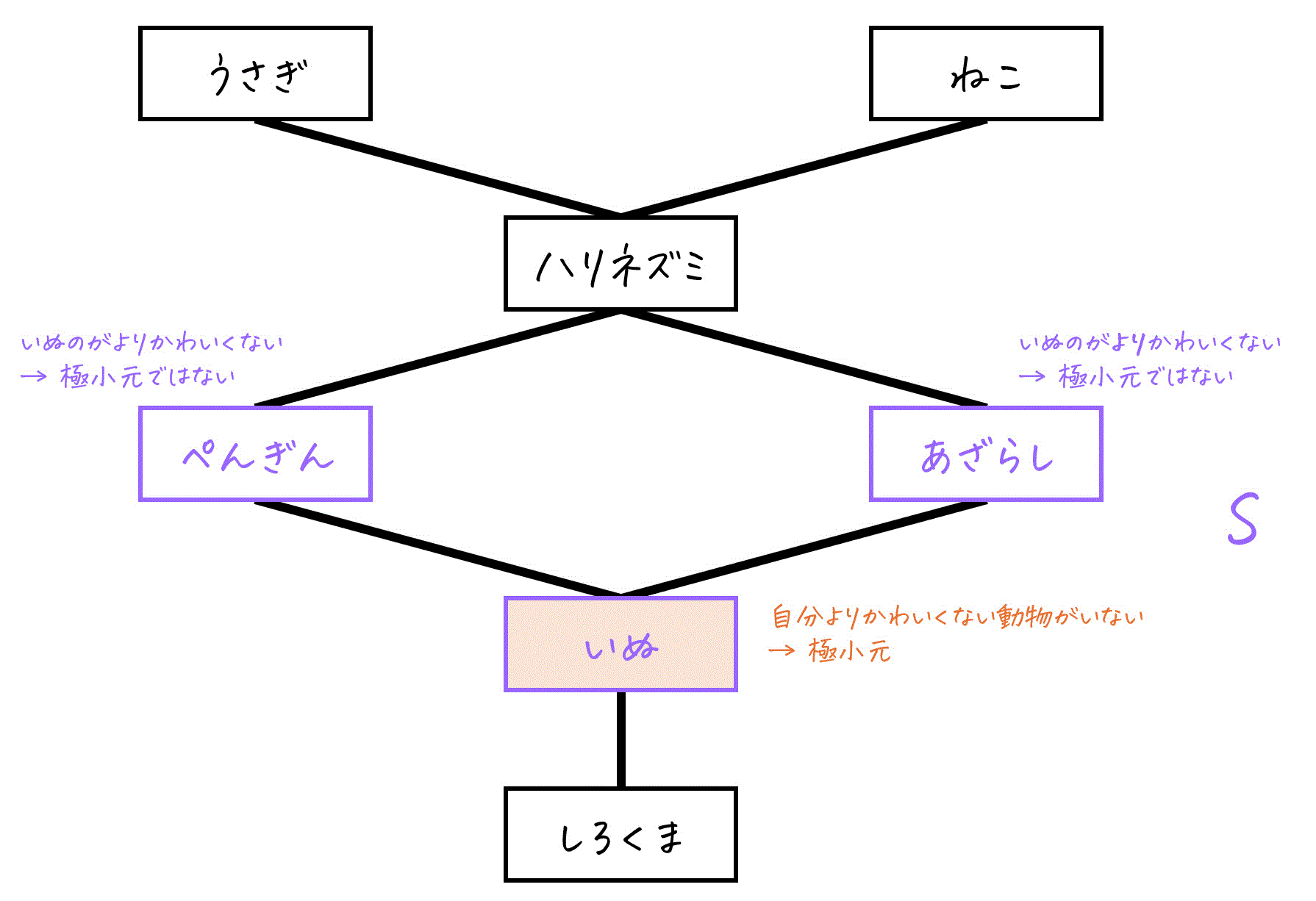
具体例で確認

先ほどと同じハッセ図で、S = {ぺんぎん, あざらし, いぬ} の極小元を考えてみましょう。

• ぺんぎん → いぬがS内でよりかわいくないため、極小元ではありません。
• あざらし → いぬがS内でよりかわいくないため、極小元ではありません。
• いぬ → S内でこれよりかわいくない動物がいないため極小元です。

したがって、S = {ぺんぎん, あざらし, いぬ} の極小元は「いぬ」だけです。

テストでの注意ポイント！

極小元は、極大元と不等号の向きが反対なだけで、考え方は同じです！

• 極小元は複数存在することがあります（この例では2つ）。
  ※ 極小元は存在する場合は必ず1つ！
• 最小元とは異なり、互いに比較できない要素が極小元になることがあります。
• 極小元が1つだけ存在する場合、最小元と必ず等しくなります。

(7) 上限(最小上界) [じょうげん／さいしょうじょうかい]

直感的理解

「グループ \( S \) 内のどのメンバーよりも、大きい or 等しい要素（＝上界）」の中で、一番小さいもの。

かわいさで言うと、「グループS内の全ての動物以上にかわいい動物（上界）」の中で、かわいさの序列が最も低といえる動物（つまり、ギリギリで上界の条件を満たす動物）が「Sの上限」です。

数学的な理解

上界の要素を部分集合 S' としたときの、S' の最小元。

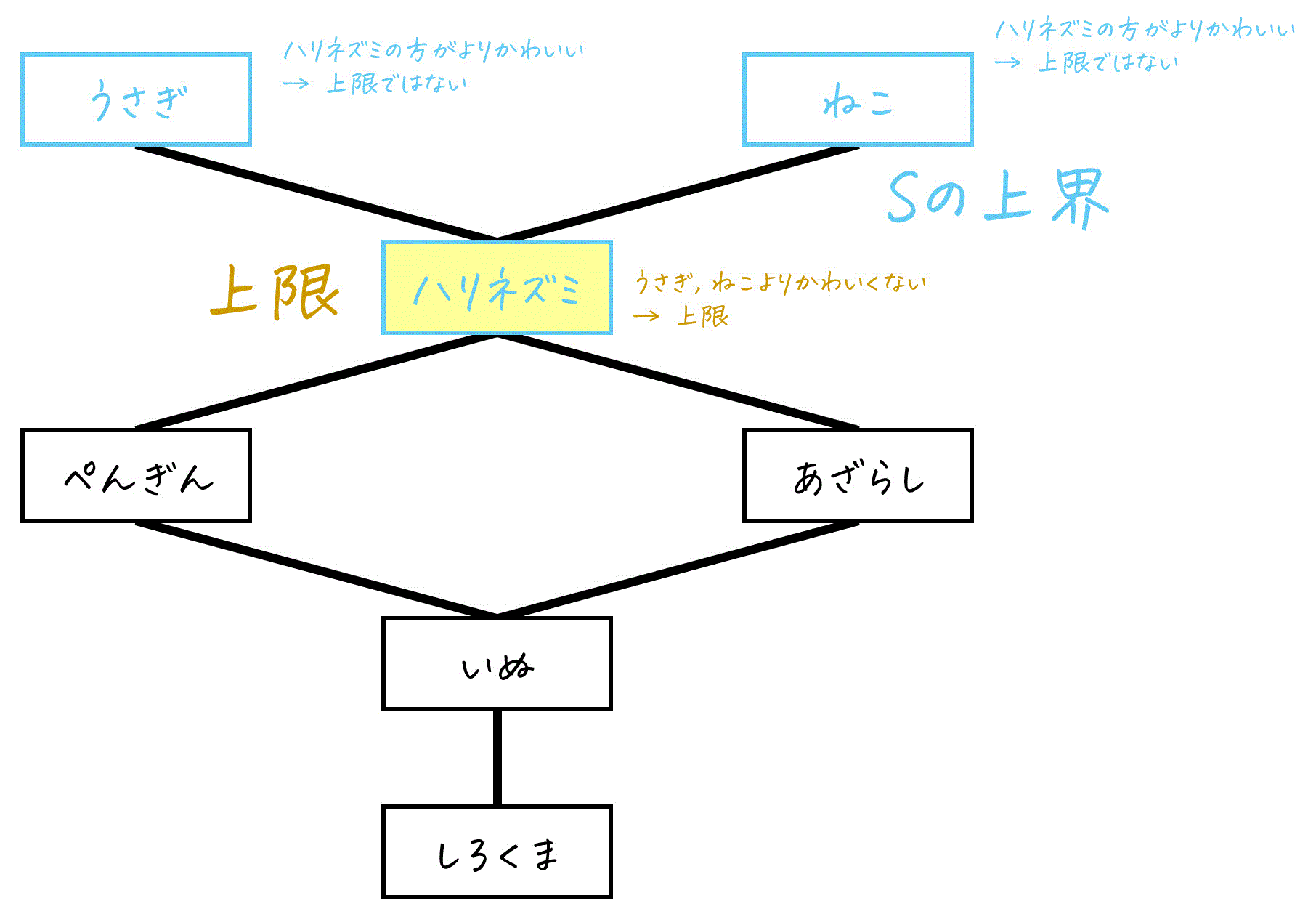
具体例で確認

同じハッセ図で、S = {ぺんぎん, あざらし, いぬ} の上限を考えてみましょう。

まず、Sの上界は「うさぎ、ねこ、ハリネズミ」でしたね。この2つの要素のうち、最小（かわいさが控え目）と言える要素があるかどうか確認します。

• うさぎ → ハリネズミが、よりかわいさが控え目（小さい）なので上限とはなりません。
• ねこ → ハリネズミが、よりかわいさが控え目（小さい）なので上限とはなりません。
• ハリネズミ → うさぎ、ねこともにかわいさに負けるため、上限と言える。

よって、Sの上限は「ハリネズミ」となります。

テストでの注意ポイント！

• 上限は、存在する場合必ず1つだけです。
• 上限は、存在しないこともあります。

(8) 下限(最大下界) [かげん／さいだいかかい]

直感的理解

「グループ \( S \) 内のどのメンバーよりも、小さい or 等しい要素（＝下界）」の中で、一番大きいもの。

かわいさで言うと、「グループS内の全ての動物以下にかわいい動物（下界）」の中で、かわいさの序列が最も高いといえる（つまり、ギリギリで下界の条件を満たす）動物が「Sの下限」です。

数学的な理解

下界の要素を部分集合 S' としたときの、S' の最大元。

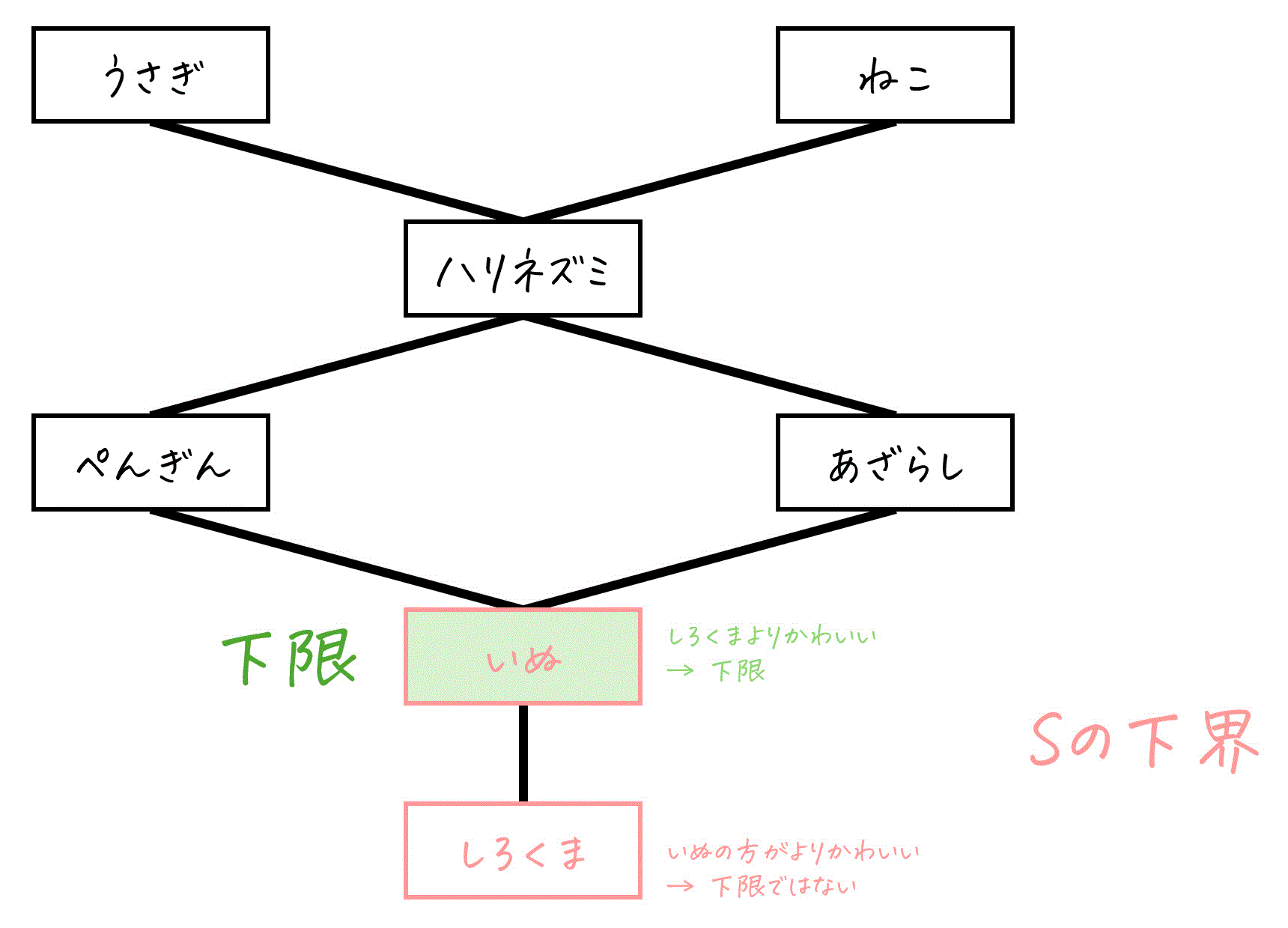
具体例で確認

同じハッセ図で、S = {ぺんぎん, あざらし, いぬ} の下限を考えてみましょう。

ここで、Sの下界は「いぬ、しろくま」でしたね。

• いぬ → しろくまよりかわいいため、下界の中で一番かわいいと言える。よって下限。
• しろくま → いぬの方がよりかわいいため、下限とは言えない。

よって、Sの下限は「いぬ」となります。

テストでの注意ポイント！

• 上限は、存在する場合必ず1つだけです。
• 上限は、存在しないこともあります。

5. 練習問題にチャレンジ！

順序関係の8つの性質は、テストでも頻出です！

なので、練習問題で理解度を確認していきましょう。

問題

練習問題

半順序集合\[
X = \{ a,b,c,d,e,f,g,h,i,j,k \}
\]上の半順序関係 \( \sqsubseteq \) が以下のハッセ図のように定義されている。

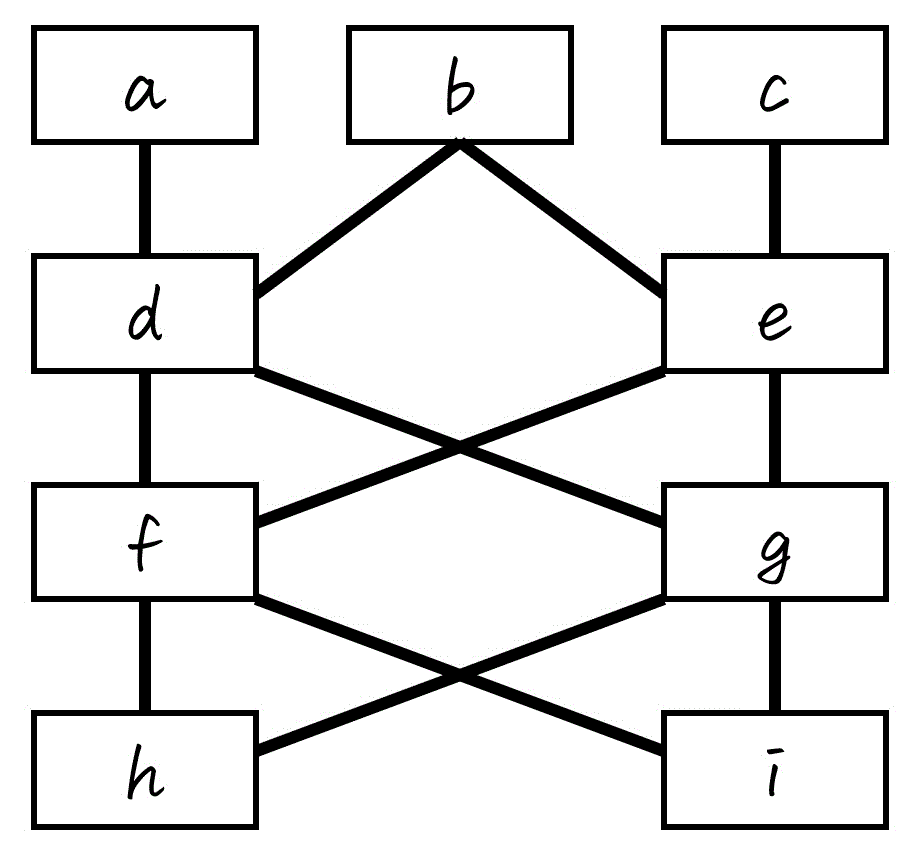
つぎの(1), (2)の問いに答えなさい。

(1) 要素 \( d \) について、つぎの[a], [b], を満たすような \( x \) をそれぞれすべて求めなさい。ただし、\( x \in X \) とする。

[a] \( d \sqsubseteq x \) を満たすような \( x \)
[b] \( x \sqsubseteq d \) を満たすような \( x \)
\( \lnot ( (x \sqsubseteq d) \lor (d \sqsubseteq x) ) \)

(2) 部分集合を \( S = \{ d, f, g \} \) とする。\( S \) について、次の [ア] ～ [ク] に当てはまる要素をすべて答えなさい。ただし、存在しない場合は「×」と答えること。

[ア] 上界
[イ] 下界
[ウ] 最大元
[エ] 最小元
[オ] 極大元
[カ] 極小元
[キ] 上限
[ク] 下限

解説

(1) ハッセ図の読み方

[a] \( d \sqsubseteq x \): \( x \) は \( d \) と同じか、より上である。

ハッセ図で \( d \) と同じ位置にあるか、\( d \) から出発して線を上にたどっていくと到達できる要素 \( x \) をすべて列挙していきます。

• \( d \) 自身：まず \( d \) が当てはまります
• \( d \) から上へ:
  • \( d \) から直接線で上に繋がっているのは \( a \) と \( b \) です。
  • \( a \) や \( b \) からさらに上へたどれる要素はありません。

したがって、\( a , b , d \) が条件を満たします。

答え：\( a , b , d \)

[b] \( x \sqsubseteq d \): \( x \) は \( d \) と同じか、より下である。

ハッセ図で \( d \) と同じ位置にあるか、\( d \) から出発して線を下にたどっていくと到達できる要素 \( x \) をすべて見つけられればOKです。

• \( d \) 自身：まず \( d \) が当てはまります
• \( d \) から下へ:
  • \( d \) から直接線で下に繋がっているのは \( f \) と \( g \) です。
  • \( f \) からさらに下にたどると、\( h \) と \( i \) が出てきます。
  • \( g \) からさらに下にたどると、\( h \) と \( i \) が出てきます。
  • \( h \) や \( i \) から、さらに下へたどれる要素はありません.。

したがって、\( d, f, g, h, i\) が条件を満たします。

答え：\( d, f, g, h, i\)

\( \lnot ( (x \sqsubseteq d) \lor (d \sqsubseteq x) ) \)

これは、\( d \) との間に上下関係が全くない（ハッセ図で、\( d \) から上にも下にも辿れない）要素を探すということです。比較できないということですね。

具体的には、[a], [b] で見つからなかった要素が比較不能となります。

• [a] \( d \sqsubseteq x \) となる要素: \( a , b , d \)
• [b] \( x \sqsubseteq d \) となる要素: \( d, f, g, h, i\)

[a] と [b] で見つかっていない出てきていない要素

\( x \sqsubseteq d \) ( \( d \) 以上である ）でも \( d \sqsubseteq x \) （ \( d \) 以下である）の否定は、比較が出来ないもの。

よって、答えは \( c, e \) となります。

答え：\( c, e \)

(2) 重要な性質の復習

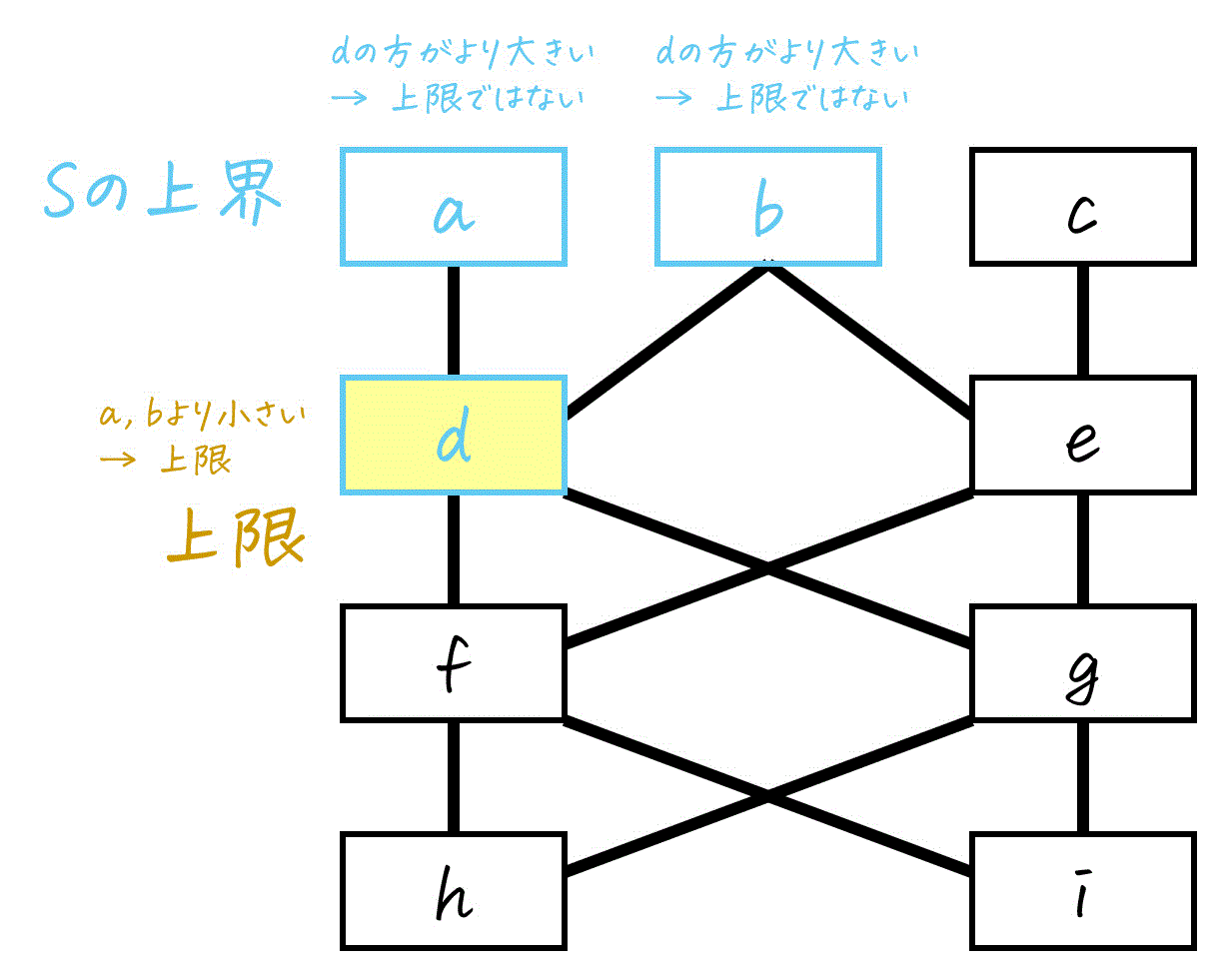
[ア] 上界

\( S \) のメンバーである \( d \), \( f \), \( g \) のすべてに対して、「その要素と同じか、それより上にある」ような要素を \( X \) の中からすべて見つけます。

• \( d \) 以上の要素：\( a \), \( b \), \( d \)
• \( f \) 以上の要素：\( a \), \( b \), \( c \), \( d \), \( e \), \( f \)
• \( g \) 以上の要素：\( a \), \( b \), \( c \), \( d \), \( e \), \( g \)

これら3つのもので、共通して含まれている要素は \( a \), \( b \), \( d \) ですね。

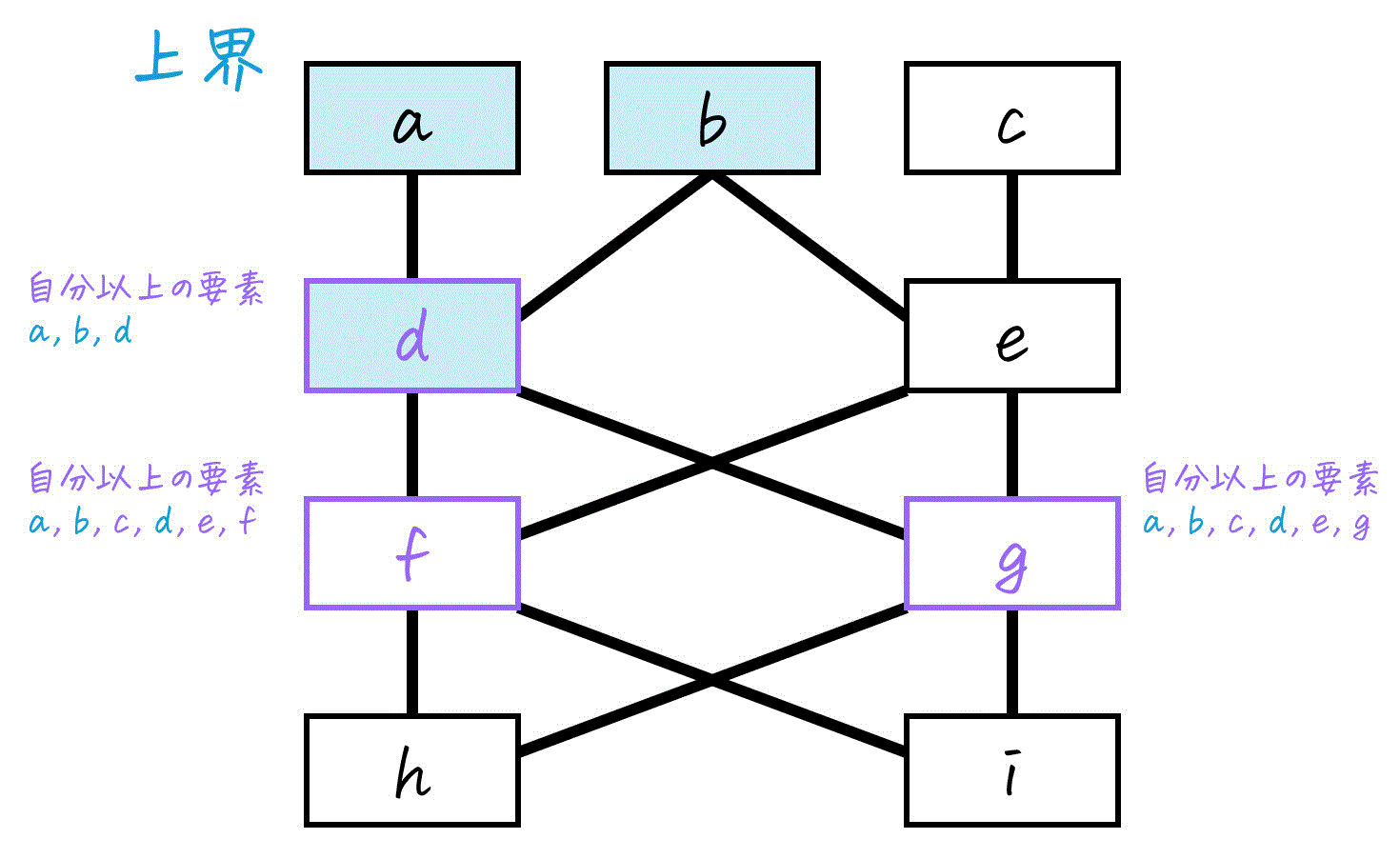
よって、\( S \) の上界は \( a,b,d \) です。

[イ] 下界

\( S \) のメンバーである \( d \), \( f \), \( g \) のすべてに対して、「その要素と同じか、それより下にある」ような要素を \( X \) の中からすべて見つけます。

• \( d \) 以下の要素：\( d \), \( f \), \( g \), \( h \), \( i \)
• \( f \) 以下の要素：\( f \), \( g \), \( i \)
• \( g \) 以下の要素：\( g \), \( h \), \( i \)

これら3つのもので、共通して含まれている要素は \( i \) だけですね。

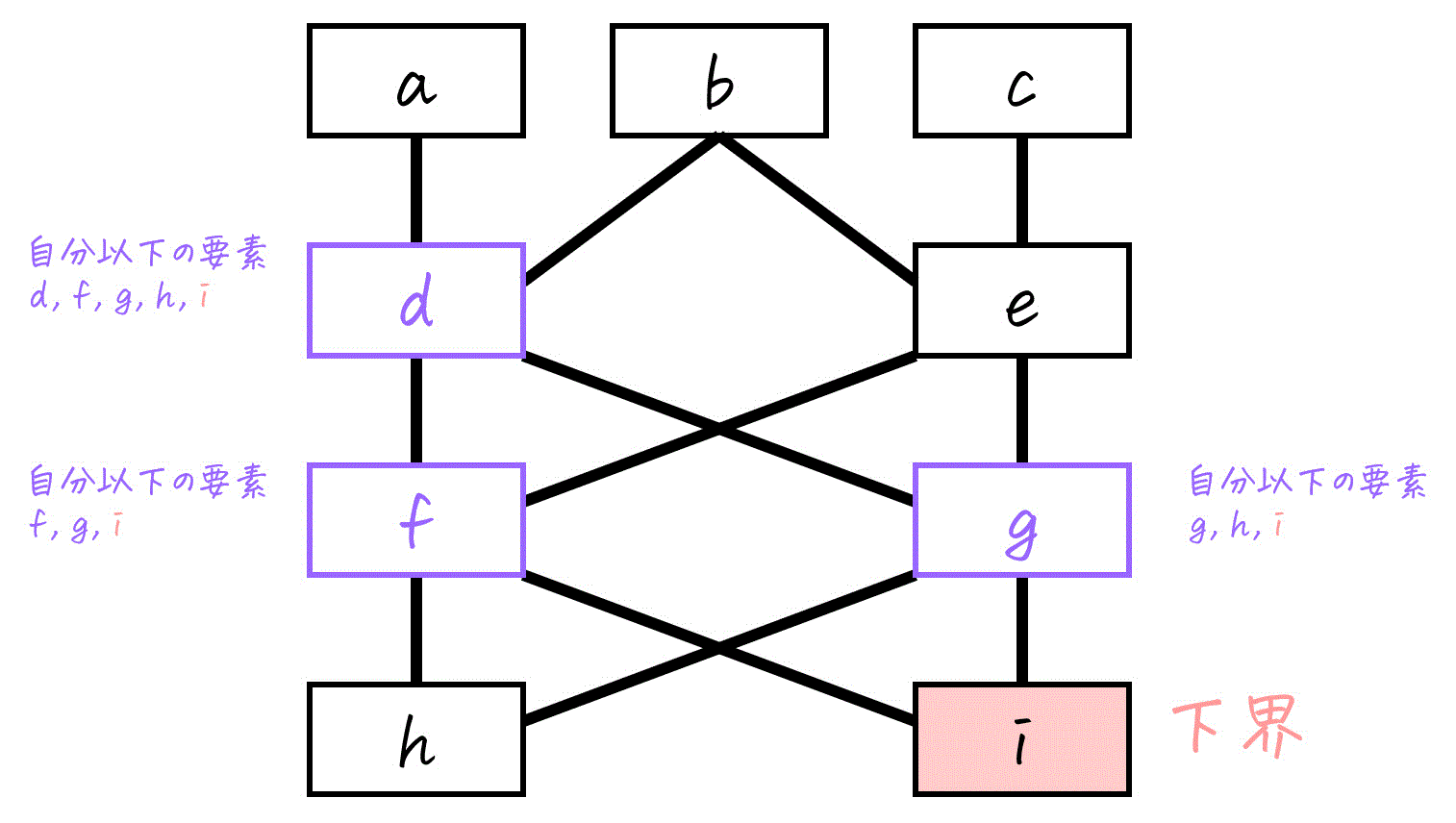
よって、\( S \) の下界は \( i \) です。

[ウ] 最大元

\( S \) のメンバーである \( d \), \( f \), \( g \) の中で、他のどの \( S \) のメンバーと比べても文句なしの1番大きいものを見つけていきましょう。

• \( d \): \( f \), \( g \) より大きいですね。
  → 最大元
• \( f \): \( d \) より小さいですね。
  → 最大元ではない
• \( g \): \( d \) より小さいですね。
  → 最大元ではない。

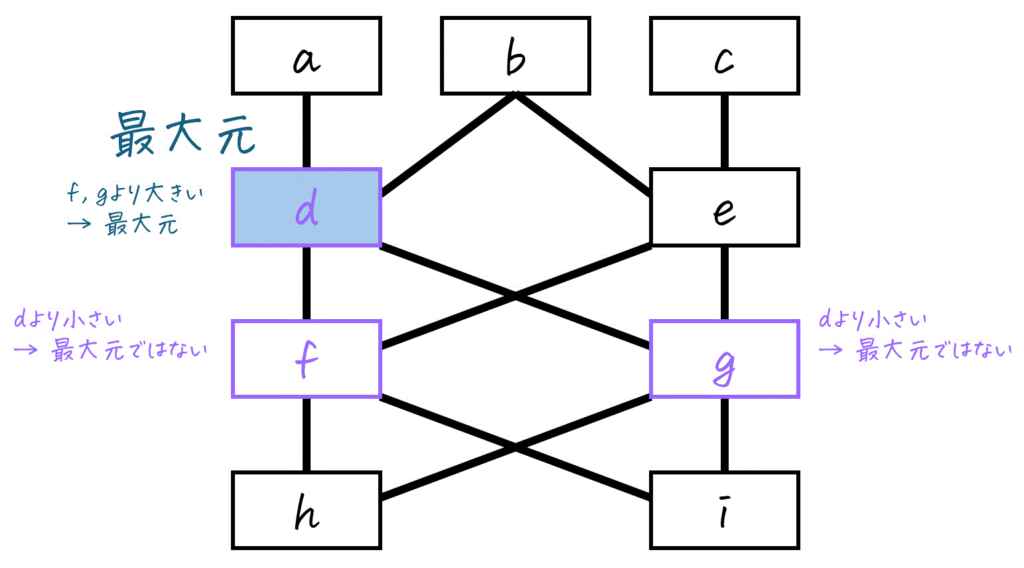
よって、\( S \) の最大元は \( d \) です。

[エ] 最小元

\( S \) のメンバーである \( d \), \( f \), \( g \) の中で、他のどの \( S \) のメンバーと比べても文句なしの1番小さいものを見つけていきましょう。

• \( d \): \( f \), \( g \) より大きいですね。
  → 最小元ではありません。
• \( f \): \( g \) と比較できません。
  → 最小元ではありません。
• \( g \): \( f \) と比較できません。
  → 最小元ではありません。

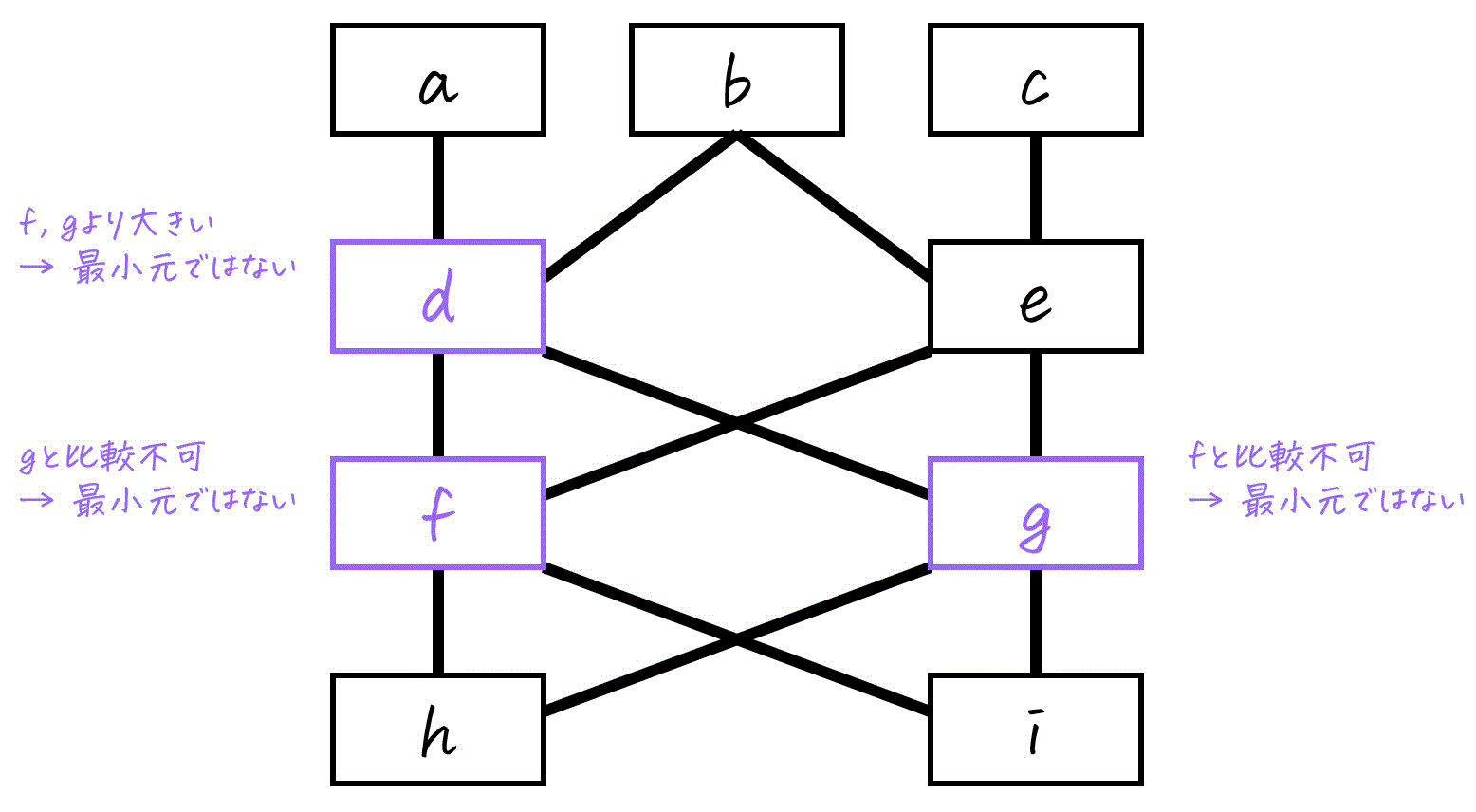
よって、\( S \) の最小元は存在しません。（×）

[オ] 極大元

\( S \) のメンバーである \( d \), \( f \), \( g \) それぞれで、自分より上に \( S \) のメンバーがいないかどうか見ていきましょう。

• \( d \): これ以上大きい要素は \( S \) の中にはいませんね。
  → 極大元。
• \( f \): \( d \) がより大きいですね。
  → 極大元ではありません。
• \( g \): \( d \) がより大きいですね。
  → 極大元ではありません。

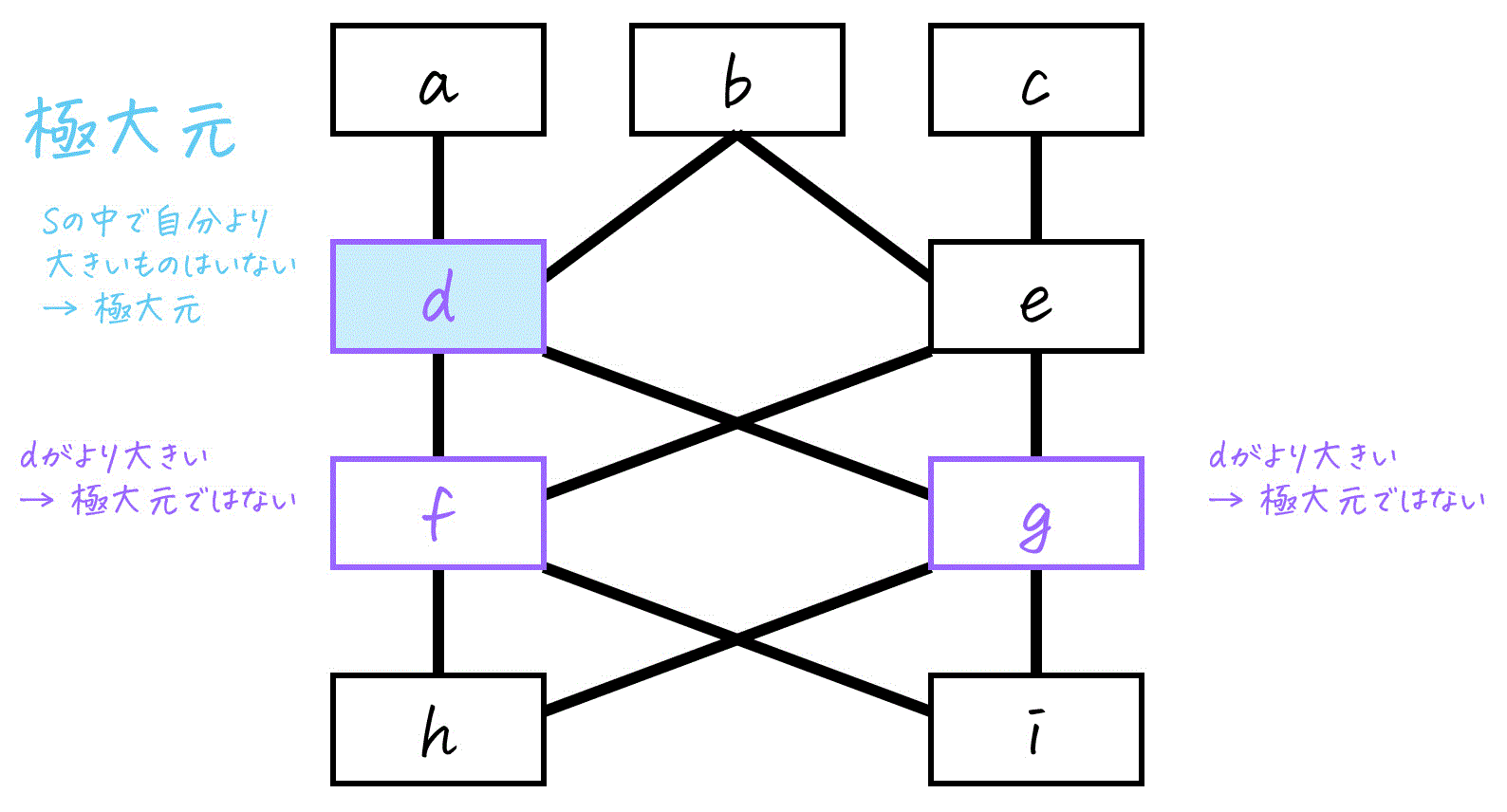
よって、\( S \) の極大元は \( d \) です。

※ 最大元が \( d \) なので、極大元は自動的に \( d \) となります。（最大元があれば、それは必ず極大元です。）

[カ] 極小元

\( S \) のメンバーである \( d \), \( f \), \( g \) それぞれで、自分より下に \( S \) のメンバーがいないかどうか見ていきましょう。

• \( g \): \( f \), \( g \) がより小さいですね。
  → 極小元ではありません。
• \( d \): これより小さい要素は \( S \) の中にはいませんね。
  → 極小元。
• \( f \): これより小さい要素は \( S \) の中にはいませんね。
  → 極小元。

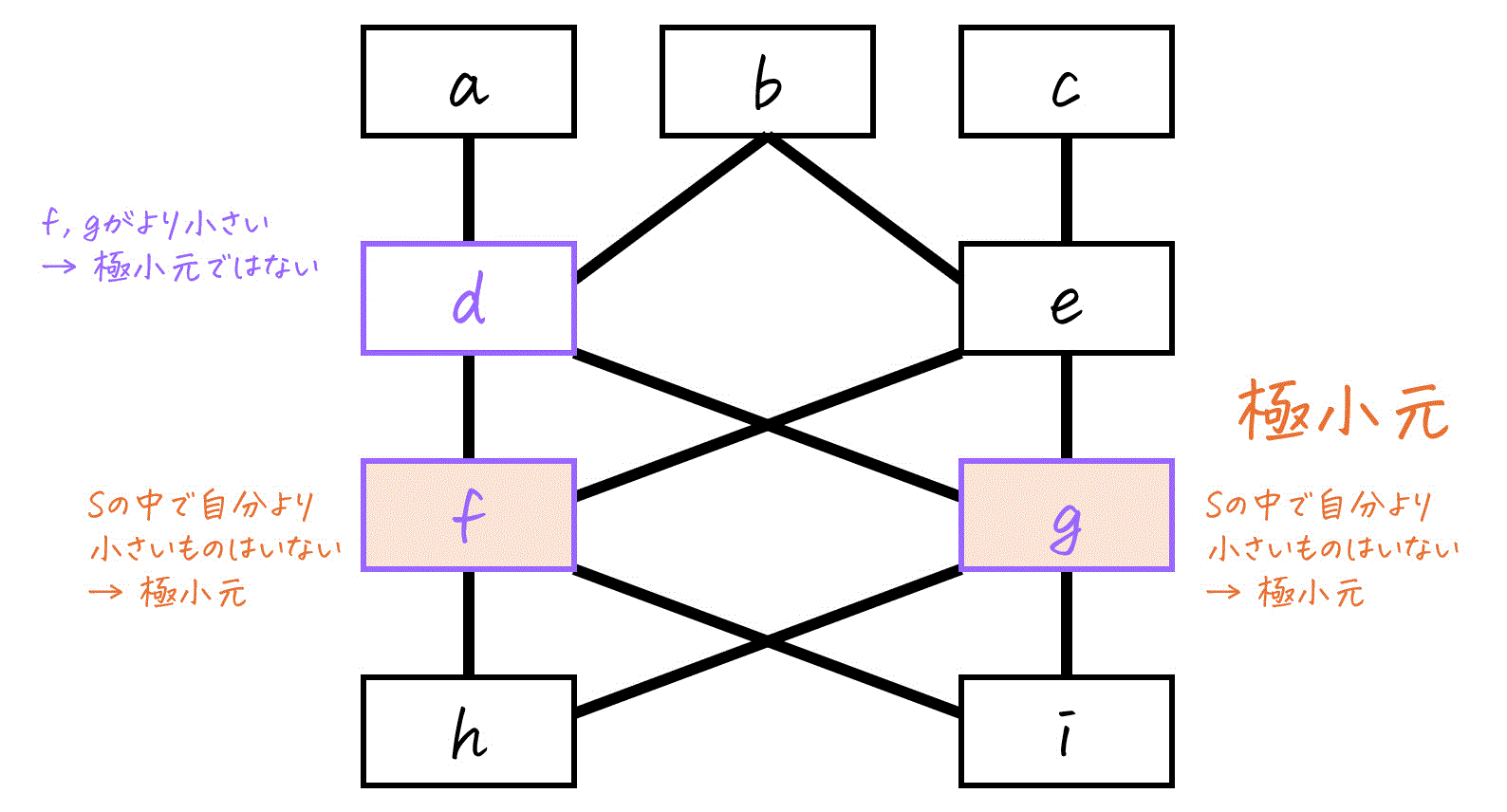
よって、\( S \) の極小元は \( d, f \) です。

[キ] 上限(最小上界)

[ア] で見つけた「上界」の要素たちの中で、文句なしに最も小さいと言える要素を探していきましょう。

ここで、\( S \) の上界は \( a,b,d \) でしたね。

• \( a \): \( d \) の方が小さいですね。
  → 上限ではありません。
• \( b \) \( d \) の方がより小さいですね。
  → 上限ではありません
• \( d \): \( a \), \( b \) より小さいですね。
  → 上限。

[ク] 下限(最大上界)

[イ] で見つけた「下界」の要素たちの中で、文句なしに最も大きいと言える要素を探していきましょう。

ここで、\( S \) の下界は \( i \) でしたね。

下界が1つしかないので、自動的に下限も \( i \) と決定します。

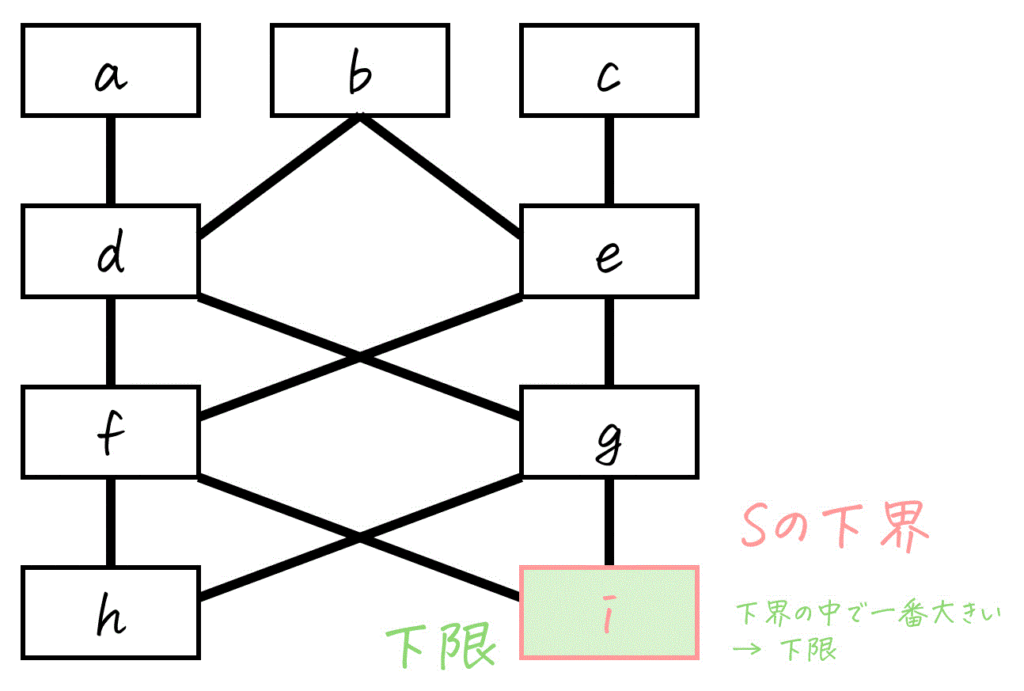
よって、\( S \) の極小元は \( i \) です。

6. テスト勉強の最強の味方！　うさぎ塾オリジナルの学習ツール

(1) 判定ツール（問題を入れると結果を自動で出力！）

「課題の答え合わせをしたいけど、自分の考え方が合っているか不安……」という方におすすめ！

スマホからでもサクサク入力できる「専用ボタン」を搭載した、2つの自動判定ツールを作成しました。

ツール①：述語論理 × ハッセ図 判定ツール

ハッセ図と論理式を入力するだけで、述語論理で記載された式の真偽（成り立つかどうか）を自動で判定・確認できます。

ツール②：順序集合の各種要素 判定ツール

ハッセ図と部分集合 $S$ を指定するだけで、上界/下界、最大元/最小元、極大元/極小元、上限(最小上界)/下限(最大下界) を瞬時に計算して出力します。

(2) ガチ演習ドリル（テスト前の練習に！）

テスト前に「もっとたくさん問題を解いて慣れたい！」という方のために、問題を無限に生成できる演習ツールを作成しました。

テスト前の追い込みや実力試しに、ぜひご活用ください！

ドリル①：述語論理 × ハッセ図 判定ドリル

述語論理で与えられた式が、ハッセ図内で成立するかどうか（真偽）を判定する問題を無限に特訓できます。

ドリル②：上界/下界・最大/最小・極大/極小・上限/下限 判定ドリル

ハッセ図と部分集合が与えられた際に、ややこしい各要素（上界/下界、最大元/最小元、極大元/極小元、上限(最小上界)/下限(最大下界) ）を正確に見つけ出すトレーニングが無限に可能です。

手を動かして、テスト本番でのケアレスミスをなくしましょう！

7. 確認テスト！

最後に、今回の記事で勉強した内容が、理解できているかどうかをどうかを確認するための小テストを作りました！

理解度確認に是非チャレンジしてみてください！

※ 回答フォームに入力後、自動採点 & 自動解説表示が行われます。

※ 小テストは2026年5月下旬～6月上旬にかけてリニューアル予定です。リニューアルまで、半順序の記号が \( \sqsubseteq \) ではなく、\( \preceq \) となっております。ご注意ください。

確認テストだけでは足りないよという人がいましたら、追加の練習フォームもどうぞ。