スポンサードリンク
こんにちは、ももやまです。
今回は最大フロー・最小カットの求め方をメインにまとめていきたいと思います。
前回の記事(第14羽)はこちら!
ダイクストラ法を用いた最短経路の出し方ついてです!
目次
スポンサードリンク
1.フロー・最大フローとは
まず最初に最大フローの「フロー」とはなにかを簡単にですが説明しましょう。
フローとは、ある場所(スタート)からある場所(ゴール)まで「運んだ荷物の量」、「流した水の量」などを表します。
しかし、無制限に流せるなんてことはありませんね。荷物であれば「制限重量」、水であれば「流量制限」などがかかることが多いです。
最大フローとは、それぞれのルートの間に「制限重量」や「流量制限」などがかかっている場合に、ある場所(スタート)からある区間(ゴール)まで最も多く運べる(流せる)ルートを表します。
スポンサードリンク
2.重みつき有向グラフ
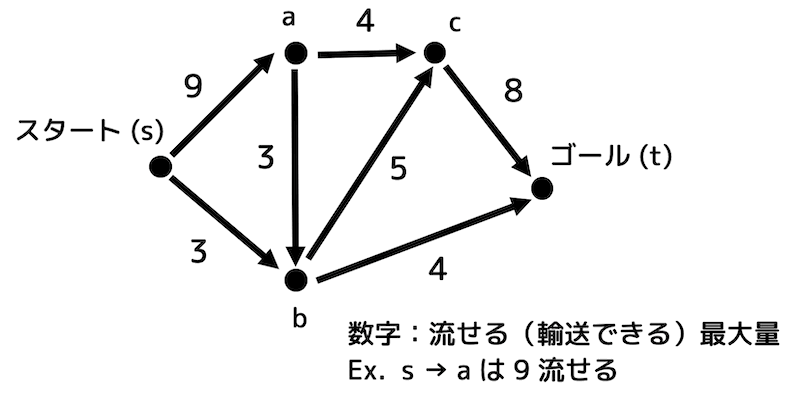
フローを考える際に出てくる「流量制限」や「制限重量」は下のような重みがついた有向グラフで考えます。この有向グラフのことをネットワークと呼んだりします。
例えば、\( s \) から \( a \) には最大9まで流せる(運べる)ことを示しています。
また、それぞれの点から点まで流せる(運べる)上限値のことを容量と呼びます。
実際にフローをグラフで示すときは、下のように「(フロー) / (容量)」と書くことが多いです。
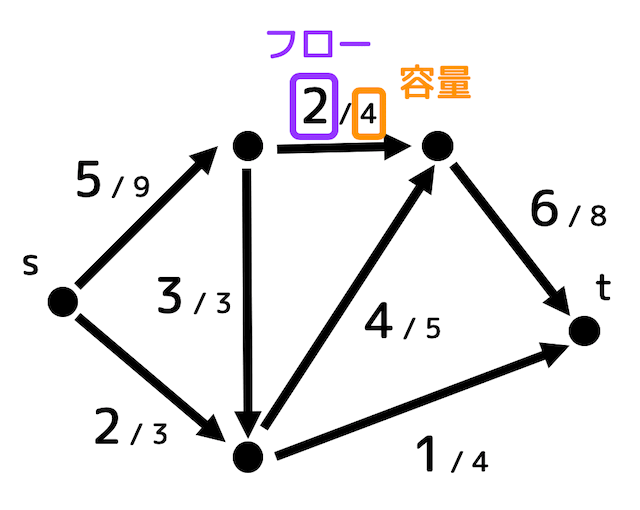
このように書くことで、上限値に対し、現在どれだけ運んでいるかが明確になるからです。
この図の場合、スタート \( s \) からゴール \( t \) まで合計7運んでいる(流している)ので \( s \) から \( t \) までのフローは7となります。。
スポンサードリンク
3.残余ネットワーク
最大フローを求める際には残余ネットワークを考えます。
残余ネットワークとは、あとフローをどれだけ追加でき、どれだけ戻すことができるかを重みつき有向グラフで表したものです。
例えば下のようなフローを考えてみましょう。
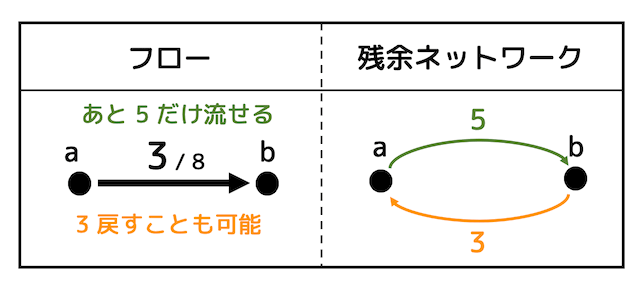
\( a \) から の容量は8に対し、現在のフローは3ですね。
なので、\( a \) から \( b \) にさらに5流すことができますね。
また、今まで流したフローを戻すこともできますね。言い換えると \( b \) から \( a \) に今まで流した3を戻してあげられますね。
なので残余ネットワークは \( a \) から \( b \) まであと5流せる緑色の辺と \( b \) から \( a \) まであと3流せるオレンジの辺で構成されます。
4.最大フローの求め方
では最大フローを求める方法(アルゴリズム)を説明していきます。
最大フローは下のような手順で求めることができます。
あるネットワークのスタート \( s \) からゴール \( t \) までの最大フローは下のような手順で求めることができる。
- 全部のフローが0の状態をはじめの状態(初期フロー)とし、初期フローのときの残余ネットワーク(与えられたネットワークと同じ)を考える。
- 残余ネットワークで \( s \) から \( t \) までたどれるような道(ルート)を見つけ、その道に流せるだけのフローを流す。(この道のことを増大道と呼びます)
- 2を繰り返し、\( s \) から \( t \) まで流せる道がなくなったときのフローが最大フローとなる。
最大フローの求め方
例として最初に説明したこちらのネットワークの最大フローをもとめていきたいと思います。

最初は何も流していないので当然どのフローも0です。
なので残余ネットワークは例で与えられたネットワークと同じになります。
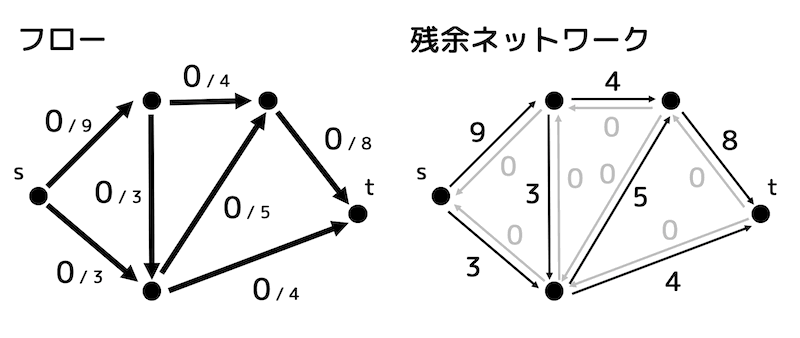
適当に \( s \) から \( t \) までの道を1つ考えます。
下の図のような道(ルート)を選ぶと最大で4流せますね。なので流した部分のフローすべてに4を追加します。
このような流す道のことを増大道と呼びます。
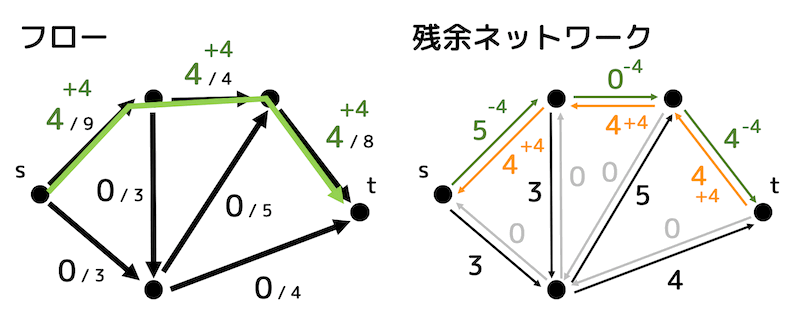
追加したら残余ネットワークも変化するので、残余ネットワークも書き換えておきましょう。
残余ネットワークを見てみると、まだ \( s \) から \( t \) までたどる道がありそうですね。なので今度は別の道を選んでみましょう。
下の図の道であれば最大で3流せますね。なので流した部分のフローすべてに3を追加します。残余ネットワークの書き換えも忘れずに。
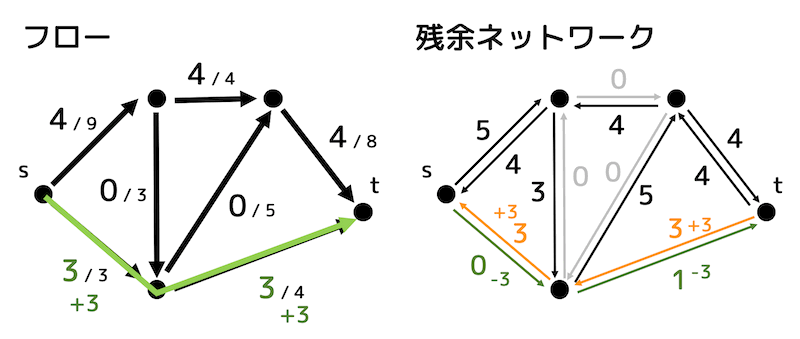
また別の道を考えてみましょう。
下のような道でも最大3流すことができますね。なので流した部分のフローに3を追加します。
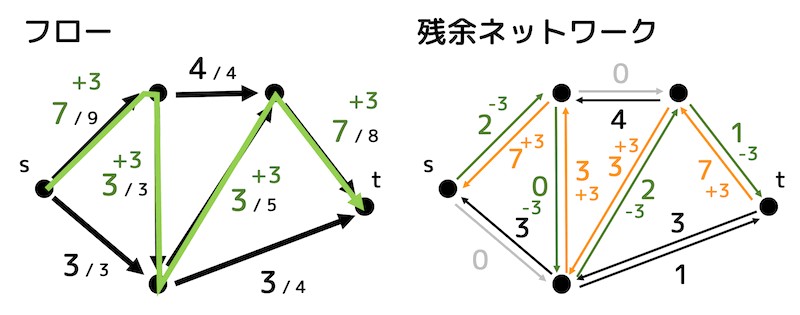
残余ネットワークを見てみると、 \( s \) から \( t \) までたどれる道がもうありませんね。
なのでこれ以上フローが増やせないことがわかります。
つまり、今のフローが最大フローであることがわかります。
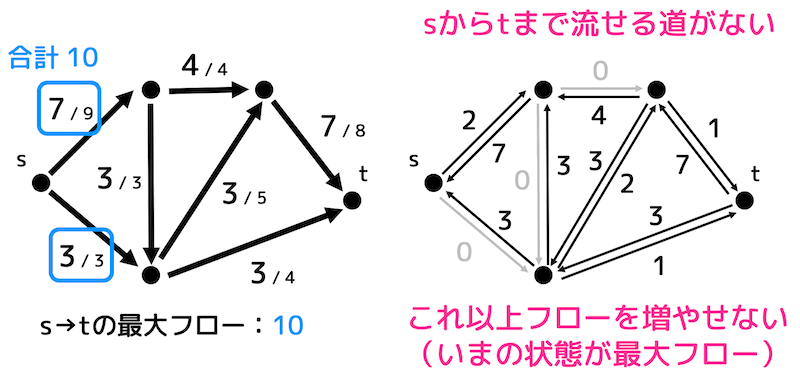
今回の場合、\( s \) から \( t \) まで最大10流せることがわかりますね。
(\( s \) から7と3流しているので合計10流していることがわかる。)
5.残余ネットワークを考える理由
フローを追加するのに残余ネットワークをみていきましたね。
しかし、なぜ残余ネットワーク(どれだけ戻すことができるのか)を見る必要があるのでしょうか。
戻すことを考えずに(あとどれくらい追加できるのかだけを考えて)やってみましょう。
下の4本の増大道(運び方)を考えます。
すると、フローは9になりますね。しかしこれ以上追加できる辺はありませんね。
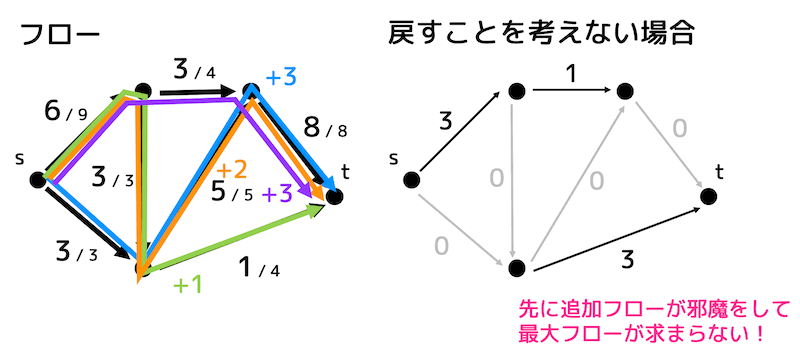
先に追加した増大道が邪魔をして最大フローである10を求めることができませんね。
上のフローが9の状態から残余ネットワーク(戻すこと)を考えてやってみましょう。
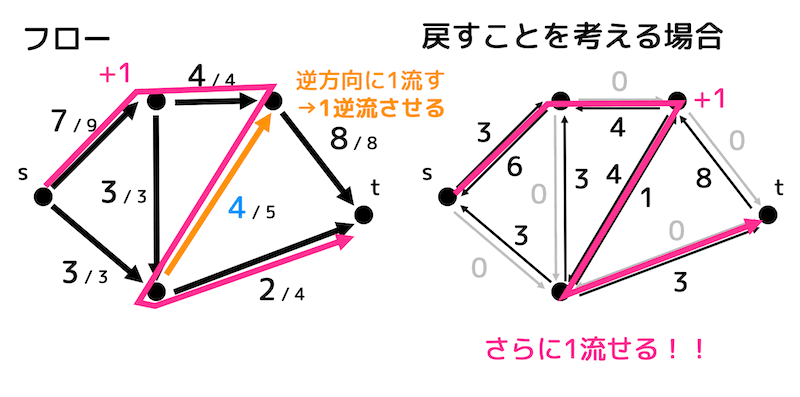
すると、オレンジ色の辺を1逆流させることでさらに1流せますね!
このように残余ネットワークを考えることで、最初追加した増大道が邪魔をしても後から逆流させることで正しく最大フローを求めることができるのです!
6.カット・最小カット
(1) カットとは
ネットワークのそれぞれの点を2つのグループにわけることカットといい、\( E ( S, \overline{S} ) \) と表します。
一方のグループをフローのスタート点 \( s \) が含まれる \( S \)、\( S \) に属さないもう一方のグループ \( \overline{S} \) をゴール点 \( t \) が含まれるようにします*1。
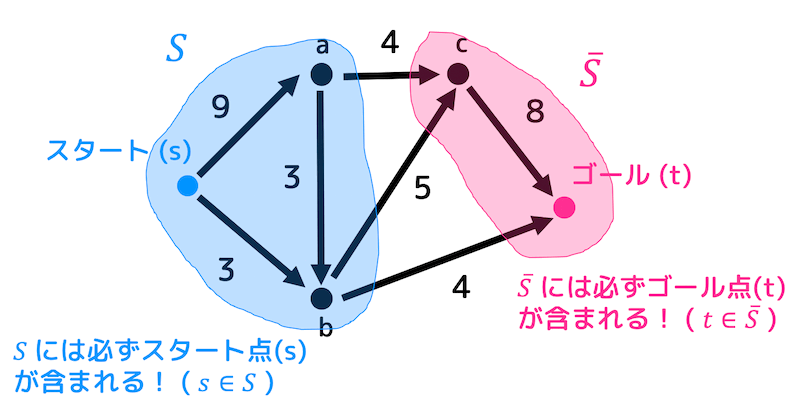
上の図の場合、\( S = \{s,a,b\} \) となりますね。
スタート点 \( s \) とゴール点 \( t \) 以外の頂点は \( S \), \( \overline{S} \) どちらに属してもよいので、頂点数 \( n \) のときのカットの種類の数は \( 2^{n-2} \) 通りあります。
また、\( S \) に属する点から \( S \) に属さないグループ(つまり \( \overline{S} \) に属するグループ)にたどる辺の重みの合計のことをカットの容量と呼び、\( U(S, \overline{S} \) や \( c( S, \overline{S}) \) と表します。
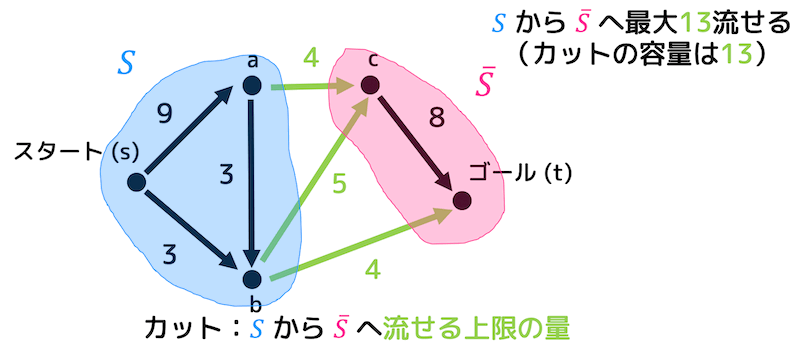
上の図の場合、緑色の辺で表された3つの辺が \( S \) から \( \overline{S} \) にたどる辺となります。また3つの辺の重みの合計は13なので、カットの容量も13となります。
つまり、\( S \) から \( \overline{S} \) へ最大13流せることがわかりますね。
カットの容量 \( U(S, \overline{S}) \) と最大フロー \( f_{max} \) には常に以下のような関係が成り立ちます\[
f_{max} \leqq U(S, \overline{S})
\]つまり、カットの容量は常に最大フロー以上となるのです!
簡単な理由
カットの容量はスタート \( s \) が含まれるグループ \( S \) から、ゴール \( t \) が含まれるグループ \( \overline{S} \) まで流すことのできる最大量を表していますね。
\( S \) から \( \overline{S} \) へ流せる最大量がスタート \( s \) からゴール \( t \) を超えることはありえませんよね。
なので、カットの容量 \( U(S, \overline{S}) \) は少なくとも最大フロー \( f_{max} \) 以上である必要がありますね。
あるネットワークの点を2つのグループ \( S \), \( \overline{S} \) にわけることをカットと呼ぶ。(ただし \( S \) はスタート点 \( s \)、\( \overline{S} \) はゴール点 \( t \) が入っている必要あり。)
また、グループ \( S \) からグループ \( \overline{S} \) に流せる上限量のことをカットの容量 \( U(S, \overline{S} \) と呼び、必ず最大フロー以上となる。
(2) 最小カットとは
あるネットワークのカット中で、カットの容量が最小になるカットのことを最小カットと呼びます。
先程のネットワークの場合、下のようなカットが最小カットとなります。
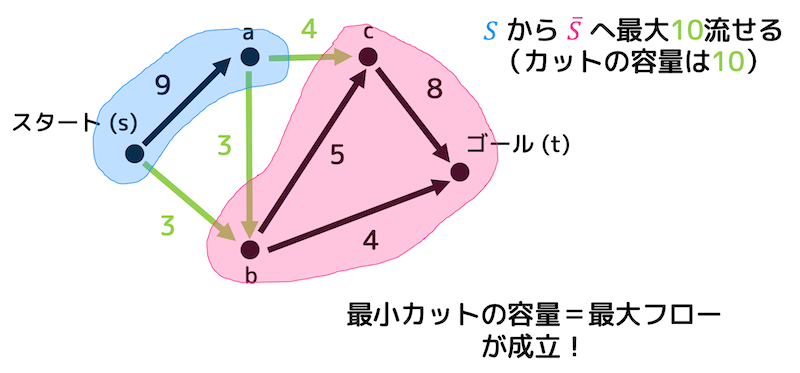
最小カットにおける重要な性質の1つに、最小カットと最大フローは必ず等しいというのがあります。
簡単な理由(?)
上の図の最小カットのときの残余ネットワークをみてみましょう。
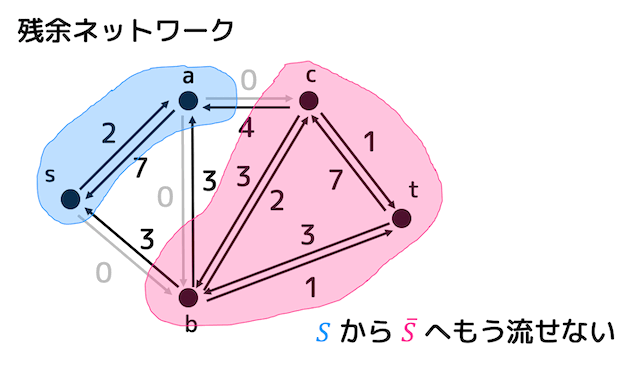
\( S \) から \( \overline{S} \) に流せるような辺が1つも存在しませんね。
つまり、\( S \) から \( \overline{S} \) に流せる最大量をすべて流している状態となっていますね。
なので、最小カットの容量は最大フローと等しくなるのです!
ちなみに最小カット \( S \) から \( \overline{S} \) に流せるような辺が存在しないということは、スタート点 \( s \) からたどれる点はすべて \( S \) のグループに属するということができます。
つまり、スタート点 \( s \) からたどれる点からなる集合が最小カット \( S \) になることがわかりますね。
(最小カット \( S \) は残余ネットワーク内の \( s \) からたどれるすべての点の集合からなる。今回の場合だと最小カットは \( S = \{s,a \} \) となる。)
あるネットワークの中でカットの容量が最小となるようなカットを最小カットと呼ぶ。
また、最小カット の容量と最大フローは必ず等しくなるので、最大フローを求めることで最小カットの容量を求めることができる。
さらに最小カット \( S \) はスタート点 \( s \) からたどれる点をすべて集めた集合となる。
7.練習問題
では、1問だけですが練習してみましょう!
問題
現在渋谷はイベント終了直後で、東京まで帰る人で人がごった返している。
そこで1人でも多く東京駅まで届けるためにはそれぞれのルート間で何人ずつ輸送すればいいかを調べたい。
ただし、下の図(グラフ)の矢印の方向にしか人は輸送できないものとし、矢印の上に書かれている数字は輸送できる人数の上限を表している(1単位は1,000人)。
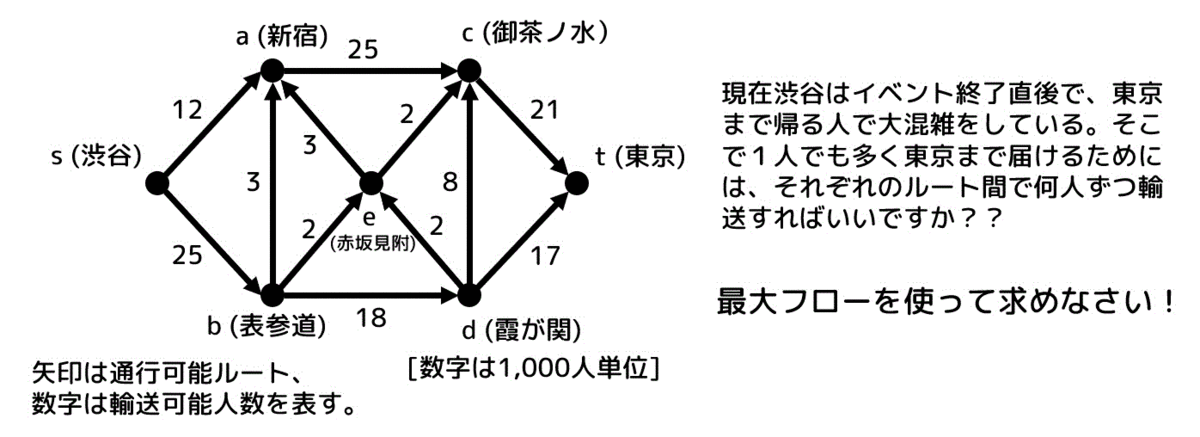
(1) それぞれのルート間で何人ずつ輸送すればいいかを答えなさい。また、全体で何人輸送することができるのかも答えなさい。
(2) グラフの最小カット、および最小カットの容量を求めなさい。
(地名ではなく、アルファベットを使って答えてもOK)
8.練習問題の答え
(1)
最大フローが35と求められるので最大で35,000人輸送することができる。
最大フローのときのそれぞれのフロー値、および残余ネットワークは下のようになる。
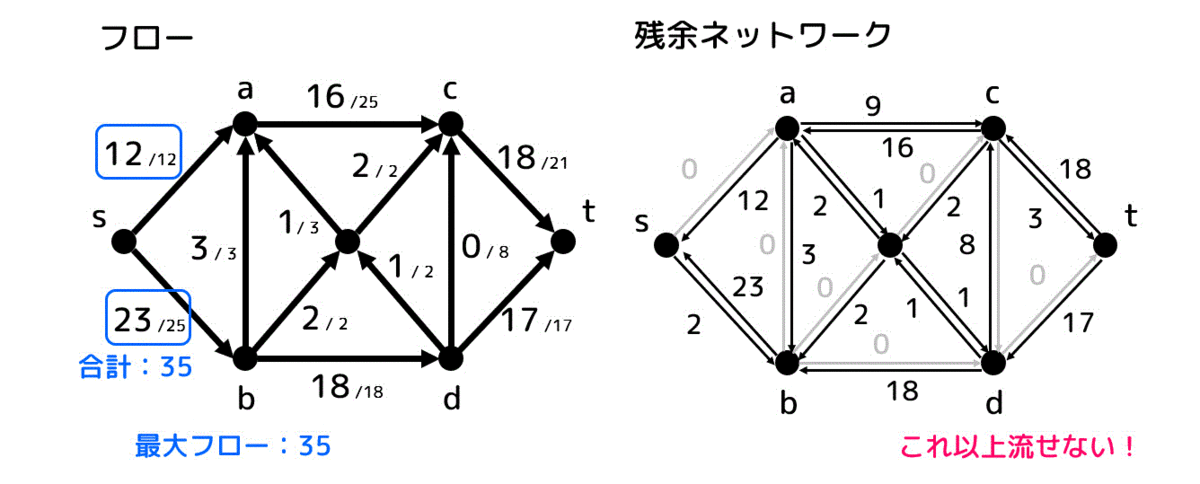
フローを追加していくときの過程をアニメーションにしています(増大道の選び方)

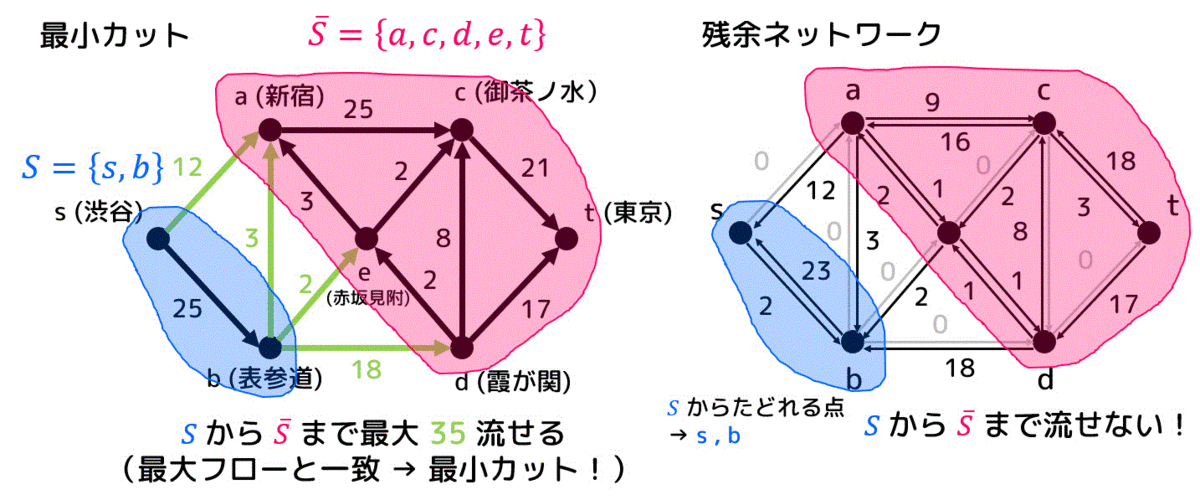
(2)
残余ネットワークのグラフを見ると、スタート点 \( s \) からたどれる点は \( s \), \( b \) の2つである。
よって、\( S = \{s,b\} \) とすることで最小カット \( E(S, \overline{S} ) \) を求められる。
また、最小カットの容量は \( S \) から \( \overline{S} \) に流せる最大量なので35(35,000)となり、最大フローと一致する。
9.さいごに
今回は最大フロー、最小カットを求める方法をまとめました。
最大フロー問題は運送問題などはもちろんのこと、通信分野などでも応用されています。
次回はグラフの点連結・辺連結についてまとめていきたいとおもいます。
*1:一応念のため補足すると \( \overline{S} \) は \( S \) の補集合です。
関連広告・スポンサードリンク