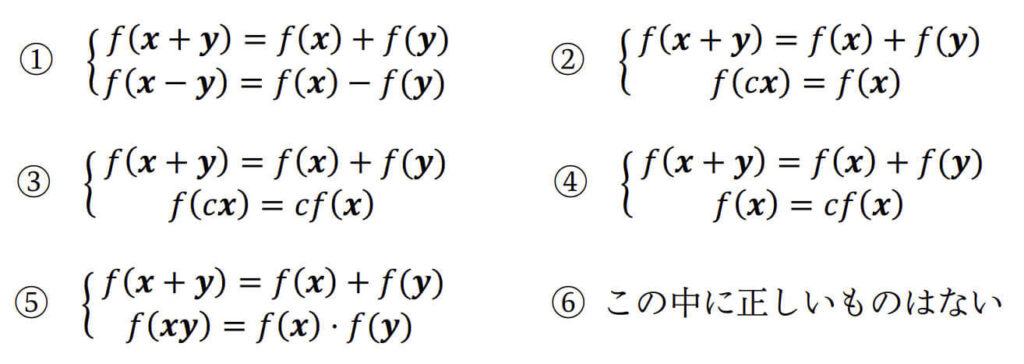
スポンサードリンク
こんにちは、ももやまです。
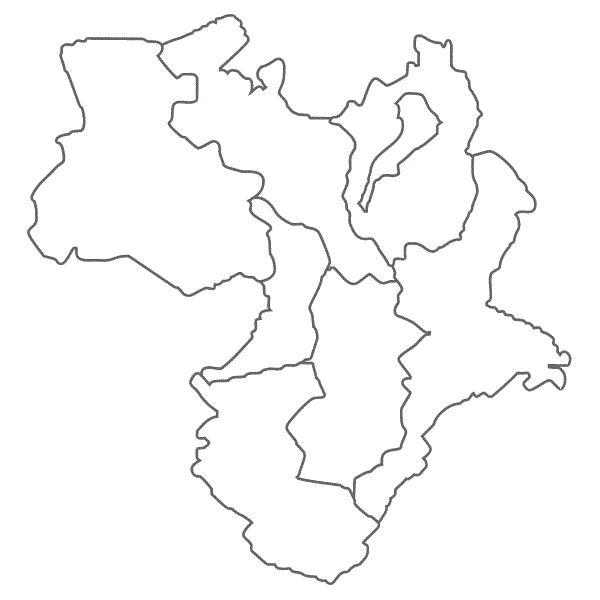
今回はグラフの彩色問題や、彩色問題を応用して下のような地図を塗り分ける方法などについてまとめています。
前回の離散数学(グラフ理論)の記事はこちら!
平面グラフ・平面的グラフについてです。
目次
スポンサードリンク
0.はじめに
彩色問題は点彩色(頂点を塗り分けていく)と辺彩色(辺を塗り分けていく)の2つにわかれます。
今回は点彩色、辺彩色の両方についてまとめていきます。
後ほど説明しますが、下のような地図を塗り分ける問題は点彩色を用いることで解くことができます。
考えてみよう!
何色あれば上の地図(近畿地方)を府県ごとに色分けすることができるでしょうか?
スポンサードリンク
1.点彩色
(1) 点彩色とは
隣り合うどの2点も異なる色になるようにグラフの頂点を色わけすることを点彩色といいます。(頂点彩色、もしくは単に彩色とも呼ばれることもあります。 )
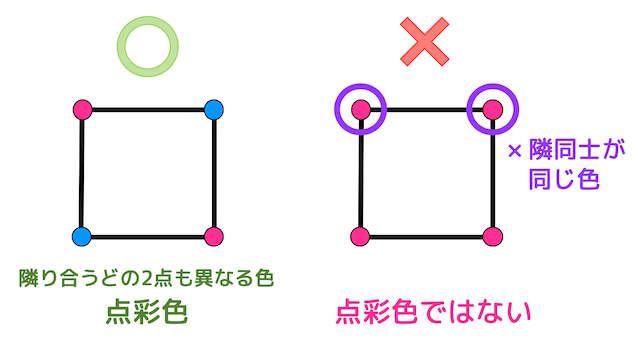
例えば左側のグラフは隣り合うどの2点も異なる色に色分けしているので点彩色となっていますが、右側のグラフは隣同士を同じ色に色分けしてしまっているので点彩色ではありません。
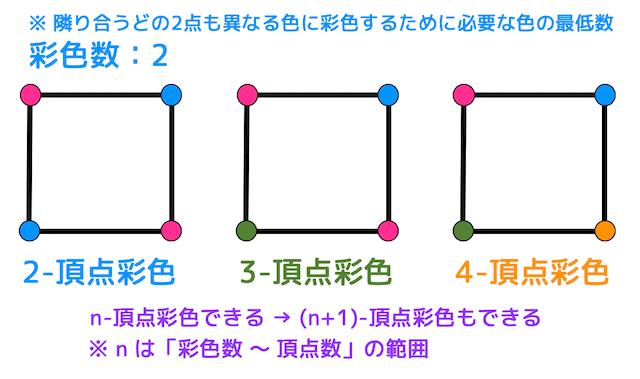
(2) n-頂点彩色
あるグラフを \( n \) 色で彩色することを、n-頂点彩色といいます。
例えば、左側のグラフは2色で彩色していますね。なので2-頂点彩色となります。
また、真ん中や右側にあるグラフのように、より多くの色を使って3色(3-頂点彩色)や4色(4-頂点彩色)で彩色を行うこともできます。
なのでn-頂点彩色できるグラフは必ず(n+1)-頂点彩色もできます*1。
(3) 彩色数
あるグラフ \( G \) がn-頂点彩色可能なときの \( n \) の最小値のことを彩色数と呼びます。
言い換えると、グラフ \( G \) を彩色するために必要な色の最低数を彩色数といいます。

上のグラフの場合、彩色するために少なくとも2色は必要ですよね(明らかに1色では彩色できない)。
なので、彩色数は2となります。
あるグラフ \( G \) の頂点を隣り合っているどの2点も異なる色になるように色分けすることを点彩色(彩色)と呼ぶ。
また、グラフ \( G \) の頂点を \( n \) 色で彩色することを n-頂点彩色と呼び、最小の \( n \)、つまりグラフ \( G \) の頂点を彩色するために必要な色の最低数のことを彩色数と呼ぶ。
(4) 彩色数に関する2つの定理
彩色数に関する定理が2つあるので紹介していきたいと思います。
まずは完全グラフと彩色数についての定理です。
頂点数 \( n \) の完全グラフ \( K_n \) の彩色数は \( n \) である。
完全グラフはどの2点の間にも辺があるため、どの2点とも隣り合っていますね。なので、どの頂点も異なる色で着色しないと、隣同士が同じ色になってしまいますね。
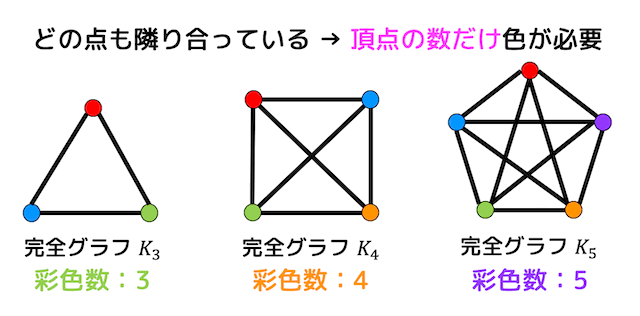
また、2部グラフと彩色数に関する定理もあるので紹介したいと思います。
2部グラフの彩色数は2である。
2部グラフは頂点を2つのグループにわけたときに同じグループ同士で辺を結んでいない(隣り合わない)ようなグラフでしたね。
なので一方のグループすべてに同じ色 \( C_1 \) を塗り、もう一方のグループすべてに最初のグループとは異なる色 \( C_2 \) を塗ると2色で彩色することができますね。
なので2部グラフの彩色数は必ず2となります!
スポンサードリンク
2.Welch-Powellの点彩色アルゴリズム
(1) アルゴリズムの紹介
実際にグラフを点彩色するときに大変便利なアルゴリズムとして、Welch-Powellの点彩色アルゴリズムがあります。
Welch-Powerllの点彩色アルゴリズムを使うことでなるべく少ない色数で点彩色を求めることができます。
(なるべく少ない色数で彩色を行うため、グラフの彩色数も求めることができます)
ループを持たないグラフの点彩色は以下のようにして求めることができる。
- それぞれの頂点における次数を調べ、次数が大きい順に頂点を並び替える。
- 次数が一番大きい点に色 \( C_1 \) を塗る。さらに、次数が大きい順に色 \( C_1 \) を塗った点と隣接してない点に同じ色 \( C_1 \) を塗る。
- まだ塗られていない点の中で次数が一番大きい点に別の違う色 \( C_2 \) を塗る。さらに次数が大きい順に色 \( C_2 \) を塗った点と隣接してない点に同じ色 \( C_2 \) を塗る。
- すべての頂点が塗られるまで3を繰り返す。
Welch-Powellの点彩色アルゴリズム
※注意:次数が大きい順に点を選ぶ際に次数が同じ点がある場合、選んだ点によって正しく彩色数が求められないことがあります。
(どの点を選んでも必ず最小の色数になるとは限らない)
(2) アルゴリズムの動きかたの例
アルゴリズムの動きを確認してもらうため、実際に1つグラフを彩色してみましょう。
今回は最初の例に出した下の地図をグラフとみなして色塗りしていきたいと思います。
例題1
次の2府5県(近畿地方)をなるべく少ない色数で塗り分けなさい。
(ただし隣り合っている府県が同じ色にならないように塗り分けること)

ヒント
それぞれの府県を頂点、隣り合っている県同士を辺で結び、作成したグラフの点彩色を行うことで、隣り合っている府県が同じ色にならないように彩色することができます。
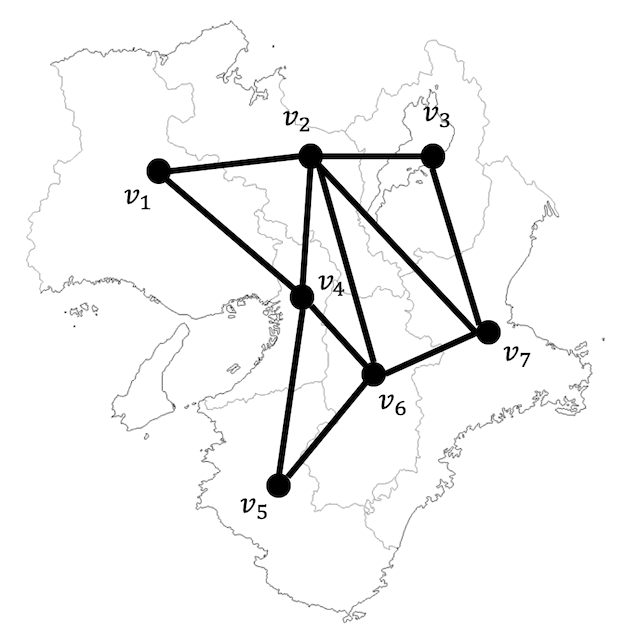
つまり、「上のグラフをなるべく少ない色数で点彩色」すればOK。
解説1
Welch-Powellの点彩色アルゴリズムを用いて作成したグラフの点彩色を求めていきます。
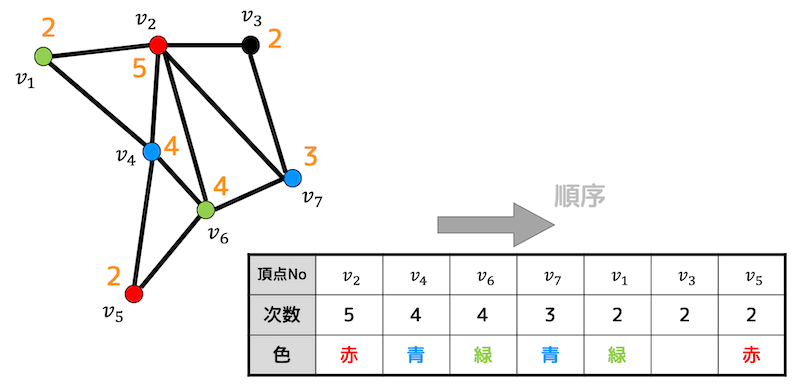
Step1 それぞれの頂点の次数を並べ、次数が大きい順に並べる
まずはグラフの次数を並べ、次数が大きい順に頂点を並べてみましょう。
するとそれぞれの次数は下のようになります。さらに次数が大きい順に頂点を並べましょう。
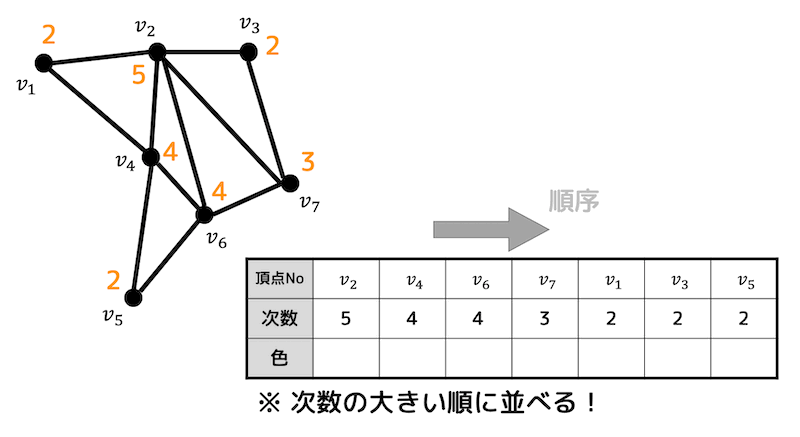
Step2 1色目(赤)を塗る
まず、次数が一番大きい点 \( v_2 \) に1色目(赤)を塗ります。
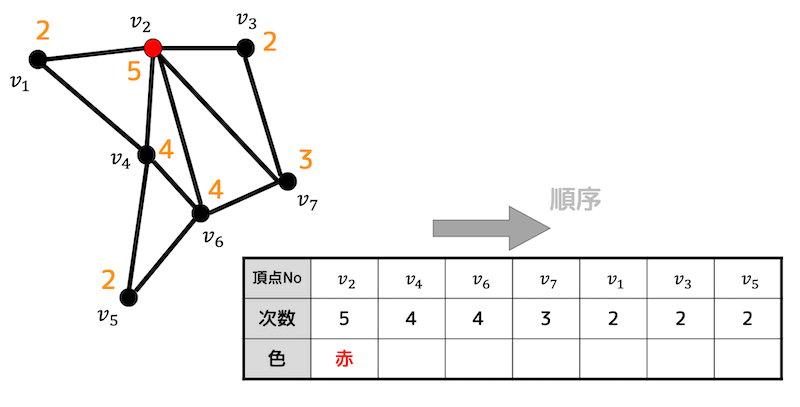
つぎに \( v_2 \) と隣り合っていない点を探します。
\( v_5 \) 以外はすべて \( v_2 \) と隣り合ってしまっているので \( v_5 \) に赤色を塗ります。
(もしここで隣り合っていない頂点が2つ以上ある場合は、隣り合っていない頂点の中で一番次数が大きい頂点に赤色を塗ります)
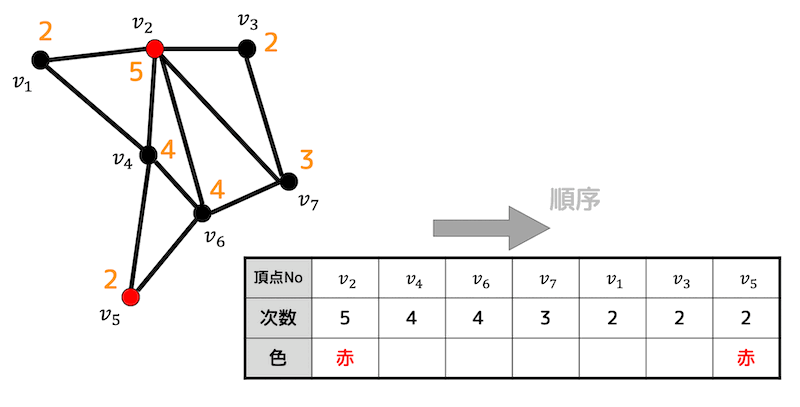
赤色で塗れる点がなくなったのでStep1終了です。
Step3 2色目(青)を塗る
つぎにまだ塗られていない5点の中で一番次数が大きい点(\( v_4 \), \( v_6 \) のどちらか)に2色目(青)を塗ります。
\( v_4 \), \( v_6 \) のどちらを選んでもいいですのですが、今回は番号が小さい \( v_4 \) に2色目(青)を塗ろうと思います。
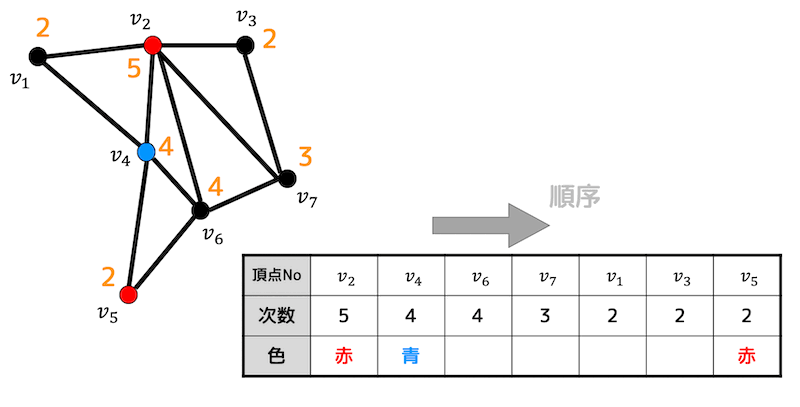
つぎに青色に塗った \( v_4 \) と隣り合っていない点を探します。すると \( v_3 \), \( v_7 \) が隣り合っていないことがわかりますね。
2つの点のうち、より次数が大きいのは \( v_7 \) なので、\( v_7 \) に青色を塗ります。
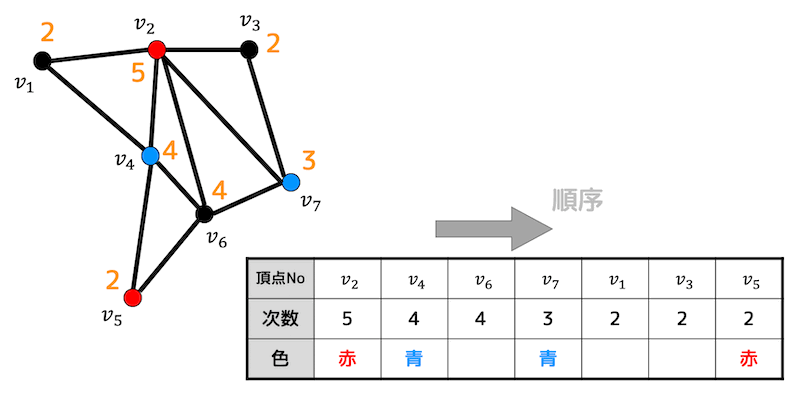
青色で塗れる点がなくなりましたね。
なのでStep3終了です。
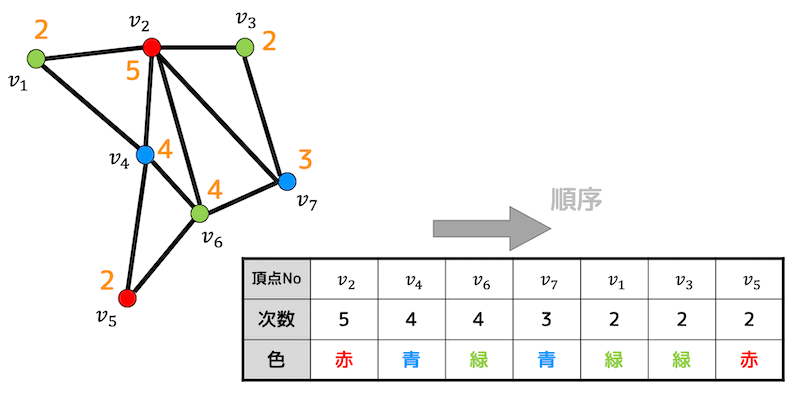
Step4 3色目(緑)を塗る
まだ塗られていない3点の中で一番次数が大きい点は \( v_6 \) なので \( v_6 \) に3色目(緑)を塗ります。
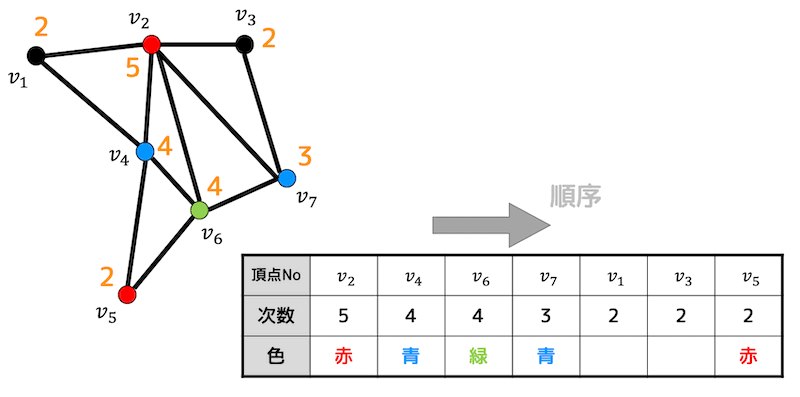
つぎに緑色に塗った \( v_6 \) と隣り合っていない点を探します。すると \( v_1 \), \( v_3 \) が隣り合っていないことがわかりますね。
2点の次数はともに同じ(両方とも2)なので、番号が先の \( v_1 \) から緑色で塗ります。
\( v_3 \) を緑に着色しても、緑色に着色した \( v_1 \), \( v_6 \) とは隣り合わないので \( v_3 \) も緑で着色します。
すべての点が着色できたので彩色完了です!
着色済みのグラフより、彩色数は3となります。
また、実際に上の結果を用いて近畿地方を彩色すると下のようなります。
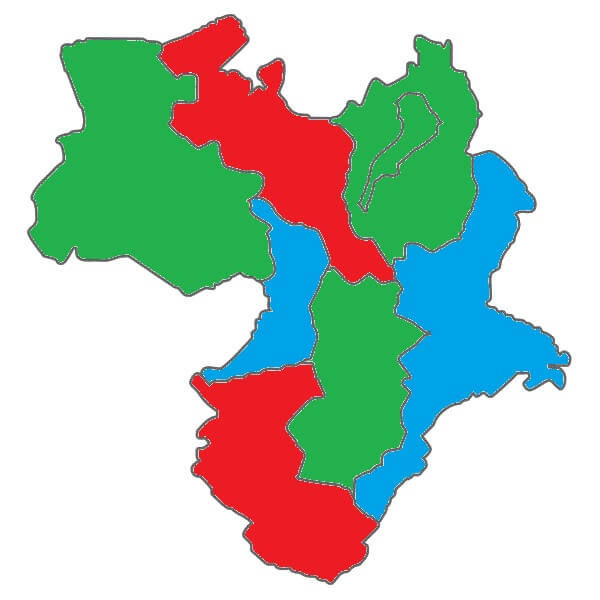
確かに3色あれば隣り合う府県が異なる色になるように彩色することができますね!
3.点彩色と平面グラフ
平面グラフと点彩色には一定色以内で塗ることができるという面白い定理があるので紹介したいと思います。
また、地図は必ず平面グラフを用いて表すことができるので、地図も一定色で塗ることができるのです!
今回は平面グラフ(地図)が一定色で塗ることができることを(一部を除いて)簡単な理由、証明とともにまとめていきたいと思います。
※ 平面グラフとは2辺が途中で交差していないようなグラフのことを表します。平面グラフについての詳しい記事はこちらをご覧ください。
(1) 6色定理
まずは簡単に証明できる6色定理からいきましょう。
平面グラフは必ず6-頂点彩色ができる。
つまり、平面グラフの彩色数は必ず6以下となる。
(どんな地図でも6色以内で彩色することができる。)
では簡単にですが証明していきましょう。頂点数に関する数学的帰納法で証明します。
(i) 頂点数が6以下のとき
頂点数が6以下であれば、すべての頂点を異なる色で塗っても彩色数は6以下ですよね。なので頂点数が6以下であれば必ず6色定理が成立します。
(ii) 頂点数がn+1のとき
では頂点数 \( n \) のときに6色定理が成り立つことを仮定してから頂点数が \( n+1 \) 個のときに6色定理が成り立つことを示しましょう。
まず、平面グラフには次のような定理がありましたね。
連結で単純な平面的グラフであれば、次数5以下の点が必ず1つ以上存在する。
(当然平面グラフも平面的グラフであるので成立する)
平面グラフには次数が5以下の点が必ず1つは存在しますよね。
頂点数が \( n+1 \) の平面グラフ \( G_1 \) から、次数が5(以下)の点 \( v_1 \) を削除したグラフ \( G_2 \) を考えます。
すると、\( G_2 \) の頂点数は1つ減って \( n \) となりますね。このグラフ \( G_2 \) が平面グラフであると仮定します。(帰納法の仮定)
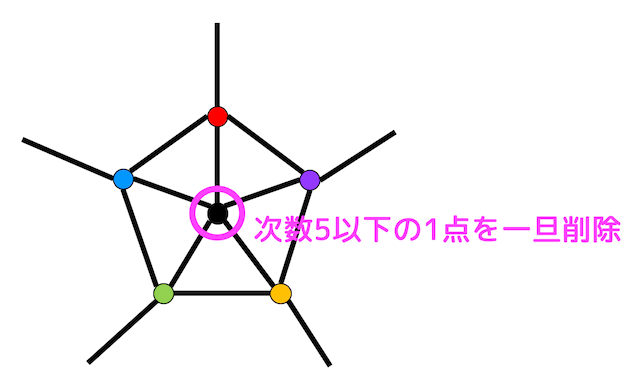
グラフ \( G_2 \) に先程削除した点 \( v_1 \) を追加します(もとに戻します)。
\( v_1 \) は次数が5(以下)の点なので、\( v_1 \) のまわりにあるどの点とも異なる色を彩色することでグラフ \( G_1 \) も6色で彩色することができますね*2!
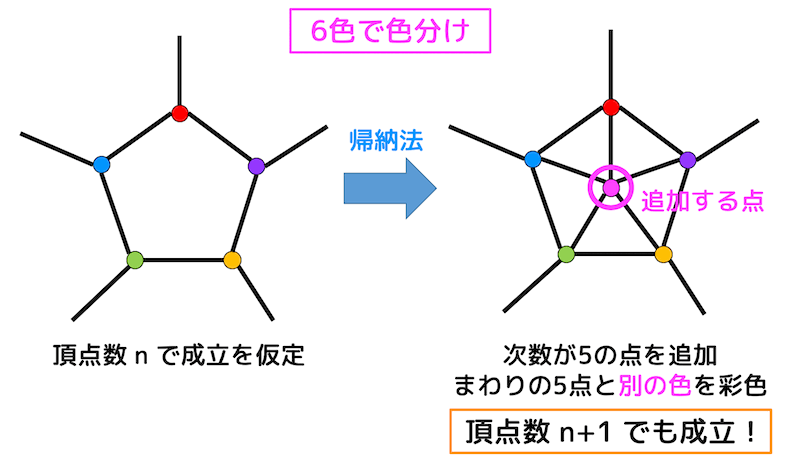
なのでどんな平面グラフであっても6色以内で彩色できる、つまり6-頂点彩色ができることが示されましたね!
(2) 5色定理
平面グラフは1色減らして5色でも必ず彩色ができるのです!
しかし、証明難易度が少しだけ上がります。
平面グラフは必ず5-頂点彩色ができる。
つまり、平面グラフの彩色数は必ず5以下となる。
(どんな地図でも5色以内で彩色することができる。)
では証明していきましょう。こちらも頂点数に関する数学的帰納法で証明します。
(i) 頂点数が5以下のとき
頂点数が5以下であれば、すべての頂点を異なる色で塗っても彩色数は5以下ですよね。なので頂点数が5以下であれば必ず5色定理が成立します。
(ii) 頂点数がn+1のとき
先程と同じように、頂点数 \( n \) のときに5色定理が成り立つことを仮定してから頂点数が \( n+1 \) 個のときに5色定理が成り立つことを示しましょう。
6色定理のときと同じように頂点数が \( n+1 \) の平面グラフ \( G_1 \) から、次数が5(以下)の点 \( v_1 \) を削除したグラフ \( G_2 \) を考えます。
しかし、そのままでは5色以内で塗りわけることを示せないので、5色定理では6色定理の証明では使わなかった定理を1つ使います*3。
平面グラフには、次数5以下の点が存在するのに加え、次のような定理も成り立ちましたね。
頂点数5の完全グラフ \( K_5 \) は平面的グラフではない。
(もちろん平面グラフでもない)
この定理から、頂点数5の平面グラフは必ずどこか隣り合っていない点があると言うことができます。
(完全グラフはどの頂点も隣り合っているグラフなので、完全グラフではないグラフは必ずどこかの2点は隣り合っていない)
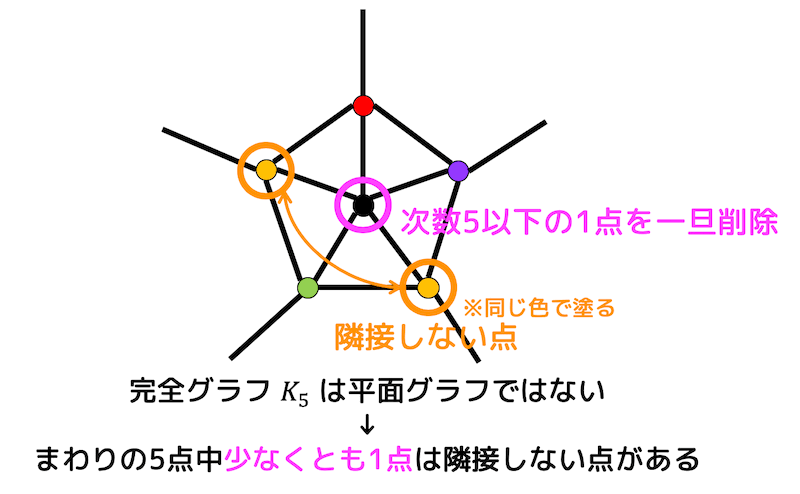
なので次数5のまわりの点の中で、隣り合っていない2点を同じ色で塗ってから平面グラフ \( G_1 \) から次数5の点 \( v_1 \) を一端消してグラフ \( G_2 \) とします。
そして、頂点数 \( n \) のグラフ \( G_2 \) が平面グラフであると仮定します。
あとは6色定理と同じ流れで証明ができます。
先程消した次数5の点 \( v_1 \) を復活させ、まわりの5点(4色)とは異なる色で塗ることで頂点数 \( n+1 \) のグラフ \( G_1 \) も5色で色分けすることができますね。
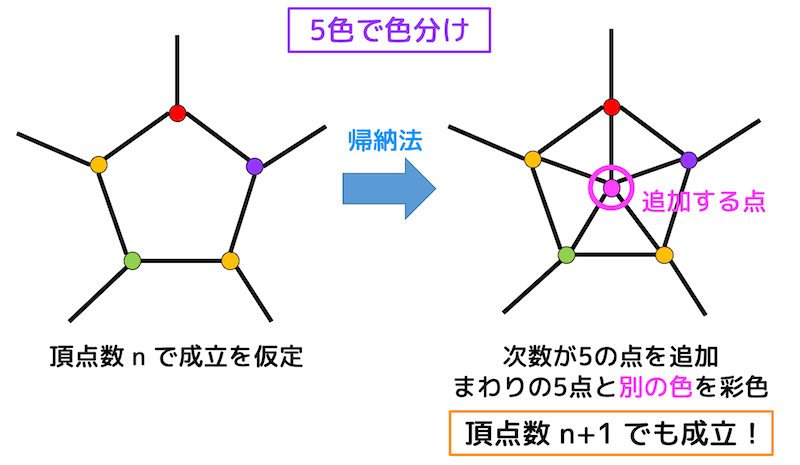
なのでどんな平面グラフであっても5色以内で彩色できる、つまり5-頂点彩色ができることが示されましたね!
(3) 4色定理
さらに1色減らして平面グラフは4色で彩色することができます!
ですが定理の証明はコンピュータの補助がないと証明ができない大変むずかしい証明となっています。
なので定理だけ紹介したいと思います。
平面グラフは必ず4-頂点彩色ができる。
つまり、平面グラフの彩色数は必ず4以下となる。
(どんな地図でも4色以内で彩色することができる。)
この定理は、どんな平面グラフ(地図)であっても必ず4色使えば必ず塗り分けができるという大変面白い定理となっております。
(中には3色、2色で塗り分けられる平面グラフや地図もある)
暇な人は日本地図や世界地図を4色で塗りわけてみましょう。
4.辺彩色
点彩色に引き続き、辺彩色も少しだけですがまとめていきます。
(1) 辺彩色とは
隣り合うどの2辺も異なる色になるようにグラフの辺を色わけすることを辺彩色といいます。
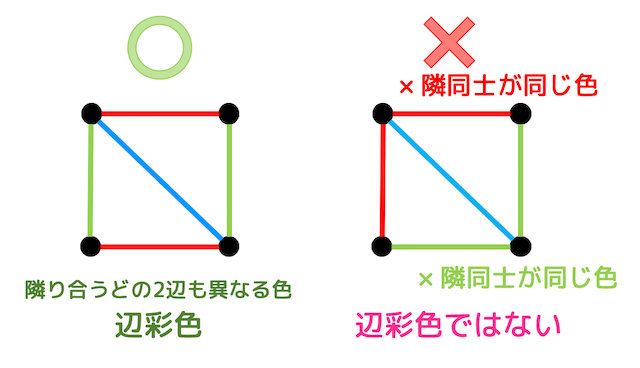
例えば左側のグラフは隣り合うどの2辺も異なる色に色分けしているので辺彩色となっていますが、右側のグラフは隣同士を同じ色に色分けしてしまっているので辺彩色ではありません。
(2) n-辺彩色
あるグラフの辺を \( n \) 色で彩色することを、n-辺彩色といいます。
例えば、左側のグラフの辺は3色で彩色していますね。なので3-辺彩色となります。
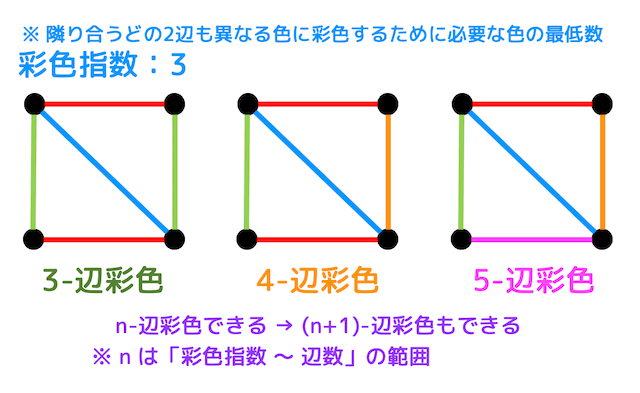
点彩色と同じように真ん中や右側にあるグラフのように、より多くの色を使って4色(4-辺彩色)や5色(5-辺彩色)で彩色を行うこともできます。
なのでn-辺彩色できるグラフは必ず(n+1)-辺彩色もできます*4。
(3) 彩色指数
あるグラフ \( G \) がn-辺彩色可能なときの \( n \) の最小値のことを彩色指数と呼びます。
言い換えると、グラフ \( G \) を辺彩色するために必要な色の最低数を彩色指数といいます。

上のグラフの場合、彩色するために少なくとも3色は必要ですよね。
なので、彩色指数は3となります。
あるグラフ \( G \) の辺を隣り合っているどの2辺も異なる色になるように色分けすることを辺彩色と呼ぶ。
また、グラフ \( G \) の辺を \( n \) 色で彩色することを n-辺彩色と呼び、最小の \( n \)、つまりグラフ \( G \) の辺を彩色するために必要な色の最低数のことを彩色指数と呼ぶ。
(4) 彩色指数に関する4つの定理
辺彩色は点彩色と異なり、Welch-Powerllの点彩色アルゴリズムのような便利なアルゴリズムがありません。
その代わりに今から説明する4つの強力な定理のおかげで点彩色よりも簡単に彩色指数を求めることができます。
定理その1 最大次数と彩色指数
まずは最大次数と彩色指数に関する定理です。
あるグラフ \( G \) の彩色指数は、必ずグラフ \( G \) の最大次数以上になる。
隣り合う2辺を異なる色にするためには、それぞれの点において次数の数だけ異なる色で辺を塗る必要がありますね。
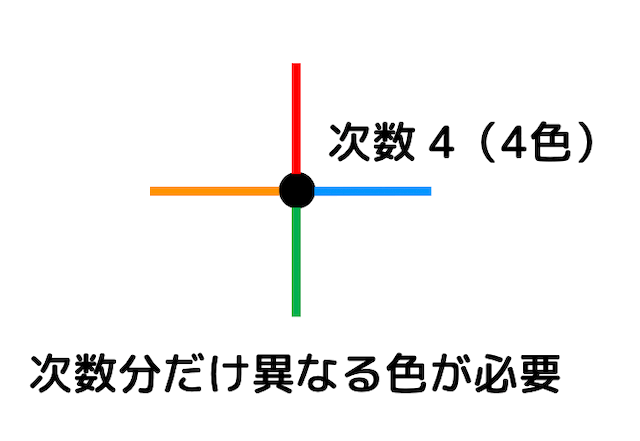
なので、辺彩色を行うためには最低でも最大次数以上の異なる色が必要ですよね。
定理その2 Vizingの定理
つぎにVizingの定理です。
定理1と組み合わせることで彩色指数を簡単に求めることができます。
単純グラフ \( G \) は (\( G \) の最大次数+1)色あれば必ず辺彩色できる。
つまり、単純グラフ \( G \) の彩色指数は必ず「最大次数-1」以下となる。
定理1と組み合わせると、単純グラフの彩色指数に対し、つぎのような公式が成り立ちます。
単純グラフ \( G \) の彩色指数は必ず「最大次数」もしくは「最大次数+1」となる。
グラフの彩色指数
彩色数(頂点の色分けに必要な最低色数)はグラフによって「2〜頂点数」と大きな幅がありますが、彩色指数(辺の色分けに必要な最低色数)は単純グラフであれば「最大次数」or「最大次数+1」に絞られるので、彩色指数は簡単に求められそうですよね。
定理その3 完全グラフと彩色指数
どの辺も隣り合っている完全グラフの彩色指数に関して次のような定理が成り立ちます。
頂点数 \( n \) の完全グラフ \( K_n \) の彩色指数は以下の通りである。
\( n \) が偶数のとき:彩色指数は \( n-1 \)
\( n \) が奇数のとき:彩色指数は \( n \)
試しに \( K_3 \), \( K_4 \), \( K_5 \) を辺彩色してみましょう。
辺彩色は下のようになりますね。
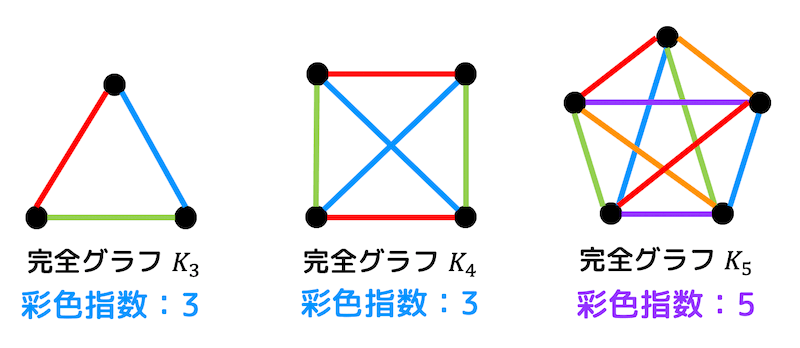
辺彩色より、確かに偶数のときは彩色指数が \( n-1 \)、奇数のときは \( n \) になることがわかりますね。
(ちなみに奇数個の点を持つ完全グラフは、彩色指数が「最大次数+1」となるパターンです。)
ところで \( K_3 \), \( K_4 \) は頂点の数が異なるにも関わらず、彩色指数が同じですよね。
実は、頂点が奇数個の完全グラフに点を1つ加えて完全グラフを作っても、色を増やさずに辺彩色を行えるのです!
\( K_3 \) を用いて簡単に理屈を説明しましょう。
まず、頂点を1本追加し、完全グラフになるように辺も追加します。
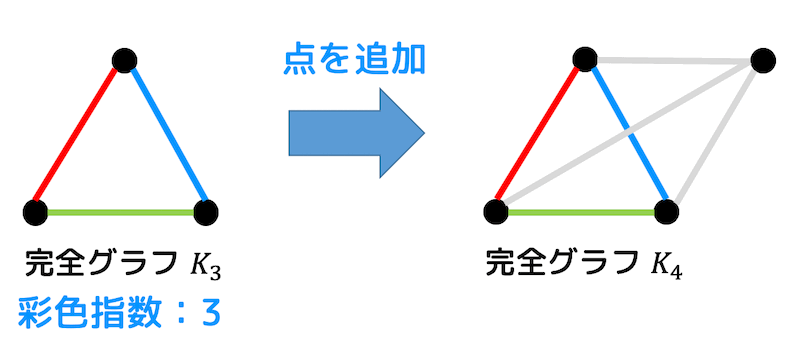
次に頂点ごとに3色のうち、まだ使っていない残りの色で彩色します*5。
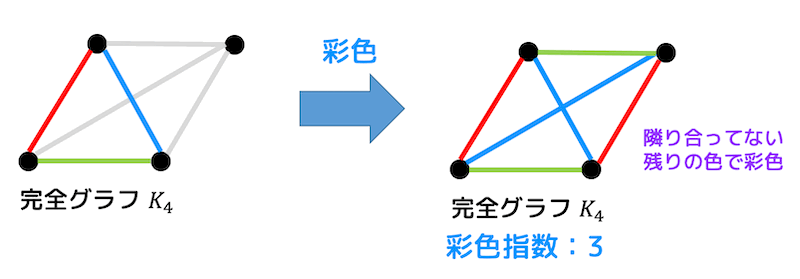
すると、彩色指数を増やすことなく \( K_4 \) を作ることができましたね。
なので \( n \) が奇数であれば \( K_n \) と \( K_{n+1} \) の彩色指数は等しくなるのです。
定理その4 Konigの定理
2部グラフと彩色指数に関する定理としてKonigの定理があるので紹介しておきます。
2部グラフ \( G \) は \( G \) の最大次数だけ色あれば必ず辺彩色できる。
つまり、2部グラフの彩色指数は必ず「最大次数」となる。
例えば、完全2部グラフ \( K_{3,3} \) を彩色することを考えましょう(最大次数は3)。
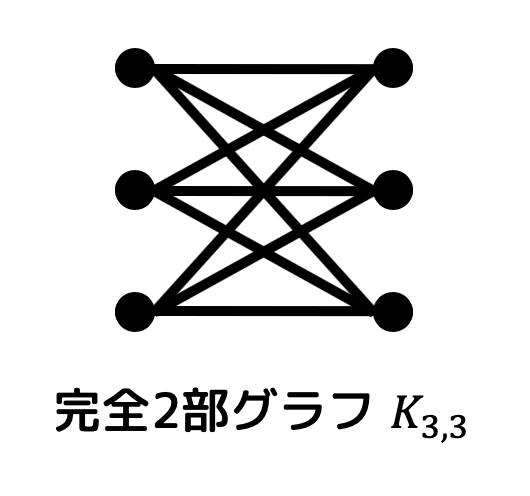
すると、次のように彩色することができますね。
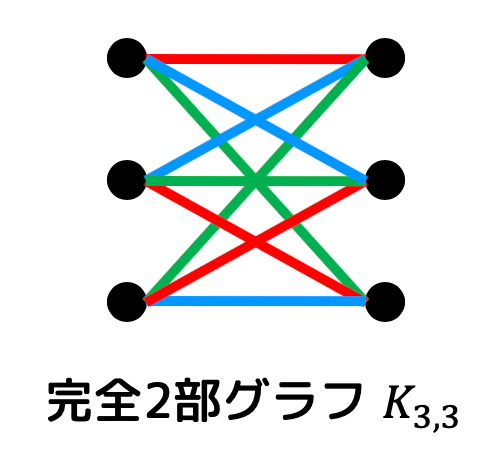
確かに彩色指数が3と最大次数と等しくなってますね。
5.練習問題
では、2問ほど実際に点彩色、辺彩色をやってみましょう!
練習1
つぎのグラフ(ピーターセングラフ)に点彩色、辺彩色をし、彩色数および彩色指数を求めなさい。
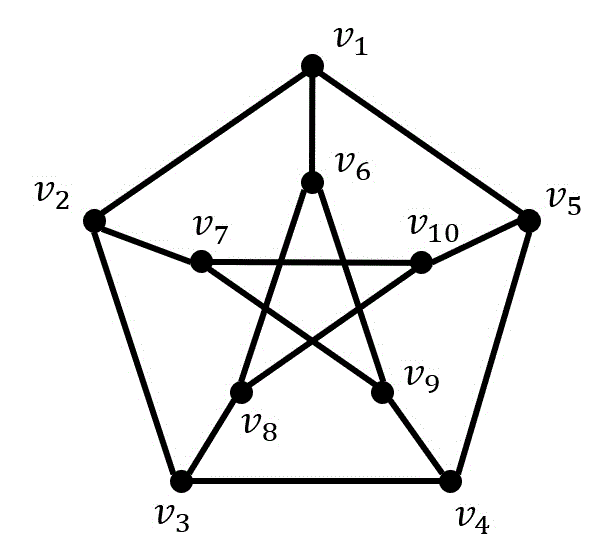
練習2
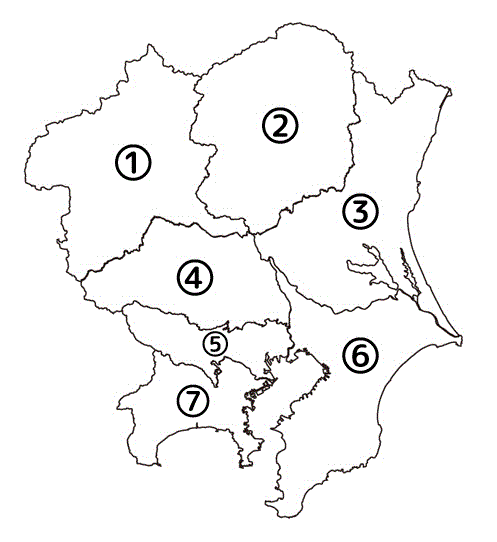
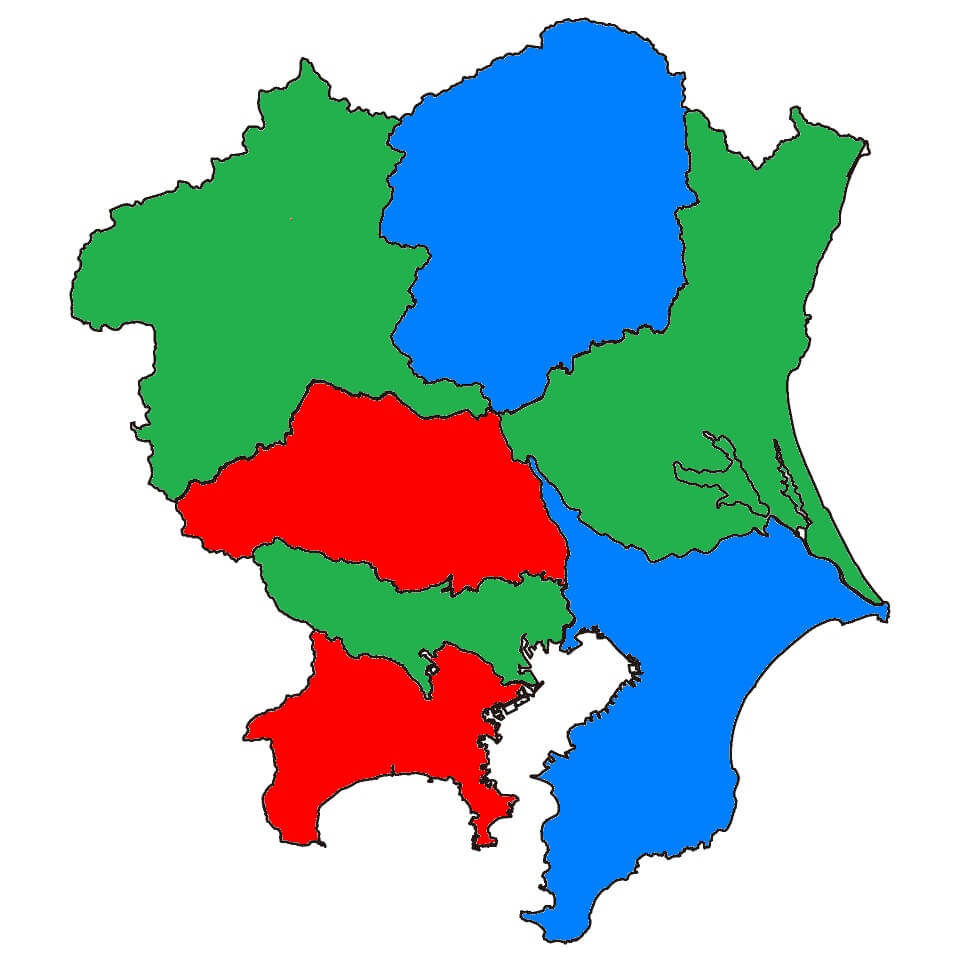
下の地図の①~⑦の都県を他の県が隣り合わないように彩色しなさい。
また、塗り分けるのに何色必要か答えなさい。
(②と④は隣り合っていることに注意!)
6.練習問題の答え
解答1
点彩色
まずはそれぞれの点 \( v_1 \) ~ \( v_{10} \) の次数を求め、次数の順番に頂点を並べます。
しかし、全部の頂点の次数が3なので今回は番号順に並べることにします。
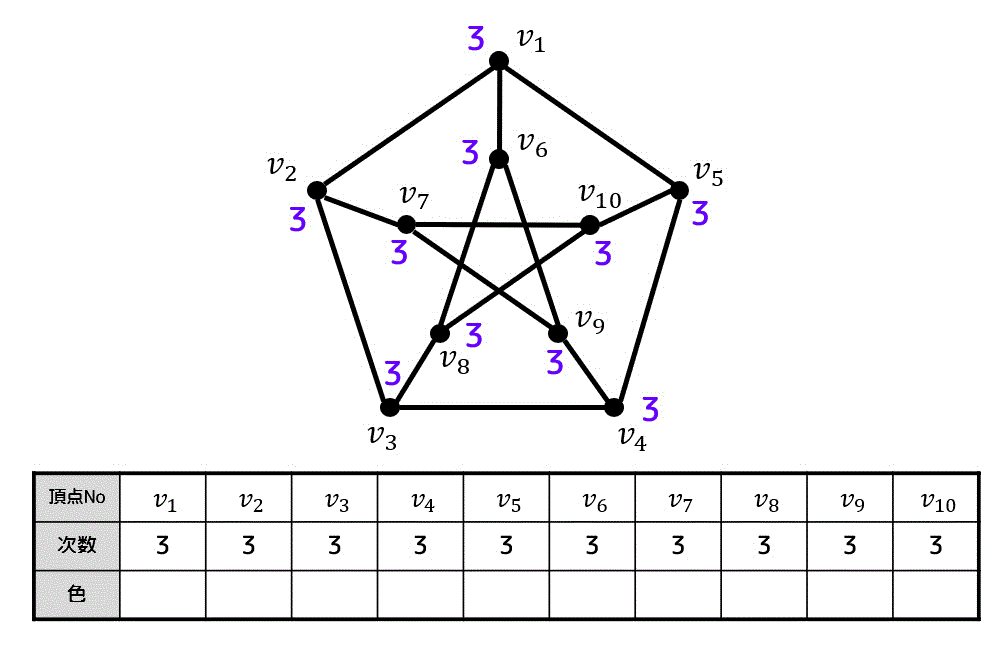
あとはWelch-Powerllのアルゴリズムを適用するだけ。
アルゴリズムの動きがわかるようにアニメーションを用意しました。
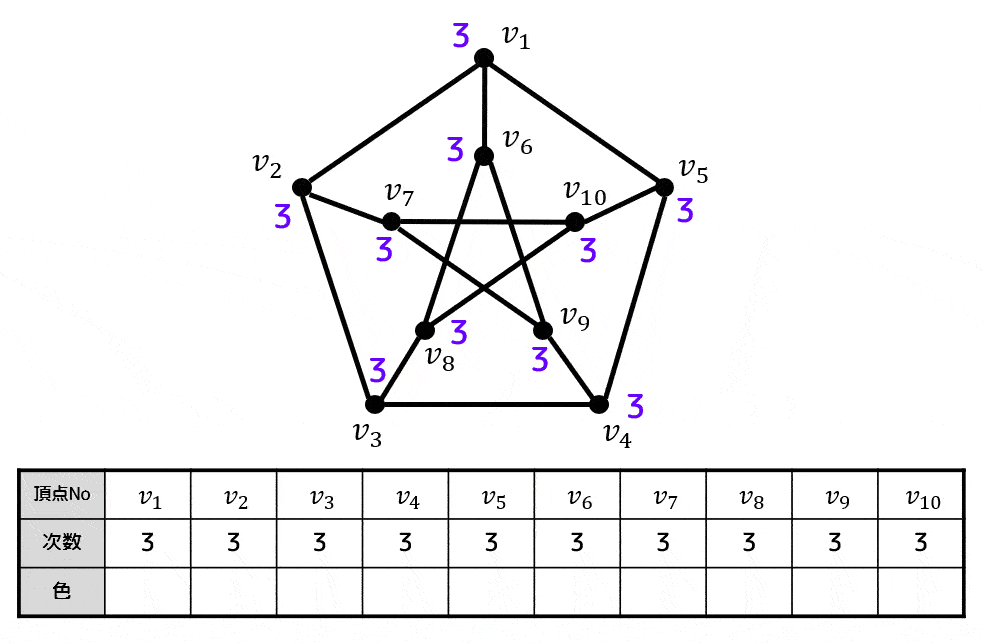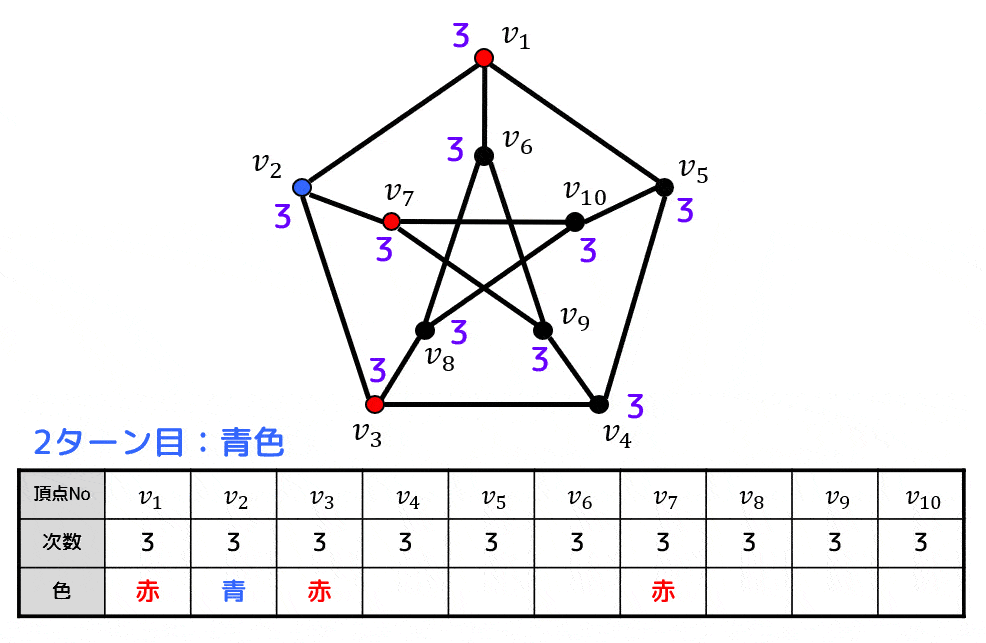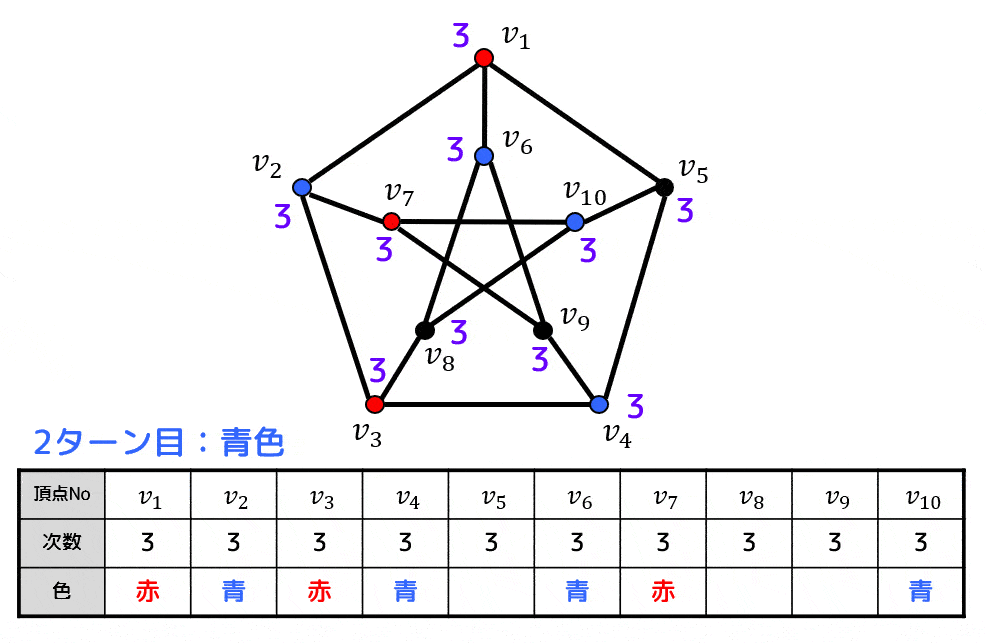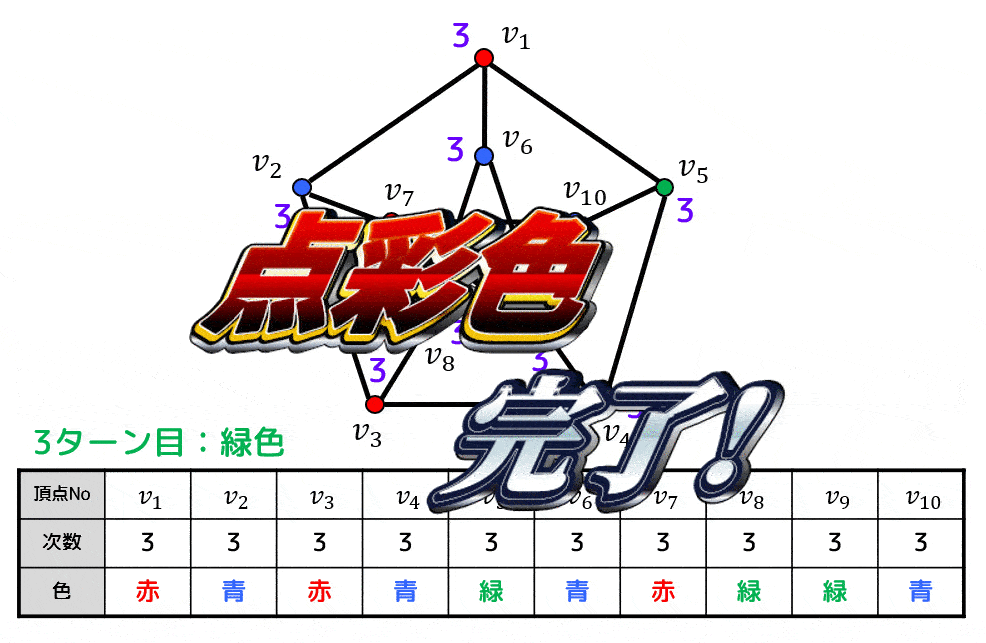
よって、点彩色は下のようになる。
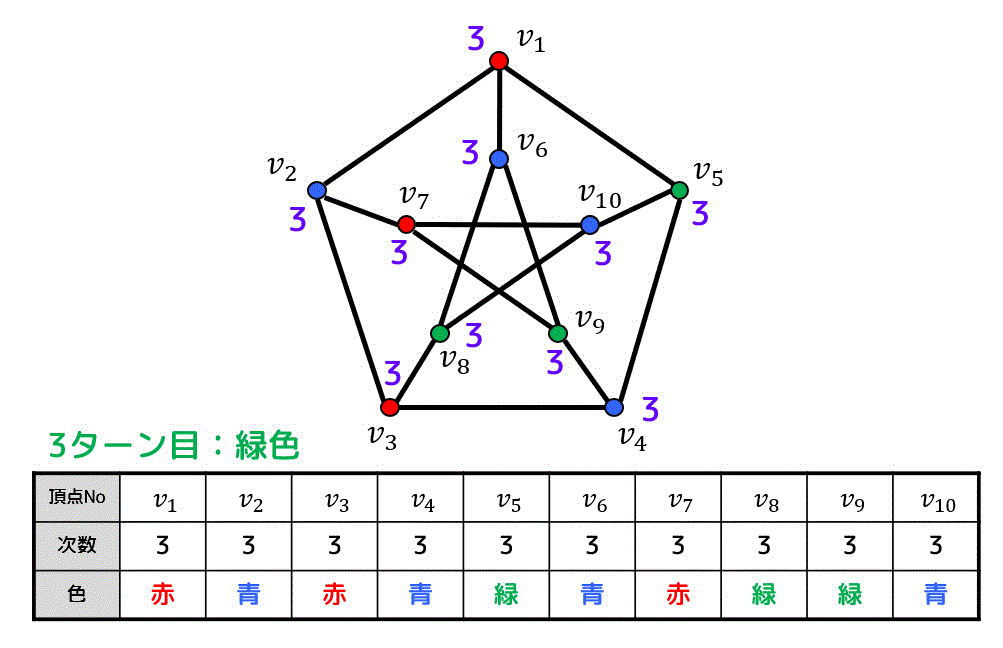
よって彩色数は3となる。
また、グラフの最大次数が3のため、彩色指数は3か4のいずれかである。(単純グラフなので)
あとは実際に辺彩色をして確かめるだけ。
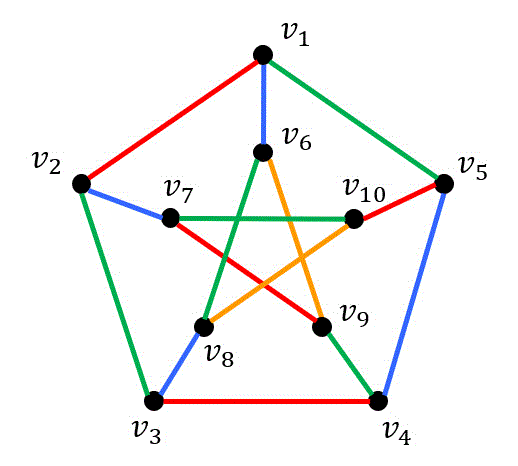
下のように辺彩色できるので、彩色指数は4となる。
(3色で辺彩色することはできません。)
解答2
まずは、①~⑦の都県を点、隣り合っている都県を辺とみなしたグラフを書きます。
すると、下のようなグラフが出来上がります。
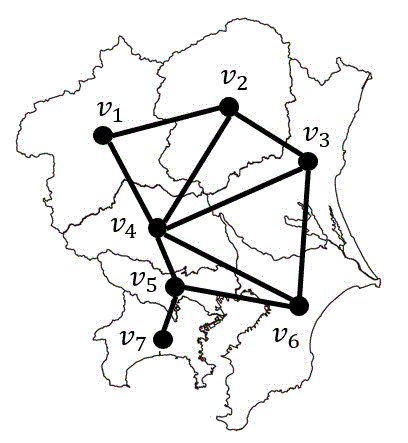
あとは上のグラフの点彩色と彩色数を求めればOKです。
まずはグラフの次数を求めてから頂点を次数の大きい順に並べます。
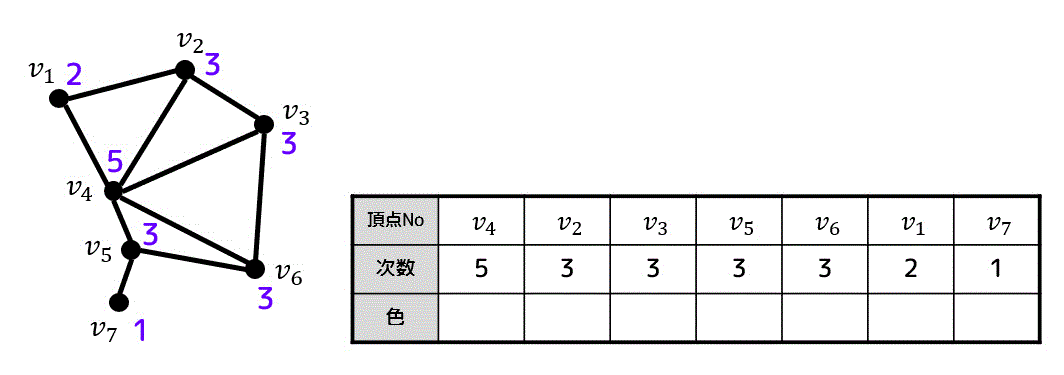
あとはWelch-Powerllのアルゴリズムを適用すればOKです。
途中過程をアニメーションで表しています。
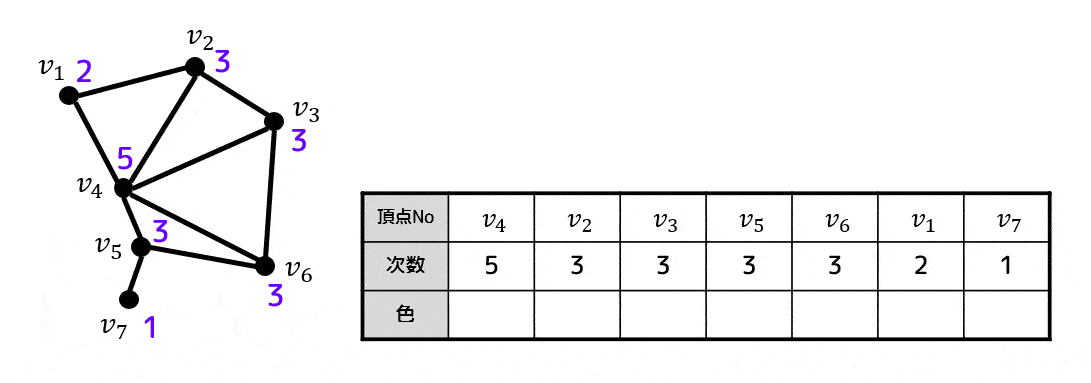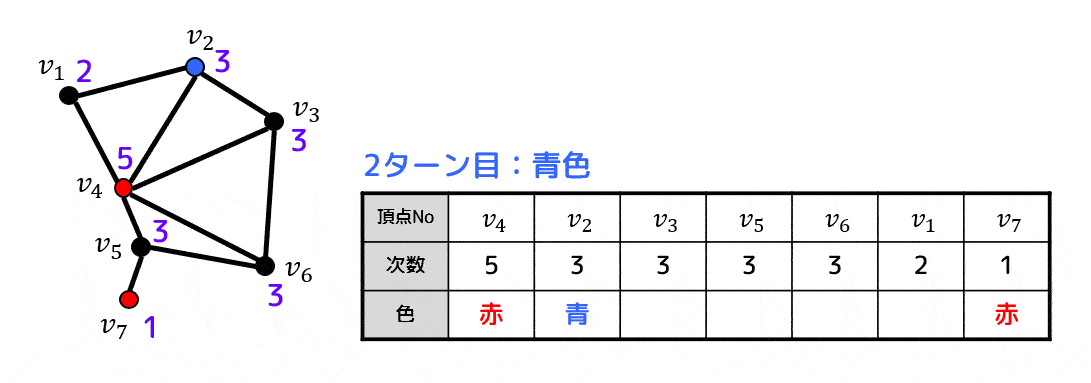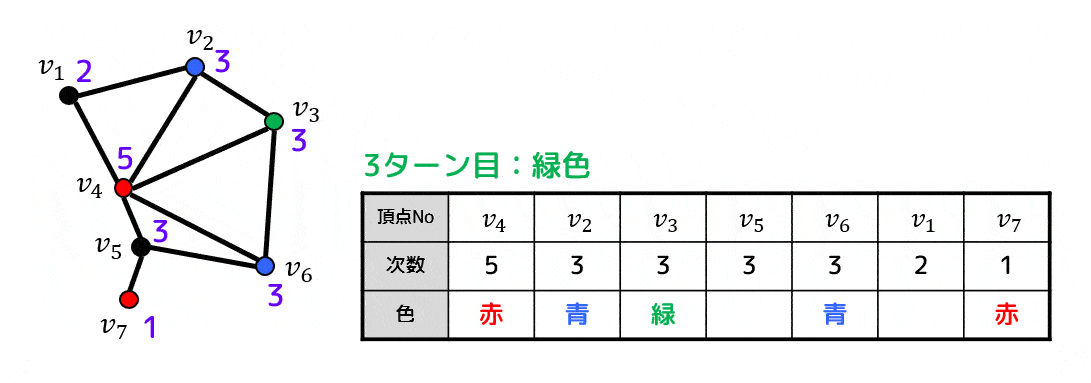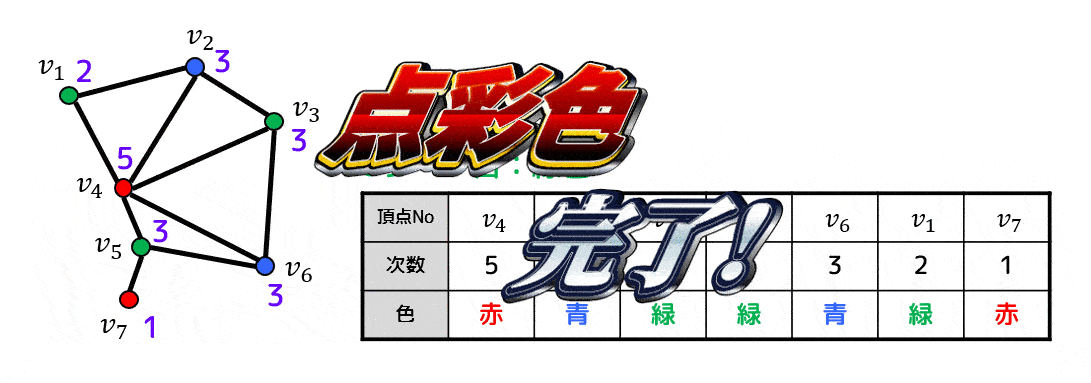
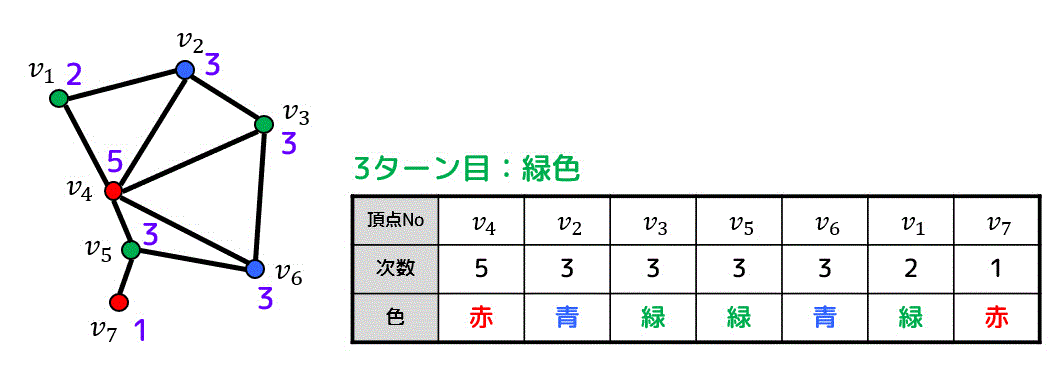
※青色を彩色する際に次数3の点として \( v_5 \) と \( v_6 \) の候補があるのですが、この際に \( v_6 \) を選択しないと3色で彩色することができないので注意してください。
( \( v_5 \) を選ぶと4色で彩色することになってしまい、最小色数で彩色することができません)
Welch-Powerllのアルゴリズムは次数の大きい順に頂点を選ぶのですが、同じ次数の候補点が複数ある場合に同じ次数のどの点を選んでも彩色数が求まるとは限らないことに注意!
よって下のように点彩色をすることができ、彩色数は3と求められます。
よって、下のように3色で関東地方を塗り分けることができますね。
7.さいごに
今回は彩色問題として頂点や辺を隣り合わないように彩色していく問題や、平面グラフ(地図)が4色以内に彩色できることなどについてまとめました。
もし暇なら白地図を彩色していきましょう。絶対に4色以内で彩色できることが身に染みるはずです()。
離散数学(グラフ理論)の記事は今回が最終回(の予定)です!
今まで読んでいただきありがとうございました!
*1:当然といえば当然なのですが \( n \) の上限は頂点数です。
*2:\( v_1 \) のまわりの点以外はすでに \( G_1 \) で成立を仮定しているので考える必要がありません。
*3:実は次数が4以下の点がある場合は次数が4以下の点を削除し、削除したグラフが平面グラフと仮定し、削除した点をもとに戻すことで6色定理と同様に証明することができる(削除した点のまわりに存在する点は4点以下なのですべての点が異なる点であっても自分を含めて5色以内で彩色することができるため)。
*4:当然といえば当然なのですが \( n \) の上限は辺数です。
*5:例えばある点に赤と青の辺がつながっている場合、残りの緑色の辺がつながっていないので緑色の辺で彩色を行う。
関連広告・スポンサードリンク