スポンサードリンク
こんにちは、ももやまです。
前編の「うさぎ模試 グラフ理論 フォーム編」にて、グラフ理論で使う知識を浅く広く確認はできましたでしょうか。
後編ではグラフ理論の中でも特に重要な項目を、実践的な問題として、記述式で5題(問題4~問題8)を用意しました!
時間がある人はじっくり、時間がない人は素早くこの記事にてグラフ理論の復習をしましょう!
↓ まだ問題をダウンロードしていない人はこちらからしましょう!(フォーム式の問題から解くことをおすすめします)
※ 採点は各自でお願いします。
目次
スポンサードリンク
問題4. 中問集合
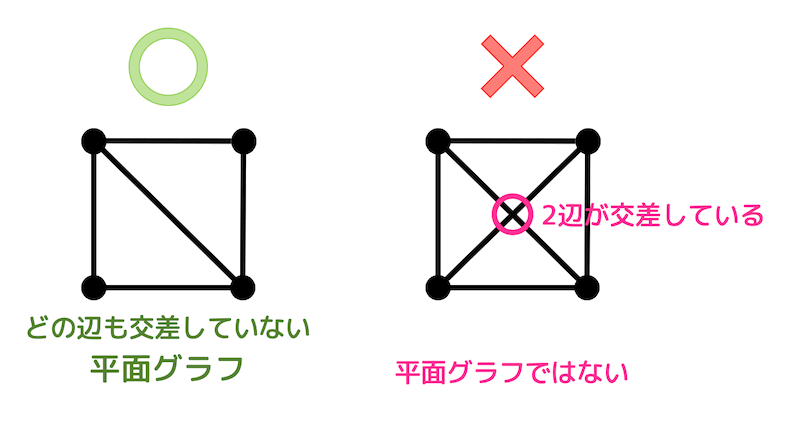
(1) 平面グラフの確認
次のグラフ \( G_1 \), \( G_2 \) について(1), (2)の問いに答えなさい。
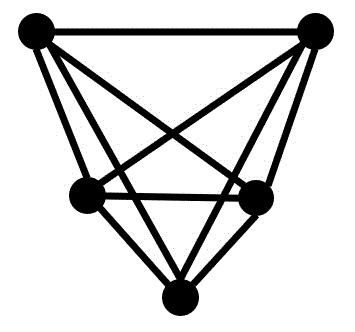
(1) グラフ \( G_1 \) は平面的グラフか、理由とともに答えなさい。
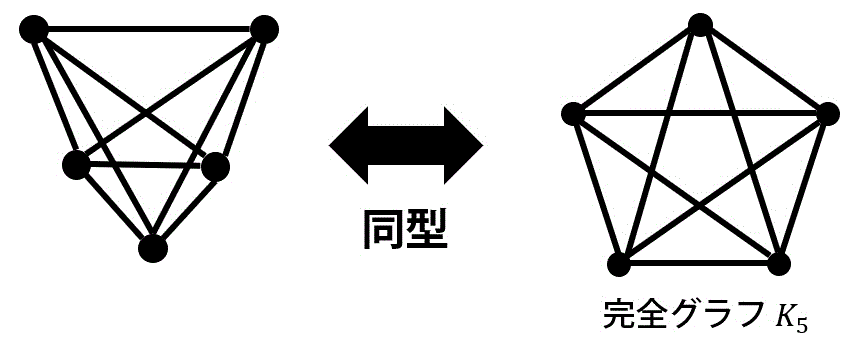
グラフ \( G_1 \) が完全グラフと仮定する。
すると、頂点数 \( p \)、辺数 \( q \) に対して \( q \leqq 3p -6 \) の関係が成立する。
ここで、グラフ \( G_1 \) の頂点数は、\( p = 5 \)、辺数 \( q = 10 \) となるため、\( 10 \leqq 3 \cdot 5 -6 = 9 \) と \( q \leqq 3p - 6 \) の関係に矛盾する。
よって、グラフ \( G_1 \) は平面グラフではない。
平面グラフでないことを示す方法は次の2通り。
[1] 完全グラフ \( K_5 \), \( K_{3,3} \) の一部分を含んでいないこと(クラトフスキーの定理) [2] グラフの点の数 \( p \)、辺の数 \( q \) に対して以下の数式を満たすこと。
- グラフに長さが奇数の閉路がある場合 → \( p \leqq 3p - 6 \) を満たさないこと
- グラフに長さが奇数の閉路がない場合 → \( p \leqq 2p - 4 \) を満たさないこと
平面グラフについて、さらに復習したい人は下の記事を御覧ください!
(2) 最小分離集合
次のグラフ \( G_1 \), \( G_2 \) について(1), (2)の問いに答えなさい。
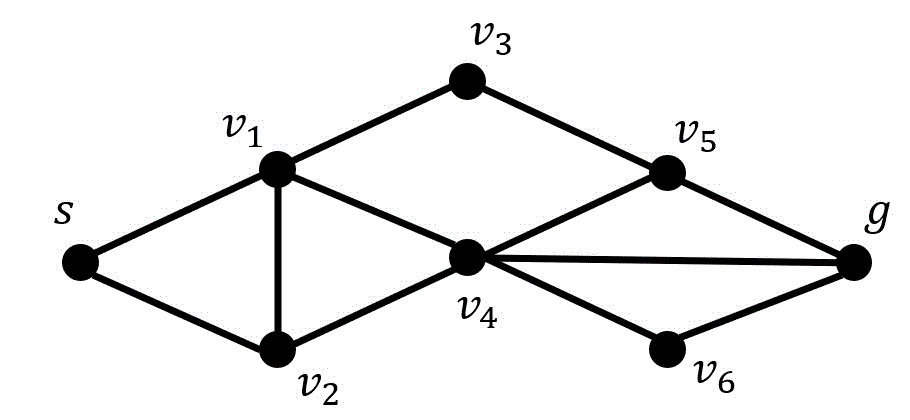
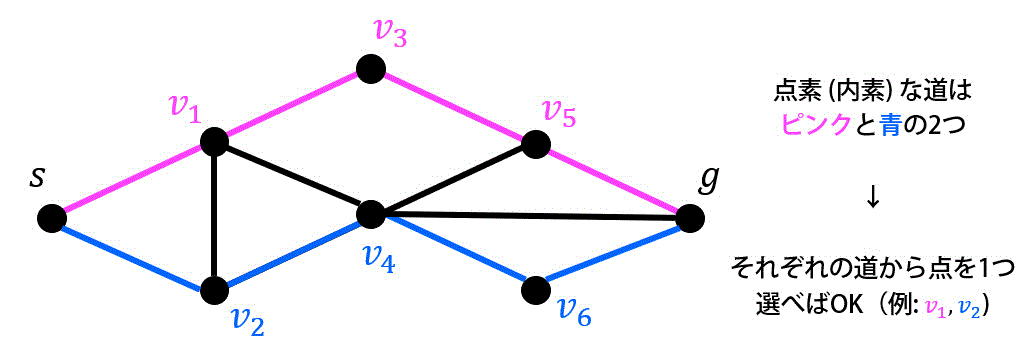
(2) グラフ \( G_2 \) の \( s-g \) 間の最小分離(点)集合を理由とともに答えなさい。
s-g間の点素(内素)な道は、下の2つ(ピンクと青)である。
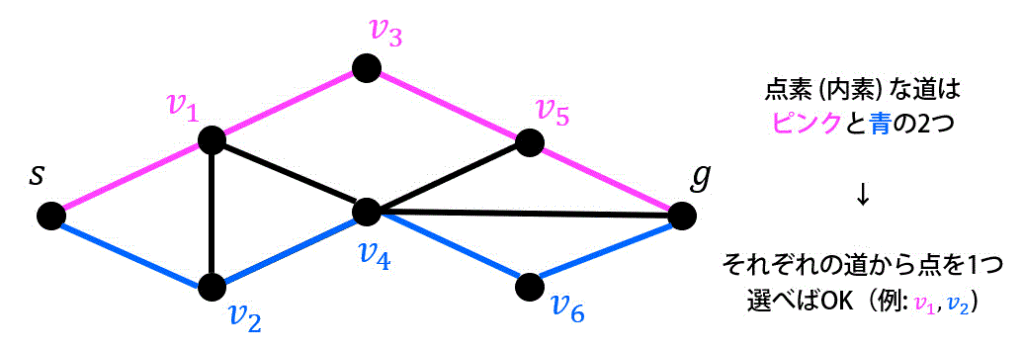
この道から点を1つずつ選べば最小分離集合となる。(答えは9通りあります)
ある点 \( s \) からある点 \( g \) 間の最小分離(点)集合、最小分離辺集合は次のように求めればOK。
最小分離(点)集合
→ \( s \) - \( g \) 間の点素(内素)な道から各1点ずつ選べばOK
最小分離辺集合
→ \( s \) - \( g \) 間の辺素な道から各1辺ずつ選べばOK
最小分離集合についてさらに復習をしたい人はこちらの記事をご覧ください!
スポンサードリンク
問題5. オイラーグラフとハミルトングラフ
(1) ハミルトングラフかどうかの確認
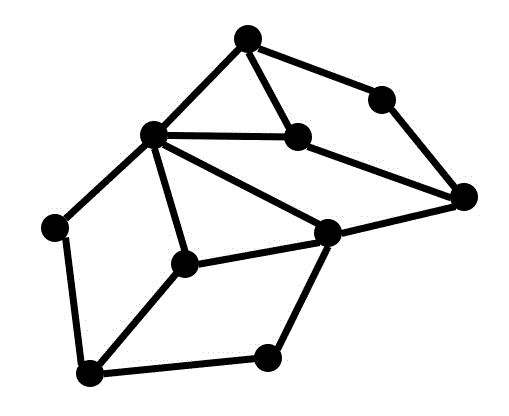
ヒビキくんとアキさんは下のようなグラフ \( G \) で表される地域に住んでいる。
ここで、それぞれのグラフの頂点は街を表し、辺は街に行くための道路を表している。次の会話を読み、(1), (2)の問いに答えなさい。(配点 12)
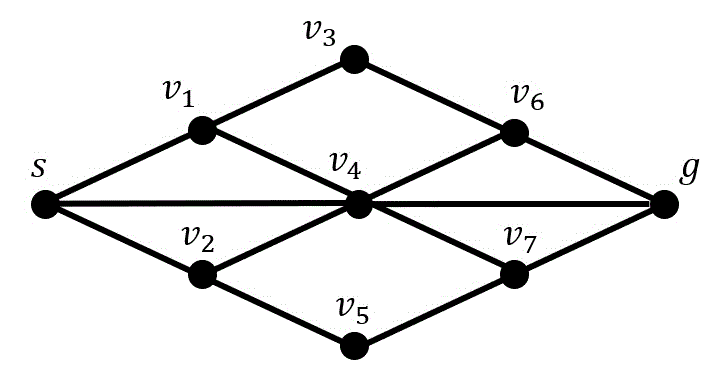
アキ:ヒビキくん、もしよかったら一緒に散歩しない?
ヒビキ:いいね! 今日はどの道を散歩する?
アキ:うーん、じゃあ1回通った街を2回以上通らないように地域全部の街を回るルートで散歩がしたいんだけど、そんなルートはあると思う?
ヒビキ:なるほど、つまりグラフ \( G \) がハミルトングラフになるかどうか確認すればいいってことね!
(1) グラフ \( G \) はハミルトングラフか。理由も合わせて答えなさい。
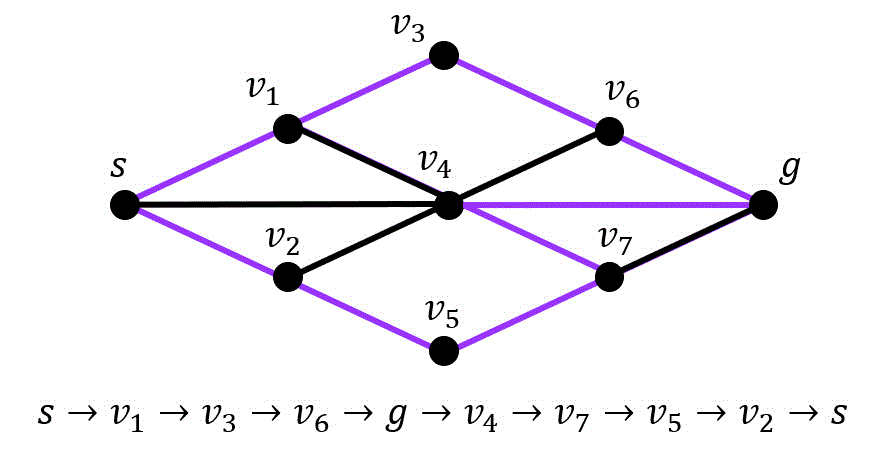
※ すべての点を1度だけたどって起点に戻るようなたどり方を1個示せていたらOK。
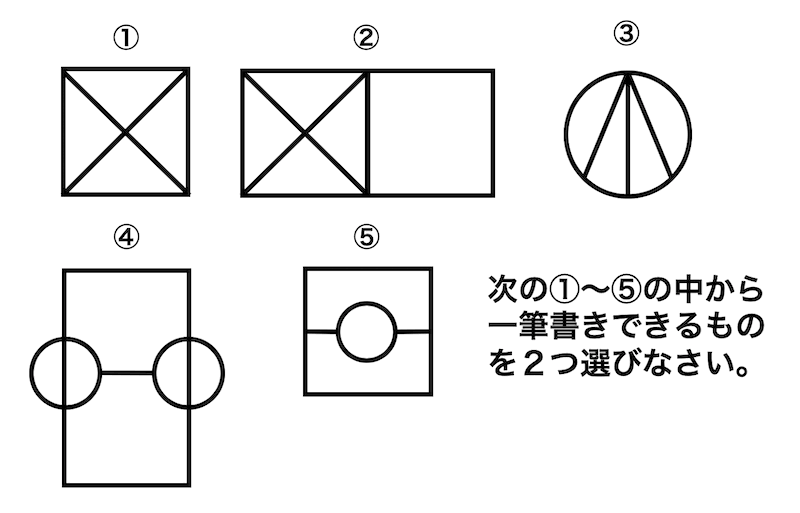
オイラーグラフ
→ すべての辺を1度ずつ通って元の点に帰ってこれるグラフ(一筆書きの辺Ver)
ハミルトングラフ
→ すべての点を1度ずつ通って元の点に帰ってこれるグラフ(一筆書きの点Ver)
※ 実際にオイラーグラフ・ハミルトングラフであることを示す場合は、一筆書きができる例を1つ示せばOK
(2) オイラーグラフかどうかの確認
散歩後、ヒビキくんとアキさんがまた会話をしている。

アキ:散歩楽しかったね!
ヒビキ:うん!
アキ:ねぇ、明日は1回通った道路を2回以上通らないように地域全部の道路を回るルートで散歩がしたいな!
ヒビキ:ってことは、グラフ \( G \) がオイラーグラフになるかどうか確認すればいいのね。でも、もうぽれ*1疲れたよ〜。明日は休ませて…。
アキ:そうそう! でも2日連続散歩するのはちょっとしんどいわね。明日は一緒にゲームしよっか! ヒビキ:おけおけ!*2
*1 ぽれ … 1人称
*2 おけおけ! … 賛同を表している。OKとほぼ同じ。
(2) グラフ \( G \) はオイラーか。理由も合わせて答えなさい。
オイラーグラフは、次数が奇数の点が存在しないことが条件なので、1つでも次数が奇数の点が存在したその時点でオイラーグラフでないことが確定します。
オイラーグラフ・ハミルトングラフではないことを示す方法
[オイラーグラフ]次数が奇数の点が1つでもあることを言えばOK。
(オイラーグラフは次数がすべて偶数のグラフなため)
次の条件のどちらかを満たしていないことを言えばOK。
- グラフの最小次数 \( d(v)_{min} \)、頂点数 \( n \) のとき、\( 2 d(v)_{min} \geqq n \)
- 隣接していないどの2点を選んでも、次数の合計が頂点数以上になっていること。
オイラーグラフ、ハミルトングラフについてさらに復習したい人はこちらの記事をご覧ください!
スポンサードリンク
問題6. 最短経路問題・最小全域木
(1) 最短経路問題
ヒビキ家の住民は、下のようなグラフ \( G \) で表される地域の街 \( s \) に住んでいる。

ここで、それぞれのグラフの頂点は街を表し、辺は街に行くための道路を表している。また、それぞれの辺の数字は距離[km]を表している。
ヒビキ母:ねぇ、明日街 \( g \) に出張なんだけど、普段使っているルート*3が工事中なのよね。街 \( s \) から街 \( g \) までの最短距離ってどうやったらわかる?
ヒビキ:それなら、ダイクストラ法で計算すればかんたんに計算できるかな。
ヒビキ母:なるほど〜。ちょっとヒビキ計算してみてよ。
ヒビキ:えぇ、めんどくさいなぁ。(計算を始める)
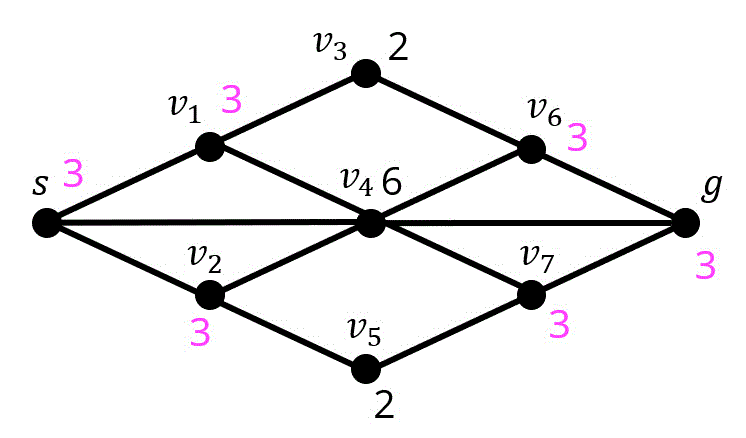
(1) 街 \( s \) から街 \( g \) までの最短距離をダイクストラ法で計算しなさい。
最短距離: 12(8点)
※経路は \( s \to v_2 \to v_5 \to v_7 \to v_4 \to g \)
各点にかかれている数字の色の意味は下の通り。ここで、数字の右に書かれているかっこは、どの点から来たかを表す。
- 桃 … すでに距離が確定した点
- 赤 … ちょうど距離が確定した点
- 紫 … 新たに暫定距離が求まった(更新された)点
- 緑 … すでに暫定距離が求まっている点
- 水 … 新たな暫定距離が求まったが、前の暫定距離の方が短かったため更新されなかった点
Step1. 点 \( s \) の距離確定
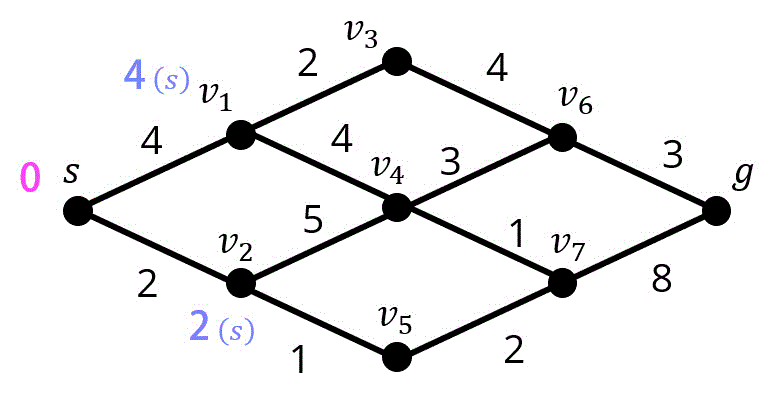
Step2. 点 \( v_2 \) の距離確定
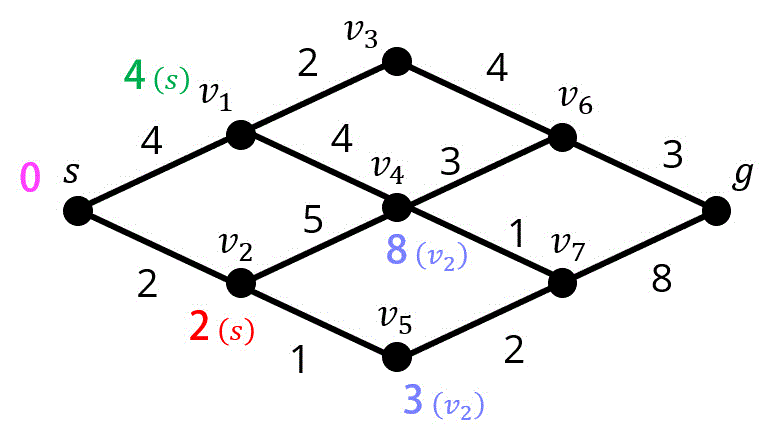
Step3. 点 \( v_5 \) の距離確定
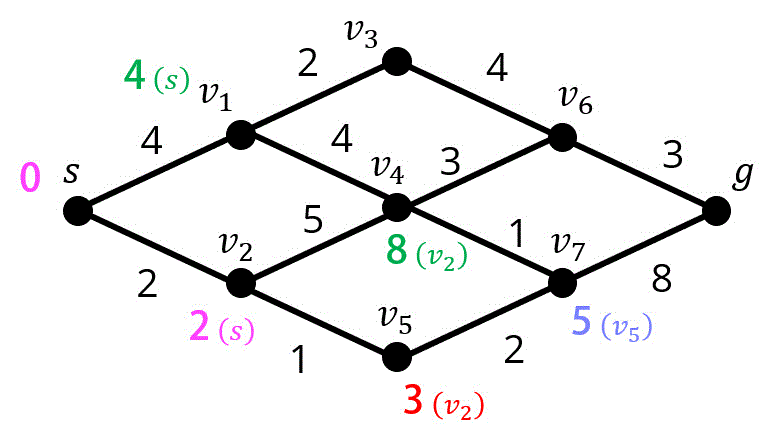
Step4. 点 \( v_1 \) の距離確定、\( v_4 \) の暫定距離は更新されない
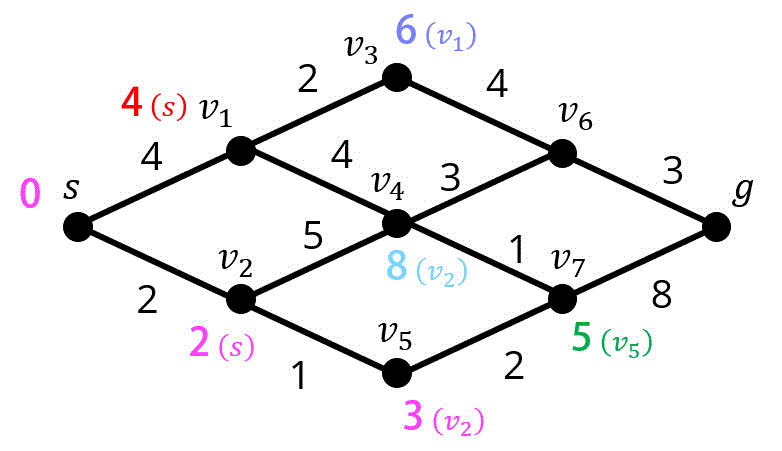
Step5. 点 \( v_7 \) の距離確定、\( v_4 \) の暫定距離が更新される
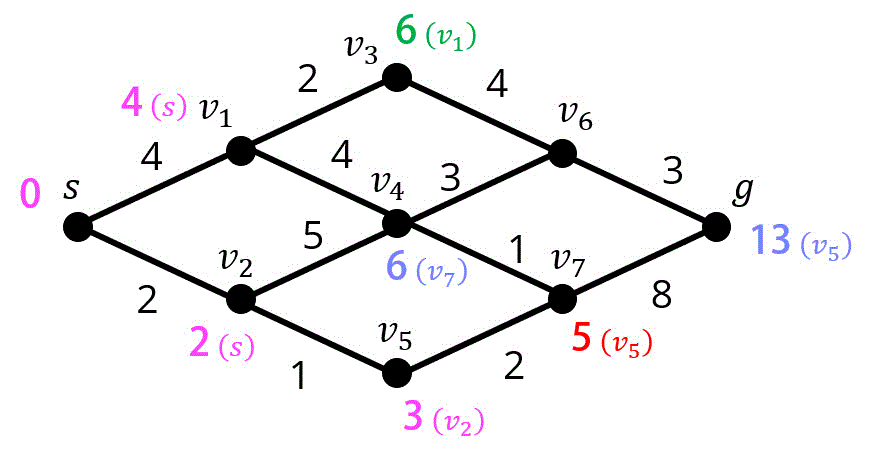
Step6. 点 \( v_1 \) の距離確定
※ 暫定距離が最も短い点が2つ以上ある場合は、\( v \) の番号が小さい順に確定させることにします。
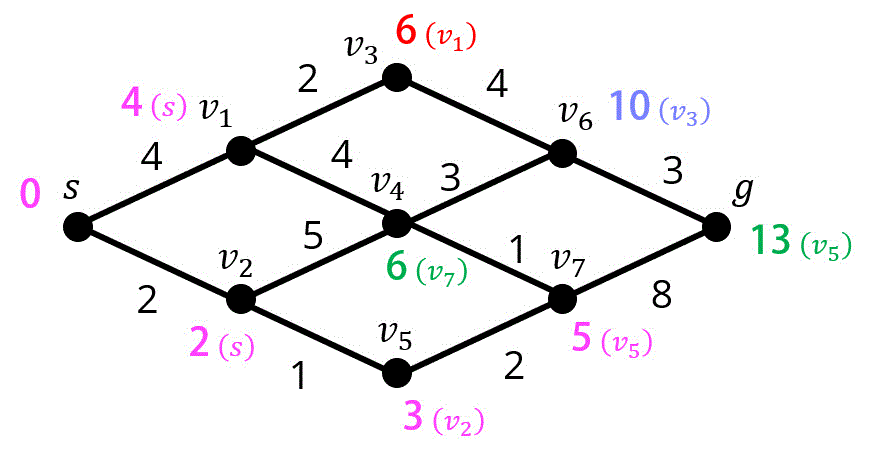
Step7. 点 \( v_7 \) の距離確定、点 \( v_6 \) の暫定距離更新
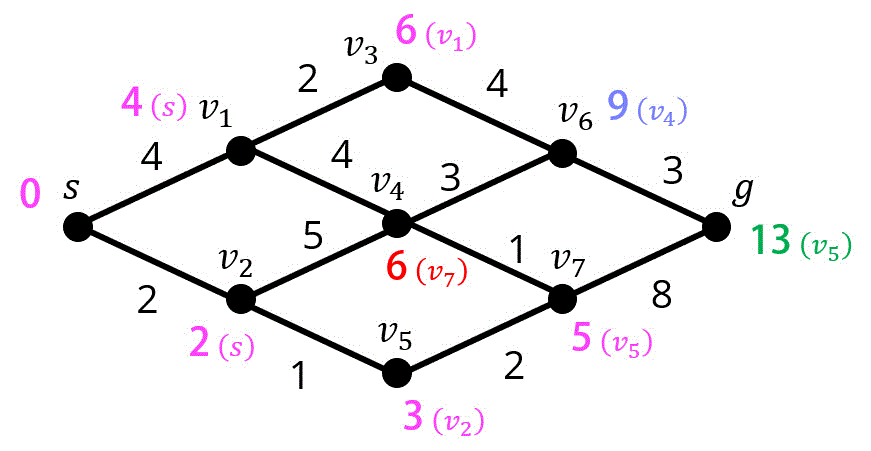
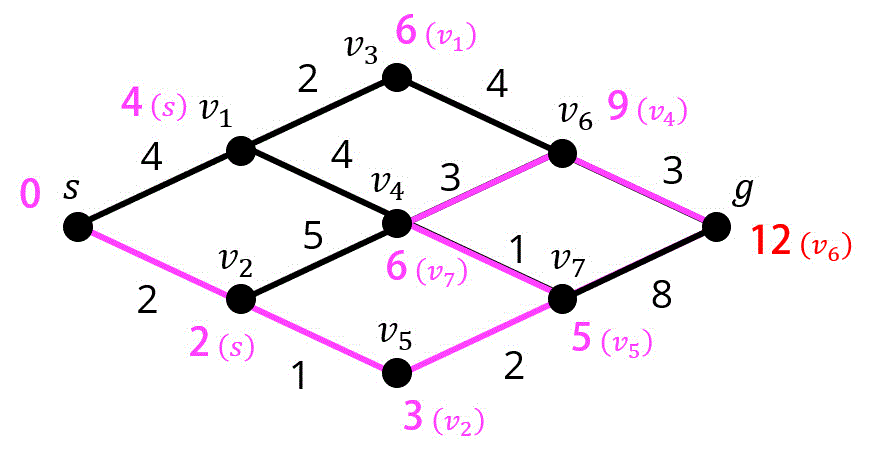
Step8. 点 \( v_4 \) の距離確定、点 \( g \) の暫定距離更新
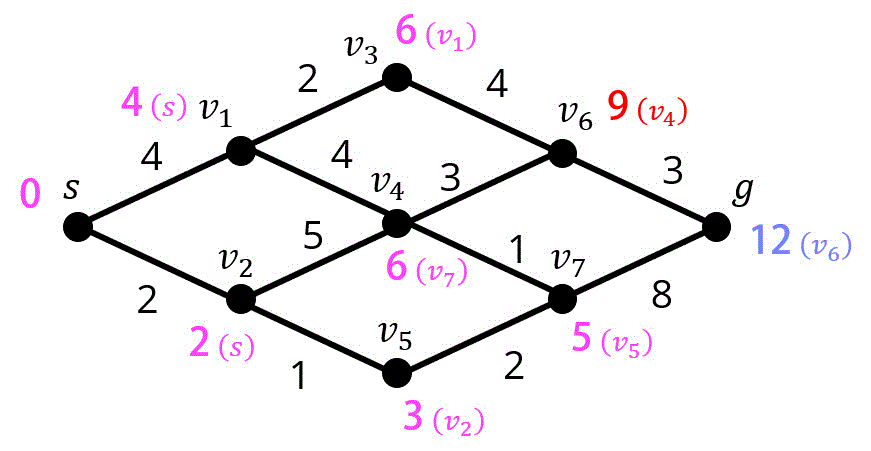
Step9. 点 \( g \) の距離確定

それぞれの点から点までの距離が確定したものを確定距離、確定はしてないものの距離を計算している点を暫定距離とする。
Step1. 始点から始点までの確定距離を0とする。
Step2. 距離が確定した点と隣り合っている点までの暫定距離とたどる元の点を求める。(暫定距離 = 確定距離 + 隣り合っている点までの移動距離)
ただし、隣り合っている点の暫定距離がすでに求まっている場合、より短い暫定距離が出た場合のみ上書きする。また、隣り合っている点の確定距離がすでに求まっている場合は無視する(すでに確定してるので更新されない)。
Step3. 暫定距離が出ている点の中で、一番暫定距離が小さいものを確定距離とする。
すべての距離が確定するまでStep2, Step3を繰り返す。また、各点の経路は、ゴールから元の点をたどることで求めることができる。
ダイクストラ法のアルゴリズムについてさらに確認したい人はこちらをご覧ください!
(2) 最小全域木
ヒビキとその父親が夕食後、会話をしている。

ヒビキ父:今度この街に渋滞緩和のための有料道路を作ろうと思ってるだよね。
ヒビキ:え? 本当に? どことどこを結ぶの?
ヒビキ父:この地域にある街を有料道路だけで行き来できるようにいろんな区間に建設するんだ*4。
ヒビキ:まじか、それ予算すごくかからない?
ヒビキ父:そうなんだよ。ちょっとヒビキ、どの街間に有料道路を設置すれば費用が一番安くなるか、計算できる?
ヒビキ:グラフ G の最小全域木を計算すれば求まるけどさぁ…。
[注釈] *4 普通の家庭ではこんな話はしない。(2) グラフ \( G \) の最小全域木を計算し、どの街間に有料道路を設置すれば費用が一番安くなるかを求めなさい。ただし、設置費用は1km = 10億円とする。
クラスカル法とプリム法のどちらでもやってもOK。
解く際には、辺の数が (頂点数) - 1 になることを必ず意識すること!!(今回は8)
(i) クラスカル法で解く場合
辺の重み(設置費用)が小さい順に追加すればOK。ただし、途中で閉路ができないように注意すること。
※ ピンク色の辺は追加した辺、灰色の辺は追加すると閉路ができてしまう辺を表しています。
1つ目 / 8つ目. 同じ重みの辺が複数ある場合、\( v \) の番号が小さい方[1]辺につながっている2つの点のうち、小さい方の点を基準に考えます。例えば \( (v_2,v_3) \) であれば \( v_2 \) を基準で考えています。から順に追加しています。
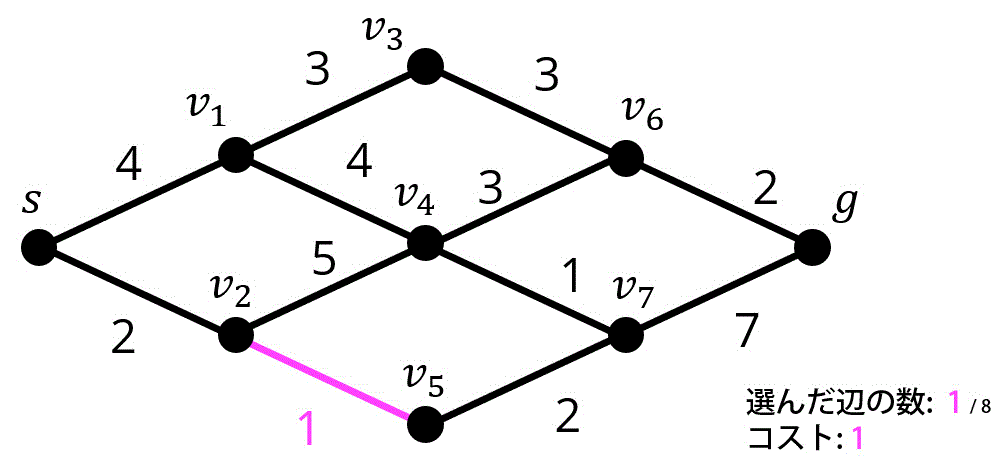
2つ目 / 8つ目
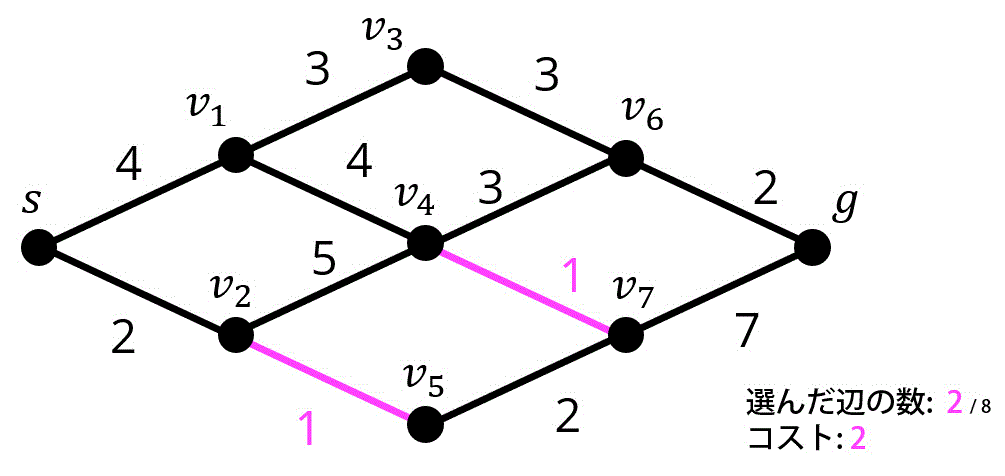
3つ目 / 8つ目
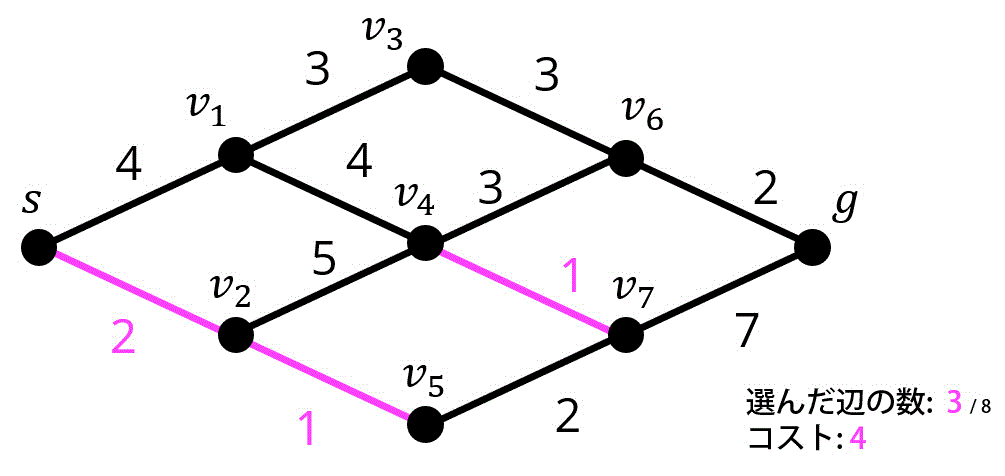
4つ目 / 8つ目
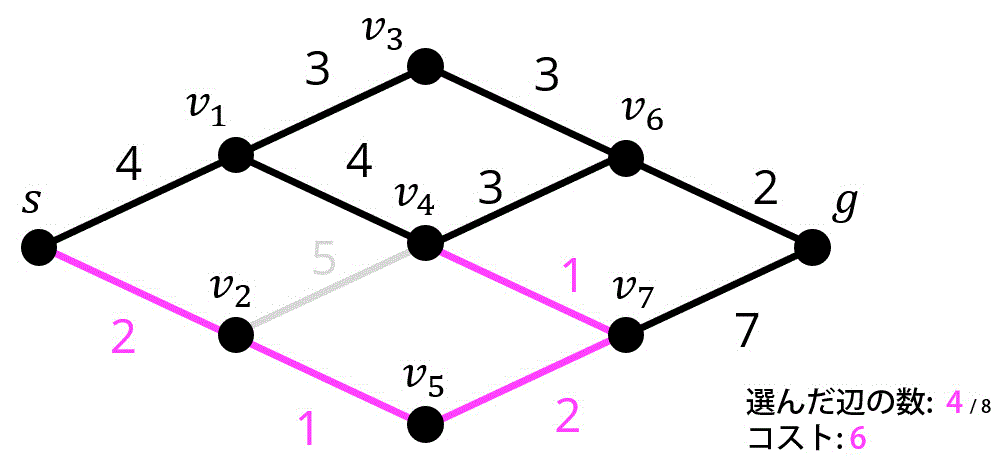
5つ目 / 8つ目
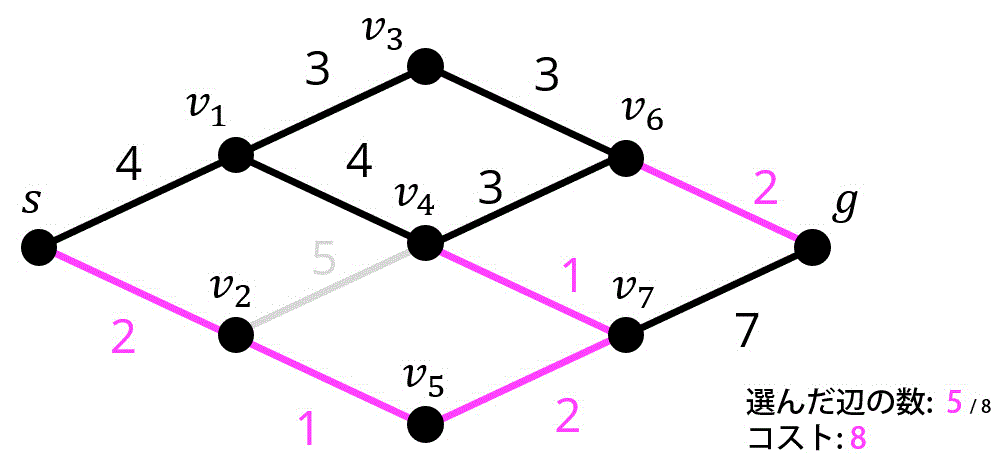
6つ目 / 8つ目
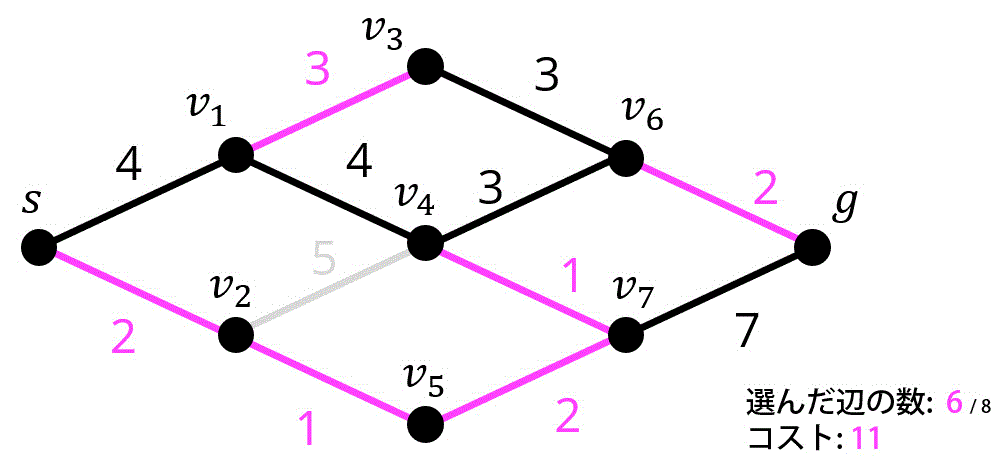
7つ目 / 8つ目
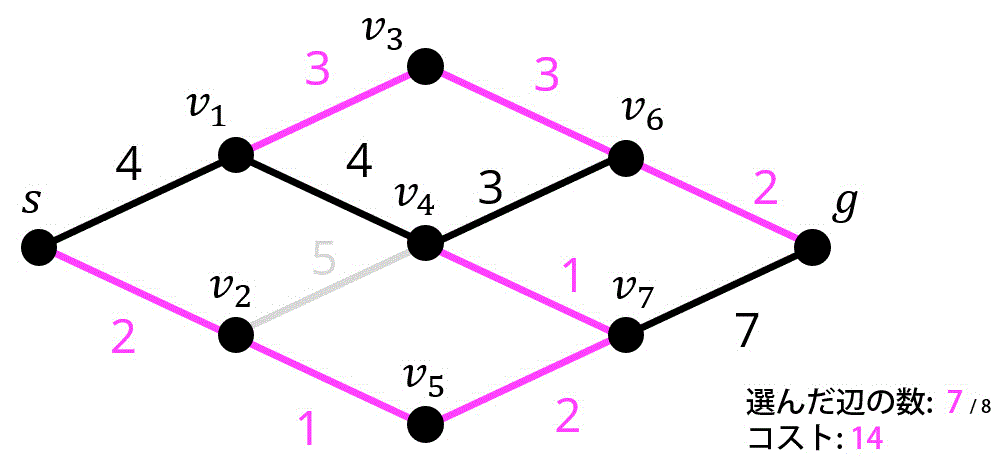
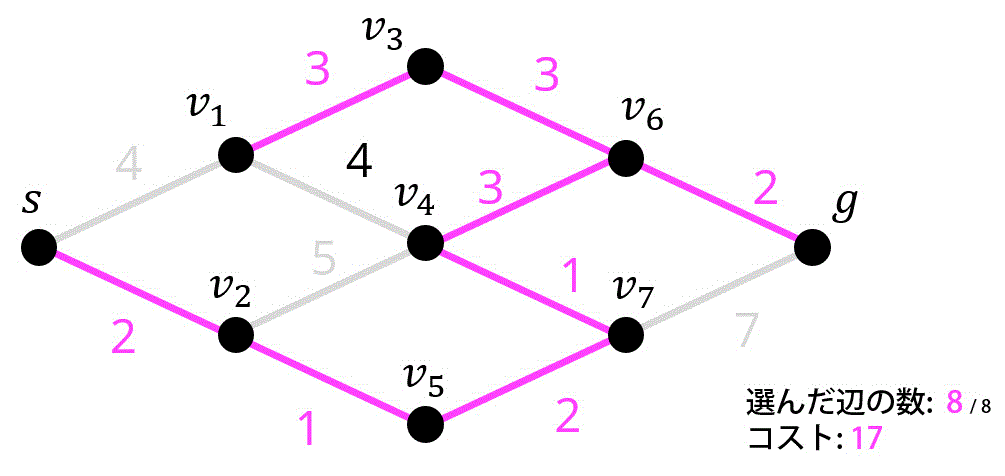
8つ目 / 8つ目

Step1. まだ追加していないグラフ内の辺の中で、重みが最も小さい辺を取り出す。
(複数存在する場合は指示がない限り、どれを取り出してもOK)
Step2. チェックした辺を追加しても閉路ができなければ辺を追加し、Step1に戻る。追加して閉路ができてしまう場合は無視。
Step3. すべての辺をチェックし終わったときに追加された辺が最小全域木である。
(ii) プリム法で解く場合
辺の重みが最も小さい辺が含まれている点をスタートとして、辺をどんどんつなげていく形で最小全域木を作り上げましょう。ただし、閉路ができないように注意。
※ ピンク色の辺は追加した辺、水色の辺は追加する候補の辺、灰色の辺は追加すると閉路ができてしまう辺を表しています。
1つ目 / 8つ目. 点 \( v_5 \) をスタート点としましょう。
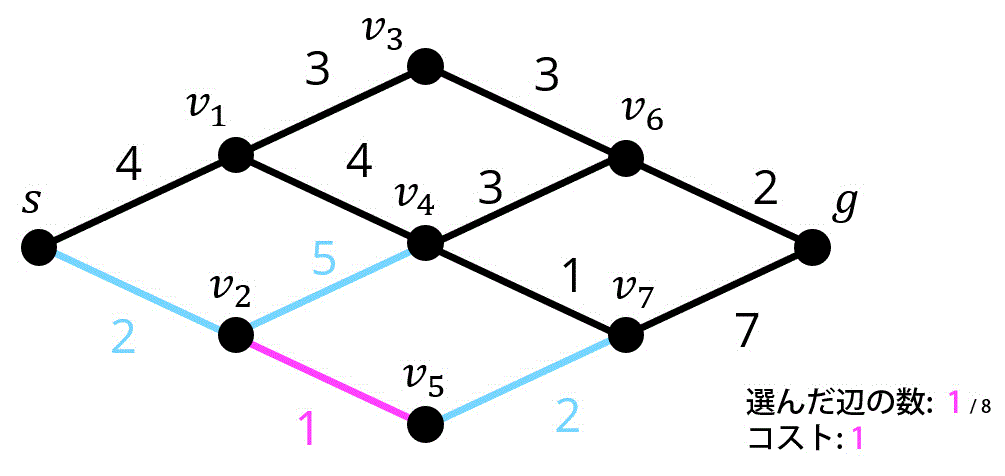
2つ目 / 8つ目.
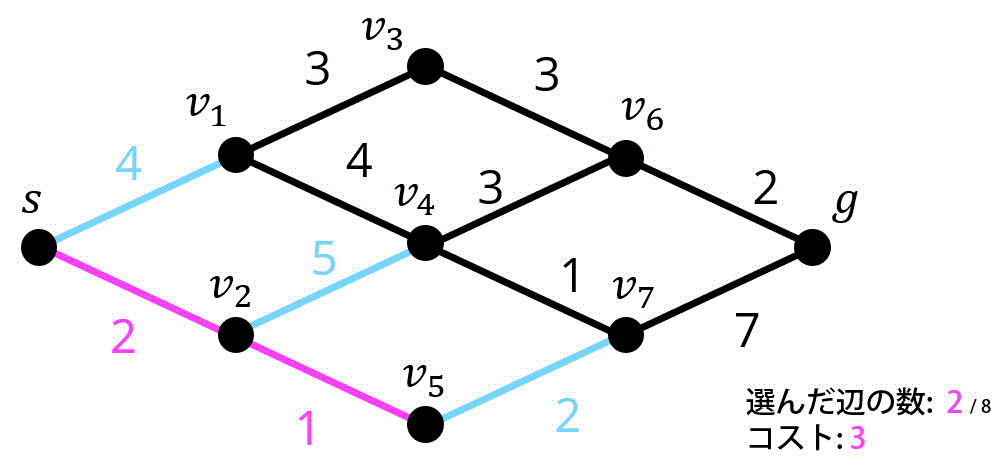
3つ目 / 8つ目.
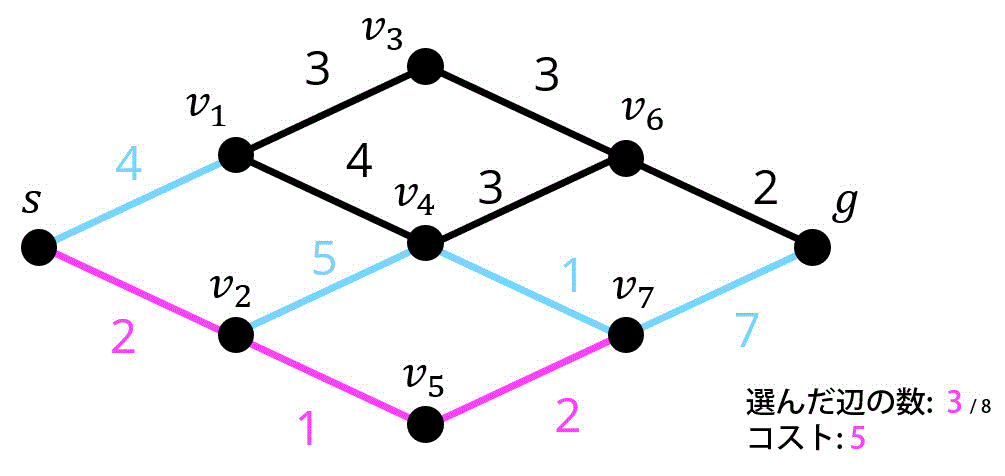
4つ目 / 8つ目.
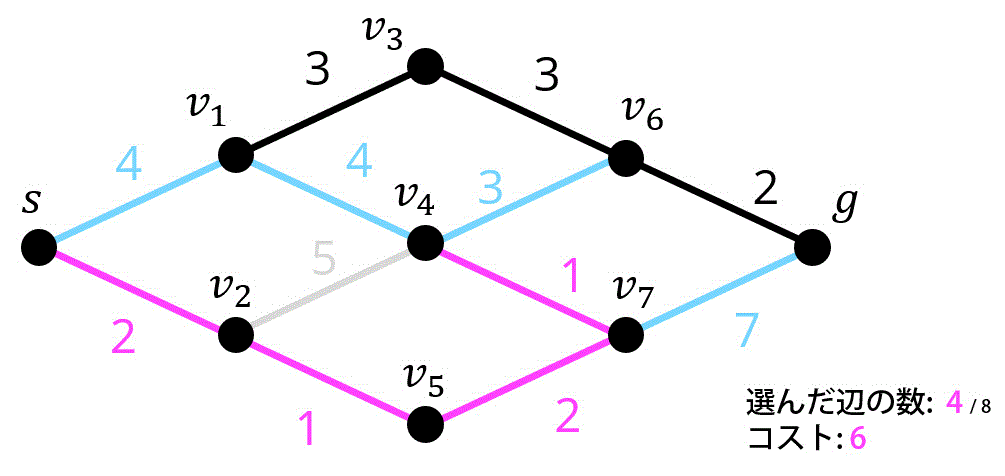
5つ目 / 8つ目.
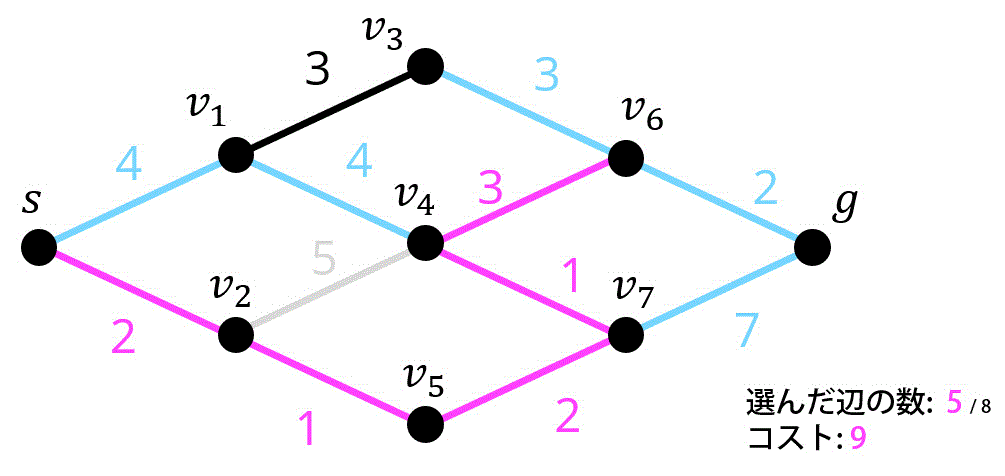
6つ目 / 8つ目.
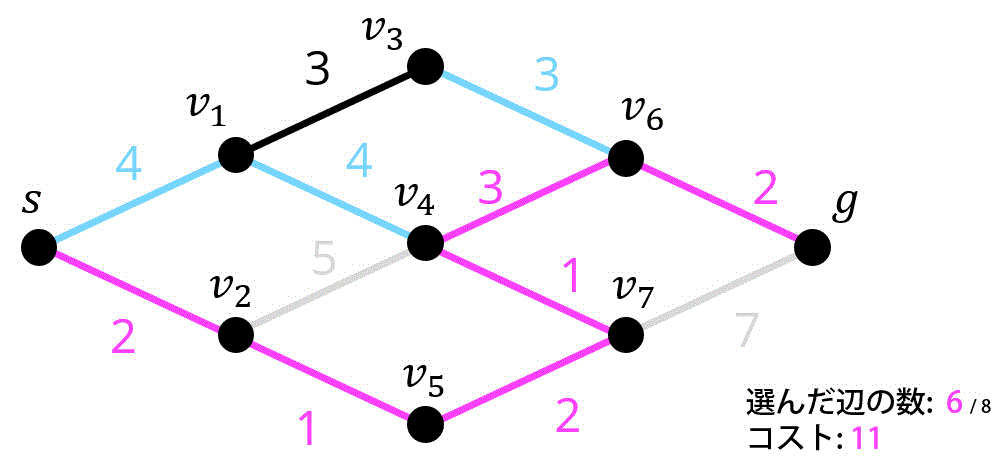
7つ目 / 8つ目.
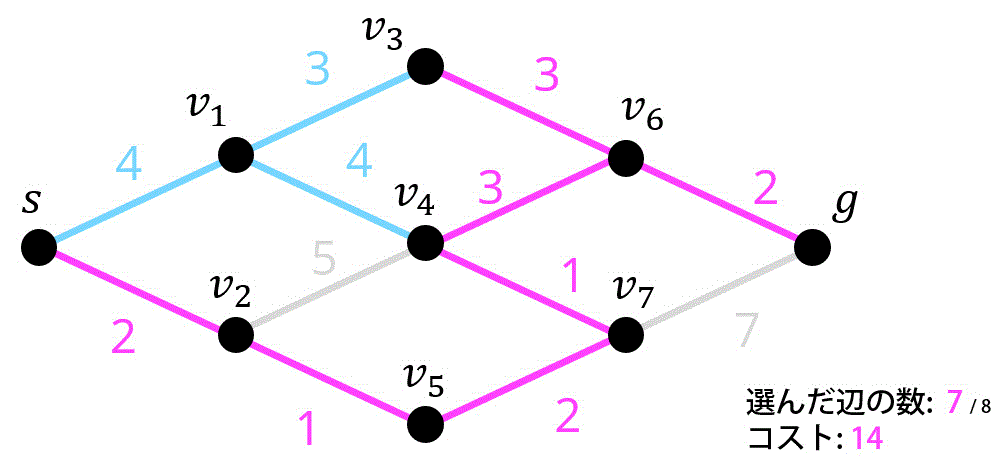
8つ目 / 8つ目.

Step1. スタートの点を1つ決める(どこでもOK)
Step2. スタート点、およびすでに追加した辺からたどれる辺の中で一番重みが小さい辺を追加することを繰り返す。
(一番重みが小さい辺が複数ある場合は重みが一番小さいどの辺をチェックしてもOK)
Step3. 追加できる辺がなくなったらおしまい
最小全域木についてさらに練習したい人はこちらの記事をご確認ください!
問題7. 最大フロー・最小カット
ヒビキ達が住んでいる地域は、下のようなグラフ \( G \) で表される。
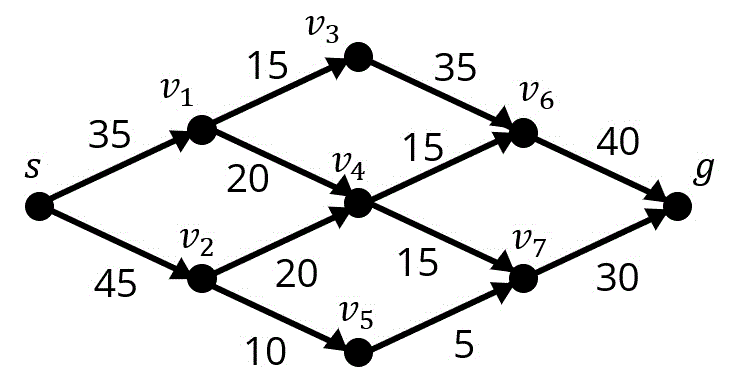
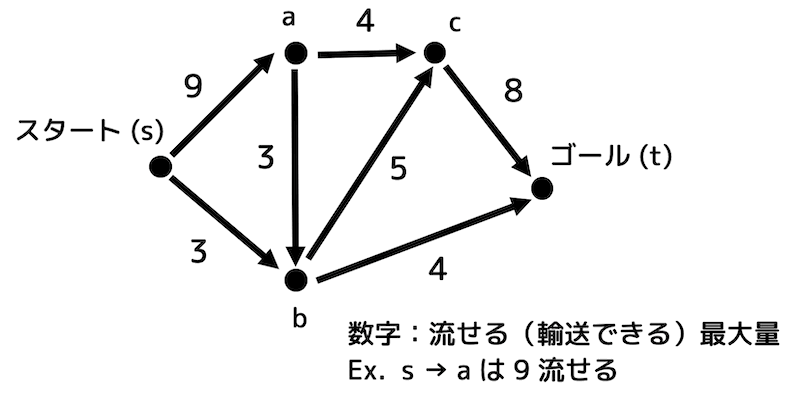
ここで、それぞれのグラフの頂点は街を表し、辺は街に行くための道路を表している。辺に書かれている数字は、1時間あたりに移動できる人数の上限[×100人]を表している。ここで、この地域では、年に1度、地域の誕生を祝う祭りが開かれる。その祭りの際に、街 \( s \) から街 \( g \) へ大量の人が移動する。そこで1時間あたりに街 \( s \) から街 \( g \) へ移動できる人数の限度を知りたい。次の(1), (2)の問いに答えなさい。
(1) このグラフ \( G \) の最大フローを求めることで、1時間あたりに街 \( s \) から街 \( g \) へ移動できる人数の限度を求めなさい。ただし、年に1度の祭りの際には交通規制が行われるため、人々は矢印の方向にしか進めないものとする*5。
(2) グラフ \( G \) の最小カット、および最小カットの容量を求めなさい。
[注釈] *5 祭りのときによるある一方通行規制だと思ってください。(1) [解答] 5,000人/h(最大フローは50×100人)(7点)
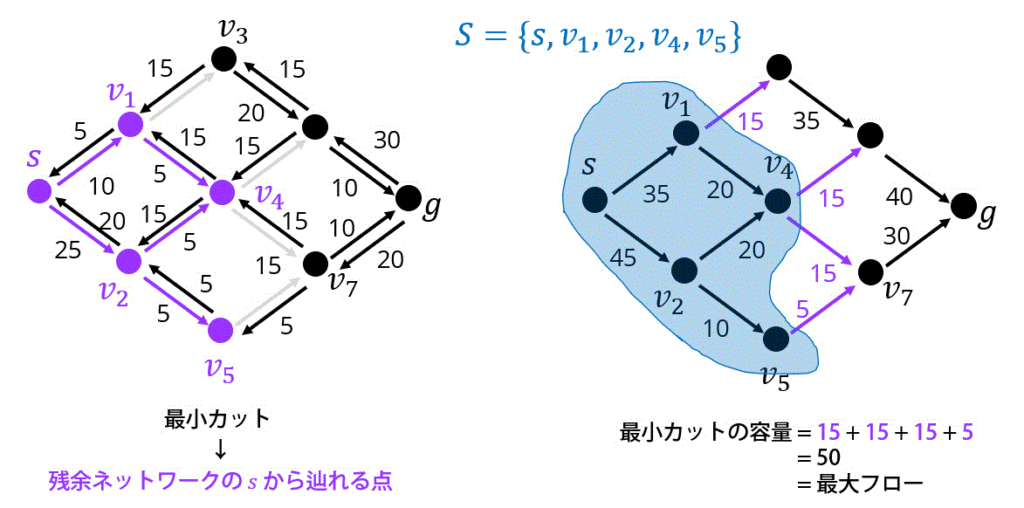
(2) 最小カット \( \{ s, v_1, v_2, v_4, v_5 \} \) 、最小カットの容量 5,000(人)
[解説](1) フローと残余ネットワークは下の通り。
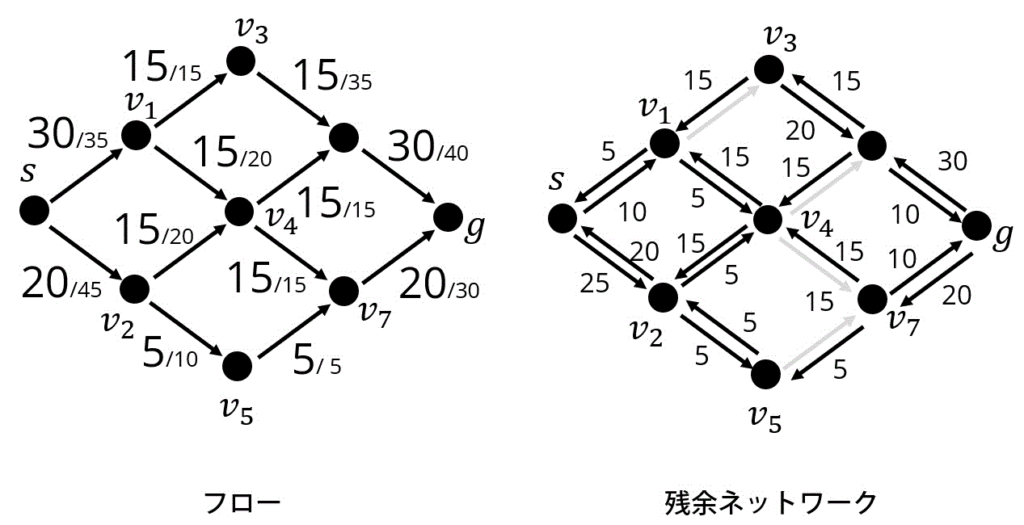
残余ネットワークのグラフにおいて、\( s \) から \( g \) までの道が存在しなくなるまでフローに追加していけばOK。
初期状態(何も追加していない状態)
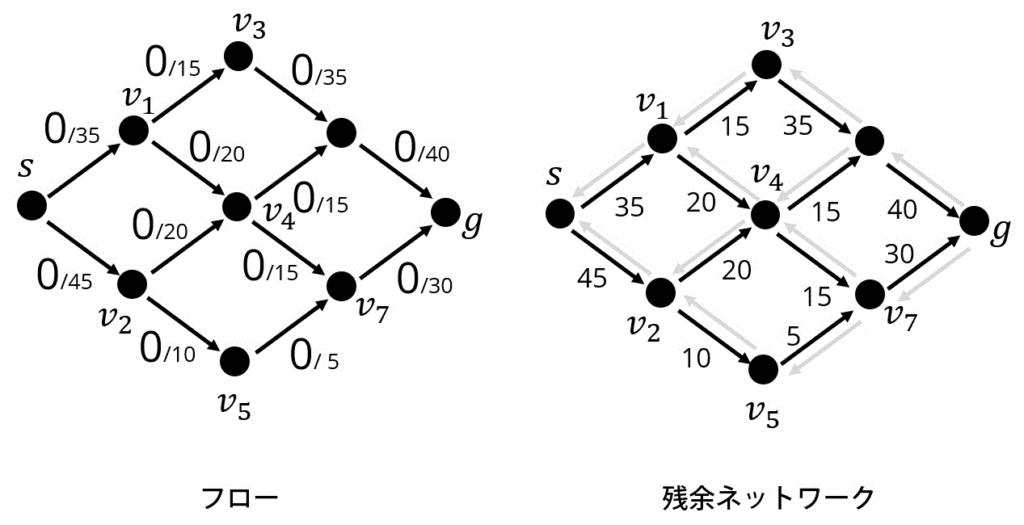
Attempt1. 緑色の矢印方向に15追加
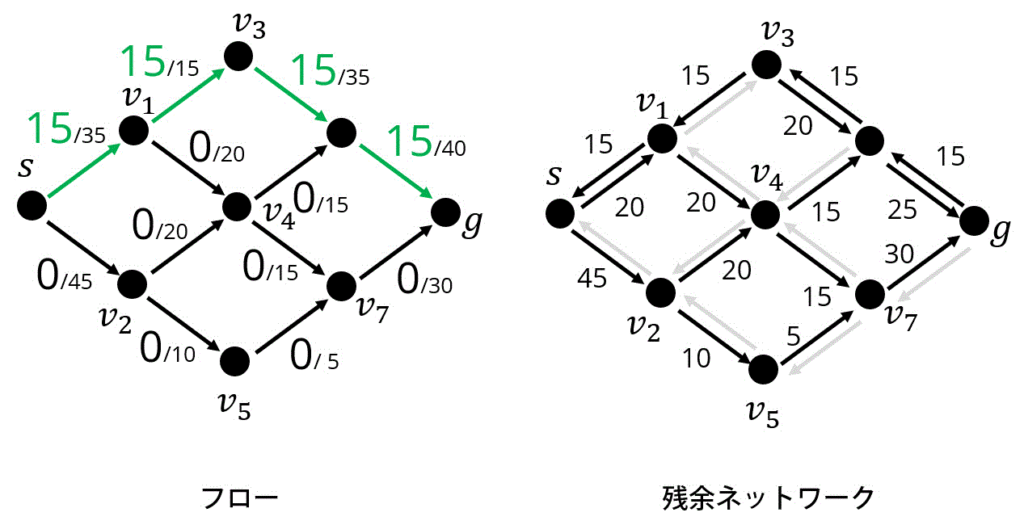
Attempt2. 緑色の矢印方向に15追加
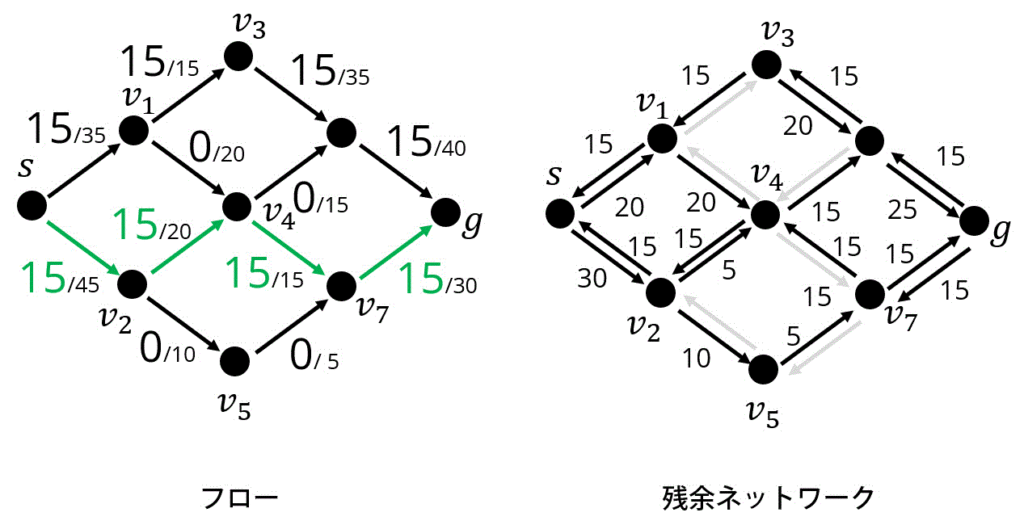
Attempt3. 緑色の矢印方向に15追加
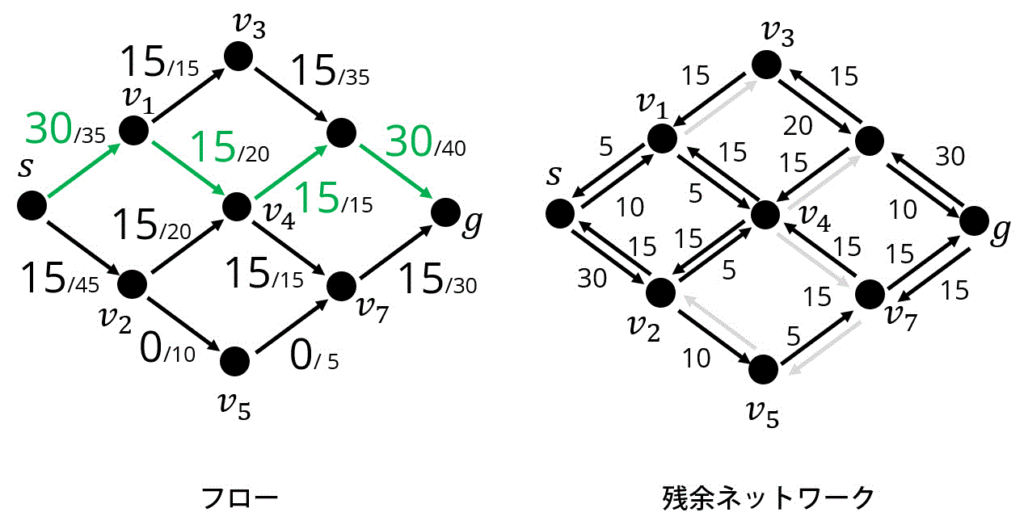
Attempt4. 緑色の矢印方向に5追加
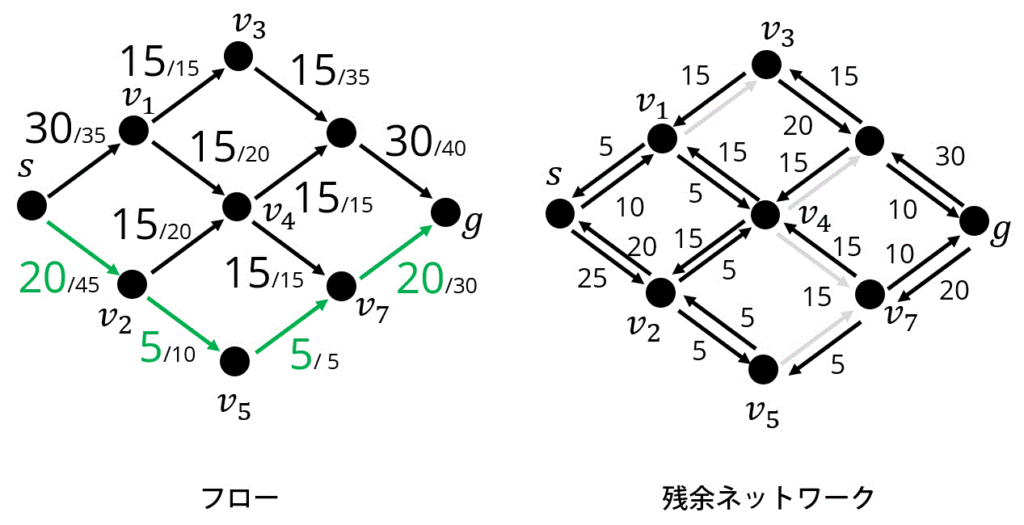
ここで、残余ネットワークのグラフを見ると、\( s \) から \( g \) まで辿れる道がなくなっている。
よって、この状態が最大フローであることがわかる。
あるネットワークのスタート \( s \) からゴール \( g \) までの最大フローは下のような手順で求めることができる。
Step1. 全部のフローが0の状態をはじめの状態(初期フロー)とし、初期フローのときの残余ネットワーク(与えられたネットワークと同じ)を考える。
Step2. 残余ネットワークで から までたどれるような道(ルート)を見つけ、その道に流せるだけのフローを流す。(増大道と呼ばれる)
Step3. Step2を繰り返し、\( s \) から \( g \) まで流せる道がなくなったときのフローが最大フローとなる。
(2)
最小カットは、「最大フローの状態のときの残余ネットワークのグラフ」において、スタート点 \( s \) から辿れる点を集めた集合である。
よって、最小カットは \( S = \{ s, v_1, v_2, v_4, v_5 \} \) となる。(4点)
また、最小カットの容量は、「\( S \) の集合の要素である点」から「\( S \) 以外の集合 \( \overline{S} \) の要素である点」へ流せるフローの合計値に等しい。
よって、最小カットの容量の答えは50(5,000人)となる。(3点)
なお、最大フローと最小カットの容量は必ず等しくなるため、最小カットの集合を問われていない場合は、最大フローを求めるだけで最小カットの容量を求めることができる。
(最大フローと最小カットの容量を両方求めることで、検算に使うのももちろんOK)
最大フローのときの残余ネットワークのグラフにおいて、始点 \( s \) から辿れるグラフが最小カット \( S \) となる。
また、最小カット \( S \) からそれ以外の点 \( \overline{S} \) へのフローの和が最小カットの容量となり、最大フローと必ず一致する。
最大フロー・最小カットについてもう少し練習したい人はこちらの記事をご覧ください。
問題8. マッチング
ヒビキとその友達(リクオ、マツ、ノゾミ、ユメ、サキ)は肝試しをすることにした。そこで、肝試しを楽しんでもらうために、お互いに仲が良い人同士で組むことを考えたい。ここで、男性陣はヒビキ、リクオ、マツの3人、女性陣はノゾミ、ユメ、サキの3人である。
(1) まずは、男女考えずに2人組を作ることを考えた。事前に仲良しな人を調査した結果、6人の関係は下の表となった。次の(i), (ii)の問いに答えなさい。ここで、○がついている人同士がお互いに仲が良い人を表す。例えば、ヒビキとリクオは○がついているため、お互いに仲が良い。
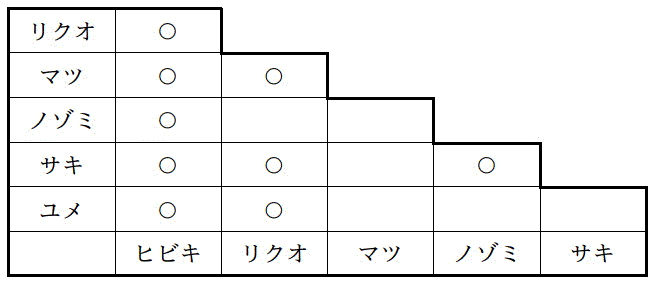
(i) 人を点、仲良し関係を辺としたときの状態をグラフで書きなさい。
(ii) 互いに仲が良い人同士で組むことは可能か。理由とともに答えなさい。
(2) 次に男女ペアで2人組を作ることを考えた。事前に組んでもいい人を調査した結果、関係は下の表ようになった。((1)と同じく、○がついている人同士が互いに仲が良い)
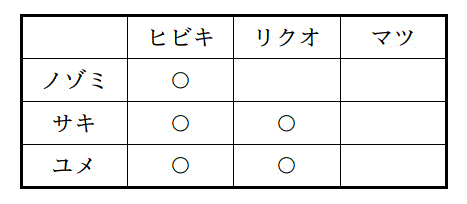
(i) 仲良し関係を辺としたときの状態をグラフで書きなさい。
(ii) 互いに仲が良い人同士で組むことは可能か。理由とともに答えなさい。
(1-i) グラフは以下の通り。特に解説はなし。(3点)
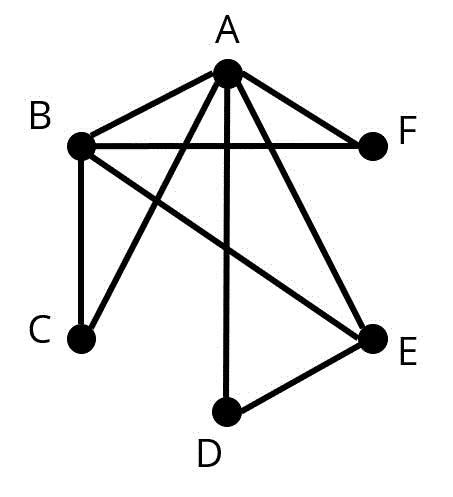
(1-ii) 可能。(2点)
理由:(i)で作ったグラフの完全マッチングが下のグラフのようになるから。(解答として書く際には、ピンクの辺を取り出してグラフを書けばOK)(3点)
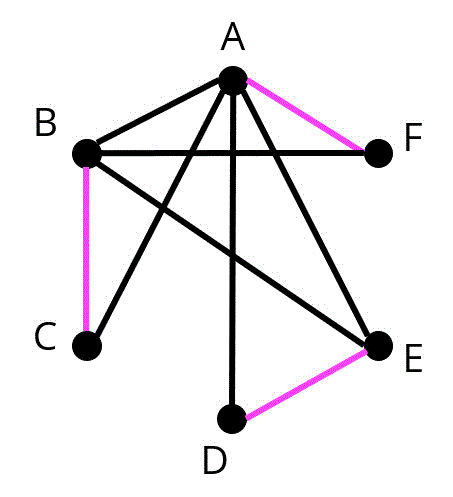
どの点にも辺がつながっているマッチングのことを完全マッチングと呼ぶので、覚えておきましょう。
なお、完全マッチングが存在する場合、完全マッチングのグラフの辺の数は必ず頂点の数の半分となるので、頭に入れておくと便利です。
極大マッチング:マッチングの中でこれ以上辺(ペア)を追加できないもの
最大マッチング:あるグラフに追加できる上限数分の辺(ペア)を追加したもの
(最大マッチングであるものは必ず極大マッチングであるが、極大マッチングだからといって最大マッチングであるとは限らない)
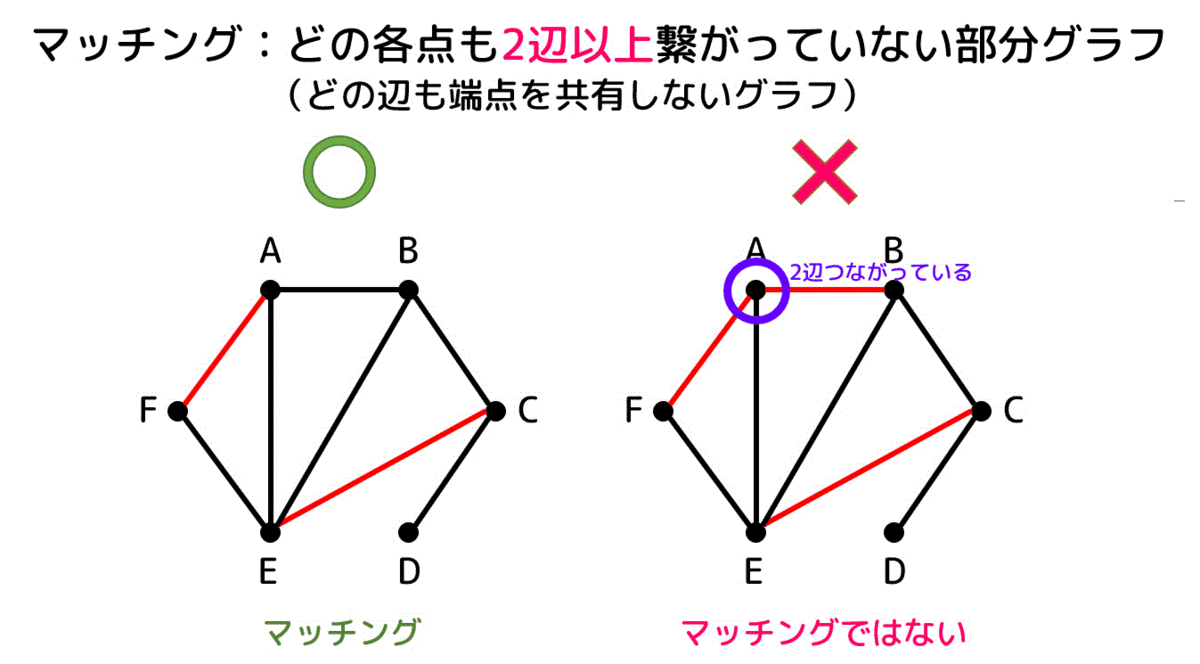
完全マッチング:どの点にも辺がつながっている(ペアになっている)マッチング
(完全マッチングであれば必ず最大マッチングとなる、一方最大マッチングが完全マッチングになるかはわからない。)
また、あるグラフが完全マッチングとなる場合、頂点数 \( n \) に対して追加した辺の数は必ず \( \frac{1}{2} n \) となる。
(2-i) グラフは以下の通り。今回は、2部グラフとなる。(3点)
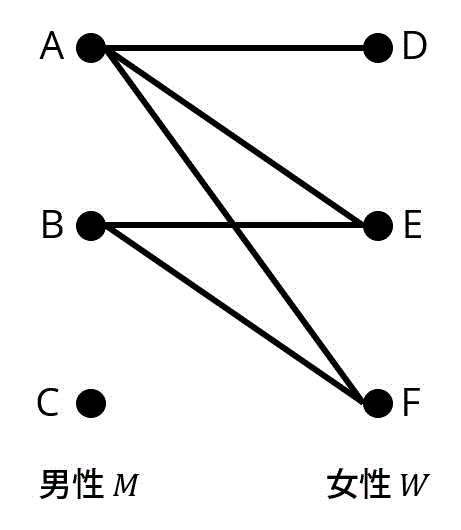
(ii) 不可能。(2点)
[理由] (3点)(i)のグラフが \( M \) から \( W \) への完全マッチングを持つと仮定する。すると、ホールの定理より、どのような \( S \) ただし \( S \subseteq M \) であっても \( S \leqq N(S) \) が成立する[2]\( N(S) \) は、\( S \) の集合から辿れる \( W \) への点を表している。例えば \( S = \{ A,B \} とした場合、\( N(S) = \{D,E,F\} \) となる。。
しかし、\( S = \{ C \} \) とした場合、\( |S| = 1 \) になるのに対し、\( N(S) = 0 \) となるため、仮定は矛盾する。よって、完全マッチングは持たない。
\( A \) から \( B \) への完全マッチングを持たないことを示すためには、グラフ \( A \) の中から要素を何個か選んだとき(\( S \subseteq A \) )に、\( A \) から辿れる集合の要素 \( N(S) \) について、以下の関係になる \( S \) を1つでも見つけたらOK。\[
|S| > |N(S)|
\]
マッチングについてさらに復習したい人はこちらの記事にて復習しましょう!
関連広告・スポンサードリンク