うさぎでもわかる信号処理　第01羽　z変換のいろは

こんにちは、ももやまです。

数か月ぶりですが、大学数学の記事を書き進めていきたいと思います。

今回からしばらくの間は、制御数学（信号処理で使う数学）について不定期ですが更新していきたいと思います。

最初となる第01羽は、z変換の基本について説明していきます。

スポンサードリンク

１．z変換の定義・ラプラス変換との関係性

(1) z変換の定義

まずいきなりですが、z変換の定義を見てみましょう。

ある数列 \( x_n \) に対して、\[
X(z) = \sum^{\infty}_{n = 0} x_n z^{-n}
\]の無限級数の形で表される \( z \) の関数 \( X(z) \) のことをz変換と呼びます。

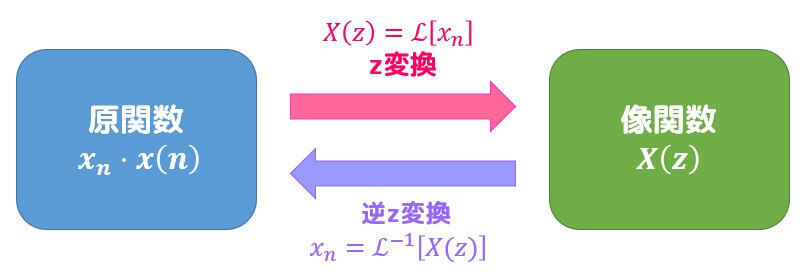
さらに、z変換を行う元の数列 \( x_n \) を原関数と呼び*1、z変換後の \( z \) の関数 \( X(z) \) のことを像関数と呼び、1対1に対応しています。

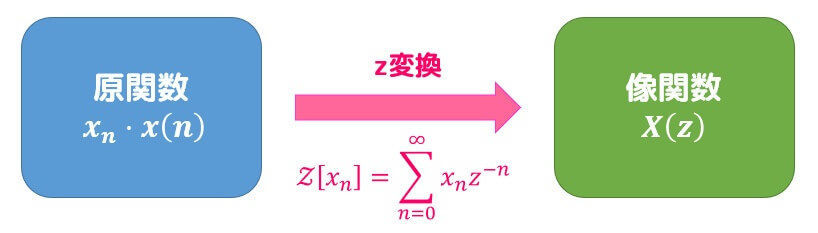
(2) ラプラス変換との関係性

いきなり定義を暗記しろ、って言われても腑に落ちない人もいると思います。

なので、z変換がなぜ(1)で説明した公式の形が出てきたかを（ラプラス変換との関係性を踏まえながら）説明したいと思います。

なお、ラプラス変換についてはこちらで記事にしているため、もしよかったらご覧ください。

まず、ラプラス変換の公式は、\[
F(s) = \int^{\infty}_{0} f(t) e^{-st}
\]でしたね。

この \( F(s) \) は、下の図の \( x \) 軸と \( f(t) e^{-st} \) で囲まれた部分の面積 \( S \) と一致しますね。

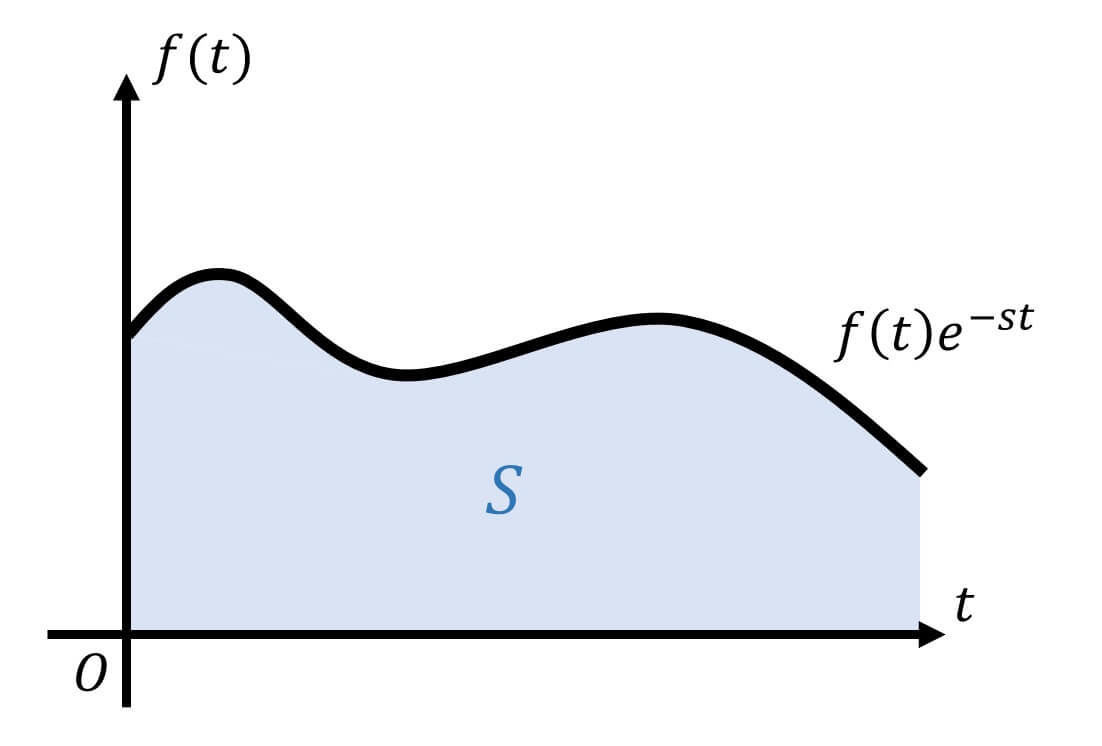
つぎに、\( S \) を、微小な間隔 \( \Delta t \) ごとに刻んでいきます*2。

（信号処理・制御数学の世界では、「刻む」ことをサンプリング or 標本化と呼びます。）

さらに、刻んだ部分それぞれの面積を \( \Delta S_0 \), \( \Delta S_1 \), \( \Delta S_2 \) … としていきます。

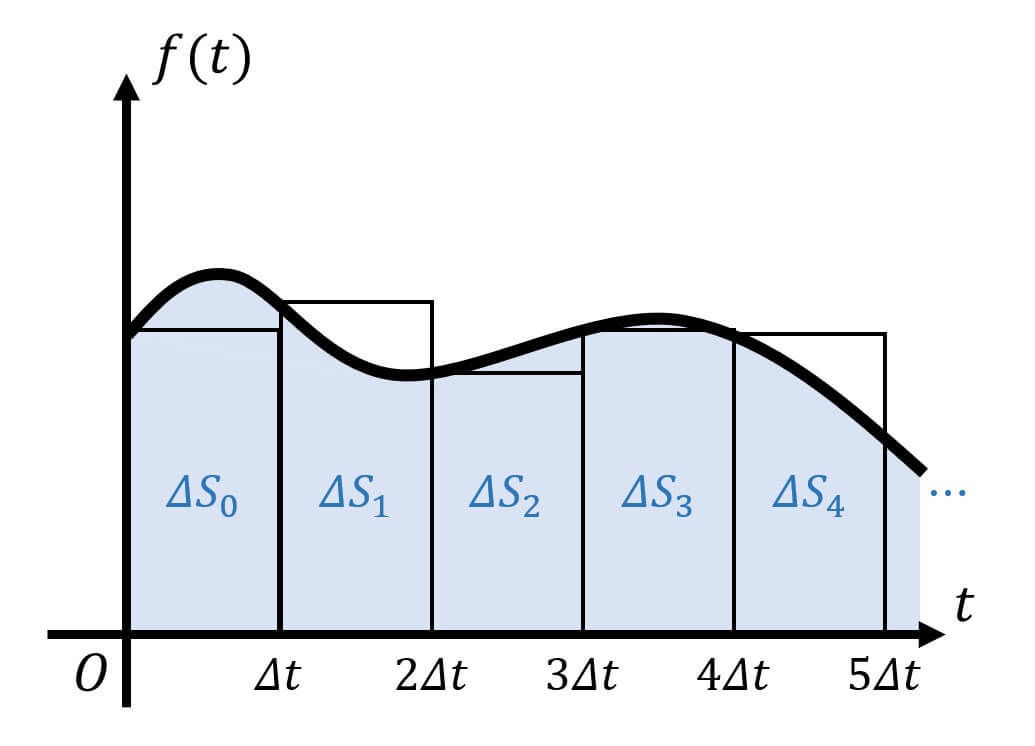
すると、例えば \( \Delta S_0 \) の面積は、\[\begin{align*}
\Delta S_0 & = f(0) e^{-s \cdot 0} \cdot \Delta t
\\ & = f(0) \Delta t
\end{align*}\]と長方形の面積を求めるノリで求められますね。

同様に、\( \Delta S_2 \) の面積であれば、\[\begin{align*}
\Delta S_2 & = f( 2 \Delta t ) e^{-s \cdot 2 \Delta t} \cdot \Delta t
\\ & = f (2 \Delta t ) e^{ - 2 s \Delta t} \ \Delta t
\end{align*}\]となりますね。

では、\( \Delta S_n \) の面積はどうなるかを考えてみましょう。

\( n \) と具体的な数値ではありませんが、上の \( S_2 \) などの計算と同じように\[\begin{align*}
\Delta S_n & = f( n \Delta t ) e^{-s \cdot n \Delta t} \cdot \Delta t
\\ & = f (n \Delta t ) e^{ - n s \Delta t} \ \Delta t
\end{align*}\]と計算することができます。

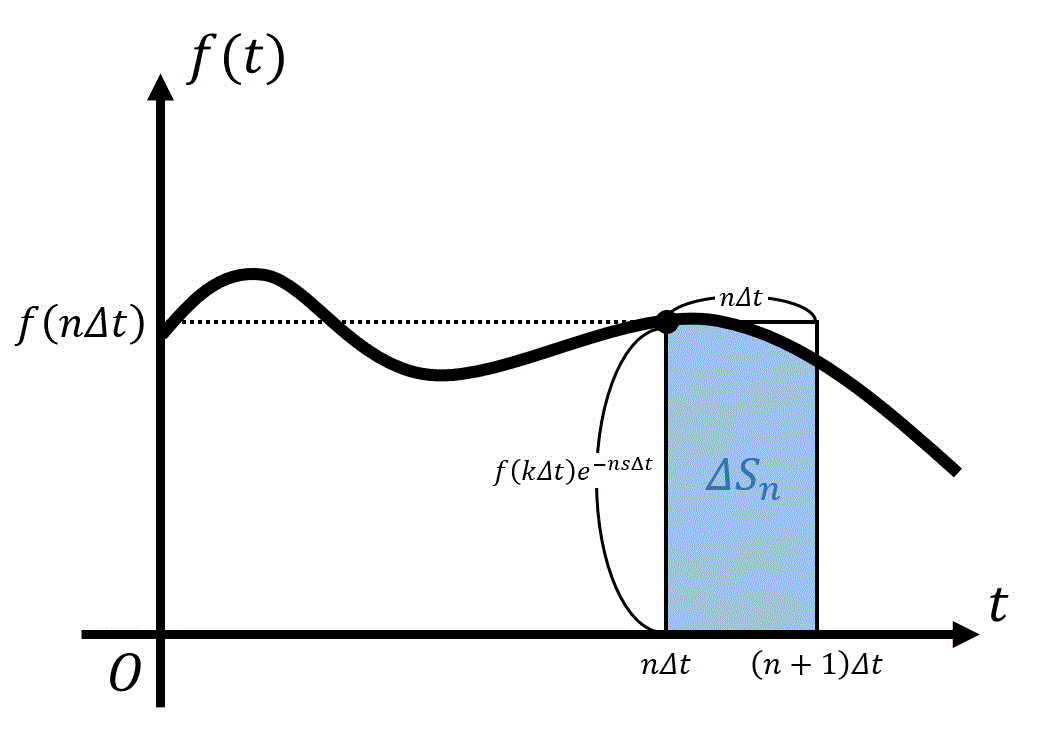
ここで、刻んだ面積 \( \Delta S_0 \), \( \Delta S_1 \), … の総和は当然 \( S \) と一致しますよね。

よって総和 \( S \) を\[\begin{align*}
S & = \Delta S_0 + \Delta S_1 + \Delta S_2 + \cdots
\\ & =  \sum^{\infty}_{n = 0} \Delta S_n
\\ & =  \sum^{\infty}_{n = 0}  f (n \Delta t ) e^{ - n s \Delta t} \ \Delta t
\\ & = \Delta t  \sum^{\infty}_{n = 0}  f (n \Delta t ) e^{ - n s \Delta t}
\end{align*}\]と書き換えることができますね。

ここで、両辺を \( \Delta t \) で割り、さらに\[
e^{-s \Delta t} = z^{-1} , \ \ \ x_n =  f (n \Delta t )
\]とおきます。

すると、\[\begin{align*}
\frac{S}{ \Delta t} & = \sum^{\infty}_{n = 0}  f (n \Delta t ) e^{ - n s \Delta t}
\\ & = \sum^{\infty}_{n = 0} f (n \Delta t ) z^{-n} \tag{*}
\\ & = \sum^{\infty}_{n = 0} x_n z^{-n}
\end{align*}\]と変形することができます。

この、\[
\sum^{\infty}_{n = 0} x_n z^{-n}
\]の形が \( z \) 変換の公式となり、\( \mathcal{Z}[x_n] \) と表記されます。

(3) 定義に沿ってz変換を求めてみよう

では、(1)で紹介した定義に沿ってz変換を計算してみましょう！

 例題1 

つぎの(1), (2)で表される数列 \( x_n \) のz変換 \( \mathcal{Z}[x_n] \) を求めなさい。

(1) \( \mathcal{Z}[1] \)

(2) \( \mathcal{Z}[n] \)

[解説1]

(1)

まずは、\( x_n = 1 \) をz変換の公式に代入してみましょう。すると、\[\begin{align*}
\mathcal{Z}[1] & = \sum^{\infty}_{n = 0} x_n z^{-n}
\\ & = 1 + z^{-1} + z^{-2} + \cdots
\end{align*}\]の形になりますね。

すると、初項1、公比 \( z \) の無限等比数列の総和の形になっていることがわかりますね。

よって、\[\begin{align*}
\mathcal{Z}[1] & = 1 + z^{-1} + z^{-2} + \cdots
\\ & = \frac{1}{1 - z^{-1}}
\\ & = \frac{z}{z-1}
\end{align*}\]とz変換を求めることができますね。

[別解]

マクローリン展開\[
\frac{1}{1 - z^{-1}} = 1 + z^{-1} + z^{-2} + \cdots
\]の形からz変換を求めてもOKです。

(2)

(1)と同じように \( x_n = n \) をz変換の公式に代入してみましょう。すると、\[\begin{align*}
\mathcal{Z}[n] & = \sum^{\infty}_{n = 0} x_n z^{-n}
\\ & = z^{-1} + 2 z^{-2} + 3 z^{-3} + 4 z^{-4} + \cdots \cdots
\end{align*}\]の形になりますね。

(1)のように無限等比数列の総和の形になんとか持ち込みたいですよね。

しかし、今回の問題はどう頑張っても無限等比数列の形には持ち込めません。

なので別の方法を考えてみましょう。

ここで、\[
\frac{1}{1 - z^{-1}} = 1 + z^{-1} + z^{-2} + \cdots
\]の両辺を微分してみましょう。

すると、\[\begin{align*}
\frac{d}{dz} \frac{1}{1 - z^{-1}} & = - z^{-2} - 2z^{-3} - 3z^{-4} - 4z^{-5} \cdots \\
\frac{ - z^{-2} }{ (1-z^{-1})^{2} } & = - z^{-2} - 2z^{-3} - 3z^{-4} - 4z^{-5} \cdots
\end{align*}\]が出てきますね。

さらに、両辺に \( - z \) を掛けると、\[\begin{align*}
- z \cdot \frac{ - z^{-2} }{ (1-z^{-1})^{2} } & = - z \left( - z^{-2} - 2z^{-3} - 3z^{-4} - 4z^{-5} \cdots \right) \\
\frac{z^{-1}}{ ( 1 - z^{-1} )^{2} } & = z^{-1} + 2z^{-2} + 3z^{-3} + 4z^{-4} + \cdots
\end{align*}\]となる。

よって、z変換は\[\begin{align*}
\mathcal{Z}[n] & = \sum^{\infty}_{n = 0} x_n z^{-n}
\\ & = z^{-1} + 2 z^{-2} + 3 z^{-3} + 4 z^{-4} + \cdots \cdots
\\ & = \frac{z^{-1}}{ ( 1 - z^{-1} )^{2} }
\\ & = \frac{z^2 \cdot z^{-1}}{z^2 ( 1 - z^{-1} )^{2} }
\\ & = \frac{z}{(z-1)^2}
\end{align*}\]と求められる。

※ しれっと無限級数 \( 1 + z^{-1} + z^{-2} + \cdots \) を \( z \) で微分しましたが、厳密には無限級数が収束するかどうかを確かめてから微分する必要があるので、答案などを書く際には注意しましょう。

(4) 片側z変換と両側z変換

先程(1), (2)で取り上げたz変換は、\( n \geqq 0 \) の整数 \( n \) のみで定義される \( x_n \) が対象でしたね。

正と負のうちの片方（正）でのみ定義されてるz変換なので、片側z変換と呼ばれることもります。

一方、 \( x_n \) に \( x_{-1} \), \( x_{-2} \), … のような \( n < 0 \) でも定義されるz変換のことを両側z変換と呼びます。

式で書くと、下のような形になります。\[
\sum^{\infty}_{n = - \infty} x_n z^{-n}
\]

※ 本記事では特に指示がない限り、z変換と呼ばれたら片側z変換を指していると思ってください。

スポンサードリンク

２．逆z変換

z変換を行う前の数列 \( x_n \) とz変換後の関数 \( X(z) \) は1対1に対応しているのでしたね。

1対1に対応していることを利用することで、z変換後の関数 \( X(z) \) からz変換前の数列 \( x_n \) に戻す逆z変換 \( \mathcal{Z}^{-1}] \) が定義されます。

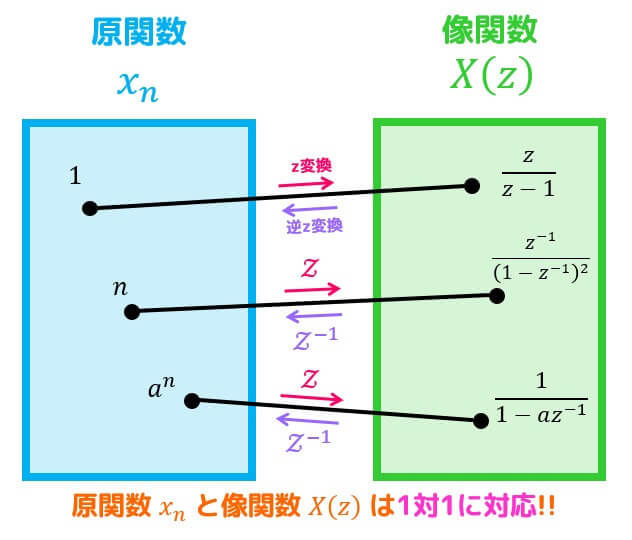
先程、\( x_n = 1 \) をz変換した結果が \( X(z) = \frac{z}{z-1} \) であることを確認しましたね。

z変換前・変換後の関数は1対1の関係にあるため、\(X(z) = \frac{z}{z-1} \) を逆z変換した結果は\[\begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ X(z) \right] \\ & = \mathcal{Z}^{-1} \left[ \frac{z}{z-1} \right] \\ & = 1
\end{align*}\]と求めることができます。

スポンサードリンク

３．重要なz変換の6つの公式

つぎに、z変換で重要な6つの公式

• 線形の法則（重要度：★★★★★）
• 微分の法則（重要度：★★★★★）
• 指数倍の法則（重要度：★★★★★）
• シフトの法則（重要度：★★★★☆）
• 初期値定理（重要度：★★★☆☆）
• 最終値定理（重要度：★★☆☆☆）

を見ていきましょう。

時間がないという人は、赤色で示された4つの公式を確認すればOKです。

その1 　線形(定数)の法則

積分でも、\[
\int 5x^2 + 3x \ dx = 5 \int x^2 \ dx + 3 \int x \ dx
\]と足し算引き算、定数倍を分離できるように、z変換においても足し算引き算、定数倍を分離することができます。

[導出過程]

数列 \( x_n \), \( y_n \) のz変換が\[
\mathcal{Z}[x_n] = X(z) \\
\mathcal{Z}[y_n] = Y(z)
\]で表せるとする。

\[\begin{align*}
\mathcal{Z}[a \ x_n + b \ y_n] & =  \sum^{\infty}_{n = 0} (a \ x_n + b \ y_n) z^{-n}
\\ & = \sum^{\infty}_{n = 0} a \ x_n + \sum^{\infty}_{n = 0} b \ y_n
\\ & = a \sum^{\infty}_{n = 0} x_n + b \sum^{\infty}_{n = 0} y_n
\\ & = a \ X(z) + b \ Y(z)
\\ & = a \ \mathcal{Z}[x_n] + b \ \mathcal{Z}[y_n] \end{align*}\]

逆変換でも線形の法則は成り立つ！

なお、逆z変換であっても、\[
\mathcal{Z}^{-1}[a \ X(z) + b \ Y(z)] = a \ \mathcal{Z}^{-1}[X(z)] + b \ \mathcal{Z}^{-1}[Y(z)] \]と、定数倍・足し算を分離することができます。

その2 　微分の法則

z変換前の数列 \( x_n \) が \( x_n = n^2 + 4n + 3 \) のような \( n^a \) の多項式の形になっているときに使える法則です。

まずは公式を見てみましょう。

微分の法則を使うことで、元の数列 \( x_n \) に \( n^a \) の形が含まれている場合に、z変換の定義式を使うことなしにz変換を行うことができます。

早速導出していきましょう。

まず、z変換の定義式\[\begin{align*}
\mathcal{Z}[n] & = \sum^{\infty}_{n = 0} x_n z^{-n}
\\ & = x_0 + x_1 z^{-1} + x_2 z^{-2} + \cdots + x_{n} z^{-n} + \cdots
\\ & = f(z)
\end{align*}\]の両辺を微分してみましょう。

すると、\[\begin{align*}
f'(z) & =  - x_1 z^{-2} - 2 x_2 z^{-3} - 3 x_3 z^{-4} \cdots - n x_{n} z^{-(n+1)} - \cdots
\\ & = - z^{-1} \left( x_1 z^{-1} + 2 x_2 z^{-2} + 3 x_3 z^{-3} + \cdots + n z^{-n} + \cdots \right)
\\ & = - z^{-1} \left( x_1 z^{-1} + 2 x_2 z^{-2} + 3 x_3 z^{-3} + \cdots + n z^{-n} + \cdots \right)
\\ & = - z^{-1} \sum^{\infty}_{n = 0} n x_n z^{-n}
\\ & = - z^{-1} \mathcal{Z}[n x_n] \end{align*}\]の形になりますね。

よって、\[
\frac{d}{dz}  \mathcal{Z}[n] = - z^{-1} \mathcal{Z}[n x_n] \\
\mathcal{Z}[n x_n] = -z \cdot \frac{d}{dz}  \mathcal{Z}[n] \]の関係式を導出することができます。

※ 本記事の1章同じく、しれっと無限級数 \( 1 + z^{-1} + z^{-2} + \cdots \) を \( z \) で微分しましたが、厳密には無限級数が収束するかどうかを確かめてから微分する必要があるので、答案などを書く際には注意しましょう。

使用例

実際に使用する場合には、ベースとなるz変換の公式\[
\mathcal{Z}[1] = \frac{z}{z-1}
\]に多項式の次数の数だけ微分します。

例えば、\( \mathcal{Z}[n^2] \) を導出する場合は、

1. \( \mathcal{Z}[1] \) に1回目の微分の公式を適用し、\( \mathcal{Z}[n] \) をつくる
2. \( \mathcal{Z}[n] \) に2回目の微分の公式を適用し、\( \mathcal{Z}[n^2] \) をつくる

の2ステップで導出が可能です。

具体的に微分の法則を用いてz変換を導出する方法は、第02羽のz変換計算編にて説明しますが、非常に重要なため、忘れないうちに1題だけ例題を解いてみましょう。

 例題2 

数列 \( x_n = n^2 \) のz変換 \( \mathcal{Z}[n^2] \) を微分の公式を用いて導出しなさい。必要であれば\[
\mathcal{Z}[1] = \frac{z}{z-1}
\]となることを使ってもよい。

[解説2]

まずは \( \mathcal{Z}[n] \) を作りましょう。\[\begin{align*}
\mathcal{Z}[n] & = \mathcal{Z}[n \cdot \color{red}{1}] \\ & = - z \cdot \frac{d}{dz} \mathcal{Z}[\color{red}{1}] \\ & = - z \cdot \frac{d}{dz} \frac{z}{z-1}
\\ & = - z  \cdot \frac{1 \cdot (z-1) - z \cdot 1}{(z-1)^2}
\\ & =  - z \cdot  \frac{-1}{(z-1)^2}
\\ & =  \frac{z}{(z-1)^2}
\end{align*}\]

つぎに目標の \( \mathcal{Z}[n^2] \) を作りましょう。\[\begin{align*}
\mathcal{Z}[n^2] & = \mathcal{Z}[n \cdot \color{red}{n}] \\ & = - z \cdot \frac{d}{dz} \mathcal{Z}[\color{red}{n}] \\ & = - z \cdot \frac{d}{dz} \frac{z}{(z-1)^2}
\\ & =  - z \cdot \frac{d}{dz} \frac{1 \cdot (z-1)^2 - z \cdot 2 (z-1)}{(z-1)^4}
\\ & =  - z \cdot  \frac{-z-1}{(z-1)^3}
\\ & =  \frac{z(z+1)}{(z-1)^3}
\end{align*}\]となるので、\( x_n = n^2 \) の z 変換は、\[
\mathcal{Z}[n^2] = \frac{z(z+1)}{(z-1)^3}
\]と求められる。

その3 　指数倍の法則

z変換前の数列 \( x_n \) が \( x_n = 3^n \) のような \( a^n \) のような指数関数の形になっているときに使える法則です。

微分の公式と同じく、z変換、逆z変換の導出に重要な公式の1つです。

同じく、公式を見てみましょう。

指数倍の法則を使うことで、元の数列 \( x_n \) に \( a^n \) の形が含まれている場合でも、あっという間にz変換の結果を出すことができます。

早速導出していきましょう。

z変換の定義式\[\begin{align*}
\mathcal{Z}[n] & = \sum^{\infty}_{n = 0}  a^n x_n z^{-n}
\\ & = a^0 x_0 + a^1 x_1 z^{-1} + a^2 x_2 z^{-2} + \cdots + a^n x_{n} z^{-n} + \cdots
\\ & = \sum^{\infty}_{n = 0} a^n x_n z^{-n}
\\ & = \sum^{\infty}_{n = 0} x_n (a^{-1} z)^{-n}
\\ & = X(a^{-1} z)
\end{align*}\]と導出することができます。

指数倍の公式は、微分の公式と組み合わせて使うことができます。

例えば、\( \mathcal{Z}[3^n n^2] \) であれば、

• \( \mathcal{Z}[1] \) に対して微分の公式を2回適用することで \( \mathcal{Z}[n^2] \) を作成
•  \( \mathcal{Z}[n^2] \) に対して指数倍の公式を適用することで \( \mathcal{Z}[3^n n^2] \) を作成

の2ステップで行うことができます。

指数倍の公式が微分の公式と組み合わせて使えることを体感してもらうために、また1問例題を用意してみたので、解いてみましょう。

 例題3 

数列 \( x_n = 4^n n^2 \) のz変換を指数倍の公式を用いて導出しなさい。必要であれば例題2の答えを使ってもよい。

[解説3]

\( n^2 \) のz変換を \( X(z) \) とする。\[
\mathcal{Z}[n^2] = \frac{z(z+1)}{(z-1)^3} = X(z)
\]

あとは \( z \to 4^{-1} z \) に置き換えるだけでOK。\[\begin{align*}
\mathcal{Z}[\color{red}{4}^n n^2] & = X(\color{red}{4}^{-1} z)
\\ & = \frac{4^{-1} z(4^{-1} z+1)}{(4^{-1} z-1)^3}
\\ & = \frac{( 4^{-1} z(4^{-1} z+1) ) \cdot 4^3}{( (4^{-1} z-1)^3 ) \cdot 4^3}
\\ & = \frac{4 z(z+4)}{(z-4)^3}
\end{align*}\]

その4 　シフトの法則

シフト変換は、数列 \( x_n \) をz変換、逆z変換する際にはあまり使いませんが、z変換を用いて差分方程式（漸化式）を解く際に必ずお世話になる法則です。

\( x_{n+2} \) のときまで導出してみましょう。

基本的な導出ステップとしては、

1. z変換の定義式\[
   \mathcal{Z}[x_{n+k}] = \sum^{\infty}_{n = 0} x_{n+k} z^{-n}
   \]によりz変換。
2. \( x_{n + k} \) のとき、 \( n' = n + k \) とおき、\[
   \sum^{\infty}_{n' = 0} x_{n'} z^{-n'} = X(z)
   \]の形に持ち込み、逆z変換を行う。

の2つです。

\( \mathcal{Z}[x_{n+1}] \) の導出\[\begin{align*}
\mathcal{Z}[x_{n+1}] & = \sum^{\infty}_{n = 0} x_{n+1} z^{-n}
\\ & = z \sum^{\infty}_{n = 0} x_{n+1} z^{-n-1}
\\ & = z \sum^{\infty}_{n = -1} x_{n+1} z^{-n-1} - x_0 z
\\ & = z \sum^{\infty}_{n' = 0} x_{n'} z^{-n'} - x_0 z
\\ & = z X(z) - x_0 z
\end{align*}\]

\( \mathcal{Z}[x_{n+2}] \) の導出\[\begin{align*}
\mathcal{Z}[x_{n+2}] & = \sum^{\infty}_{n = 0} x_{n+2} z^{-n}
\\ & = z^2 \sum^{\infty}_{n = 0} x_{n+2} z^{-n-2}
\\ & = z^2 \sum^{\infty}_{n = -2} x_{n+2} z^{-n-2} - x_0 z^2 - x_1 z
\\ & = z^2 \sum^{\infty}_{n' = 0} x_{n'} z^{-n'} - x_0 z^2 - x_1 z
\\ & = z^2 X(z) - x_0 z^2 - x_1 z
\end{align*}\]

なお、 \( x_{n-1} \), \( x_{n-2} \) のように負のシフト法則も同じように導出が可能です。導出結果（公式）のみを下に載せておきます。

\( \mathcal{Z}[x_{n-1}] \) の導出（途中で \( n' = n - 1 \) とおいています）

\[\begin{align*}
\mathcal{Z}[x_{n-1}] & = \sum^{\infty}_{n = 0} x_{n-1} z^{-n}
\\ & = z^{-1} \sum^{\infty}_{n = 0} x_{n-1} z^{-n+1}
\\ & = z^{-1} \sum^{\infty}_{n = 1} x_{n-1} z^{-n+1} + x_{-1}
\\ & = z^{-1} \sum^{\infty}_{n' = 0} x_{n'} z^{-n'} + x_{-1}
\\ & = z^{-1} X(z) + x_{-1}
\end{align*}\]

\( \mathcal{Z}[x_{n-2}] \) の導出（途中で \( n' = n - 2 \) とおいています）

\[\begin{align*}
\mathcal{Z}[x_{n-2}] & = \sum^{\infty}_{n = 0} x_{n-2} z^{-n}
\\ & = z^{-2} \sum^{\infty}_{n = 0} x_{n-2} z^{-n+2}
\\ & = z^{-2} \sum^{\infty}_{n = 2} x_{n-2} z^{-n+2} + x_{-2} + x_{-1} z^{-1}
\\ & = z^{-2} \sum^{\infty}_{n' = 0} x_{n'} z^{-n'} + x_{-1} z^{-1} + x_{-2}
\\ & = z^{-2} X(z) + x_{-1} z^{-1} + x_{-2}
\end{align*}\]

その5　初期値定理

初期値定理は、初項 \( x_0 \) がわからない数列に対して、初項を求めるときに使うことができます。

導出もかなり簡単です。

定義式に \( z \to \infty \) の極限を適用するだけです。\[\begin{align*}
\lim_{z \to \infty} X(z) & = \lim_{z \to \infty} \sum^{\infty}_{n = 0} x_n z^{-n}
\\ & = \lim_{z \to \infty} \left( x_0 + x_1 z^{-1} + x_2 z^{-2} + \cdots + x_{n} z^{-n} + \cdots \right)
\\ & = x_0
\end{align*}\]

なお、「その4　シフト法則」と組み合わせることで、\[
x_1 = \lim_{z \to \infty} \left( zX(z) - x_0 z   \right)
\]のように、\( x_0 \) 以外の項も計算を行うことも可能です。

その6　最終値定理

最終値定理は、数列 \( x_n \) の \( n \) を極限まで増やしたとき、つまり \( n \to \infty \) のときに収束する値を調べる際に使用します。

最終値定理のゆるめな導出（※厳密ではないため注意！！）

\[
z X(z) - x_0 z = \mathcal{Z}[x_{n+1}] =  \sum^{\infty}_{n = 0} x_{n+1} z^{-n} \\
z X(z) = \sum^{\infty}_{n = 0} x_{n+1} z^{-n} + x_0 z
\]より、\[\begin{align*}
(z - 1) X(z) & =  \lim_{n \to \infty} \left( \sum^{n}_{k = 0} x_{k+1} z^{-k} + x_0 z - \sum^{n}_{n = k} x_k z^{-k} \right)
\\ & = \lim_{n \to \infty} \left( x_0 (z-1) + x_1 (1 - z^{-1}) + \cdots + x_n z^{-(n-1)} (1-z^{-1}) + x_{n+1} z^{-n} \right)
\\ & =  x_0 (z-1) + x_1 (1 - z^{-1}) + \cdots + \lim_{n \to \infty}  x_n z^{-(n-1)} (1-z^{-1}) + \lim_{n \to \infty} x_{n+1} z^{-n}
\end{align*}\]となるため、

\[\begin{align*}
&  \lim_{z \to 1} (z - 1) X(z)
\\ = \ & \lim_{z \to 1} \left( x_0 (z-1) + x_1 (1 - z^{-1}) + \cdots + \lim_{n \to \infty}  x_n z^{-(n-1)} (1-z^{-1}) + \lim_{n \to \infty} x_{n+1} z^{-n} \right)
\\ = \ & \lim_{z \to 1} \lim_{n \to \infty} x_n z^{-(n-1)} (1-z^{-1}) + \lim_{z \to 1} \lim_{n \to \infty} x_{n+1} z^{-n}
\\ = \ & \lim_{n \to \infty} \lim_{z \to 1} x_n z^{-(n-1)} (1-z^{-1}) +  \lim_{n \to \infty} \lim_{z \to 1} x_{n+1} z^{-n}
\\ = \ & \lim_{n \to \infty}  x_{n+1}
\\ = \ & \lim_{n \to \infty}  x_{n} \left( \because n \to \infty \ のとき、n+1 \fallingdotseq n \right)
\end{align*}\]

※ 厳密に証明する場合、極限の入れ替えが可能なことの証明が必要

途中の式\[
\sum^{n}_{k = 0} x_{k+1} z^{-k} + x_0 z - \sum^{n}_{n = k} x_k z^{-k}
\]の詳しい計算過程は下の画像をご覧ください。

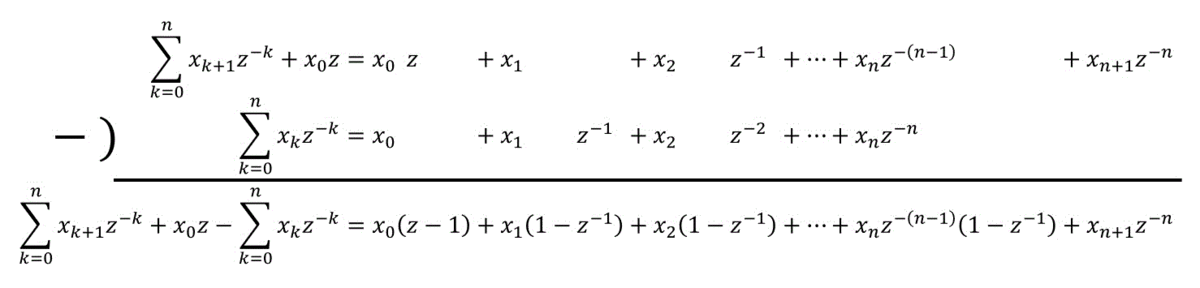
４．三角関数のz変換

第3章で説明した「微分の法則」、「指数倍の法則」を直接使うだけでは導出できない三角関数 \( \sin bn \), \( \cos bn \) のz変換も導出してみましょう。

今回は、オイラーの公式\[
e^{ibn} = \color{deepskyblue}{ \cos bn } + i \color{magenta}{ \sin bn }
\]を使って導出を行いたいと思います。

指数関数 \( a^{n} \) が含まれている場合のz変換は、以下の2ステップの公式で導出が可能ですね。\[\begin{align*}
\mathcal{Z}[1] = X(z) = \frac{z}{z-1} \\
\mathcal{Z}[a^n x_n] = X(a^{-1} z)
\end{align*}\]

今回ほしいのは、\( e^{ibn} \) のz変換なので、\[\begin{align*}
\mathcal{Z}[1] = X(z) = \frac{z}{z-1} \\
\mathcal{Z}[e^{ibn} x_n] & = X(e^{-ib} z)
\\ & = \frac{e^{-ib}z}{e^{-ib}z-1}
\\ & = \frac{z}{z - e^{ib}}
\end{align*}\]で計算が可能です。

ここで、\[
e^{ib} = \cos b + i \sin b
\]を適用し、さらに \( t = z - \cos b \) とおくと、\[\begin{align*}
\frac{z}{z - e^{ib}} & = \frac{z}{z - \cos b - i \sin b}
\\ & = \frac{z}{t - i \sin b}
\\ & = \frac{z(t + i \sin b)}{(t - i \sin b)(t + i \sin b)}
\\ & = \frac{zt + i z \sin b}{t^2 + \sin^2 b}
\\ & = \frac{z(z - \cos b) + i z \sin b}{(z - \cos b)^2 + \sin^2 b}
\\ & = \frac{z^2-  z \cos b + i z \sin b}{z^2 - 2 z \cos b + \cos^2 b + \sin^2 b}
\\ & = \frac{z^2-  z \cos b + i z \sin b}{z^2 - 2 z \cos b + 1}
\\ & = \color{deepskyblue}{ \frac{z^2-  z \cos b}{z^2 - 2 z \cos b + 1} } + i \color{magenta}{ \frac{z \sin b}{z^2 - 2 z \cos b + 1} }
\end{align*}\]

となるため、\[\begin{align*}
\mathcal{Z}[e^{ibn} x_n] & = \color{deepskyblue}{ \mathcal{Z}[\cos bn] } + i \color{magenta}{ \mathcal{Z}[\sin bn] }
\\ & =  \frac{z}{z - e^{ib}}
\\ & = \color{deepskyblue}{ \frac{z^2-  z \cos b}{z^2 - 2 z \cos b + 1} } + i \color{magenta}{ \frac{z \sin b}{z^2 - 2 z \cos b + 1} }
\end{align*}\]の関係式が成り立ちますね。

よって、三角関数のz変換\[
\color{deepskyblue}{ \mathcal{Z}[\cos bn] = \frac{z^2-  z \cos b}{z^2 - 2 z \cos b + 1}  } \\
\color{magenta}{ \mathcal{Z}[\sin bn] = \frac{z \sin b}{z^2 - 2 z \cos b + 1}  }
\]を2つまとめて導出することができました！

５．z変換と信号処理

z変換を行うと、数式で表されたディジタル信号 \( x_n \) の信号の特徴を

• 時刻
• （ある時刻における）信号の値

の2つで捉えることができます。

まず、z変換の公式は\[\begin{align*}
\mathcal{Z}[x_n] & =  \sum^{\infty}_{n = 0} x_n z^{-n}
\\ & = \sum^{\infty}_{n = 0} f (n \Delta t ) z^{-n}
\\ & = f(0) z^0 + f( \Delta t ) z^{-1} + f(2 \Delta t ) z^{-2} + \cdots
\end{align*}\]と変形できます。

ここで、\( x_n = f( n \Delta t \) は、時刻 \( n \Delta t \) における信号の値を表しています*3。

そのため、\( x_n \) の値、つまりそれぞれの \( z^{-n} \) の係数部分を見ると、 ディジタル信号がどの時刻にどれくらいの信号値を持っているかがすぐにわかってしまうということなのです！

言い換えると、見た目は数式で表されていてよくわからないディジタル信号 \( x_n \) でも、z変換という魔法をかけるだけで、時間に対する信号値のグラフを簡単に書くことができるということです！

試しに例題を解いてみましょう。

 例題4 

ある数列 \( x_n \) で表されるディジタル信号をz変換したところ、以下のようになった。\[
4 + 2 z^{-1} - z^{-2} + z^{-4}
\]

(1) 時刻 \( 2 Delta t \) における信号の値を答えなさい。
(2) ディジタル信号を縦軸を時刻、横軸を信号としたグラフで表現しなさい。

[解説4]

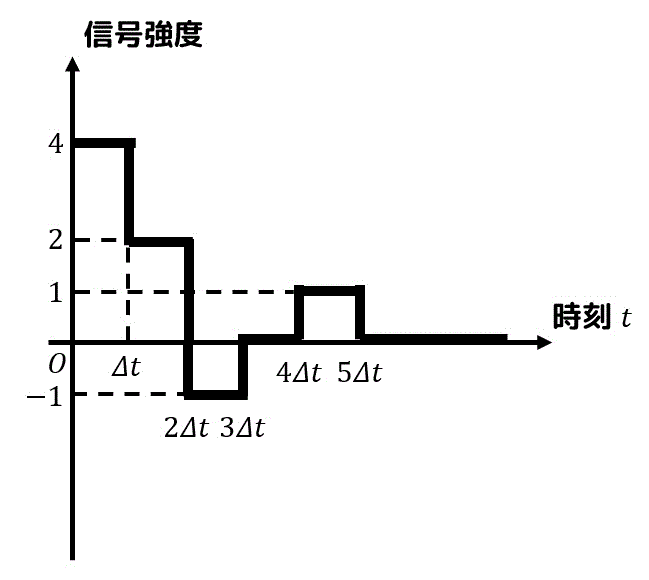
(1)

\( \color{red}{2} \Delta t \) のときの信号は、\( z^{-\color{red}{2}} \) の係数部分に着目すればOK。係数は-1なので、信号の値は-1となる。

(2)

与えられた数列 \( x_n \) のz変換の結果から、

• 時刻 \( 0 \) のときの信号の値：4
• 時刻 \( \Delta t \) のときの信号の値：2
• 時刻 \( 2 \Delta t \) のときの信号の値：-1
• 時刻 \( 3 \Delta t \) のときの信号の値：0
  （忘れたり、-1にしないように注意！）
• 時刻 \( 4 \Delta t \) のときの信号の値：1
• 時刻 \( 5 \Delta t \) 以降の信号の値：0

となることがわかる。あとはこれをグラフにすればOK。

６．さいごに

今回は、制御数学で頻出のz変換を数学的に説明していきました。

次回は、今回説明した公式を使って、実際にz変換や逆z変換を解く練習をしていきましょう！