スポンサードリンク
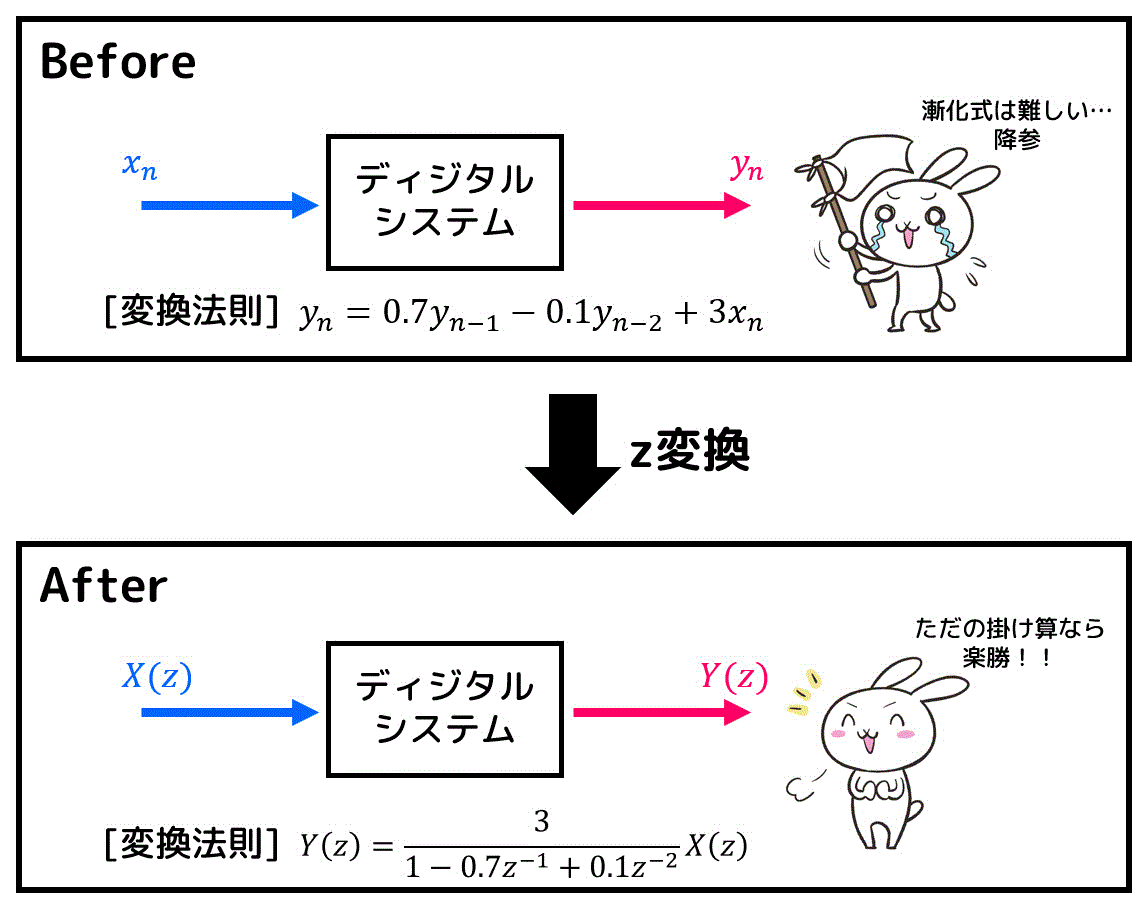
※ 動的システムではなく、ディジタルシステムについて(伝達関数、インパルス応答、ステップ応答の求め方など)知りたい人は、こちらの記事ではなく、下のリンク先の記事をご覧ください。
こんにちは、ももやまです!
今回からは、動的システムの振る舞いについて書いていきます。
前編となる第06羽では、下の5つの内容についてみていきましょう。
- 動的システムとは何か
- 動的システムを見るために必要なラプラス変換の復習
- 伝達関数の定義と求め方
- 単位インパルス関数と単位ステップ関数について
- インパルス応答とステップ応答の求め方
目次 [hide]
スポンサードリンク
1. 静的システムと動的システム
最初に動的システムとはどのようなシステムかについて、対になる静的システムと比べながら見ていきましょう。
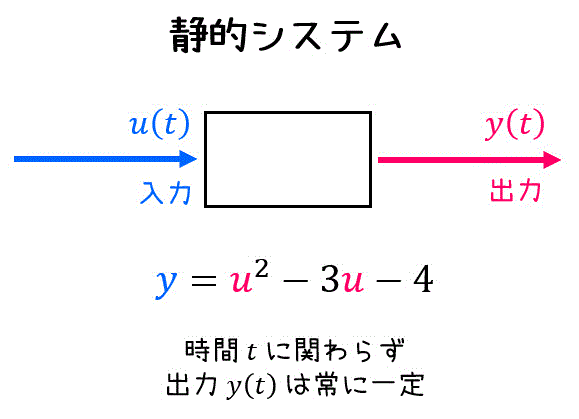
(1) 静的システム
静的システムとは、時間
言い換えると、ある入力
高校物理で習う物理公式の中で、時間
例えば、力学分野で出てくるフックの法則
静的システムは簡単に解ける!
静的システムの大きな特徴に、ある入力
例えば、上の例で示したシステム
このように、静的システムは中学数学レベルでも入出力関係がわかる簡単なシステムと言えるのです!
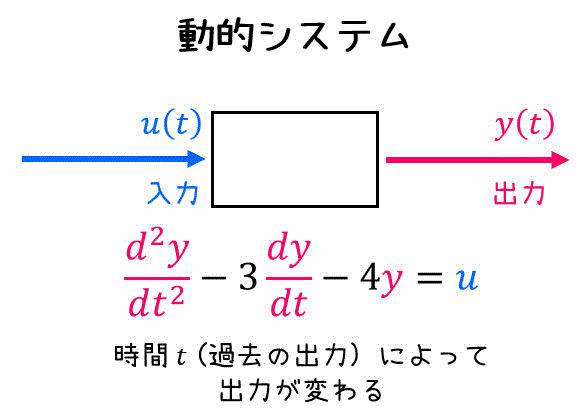
(2) 動的システム
動的システムとは、時間
言い換えると、入力

動的システムは、微積が頻繁に出てくる大学物理で登場し、微分方程式の形で表されます。
例えば、ある加速度
動的システムは難しい!
動的システムの振る舞いは、先ほども説明した通り微分方程式の形で表されます。そのため、中3レベルの方程式を解くだけでよかった静的システムに比べて、入出力関係を把握するための難易度が一気に上昇します。
例えば上で出てきたシステム
どう考えても静的システムより解く難易度が高いです。
そこで、動的システムをより簡単に解く方法について、次の章から説明していきましょう!
スポンサードリンク
2. 動的システムを解読する魔法・ラプラス変換
※ 「ラプラス変換をまだ習っていない or 習っているけど理解があいまいだ」という人は、下の2つの記事にて内容を確認してからこちらの内容に戻ることをおすすめします。
ラプラス変換と微分方程式
微分方程式はラプラス変換という道具を使うことで、微分方程式という難しい問題から中3レベルの方程式を解く簡単な問題に持ち込むことができるのでしたね。
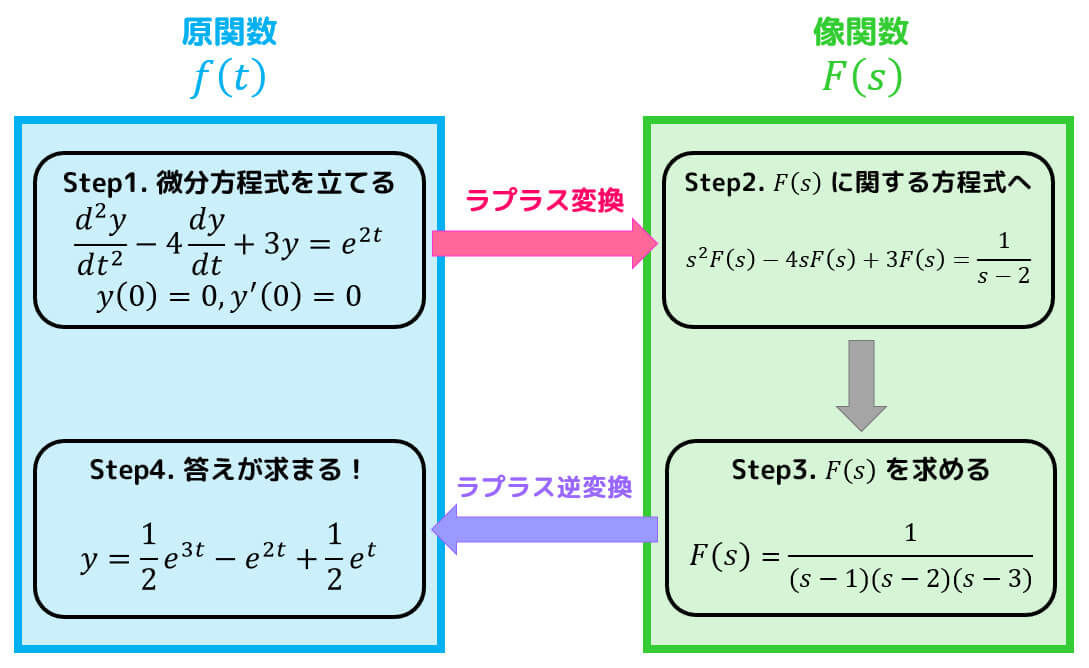
そのため、「微分方程式で振る舞いが表されている動的システム」もラプラス変換を使うことで、簡単に解くことができそうですね。
そこで、第2章では動的システムを解くために必要なラプラス変換の知識について復習しましょう。
(1) ラプラス変換の基本法則
まずは、ラプラス変換で使える法則について軽く復習しましょう。
ただし、微分の法則については少し補足があります。

★ 動的システムで使う微分方程式の初期値は…?
微分方程式の解を解くためには、下のように初期値が与えられますね。
動的システムの振る舞いを考える場合でも同じように初期値を考える必要がありますが、将来的にどのような振る舞いをするかを調べればOKです。
ここで、十分先の未来においては初期値の値が少しくらい変わったところでほとんど影響がなさそうですね。そのため、動的システムの振る舞いを考える際には、基本的にすべての初期条件
そのため、ラプラス変換の微分の法則を下のように簡略化することができます。
動的システムの振る舞いを考える際は、初期条件
そのため、ラプラス変換の微分の法則を以下のように簡略化できる。
※
(2) 基本的なラプラス変換・ラプラス変換表
(i) 最低限頭に入れておいたほうがいい公式
魔法の技だって言われても、それを発動する方法がわからければ使いませんね。
同じように、ラプラス変換も最低限の公式を頭に入れておかないと実際に使うことはできません。
そこで、最低限覚える必要がある公式を紹介します。
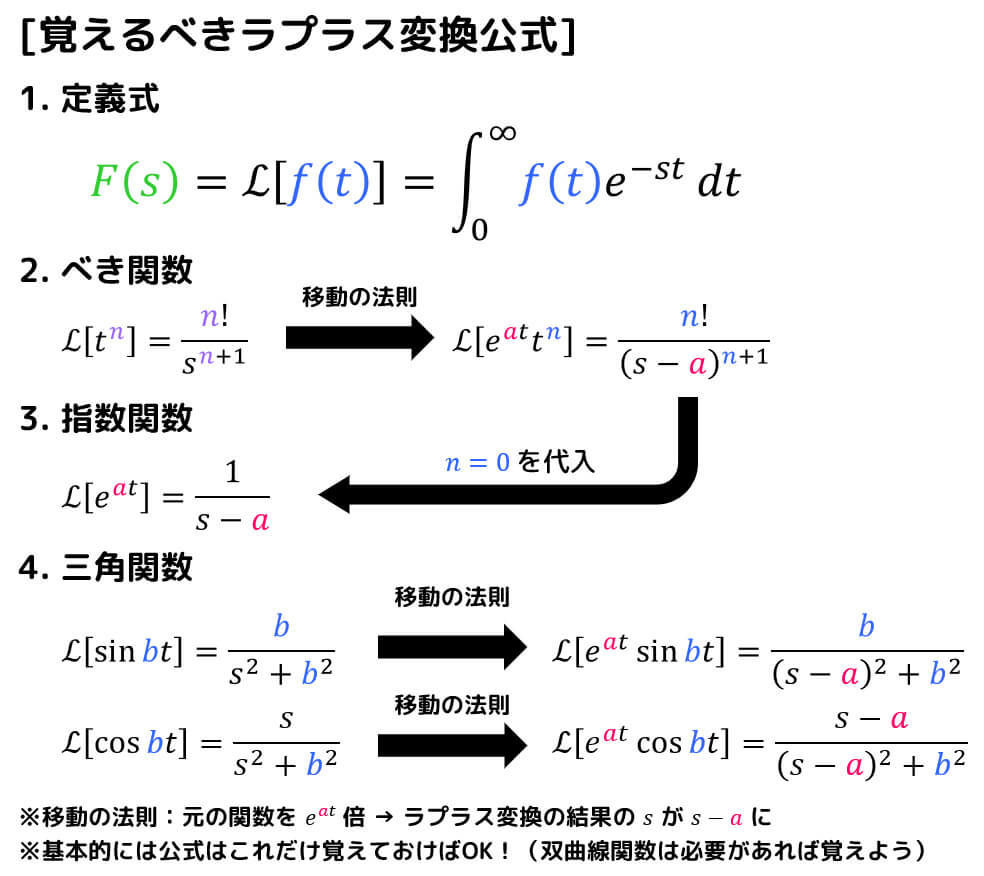
例えば、
(ii) ラプラス変換表の使い方
また、試験によっては下のようにラプラス変換表が与えられていることがあります。
この場合、それぞれの関数
| 時間関数 | ラプラス変換 | 時間関数 | ラプラス変換 |
|---|---|---|---|
| | |||
| | | ||
| | | | |
| | | | |
ただし、試験前にラプラス変換表の使い方は確認しておきましょう。
例えば、上の表から
なお、PDF版のラプラス変換表がもしほしい方がいらっしゃれば、下からダウンロードをしてください!
スポンサードリンク
3. 動的システムと伝達関数
動的システムの入出力をラプラス変換上の値で表現したものを伝達関数と呼びます。
といきなり日本語で言われてもよくわからないと思うので、伝達関数がどのように定義されているかを、例題を使いながら見ていきましょう!
下の式で表されるような振る舞いをする動的システムがある。
[解説1]
まずは、両辺をラプラス変換しましょう。ここで、入力
さらに、左辺、右辺の項を線形の法則を用いてバラバラにします。
最後に、
どうでしょう、元々は微分方程式という難しい方程式で表されていた動的システムが、ラプラス変換上では
ここで、ラプラス変換上で表される出力

ラプラス変換上にて、出力
4. インパルス応答とステップ応答
3章では、ラプラス変換上による入力
ただし、ラプラス変換上にて入出力の関係を表されても、少しよくわかりませんよね。我々が知りたいのはラプラス変換する前の世界線(実世界線上と呼びましょう)における入力
そこで、動的システムの振る舞いをラプラス変換上でなく、実世界線上の値で把握するために使われるインパルス応答とステップ応答について見ていきましょう。
(1) インパルス応答
まずは、インパルス応答から見ていきましょう。
(i) (単位)インパルス関数 [デルタ関数] とは
インパルス応答では、下のように定義されるちょっと不思議な関数である(単位)インパルス関数(別名:デルタ関数)
この(単位)インパルス関数は、下のように
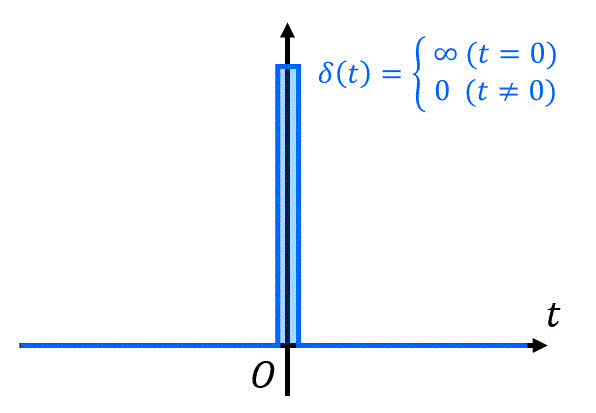
この関数の大きな特徴として、実数領域全体(負の無限大から正の無限大まで)積分をすると、1になるという特徴があります。
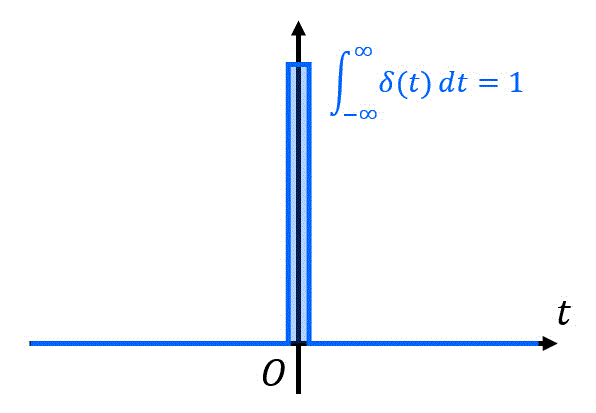
なお、積分範囲は
(ii) (単位)インパルス関数をラプラス変換すると…
次に(単位)インパルス関数をラプラス変換してみましょう。
ラプラス変換の定義は
ここで、
すると、
つまり、(単位)インパルス関数は、ラプラス変換をすると1になる不思議な関数であることが確認できましたね!
(iii) インパルス応答の計算方法
単位インパルス応答とは、入力
ここで、単位インパルス関数
そのため、
単位インパルス関数
また、この(単位)インパルス関数 [デルタ関数]
(2) ステップ応答
続いてステップ応答も見てきましょう。
(i) (単位)ステップ応答
(単位)ステップ関数は、下のように
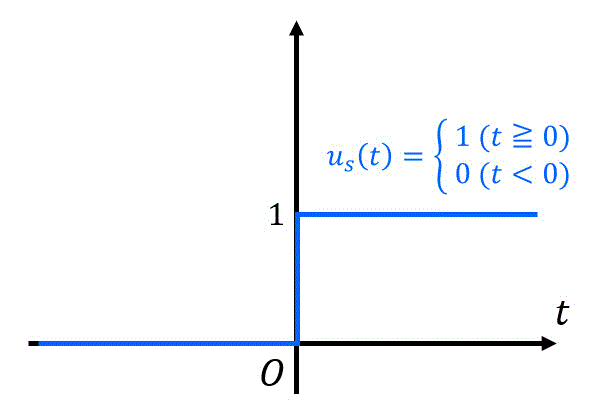
単位ステップ応答
(ii) ステップ応答の計算方法
ステップ応答とは、入力
ここで、(単位)ステップ関数
そのため、
単位ステップ関数
また、この(単位)ステップ関数
(3) (単位)ランプ応答
(i) (単位)ランプ応答
(単位)ランプ関数は、下のように
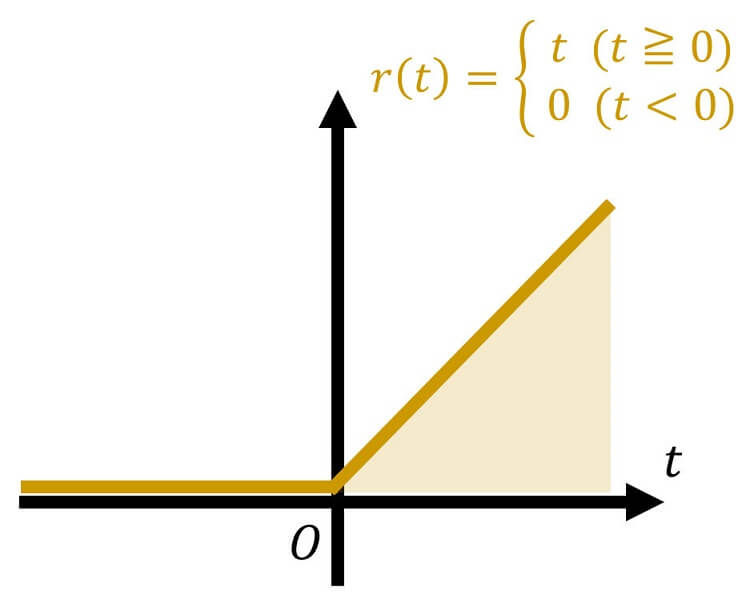
単位ランプ応答のラプラス変換
(ii) ランプ応答の計算方法
ランプ応答とは、入力
ここで、(単位)ランプ関数
よって、
そのため、
(4) 例題で確認!
インパルス応答とステップ応答についてさらに理解を深めるため、ここで例題を見ていきましょう。
以下の伝達関数
(1) インパルス応答を求めなさい。
(2) ステップ応答を求めなさい。
(3) ランプ応答を求めなさい。
[解答2]
(1) [インパルス応答]
インパルス応答なので、単位インパルス関数を入力としたときの出力を求めればOK。ここで、単位インパルス関数のラプラス変換は1、つまり
ここで、
と係数を求めることができるため、
よって、インパルス応答は
※ 最後に初期条件
(2) [ステップ応答]
ステップ応答なので、単位ステップ関数を入力としたときの出力を求めればOK。ここで、単位ステップ関数のラプラス変換は
ここで、
と係数を求めることができるため、
よって、ステップ応答は
(3) [ランプ応答]
ランプ応答なので、単位ランプ関数
ここで、単位ランプ関数のラプラス変換は
よって、出力をラプラス変換したもの
ここで、
すると、
と係数を求めることができるため、
よって、ランプ応答は
※ 最後に初期条件
※ 部分分数分解の計算に慣れていない人は、こちらの記事にて練習をすることをお勧めします。
(5) インパルス応答、ステップ応答、ランプ応答の関係
インパルス応答、ステップ応答、ランプ応答のすべてを計算すると結構な時間がかかりますよね。そこで、計算量を減らすための工夫をしましょう。
まず、ある関数
さらに、
よって、
さらに、伝達関数を
まず、インパルス応答は
つぎにステップ応答は
さらにランプ応答は
この2つに着目すると、
- ランプ応答
- ステップ応答
となることが分かります。
言い換えると、
- インパルス応答
- ステップ応答
となります!
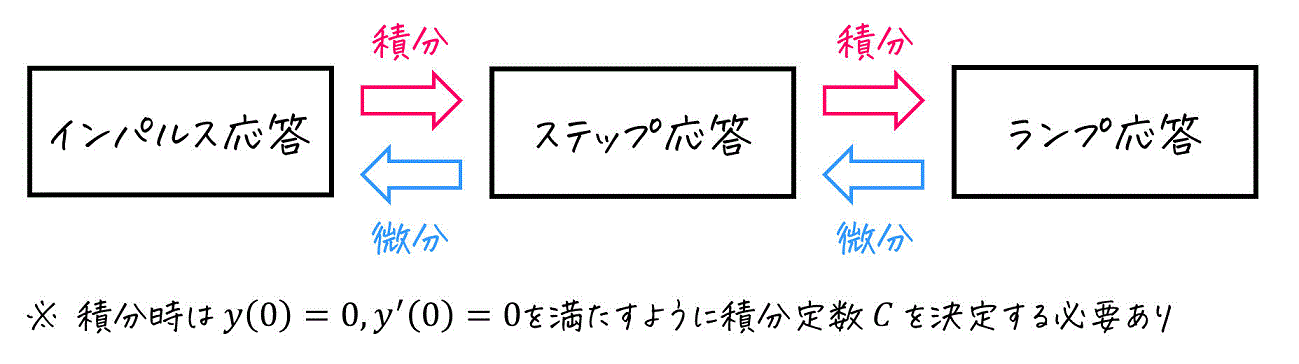
この微分、積分の関係を使うことで、ステップ応答、インパルス応答、ランプ応答のうちの1つを求めることができれば、いちいち部分分数分解しなくても簡単に残りの2つを求めることができるということですね!
※ 積分してステップ応答、ランプ応答を求める際には積分定数
(1) ランプ応答
(2) インパルス応答
以下の伝達関数
(1) ステップ応答を
(2) インパルス応答を
(3) この動的システムのランプ応答を求めなさい。
[解説3]
(1) ステップ応答
(2) インパルス応答
ここで、
(3) ランプ応答は、
- ステップ応答を1回積分
で求めることができる。
実際にステップ応答
あとは、
よって、ランプ応答は、
ステップ応答さえも求まっていれば、積分を用いることでランプ応答を少し簡単に求めることができることがわかりましたね。
5. 練習問題
では、実際に練習問題を解いて、今回の内容を復習しましょう。
下の式で表されるような振る舞いをする動的システムがある。
(1) 伝達関数
(2) 入力を単位インパルス関数
(3) 入力を単位ステップ関数
(1)
両辺をラプラス変換して、
(2)
単位インパルス関数を入力とするので、
最初に
ここで
さらに、
よって、
(3)
[方針1:普通に計算する]
単位ステップ関数を入力とするので、
ここで、
ここで、(a)式の両辺を微分を微分しても恒等式は成立する。実際に微分をすると、
と係数を求めることができるため、
よって、
[方針2:インパルス応答を積分する]
インパルス応答を積分し、初期条件
ここで、インパルス応答を
これを積分したものがステップ応答
ここで部分積分を2回適用する。
ここで、初期条件
6. さいごに
今回は、動的システムの振る舞いを確認する手段の中でも、伝達関数、インパルス応答、ステップ応答の3つを中心に説明しました。
次回は、動的システムの安定性について見ていきましょう。それではさようなら。
関連広告・スポンサードリンク