うさぎでもわかる信号処理・制御工学　第12羽　離散時間フーリエ変換(DTFT)

こんにちは、ももやまです。

前回まで理工系の数学の授業では必ずと言って出てくるフーリエ変換についてお勉強していきました。

ただ、実際にフーリエ変換を使う際にはいちいち計算するなんてことはしたくありませんよね。できればコンピュータ上で計算をさせたいです。

しかし、前回説明したフーリエ変換をそのままコンピュータ上で計算させるのには、

• 無限大の積分が登場する
• コンピュータに波を認識させる際に標本化^[1]連続信号を一定の間隔ごとにあつめ、離散的な離散信号として収集することされるため、連続的な関数 \( f(t) \) を考えることができない

などの問題点があります。

ここから先は、「フーリエ変換の解き方」ではなく、「コンピュータ上でフーリエ変換を扱う方法」についての説明を3回にわたってしていきます。

今回は、離散時間フーリエ変換 (Discrete-Time Fourier Transform / DTFT) についての説明です！

スポンサードリンク

1. [復習] (連続)フーリエ変換

まずは、離散時間フーリエ変換(DTFT)の導出に使う(連続)フーリエ変換についておさらいしておきましょう。

※ 連続的であることを強調するために、本記事ではフーリエ変換のことを連続フーリエ変換と書いています。

スポンサードリンク

2. 離散時間フーリエ変換の導出

(1) 離散的な関数は積分できない？

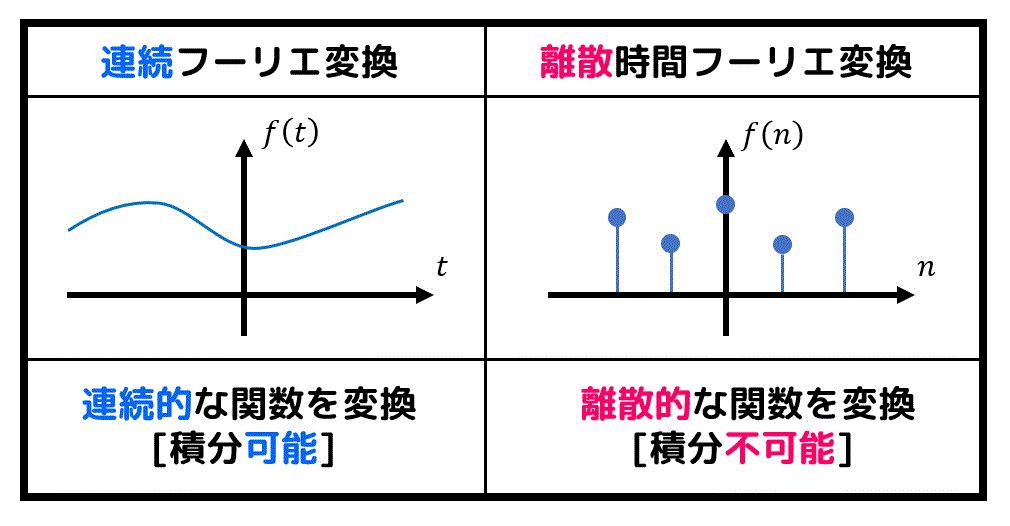
離散時間フーリエ変換が、第09羽で学習した(連続)フーリエ変換と決定的に違う点として、変換の対象が連続的ではなく離散的な関数であるという点にあります。

ここで連続的な関数 \( f(t) \) をフーリエ変換する際に\[
F( \omega ) = \int^{\infty}_{- \infty} f(t) e^{- i \omega t} \ dt
\]のように、積分の式を使って表せるのでしたね。

一方離散的な関数 \( f(n) \) は、連続的な関数 \( f(t) \) と同じような積分計算\[
F( \omega ) = \int^{\infty}_{- \infty} f(n) e^{- i \omega n} \ dn
\]をしても、離散的な点を積分するだけなので、計算結果が0になってしまいます。

そこで、離散的な関数 \( f(n) \) に対してもフーリエ変換を計算できるように式の形を書き換える必要があります。

(2) 連続フーリエ変換から離散時間フーリエ変換へ

積分というのは、下の図のように細かく刻んだ長方形の面積の和を計算する演算でしたね。

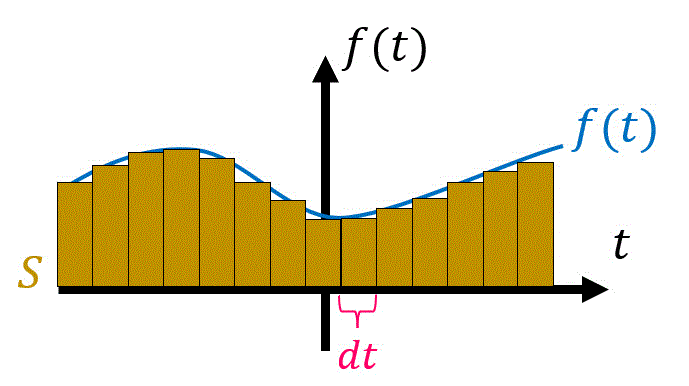
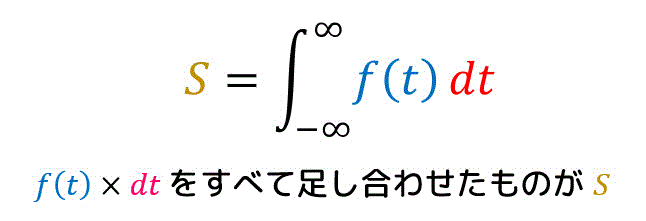
ここで、長方形の面積の和を計算するというのは、下のようにΣを用いて表すこともできますね。\[
F( \omega ) = \sum^{\infty}_{n = - \infty} f(n) e^{- i \omega n}
\]この式が離散時間フーリエ変換の定義式となります。

なお、\( n \) は整数なため、\( F ( \omega ) \) は必ず \( G( \omega ) e^{i \omega} \) の形になります。

そこで、離散時間フーリエ変換であることを強調するために、離散時間フーリエ変換では、フーリエ変換後の関数のことを \( F ( \omega ) \) ではなく \( F ( e^{i \omega } ) \) と記すことが多いです。

※ ここから先は、この記事内でも離散時間フーリエ変換後の関数を \( F ( e^{i \omega} ) \) と表記します。

(3) 離散時間逆フーリエ変換も定義してみよう

連続逆フーリエ変換の式は\[
f(t) = \frac{1}{2 \pi} \int^{\infty}_{- \infty} F ( e^{i \omega} ) e^{i \omega t} \ d \omega
\]でしたね。

離散時間フーリエ変換では、変数 \( n \) は離散的な値（整数）なため積分を行うことができませんでしたね。一方、角周波数 \( \omega \) は離散時間フーリエ変換（nが整数）であっても連続的な値を取ります。

そのため、(2)のように積分式をΣ（シグマ式）に書き換える必要がありません。

ただし、離散時間フーリエ変換の変換元の変数 \( n \) は整数です。

言い換えると、\( n \) の値は1刻みになっていますね。
（\( n \) の周期は1といえますね）

ここで、離散時間フーリエ変換の変換式は、\[
F( e^{i \omega} ) = \sum^{\infty}_{n = - \infty} f(n) e^{- i \omega n}
\]と、\( f(n) e^{- i \omega n} \) の和を計算していますね。

さらに、\( e^{- i \omega n} \) は、\[
e^{-i \omega n} = \cos \omega n - i \sin \omega n
\]と変形できます。

\( \sin \omega n \), \( \cos \omega n \) の周期は2πなため、\( \omega \) の周期は\[
\frac{\omega n \mathrm{の周期}}{n \mathrm{の周期}} = 2 \pi
\]となります。

フーリエ級数展開・フーリエ変換では、1周期分の波に着目して変換を行ったため、フーリエ逆変換でも同じように1周期分の波に着目をして逆変換を行います。

すると、離散時間逆フーリエ変換の式は、下のように \( \omega \) 1周期分を積分した式になります。\[\begin{align*}
f(t) & = \frac{1}{2 \pi} \int^{\pi}_{- \pi } F ( e^{i \omega} ) \cdot e^{i \omega n} \ d \omega
\\ & = \frac{1}{2 \pi} \int^{2 \pi}_{0 } F ( e^{i \omega} ) \cdot e^{i \omega n} \ d \omega
\end{align*}\]

スポンサードリンク

3. デルタ関数（インパルス関数）と離散時間フーリエ変換

(1) デルタ関数（インパルス関数）とは

デルタ関数 \( \delta (t) \) とは、\( t = 0 \) のときのみ値をもつ^[2]つまり \( t \not = 0 \) のときは常に0特殊な関数です。制御の世界だとインパルス関数とも呼ばれます。

この関数の大きな特徴として、\[\int^{\infty}_{- \infty} \delta (t) f(t) = f(0)\]という大きな特徴があります。

(2) デルタ関数（インパルス関数）と離散時間フーリエ変換の関係

連続的なフーリエ変換では、\( f(t) = e^{- i \omega t} \) とおくことで、\[
\int^{\infty}_{- \infty} \delta (t) e^{- i \omega t} =1
\]という関係式、つまりフーリエ変換の結果が1となる関数がデルタ関数 \( \delta (t) \) でしたね。

離散時間フーリエ変換の世界でも、「2(2)連続フーリエ変換から離散時間フーリエ変換へ」と同じように積分の式をシグマ式に書き換えることで、\[
\sum^{\infty}_{n = - \infty} \delta (n) e^{- i \omega n} = 1
\]の式に変形することができます。

つまり、離散時間フーリエ変換の世界でも変換の結果が1となる関数がデルタ関数 \( \delta (n) \) となるのです！

当然、1を離散時間フーリエ変換を行うとデルタ関数 \( \delta (n) \) になると言い換えることもできます。\[
\frac{1}{2 \pi} \int^{\pi}_{- \pi } 1 \cdot e^{i \omega n} = \delta (n)
\]

4. 例題で確認してみよう！

では、実際に例題を1問使って、離散時間フーリエ変換(DTFT)の確認をしましょう！

★解説★

(1)

デルタ関数の離散時間フーリエ変換の定義\[
\sum^{\infty}_{n = - \infty} \delta (\textcolor{orange}{n}) e^{- i \omega \textcolor{orange}{n}} = 1
\]を使う。

ここで、\[\begin{align*}
\sum^{\infty}_{n = - \infty} \delta (n+1) e^{- i \omega n} & = \sum^{\infty}_{n = - \infty} \delta (\textcolor{red}{n+1}) e^{- i \omega (\textcolor{red}{n+1}) } \cdot e^{i \omega}
\\ & = e^{i \omega} \underbrace{\sum^{\infty}_{n = - \infty} \delta (\textcolor{red}{n+1}) e^{- i \omega (\textcolor{red}{n+1})}}_{1}
\\ & = e^{i \omega}
\end{align*}\] \[\begin{align*}
\sum^{\infty}_{n = - \infty} \delta (n-1) e^{- i \omega n} & = \sum^{\infty}_{n = - \infty} \delta (\textcolor{blue}{n-1}) e^{- i \omega (\textcolor{blue}{n-1}) } \cdot e^{-i \omega}
\\ & = e^{i \omega} \underbrace{\sum^{\infty}_{n = - \infty} \delta (\textcolor{blue}{n-1}) e^{- i \omega (\textcolor{blue}{n-1})}}_{1}
\\ & = e^{- i \omega}
\end{align*}\]と計算できる。

よって、\( f(n) \) をフーリエ変換した結果 \( e^{i \omega} \) は\[\begin{align*}
F ( e^{i \omega} ) & = e^{i \omega} + 1 + e^{- i \omega}
\\ & = ( e^{i \omega} + e^{- i \omega} ) + 1
\\ & = 2 \cos \omega + 1
\end{align*}\]となる。

(2)

\( F( e^{i \omega} ) = 2 \cos \omega + 1 \) を離散時間逆フーリエ変換する。

ここで、\[
\frac{1}{2 \pi} \int^{\pi}_{- \pi} 1 \cdot e^{i \omega \textcolor{orange}{n}} \ d \omega = \delta( \textcolor{orange}{n} )
\]を利用する。（積分範囲は0から2πでもOK）

すると、\[\begin{align*}
f(n) & = \frac{1}{2 \pi} \int^{\pi}_{- \pi} (2 \cos \omega + 1) e^{i \omega n} \ d \omega
\\ & = \frac{1}{2 \pi} \int^{\pi}_{- \pi} (e^{i \omega} + e^{- i \omega} + 1) e^{i \omega n} \ d \omega
\\ & = \frac{1}{2 \pi} \int^{\pi}_{- \pi} 1 \cdot e^{i \omega (\textcolor{red}{n+1})} \ d \omega + \frac{1}{2 \pi} \int^{\pi}_{- \pi} 1 \cdot e^{i \omega n} \ d \omega + \frac{1}{2 \pi} \int^{\pi}_{- \pi} 1 \cdot e^{i \omega (\textcolor{blue}{n-1}) } \ d \omega
\\ & = \delta (n) + \delta( \textcolor{red}{n+1} ) + \delta( \textcolor{blue}{n-1} )
\\ & = \delta (n+1) + \delta (n) + \delta (n-1)
\end{align*}\]と離散時間逆フーリエ変換でき、元の問題の答えと一致することがわかる。

5. さいごに

今回は、離散時間フーリエ変換 (Discrete-Time Fourier Transform / DTFT) について説明をしていきました。

この変換を使うことで、「無限大の積分が登場する」ということはなくなりますね。

一方、変換の式に\[
\sum^{\infty}_{n = - \infty}
\]が出てくるため、まだまだコンピュータ上で計算させるのは難しそうですね。

そこで次回は、「無限和」をなくし、コンピュータ上でも計算ができるようにした離散フーリエ変換 (DFT) について説明していきたいと思います！