スポンサードリンク
こんにちは、ももやまです。
前回の第10羽では、離散的な関数 \( f(n) \) に対するフーリエ変換である離散時間フーリエ変換について説明しました。
今回は、離散時間フーリエ変換の式をさらに変形することでコンピュータ上でもフーリエ変換の処理が行える離散フーリエ変換(DFT)について説明をしていきましょう。
目次
スポンサードリンク
1. 離散フーリエ変換(DFT)へ
(1) 離散時間フーリエ変換
まずは、離散時間フーリエ変換の定義を確認しましょう。
\[
F( \omega ) = \sum^{\infty}_{n = - \infty} f(n) e^{- i \omega n}
\]
これが離散時間フーリエ変換です。
しかし、この式に出てくる \( n \) が負の無限大から正の無限大となっています。そのため、このままではコンピュータ上で処理に適した形とは言えません。
そこで、この式をコンピュータ上で処理できるように無限大の範囲を有限に近似していきましょう。
(2) 離散フーリエ変換と複素フーリエ級数
離散時間フーリエ変換は、フーリエ変換を離散的な値を持つ関数に対しても適用ができるように考えられた変換です。
このフーリエ変換は、複素フーリエ級数変換の周期 \( T \) を極限まで長いと仮定、つまり \( T \to \infty \) と仮定した変換を指すのでしたね。
ここで今回欲しいのは、有限な周期を持つ離散的な関数に対して適用可能なフーリエ変換ですね。
そこで、周期が \( T \) と有限な複素フーリエ級数変換を、離散的な値を持つ関数に対しても適用できるように変形してあげましょう。
(3) 複素フーリエ級数 → 離散フーリエ変換の導出
まずは周期 \( T \) の複素フーリエ変換の式を確認しましょう。\[
f(t) = \sum^{\infty}_{k = - \infty} c_k e^{i \frac{2 \pi k}{T} t}
\]\[
c_k = \frac{1}{T} \int^{T}_{0} f(t) e^{- i \frac{2 \pi k}{T} t } \ dt
\]
まず、複素フーリエ係数 \( c_k \) を \( k \) の関数 \( F(k) \) とみます。

すると、ある関数 \( f(t) \) を変換すると \( F(k) \) になるという関係式が出来ますね。
次に、連続的な変数 \( t \), \( T \) を離散的な変数 \( n \), \( N \) に置き換えます。ここで注意が必要なのは離散的な変数 \( n \) は積分ができないということです。
なので、積分記号を和の記号に置き換えてあげましょう。

ここで周期が \( N \) なので、和の記号の範囲に含まれる整数 \( n \) の数も \( N \) 個になるようにしましょう。そのため、和の記号の範囲は \( 0 \leqq n \leqq N \) ではなく、\( 0 \leqq n \leqq N-1 \) となります[1]\( 0 \leqq n \leqq N \) とすると、範囲内に含まれる \( n \) の数が \( N + 1 \) 個になってしまい、周期も \( N + 1 \) になってしまうから。。
すると、\( f(n) \) から \( F(k) \) への変換式が出てきます。\[
F(k) = \frac{1}{N} \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n }
\]
この式が離散フーリエ変換の1つの定義式となります。
(4) 複素フーリエ級数 → 逆離散フーリエ変換の導出
逆離散フーリエ変換の式(\( F(k) \) から \( f(n) \) への変換式)も考えましょう。
逆離散フーリエ変換の元になるのは、複素フーリエ変換の計算式です。\[
f(t) = \sum^{\infty}_{k = - \infty} c_k e^{i \frac{2 \pi k}{T} t}
\]
まず、(3)の離散フーリエ変換のときと同じように、複素フーリエ係数 \( c_k \) を \( k \) の関数 \( F(k) \) とみます。
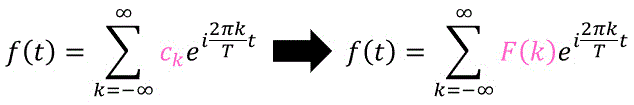
すると、\( F(k) \) から \( f(t) \) への変換式っぽいものが出てきますね。
次に、連続的な変数 \( t \), \( T \) を離散的な変数 \( n \), \( N \) に置き換えます。
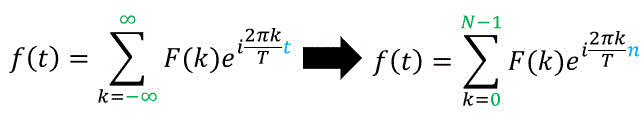
さらに、(3)の離散フーリエ変換の時と同じように、和の記号の範囲に含まれる整数 \( k \) の数が \( N \) 個になるようにしましょう。
すると、\( F(k) \) から \( f(n) \) への変換式が出てきます。\[
f(n) = \sum^{N-1}_{k = 0} F(k) e^{i \frac{2 \pi k}{N} n }
\]
この式が離散逆フーリエ変換の1つの定義式となります。
(5) 色んな離散フーリエ変換・離散逆フーリエ変換の定義の仕方
(3), (4)で離散フーリエ変換、逆離散フーリエ変換の定義を紹介しましたが、実は教科書によっては変換、逆変換式が別の式で定義されていることがあります[2]離散フーリエ変換、逆離散フーリエ変換の対応付けが正しければ(3), … Continue reading。よく見かける3例を紹介しましょう。
※ 本ブログでは赤色の変換式で説明します。
| 離散フーリエ変換 | 離散逆フーリエ変換 |
|---|---|
| \[ F(k) = \frac{1}{N} \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } \] | \[ f(n) = \sum^{N-1}_{k = 0} F(k) e^{i \frac{2 \pi k}{N} n } \] |
| \[ F(k) = \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } \] | \[ f(n) = \frac{1}{N} \sum^{N-1}_{k = 0} F(k) e^{i \frac{2 \pi k}{N} n } \] |
| \[ F(k) = \frac{1}{\sqrt{N}} \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } \] | \[ f(n) = \frac{1}{\sqrt{N}} \sum^{N-1}_{k = 0} F(k) e^{i \frac{2 \pi k}{N} n } \] |
ここで、2番目と3番目を導出するために(3), (4)で求めた式をひとまとめに書いてみましょう。\[
f(n) = \sum^{N-1}_{n = 0} \left( \underbrace{ \frac{1}{N} \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } }_{F(k)} \right) e^{i \frac{2 \pi k}{N} n }
\]
(i) 1番目の式 → 2番目の式の導出
ここで、係数 \( \frac{1}{N} \) は定数なので、下のようにΣや括弧の外に出すことができます。\[
f(n) = \frac{1}{N} \sum^{N-1}_{n = 0} \left( \underbrace{ \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } }_{F(k)} \right) e^{i \frac{2 \pi k}{N} n }
\]
このとき、青部分を離散フーリエ変換、赤線部分を逆離散フーリエ変換とすることで2番目の離散フーリエ変換、逆離散フーリエ変換を導くことができます。

なお、教科書では(i)の組み合わせで離散フーリエ変換、逆離散フーリエ変換が定義されていることが多いです。そのため、本記事では、離散フーリエ変換、離散逆フーリエ変換を2番目の式\[\begin{align*}
F(k) & = \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } \\
f(n) & = \frac{1}{N} \sum^{N-1}_{n = 0} F(k) e^{i \frac{2 \pi k}{N} n }
\end{align*}\]で定義したいと思います。
(ii) 1番目の式 → 3番目の式の導出
離散フーリエ変換、逆離散フーリエ変換に出てくる係数を同じにするために、\( \frac{1}{ \sqrt{N} } \) を括弧の外に出しましょう。\[
f(n) = \frac{1}{\sqrt{N}} \sum^{N-1}_{n = 0} \left( \underbrace{ \frac{1}{\sqrt{N}} \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n } }_{F(k)} \right) e^{i \frac{2 \pi k}{N} n }
\]
ここで、青部分を離散フーリエ変換、赤線部分を逆離散フーリエ変換とすることで3番目の離散フーリエ変換、逆離散フーリエ変換を導くことができます。

(ii)のパターンの場合、係数に \( \frac{1}{\sqrt{N}} \) が含まれるため、実際に計算する際に少しややこしく計算が必要になりますが、この形にすることで得られる理論的なメリットもあります。
(理論的なメリットについては機会があれば別記事にて説明したいと思います)
スポンサードリンク
2. 離散フーリエ変換と行列
離散フーリエ変換も、線形変換で表すことができればコンピュータ上で簡単に計算できるのに、って思いませんか? 実は、離散フーリエ変換は、線形変換で表すことができるのです!
そこで、2章では線形変換に変形するための下準備をしていきたいと思います。
まず、離散フーリエ変換は、下のように \( N \) 個 (有限) の実数値をまとめてフーリエ変換するもの、ということができますね。
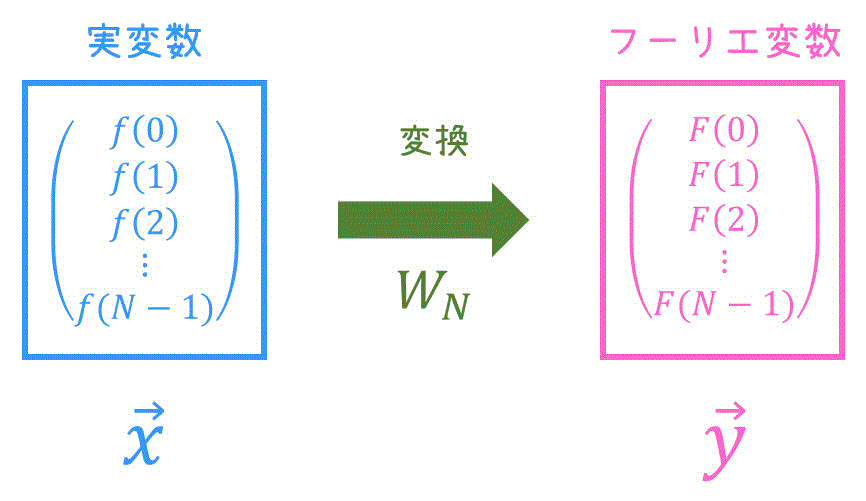
そこでまず、\( N \) 個の実数値を集めたベクトル \( \vec{x} \) を下のように定義しましょう。\[
\vec{x} = \left( \begin{array}{ccc} f(0) \\ f(1) \\ \vdots \\ f(N-1) \end{array} \right)
\]
同じように、フーリエ変換を適用したあとの答えとなるベクトル \( \vec{y} \) も定義しましょう。\[
\vec{y} = \left( \begin{array}{ccc} F(0) \\ F(1) \\ \vdots \\ F(N-1) \end{array} \right)
\]
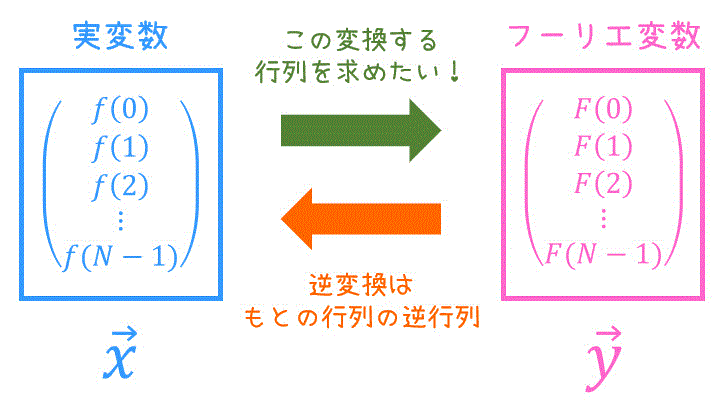
ここで、線形変換とは、あるベクトル \( \vec{x} \) からあるベクトル \( \vec{y} \) への変換を正方行列 \( A \) を用いて、\[ \vec{y} = A \vec{x} \]と表せる変換のことでしたね。

また、1回線形変換を適用したベクトル \( \vec{y} \) を元のベクトル \( \vec{x} \) へ戻すような変換(逆変換)は、元の変換行列 \( A \) の逆行列 \( A^{-1} \) で表せますね。

そこで、3章以降では離散フーリエ変換を線形変換 \( \vec{y} = A \vec{x} \) で表す方法を見ていきたいと思います!
スポンサードリンク
3. [具体例] N=2の離散フーリエ変換
とはいってもいきなり \( N \) 次のときに試すのはちょっとむずかしいですね。
そこで、まずは \( N = 2 \) の離散フーリエ変換で見ていきましょう。
(i) N=2の離散フーリエ変換
\( N = 2 \) のときの離散フーリエ変換を思い出しましょう。\[
F(k) = \sum^{1}_{ \textcolor{deepskyblue}{n} = 0} f(n) e^{- i \frac{2 \pi \textcolor{magenta}{k}}{2} \textcolor{deepskyblue}{n} }
\]
この離散フーリエ変換の \( F( \textcolor{magenta}{0} ) \), \( F( \textcolor{magenta}{1} ) \) の値は下の式で求めることができますね。
\[\begin{align*}
F( \textcolor{magenta}{0} ) & = \sum^{1}_{n = 0} f( \textcolor{deepskyblue}{n} ) e^{- i \frac{2 \pi \cdot \textcolor{magenta}{0} }{2} \cdot \textcolor{deepskyblue}{n} }
\\ & = f( \textcolor{ deepskyblue }{0} ) e^{- i \frac{2 \pi \cdot \textcolor{magenta}{0} }{2} \cdot \textcolor{deepskyblue}{0} } + f( \textcolor{ deepskyblue }{1} ) e^{- i \frac{2 \pi \cdot \textcolor{magenta}{0} }{2} \cdot \textcolor{deepskyblue}{1} }
\\ & = f(0) + f(1)
\end{align*}\]
\[\begin{align*}
F( \textcolor{magenta}{1} ) & = \sum^{1}_{n = 0} f( \textcolor{deepskyblue}{n} ) e^{- i \frac{2 \pi \cdot \textcolor{magenta}{1} }{2} \cdot \textcolor{deepskyblue}{n} }
\\ & = f( \textcolor{ deepskyblue }{0} ) e^{- i \frac{2 \pi \cdot \textcolor{magenta}{1} }{2} \cdot \textcolor{deepskyblue}{0} } + f( \textcolor{ deepskyblue }{1} ) e^{- i \frac{2 \pi \cdot \textcolor{magenta}{1} }{2} \cdot \textcolor{deepskyblue}{1} }
\\ & = f(0) + e^{- i \pi} f(1)
\\ & = f(0) + e^{- i \pi} f(1)
\\ & = f(0) - f(1)
\end{align*}\]
この2つの式をまとめて書くと、 \[ \left. \begin{array}{l} F(0) & = f(0) + f(1) \\ F(1) & = f(0) - f(1) \end{array} \right. \]となりますね。
これを行列を用いて書くと、下のように表すことができます。\[
\underbrace{ \left( \begin{array}{ccc} F(0) \\ F(1) \end{array} \right) }_{\vec{y}}= \underbrace{ \left( \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right) }_{\mathrm{変換行列} \ W_2} \underbrace{ \left( \begin{array}{ccc}f(0) \\ f(1) \end{array} \right) }_{ \vec{x} }
\]
これは、まさしく線形変換 \( \vec{y} = A \vec{x} \) の形ですね!
よって、\( N = 2 \) のときに離散フーリエ変換を行列で表すことに成功しました。今回は \( N = 2 \) の離散フーリエ変換なので、この行列を \( W_2 \) と定義しましょうか。。
(ii) N=2 の逆離散フーリエ変換
(i)と同じように、逆離散フーリエ変換の変換行列 \( W_2' \) も出してみましょう。
まず、\( N = 2 \) のときの逆離散フーリエ変換を思い出しましましょう。\[\begin{align*}
f(\textcolor{deepskyblue}{n}) & = \frac{1}{2} \sum^{1}_{\textcolor{magenta}{k} = 0 } F( \textcolor{magenta}{k} ) e^{i \frac{2 \pi \textcolor{deepskyblue}{n} }{N} \cdot \textcolor{magenta}{k} }
\end{align*}\]
この逆離散フーリエ変換の \( f( \textcolor{deepskyblue}{0} ) \), \( f( \textcolor{deepskyblue}{1} ) \) の値は下の式で求めることができますね。
\[\begin{align*}
f(\textcolor{deepskyblue}{0}) & = \frac{1}{2} \sum^{1}_{\textcolor{magenta}{k} = 0 } F( \textcolor{magenta}{k} ) e^{i \frac{2 \pi \cdot \textcolor{deepskyblue}{0} }{N} \cdot \textcolor{magenta}{k} }
\\ & = \frac{1}{2} F( \textcolor{magenta}{0} ) e^{i \frac{2 \pi \cdot \textcolor{deepskyblue}{0} }{N} \cdot \textcolor{magenta}{0} } + \frac{1}{2} F( \textcolor{magenta}{1} ) e^{i \frac{2 \pi \cdot \textcolor{deepskyblue}{0} }{0} \cdot \textcolor{magenta}{1} }
\\ & = \frac{1}{2} F(0) + \frac{1}{2} F(1)
\end{align*}\]
\[\begin{align*}
f(\textcolor{deepskyblue}{0}) & = \frac{1}{2} \sum^{1}_{\textcolor{magenta}{k} = 0 } F( \textcolor{magenta}{k} ) e^{i \frac{2 \pi \cdot \textcolor{deepskyblue}{1} }{N} \cdot \textcolor{magenta}{k} }
\\ & = \frac{1}{2} F( \textcolor{magenta}{0} ) e^{i \frac{2 \pi \cdot \textcolor{deepskyblue}{1} }{N} \cdot \textcolor{magenta}{0} } + \frac{1}{2} F( \textcolor{magenta}{1} ) e^{i \frac{2 \pi \cdot \textcolor{deepskyblue}{1} }{0} \cdot \textcolor{magenta}{1} }
\\ & = \frac{1}{2} F(0) + \frac{1}{2} e^{- i \pi} F(1)
\\ & = \frac{1}{2} F(0) - \frac{1}{2} F(1)
\end{align*}\]
この2つの式をまとめて書くと、 \[ \left. \begin{array}{l} f(0) & = \frac{1}{2} F(0) + \frac{1}{2} F(1) \\ f(1) & = \frac{1}{2} F(0) - \frac{1}{2} F(1) \end{array} \right. \]となりますね。
これを行列を用いて書くと、下のように表すことができます。\[\begin{align*}
\underbrace{ \left( \begin{array}{ccc} f(0) \\ f(1) \end{array} \right) }_{\vec{x}} & = \underbrace{ \left( \begin{array}{ccc} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \end{array} \right) }_{\mathrm{変換行列} \ W_2'} \underbrace{ \left( \begin{array}{ccc} F(0) \\ F(1) \end{array} \right) }_{ \vec{y} }
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right) \left( \begin{array}{ccc} F(0) \\ F(1) \end{array} \right)
\end{align*}\]
確かに逆変換 \( \vec{x} = A^{-1} \vec{y} \) の形になっていますね。
そこで、本当に \( W_2' \) が離散フーリエ変換の変換行列の逆行列 \( W_2^{-1} \) となっているかを、実際に逆行列を計算することで確かめましょう。\[\begin{align*}
| W_2 | & = \left| \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right|
\\ & = -1 - 1
\\ & = -2
\end{align*}\]より、\[\begin{align*}
W_2^{-1} & = \frac{1}{|W_N|} \left( \begin{array}{ccc} -1 & -1 \\ -1 & 1 \end{array} \right)
\\ & = \frac{1}{-2} \left( \begin{array}{ccc} -1 & -1 \\ -1 & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right)
\end{align*}\]
確かに \( W_2' = W_2^{-1} \) となり、一致していますね。
よって、\( N = 2 \) のときの離散逆フーリエ変換は、元の離散フーリエ変換の変換行列がわかってしまえば簡単に求められることがわかりました。
4. 式を簡単にする救世主:回転因子
今度は、\( N = 2 \) と限定せず、一般化していきましょう。
しかし、\( N \) の数が増えて複雑になればなるほど、式に \( e^{- i \frac{2 \pi k}{N} n } \) や \(e^{ i \frac{2 \pi n}{N} k } \) が沢山出てきて、見るだけでも嫌な数式になりそうですね。
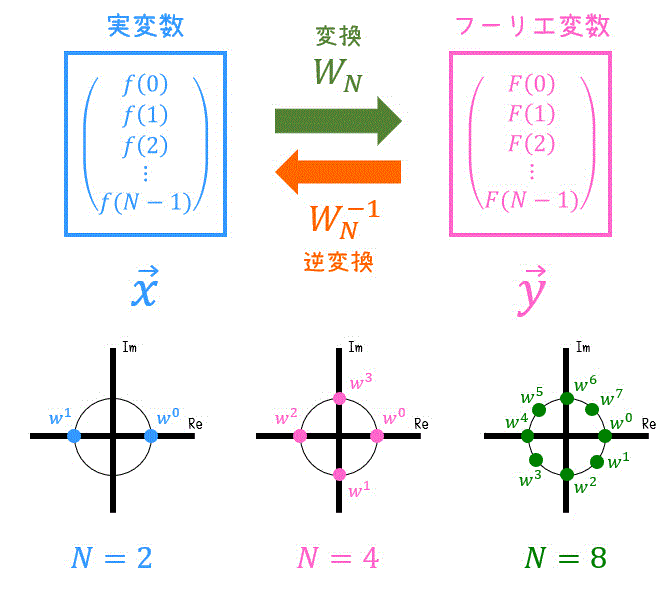
そこで、\( w = e^{- \frac{2 \pi}{N} i } \) とおきましょう。すると、\( w^a \) は単位円(半径1の円)に現れます。
例えば、\( N = 8 \) であれば \( w = e^{- \frac{\pi}{4} ai} \) となるため、\( w^a \) は時計回りに45°進むごとに登場します。

このように、\( w^a \) は半径1の円上に一定間隔に回転しながら現れているので、\( w = e^{- \frac{2 \pi}{N} i } \) のことを回転因子と呼びます。
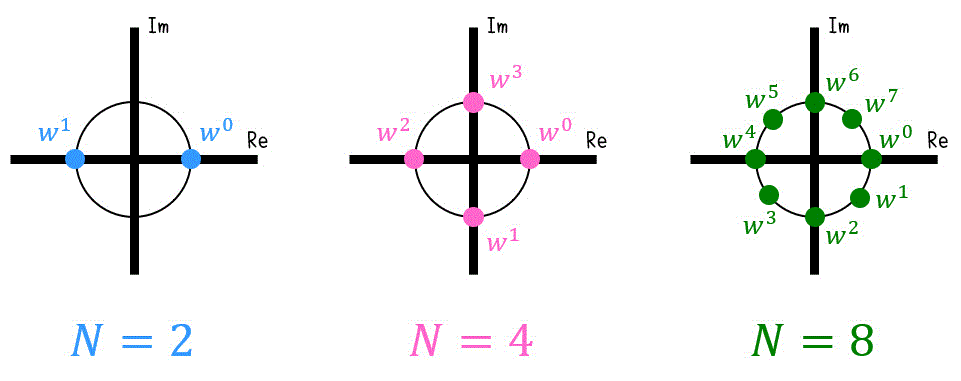
では、回転因子 \( w = e^{- \frac{2 \pi}{N} i } \) を使って離散フーリエ変換の式を変形しましょう。\[\begin{align*}
F(k) & = \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n }
\\ & = \sum^{N-1}_{n = 0} f(n) e^{ \left(- \frac{2 \pi}{N} i \right) kn }
\\ & = \sum^{N-1}_{n = 0} f(n) w^{kn}
\end{align*}\]
同じように、逆離散フーリエ変換の式も回転因子 \( w \) を用いて変形できます。\[\begin{align*}
f(n) & = \frac{1}{N} \sum^{N-1}_{k = 0} e^{i \frac{2 \pi n}{N} k}
\\ & = \frac{1}{N} \sum^{N-1}_{k = 0} e^{- \frac{2 \pi }{N} i (-nk)}
\\ & = \frac{1}{N} \sum^{N-1}_{k = 0} w^{-nk}
\end{align*}\]
と変形できます[3]逆変換に出てくる \( w^{-nk} \) は、もちろん \( w^{-kn} \) でもOKです。。
離散フーリエ変換を簡潔に示すために \( w = e^{- \frac{2 \pi}{N} i } \) のことを回転因子と呼ぶ。
また、\( w^{ \frac{N}{2} } = -1 \),\( w^{ N } = 1 \) である。
さらに、離散フーリエ変換、離散逆フーリエ変換を以下のように変形できる。
[離散フーリエ変換]\[F(k) = \sum^{N-1}_{n = 0} f(n) w^{kn}
\] [離散逆フーリエ変換]\[
f(n) = \frac{1}{N} \sum^{N-1}_{k = 0} w^{-nk}
\]
5. 離散フーリエ変換とDFT行列
では実際に回転因子 \( w \) を使うことで式\[
F(k) = \sum^{N-1}_{n=0} f(n) w^{kn}
\]を行列で表してみましょう。
まずは、\( F(0) \), \( F(1) \), \( F(2) \) , …, \( F(N-1) \) をそれぞれ \( f(0) \), \( f(1) \), …, \( f(N-1) \) の線形結合(和)で表します。
\[
\begin{align}
F(\textcolor{magenta}{0}) & = \ \ \ \ \ \ \ w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0}} f(\textcolor{deepskyblue}{0}) + \ \ \ \ \ \ \ w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1}} f(\textcolor{deepskyblue}{1}) + \ \ \ \ \ \ \ w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2}} f(\textcolor{deepskyblue}{2}) + \cdots + \ \ \ \ \ \ \ w^{\textcolor{magenta}{0} \cdot ( \textcolor{deepskyblue}{N-1})} f(\textcolor{deepskyblue}{N-1})
\\ F(\textcolor{magenta}{1}) & = \ \ \ \ \ \ \ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0}} f(\textcolor{deepskyblue}{0}) + \ \ \ \ \ \ \ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1}} f(\textcolor{deepskyblue}{1}) + \ \ \ \ \ \ \ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2}} f(\textcolor{deepskyblue}{2}) + \cdots + \ \ \ \ \ \ \ w^{\textcolor{magenta}{1} \cdot ( \textcolor{deepskyblue}{N-1})} f(\textcolor{deepskyblue}{N-1})
\\ F(\textcolor{magenta}{2}) & = \ \ \ \ \ \ \ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0}} f(\textcolor{deepskyblue}{0}) + \ \ \ \ \ \ \ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1}} f(\textcolor{deepskyblue}{1}) + \ \ \ \ \ \ \ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2}} f(\textcolor{deepskyblue}{2}) + \cdots + \ \ \ \ \ \ \ w^{\textcolor{magenta}{2} \cdot ( \textcolor{deepskyblue}{N-1})} f(\textcolor{deepskyblue}{N-1})
\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots
\\ F(\textcolor{magenta}{N-1}) & = w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{0}} f(\textcolor{deepskyblue}{0}) + w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{1}} f(\textcolor{deepskyblue}{1}) + w^{(\textcolor{magenta}{N-1}) \cdot \textcolor{deepskyblue}{2}} f(\textcolor{deepskyblue}{2}) + \cdots + w^{(\textcolor{magenta}{N-1}) \cdot ( \textcolor{deepskyblue}{N-1})} f(\textcolor{deepskyblue}{N-1})
\end{align}
\]
次に、この式を行列で表します。\[
\left( \begin{array}{ccc} F(\textcolor{magenta}{0}) \\ F(\textcolor{magenta}{1}) \\ F(\textcolor{magenta}{2}) \\ \vdots \\ F( \textcolor{magenta}{N-1} ) \end{array} \right) =
\underbrace{ \left( \begin{array}{ccc} w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{0} \cdot \ ( \textcolor{deepskyblue}{N-1} )}
\\ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{1} \cdot ( \textcolor{deepskyblue}{N-1} )} \\ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{2} \cdot ( \textcolor{deepskyblue}{N-1} )}
\\ & & & \ddots & \\
w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{0}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{1}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{( \textcolor{magenta}{N-1} ) \cdot ( \textcolor{deepskyblue}{N-1} )}
\end{array} \right) }_{{\mathrm{DFT行列 (変換行列)} \ W_N}}
\left( \begin{array}{ccc} f(\textcolor{deepskyblue}{0}) \\ f(\textcolor{deepskyblue}{1}) \\ f(\textcolor{deepskyblue}{2}) \\ \vdots \\ f( \textcolor{deepskyblue}{N-1} ) \end{array} \right)
\]
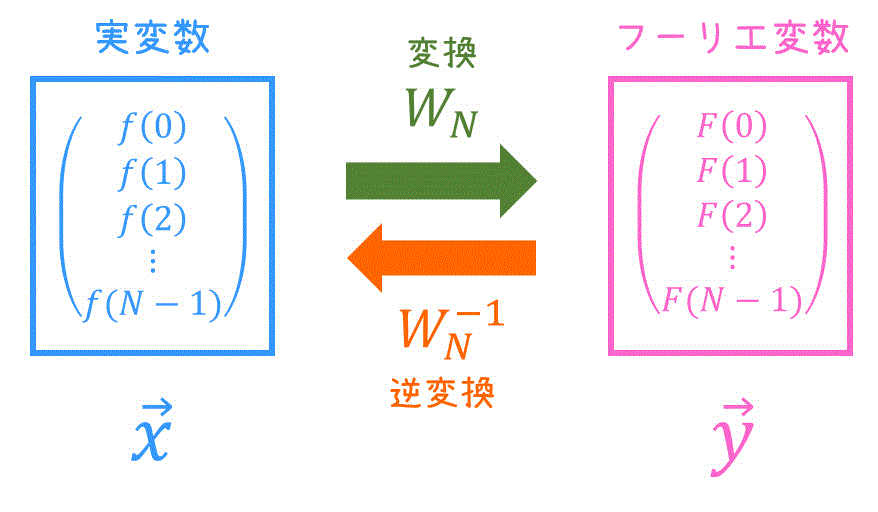
よって、実変数ベクトル \( \vec{x} \) からフーリエ変数ベクトル \( \vec{y} \) の線形変換式\[
\vec{y} = W_N \vec{x}
\]が完成しましたね。
この変換行列 \( W_N \) のことをDFT行列と呼びます。
\( w = e^{- \frac{2 \pi}{N} i } \) とおくことで、離散フーリエ変換を下のように書き換えることができる。\[
F(k) = \sum^{N-1}_{n=0} f(n) w^{kn}
\]
さらに、DFT行列\[
W_N = \left( \begin{array}{ccc} w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{0} \cdot \ ( \textcolor{deepskyblue}{N-1} )}
\\ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{1} \cdot ( \textcolor{deepskyblue}{N-1} )} \\ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{2} \cdot ( \textcolor{deepskyblue}{N-1} )}
\\ & & & \ddots & \\
w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{0}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{1}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{( \textcolor{magenta}{N-1} ) \cdot ( \textcolor{deepskyblue}{N-1} )}
\end{array} \right)
\]を用いることで、フーリエ変換を線形変換で表すことができる。\[
\vec{y} = W_N \vec{x}
\]
6. 離散逆フーリエ変換と逆DFT行列
5章の離散フーリエ変換と同じように、逆離散フーリエ変換\[
f(n) = \frac{1}{N} \sum^{N-1}_{k = 0} w^{-nk}
\]の変換行列(逆DFT行列)も求めてみましょう。
つぎに \( f(0) \), \( f(1) \), \( f(2) \) , …, \( f(N-1) \) をそれぞれ \( F(0) \), \( F(1) \), …, \( F(N-1) \) の線形結合(和)で表します。
\[
\begin{align}
f(\textcolor{deepskyblue}{0}) & = \frac{1}{N} \left\{ \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{0}} F(\textcolor{magenta}{0}) + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{1}} F( \textcolor{magenta}{1} ) + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{2}} F(\textcolor{magenta}{2}) + \cdots + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{0} \cdot ( \textcolor{magenta}{N-1} ) } F(\textcolor{magenta}{N-1}) \right\}
\\ f(\textcolor{deepskyblue}{1}) & = \frac{1}{N} \left\{ \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{0}} F(\textcolor{magenta}{0}) + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{1}} F( \textcolor{magenta}{1} ) + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{2}} F(\textcolor{magenta}{2}) + \cdots + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{1} \cdot ( \textcolor{magenta}{N-1} ) } F(\textcolor{magenta}{N-1}) \right\}
\\ f(\textcolor{deepskyblue}{2}) & = \frac{1}{N} \left\{ \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{0}} F(\textcolor{magenta}{0}) + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{1}} F( \textcolor{magenta}{1} ) + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{2}} F(\textcolor{magenta}{2}) + \cdots + \ \ \ \ \ \ \ w^{- \textcolor{deepskyblue}{2} \cdot ( \textcolor{magenta}{N-1} ) } F(\textcolor{magenta}{N-1}) \right\}
\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots
\\ f(\textcolor{deepskyblue}{N-1}) & = \frac{1}{N} \left\{ w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{0}} F(\textcolor{magenta}{0}) + w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{1}} F( \textcolor{magenta}{1} ) + w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{2}} F(\textcolor{magenta}{2}) + \cdots +w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot ( \textcolor{magenta}{N-1} ) } F(\textcolor{magenta}{N-1}) \right\}
\end{align}
\]
さらに、上の式を行列で表してみましょう。\[
\left( \begin{array}{ccc} f(\textcolor{deepskyblue}{0}) \\ f(\textcolor{deepskyblue}{1}) \\ f(\textcolor{deepskyblue}{2}) \\ \vdots \\ f( \textcolor{deepskyblue}{N-1} ) \end{array} \right) =
\underbrace{
\frac{1}{N} \left( \begin{array}{ccc} w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{0} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{1} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{2} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ & & & \ddots & \\
w^{(- \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{0}} & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{1}} & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{2}} & \cdots & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot ( \textcolor{magenta}{N-1} )}
\end{array} \right) }_{{\mathrm{逆DFT行列 (変換行列)} \ W_N^{-1}}}
\left( \begin{array}{ccc} F(\textcolor{magenta}{0}) \\ F(\textcolor{magenta}{1}) \\ F(\textcolor{magenta}{2}) \\ \vdots \\ F( \textcolor{magenta}{N-1} ) \end{array} \right)
\]
よって、フーリエ変数ベクトル \( \vec{y} \) から実ベクトル \( \vec{x} \) への線形変換式\[
\vec{x} = W_N^{-1} \vec{y}
\]を導出することができましたね。
この変換行列 \( W_N^{-1} \) のことを逆DFT行列と呼ぶことにしましょう。
\( w = e^{- \frac{2 \pi}{N} i } \) とおくことで、逆離散フーリエ変換を下のように書き換えることができる。\[
f(n) = \frac{1}{N} \sum^{N-1}_{k = 0} w^{-nk}
\]
さらに、逆DFT行列\[
W_N^{-1} = \frac{1}{N} \left( \begin{array}{ccc} w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{0} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{1} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{2} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ & & & \ddots & \\
w^{(- \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{0}} & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{1}} & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{2}} & \cdots & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot ( \textcolor{magenta}{N-1} )}
\end{array} \right)
\]を用いることで、フーリエ変換を線形変換で表すことができる。\[
\vec{x} = W_N^{-1} \vec{y}
\]
7. 逆DFT行列からDFT行列を求める方法
DFT行列、逆DFT行列をいちいち導出するのはめんどくさいですね。かと言って、\( W_N \) の逆行列を計算するのはさらにしんどいです。
そこで、DFT行列 \( W_N \) から逆DFT行列 \( W_N^{-1} \) を出す方法を見ていきましょう。
まず、DFT行列 \( W_N \) は\[
W_N = \left( \begin{array}{ccc} w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{0} \cdot \ ( \textcolor{deepskyblue}{N-1} )}
\\ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{1} \cdot ( \textcolor{deepskyblue}{N-1} )} \\ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{2} \cdot ( \textcolor{deepskyblue}{N-1} )}
\\ & & & \ddots & \\
w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{0}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{1}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{( \textcolor{magenta}{N-1} ) \cdot ( \textcolor{deepskyblue}{N-1} )}
\end{array} \right)
\]でしたね。
つぎに、逆DFT行列 \( W_N^{-1} \) を見てみましょう。\[
W_N^{-1} = \frac{1}{N} \left( \begin{array}{ccc} w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{0} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{0} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{1} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{1} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{0}} & w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{1}} & w^{- \textcolor{deepskyblue}{2} \cdot \textcolor{magenta}{2}} & \cdots & w^{- \textcolor{deepskyblue}{2} \cdot \ ( \textcolor{magenta}{N-1} )}
\\ & & & \ddots & \\
w^{(- \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{0}} & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{1}} & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot \textcolor{magenta}{2}} & \cdots & w^{- ( \textcolor{deepskyblue}{N-1} ) \cdot ( \textcolor{magenta}{N-1} )}
\end{array} \right)
\]
すると、DFT行列 \( W_N \) に出てくる \( w^a \) の指数部分の正負を入れ替え(共役複素数をとり)、\( w^{-a} \) としてから \( \frac{1}{N} \) 倍したものが逆DFT行列になっていることがわかりますね!
つまり、DFT行列(離散フーリエ変換の変換行列)さえ求めてしまえば、
- 出てくる \( w^a \) の正負を入れ替え(共役複素数を取る)
- 全体を \( \frac{1}{N} \) 倍する
だけで簡単に逆DFT行列(逆離散フーリエ変換の変換行列)を求めることができちゃうのです!
離散フーリエ変換の変換行列 (DFT行列) が \( W_N \) とわかっている場合、離散逆フーリエ変換の変換行列 (逆DFT行列) \( W_N^{-1} \) は、下のように求められる。\[
W_N^{-1} = \frac{1}{N} \overline{W_N}
\]
※ \( \overline{W} \) は複素共役行列
→ 行列内の全要素に対して共役複素数を取った行列
→ \( w^a \) の共役複素数は \( w^{-a} \)
※ \( \overline{W} \) の代わりに随伴行列 \( W^* \) としてもOK[4]転置しても行列が変わらないため。
→ 複素共役行列を転値させた行列が随伴行列)
8. [例題] N = 4 の離散フーリエ変換・逆変換
ここからは、実際に例題を解くことで離散フーリエ変換の知識が身についているかを確認しましょう。
ある実変数\[
\vec{x} = \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 1 \end{array} \right)
\]を離散フーリエ変換したい。
(1) \( N = 4 \) のとき、離散フーリエ変換の変換行列(DFT行列)を求めなさい。
(2) \( \vec{x} \) を4点離散フーリエ変換しなさい。
(3) 逆離散フーリエ変換の変換行列(逆DFT行列)を求めなさい。
(4) \( \vec{y} \) に逆離散フーリエ変換を適用することで \( \vec{x} \) に戻るかを確認しなさい。
(1)
\( w = e^{- \frac{2 \pi}{4} i } \)、つまり \( w = - e^{ \frac{\pi}{2} i } \) とおく。
ここで、次の計算をしておく。\[\begin{align*}
w^0 & = 1
\\ w^1 & = e^{- \frac{\pi}{2} i } = -i
\\ w^2 & = e^{- \pi i } = -1
\\ w^3 & = e^{- \frac{3 \pi}{2} i } = i
\\ w^4 & = e^{- 2 \pi i } = 1
\end{align*}\]必要であれば下のように円を書いておくのもあり。
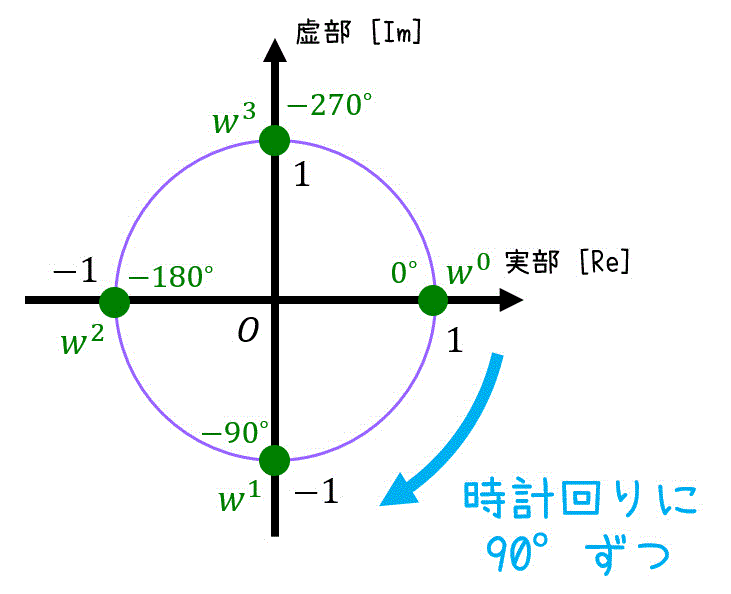
すると、離散フーリエ変換の変換行列 \( W_4 \) は、下のように求められる。\[\begin{align*}
W_4 & = \left( \begin{array}{ccc} w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{3} }
\\ w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{3} }
\\ w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{3} }
\\ w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{3} }
\end{array} \right)
\\ & = \left( \begin{array}{ccc} w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 }
\\ w^{ 0 } & w^{ 1 } & w^{ 2 } & w^{ 3 }
\\ w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 }
\\ w^{ 0 } & w^{ 3 } & w^{ 6 } & w^{ 9 }
\end{array} \right)
\\ & = \left( \begin{array}{ccc} w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 }
\\ w^{ 0 } & w^{ 1 } & w^{ 2 } & w^{ 3 }
\\ w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 2 } w^{ 4 }
\\ w^{ 0 } & w^{ 3 } & w^{ 2 } w^{ 4 } & w^{ 1 } w^{8 }
\end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 1 & 1 & 1
\\ 1 & -i & -1 & i
\\ 1 & -1 & 1 & -1
\\ 1 & i & -1 & -i
\end{array} \right)
\end{align*}\]※ 途中の変形で \( w^4 = 1 \) を利用しています。
(2)
\( \vec{y} = W_4 \vec{x} \) を計算すればOK。
\[\begin{align*}
\vec{y} & =
\left( \begin{array}{ccc} 1 & 1 & 1 & 1 \\ 1 & -i & -1 & i \\ 1 & -1 & 1 & -1 \\ 1 & i & -1 & -i \end{array} \right) \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1+1+1 \\ 1-1+i \\ 1+1-i \\ 1-i-i \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 \\ i \\ 1 \\ -i \end{array} \right)
\end{align*}\]
(3)
逆DFT行列は、DFT行列の要素全体の共役複素数を取り、\( \frac{1}{N} \) 倍すればOK。
計算前に、次の計算をしておく。\[\begin{align*}
w^1 & = e^{ \frac{\pi}{2} i } = i \\
w^2 & = e^{ \pi i } = -1 \\
w^3 & = e^{ \frac{3 \pi}{2} i } = -i \\
w^4 & = e^{ 2 \pi i } = 1
\end{align*}\]必要であれば下のように円を書いて求めるのもあり。
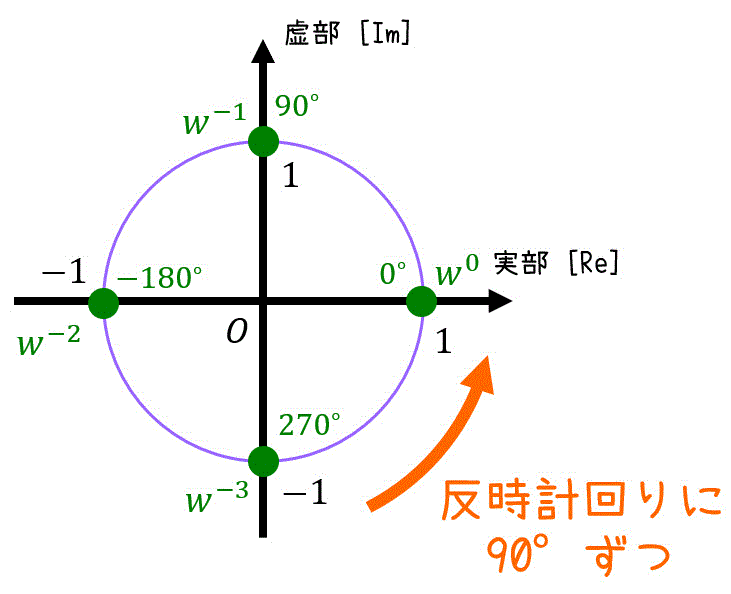
今回は、\( N = 4 \) なので、\[\begin{align*}
W_4^{-1} & = \frac{1}{4} \overline{W_4}
\\ & = \left( \begin{array}{ccc} w^{ -0 } & w^{ -0 } & w^{ -0 } & w^{ -0 }
\\ w^{ -0 } & w^{ -1 } & w^{ -2 } & w^{ -3 }
\\ w^{ -0 } & w^{ -2 } & w^{ -4 } & w^{ -6 }
\\ w^{ -0 } & w^{ -3 } & w^{ -6 } & w^{ -9 }
\end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} w^{ -0 } & w^{ -0 } & w^{ -0 } & w^{ -0 }
\\ w^{ -0 } & w^{ -1 } & w^{ -2 } & w^{ -3 }
\\ w^{ -0 } & w^{ -2 } & w^{ -4 } & w^{ -2 } w^{ -4 }
\\ w^{ -0 } & w^{ -3 } & w^{ -2 } w^{ -4 } & w^{ -1 } w^{ -8 }
\end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \end{array} \right)
\end{align*}\]※ 途中の変形で \( w^{-4} = 1 \) を利用しています。
(4)
確認するだけ。\[\begin{align*}
\vec{x} & = W_4^{-1} \vec{y}
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \end{array} \right) \left( \begin{array}{ccc} 3 \\ i \\ 1 \\ -i \end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 3+i+1-i \\ 3+i^2-1+i^2 \\ 3-i+1+i \\ 3-i^2-1-i^2 \end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 4 \\ 0 \\ 4 \\ 4 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 1 \end{array} \right)
\end{align*}\]
9. [練習問題] N = 8 の離散フーリエ変換にチャレンジ!
最後に、\( N = 8 \) の離散フーリエ変換にもチャレンジしてみましょう!
ある実変数\[
\vec{x} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{array} \right)
\]を離散フーリエ変換したい。
(1) \( N = 8 \) のとき、離散フーリエ変換の変換行列(DFT行列)を求めなさい。
(2) \( \vec{x} \) を8点離散フーリエ変換しなさい。
(1)
\( w = e^{- \frac{2 \pi}{8} i } \)、つまり \( w = - e^{ \frac{\pi}{4} i } \) とおく。
まず、離散フーリエ変換の変換行列 \( W_8 \) を \( w \)を用いて表す。\[\begin{align*}
W_8 & = \left( \begin{array}{ccc} w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}
{3} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}
{4} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}
{5} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}
{6} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{7} }
\\ w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{0} } & w^{ \textcolor{magenta}
{7} \cdot \textcolor{deepskyblue}{1} } & w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{2} } & w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{3} } & w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{4} } & w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{5} } & w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{6} } & w^{ \textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{7} }
\end{array} \right)
\\ & = \left( \begin{array}{ccc} w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 }
\\ w^{ 0 } & w^{ 1 } & w^{ 2 } & w^{ 3 } & w^{ 4 } & w^{ 5 } & w^{ 6 } & w^{ 7 }
\\ w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 } & w^{ 8 } & w^{ 10 } & w^{ 12 } & w^{ 14 }
\\ w^{ 0 } & w^{ 3 } & w^{ 6 } & w^{ 9 } & w^{ 12 } & w^{ 15 } & w^{ 18 } & w^{ 21 }
\\ w^{ 0 } & w^{ 4 } & w^{ 8 } & w^{ 12 } & w^{ 16 } & w^{ 20 } & w^{ 24 } & w^{ 28 }
\\ w^{ 0 } & w^{ 5 } & w^{ 10 } & w^{ 15 } & w^{ 20 } & w^{ 25 } & w^{ 30 } & w^{ 35 }
\\ w^{ 0 } & w^{ 6 } & w^{ 12 } & w^{ 18 } & w^{ 24 } & w^{ 30 } & w^{ 36 } & w^{ 42 }
\\ w^{ 0 } & w^{ 7 } & w^{ 14 } & w^{ 21 } & w^{ 28 } & w^{ 35 } & w^{ 42 } & w^{ 49 }
\end{array} \right)
\\ & = \left( \begin{array}{ccc} w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 }
\\ w^{ 0 } & w^{ 1 } & w^{ 2 } & w^{ 3 } & w^{ 4 } & w^{ 5 } & w^{ 6 } & w^{ 7 }
\\ w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 } & w^{ 8 } & w^{ 2 } w^{8} & w^{ 4 } w^{8} & w^{ 6 } w^{8}
\\ w^{ 0 } & w^{ 3 } & w^{ 6 } & w^{ 1 } w^{8} & w^{ 4 } w^{8} & w^{ 7 } w^{8} & w^{ 2 } \left( w^{8} \right)^2 & w^{ 5 } \left( w^{8} \right)^2
\\ w^{ 0 } & w^{ 4 } & w^{ 8 } & w^{ 4 } w^8 & \left( w^{8} \right)^2 & w^{ 4 } \left( w^{8} \right)^2 & \left( w^{8} \right)^3 & w^{ 4 } \left( w^{8} \right)^3
\\ w^{ 0 } & w^{ 5 } & w^{ 2 } w^{8} & w^{ 7 } w^{8} & w^{ 4 } \left( w^{8} \right)^2 & w^{ 1 } \left( w^{8} \right)^3 & w^{ 6 } \left( w^{8} \right)^2 & w^{3} \left( w^{8} \right)^4
\\ w^{ 0 } & w^{ 6 } & w^{ 4 } w^8 & w^{ 2 } \left( w^{8} \right)^2 & \left( w^{8} \right)^3 & w^{ 6 } \left( w^{8} \right)^3 & w^{ 4 } \left( w^{8} \right)^4 & w^{ 2 } \left( w^{8} \right)^5
\\ w^{ 0 } & w^{ 7 } & w^{ 6 } w^8 & w^{5} \left( w^{8} \right)^2 & w^{ 3 } \left( w^{8} \right)^3 & w^{ 3 } \left( w^{8} \right)^4 & w^{ 2 } \left( w^{8} \right)^5 & w^{ 1 } \left( w^{8} \right)^6
\end{array} \right)
\\ & = \left( \begin{array}{ccc} w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 }
\\ w^{ 0 } & w^{ 1 } & w^{ 2 } & w^{ 3 } & w^{ 4 } & w^{ 5 } & w^{ 6 } & w^{ 7 }
\\ w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 } & w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 }
\\ w^{ 0 } & w^{ 3 } & w^{ 6 } & w^{ 1 } & w^{ 4 } & w^{ 7 } & w^{2 } & w^{ 5 }
\\ w^{ 0 } & w^{ 4 } & w^{ 0 } & w^{ 4 } & w^{ 0 } & w^{ 4 } & w^{ 0 } & w^{ 4 }
\\ w^{ 0 } & w^{ 5 } & w^{ 2 } & w^{ 7 } & w^{ 4 } & w^{ 1 } & w^{ 6 } & w^{ 3 }
\\ w^{ 0 } & w^{ 6 } & w^{ 4 } & w^{ 2 } & w^{ 0 } & w^{ 6 } & w^{ 4 } & w^{ 2 }
\\ w^{ 0 } & w^{ 7 } & w^{ 6 } & w^{ 5 } & w^{ 4 } & w^{ 3 } & w^{ 2 } & w^{ 1 }
\end{array} \right)
\end{align*}\]※ 最後の変形では \( w^8 = 1 \) を利用しています。
ここで、次の計算をしておく。\[\begin{align*}
w^0 & = 1
\\ w^1 & = e^{ - \frac{\pi}{4} i } = \frac{ \sqrt{2} }{2} - \frac{ \sqrt{2} }{2} i
\\ w^2 & = e^{- \frac{\pi}{2} i } = - i
\\ w^3 & = e^{- \frac{3 \pi}{4} i } = - \frac{ \sqrt{2} }{2} - \frac{ \sqrt{2} }{2} i
\\ w^4 & = e^{- \pi i } = - 1
\\ w^5 & = e^{- \frac{5 \pi}{4} i } = - \frac{ \sqrt{2} }{2} + \frac{ \sqrt{2} }{2} i
\\ w^6 & = e^{- \frac{3 \pi}{2} i } = i
\\ w^7 & = e^{- \frac{7 \pi}{4} i } = \frac{ \sqrt{2} }{2} + \frac{ \sqrt{2} }{2} i
\\ w^8 & = e^{- \pi i } = 1
\end{align*}\]必要であれば下のように円を書いておくのもあり。
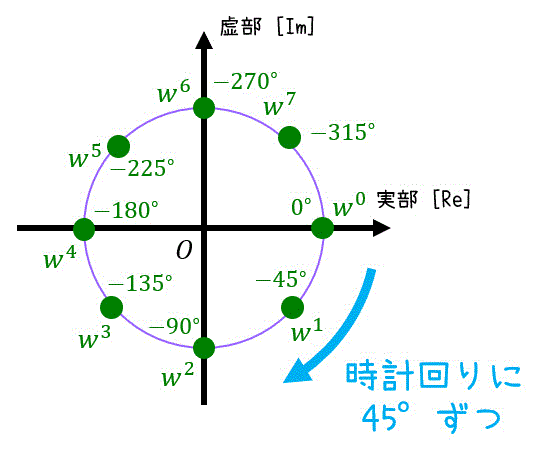
よって、
\[\begin{align*}
W_8 & = \left( \begin{array}{ccc} w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 } & w^{ 0 }
\\ w^{ 0 } & w^{ 1 } & w^{ 2 } & w^{ 3 } & w^{ 4 } & w^{ 5 } & w^{ 6 } & w^{ 7 }
\\ w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 } & w^{ 0 } & w^{ 2 } & w^{ 4 } & w^{ 6 }
\\ w^{ 0 } & w^{ 3 } & w^{ 6 } & w^{ 1 } & w^{ 4 } & w^{ 7 } & w^{2 } & w^{ 5 }
\\ w^{ 0 } & w^{ 4 } & w^{ 0 } & w^{ 4 } & w^{ 0 } & w^{ 4 } & w^{ 0 } & w^{ 4 }
\\ w^{ 0 } & w^{ 5 } & w^{ 2 } & w^{ 7 } & w^{ 4 } & w^{ 1 } & w^{ 6 } & w^{ 3 }
\\ w^{ 0 } & w^{ 6 } & w^{ 4 } & w^{ 2 } & w^{ 0 } & w^{ 6 } & w^{ 4 } & w^{ 2 }
\\ w^{ 0 } & w^{ 7 } & w^{ 6 } & w^{ 5 } & w^{ 4 } & w^{ 3 } & w^{ 2 } & w^{ 1 }
\end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 2 & 2 & 2 & 2 & 2 & 2 & 2 & 2
\\ 2 & \sqrt{2} - \sqrt{2} i & -2i & - \sqrt{2} - \sqrt{2} i & -2 & - \sqrt{2} + \sqrt{2} i & 2i & \sqrt{2} + \sqrt{2} i
\\ 2 & -2i & -2 & 2i & 2 & -2i & -2 & 2i
\\ 2 & - \sqrt{2} - \sqrt{2} i & 2i & \sqrt{2} - \sqrt{2} i & -2 & \sqrt{2} + \sqrt{2} i & -2i & - \sqrt{2} + \sqrt{2} i
\\ 2 & -2 & 2 & -2 & 2 & -2 & 2 & -2
\\ 2 & - \sqrt{2} + \sqrt{2} i & -2i & \sqrt{2} + \sqrt{2} i& -2 & \sqrt{2} - \sqrt{2} i & 2i & - \sqrt{2} - \sqrt{2} i
\\ 2 & 2i & -2 & -2i & 2 & 2i & -2 & -2i
\\ 2 & \sqrt{2} + \sqrt{2} i & 2i & - \sqrt{2} + \sqrt{2} i & -2 & - \sqrt{2} - \sqrt{2} i & -2i & \sqrt{2} - \sqrt{2} i
\end{array} \right)
\end{align*}\]
と計算できる。
※ 特に指示がない場合を除き、\( w \) のままで答えることを強くおすすめします。
(2)
\( w \) でおいた状態の行列から求めることを強くおすすめします。
\( w \) に値を代入した行列を使って計算するとわけがわからなくなります。
\[\begin{align*}
\vec{y} & = W_8 \vec{x}
\\ & = \left( \begin{array}{ccc} \textcolor{red}{ w^{ 0 } } & w^{ 0 } & w^{ 0 } & \textcolor{red}{ w^{ 0 } } & w^{ 0 } & w^{ 0 } & w^{ 0 } & \textcolor{red}{ w^{ 0 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 1 } & w^{ 2 } & \textcolor{red}{ w^{ 3 } } & w^{ 4 } & w^{ 5 } & w^{ 6 } & \textcolor{red}{ w^{ 7 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 2 } & w^{ 4 } & \textcolor{red}{ w^{ 6 } } & w^{ 0 } & w^{ 2 } & w^{ 4 } & \textcolor{red}{ w^{ 6 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 3 } & w^{ 6 } & \textcolor{red}{ w^{ 1 } } & w^{ 4 } & w^{ 7 } & w^{2 } & \textcolor{red}{ w^{ 5 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 4 } & w^{ 0 } & \textcolor{red}{ w^{ 4 } } & w^{ 0 } & w^{ 4 } & w^{ 0 } & \textcolor{red}{ w^{ 4 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 5 } & w^{ 2 } & \textcolor{red}{ w^{ 7 } } & w^{ 4 } & w^{ 1 } & w^{ 6 } & \textcolor{red}{ w^{ 3 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 6 } & w^{ 4 } & \textcolor{red}{ w^{ 2 } } & w^{ 0 } & w^{ 6 } & w^{ 4 } & \textcolor{red}{ w^{ 2 } }
\\ \textcolor{red}{ w^{ 0 } } & w^{ 7 } & w^{ 6 } & \textcolor{red}{ w^{ 5 } } & w^{ 4 } & w^{ 3 } & w^{ 2 } & \textcolor{red}{ w^{ 1 } }
\end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{1} \\ 0 \\ 0 \\ \textcolor{red}{1} \\ 0 \\ 0 \\ 0 \\ \textcolor{red}{1} \end{array} \right)
\\ & = \left( \begin{array}{ccc} w^0 + w^0 + w^0 \\ w^0 + w^3 + w^7 \\ w^0 + w^6 + w^6 \\ w^0 + w^1 + w^5 \\ w^0 + w^4 + w^4 \\ w^0 + w^7 + w^3 \\ w^0 + w^2 + w^2 \\ w^0 + w^5 + w^1 \end{array} \right) = \left( \begin{array}{ccc} 3 w^0 \\ w^0 + w^3 + w^3 w^4 \\ w^0 + 2 w^6 \\ w^0 + w^1 + w^1 w^4 \\ w^0 + 2 w^4 \\ w^0 + w^3 w^4 + w^3 \\ w^0 + 2w^2\\ w^0 + w^1 w^4 + w^1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 w^0 \\ w^0 + w^3 - w^3 \\ w^0 + 2 w^6 \\ w^0 + w^1 - w^1 \\ w^0 + 2 w^4 \\ w^0 - w^3 + w^3 \\ w^0 + 2w^2\\ w^0 + w^1 w^4 + w^1 \end{array} \right)
= \left( \begin{array}{ccc} 3 \\ 1 \\ 1 + 2i \\ 1 \\ -1 \\ 1 \\ 1 - 2i \\ 1 \end{array} \right)
\end{align*}\]
※ \( w^4 = -1 \) を使うと若干計算が楽になります。
10. さいごに
今回は、離散フーリエ変換(DFT)について説明していきました。
離散フーリエ変換を学ぶことで、無限や極限を扱えないコンピュータ上でも、フーリエ変換を適用する方法が理解できたのであれば幸いです。
次回は、離散フーリエ変換(DFT)を高速で計算する方法について書いていきたいと思います!
注釈
| ↑1 | \( 0 \leqq n \leqq N \) とすると、範囲内に含まれる \( n \) の数が \( N + 1 \) 個になってしまい、周期も \( N + 1 \) になってしまうから。 |
|---|---|
| ↑2 | 離散フーリエ変換、逆離散フーリエ変換の対応付けが正しければ(3), (4)の変換式で定義しなくてもOKです。具体的には、「離散フーリエ変換の正規化係数×逆離散フーリエ変換の正規化係数=1/N」と、「離散フーリエ変換、離散逆フーリエ変換の指数部の符号が異なっている」ことを満たしていればOKです。 |
| ↑3 | 逆変換に出てくる \( w^{-nk} \) は、もちろん \( w^{-kn} \) でもOKです。 |
| ↑4 | 転置しても行列が変わらないため。 |
関連広告・スポンサードリンク