スポンサードリンク
こんにちは、ももやまです。
今日は、確率・統計に出てくる「累積分布関数」についてお勉強していきましょう!
目次
スポンサードリンク
1. 確率密度関数の復習
累積分布関数を知るためには、確率密度関数の知識が前提となってきます。
なので、まずは確率密度関数について簡単におさらいしましょう。
(1) 確率分布関数のイメージ
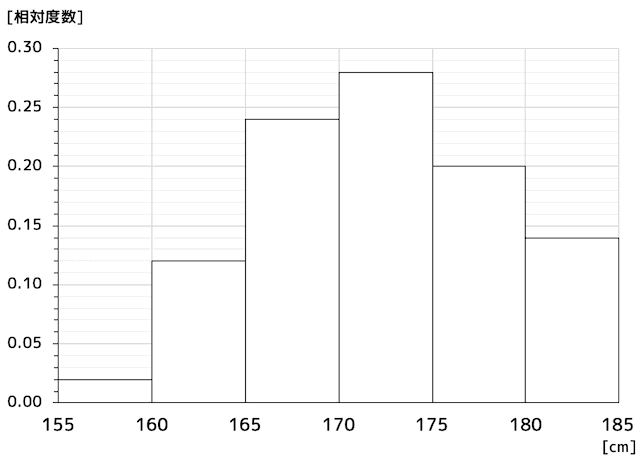
確率密度関数は、ヒストグラムに出てくる相対度数を細かく細かく刻んで、滑らかな曲線になったものを関数にしたものです。
(2) 確率分布関数で重要な6つの性質・公式
確率分布関数 \( f(x) \) で出てくる重要な6つの公式を、復習しましょう。
確率密度関数 ( f(x) ) で与えられる確率変数 ( X ) 。ただし、\( X \) は、 の値を取るとする。
その1. 確率の密度は、必ず正である。\[
f(x) \geqq 0
\]
その2. 確率の密度 \( f(x) \) は1を超えることもある。
※ 確率の密度は、確率とは異なるもの
その3. 確率変数 \( X \) が、\( a \leqq x \leqq b \) となる確率は、以下の積分式で求められる。\[
\int^{b}_{a} f(x) \ dx
\]
その4. 確率の和は1であるため、以下の積分式が成立する。\[
\int^{\infty}_{- \infty}f(x) \ dx = 1
\]※ 高校数学の数Bで「確率分布と統計的な推測」を勉強してきた人は、取りうる値が \( m \leqq x \leqq M \) の確率変数 \( X \) に対して、\[
\int^{M}_{m} f(x) \ dx = 1
\]が成立する、という表記法のほうが馴染みがあると思います。(高校数学では広義積分を習わないため)
その5. 期待値(平均) \( E(X) \) は、次の積分式で計算ができる。\[
\int^{\infty}_{- \infty} x f(x) \ dx
\]※ 取りうる値が \( m \leqq x \leqq M \) の確率変数 \( X \) の場合、期待値は\[
\int^{M}_{m} x f(x) \ dx
\]で計算できる。(数Bの「確率分布と統計的推測」ではこの表記を使用)
その6. 分散 \( V(X) \) は、期待値(平均) \( \mu = E(X) \) を用いて以下の(1), (2)の式のいずれかで計算ができる。(推奨: (1)の式)
(1) 2乗した値の期待値 - 期待値の2乗で計算\[\begin{align*}
V(X) & = E(X^2) - \left[ E(X) \right]^2
\\ & = \int^{\infty}_{- \infty} x^2 f(x) \ dx - \left( \int^{\infty}_{- \infty} x f(x) \ dx \right)^2
\\ & = \int^{\infty}_{- \infty} x^2 f(x) \ dx - \mu^2
\end{align*}\]
※ 取りうる値が \( m \leqq x \leqq M \) の確率変数 \( X \) の場合は、分散を\[\begin{align*}
V(X) = \int^{M}_{m} x^2 f(x) \ dx - \left( \int^{M}_{m} x f(x) \ dx \right)^2
\\ & = \int^{M}_{m} x^2 f(x) \ dx - \mu^2
\end{align*}\]と計算できる。(数Bの「確率分布と統計的推測」ではこの表記を使用)
(2) 各値とその期待値(平均)の差を2乗したものの期待値(平均)\[
V(X) = \int^{\infty}_{- \infty} (x- \mu)^2 f(x) \ dx
\]※ とりうる値が \( m \leqq x \leqq M \) の確率変数 \( X \) の場合は、\[
V(X) = \int^{M}_{m} (x- \mu)^2 f(x) \ dx
\]で計算できる。
軽くおさらいしても、「確率密度関数があまりよくわからないなぁ。」という人は、以下の記事にて確率密度関数について解説しているので、リンク先の記事をご覧ください。
スポンサードリンク
2. 累積分布関数のイメージ
(1) 相対度数と累積相対度数
累積分布関数について説明する前に、まずは「相対度数」と「累積相対度数」について復習しましょう。
※ 「累積相対度数」というのが、累積分布関数のベースとなってきます。
[a] 相対度数
相対度数とは、データをある範囲ごとに区切ったときに、その範囲内にどれくらいの割合のデータがあるかを、それぞれの範囲ごと(階級ごと)に表したものです。
式で書くと、
(相対度数)=(各階級ごとの度数)÷(全体の度数)
となります。
例えば、階級「身長170cm以上175cm未満」の相対度数は\[
28 \div 100 = 0.28
\]と計算できます。
表1. 度数と相対度数の関係
| 身長 | 度数 | 相対度数 |
|---|---|---|
| 155 - 160 | 2 | 0.02 |
| 160 - 165 | 12 | 0.12 |
| 165 - 170 | 24 | 0.24 |
| 170 - 175 | 28 | 0.28 |
| 175 - 180 | 20 | 0.20 |
| 180 - 185 | 14 | 0.14 |
| 合計 | 100 | 1.00 |
[b] 累積相対度数
累積相対度数は、相対度数を累積していったものです。つまり、「(小さい階級から数えていったときに)ある区間までのデータの割合を累積したもの」と言えます。
例えば、先ほどの表1のデータを見てみましょう。
表1の各階級ごとの累積相対度数は、
- 155cm以上160cm未満 → 累積相対度数は、そのまま相対度数0.02。
- 160cm以上165cm未満 → 160cm未満までの累積相対度数0.02に、160cm以上165cm未満の相対度数0.12を足すので、0.02 + 0.12 = 0.14。
- 165cm以上170cm未満 → 165cm未満までの累積相対度数0.14に、165cm以上170cm未満の相対度数0.24を足すので、0.14 + 0.24 = 0.38。
- 170cm以上175cm未満 → 170cm未満までの累積相対度数0.38に、170cm以上175cm未満の相対度数0.28を足すので、0.38 + 0.28 = 0.66。
- 175cm以上180cm未満 → 175cm未満までの累積相対度数0.66に、175cm以上180cm未満の相対度数0.20を足すので、0.66 + 0.20 = 0.86。
- 180cm以上185cm未満 → 180cm未満までの累積相対度数0.86に、180cm以上185cm未満の相対度数0.14を足すので、0.86 + 0.14 = 1.00。
と計算できます。
表2. 相対度数と累積相対度数の関係
| 身長 | 度数 | 相対度数 | 累積相対度数 | 計算式 (累積相対度数) |
|---|---|---|---|---|
| 155 - 160 | 2 | 0.02 | 0.02 | 0.02 |
| 160 - 165 | 12 | 0.12 | 0.14 | 0.02 + 0.12 |
| 165 - 170 | 24 | 0.24 | 0.38 | 0.14 + 0.24 |
| 170 - 175 | 28 | 0.28 | 0.66 | 0.38 + 0.28 |
| 175 - 180 | 20 | 0.20 | 0.86 | 0.66 + 0.20 |
| 180 - 185 | 14 | 0.14 | 1.00 | 0.86 + 0.14 |
| 合計 | 100 | 1.00 | - | - |
(2) 累積相対度数から累積分布関数へ
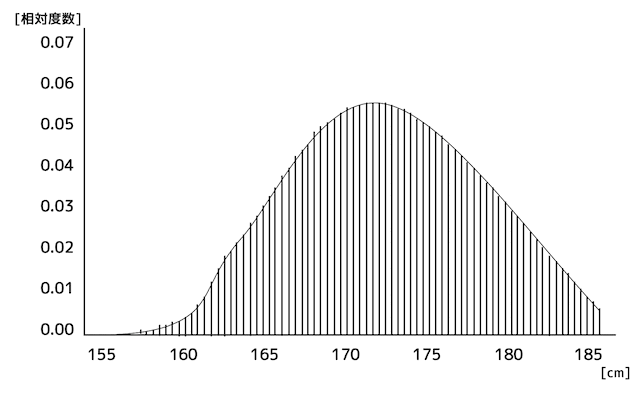
表2で求めた、各階級ごとの累積相対度数を、下のようなヒストグラムの形にします。
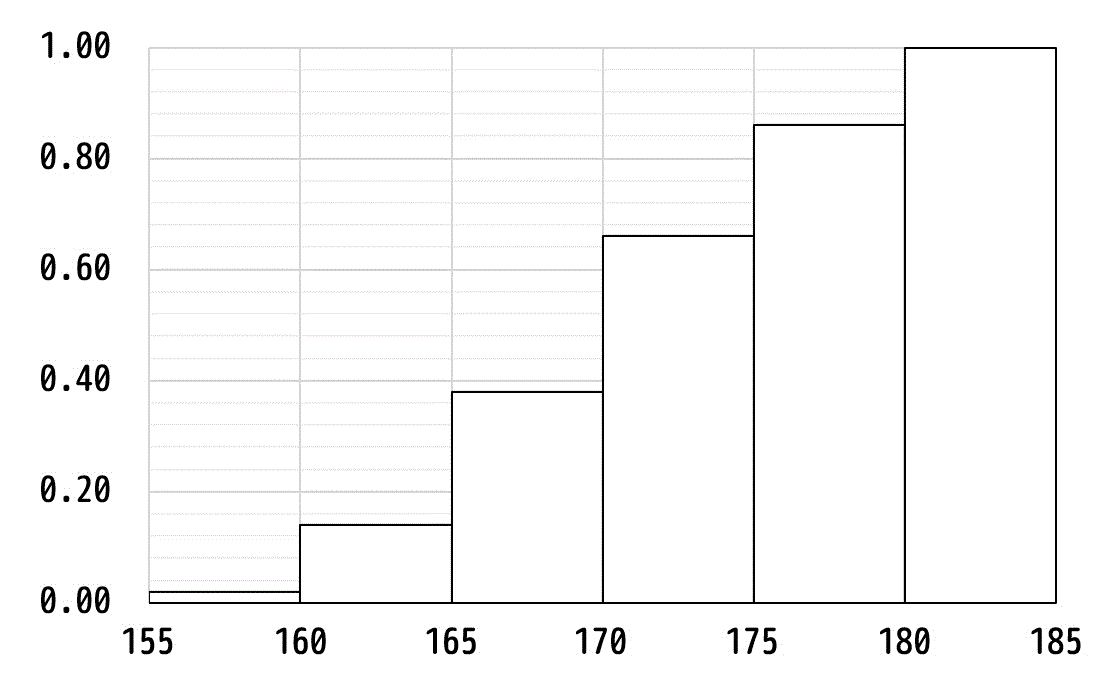
さらに、このヒストグラムの横軸をどんどん細かくしていくことを考えていきます。
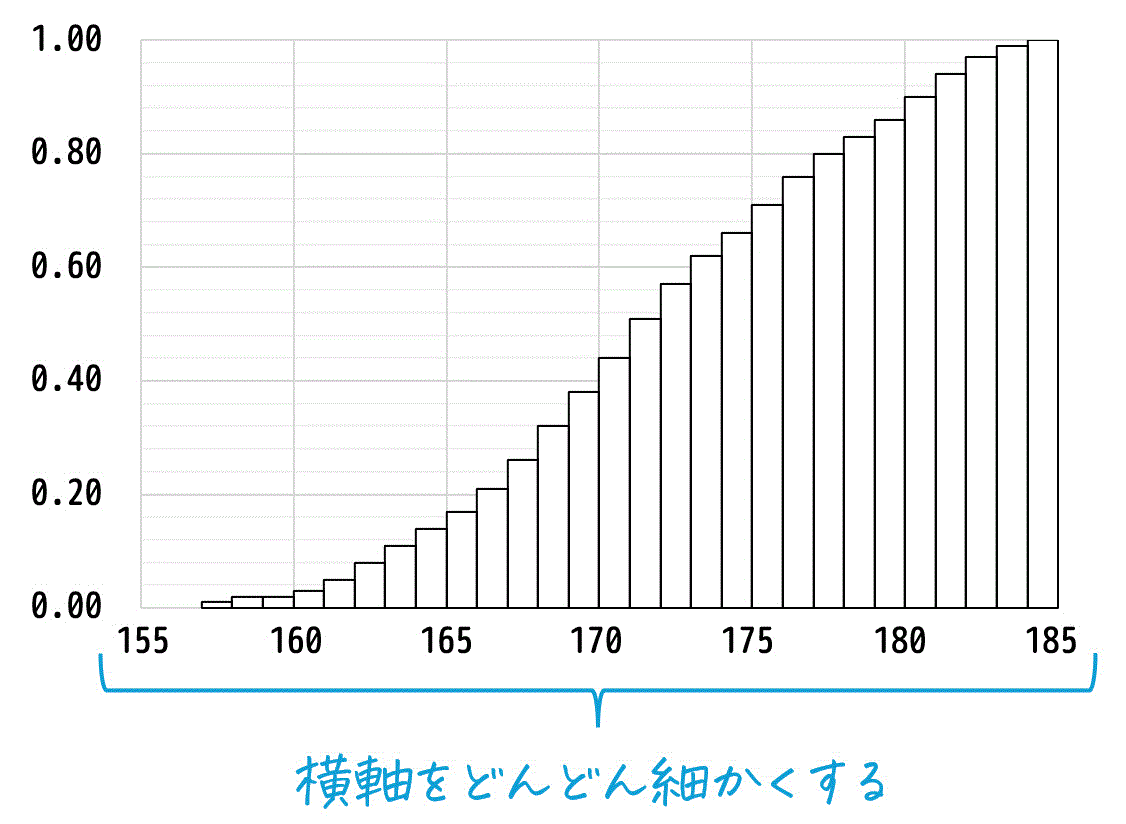
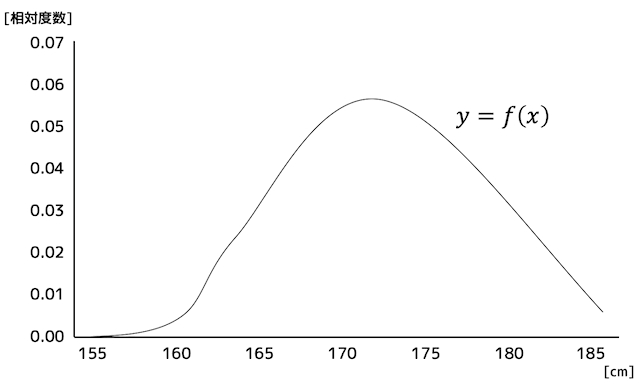
累積分布関数 \( F(x) \) は、この細かくなったヒストグラムをなめらかかつ連続的にしたもの、だと思っていただければOKです。
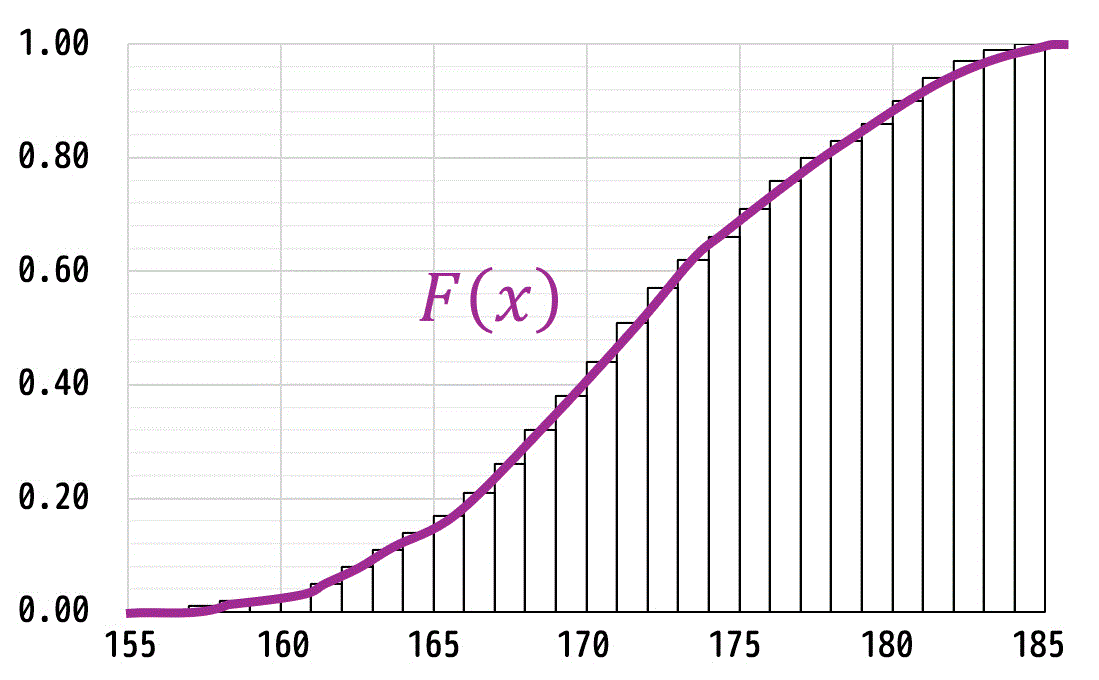
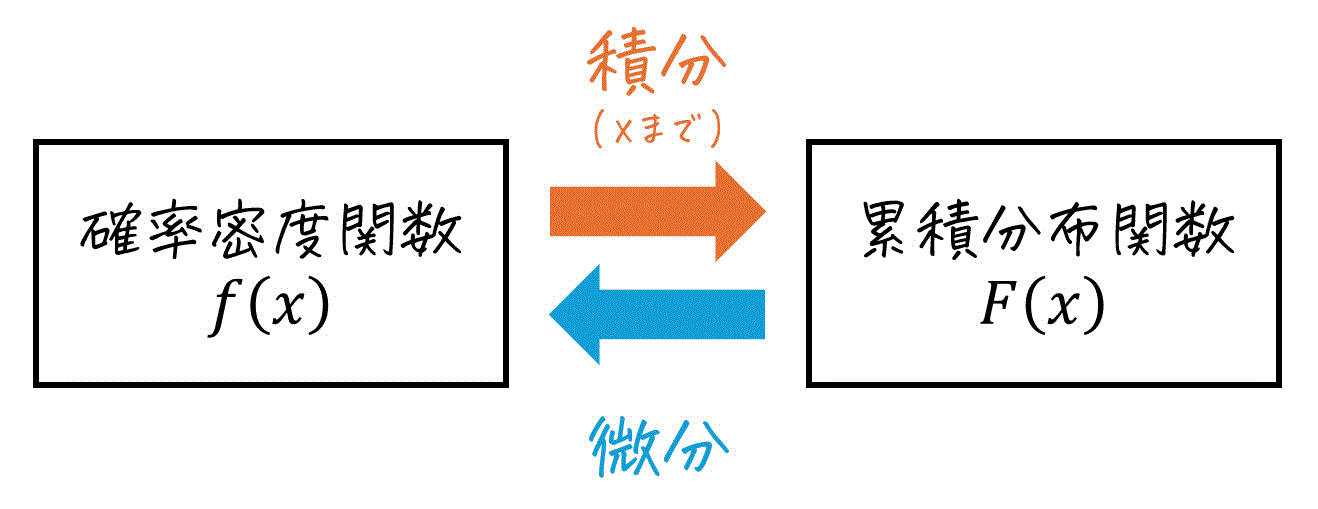
(3) 確率密度関数 f(x) と累積分布関数 F(x) の関係
[a] f(x)からF(x)を求める方法
累積相対度数というのは、ある区間までの相対度数を累積したものでした。
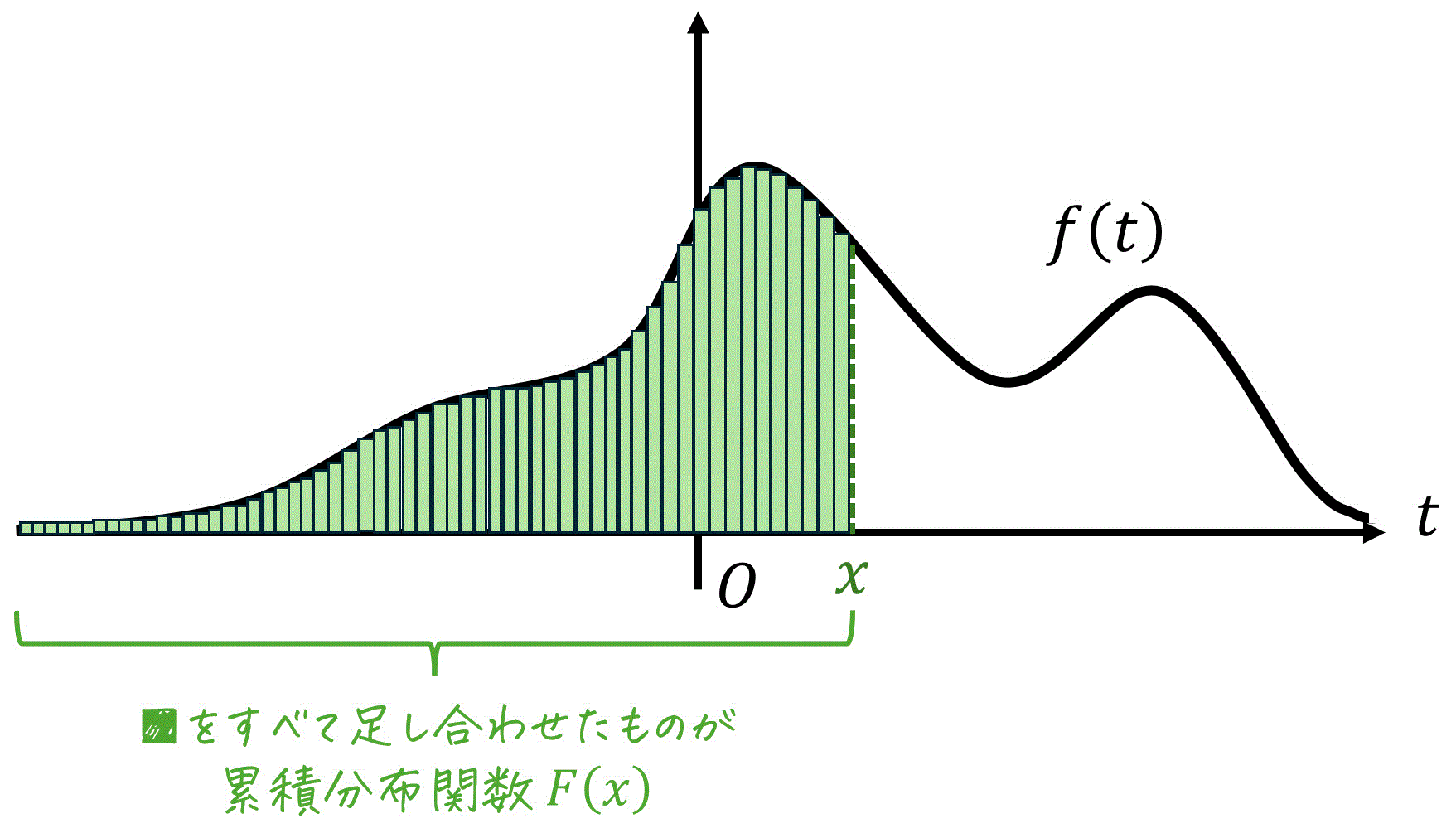
この考えは、累積分布関数でも言えます。つまり、累積分布関数 \( F(x) \) は、それまでの値 \( x \) までの確率密度関数 \( f(x) \) をすべて累積した(=足し合わせた)ようなものと言えます。

ここで、確率密度関数 \( f(x) \) は連続なので、ある値 \( x \) までの累積は、積分を使って計算することが出来ます。
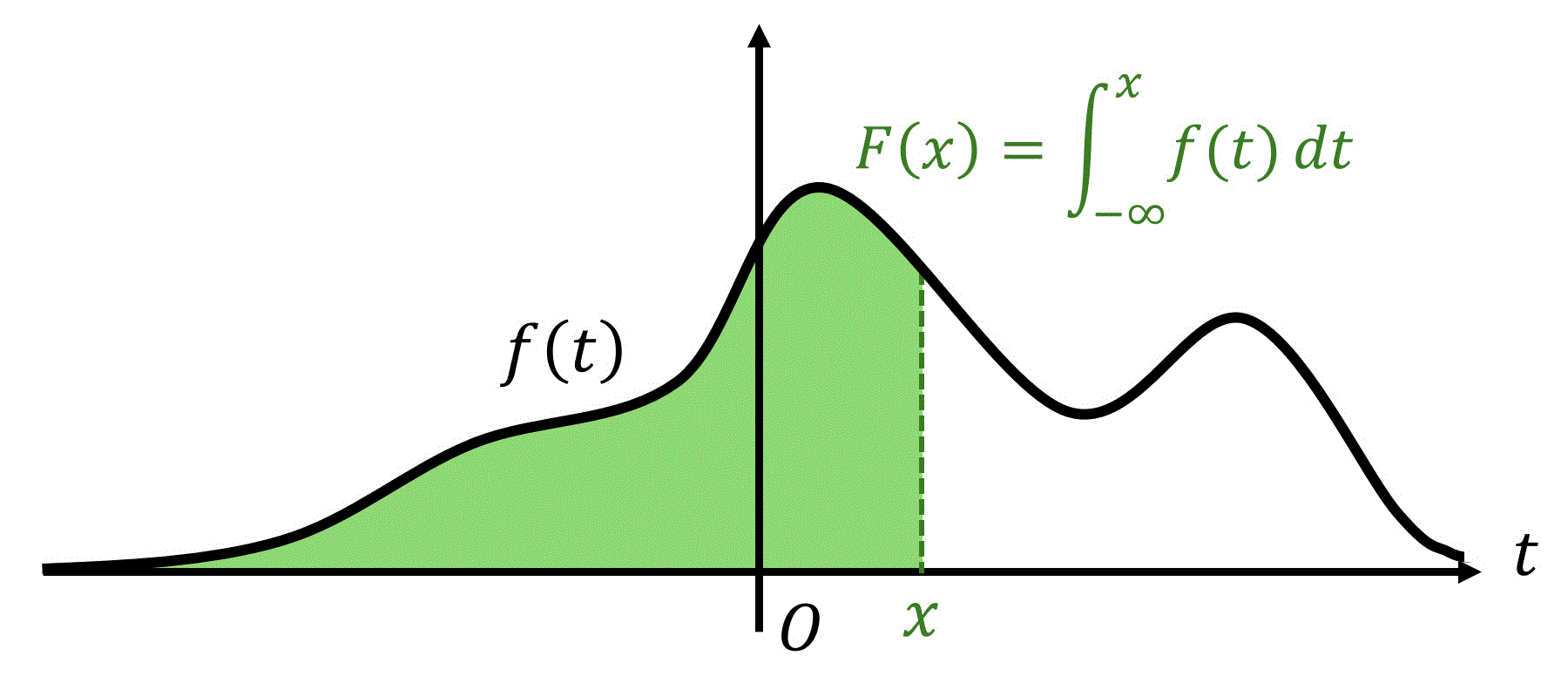
具体的に、ある値 \( x \) における累積分布関数 \( F(x) \)、つまり値 \( x \) までの確率密度関数 \( f(x) \) をすべて累積したものは、確率密度関数 \( f(x) \) を用いて次のように計算できます。\[
F(x) = \int^{x}_{- \infty} f(t) \ dt
\]※ \( f(t) \) は確率密度関数 \( f(x) \) の \( x \) を \( t \) におきかえたもの。
[b] F(x)からf(x)を求める方法
確率密度関数 \( f(x) \) から累積分布関数 \( F(x) \) は、積分をすることで求めることが出来ましたね。
そのため、累積分布関数 \( F(x) \) から確率密度関数 \( f(x) \) を求める際には、累積分布関数 \( F(x) \) を微分することで求めることが出来ます。式で書くと、以下の通りです。\[
f(x) = \frac{d}{dx} F(x)
\]
まとめ: f(x)とF(x)の関係
(4) 累積分布関数 F(x)で覚えておきたい3つの性質
つぎに、累積分布関数で覚えておきたい3つの性質を紹介します。
性質1. \( F(x) \) は必ず0以上1以下
累積分布関数 \( F(x) \) は確率なので、値は必ず0以上1以下の値を取ります。\[
0 \leqq F(x) \leqq 1
\]
性質2. \( F(x) \) は単調増加
累積相対度数では、前の階級値の相対度数をどんどん累積していって求めるため、前の階級値の累積相対度数よりも累積相対度数が小さくなることは絶対にありません。
累積分布関数 \( F(x) \) でも累積相対度数の考え方と同じように、それまでの確率密度 \( f(x) \) をすべて足し合わせて求めていくため、\( x \) の値が増えると、必ず \( F(x) \) は大きい or 同じ値を取ります。
数式で書くと、\[
x_1 < x_2 \to F(x_1) \leqq F(x_2)
\]となります。
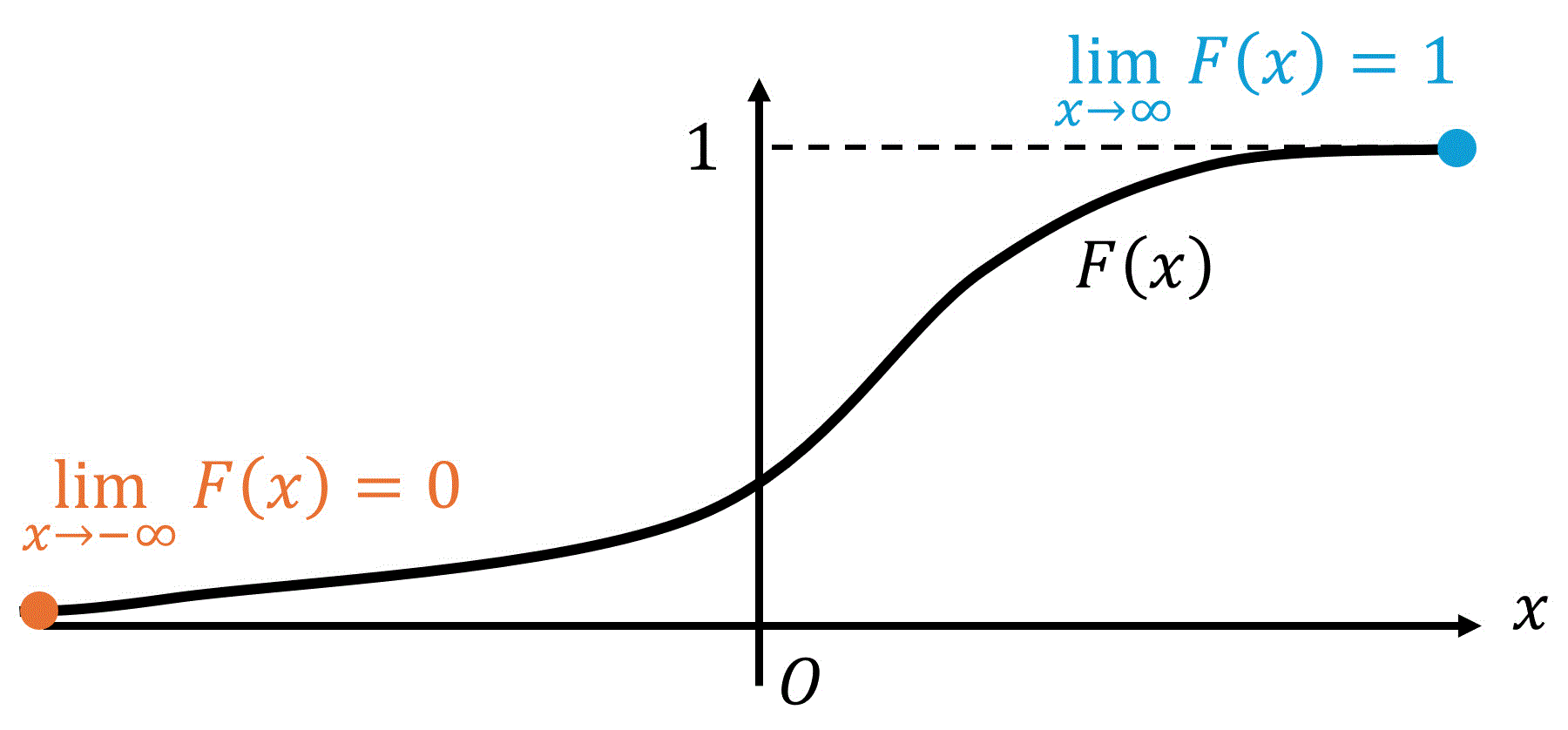
性質3. \( F(x) \) と極限
累積分布関数 \( F(x) \) では、つぎの2つの極限式が成り立ちます[1]直接試験で出てくることは少ないですが、求めた累積分布関数 \( F(x) \) が正しいかどうかの検算に使えます。。
[1]\[\lim_{x \to - \infty} F(x) = 0
\]解説: \( x \) が限りなく小さいときは、何も累積されていない状態なので、0となる。 [2]\[
\lim_{x \to \infty} F(x) = 1
\]解説: \( x \) が限りなく大きいときは、すべての確率密度 \( f(x) \) が累積されている状態のため、1となる。
この2つの性質は、図で見るとより分かりやすくなると思うので、図でも確認しましょう。
スポンサードリンク
3. 例題を解いてみよう
ここからは、実際に例題を解くことで、試験でよく出題される確率密度関数 \( f(x) \) と累積分布関数 \( F(x) \) の変換計算に慣れましょう。
例題1. 確率密度関数から累積分布関数への変換
確率変数 \( X \) の確率密度関数 \( f(x) \) が、つぎのように定義されている。\[\begin{align*}
f(x) = \left\{ \begin{array}{l}
0 \ & ( x < 0 ) \\
\frac{1}{4} \ & ( 0 \leqq x < 2 ) \\
\frac{1}{2} \ & ( 2 \leqq x < 3 ) \\
0 \ & ( 3 \leqq x )
\end{array}\right.
\end{align*}\]
このとき、累積分布関数 \( F(x) \) を求めなさい。
解説1
確率密度関数が
- \( x < 0 \) … [i]
- \( 0 \leqq x < 2 \) … [ii]
- \( 2 \leqq x < 3 \) … [iii]
- \( 3 \leqq x \) … [iv]
で分かれているので、この4つに場合分けして計算しましょう。
[i] \( x < 0 \) のとき\[\begin{align*}F(x) & = \int^{x}_{- \infty} f(t) \ dt
\\ & = \int^{x}_{- \infty} 0 \ dt
\\ & = 0
\end{align*}\]※ 試験では、わざわざ式で書かなくていいレベル。 [ii] \( 0 \leqq x < 2 \) のとき\[\begin{align*}
F(x) & = \int^{x}_{- \infty} f(t) \ dt
\\ & = \int^{0}_{- \infty} 0 \ dt + \int^{x}_{0} \frac{1}{4} \ dt
\\ & = 0 + \left[ \frac{1}{4} t \right]^{x}_{0}
\\ & = \frac{1}{4} x
\end{align*}\] [iii] \( 2 \leqq x < 3 \) のとき\[\begin{align*}
F(x) & = \int^{x}_{- \infty} f(t) \ dt
\\ & = \int^{0}_{- \infty} 0 \ dt + \int^{2}_{0} \frac{1}{4} \ dt + \int^{x}_{2} \frac{1}{2} \ dt
\\ & = 0 + \left[ \frac{1}{4} t \right]^{2}_{0} + \left[ \frac{1}{2} t \right]^{x}_{2}
\\ & = \left( \frac{1}{4} \cdot 2 - \frac{1}{4} \cdot 0 \right) + \left( \frac{1}{2} x - \frac{1}{2} \cdot 2 \right)
\\ & = \frac{1}{2} x - \frac{1}{2}
\end{align*}\] [iv] \( 3 \leqq x \) のとき\[\begin{align*}
F(x) & = \int^{x}_{- \infty} f(t) \ dt
\\ & = \int^{0}_{- \infty} 0 \ dt + \int^{2}_{0} \frac{1}{4} \ dt + \int^{3}_{2} \frac{1}{2} \ dt + \int^{x}_{3} 0 \ dt
\\ & = 0 + \left[ \frac{1}{4} t \right]^{2}_{0} + \left[ \frac{1}{2} t \right]^{3}_{2} + 0
\\ & = \left( \frac{1}{4} \cdot 2 - \frac{1}{4} \cdot 0 \right) + \left( \frac{1}{2} \cdot 3 - \frac{1}{2} \cdot 2 \right)
\\ & = \frac{1}{2} + \frac{1}{2}
\\ & = 1
\end{align*}\]※ 累積分布関数の性質として、\[
\lim_{x \to \infty} F(x) = 1
\]
よって、累積分布関数 \( F(x) \) は、\[\begin{align*}
F(x) = \left\{ \begin{array}{l}
0 \ & ( x < 0 ) \\
\frac{1}{4} x \ & ( 0 \leqq x < 2 ) \\
\frac{1}{2} x - \frac{1}{2} \ & ( 2 \leqq x < 3 ) \\
1 \ & ( 3 \leqq x )
\end{array}\right.
\end{align*}\]と計算できる。
例題2. 累積分布関数から確率密度関数への変換
確率変数 \( X \) の累積分布関数 \( F(x) \) が、つぎのように定義されている。\[\begin{align*}
f(x) = \left\{ \begin{array}{l}
0 \ & ( x < 0 ) \\
\frac{1}{4} x \ & ( 0 \leqq x < 1 ) \\
\frac{1}{4} x^2 \ & ( 1 \leqq x < 2 ) \\
1 \ & (2 \leqq x )
\end{array}\right.
\end{align*}\]
このとき、確率密度関数 \( f(x) \) を求めなさい。
解説2
累積分布関数が
- \( x < 0 \) … [i]
- \( 0 \leqq x < 1 \) … [ii]
- \( 1 \leqq x < 2 \) … [iii]
- \( 2 \leqq x \) … [iv]
で分かれているので、この4つに場合分けして計算しましょう。
[i] \( x < 0 \) のとき\[\begin{align*}f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left( 0 \right)
\\ & = 0
\end{align*}\]※ 試験では、わざわざ式で書かなくていいレベル。 [ii] \( 0 \leqq x < 1 \) のとき\[\begin{align*}
f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left( \frac{1}{4} x \right)
\\ & = \frac{1}{4}
\end{align*}\] [iii] \( 1 \leqq x < 2 \) のとき\[\begin{align*}
f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left( \frac{1}{4} x^2 \right)
\\ & = \frac{1}{2}x
\end{align*}\] [iv] \( 2 \leqq x\) のとき\[\begin{align*}
f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left( 0 \right)
\\ & = 0
\end{align*}\]※ 試験では、わざわざ書く必要なし。
よって、確率密度関数 \( f(x) \) は、\[\begin{align*}
f(x) = \left\{ \begin{array}{l}
0 \ & ( x < 0 ) \\
\frac{1}{4} \ & ( 0 \leqq x < 1 ) \\
\frac{1}{2} x \ & ( 1 \leqq x < 2 ) \\
0 \ & ( 2 \leqq x )
\end{array}\right.
\end{align*}\]と計算できる。
4. 練習問題にチャレンジ
それでは、累積分布関数の理解が出来ているか、実際に練習問題を解くことで確認しましょう!
練習1.
確率変数 \( X \) の確率密度関数 \( f(x) \) が、つぎのように定義されている。\[\begin{align*}
f(x) = \left\{ \begin{array}{l}
2 x e^{-x^2} \ & ( x \geqq 0 ) \\
0 \ & ( x < 0 )
\end{array}\right.
\end{align*}\]
このとき、累積分布関数 \( F(x) \) を求めなさい。
練習2.
確率変数 \( X \) の累積分布関数 \( F(x) \) が、つぎのように定義されている。\[\begin{align*}
f(x) = \left\{ \begin{array}{l}
0 \ & ( x < 1 ) \\
(x-1)^2 \ & ( 1 \leqq x < 2 ) \\
1 \ & (2 \leqq x )
\end{array}\right.
\end{align*}\]
(1) 確率密度関数 \( f(t) \) を求めなさい。
(2) 確率変数 \( X \) の期待値 \( E(X) \) を求めなさい。
(3) 確率変数 \( X \) の分散 \( V(X) \) を求めなさい。
5. 練習問題の答え
解答1
確率密度関数が
- \( x \geqq 0 \) … [i]
- \( x < 0 \) … [ii]
で分かれているので、この4つに場合分けして計算しましょう。
[i] \( x \geqq 0 \) のとき\[\begin{align*}F(x) & = \int^{x}_{- \infty} f(t) \ dt
\\ & = \int^{0}_{- \infty} 0 \ dt + \int^{x}_{0} 2te^{-t^2} \ dt
\\ & = 2 \int^{x}_{0} te^{-t^2} \ dt
\\ & = - \int^{x}_{0} -2t e^{-t^2} \ dt
\\ & = - \left[ e^{-t^2} \right]^{x}_{0}
\\ & = - \left( e^{-x^2} - e^{0^2} \right)
\\ & = - \left( e^{-x^2} - 1 \right)
\\ & = 1 - e^{-x^2}
\end{align*}\] [ii] \( x < 0 \) のとき\[\begin{align*}
F(x) & = \int^{x}_{- \infty} f(t) \ dt
\\ & = \int^{x}_{- \infty} 0 \ dt
\\ & = 0
\end{align*}\]※ 試験では、わざわざ式で書かなくていいレベル。
よって、累積分布関数 \( F(x) \) は、\[\begin{align*}
F(x) = \left\{ \begin{array}{l}
1 - e^{-x^2} \ & ( x \geqq 0 ) \\
0 \ & ( x < 0 )
\end{array}\right.
\end{align*}\]と計算できる。
※ [i]の積分が合っているか不安な人は、累積分布関数 \( F(x) \) の極限式\[
\lim_{x \to \infty} F(x) = 1
\]が成り立つか確認するのがおススメです。実際に計算してみると、\[\begin{align*}
\lim_{x \to \infty} F(x) & = \lim_{x \to \infty} 1 - e^{-x^2}
\\ & = 1 - \lim_{x \to \infty} e^{-x^2}
\\ & = 1 - 0
\\ & = 1
\end{align*}\]となり、問題ないことが分かります。
解答2
(1)
累積分布関数が
- \( x < 1 \) … [i]
- \( 1 \leqq x < 2 \) … [iii]
- \( 2 \leqq x \) … [iv]
で分かれているので、この4つに場合分けして計算する。
[i] \( x < 1 \) のとき\[\begin{align*}f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left( 0 \right)
\\ & = 0
\end{align*}\]※ 試験では、わざわざ式で書かなくていいレベル。 [ii] \( 1 \leqq x < 2 \) のとき\[\begin{align*}
f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left\{ (x-1)^2 \right\}
\\ & = \frac{d}{dx} \left( x^2 - 2x + 1 \right)
\\ & = 2x - 2
\end{align*}\] [iii] \( 2 \leqq x \) のとき\[\begin{align*}
f(x) & = \frac{d}{dx} F(x)
\\ & = \frac{d}{dx} \left( 0 \right)
\\ & = 0
\end{align*}\]※ 試験では、わざわざ式で書かなくていいレベル。
よって、確率密度関数 \( f(x) \) は、\[\begin{align*}
f(x) = \left\{ \begin{array}{l}
0 \ & ( x < 1 ) \\
2x-2 \ & ( 1 \leqq x < 2 ) \\
0 \ & ( 2 \leqq x )
\end{array}\right.
\end{align*}\]と計算できる。
(2)
確率密度関数 \( f(x) \) が求まっているので、求めた \( f(x) \) を、期待値の公式\[
E(X) = \int^{\infty}_{- \infty} x f(x) \ dx
\]に入れればOK。
実際に計算すると、\[\begin{align*}
E(X) & = \int^{\infty}_{- \infty} x f(x) \ dx
\\ & = \int^{1}_{- \infty} x \cdot 0 \ dx + \int^{2}_{1} x (2x-2) \ dx + \int^{\infty}_{2} x \cdot 0 \ dx
\\ & = \int^{2}_{1} 2x^2 - 2x \ dx
\\ & = 2 \int^{2}_{1} x^2 - x \ dx
\\ & = 2 \left[ \frac{1}{3} x^3 - \frac{1}{2} x^2 \right]^{2}_{1}
\\ & = 2 \left\{ \left( \frac{1}{3} \cdot 2^3 - \frac{1}{2} \cdot 2^2 \right) - \left( \frac{1}{3} \cdot 1^3 - \frac{1}{2} \cdot 1^2 \right) \right\}
\\ & = 2 \left\{ \left( \frac{8}{3} - 2 \right) - \left( \frac{1}{3} - \frac{1}{2} \right) \right\}
\\ & = 2 \left\{ \frac{2}{3} - \left( - \frac{1}{6} \right) \right\}
\\ & = 2 \cdot \frac{5}{6}
\\ & = \frac{5}{3}
\end{align*}\]と計算できる。
(3)
確率密度関数 \( f(x) \) を、分散の公式\[\begin{align*}
V(X) & = E(X^2) - \left[ E(X) \right]^2
\\ & = \int^{\infty}_{- \infty} x^2 f(x) \ dx - \left[ E(X) \right]^2
\end{align*}\]に入れればOK。
ここで、\[\begin{align*}
E(X^2) & = \int^{\infty}_{- \infty} x^2 f(x) \ dx
\\ & = \int^{1}_{- \infty} x^2 \cdot 0 \ dx + \int^{2}_{1} x^2 (2x-2) \ dx + \int^{\infty}_{2} x^2 \cdot 0 \ dx
\\ & = \int^{2}_{1} 2x^3 - 2x^2 \ dx
\\ & = 2 \int^{2}_{1} x^3 - x^2 \ dx
\\ & = 2 \left[ \frac{1}{4} x^4 - \frac{1}{3} x^3 \right]^{2}_{1}
\\ & = 2 \left\{ \left( \frac{1}{4} \cdot 2^4 - \frac{1}{3} \cdot 2^3 \right) - \left( \frac{1}{4} \cdot 1^4 - \frac{1}{3} \cdot 1^3 \right) \right\}
\\ & = 2 \left\{ \left( 4 - \frac{8}{3} \right) - \left( \frac{1}{4} - \frac{1}{3} \right) \right\}
\\ & = 2 \left\{ \frac{4}{3} - \left( - \frac{1}{12} \right) \right\}
\\ & = 2 \cdot \frac{17}{12}
\\ & = \frac{17}{6}
\end{align*}\]と計算できるので、分散は、\[\begin{align*}
V(X) & = E(X^2) - \left[ E(X) \right]^2
\\ & = \frac{17}{6} - \left( \frac{5}{3} \right)^2
\\ & = \frac{17}{6} - \frac{25}{9}
\\ & = \frac{51}{18} - \frac{50}{18}
\\ & = \frac{1}{18}
\end{align*}\]と計算できる。
6. まとめ
最後に、累積分布関数 \( F(x) \) で出てきた公式たちを振り返りましょう。
1.累積分布関数 \( F(x) \) は、確率密度関数 \( f(x) \) をある値 \( x \) まで積分することで求められる。\[
F(x) = \int^{x}_{- \infty} f(t) \ dt
\]※ \( f(t) \) は、確率密度関数 \( f(x) \) の \( x \) を \( t \) におきかえた関数。
2.累積分布関数 \( F(x) \) が分かれば、ある値 \( x \) における確率密度関数 \( f(x) \) は、累積分布関数 \( F(x) \) を微分することで求められる。\[
f(x) = \frac{d}{dx} F(x)
\]
3.累積分布関数は、必ず \( 0 \leqq F(x) \leqq 1 \) となる。
4.累積分布関数 \( F(x) \) は単調増加である。つまり、\[
x_1 < x_2 \to F(x_1) \leqq F(x_2)
\]が必ず成り立つ。
5.累積分布関数の極限値について、次の式が成立する。\[
\lim_{x \to - \infty} F(x) = 0 , \ \ \ \lim_{x \to \infty} F(x) = 1
\]
注釈
| ↑1 | 直接試験で出てくることは少ないですが、求めた累積分布関数 \( F(x) \) が正しいかどうかの検算に使えます。 |
|---|
関連広告・スポンサードリンク