スポンサードリンク
サイコロを使ったゲームって色々ありますよね。すごろく、桃鉄、TRPG、チンチロリン、色々あります。
その中で、相手の人が降った出目がやたら良かったら「この人イカサマなサイコロ使ってるんじゃね?」と思うこと、ありますよね。
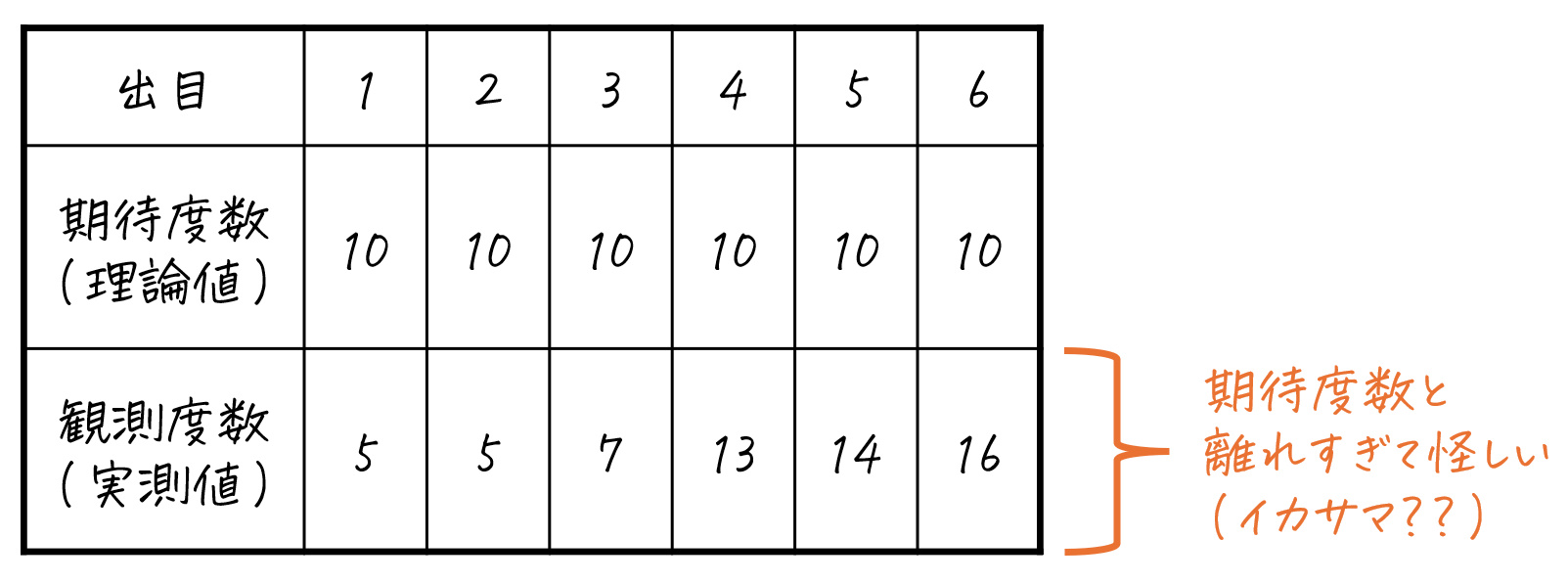
表1. サイコロを60回振ったときの期待度数(理論値)と実際の観測度数の例

今回は、「この人あきらかにイカサマしてるだろ!」というのを、数値で表すための指標である適合度と、適合度を使った検定の仕方について、一緒に勉強していきましょう。
この検定法が分かると、「この人は不正をしている」というのが、数学的に言えるようになりますよ!
スポンサードリンク
1. 適合度ってなに?
まずは、「適合度ってなんだ?」というところから始めましょう。
例えば、サイコロの出目を考えてみましょう。
理論的には、サイコロ振ったときの出目は、1, 2, 3, 4, 5, 6 すべて同じ確率で出てきます。つまり、6回に1回はそれぞれの目が出てきます。(=どの目も出る確率は1/6である。)
表2. 理論的なサイコロにおいて、各目の出る確率
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 | \( \frac{1}{6} \) | \( \frac{1}{6} \) | \( \frac{1}{6} \) | \( \frac{1}{6} \) | \( \frac{1}{6} \) | \( \frac{1}{6} \) |
例えば、60回サイコロを振った場合、理論的には各目が10回(60回×1/6=10回)ずつ出てきます。
表3. サイコロを60回振ったとき、各目が出る理論的な回数
(各目ごとの期待度数)
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 期待度数 | 10 | 10 | 10 | 10 | 10 | 10 |
しかし、現実世界では「どの目も同じ確率で出る」なんてことはありません。たまたま1が多かったり、3が多かったりするなんてこともあります。
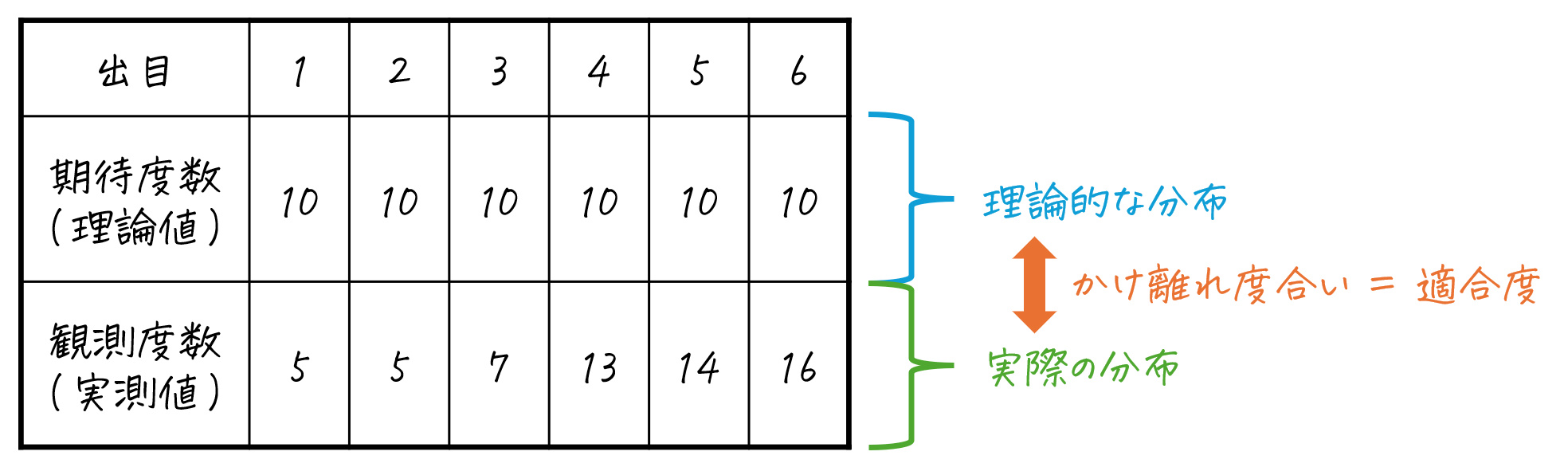
この「理論値(理想的な分布)」と「現実世界のデータ(実際の分布)」のズレを測るのが適合度という指標なのです。
スポンサードリンク
2. 適合度の定義
つぎに、適合度が、どのように定義されるかを見ていきましょう。
Step1. 各事象ごとに、次のデータを求める
- 期待度数 … 理論的に何回事象が起こるか
(期待値、理論値とも呼ばれる) - 観測度数 … 実際に事象が起こった回数
(実測値とも呼ばれる)
Step2.残差を2乗したものを、期待値で割る
※ 残差は、実測度数と期待度数の差(実測度数-期待度数)のことを言います。
Step3. 各事象ごとに求めた Step2 の値の和を取ったものが、適合度である。
【数式表記】
適合度 \( \chi^2 \) \[
\chi^2 = \sum^{n}_{k = 1} \frac{ (O_k - E_k)^2 }{ E_k }
\]
※ \( E_k \): \( k \) カテゴリ目の期待度数
※ \( O_k \): \( k \) カテゴリ目の観測度数
実際に上の定義に従って、1つ適合度を計算してみましょう。
例えば、サイコロを60回振ったとき、各出目の出た回数が下の表で与えられたとします。
表2. サイコロを60回振ったときの、各出目の出た回数(実際の分布)
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 回数 | 5 | 5 | 7 | 13 | 14 | 16 |
この表から、サイコロを60回振ったときの適合度 \( \chi^2 \) を計算します。
まず、サイコロを60回振ったとき、理論的に各出目が何回くらい出るか(=期待度数)を求めます。
期待度数は、(試行回数)×(確率)で求められるので、各目の出る回数の理論値は\[
60 \times \frac{1}{6} = 10
\]と求められます。
つぎに、各出目ごとに出た目の回数(観測度数)を使って、残差(観測度数-期待度数)を2乗して、期待度数で割ったものを求めていきます。
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 観測度数 | 5 | 5 | 7 | 13 | 14 | 16 |
| 期待度数 | 10 | 10 | 10 | 10 | 10 | 10 |
| 残差 | -5 | -5 | -3 | 3 | 4 | 6 |
| 残差2 | 25 | 25 | 9 | 9 | 16 | 36 |
| 残差2÷期待度数 | 2.5 | 2.5 | 0.9 | 0.9 | 1.6 | 3.6 |
最後に、各目で求めた残差2÷期待度数をすべて足せば、適合度が求められます。
途中式を数式で書くと、こんな感じです。\[\begin{align*}
\chi^2 & = \frac{ (5-10)^2 }{10} + \frac{ (5-10)^2 }{10} + \frac{ (7-10)^2 }{10} + \frac{ (13-10)^2 }{10} + \frac{ (14-10)^2 }{10} + \frac{ (16-10)^2 }{10}
\\ & = \frac{25}{10} + \frac{25}{10} + \frac{9}{10} + \frac{9}{10} + \frac{16}{10} + \frac{36}{10}
\\ & = 2.5 + 2.5 + 0.9 + 0.9 + 1.6 + 3.6
\\ & = 12.0
\end{align*}\]
スポンサードリンク
3. 適合度検定とカイ2乗分布
適合度についての求め方を紹介したので、いよいよ「この人あきらかにイカサマしてるだろ!(=理論的な分布とはかけ離れている)」というのを証明するための方法、適合度検定について見ていきましょう。
【適合度検定の流れ】
- ある基準となる確率(有意水準) \( \alpha \) を設定する。
※ 問題文に与えられている。 - 実際の分布となる確率と、基準値 \( \alpha \) を比べて、採択/棄却を決定する。
- 採択 … 実際に起こった現象が起こる確率 ≧ \( \alpha \)
→ 理論的な分布と一致していないとは言えない。(偶然の範囲内であり、イカサマとは言えない。) - 棄却 … 実際に起こった現象が起こる確率 < \( \alpha \)
→ 理論的な分布と一致していないといえる。(イカサマである。)
- 採択 … 実際に起こった現象が起こる確率 ≧ \( \alpha \)
ここで確率を比べる際には、適合度 \( \chi^2 \) が自由度 \( n - 1 \) のカイ2乗分布に従うことを利用します。
適合度 \( \chi^2 \) \[
\chi^2 = \sum^{n}_{k = 1} \frac{ (O_k - E_k)^2 }{ E_k }
\]は、自由度 \( n-1 \) のカイ2乗分布に従う。
※ \( n \) はカテゴリ数です。例えば、サイコロの出目の場合は、1~6の出目があるので、カテゴリ数 \( n = 6 \) となります。
【自由度が \( n-1 \) となる理由】
観測度数の合計値が分かれば、1カテゴリの観測値が分からなくても、合計値から逆算出来るからです。
例えば、サイコロの各出目がこんな感じであったとします。
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 | 合計 |
| 回数 | 5 | 5 | ★ | 13 | 14 | 16 | 60 |
このとき、★の値が分からなくても "合計" から各出目ごとの出た回数から、\[
60 - (5+5+13+14+16) = 7
\]と復元することが出来ます。
そのため、復元できる1カテゴリには情報量がないと考えられ、自由度が \( n-1 \) となります。
【適合度検定は、どんなときに使う?】
分布全体に着目して、その分布が理論的な分布とかけ離れている or 偶然の誤差であるかを判定します。
例) サイコロの例の場合、イカサマサイコロかどうかを判定するために、各出目ごとの出た回数すべてに着目して判定したい場合に使用[1]ある出目1つの出た回数に着目する場合は、母比率の検定などで可能。。
適合度検定では、実際の分布が起こる確率が有意水準 \( \alpha \) 未満かどうかを、カイ2乗値で比べる。
【用意するもの】
- 計算した適合度 \( \chi^2 \)
- 有意水準 \( \alpha \)、自由度 \( n-1 \) に対応するカイ2乗値 \( \chi_0^2 \)
※ \( n \) はカテゴリ数
【カイ2乗値での比べ方】
- \( \chi^2 \leqq \chi_0^2 \) のとき
→ 実際の分布が起こる確率は、有意水準 \( \alpha \) 以上である。
→ 仮定は採択され、理論的な分布と一致していないとは言えない。(イカサマとは言えない。) - \( \chi^2 > \chi_0^2 \) のとき
→ 実際の分布が起こる確率は、有意水準 \( \alpha \) 未満である。
→ 仮定は棄却され、理論的な分布と一致していないと言える。(イカサマと言える。)
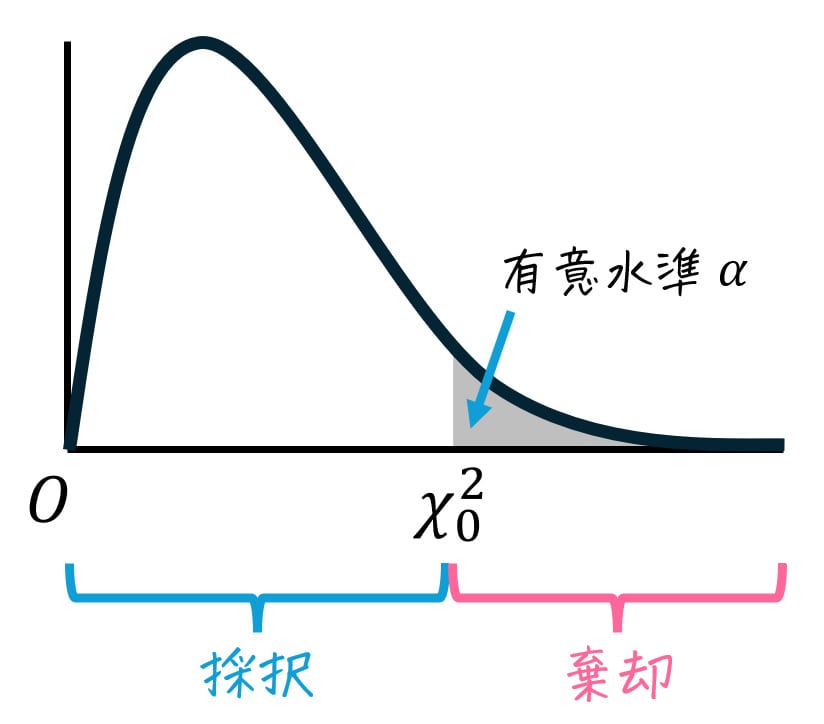
※ 適合度検定は、必ず片側検定となります。
【適合度検定が、必ず片側検定となる理由】
適合度検定では、理論的な分布と実際の分布のズレが「偶然の範囲内」か「理論分布とあっていないか」を確認する検定です。
ここで、適合度(カイ2乗値)の大小は、次の意味を持っています。
- 適合度が小さい(0に近い) … 理論分布に近い状態
- 適合度が大きい(0から遠い)… 理論分布から離れた状態
そのため、適合度が小さい状態は問題がなく、適合度が大きい状態のときのみ問題があると言えます。
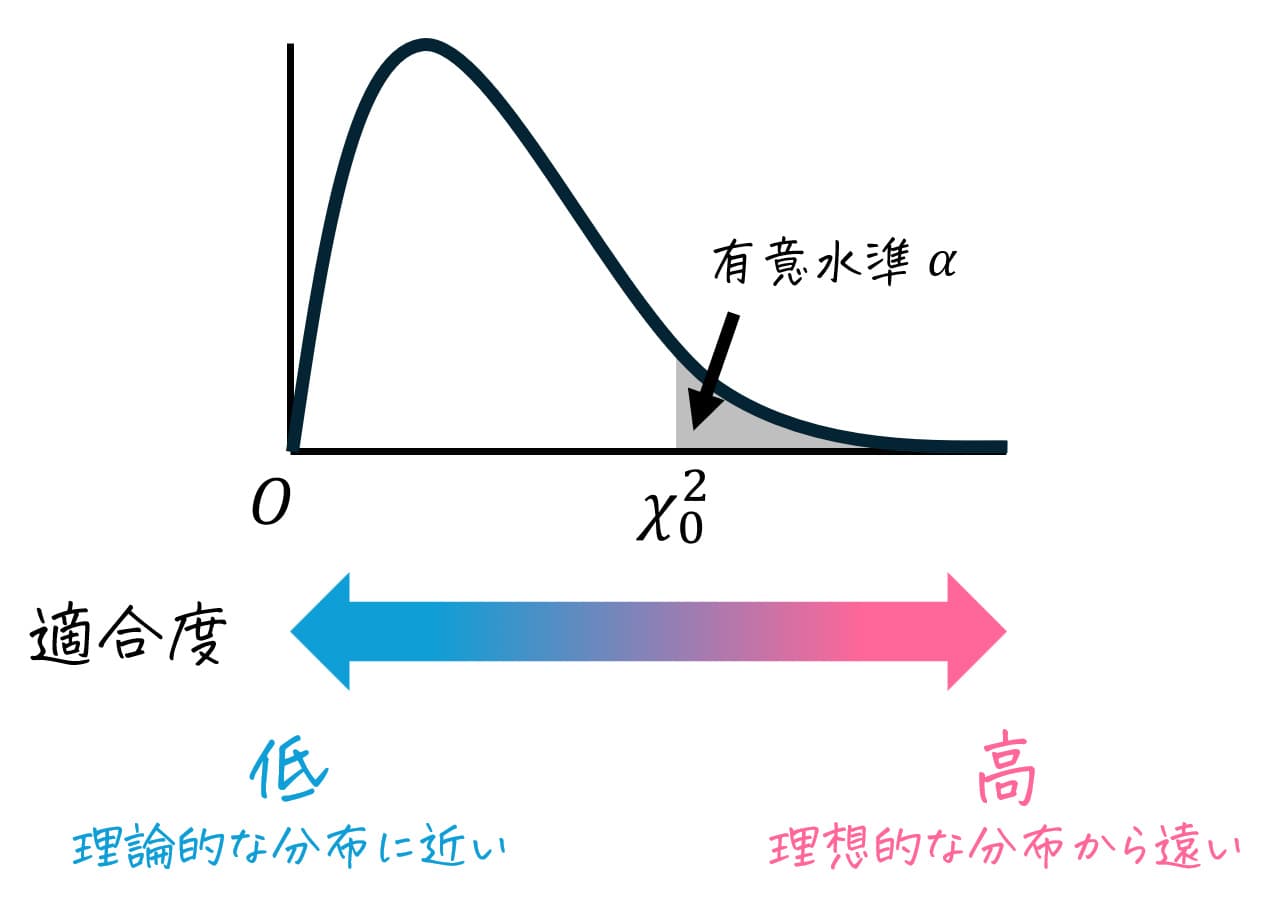
よって、適合度検定では必ず片側検定となるのです。
4. 例題にチャレンジ!
では、例題で実際に適合度検定をしてみましょう。
上田くんと、岡本さんは、サイコロを振って遊ぶゲームをした。
ゲームを振り返る際に、岡本さんが振った60回のサイコロの出目を確認したところ、以下の結果であった。
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 回数 | 5 | 5 | 7 | 13 | 14 | 16 |
※ 2章の説明で使った、サイコロの各出目と同じです。
ここで、岡本さんが振ったサイコロがまともなサイコロ(=イカサマなサイコロ)かどうかを検証したい。つぎの問いに答えなさい。
(1) 帰無仮説 \( H_0 \) と対立仮説 \( H_1 \) を述べなさい。
(2) この検証をするために必要な分布を答えなさい。(自由度がある分布の場合、自由度も答えること。)
(3) 有意水準5%で、結論(採択/棄却)を述べなさい。理由も書くこと。
※ 必要であれば、以下のリンクからカイ2乗分布表をダウンロードしてください。
解説
(1)
帰無仮説 \( H_0 \) : 岡本さんが振ったサイコロはまともなサイコロである。
→ 岡本さんが振ったサイコロの各目が出る確率は、すべて 1/6。
対立仮説 \( H_1 \) : 岡本さんが振ったサイコロはまともなサイコロではない。
→ 岡本さんが振ったサイコロの各目が出る確率が「すべて 1/6」とはいえない。
※ 帰無仮説 \( H_0 \) は、仮説検定をするにあたって立てる仮定なので、「各目の出る確率が 1/6(=サイコロがまとも)」としないと、適合度の計算が出来ない[2]サイコロがまともと仮定したときの確率を、期待度数として計算し、観測度数と期待度数のかけ離れ度合いを適合度として出している。。
(2)
今回は、サイコロの各出目に着目(=分布に着目)しているため、適合度検定を実施します。
また、カテゴリ数は6(サイコロの出目は1~6)ですね。なので、自由度は 6 - 1 = 5 です。
よって、答えは「自由度5のカイ2乗分布」となります。
(3)
次の流れで、適合度を計算していきます。
- Step1. 適合度 \( \chi^2 \) を計算する。
- Step2. 有意水準 \( \alpha = 0.05 \) [5%]、自由度5に相当するカイ2乗値 \( \chi^2_0 \) をカイ2乗分布表から求める。
- Step3. \( \chi^2 \) と \( \chi_0^2 \) を比べ、採択/棄却を決定する。
- \( \chi^2 \leqq \chi_0^2 \) → 仮説は採択。(サイコロはまともではないとは言えない。ただの偶然)
- \( \chi^2 > \chi_0^2 \) → 仮説は棄却。(サイコロはまともでないといえる。)
Step1. 適合度 \( \chi^2 \) の計算(2章と同じ計算)
各出目ごとに出た目の回数(観測度数)を使って、残差(観測度数-期待度数)を2乗して、期待度数で割ったものを求めていきます。
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 観測度数 | 5 | 5 | 7 | 13 | 14 | 16 |
| 期待度数 | 10 | 10 | 10 | 10 | 10 | 10 |
| 残差 | -5 | -5 | -3 | 3 | 4 | 6 |
| 残差2 | 25 | 25 | 9 | 9 | 16 | 36 |
| 残差2÷期待度数 | 2.5 | 2.5 | 0.9 | 0.9 | 1.6 | 3.6 |
あとは、各目ごとに求めた残差2÷期待度数をすべて足せば、OKです。\[\begin{align*}
\chi^2 & = \frac{ (5-10)^2 }{10} + \frac{ (5-10)^2 }{10} + \frac{ (7-10)^2 }{10} + \frac{ (13-10)^2 }{10} + \frac{ (14-10)^2 }{10} + \frac{ (16-10)^2 }{10}
\\ & = \frac{25}{10} + \frac{25}{10} + \frac{9}{10} + \frac{9}{10} + \frac{16}{10} + \frac{36}{10}
\\ & = 2.5 + 2.5 + 0.9 + 0.9 + 1.6 + 3.6
\\ & = 12.0
\end{align*}\]
Step2. カイ2乗表から読み取り
有意水準 \( \alpha = 0.05 \) [5%]、自由度5に相当するカイ2乗値 \( \chi^2_0 \) をカイ2乗分布表から読み取ります。
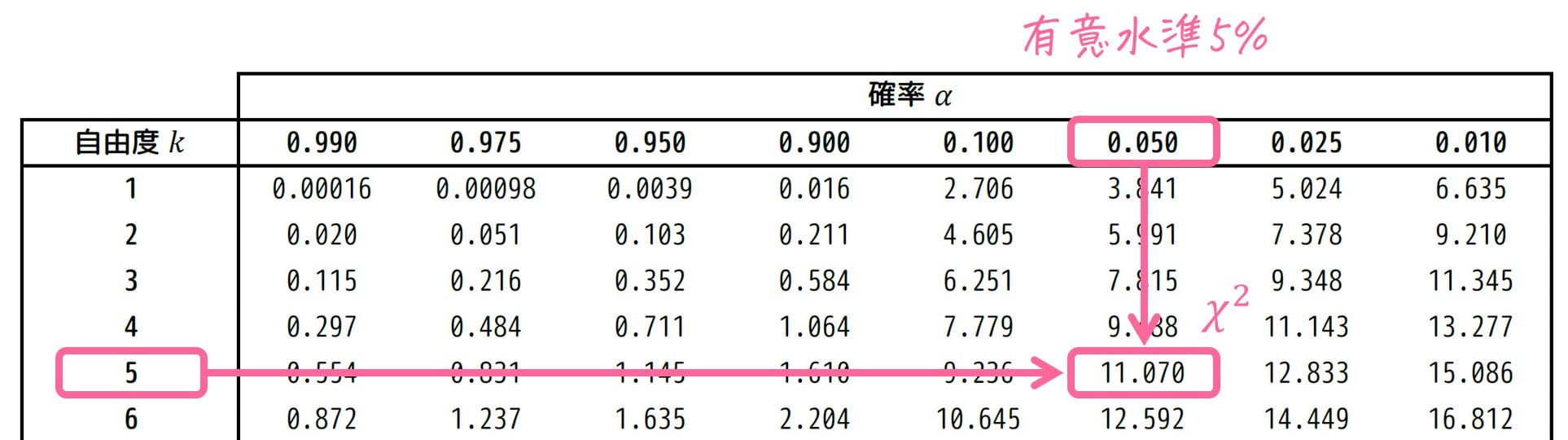
結果、11.070 と読み取れます。\( \chi^2_0 = 11.070 \) としましょう。
Step3. 採択/棄却の決定
適合度 \( \chi^2 = 12.000 \)、有意水準 \( \alpha = 0.05 \) [5%]、自由度5に相当するカイ2乗値 \( \chi^2_0 = 11.070 \) より、\[
\chi^2 = 12.000 > 11.070 = \chi^2_0
\]となります。
よって、仮説は棄却され、岡本さんが振ったサイコロはまともではない(=イカサマサイコロである)といえます。
5. 練習問題にチャレンジ!
では、最後に練習問題を解いて、適合度検定が理解できているか確認しましょう。
日本人の血液型の分布は、A型が40%、O型は30%、B型が20%、AB型が10%と言われている。
ここで、ある学年100人の血液型を調べたところ、以下の結果となった。
| 血液型 | A | O | B | AB |
| 人数 | 32 | 24 | 26 | 18 |
ここで、ある学生100人の血液型データは、日本人の血液型の分布とかけ離れていると言えるか、確認したい。
(1) 帰無仮説 \( H_0 \) と対立仮説 \( H_1 \) を述べなさい。
(2) この検証をするために必要な分布を答えなさい。(自由度がある分布の場合、自由度も答えること。)
(3) 有意水準1%で、結論(採択/棄却)を述べなさい。理由も書くこと。
※ 必要であれば、以下のリンクからカイ2乗分布表をダウンロードしてください。
6. 練習問題の答え
(1)
帰無仮説 \( H_0 \) : 学生100人の血液型データは、日本人の血液型分布と同じと言える。
→ 血液型分布は、A型が40%(100人中40人)、O型は30%(100人中30人)、B型が20%(100人中20人)、AB型が10%(100人中10人)
対立仮説 \( H_1 \) : 学生100人の血液型データは、日本人の血液型分布とはかけ離れている。
※ 血液型分布が、A型が40%、O型は30%、B型が20%、AB型が10%と仮定して、適合度を計算し、仮説検定をします。
(2)
血液型データの分布に着目しているため、適合度検定を実施します。
カテゴリ数は4(A型、O型、B型、AB型)ですね。なので、自由度は 4 - 1 = 3 です。
よって、答えは「自由度3のカイ2乗分布」となります。
(3)
Step1. 適合度 \( \chi^2 \) の計算(2章と同じ計算)
各出目ごとに出た目の回数(観測度数)を使って、残差(観測度数-期待度数)を2乗して、期待度数で割ったものを求めていきます。
| 出目 | A | O | B | AB |
| 観測度数 | 32 | 24 | 26 | 18 |
| 期待度数 | 40 | 30 | 20 | 10 |
| 残差 | -8 | -6 | 6 | 8 |
| 残差2 | 64 | 36 | 36 | 64 |
| 残差2÷期待度数 | 1.6 | 1.2 | 1.8 | 6.4 |
あとは、各目ごとに求めた残差2÷期待度数をすべて足せば、OKです。\[\begin{align*}
\chi^2 & = \frac{ (32-40)^2 }{40} + \frac{ (24-30)^2 }{30} + \frac{ (26-20)^2 }{20} + \frac{ (18-10)^2 }{10}
\\ & = \frac{ 64 }{40} + \frac{ 36 }{30} + \frac{ 36 }{20} + \frac{ 64 }{10}
\\ & = 1.6 + 1.2 + 1.8 + 6.4
\\ & = 11.0
\end{align*}\]
Step2. カイ2乗表から読み取り
有意水準 \( \alpha = 0.01 \) [1%]、自由度3に相当するカイ2乗値 \( \chi^2_0 \) をカイ2乗分布表から読み取ります。
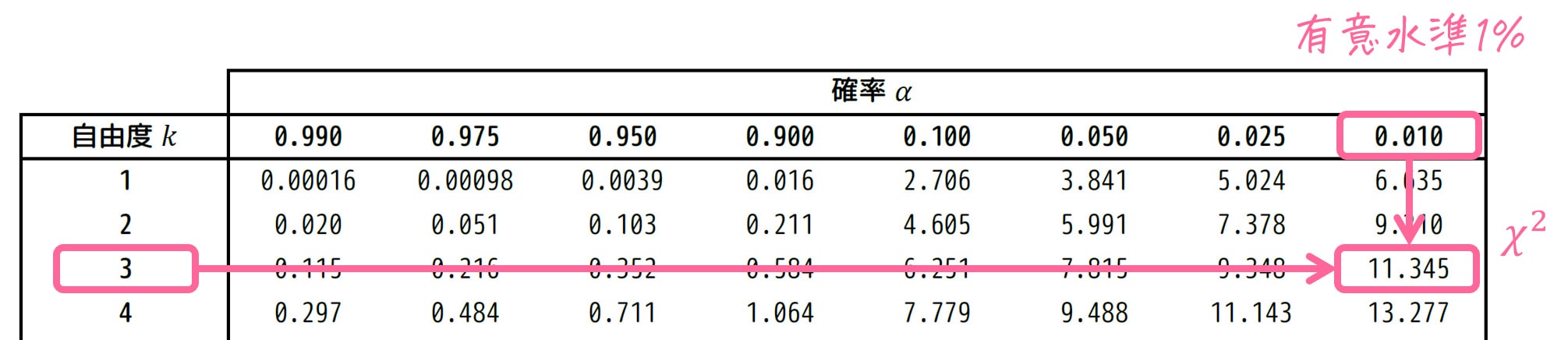
結果、11.345 と読み取れます。\( \chi^2_0 = 11.345 \) としましょう。
Step3. 採択/棄却の決定
適合度 \( \chi^2 = 11.000 \)、有意水準 \( \alpha = 0.01 \) [1%]、自由度5に相当するカイ2乗値 \( \chi^2_0 = 11.345 \) より、\[
\chi^2 = 11.000 \leqq 11.345 = \chi^2_0
\]となります。
よって、仮説は採択され、ある学生100人の血液型データは、日本人の血液型の分布とかけ離れていない(離れ具合は偶然の範囲内)と言えます。
7. さいごに
これで、サイコロ勝負で相手がイカサマなサイコロを持ってきたときでも、「このサイコロはいかさまだ!」と数学的に示すことが出来ますね。
もしイカサマだと思ったときは、適合度検定をしてみてください。
関連広告・スポンサードリンク