スポンサードリンク
こんにちは、ももやまです。
今日はカイ2乗分布で出てくる頻出テーマ「独立性の検定」についてお勉強していきましょう!
学習すると、下のような問題を解けるようになります!
表.行の属性(彼女の有無)と列の属性(工業大学 or 普通の大学)は関連がある? or 独立?

独立性の検定は、適合度検定と計算の流れが似ている部分も多いので、適合度検定をまだ勉強していない(or 理解があやふや)な人は、下の記事で適合度検定の復習をしてから、独立性の検定について学習することをおすすめします。
目次
スポンサードリンク
1. 独立性の検定の流れ
まずは、独立性の検定のフローを簡単に確認しましょう。(適合度検定と似ている部分も多いです。)
※ 詳細な計算方法は、概要の下に記述しています。
Step1. 帰無仮説/対立仮説を立てる
以下のように帰無仮説(問題を解くための仮定)、対立仮説(仮定を否定して示したいもの)をたてる。
- 帰無仮説:与えられた2つの分類は独立である(=関連がない)。
- 対立仮説:与えられた2つの分類は独立ではない(=関連がある)。
Step2. 期待度数(理論値)の計算
独立であるという仮定を元に、期待度数(理論値)を計算する。
(完全に独立である場合に、各セルの値がどうなるか求める。)
※ セルは、下の図のように表の「行属性のカテゴリ」と「列属性のカテゴリ」の交差する部分のデータをさします。
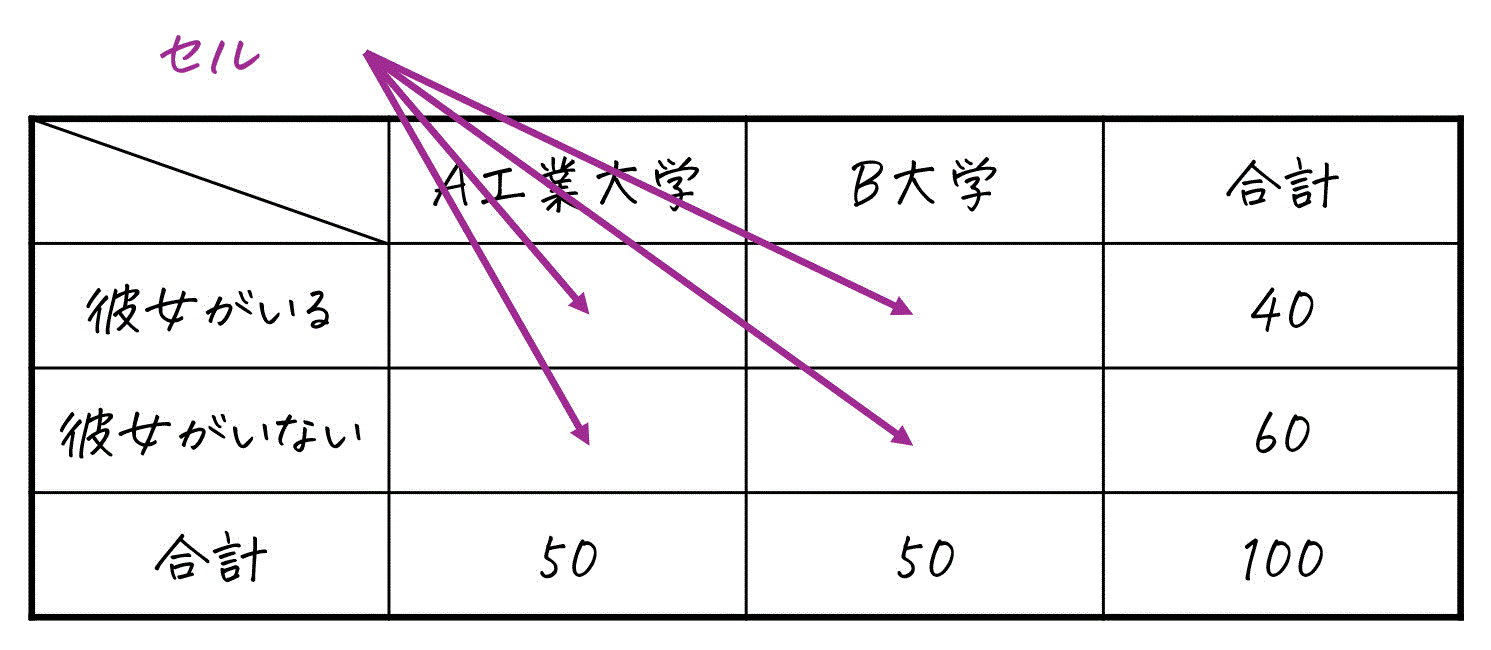
Step3. ズレの度合い(独立度と呼びます)の計算
完全に独立なデータと実際のデータのズレの度合い(=独立度)を、各セルごとに求める。
Step4. 採択/棄却の境界
独立度がカイ2乗分布に従うことを利用して、独立度に対応する自由度、および有意水準を、カイ2乗分布表から読み取る。
Step5. 結果(採択/棄却)の確認
Step3, Step4の結果を比較し、仮定が否定できない(採択) or 仮定が否定できる(棄却)の結論を出す。
実際に検定の流れでどのようなことをするか、冒頭で出した題材を例題としたものを、説明していきましょう。
工業大学生がモテないというのは、噂でも実際の会話でもたまに耳とする。そこで、この話題は本当かどうか検証してみることにした。
具体的には、あるA工業大学の大学生50人と、工業大学ではないあるB大学生の大学生50人に、「今彼女がいるか、いないか」をアンケートで調査した。
調査の結果、以下の結果が得られた。
| A工業大学 | B大学 | 合計 | |
| 彼女がいる | 16 | 24 | 40 |
| 彼女がいない | 34 | 26 | 60 |
| 合計 | 50 | 50 | 100 |
この結果から、工業大学生かそうでないかが、彼女の有無と独立であるか否かを有意水準10%で仮説検定し、結果を示しなさい。
Step1. 帰無仮説/対立仮説を立てる
独立性の検定では、「与えられた2つの属性が独立(=関連がない)」という仮定をしてから、仮定を否定出来るか出来ないかを判定します。
- 帰無仮説 \( H_0 \):与えられた2つの属性は独立である(=関連がない)。
- 対立仮説 \( H_1 \):与えられた2つの属性は独立ではない(=関連がある)。
今回の例だと、与えられた2つの属性は、
- 彼女の有無(彼女がいる/彼女がいない)
- 大学の違い(A工業大学/B大学)
となりますね。
Step2. 期待度数(理論値)の計算
つぎに、与えられたデータの2つの分類が完全に独立と仮定した際に、各セルでどれくらいの値となるか(=理論値)を計算します。
※ このステップは、適合度検定のときに比べると少し複雑になるため、丁寧に説明します。
つぎに、与えられたデータの2つの分類が独立と仮定した際に、各セルでどれくらいの値となるか(=理論値)を計算します。
では実際に、記事の冒頭で出したこのデータを例に、各セルごとの期待度数を計算してみましょう。
| A工業大学 | B大学 | 合計 | |
| 彼女がいる | 16 | 24 | 40 |
| 彼女がいない | 34 | 26 | 60 |
| 合計 | 50 | 50 | 100 |
期待度数を計算する際には、「片方の属性の合計に着目。着目した合計を、片方の属性の各カテゴリごとの割合ごとに振り分ける」ということをします。
例えば、上の表の例の場合、大学という分類(A工業大学/B大学)に着目してみます。
ここで、A工業大学の人数: B大学の人数 = 50:50 = 1:1 ですね。
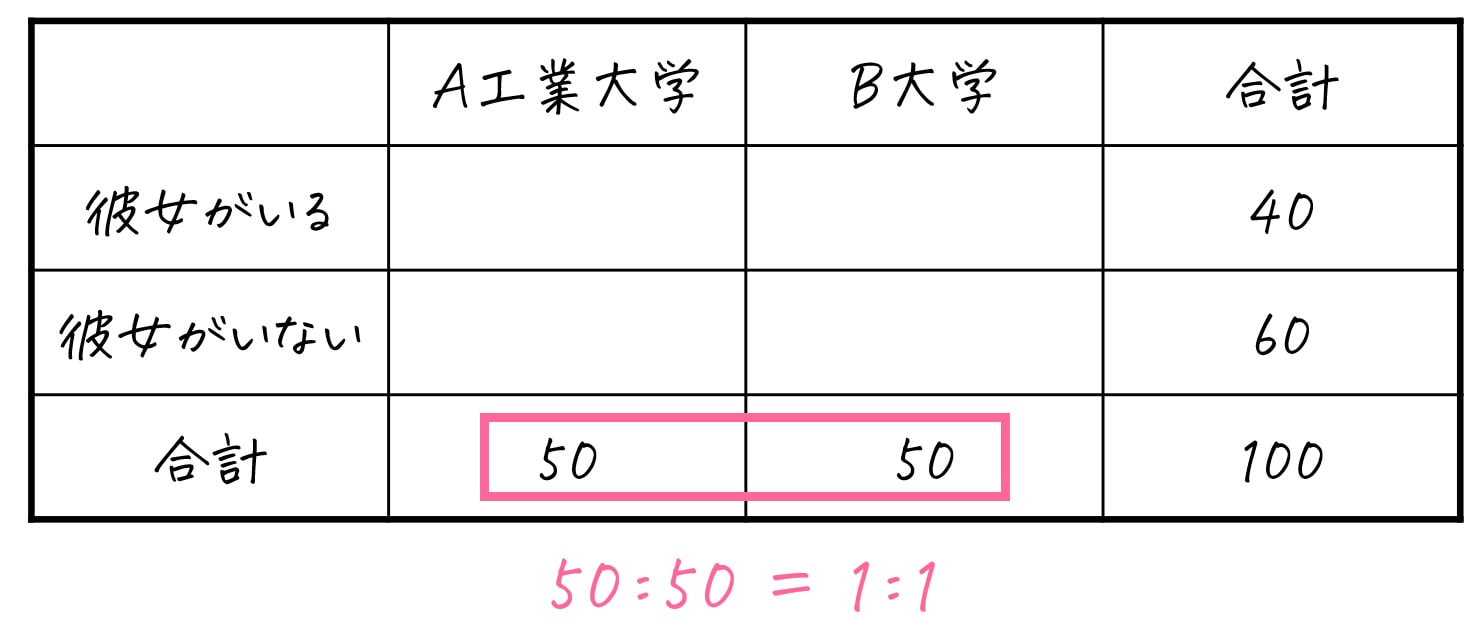
なので、彼女がいる場合(40人)、彼女がいない場合(60人)について、A工業大学: B工業大学 = 1:1 となるように振り分けます。
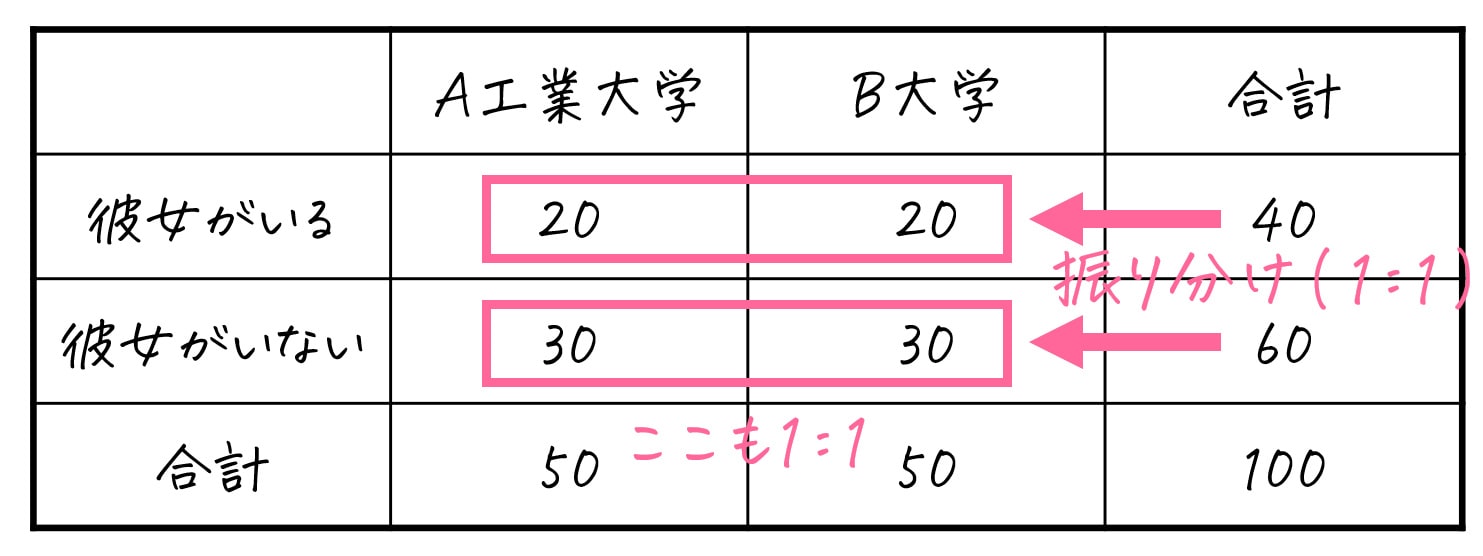
これで、各セルごとの期待度数を出すことが出来ます。
もちろん、彼女の有無(彼女がいる/彼女がいない)に着目してもOKです。
この場合、彼女がいる: 彼女がいない = 40:60 = 2:3 ですね。
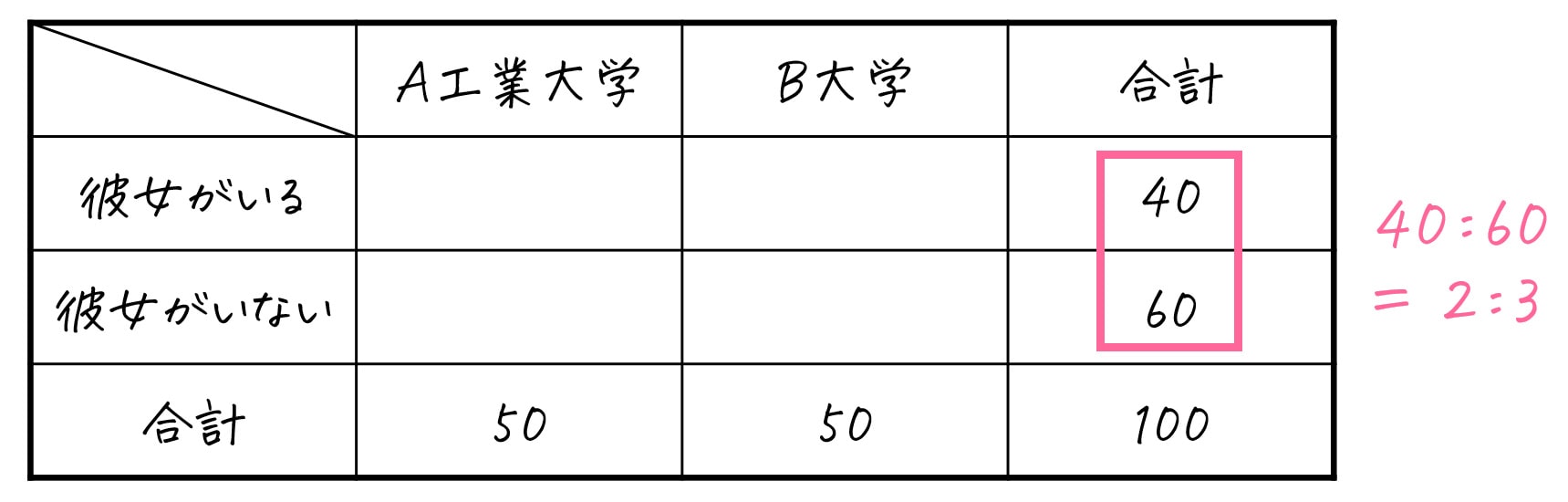
なので、A工業大学(50人)、B工業大学(50人)のそれぞれを、彼女がいる:彼女がいない = 2:3 で振り分ければOKです。
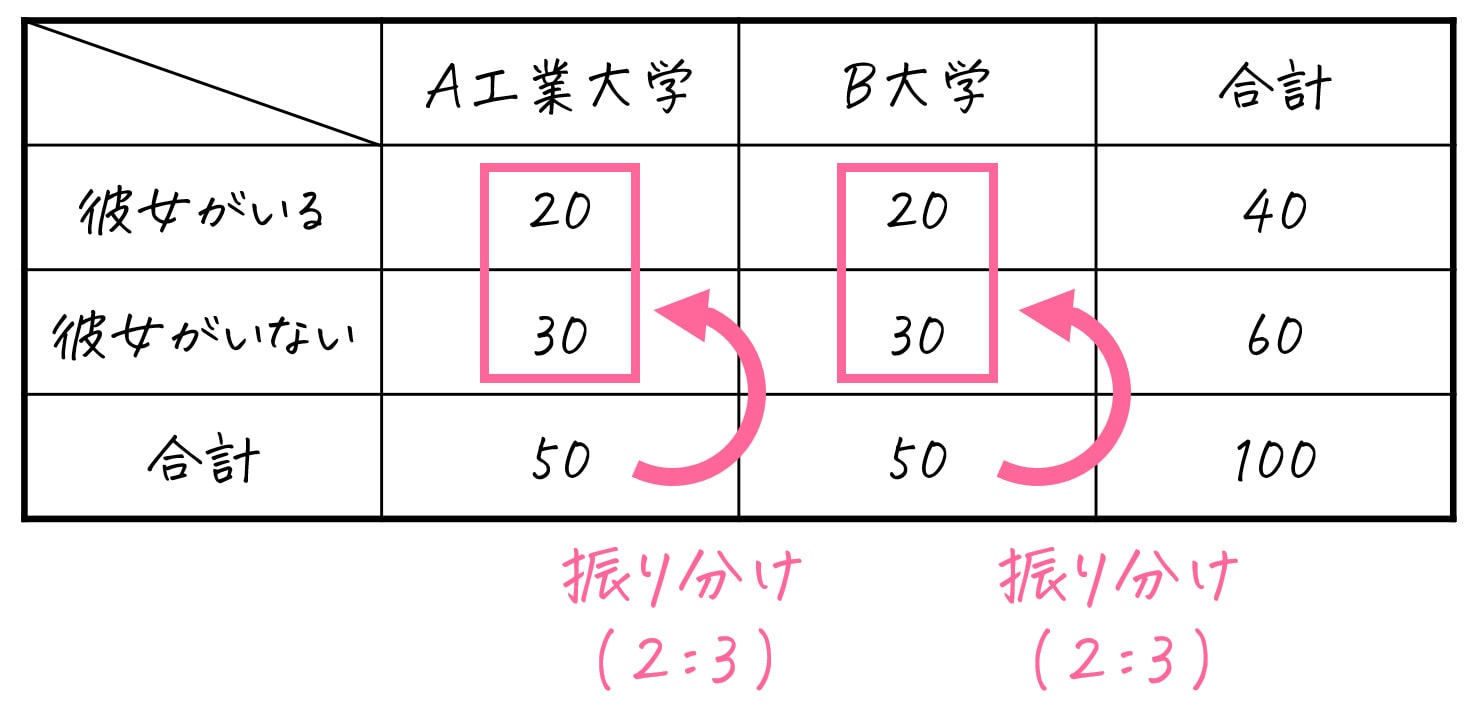
期待度数の計算を、一般化して公式化しておきます。
下のようなクロス集計表で与えられるデータがある。
| カテゴリ | 列1 | 列2 | … | 列n | 合計 |
| 行1 | \( O_{11} \) | \( O_{12} \) | … | \( O_{1n} \) | \( R_1 \) |
| 行2 | \( O_{21} \) | \( O_{22} \) | … | \( O_{2n} \) | \( R_2 \) |
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | ⋮ |
| 行m | \( O_{m1} \) | \( O_{m2} \) | … | \( O_{mn} \) | \( R_m \) |
| 合計 | \( C_1 \) | \( C_2 \) | … | \( C_n \) | \( N \) |
このとき、あるセルの期待度数 \( E_{ij} \) は、次のように計算できる。\[
E_{ij} = R_i \cdot \frac{C_j}{N}
\]※ 行 \( i \) カテゴリの合計値 \( R_i \) を、列 \( j \) カテゴリが占める割合 \( \frac{C_j}{N} \) で振り分けたものが \( E_ij \)。
※ 行 \( i \) カテゴリの合計値 \( R_i \) を、列 \( j \) カテゴリが占める割合 \( \frac{C_j}{N} \) で振り分けたものが \( E_ij \)。
※ 期待度数の計算では、各セル \( O_{ij} \) 個別の値は使わない点に注意。
もちろん、行、列の着目の仕方を変えて\[
E_{ij} = C_j \cdot \frac{R_i}{N}
\]としてもOK。(式としては同じ)
※ 列 \( j \) カテゴリの合計値 \( C_j \) を、行 \( i \) カテゴリが占める割合 \( \frac{R_i}{N} \) で振り分けたものが \( E_ij \)。
Step3. ズレの度合い(独立度)の計算
つぎに、Step2で求めた期待度数とクロス集計表で与えられたズレの度合い(独立度)を計算します。
とは言っても、計算方法は適合度のときとほぼ同じです。
【計算方法】
- 各セルごとに、残差2÷期待度数 を求める。
- 各セルごとに求めた 残差2÷期待度数 の和を取る
実際に、記事の冒頭で出したこのデータを例に、各セルごとの期待度数を計算してみましょう。
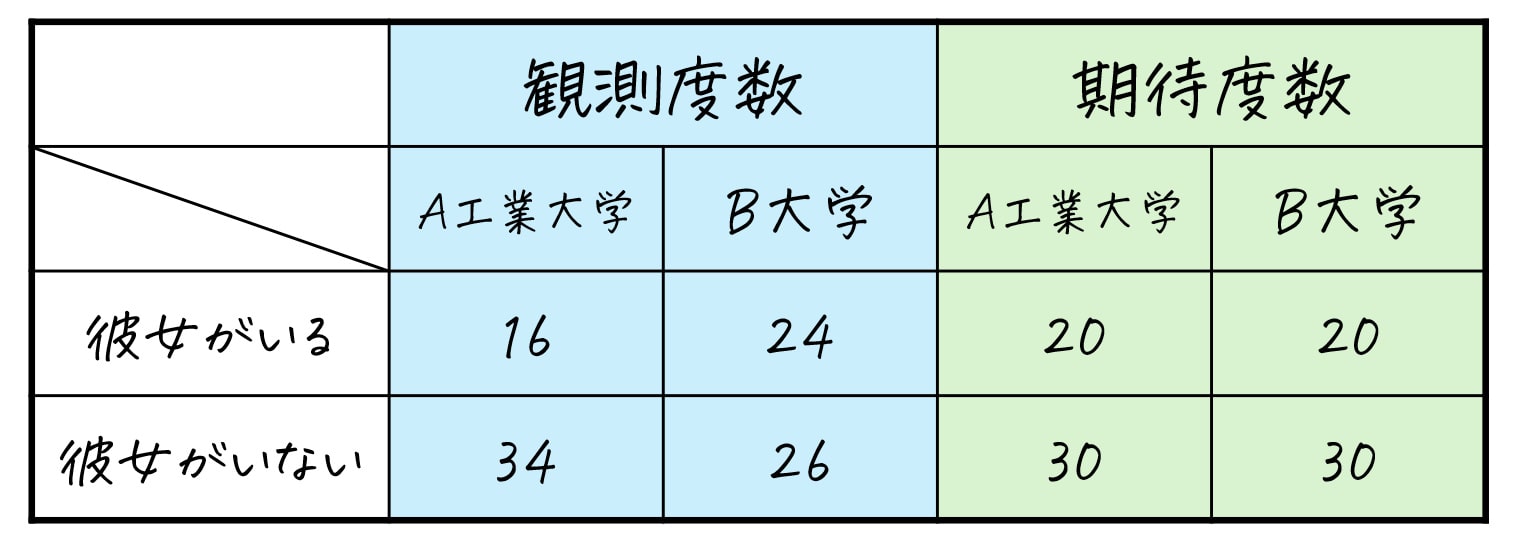
まず、各セルごとに、残差2÷期待度数 を求めていきます。
表.残差2÷期待度数(計算式)
| A工業大学 | B大学 | |
| 彼女がいる | \( \frac{(\textcolor{deepskyblue}{16}-\textcolor{lime}{20})^2}{\textcolor{lime}{20}} = \frac{16}{20} \) | \( \frac{(\textcolor{deepskyblue}{24}-\textcolor{lime}{20})^2}{\textcolor{lime}{20}} = \frac{16}{20} \) |
| 彼女がいない | \( \frac{(\textcolor{deepskyblue}{34}-\textcolor{lime}{30})^2}{\textcolor{lime}{30}} = \frac{16}{30} \) | \( \frac{(\textcolor{deepskyblue}{26}-\textcolor{lime}{30})^2}{\textcolor{lime}{30}} = \frac{16}{30} \) |
あとは、求めた 残差2÷期待度数 をすべて足して、独立度 \( \chi^2 \) を求めればOKです。
※ 小数への丸め誤差を減らすため、途中まで分数で計算して、最後に小数に直しましょう。
\[\begin{align*}
\chi^2 & = \frac{(16-20)^2}{20} + \frac{(24-20)^2}{20} + \frac{(26-30)^2}{30} + \frac{(34-30)^2}{30}
\\ & = \frac{16}{20} + \frac{16}{20} + \frac{16}{30} + \frac{16}{30}
\\ & = \frac{48}{60} + \frac{48}{60} + \frac{32}{60} + \frac{32}{60}
\\ & = \frac{160}{60}
\\ & = \frac{8}{3}
\\ & = \fallingdotseq 2.667
\end{align*}\]
より一般化して、公式を紹介します。
以下のように、\( m \) 行 \( n \) 列のクロス集計表で与えられるデータ【クロス集計表(観測度数)】、および事前に各セルごとの期待度数を計算し、表にした【クロス集計表(期待度数)】がある。
【クロス集計表(観測度数)】
| カテゴリ | 列1 | 列2 | … | 列n |
| 行1 | \( O_{11} \) | \( O_{12} \) | … | \( O_{1n} \) |
| 行2 | \( O_{21} \) | \( O_{22} \) | … | \( O_{2n} \) |
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| 行m | \( O_{m1} \) | \( O_{m2} \) | … | \( O_{mn} \) |
【クロス集計表(期待度数)】
| カテゴリ | 列1 | 列2 | … | 列n |
| 行1 | \( E_{11} \) | \( E_{12} \) | … | \( E_{1n} \) |
| 行2 | \( E_{21} \) | \( E_{22} \) | … | \( E_{2n} \) |
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| 行m | \( E_{m1} \) | \( E_{m2} \) | … | \( E_{mn} \) |
この観測度数と期待度数のクロス集計表から、独立度 \( \chi^2 \) を\[\begin{align*}
\chi^2 = \sum^{m}_{i = 1} \left\{ \sum^{n}_{j = 1} \frac{ (O_{ij} - E_{ij})^2 }{E_{ij} } \right\}
\end{align*}\]と計算できる。
Step4. 有意水準、自由度に対応するカイ2乗値を読み取る
先ほど計算した独立度 \( \chi^2 \) は、適合度と同じようにカイ2乗分布に従います。
ただし、自由度が適合度のときとは異なるので注意です。
\( m \) 行 \( n \) 列のクロス集計表で計算できる独立度 \( \chi^2 \) は、自由度 \( (m-1)(n-1) \) のカイ2乗分布に従う。
そのため、有意水準 \( \alpha \)、自由度 \( (m-1)(n-1) \) に対応するカイ2乗値 \( \chi_0^2 \) をカイ2乗表から読み取り、\( \chi^2 \) と \( \chi_0^2 \) の値を比べることで、独立度の仮説検定(採択/棄却)が判定できる。
\( \chi^2 \leqq \chi_0^2 \) のとき
→ 実際の分布が起こる確率は、有意水準 \( \alpha \) 以上である。
→ 仮定は採択され、独立性がない(関連がある)とは言えない。(2つの属性は関連があるように見えているだけ。)
\( \chi^2 > \chi_0^2 \) のとき
→ 実際の分布が起こる確率は、有意水準 \( \alpha \) 未満である。
→ 仮定は棄却され、独立性がない(関連がある)と言える。
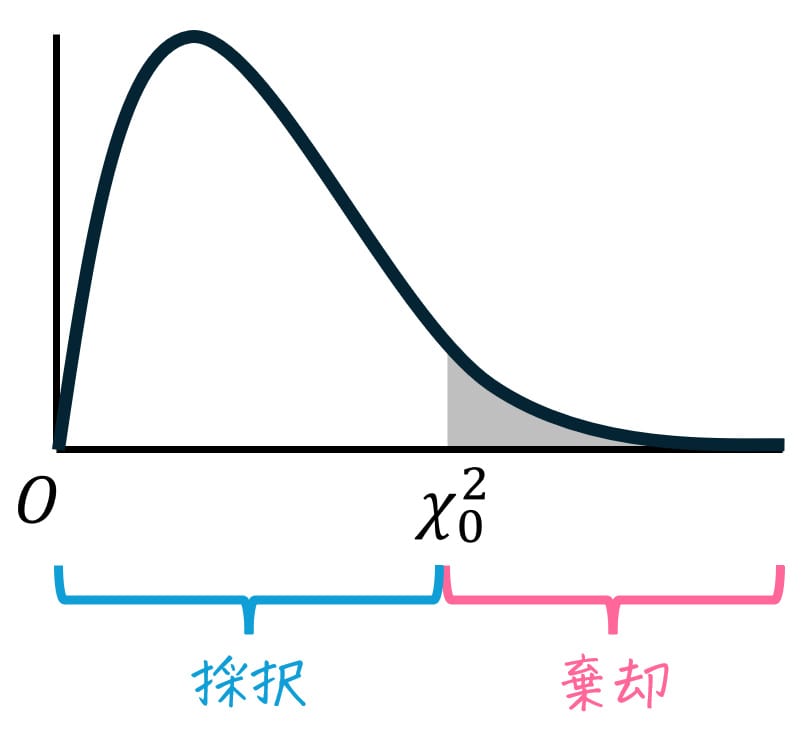
※ 独立性検定は、必ず片側検定となります。(適合度検定と同じ)
※ 自由度が \( (m-1)(n-1) \) となる理由は、Step4の末尾に記載しています。
【独立性の検定は、必ず片側検定!】
独立性検定は、理論的な分布(=完全に独立な状態)と実際の分布のズレが「偶然の範囲内」か「理論分布とあっていないか」を確認する検定です。(※ 適合度検定と理屈は同じです)
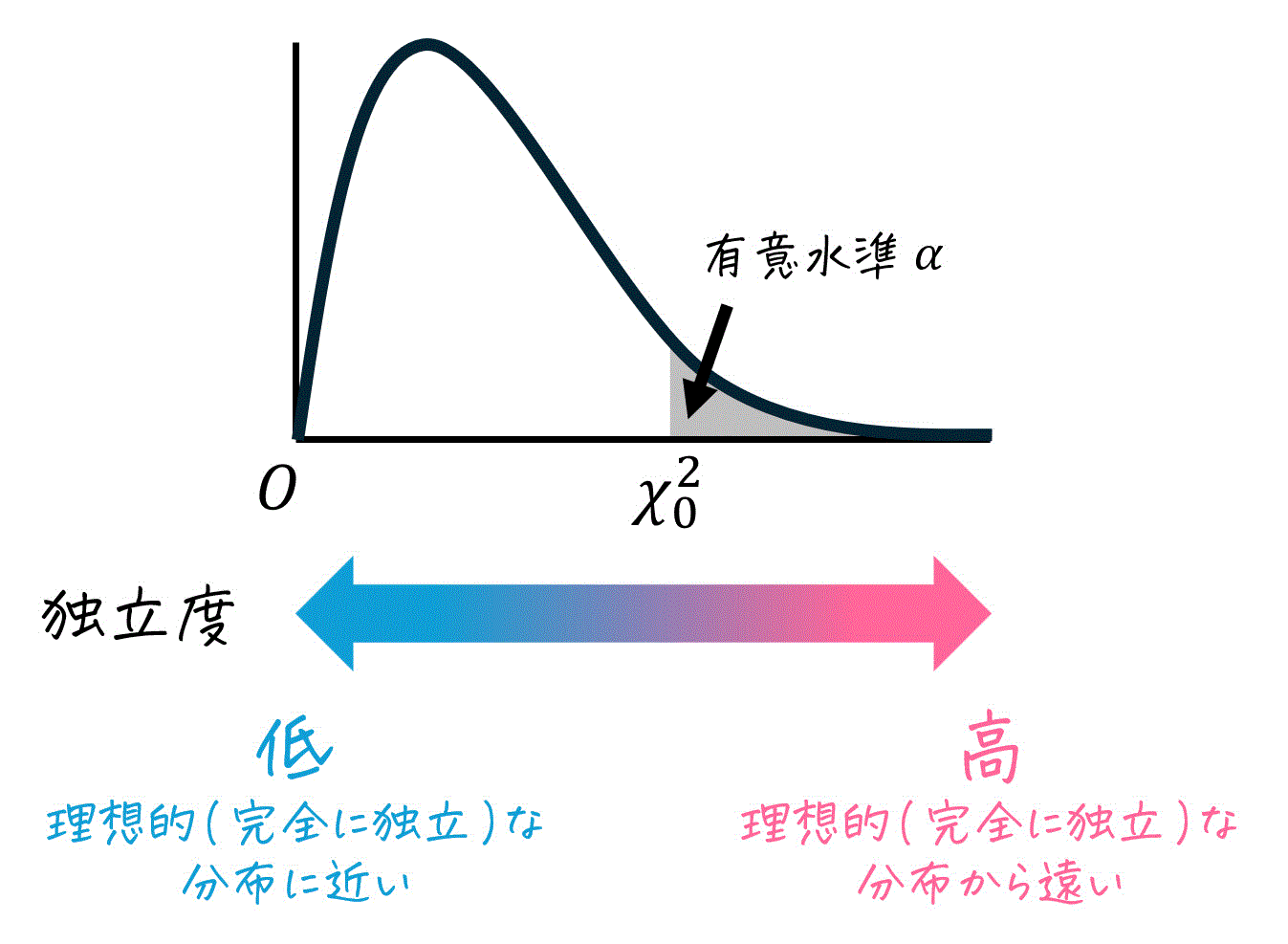
ここで、独立度(カイ2乗統計量)の大小は、次の意味を持っています。
- 独立度が小さい(0に近い) … 理論分布に近い状態
- 独立度が大きい(0から遠い)… 理論分布から離れた状態
そのため、独立度が小さい状態は問題がなく、独立度が大きい状態のときのみ問題があると言えます。
ここからは、例題について有意水準 \( \alpha = 0.10 \)、自由度 \( (m-1)(n-1) \) に対応するカイ2乗値 \( \chi_0^2 \) をカイ2乗表から読み取っていきましょう。
| A工業大学 | B大学 | 合計 | |
| 彼女がいる | 16 | 24 | 40 |
| 彼女がいない | 34 | 26 | 60 |
| 合計 | 50 | 50 | 100 |
まずは、自由度を求めてみましょう。
例題の場合、
- 行の属性:彼女がいる/彼女がいない( \( m = 2 \) )
- 列の属性:A工業大学/B大学( \( n = 2 \) )
なので、自由度は \( (2-1)(2-1) = 1 \) となりますね。
ここで、有意水準10%、自由度1に対応するカイ2乗値を、カイ2乗分布表から読み取ってみましょう。

すると、2.706 と読めますね。\( \chi_0^2 = 2.706 \) としましょうか。
【独立度の自由度が \( (m-1)(n-1) \) となる理由】
まず、クロス集計表のある1つの列に着目してみましょう。
このとき、ある列のうちの1つの値が分からなかったとしても、残りの行の値がすべてわかっていれば、分からない1つの値を計算で出すことが出来ます。言い換えると、ある列のうちの1つの値は情報量をもたない、と言えます。
例えば、下の表の★が分からないとしましょう。
| 列1 | 列2 | 列3 | 合計 | |
| 行1 | 10 | 20 | ||
| 行2 | ★ | 20 | ||
| 行3 | 7 | 30 | ||
| 行4 | 8 | 30 | ||
| 合計 | 30 | 30 | 40 | 100 |
この場合、たとえ★の値がわからなくても行1の合計 "30" と、残りのデータ "7" と "8" から、\[
30 - (10 + 7 + 8) = 5
\]と、★の値を特定することが出来ます。
| 列1 | 列2 | 列3 | 合計 | |
| 行1 | 10 | 20 | ||
| 行2 | 5 | 20 | ||
| 行3 | 7 | 30 | ||
| 行4 | 8 | 30 | ||
| 合計 | 30 | 30 | 40 | 100 |
そのため、行1~行mの \( m \) 個のセルを持つある1つの列が持つ情報量は、\( m \) から1引いた \( m - 1 \) となります。
つぎに、ある行のうちの1行すべてのデータが分からない状態であったとします。
この場合、残りの列の値がすべてわかっていれば、分からない1つ列の値をすべて計算で出すことが出来ます。言い換えると、ある列のうちの1列は全く情報量がないと言えます。
例えば、下の表の★が分からないとしましょう。
| 列1 | 列2 | 列3 | 合計 | |
| 行1 | 10 | ★ | 2 | 20 |
| 行2 | 5 | ★ | 4 | 20 |
| 行3 | 7 | ★ | 19 | 30 |
| 行4 | 8 | ★ | 15 | 30 |
| 合計 | 30 | 30 | 40 | 100 |
このときも、残りの列1、列3および各行ごとの合計から、★の部分の値を下のように計算で求めることが出来ますね。
| 列1 | 列2 | 列3 | 合計 | |
| 行1 | 10 | 8 | 2 | 20 |
| 行2 | 5 | 11 | 4 | 20 |
| 行3 | 7 | 4 | 19 | 30 |
| 行4 | 8 | 7 | 15 | 30 |
| 合計 | 30 | 30 | 40 | 100 |
そのため、\( n \) 個の列のうち、1列は全く情報量をもたないと言えます。
よって、\( m \) 行 \( n \) 列のクロス集計表から求められる独立度 \( \chi^2 \) の自由度は、\( m - 1 \) 個の情報の \( n - 1 \) 列分、つまり \( (m-1)(n-1) \) と言えるのです。
Step5. 結論(採択/棄却)を判定する
最後に、Step3で求めた独立度 \( \chi^2 \) と、Step4でカイ2乗表から読み取った値 \( \chi_0^2 \) から、結論(採択/棄却)を判定しましょう。
今回の場合、独立度 \( \chi^2 = 2.667 \)、カイ2乗表から読み取った値 \( \chi_0^2 = 2.706 \) なので、\[
\chi^2 = 2.667 \leqq 2.706 = \chi_0^2
\]となります。
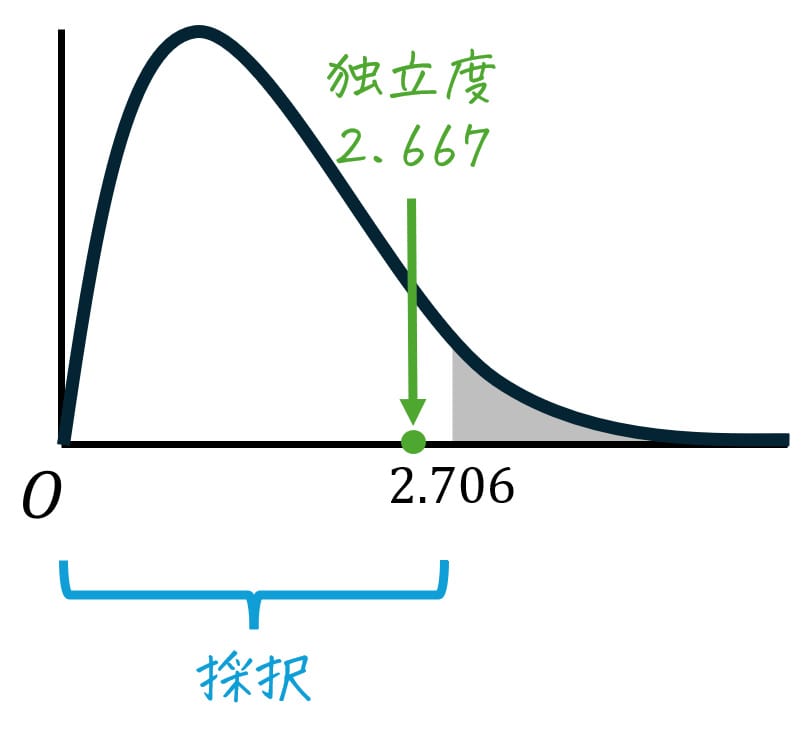
よって、仮説は採択され、「彼女の有無」と「工業大学か否か」は独立でないとは言えない(関連があるとは言えない)と結論づけられます。
スポンサードリンク
2. 独立性の検定の手順まとめ
以下の \( m \) 行 \( n \) 列のクロス集計表にあるデータについて、有意水準 \( \alpha \) にて独立性の検定を実施する場合、以下の手順を実施すればよい。
| カテゴリ | 列1 | 列2 | … | 列n | 合計 |
| 行1 | \( O_{11} \) | \( O_{12} \) | … | \( O_{1n} \) | \( R_1 \) |
| 行2 | \( O_{21} \) | \( O_{22} \) | … | \( O_{2n} \) | \( R_2 \) |
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | ⋮ |
| 行m | \( O_{m1} \) | \( O_{m2} \) | … | \( O_{mn} \) | \( R_m \) |
| 合計 | \( C_1 \) | \( C_2 \) | … | \( C_n \) | \( N \) |
Step1. 帰無仮説/対立仮説を立てる
以下のように帰無仮説(問題を解くための仮定)、対立仮説(仮定を否定して示したいもの)をたてる。
- 帰無仮説:与えられた2つの分類は独立である(=関連がない)。
- 対立仮説:与えられた2つの分類は独立ではない(=関連がある)。
Step2. 期待度数(理論値)の計算
各セルの期待度数 \( E_{ij} \) を、以下の式で計算する。\[
E_{ij} = R_i \cdot \frac{C_j}{N}
\]
※ 行 \( i \) カテゴリの合計値 \( R_i \) を、列 \( j \) カテゴリが占める割合 \( \frac{C_j}{N} \) で振り分けたものが \( E_ij \)。
※ 期待度数の計算では、各セル \( O_{ij} \) 個別の値は使わない点に注意。
Step3. ズレの度合い(独立度)の計算
独立度を\[\begin{align*}
\chi^2 = \sum^{m}_{i = 1} \left\{ \sum^{n}_{j = 1} \frac{ (O_{ij} - E_{ij})^2 }{E_{ij} } \right\}
\end{align*}\]で計算する。
Step4. 有意水準、自由度に対応するカイ2乗値を、カイ2乗表から読み取る
有意水準 \( \alpha \)、自由度 \( (m-1)(n-1) \) に対応するカイ2乗値 \( \chi_0^2 \) をカイ2乗表から読み取る。
Step5. 結果(採択/棄却)の確認
Step4, Step5の結果から、採択/棄却を決定する。
\( \chi^2 \leqq \chi_0^2 \) のとき
→ 実際の分布が起こる確率は、有意水準 \( \alpha \) 以上である。
→ 仮定は採択され、独立性がない(関連がある)とは言えない。(2つの属性は関連があるように見えているだけ。)
\( \chi^2 > \chi_0^2 \) のとき
→ 実際の分布が起こる確率は、有意水準 \( \alpha \) 未満である。
→ 仮定は棄却され、独立性がない(関連がある)と言える。

スポンサードリンク
3. 練習問題にチャレンジ!
ある大学には工学部と情報工学部の2つの学部がある。各学部の学生は、第2外国語としてドイツ語、フランス語、中国語、韓国語の中から1つを選択し、履修する。以下のクロス集計表は、各学部ごとに履修した第2外国語の人数を示している。
| 工学部 | 情報工学部 | 合計 | |
| ドイツ語 | 10 | 20 | 30 |
| フランス語 | 30 | 20 | 50 |
| 中国語 | 20 | 30 | 50 |
| 韓国語 | 40 | 30 | 70 |
| 合計 | 100 | 100 | 200 |
このデータを用いて、学部と第2外国語の選択に関連があるかどうかを調査したい。つぎの(1)~(6)の問いに答えなさい。
(1) 帰無仮説と対立仮説を述べなさい。
(2) 期待度数に関するクロス集計表を作成しなさい。
(3) この検定で使う統計量を計算しなさい。
(4) この検定に必要な分布を答えなさい。自由度がある分布であれば、自由度も述べること。
(5) 有意水準5%で仮説検定を行う際に、(4)で答えた分布の分布表から読み取った値を答えなさい。
(6) 有意水準5%で帰無仮説を採択するか棄却するか、理由も含めて答えなさい。
4. 練習問題の答え
(1) 帰無仮説と対立仮説
独立性の検定なので、「与えられた2つの属性の関連がない(=独立している)」という仮定をしてから、仮定を否定出来るか出来ないかを判定します。
- 帰無仮説 \( H_0 \):与えられた2つの属性(学部と第2外国語の選択)は関連がない(=独立している)。
- 対立仮説 \( H_1 \):与えられた2つの属性(学部と第2外国語の選択)は関連がある(=独立していない)。
(2) 期待度数に関するクロス集計表作成
期待度数の計算では、「片方の属性の合計に着目。着目した合計を、片方の属性の各カテゴリごとの割合ごとに振り分ける」ということをします。
今回は、属性「学部」の合計値に着目し、もう片方の属性、第2外国語(ドイツ語、フランス語、中国語、韓国語)の合計の割合比に振り分けていきましょう。
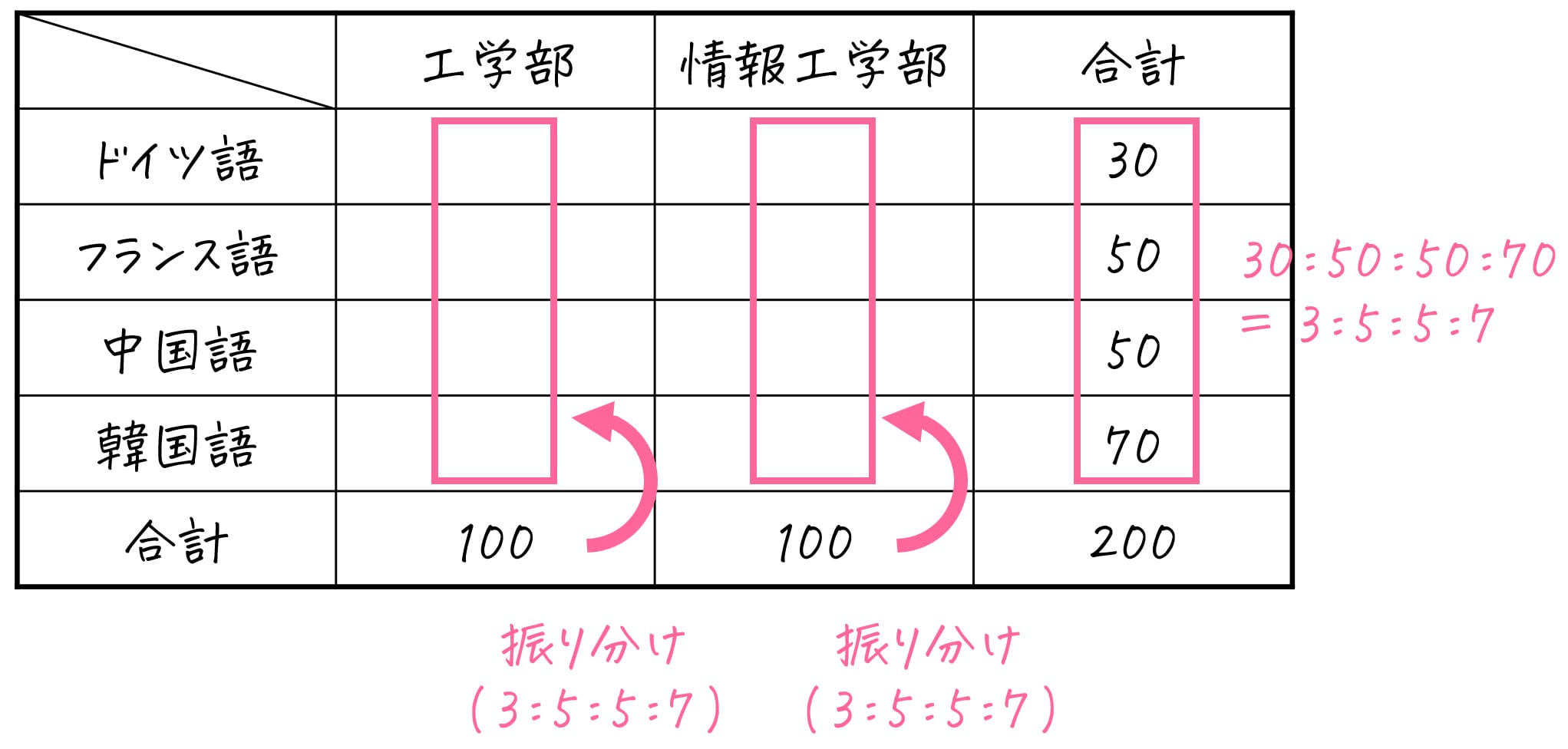
振り分けると、次の結果が得られます。
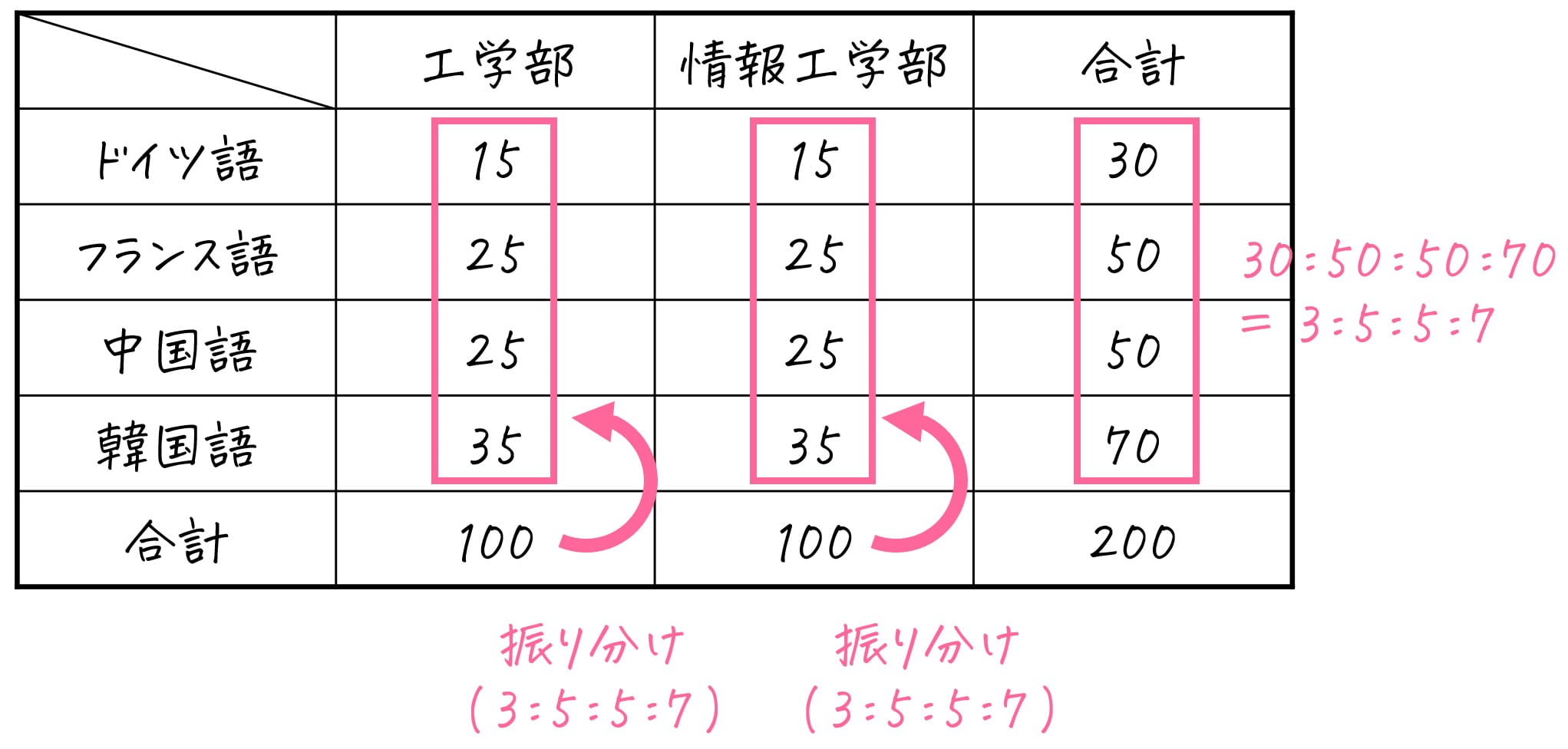
(3) カイ2乗統計量(独立度)の計算
(2)で計算した期待度数から、カイ2乗統計量(独立度)を計算しましょう。
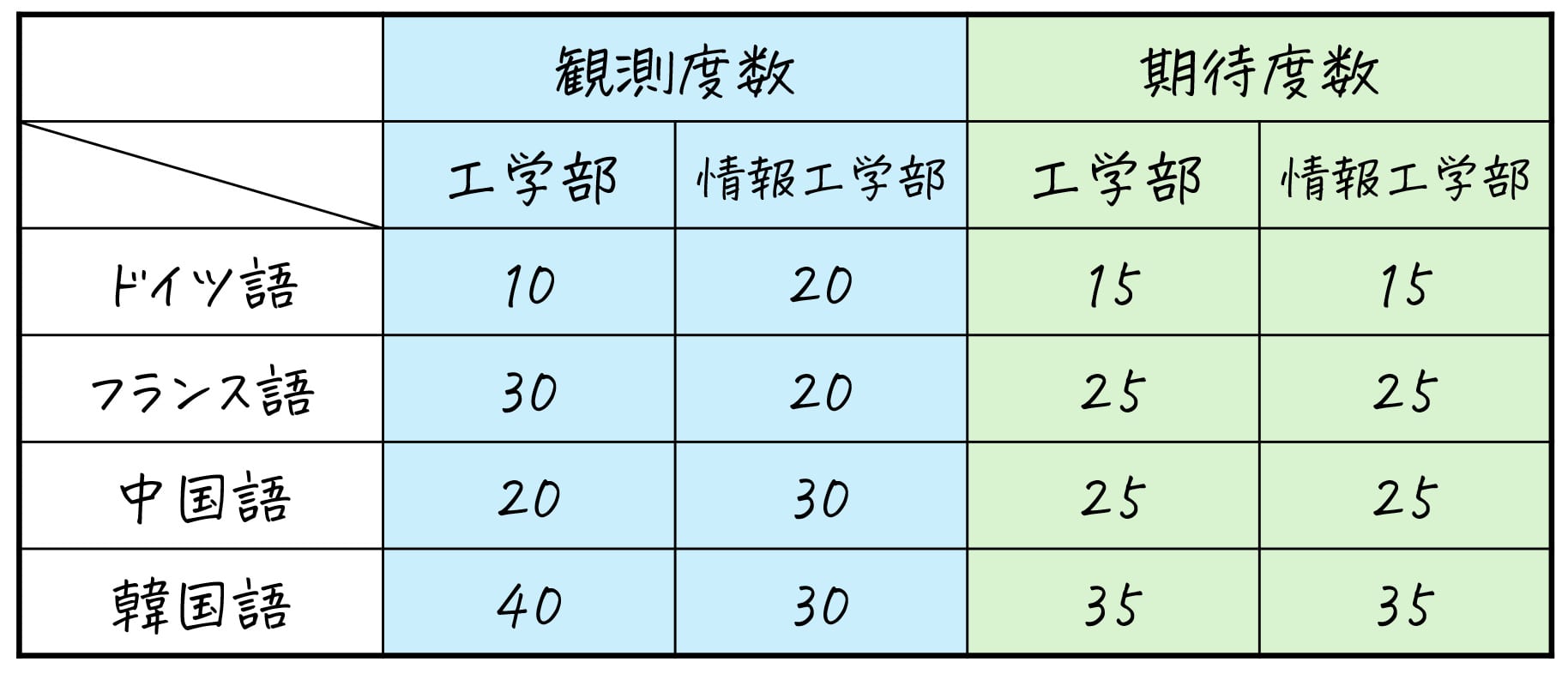
各セルごとに、残差2÷期待度数 を求めていきます。
表.残差2÷期待度数(計算式)
| 工学部 | 情報工学部 | |
| ドイツ語 | \( \frac{(\textcolor{deepskyblue}{10}-\textcolor{lime}{15})^2}{\textcolor{lime}{15}} = \frac{25}{15} \) | \( \frac{(\textcolor{deepskyblue}{20}-\textcolor{lime}{15})^2}{\textcolor{lime}{15}} = \frac{25}{15} \) |
| フランス語 | \( \frac{(\textcolor{deepskyblue}{30}-\textcolor{lime}{25})^2}{\textcolor{lime}{25}} = \frac{25}{25} \) | \( \frac{(\textcolor{deepskyblue}{30}-\textcolor{lime}{25})^2}{\textcolor{lime}{25}} = \frac{25}{25} \) |
| 中国語 | \( \frac{(\textcolor{deepskyblue}{20}-\textcolor{lime}{25})^2}{\textcolor{lime}{25}} = \frac{25}{25} \) | \( \frac{(\textcolor{deepskyblue}{30}-\textcolor{lime}{25})^2}{\textcolor{lime}{25}} = \frac{25}{25} \) |
| 韓国語 | \( \frac{(\textcolor{deepskyblue}{40}-\textcolor{lime}{35})^2}{\textcolor{lime}{35}} = \frac{25}{35} \) | \( \frac{(\textcolor{deepskyblue}{30}-\textcolor{lime}{35})^2}{\textcolor{lime}{35}} = \frac{25}{35} \) |
あとは、上の式で求めた各セルごとの統計量を足せばOKです。
\[\begin{align*}
\chi^2 & = \frac{(10-15)^2}{15} + \frac{(20-15)^2}{15} + \frac{(30-25)^2}{25} + \frac{(20-25)^2}{25} + \frac{(20-25)^2}{25} + \frac{(30-25)^2}{25} + \frac{(40-35)^2}{35} + \frac{(30-35)^2}{35}
\\ & =\frac{25}{15} + \frac{25}{15} + \frac{25}{25} + \frac{25}{25} + \frac{25}{25} + \frac{25}{25} + \frac{25}{35} + \frac{25}{35}
\\ & = \frac{5}{3} + \frac{5}{3} + 1 + 1 + 1 + 1 + \frac{5}{7} + \frac{5}{7}
\\ & = \frac{35}{21} + \frac{35}{21} + 4 + \frac{15}{21} + \frac{15}{21}
\\ & = \frac{100}{21} + 4
\\ & = 8 + \frac{16}{21}
\\ & \fallingdotseq 8.762
\end{align*}\]
(4) 使う分布、自由度の確認
独立度に関する検定なので、カイ2乗分布を使います。
また、属性が学部2カテゴリ(情報工学部、工学部)と第2外国語4カテゴリ(ドイツ語、フランス語、中国語、韓国語)なので自由度は\[
(2-1)(4-1) = 3
\]となります。
(5) カイ2乗分布表の読み取り
自由度3、有意水準5% ( \( \alpha = 0.05 \) ) に相当するカイ2乗値を読み取ります。
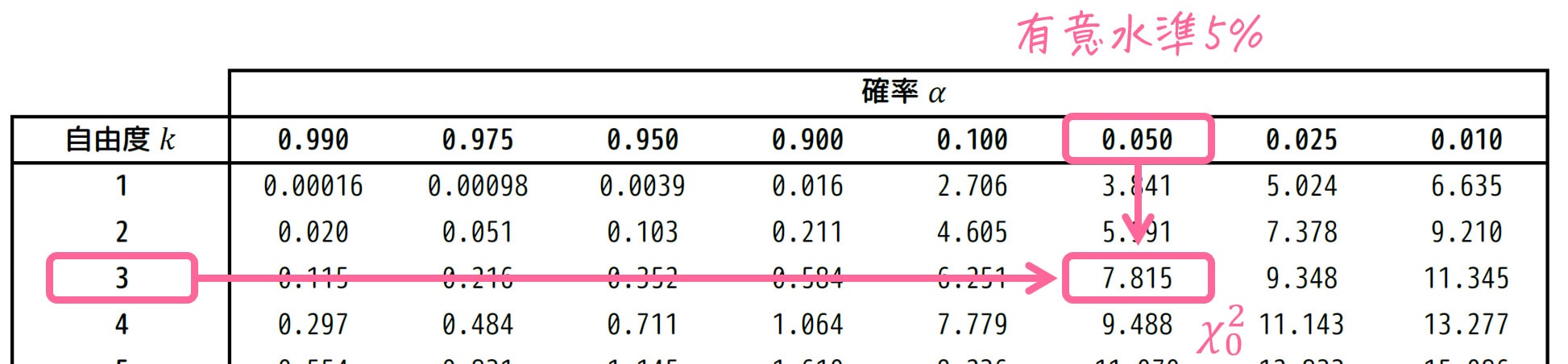
結果、7.815と読み取れますね。\( \chi_0^2 = 7.815 \) とおきましょう。
(6) 結果(採択/棄却)を判定
Step3で求めたカイ2乗統計量(独立度) \( \chi^2 = 8.762 \) と、Step5でカイ2乗表から読み取った値 \( \chi_0^2 = 7.815 \) なので、\[
\chi^2 = 8.762 > 7.815 = \chi_0^2
\]となります。
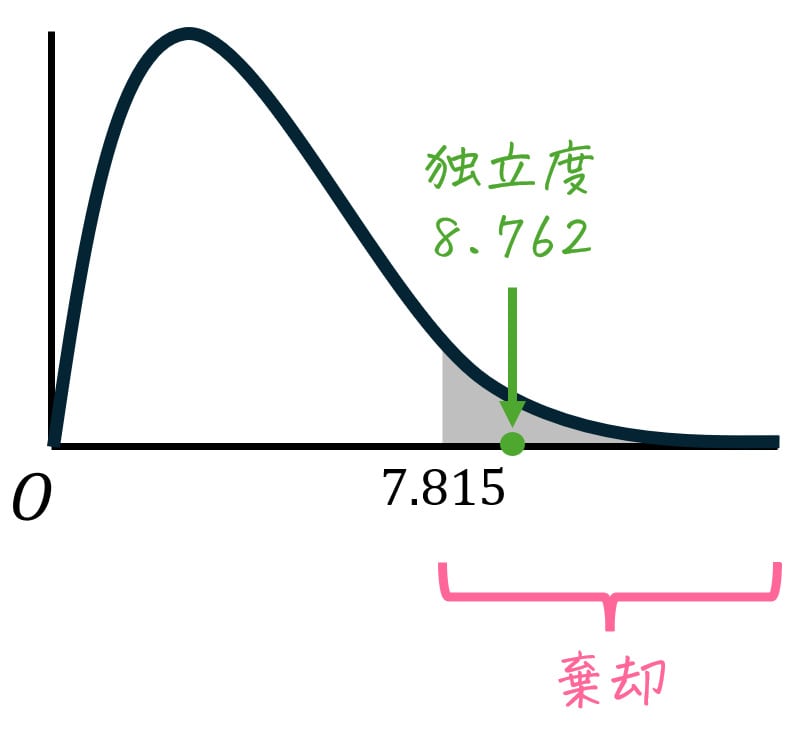
したがって、\( \chi^2 > \chi_0^2 \) より仮説は棄却され、学部と第2外国語の選択は関連がある(独立ではない)と結論づけられます。
関連広告・スポンサードリンク




![うさぎでもわかる計算機システム Part02 2の補数表現 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190615204157-1-150x150.gif)