スポンサードリンク
こんにちは、ももやまです。
皆さんは、選挙が終わった直後、まだ開票全く当選していないのに「◯◯党 △△ △△、当選確実!」という速報が出るのを見て、不思議に思ったことはありませんか?
今回は、開票がまだ進んでいないにもかかわらず、メディアがどのようにして「当選確実」と判断するのか、その仕組みを解説していきます。
スポンサードリンク
1. 出口調査の簡単なしくみ
(1) 全員分の投票情報を集めるのは不可能
投票した全員が誰に(どの党に)投票したかが分かれば、100%正確に当選者がわかります。
しかし、現実的に全員分が誰に投票したかを、開票せずに把握することは不可能です。
(2) 現実的な手段:味見=出口調査
料理を振る舞う場面を想像してください。
料理を作るとき、味付けや味の濃さを確認するために少しだけ味見をしますよね[1]料理全部を食べて確認するなんてことをしたら、振る舞う料理がなくなってしまいます。。
選挙の当選確実を出す仕組みも、この「味見」と似ています。
具体的には、投票者の一部に誰に投票したのかを選挙会場で調査(=味見)し、その結果をもとに当選者を予測します。

(3) 調査結果の判断法には要注意
今回は、候補者4人(うさぎ、ねこ、いぬ、あざらし)の中から当選者として1人を選ぶ選挙を実施したと仮定します。

ここで、10,000人がこの選挙に投票し、そのうち100人に「誰に投票したか」を出口調査した結果、以下の表の通りの得票率となったとします。
表. 100人に出口調査したときの得票率データ
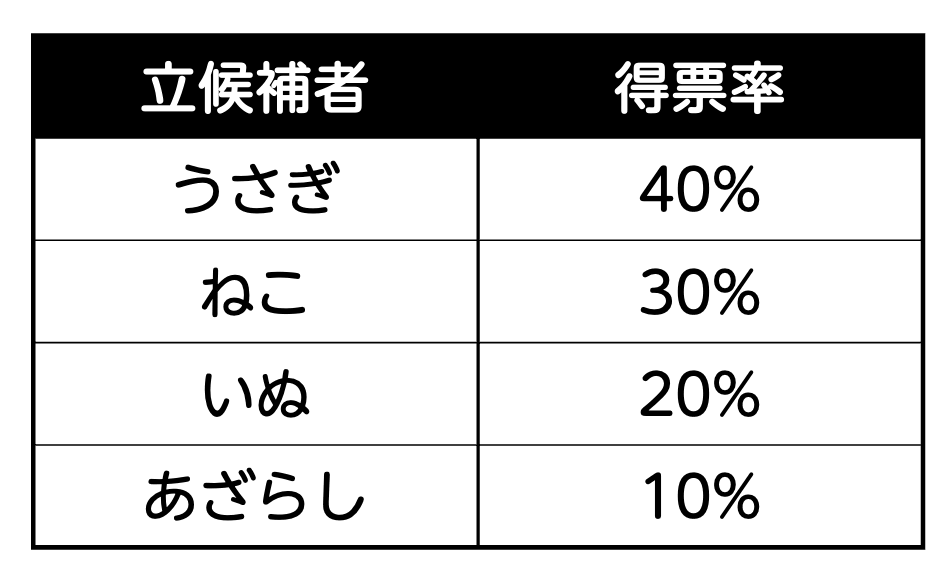
これだけ見ると、すぐに「うさぎが一番人気だな! 当選者確定!」と思うかもしれません。
しかし、ここで重要なのは、これはたった100人のデータに過ぎないという点です。実際の投票者全体(10,000人)の投票結果は、この100人のデータと一致しません。
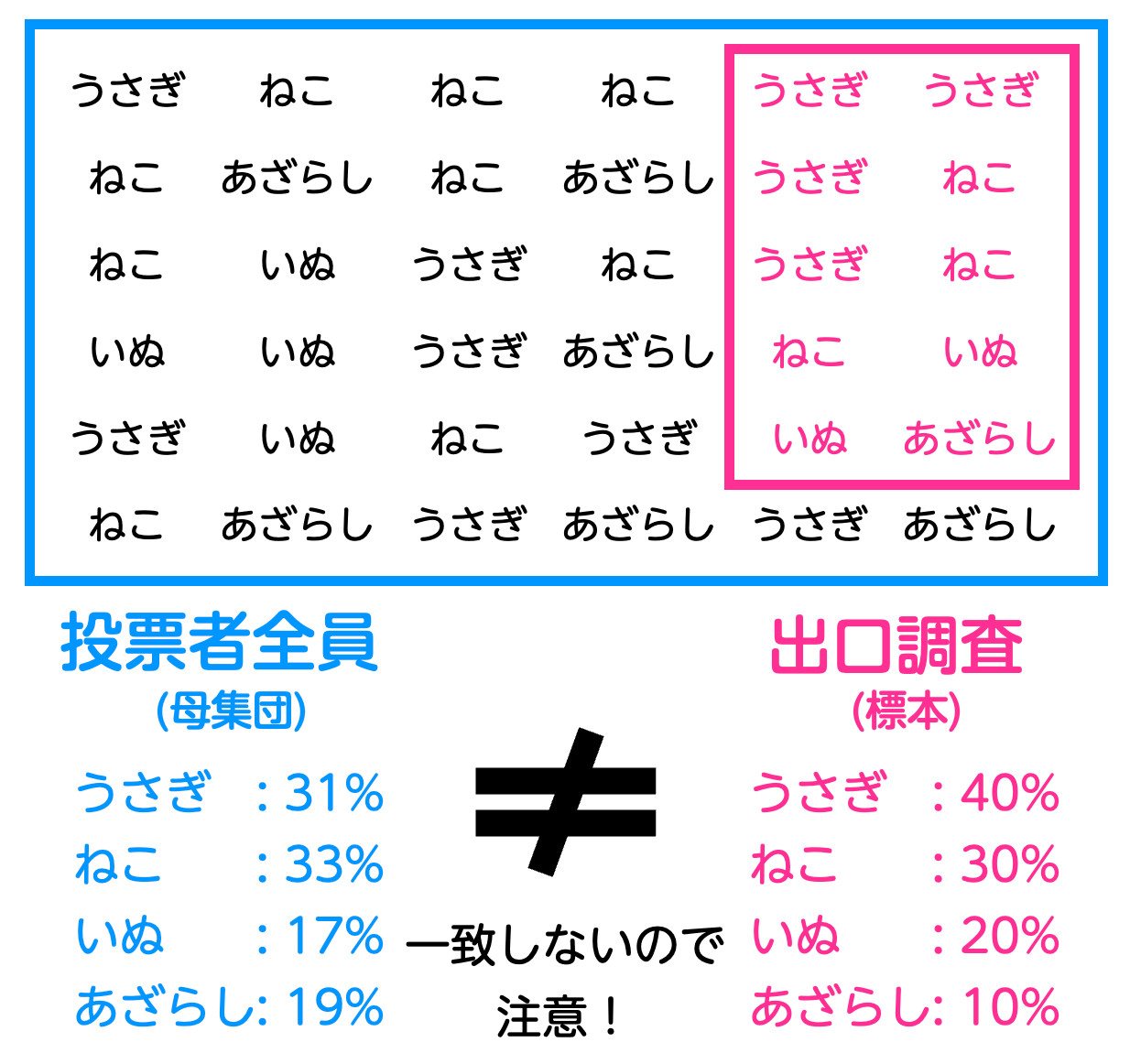
なぜなら、100人というサンプルはあくまで「一部の投票者」に過ぎないからです、全員(10,000人)の中で本当にうさぎが一番投票されているかはわからないからです。たまたま抽出した100人がうさぎに投票した人が多かっただけかもしれません。
そのため、この調査結果から「うさぎが最も投票されている(=当選確実)」ということを正確に判断するためには、数学の力を使った裏付けが必要です。
(4) 数学的な裏付け … 区間推定
では、どのように数学的に裏付けしていけばいいでしょうか?
100人のデータだけでは、全体の投票結果を完全に理解することはできません。つまり、たとえば「うさぎが40%の得票率だった」としても、実際に10,000人全体の得票率が40%であるとは限らないのです。
しかし、全体の得票率を正確に知ることができなくても、数学(統計学)の理論に基づいておおよその範囲を推測することはできます。たとえば、「うさぎの得票率は38%〜42%の間だろう」というように、得票率の範囲を推定することができるのです。この、得票率がどのくらいの範囲に収まるのかを推定するのが「区間推定」です。

★ 例え話で理解しよう。
ここで少し具体的な例えを使って考えてみましょう。
例えば、クラスのテストの平均点を調べたいとき、全員に尋ねるのは大変ですよね。そこで、100人のうち10人に「テストの平均点は何点だったか?」と聞いたとしましょう。
もし、その10人が「平均点は80点だった!」と言ったとしても、クラス全体の平均点が本当に80点だとは限りません。 もしかしたら、クラス全体の平均点はもっと高いかもしれないし、逆に低いかもしれません。そのため、10人だけのデータでは、全体の平均を完全には把握できません。
そこで、「この調査結果をもとに全体の平均点はおおよそ80点だろうと予測するけど、実際の平均点は70点から90点の間かもしれない」というように、範囲を設定することが大切なのです。
これと同じように、100人の調査データだけでは全体の得票率を正確に知ることはできませんが、「範囲」で示すことで、より現実的な予測をすることができるのです。
(5) 区間推定の結果と当選確実
当選確実を言うためには、得票率が一番高い候補者の得票率の範囲が他の候補者の範囲と重ならければOKです。
これは、他の候補者の信頼区間が一番高い候補者の範囲に含まれないことで、「この候補者よりも得票率が高い人はいない」と確定できるからです。
例えば、うさぎの得票率が「37%〜43%」と推定されていた場合、他の候補者の得票率がいくら高くても、その範囲が「37%」未満であれば、うさぎが最も高い得票率を得ていると確信できるわけです。

最も高い得票率を得ている候補者が誰か、出口調査の段階で確信できた段階で、各メディアは当選確実であることを視聴者に伝えます。
(6) 区間推定で必要な知識
区間推定をするにあたって、以下の知識が必要となります。
- 確率変数
- 平均(期待値)、分散、標準偏差
- 二項分布
これらの知識を短時間で復習するための記事を作成しています。必要な方はぜひご覧ください。
スポンサードリンク
2. 当選確実を数学的に出す方法解説
ここからは、実際に出口調査から当選確実が言えるかどうか、正確に判断するための方法を説明していきましょう。
なおこの章では、第1章と同じ以下のデータを使用します。
- 候補者4人(うさぎ、ねこ、いぬ、あざらし)の中から当選者として1人を選ぶ選挙を実施
- 選挙の投票者は全員で10,000人
- 10,000人中100人に出口調査を実施、結果は以下の表の通り
表. 100人に出口調査したときの得票率データ

(1) 区間推定の流れ
まずは、当選確実かどうかを判断するために必要な区間推定をどのように実施するか、その流れを見ていきましょう。
ここから先、数式を使った話になりますが、心配しないでください。ここでは「考え方」に焦点を当てます。区間推定では、まずサンプルデータから得られた「得票率」に、ばらつき(標準偏差)を加えたり引いたりして、範囲(区間)を求めます。
Step1: まず、出口調査での得票率(例: うさぎが40%)を求める。
Step2: Step1で求めた得票率のばらつき(標準偏差)を計算する。
Step3: Step1, Step2の結果を用いて区間推定の結果を出す。
(3) 区間推定の計算法
Step1. 出口調査での得票率の計算 … 平均
まず、100人の調査結果を使って、各候補者にに投票した人の割合(得票率)を求めます。
得票率は、次のような形で計算ができます。\[\begin{align*}
\mathrm{得票率} & = \frac{ \mathrm{各候補者に投票した人数} }{ \mathrm{調査人数} }
\end{align*}\]
たとえば、調査した100人のうち40人がうさぎに投票したとしましょう。すると、うさぎの得票率は次のように計算できます。
\[\begin{align*}
\mathrm{得票率} & = \frac{ \mathrm{うさぎに投票した人数} }{ \mathrm{調査人数} }
\\ & = \frac{40}{100}
\\ & = 0.4
\\ & = 40 [ \% ]
\end{align*}\]
Step2. 誤差の計算 … 標準偏差
次に、この得票率に基づいて、調査の結果にどれくらいの誤差があるかを計算します。
ここで、この誤差を求めるためには、二項分布という確率の理論を使います。
二項分布は、ある人が「投票する」「投票しない」のような2つの選択肢から1つを選ぶ場面で使われます。つまり、各調査対象が「各候補者に投票した」「各候補者に投票しなかった」の2通りの結果に分かれるので、このような場面にぴったり当てはまるのです。
★ 二項分布の平均と分散
調査した人数を \( n \)、ある候補者に投票された割合を \( p \) とします。この場合、得票数 \( X \) の平均 \( E(X) \)、分散 \( V(X) \) はつぎのように計算できます。
※ 投票人数が \( n \) が大きいとき、ある候補者に投票された割合 \( p \) は、出口調査での得票率と同じであるとみなして計算することができます。(大数の法則)
・平均 \( E(X) = np \)
平均は、調査した人数 \( n \) と得票率 \( p \) を掛けた数が平均です。例えば、100人を調査して、40%がうさぎに投票した場合、平均投票者数は次のように計算されます。\[\begin{align*}
E(X) & = \underbrace{ n }_{100} \times \underbrace{ p }_{0.4}
\\ & = 40
\end{align*}\]
・分散 \( V(X) = np(1-p) \)
分散とは、データがどれくらいバラついているかを示す指標で、調査した人数 \( n \)、投票された割合 \( p \)、投票されなかった割合 \( 1-p \) をすべて掛けたものです。例えば、100人を調査して、40%がうさぎに投票した場合、投票者数の分散は次のように計算されます。
\[\begin{align*}
E(X) & = \underbrace{ n }_{100} \times \underbrace{ p }_{0.4} \times ( 1 - \underbrace{ p }_{0.4} )
\\ & = 100 \times 0.4 \times 0.6
\\ & = 24
\end{align*}\]
★ 得票率のばらつき度合い(標準偏差)
次に、得票率のばらつき(誤差)を計算していきます。得票率のばらつきを示す「標準偏差」という指標を使います。標準偏差は、分散の平方根を取ったもので、データのばらつき具合を分かりやすく示します。
ここで、先程出てきた確率変数 \( X \) は、調査した人数 \( n \) に対して得票数がどれだけあるかを示したものでしたね。つまり、得票率はこの確率変数を \( n \) で割ったものとなります。
そのため、得票率の分散は、得票数の分散の \( \frac{1}{n^2} \) 倍となります[2]あるデータを \( a \) 倍すると、その分散は \( a^2 \) となるため。今回は \( a = \frac{1}{n} \) である。。そのため、得票率の分散は次のように計算ができます。
\[\begin{align*}
V \left( \frac{X}{n} \right) & = \frac{1}{n^2} V(X)
\\ & = \frac{1}{n^2} \cdot np(1-p)
\\ & = \frac{p(1-p)}{n}
\end{align*}\]
あとは、得票率の分散の平方根を取ることで、得票率の標準偏差(=ばらつき度合い)を求める事ができます。
\[\begin{align*}
\sigma & = \sqrt{ \mathrm{分散} }
\\ & = \sqrt{ \frac{p(1-p)}{n} }
\end{align*}\]
実際に分散、標準偏差を計算してみましょう。
たとえば、調査した100人のうち40人(= 得票率40%)がうさぎに投票したとします。
すると、調査人数 \( n = 100 \)、うさぎの得票率 \( p = 0.4 \) から、うさぎの得票率の分散、標準偏差は次のように計算できます。
\[\begin{align*}
\mathrm{分散} & = \frac{p(1-p)}{n}
\\ & = \frac{0.4 \cdot 0.6}{100}
\\ & = \frac{ 0.24 }{100}
\\ & = \frac{24}{10000}
\end{align*}\]
\[\begin{align*}
\mathrm{標準偏差} & = \sqrt{ \mathrm{分散} }
\\ & = \sqrt{ \frac{24}{10000} }
\\ & = \frac{ \sqrt{24} }{ \sqrt{10000} }
\\ & = \frac{ 2 \sqrt{6} }{ 100 }
\\ & = \frac{ \sqrt{6} }{50}
\\ & \fallingdotseq 0.0490
\end{align*}\]
Step3. 区間推定
得票率の平均と標準偏差を使って、得票率の区間推定を行います。
ここで調査人数が多い場合、得票率の分布は正規分布に近づくため、正規分布を用いて区間推定を行います。
(1) 信頼度
区間推定を行う際に、「どれくらいの確信度で範囲を推定するか」を示すのが信頼度です。
例えば、信頼度が95%で得票率が「35%〜45%」と推定された場合、「10,000人全体の投票結果の得票率が35%〜45%の範囲に入っている確率が95%」という意味になります。
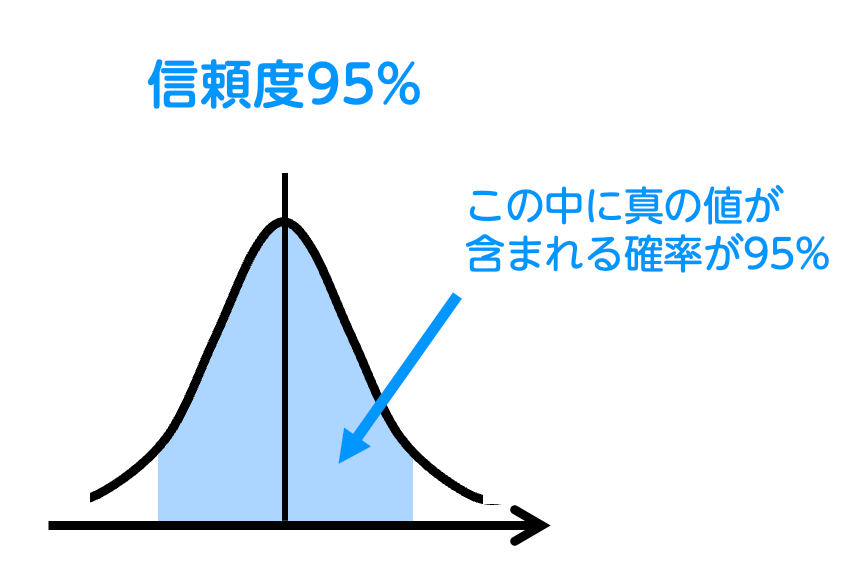
信頼度が低いほど、範囲は狭くなりますが、得票率の推定に対する確信度は弱くなります。一方、信頼度が高いほど、その範囲が広くなりますが、得票率の推定に対する確信度が強くなります。
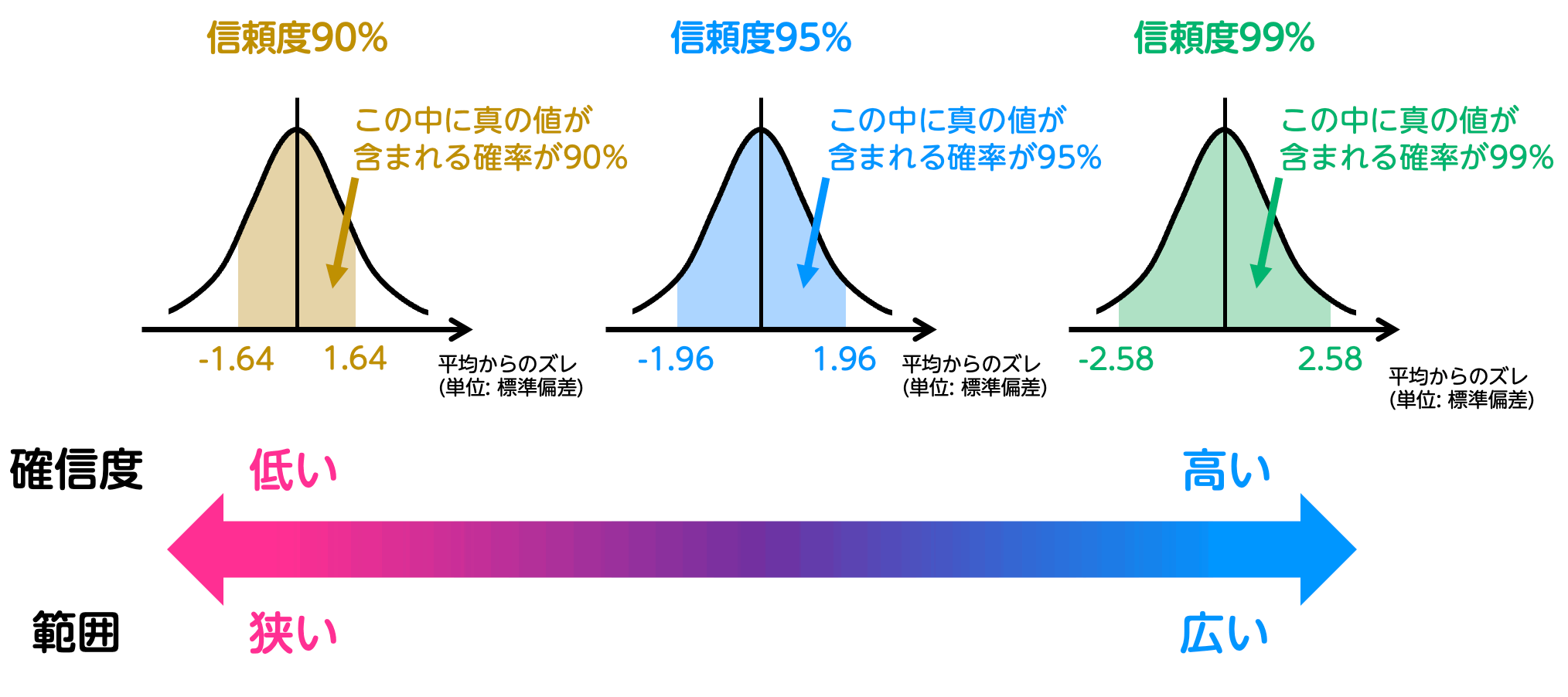
当選確実を速報する際には、嘘や誤った情報を流すと大問題となります。そのため、確実に当選確実を発表するためには高い信頼度で、区間推定を広めに取ることが重要です。
ここで、信頼度に応じて区間が具体的にどのように変わるかについては、「(2) 標準正規分布」で詳しく説明します。
(2) 標準正規分布
正規分布の中でも、平均0、標準偏差1の正規分布のことを標準正規分布と呼びます。この分布では、各値が取る範囲が具体的に決まっています。
信頼度:95%
得票率は平均 ± 標準偏差1.96個の範囲に収まります。
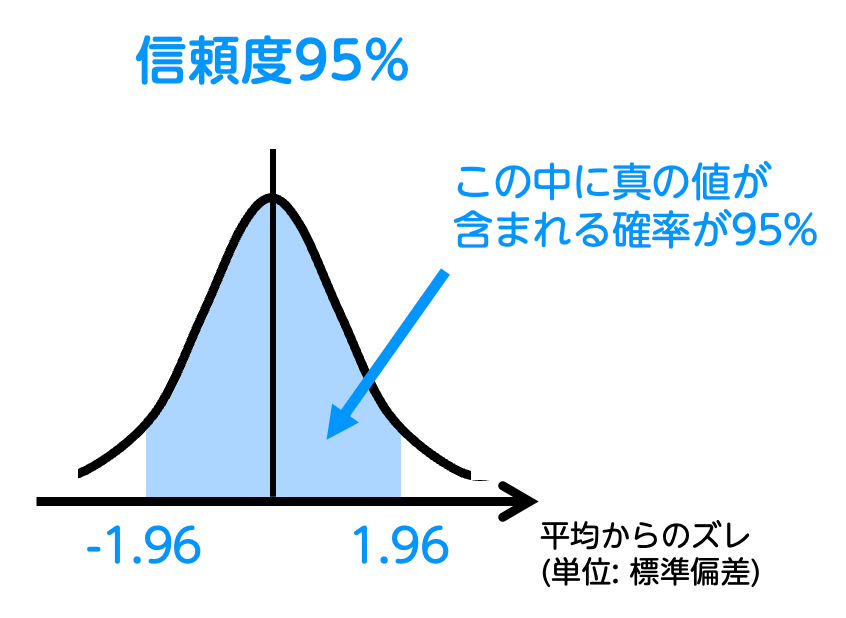
信頼度:99%(± 標準偏差2.58個分)
得票率は平均 ± 標準偏差2.58個の範囲に収まります。
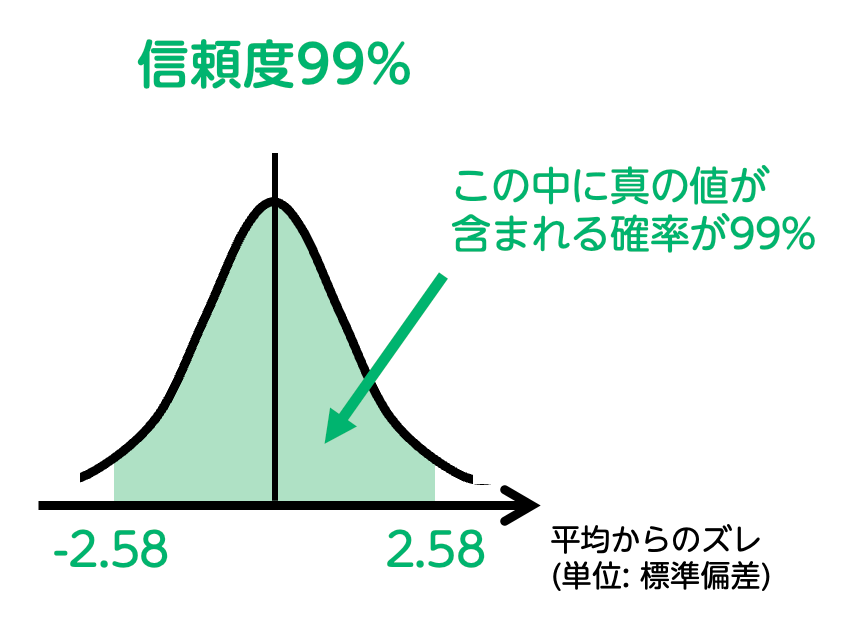
なお、実際に範囲を計算する際には、使用する正規分布に応じて、平均0、標準偏差1の標準正規分布から、変換を行います。
変化の方法については「(3) 標準正規分布 → 正規分布の変換」にて説明します。
(3) 標準正規分布 → 正規分布の変換
区間を計算するためには、平均0、標準偏差1の標準正規分布から、使用する正規分布(平均 \( p \)、標準偏差 \( \sigma \))に変換する必要があります。
まず、標準正規分布の値を \( \sigma \) 倍することで、平均0、標準偏差 \( \sigma \) の正規分布に変換します。
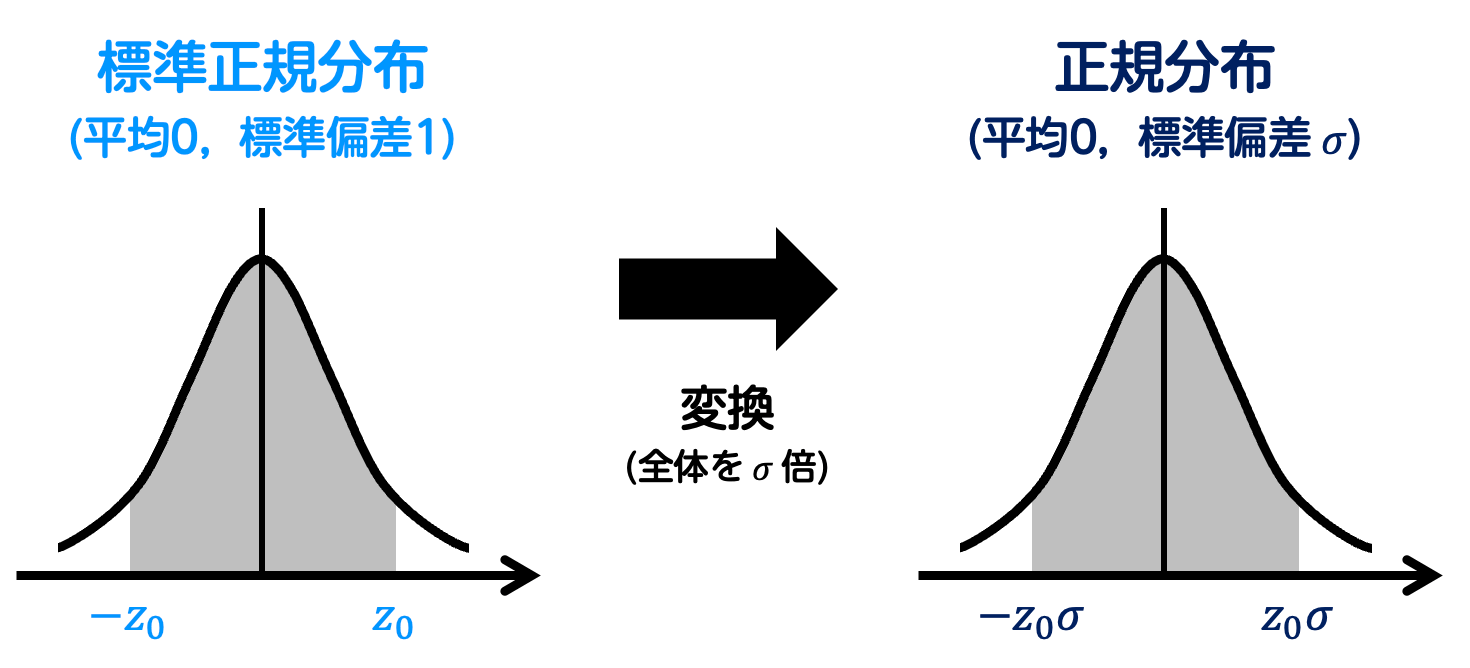
つぎに、この正規分布に値 \( p \) を加えることで、平均 \( p \) 、標準偏差 \( \sigma \) の正規分布となります。
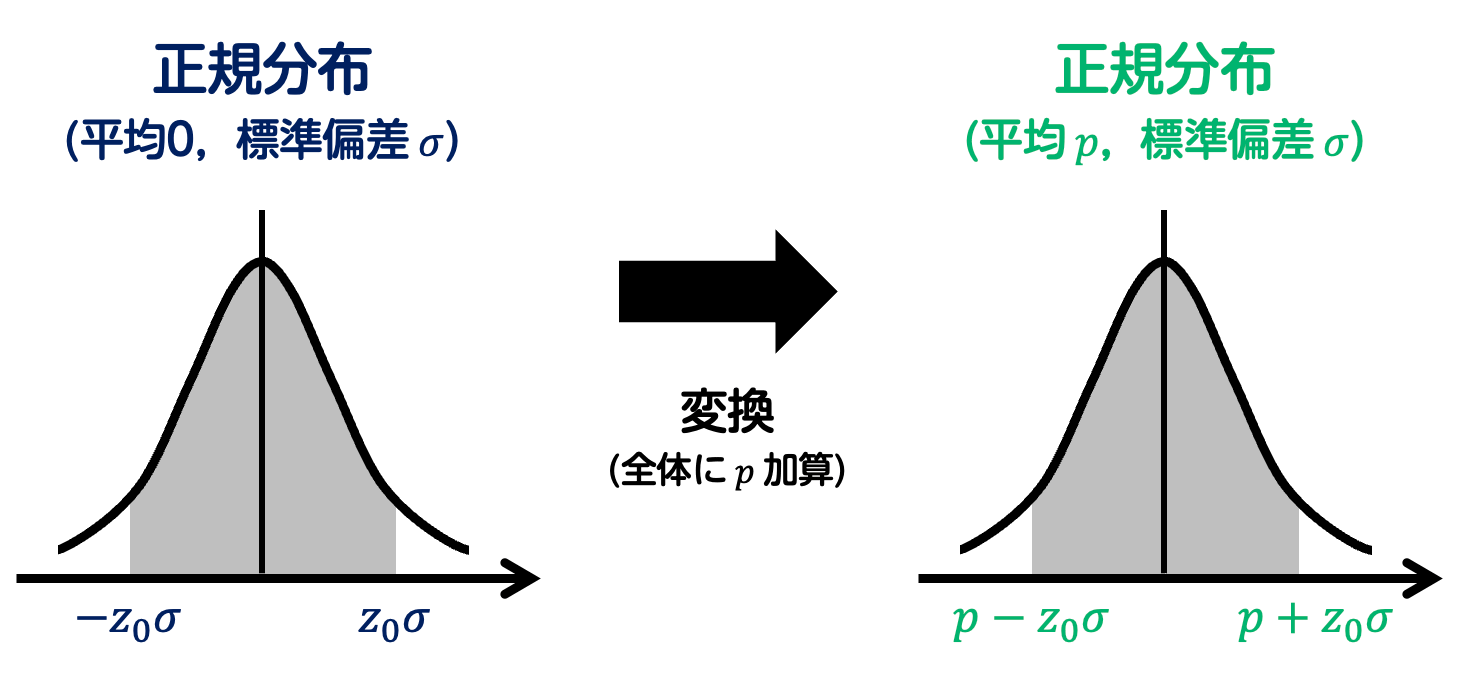
ここで、得票率 \( p \) は調査人数 \( n \) が大きいときに、調査結果内の得票率 \( \hat{p} \) と等しいとみなせます。
よって、ある信頼度における得票率 \( p \) の範囲を、次のように導出できます。\[
\hat{p} - z_0 \times \sigma \leqq p \leqq \hat{p} + z_0 \times \sigma
\]この範囲のことを、信頼区間、もしくは信頼度の情報を足してxx%信頼区間と呼びます[3]例えば、信頼度95%で区間推定した場合は、「95%信頼区間」と書きます。。
※ ここで信頼度95%のとき \( z_0 = 1.96 \)、信頼度99%のとき \( z_0 = 2.58 \) です。
なお \( \sigma \) は、Step2で求めた標準偏差\[
\sigma = \sqrt{ \frac{p(1-p)}{n} }
\]が入ります。
(4) 実際に計算してみる
では、(3)で導出した公式を使って、うさぎの得票率を推定してみましょう。
\[
\hat{p} - z_0 \times \sigma \leqq p \leqq \hat{p} + z_0 \times \sigma
\]
★ うさぎの得票率の区間推定
100人の調査結果でのうさぎの得票率は \( \hat{p} = 0.4 \)、標準偏差は \( \sigma = 0.0490 \) ですね。
[i] 信頼度95%のとき(\( z_0 = 1.96 \))\[
0.4 - 1.96 \times 0.0490 \leqq p \leqq 0.4 + 1.96 \times 0.0490
\]\[
0.304 \leqq p \leqq 0.496
\]よって、信頼度95%で区間推定した場合、うさぎの得票率は 30.4%〜49.6% となります。
\[
0.4 - 1.96 \times 0.0490 \leqq p \leqq 0.4 + 1.96 \times 0.0490
\]\[
0.274 \leqq p \leqq 0.526
\]よって、信頼度99%で区間推定した場合、うさぎの得票率は 27.4%〜52.6% となります。
※ 出口調査などで得られた得票率を区間推定することで得られた推定範囲を、信頼区間と呼びます。信頼度と合わせて95%信頼区間、99%信頼区間などと呼ばれることもあります。
例えば、上の例の場合、うさぎの得票率の信頼区間は次のようになります。
- 95%信頼区間: 30.4%〜49.6%
- 99%信頼区間: 27.4%〜52.6%
★ ねこの得票率の区間推定
同じように、ねこの得票率も区間推定してみましょう。
まずは、調査した100人での投票結果から、ねこの得票率の標準偏差を求めましょう。
調査した人数 \( n = 100 \)、100人の調査内でのねこ得票率 \( \hat{p} = 0.3 \) から、標準偏差 \( \sigma \) は次のように計算できます。
\[\begin{align*}
\sigma & = \sqrt{ \frac{p(1-p)}{n} }
\\ & = \sqrt{ \frac{0.3 \times 0.7}{100} }
\\ & = \sqrt{ \frac{0.21}{100} }
\\ & = \sqrt{ \frac{21}{10000} }
\\ & = \frac{ \sqrt{21} }{ 100 }
\\ & = 0.0458
\end{align*}\]※ 計算時、\( p = \hat{p} \) としてOK。
あとは、公式を使えば、ねこの得票率も推定できます。
\[
\hat{p} - z_0 \times \sigma \leqq p \leqq \hat{p} + z_0 \times \sigma
\]
[i] 信頼度95%のとき(\( z_0 = 1.96 \))
\[
0.3 - 1.96 \times 0.0458 \leqq p \leqq 0.3 + 1.96 \times 0.0458
\]\[
0.210 \leqq p \leqq 0.390
\]よって、信頼度95%で区間推定した場合、ねこの得票率は 21.0%〜39.0% となります。
\[
0.3 - 2.58 \times 0.0458 \leqq p \leqq 0.3 + 2.58 \times 0.0458
\]\[
0.182 \leqq p \leqq 0.418
\]よって、信頼度95%で区間推定した場合、ねこの得票率は 18.2%〜41.8% となります。
★ いぬの得票率の区間推定
同じように、いぬの得票率も区間推定してみましょう。
まずは、調査した100人での投票結果から、いぬの得票率の標準偏差を求めましょう。
調査した人数 \( n = 100 \)、100人の調査内でのいぬ得票率 \( \hat{p} = 0.2 \) から、標準偏差 \( \sigma \) は次のように計算できます。
\[\begin{align*}
\sigma & = \sqrt{ \frac{p(1-p)}{n} }
\\ & = \sqrt{ \frac{0.2 \times 0.8}{100} }
\\ & = \sqrt{ \frac{0.16}{100} }
\\ & = \sqrt{ \frac{16}{10000} }
\\ & = \frac{ 4 }{ 100 }
\\ & = 0.04
\end{align*}\]※ 計算時、\( p = \hat{p} \) としてOK。
あとは、公式を使えば、いぬの得票率も推定できます。
\[
\hat{p} - z_0 \times \sigma \leqq p \leqq \hat{p} + z_0 \times \sigma
\]
[i] 信頼度95%のとき(\( z_0 = 1.96 \))
\[
0.2 - 1.96 \times 0.04 \leqq p \leqq 0.2 + 1.96 \times 0.04
\]\[
0.122 \leqq p \leqq 0.278
\]よって、信頼度95%で区間推定した場合、いぬの得票率は 12.2%〜27.8% となります。
\[
0.2 - 2.58 \times 0.04 \leqq p \leqq 0.2 + 2.58 \times 0.04
\]\[
0.097 \leqq p \leqq 0.303
\]よって、信頼度95%で区間推定した場合、いぬの得票率は 9.7%〜30.3% となります。
★ あざらしの得票率の区間推定
最後に、あざらしの得票率も区間推定してみましょう。
まずは、調査した100人での投票結果から、あざらしの得票率の標準偏差を求めましょう。
調査した人数 \( n = 100 \)、100人の調査内でのねこ得票率 \( \hat{p} = 0.1 \) から、標準偏差 \( \sigma \) は次のように計算できます。
\[\begin{align*}
\sigma & = \sqrt{ \frac{p(1-p)}{n} }
\\ & = \sqrt{ \frac{0.1 \times 0.9}{100} }
\\ & = \sqrt{ \frac{0.09}{100} }
\\ & = \sqrt{ \frac{9}{10000} }
\\ & = \frac{ 3 }{ 100 }
\\ & = 0.03
\end{align*}\]※ 計算時、\( p = \hat{p} \) としてOK。
あとは、公式を使えば、ねこの得票率も推定できます。
\[
\hat{p} - z_0 \times \sigma \leqq p \leqq \hat{p} + z_0 \times \sigma
\]
[i] 信頼度95%のとき(\( z_0 = 1.96 \))
\[
0.1 - 1.96 \times 0.03 \leqq p \leqq 0.1 + 1.96 \times 0.03
\]\[
0.041 \leqq p \leqq 0.159
\]よって、信頼度95%で区間推定した場合、あざらしの得票率は 4.1%〜15.9% となります。
\[
0.1 - 2.58 \times 0.03 \leqq p \leqq 0.1 + 2.58 \times 0.03
\]\[
0.023 \leqq p \leqq 0.177
\]よって、信頼度99%で区間推定した場合、あざらしの得票率は 2.3%〜17.7% となります。
今まで求めた結果をすべて表にすると、次の結果となります。
表. 信頼度95%での各候補者の得票率推定結果
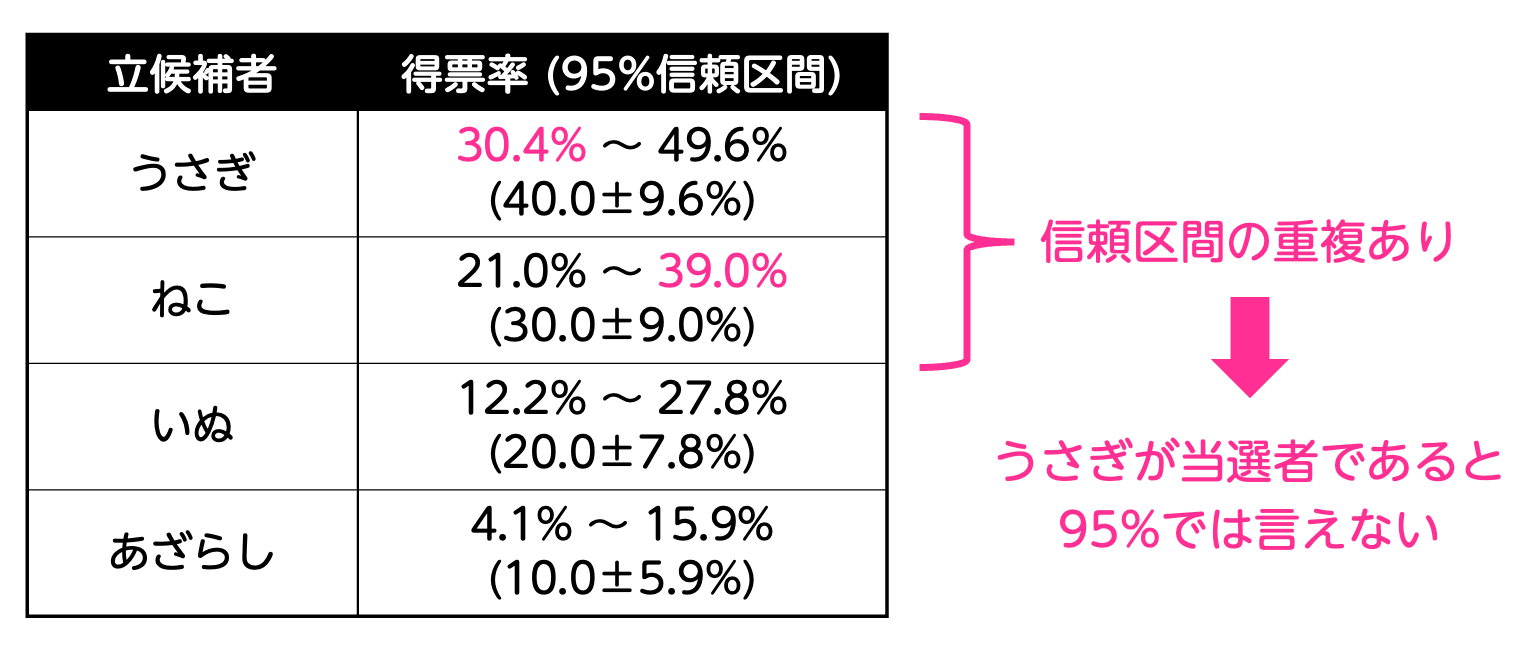
表. 信頼度99%での各候補者の得票率推定結果
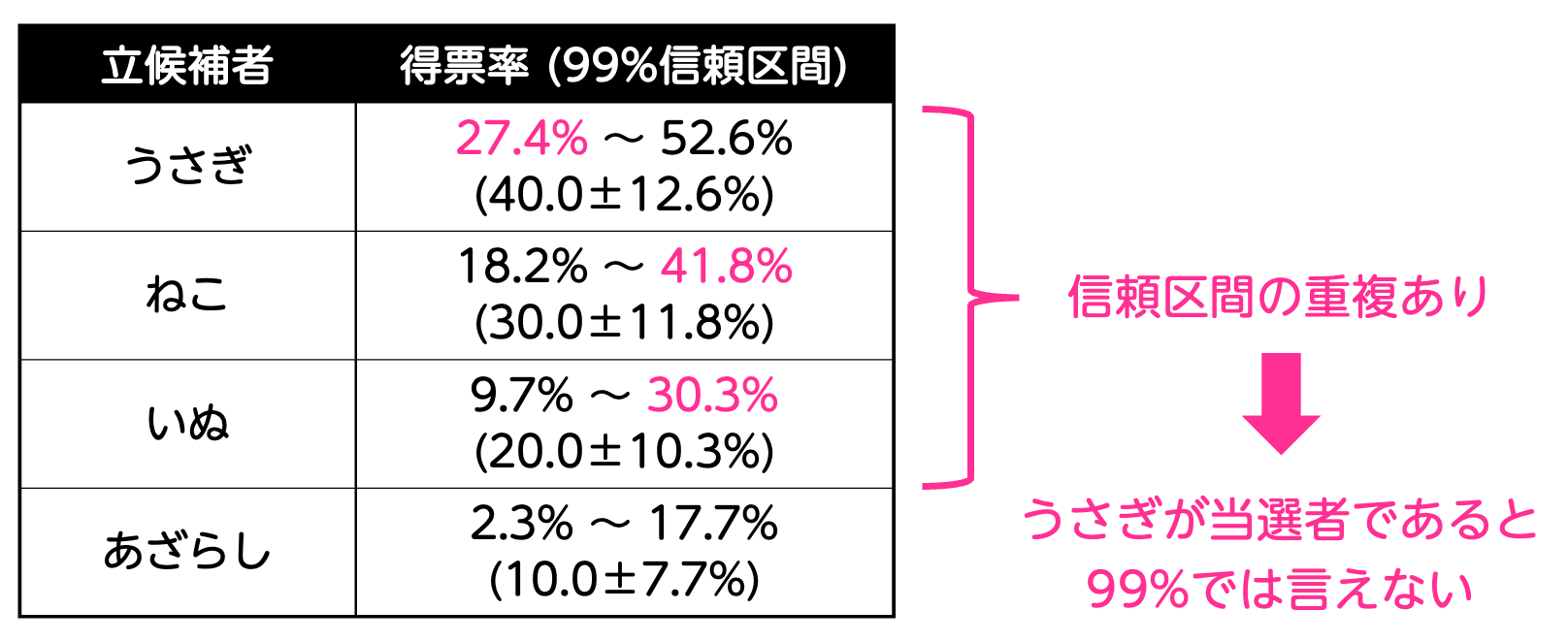
この結果を見ると、信頼度95%、99%ともに得票率1位のうさぎの信頼区間と、得票率2位のねこの信頼区間で重なっている部分がありますね。
そのため、この結果だけでは「明らかにうさぎが一番票が集まっている(=当選確実)」とは言えません。
(5) 信頼区間を狭めるには?
出口調査などで得られた信頼区間は、得票率の推定範囲を示します。しかし、もし信頼区間が広すぎると、候補者間で得票率が重なり、誰が一番票を集めているか(つまり、誰が当選するか)を確定するのが難しくなります。これを防ぐためには、信頼区間を狭めることが必要です。
ここからは、信頼区間を狭めるために何をすればよいかを考えてみましょう。
信頼区間を狭めるためには、まず標準偏差 \( \sigma \) を小さくする必要があります。標準偏差はデータのばらつきを示す指標であり、この値が小さくなると、得票率の推定値のばらつきが小さくなり、信頼区間も狭くなります。
まず、標準偏差 \( \sigma \) は次のように計算されます。\[
\sigma = \sqrt{ \frac{p(1-p)}{n} }
\]
ここで、\( p \), \( n \) は以下のとおりです。
- \( p \): 得票率
※ 出口調査での得票率 \( \hat{p} \) で計算する。 - \( n \): 調査した人数
[i] 得票率 \( \hat{p} \) は操作できない
まず、\( \hat{p} \)(出口調査内での得票率)を変えることはできません。なぜなら、得票率は実際の出口調査から導かれる数値だからです。
言い換えると、候補者に対する投票がどれくらいだったかは調査結果から決まってしまっているので、得票率を操作することは不可能です。
[ii] 調査する人数 \( n \) は増やすことができる
一方で、調査人数 \( n \) は増やすことが可能です。調査人数を増やすことで、標準偏差を小さくすることができるため、信頼区間を狭くすることができます。
なぜなら、標準偏差の式を見ると、\( n \) が分母にあるため、\( n \) を大きくすると分母が小さくなり、全体の値が小さくなるからです。つ
まり、調査人数を増やすことで、標準偏差 \( \sigma \) を小さくでき、その結果、得票率の信頼区間も狭くなるのです。
具体例を見てみよう
では、調査人数 \( n \) を増やすことで、標準偏差と信頼区間がどのように変化するか、具体的に見てみましょう。
先ほど、調査人数が100人のときの、うさぎの得票率の95%信頼区間は次のように求められましたね。(30.4%〜49.6%、40.0% ± 9.6%)\[
0.304 \leqq p \leqq 0.496
\]
ここで、調査人数を4倍の400人に増やしたとしましょう(得票率は変化なし)。すると、新しい標準偏差 \( \sigma' \) は、調査内での得票率 \( \hat{p} = 0.4 \)、調査した人数 \( n = 400 \) より、次のように求められます。
\[\begin{align*}
\sigma' & = \sqrt{ \frac{p(1-p)}{n} }
\\ & = \sqrt{ \frac{0.4 \times 0.6}{400} }
\\ & = \sqrt{ \frac{0.24}{400} }
\\ & = \sqrt{ \frac{24}{40000} }
\\ & = \frac{ 2 \sqrt{6} }{ 200 }
\\ & = \frac{ \sqrt{6} }{ 100 }
\\ & = 0.0245
\end{align*}\]※ 計算時、\( p = \hat{p} \) としてOK。
よって、新しい信頼区間は、次のように計算できます。
\[
\hat{p} - z_0 \times \sigma' \leqq p \leqq \hat{p} + z_0 \times \sigma'
\]\[
0.4 - 1.96 \times 0.0245 \leqq p \leqq 0.2 + 1.96 \times 0.0245
\]\[
0.352 \leqq p \leqq 0.448
\]
よって、95%信頼区間は 35.2%〜44.8% (40.0 ± 4.8%) となり、調査人数を4倍の400人に増やすことで、信頼区間の幅が元の信頼区間 40.0% ± 9.6% の半分に狭まっていることがわかりますね。
同じように、調査人数を4倍の400人に増やした場合のうさぎの得票率の99%信頼区間、および残りの候補者(ねこ、いぬ、あざらし)の信頼区間についても求めていきましょう。
すると、次の結果が得られます。
★ 95%信頼区間結果
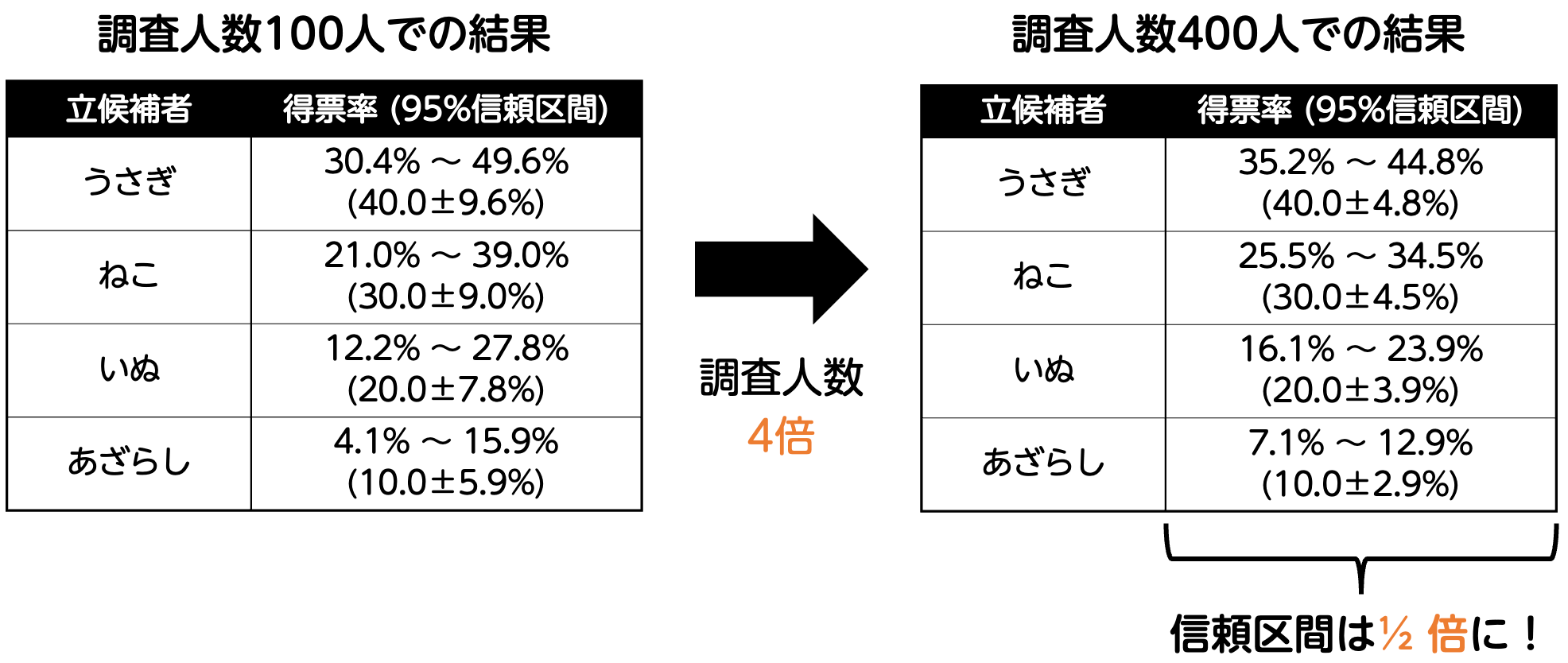
★ 99%信頼区間結果

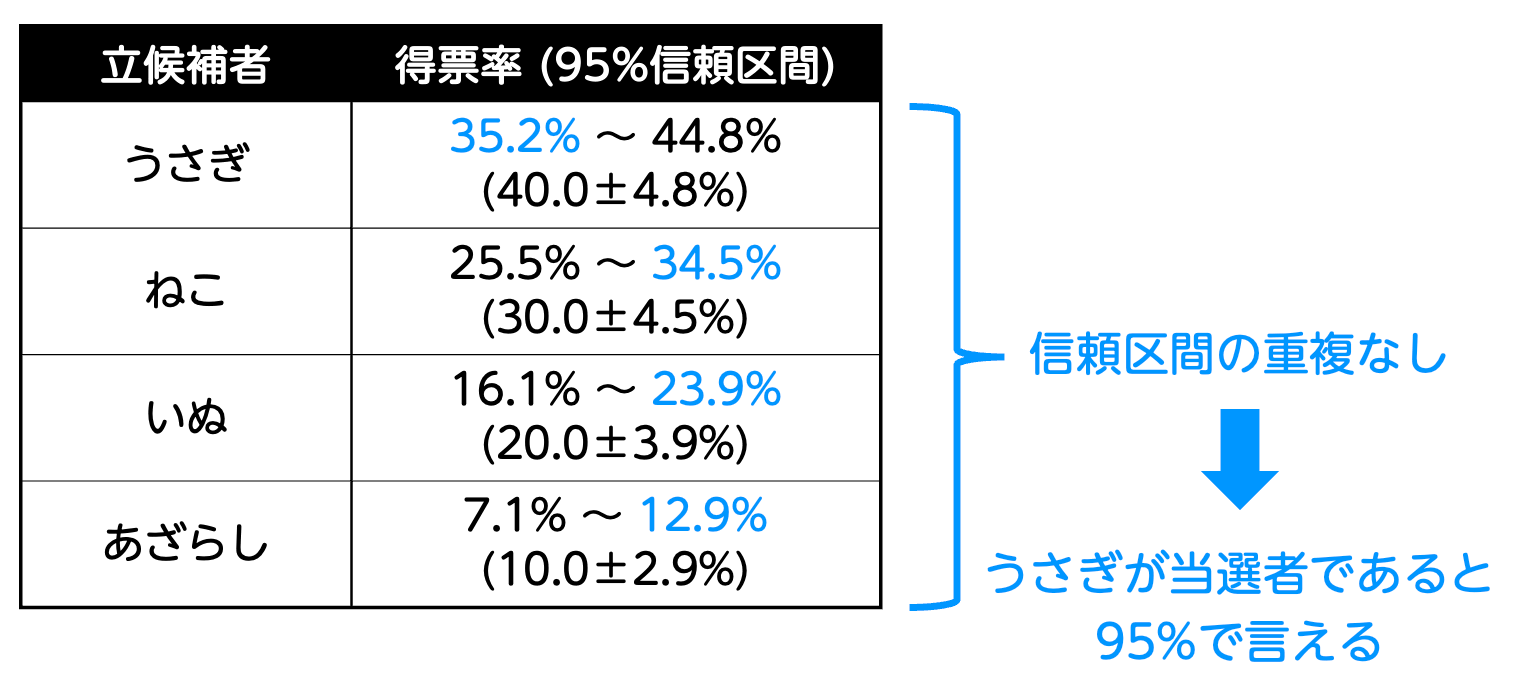
この結果を見てみると、信頼度95%での区間推定では、得票率1位の「うさぎ」の信頼区間と、得票率2位の「ねこ」の信頼区間が完全に重なっていないことがわかります。具体的には、うさぎの信頼区間はねこの信頼区間の外側にあり、重なる部分が全くありません。これは、「95%の確率でうさぎが一番票を集めている」と自信を持って言えることを意味します。
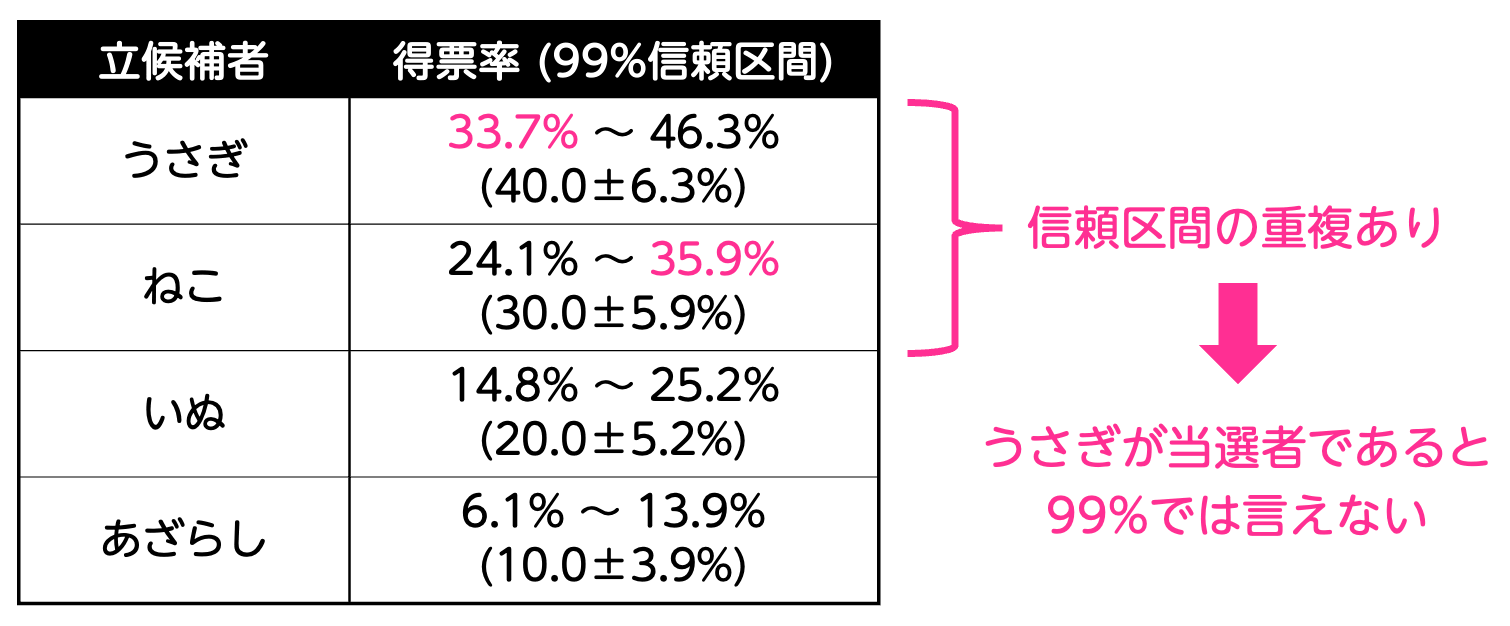
しかし、信頼度99%での区間推定では、状況が異なります。うさぎの信頼区間とねこの信頼区間が一部重なっているため、「99%の確率でうさぎが一番票を集めている」という断言はできません。なぜなら、信頼度99%の範囲では、ねこが一番票を集めている可能性も含まれてしまうからです。
ここで、調査人数を増やすと、信頼区間はどのようなるかを文字式を使った形で、一般化してみましょう。
調査人数を \( a^2 \) 倍にすると、得票率の標準偏差は \( \frac{1}{a} \) 倍 となる。
そのため、得票率の信頼区間の幅も \( \frac{1}{a} \) 倍となる。
| 調査人数 | 信頼区間 |
|---|---|
| 元の人数 | \( \hat{p} - z_0 \sigma \leqq p \leqq \hat{p} + z_0 \sigma \) \( \hat{p} \pm z_0 \sigma \) |
| 元の人数の \( a^2 \) 倍 | \( \hat{p} - \frac{1}{a} z_0 \sigma \leqq p \leqq \hat{p} + \frac{1}{a} \sigma \) \( \hat{p} \pm \frac{1}{a} z_0 \sigma \) |
★ 簡単な導出
元の人数のときの標準偏差\[
\sigma = \sqrt{ \frac{p(1-p)}{n} }
\]
人数を \( \textcolor{red}{a^2} \) 倍にした場合の標準偏差\[\begin{align*}
\sigma' & = \sqrt{ \frac{p(1-p)}{ \textcolor{red}{a^2} n} }
\\ & = \sqrt{ \frac{1}{a^2} \times \frac{p(1-p)}{ n} }
\\ & = \sqrt{ \frac{1}{a^2} } \times \sqrt{ \frac{p(1-p)}{ n} }
\\ & = \frac{1}{ \sqrt{ a^2 } } \times \sqrt{ \frac{p(1-p)}{ n} }
\\ & = \frac{1}{ a } \times \sqrt{ \frac{p(1-p)}{ n} }
\\ & = \frac{1}{ a } \sigma
\end{align*}\]
スポンサードリンク
3. 確実に当選確実を出すためには何人の調査が必要?
出口調査を行う目的は、得票率を推定し、候補者の当選確実性を判断することです。
しかし、調査の結果が精度良くないと、「誰が当選するか」を確実に判断することができません
では、「確実に当選確実を出すためには、何人の調査が必要なのか?」という疑問を解決していきましょう。
(1) 得票率がある程度予測できる場合
まず、候補者の得票率がある程度わかっている場合、つまり、出口調査の初期結果からある程度の予測投票率 \( \hat{p} \) がわかっているときに、どれくらいの人数を調査すれば良いかを計算します。
例えば、事前調査にて、うさぎ、ねこ、いぬ、あざらしの得票率が40%、30%、20%、10%程度になることがわかっていたとします。
この情報を元に、信頼度99%で当選確実を言うためには、得票率が高いうさぎ、ねこの信頼区間を重複させないようにする必要があります。
ここで、事前調査でうさぎの得票率が40%、ねこの得票率が30%であると予測されているため、得票率の信頼区間が±5%と設定すれば、うさぎの得票率が約35%~45%となり、ねこの得票率が約25%~35%となるため、信頼区間が重ならないようにすることができ、うさぎの当選確実を予測することができます。
[i] 必要な調査人数の計算1
では、実際に「当選確実を出すために、どれくらいの調査人数が必要か」を計算してみましょう。
今回のケースでは、信頼度99% で「うさぎが当選する確率を確実に知りたい」という状況を考えます。目標は、99%信頼区間の幅が ±5% 以内に収まるような調査人数の最小値を求めることです。
まず、得票率 \( \hat{p} = 0.4 \) が予測できているため、標準偏差は次の式で計算できます。\[
\sigma = \sqrt{ \frac{p(1-p)}{n} }
\]
ここで、\( n \) が大きいので、\( \hat{p} = p \) で近似できます。そのため、標準偏差 \( \sigma \) を次のように求めることができます。\[\begin{align*}
\sigma & = \sqrt{ \frac{0.4 \times 0.6}{n} }
\\ & = \sqrt{ \frac{0.24}{n} }
\\ & = \sqrt{ \frac{24}{100n} }
\\ & = \frac{ \sqrt{24} }{ \sqrt{100} \times \sqrt{n} }
\\ & = \frac{ 2 \sqrt{6} }{ 10 \sqrt{n} }
\\ & = \frac{ \sqrt{6} }{ 5 \sqrt{n} }
\end{align*}\]
ここで、信頼度99%なので、\( z_0 = 2.58 \) です。そのため、信頼区間が±5%となるように、以下の不等式を満たす調査人数 \( n \) を求めます。\[
z_0 \times \sigma \leqq 0.05
\]\[
2.58 \times \frac{ \sqrt{6} }{ 5 \sqrt{n} } \leqq 0.05
\]\[
2.58 \times \frac{ \sqrt{6} }{ 5 } \leqq 0.05 \sqrt{n}
\]\[
2.58 \times \frac{ \sqrt{6} }{ 5 \times 0.05 } \leqq \sqrt{n}
\]\[
2.58 \times 4 \sqrt{6} \leqq \sqrt{n}
\]\[
\sqrt{639.014} \leqq \sqrt{n}
\]\[
n \geqq 639.014
\]
このように、信頼区間を±5%に収めるためには、調査人数が640人以上必要であることがわかります。
[ii] 必要な調査人数の計算2
同等の計算を、得票率 \( \hat{p} = 0.3 \) が予測されているねこに対しても実施します。
すると、つぎの計算式となります。\[
z_0 \times \sqrt{ \frac{ 0.3 \times 0.7 }{n} } \leqq 0.05
\]\[
2.58 \times \sqrt{ \frac{ 0.21 }{n} } \leqq 0.05
\]
この式を解くと、調査人数 \( n \) の下限は以下のように求まります。\[
n \geqq 559.138
\]
つまり、ねこの信頼区間を±5%に収めるためには、調査人数が560人以上必要であることがわかります。
結論のまとめ
[i], [ii] の結果をあわせると、調査人数を640人以上とすることで、うさぎの信頼区間、ねこの信頼区間をともに±5%に収めることができます。そのため、調査人数を640人以上にすることで、確実に当選確実を言うことができます。
実際に、調査人数を640人にして得票率を区間推定すると、次のような結果が得られます。
確かに、99%信頼区間が重複しておらず、うさぎが当選者(=一番投票されている)といえますね。

★ 実は、ねこの計算はしなくてもOK
なお、ねこの信頼区間を±5%に収めるための計算は、実際には不要です。理由は次の通りです。
- 得票率が50%に近いほど、標準偏差が大きくなるため、信頼区間が広くなります。
- 逆に、得票率が50%から離れるほど、標準偏差が小さくなるため、信頼区間が狭くなります。
したがって、40%のうさぎに対して640人の調査が必要であれば、30%のねこに対しては、さらに多くの調査人数が必要になることはありません。そのため、ねこに対する計算は省略可能です。
実際、ねこの信頼区間も±5%に収まるために必要な人数は「560人以上」と、640人よりも小さい値となっています。
★ 得票率が50%に近いほど、信頼区間が大きくなる理由
得票率が50%に近いほど、信頼区間が広くなる理由を確認しておきましょう。\[
\hat{p} - z_0 \times \sigma \leqq p \leqq \hat{p} + z_0 \times \sigma
\]
まず、標準偏差の式は次の通りでしたね。\[
\sigma = \sqrt{ \frac{\textcolor{red}{p(1-p)}}{n} }
\]
この式の分子部分、\( \textcolor{red}{p(1-p)} \) に注目します。これを平方完成すると、つぎの式が導出できます。\[\begin{align*}
p(1-p) & = p-p^2
\\ & = - \left( p - \frac{1}{2} \right)^2 + \frac{1}{4}
\end{align*}\]
この式から、\( p = \frac{1}{2} \) のときに \( p(1-p) \) が最大値を取ることがわかります。
したがって、得票率が50%のときに、標準偏差が最も大きくなり、信頼区間も最も広くなる事がわかります。
(2) 得票率が全く予測できない場合
候補者の得票率が全く予測できない場合、どのように対処すればよいかを考えてみましょう。
このような場合、得票率が最も不確実な状況として50%(0.5)を仮定します。
なぜなら、得票率が50%のときにばらつきが最大となり、信頼区間が最も広くなるからです。この仮定をすることで、最も広い信頼区間を確保するための最悪のケースとして取り扱うことができます。
★ 必要な調査人数の計算
では、実際に「当選確実を出すために、どれくらいの調査人数が必要か」を計算してみましょう。
前提条件として、信頼度99%で「うさぎが当選する確率を確実に知りたい」という状況を考えます。ただし、得票率が全く予測できていないため、信頼区間の幅を±3%以内に収めたいと仮定します。
まず、得票率 \( \hat{p} = 0.5 \) と仮定しているため、標準偏差は次のようにで計算できます。\[
\sigma = \sqrt{ \frac{p(1-p)}{n} }
\]
ここで、調査人数 \( n \) が大きいため、近似的に \( \hat{p} = p \) とみなすことができます。したがって、標準偏差 \( \sigma \) は次のように求められます。
\[\begin{align*}
\sigma & = \sqrt{ \frac{0.5 \times 0.5}{n} }
\\ & = \sqrt{ \frac{0.25}{n} }
\\ & = \sqrt{ \frac{1}{4n} }
\\ & = \frac{ \sqrt{1} }{ \sqrt{4} \times \sqrt{n} }
\\ & = \frac{ 1 }{ 2\sqrt{n} }
\end{align*}\]
次に信頼度99%の場合の \( z_0 = 2.58 \) を使って、信頼区間の幅が±3%に収めるために必要な調査人数 \( n \) を求めます。
つまり、信頼区間の幅が±3%であるため、次の不等式を満たすような最小の \( n \) を求めればOKです。\[
z_0 \times \sigma \leqq 0.03
\]
ここから、代入して式を整理していきます。\[
2.58 \times \frac{ 1 }{ 2\sqrt{n} } \leqq 0.03
\]\[
2.58 \times \frac{ 1 }{ 2 } \leqq 0.03 \sqrt{n}
\]\[
2.58 \times \frac{ 1 }{ 2 \times 0.03 } \leqq \sqrt{n}
\]\[
43 \leqq \sqrt{n}
\]\[
\sqrt{1849} \leqq \sqrt{n}
\]\[
n \geqq 1849
\]
したがって、得票率が全く予測できない場合に、信頼区間を±3%に収めるためには、調査人数が少なくとも1849人以上必要であることがわかります。
4. まとめ:出口調査時のポイント
今回は、出口調査から得票率を正確に抽出し、当選確実を出すための仕組みについて、数学的な視点も含めて解説しました。
出口調査は、選挙や投票後に得票率を予測する重要な手段ですが、調査の方法を誤ると、誤った結果を導くことになります。そこで、出口調査を正確に行うために、以下の重要なポイントに注意しましょう。
ポイント1. 特定の地域や年代に偏った調査とならないこと
出口調査では、いろいろな地域、年代の人に実施してもらうことが重要です。
★ 重要な理由
特定の街に住んでいる人や特定の年代の人だけに調査を行うと、その結果が全体の投票結果を正確に反映しません。
例えば、ある街の住民のみを対象に調査をすると、その地域特有の意見が全体の傾向として誤って扱われてしまいます。
そのため、出口調査の結果が偏り、実際の選挙結果と異なる誤った結論に繋がる可能性があります。
★ 対策
様々な地域、年代、性別など、さまざまな背景を持つ有権者をランダムに選んで調査を実施し、偏りをなくすようにしましょう。
ポイント2. 出口調査をする人は無作為に決めること
調査対象者をランダムに選ぶことが重要です。出口調査を実施する際に、特定の人物を意図的に選んで調査を行うと、その結果が偏り、全体の得票傾向を反映しない可能性があります。
★ 重要な理由
もし調査対象者が特定の意見を持つ人々だけに偏っていると、その結果が他の有権者層の意見を正確に反映しません。
例えば、「10人に1人おきに調査を実施する」などの方法で、無作為に調査対象者を選ぶことが基本です。
意図的に調査対象者を選ぶことで、ある候補者を支持している人だけに調査が集中することになり、調査結果が偏ってしまいます。
★ 対策
調査対象者は完全にランダムに選び、全ての有権者層を公平に反映させるようにしましょう。
ポイント3. 様々な時間帯で調査をすること
出口調査は、できるだけ多くの時間帯で実施することが求められます。投票の時間帯によって投票者の層が変わるため、特定の時間帯に偏らないように調査を行う必要があります。
★ 重要な理由
例えば、投票所が閉まる直後に調査を実施すると、昼間に投票した高齢者層や、早朝に投票した働き手層の意見が反映されにくくなります。
また、特定の時間帯にのみ調査を行うと、夜間に投票した若い人々や、昼間の時間帯に投票した主婦層など、投票者層が偏ってしまう恐れがあります。
その結果、出口調査の結果が全体の投票結果と異なる偏ったものになってしまいます。
★ 対策
投票が行われているすべての時間帯でランダムに調査を実施し、時間帯による偏りを防ぎましょう。
調査の失敗例: 1936年アメリカ大統領選挙の誤り—「リッパマンの大失敗」
1936年のアメリカ大統領選挙は、世論調査の歴史における有名な誤りの事例として広く知られています。この事例を通じて、調査における偏りがどれだけ重大な影響を与えるかを学びましょう。
この選挙では、民主党候補のフランクリン・D・ルーズベルト(以下、ルーズベルト)と、共和党候補のアルフレッド・L・ランドン(以下、ランドン)が対決しました。
当時、調査会社「リッパマン(Lippmann)」が行った世論調査では、ランドン候補が勝利し、ルーズベルト候補が敗北すると予測していました。しかし、実際にはルーズベルトが圧倒的な勝利を収め、リッパマン社の予測とは全く異なる結果が出ました。
★ なぜ予測が外れたのか?
リッパマン社の予測が外れた主な理由は、調査対象に偏りがあったことにあります。具体的には、彼らが使用した調査方法に問題がありました。
リッパマン社は、電話調査を用いて選挙の結果を予測しました。彼らは、電話を所有している層が全体の投票意向を反映していると仮定して調査を行ったのですが、これは明らかに誤りでした。
当時、電話の普及率は非常に低く、特に都市部に住む裕福な層が主に電話を所有していました。そのため、調査結果は裕福な層の意見に偏ってしまったのです。
裕福な層は共和党のランドン候補を支持していた一方、貧困層や農村部に住む有権者は、民主党のルーズベルト候補を支持していました。電話調査では、裕福な層の意見だけが反映され、貧困層や農村部の意見が十分に調査に含まれなかったため、リッパマン社の予測が外れたのです。
この事例からもわかるように、出口調査を行う際には調査対象の偏りを避けることが非常に重要です。以下の3つのポイントを守ることで、偏りのない調査が実現できます。
★ 3つのポイント
ポイント1. 特定の地域や年代に偏った調査とならないこと
様々な地域や年代の人々から均等にサンプルを取ることが重要です。特定の地域や年代に偏ると、全体の投票結果を正確に反映できません。
ポイント2. 出口調査をする人は無作為に決めること
出口調査の対象者は無作為に選び、意図的に特定の人々を調査対象にしないようにしましょう。これによって、偏りがなくなり、より正確な結果が得られます。
ポイント3. 様々な時間帯で調査を実施すること
投票所が開いている時間帯によって、有権者の属性が異なる可能性があります。したがって、調査は様々な時間帯で行うべきです。特定の時間帯にだけ調査を行うと、特定の有権者層に偏った結果が得られます。
関連広告・スポンサードリンク





![うさぎでもわかる計算機システム Part01 2進数 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612102246-1-150x150.gif)