スポンサードリンク
こんにちは、ももやまです。
今回から3回に分けてF分布についてお勉強していきましょう。
第1回目は、まず「母分散の比の区間推定」方法について見ていきましょう。
※ カイ2乗分布の内容が出てくるので、カイ2乗分布がまだよくわかってない or 初見だよ、という人は、下の記事でカイ2乗分布の内容を確認することをお勧めします。
スポンサードリンク
1. F分布とは(定義)
F分布は、2つの標本のばらつき度合いを相対的に評価するために作られました。ここでは、相対的に2つの標本のばらつき度合いの評価式をどのように定義したかを見ていきましょう。
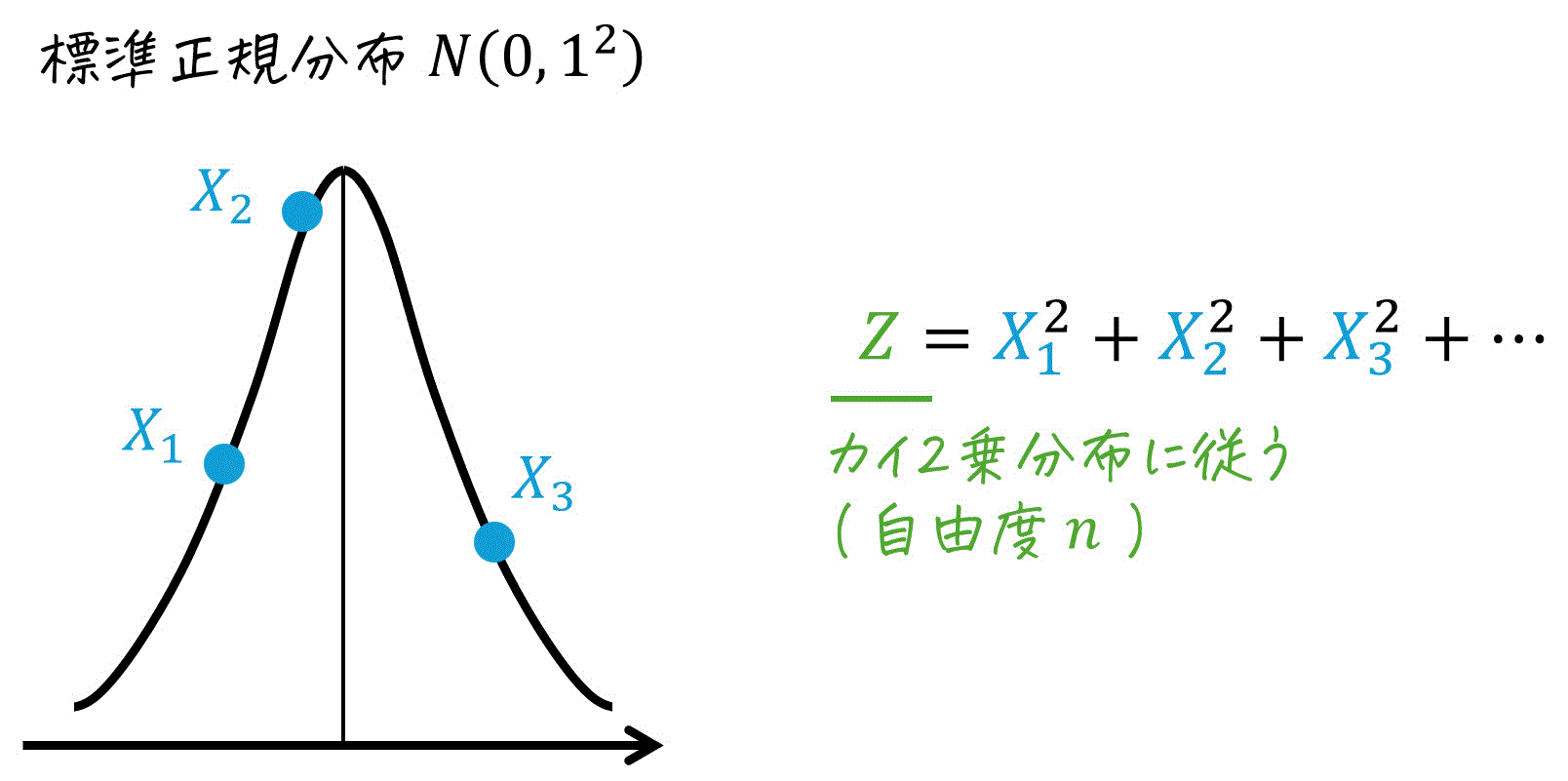
F分布での登場人物は、2つのカイ2乗分布に従う2つの \( \chi_1^2 \), \( \chi_2^2 \) です。この、\( \chi_1^2 \), \( \chi_2^2 \) は、各標本のデータのばらつき度合いを表す指標です。
しかし、カイ2乗値 \( \chi_1^2 \), \( \chi_2^2 \) の大きさは、ばらつき度合いだけでなく、自由度にも依存します。そのため、自由度が異なるカイ2乗値同士を直接的に比較することができません。
そこでF分布では、2つの標本のばらつき度合いを相対的に比較するときに「各標本ごとのカイ2乗値 \( \chi_1^2 \), \( \chi_2^2 \) を各標本ごとの自由度\( k_1 \), \( k_2 \) を割った値 \( \frac{ \chi_1^2 }{k_1} \), \( \frac{ \chi_2^2 }{k_2} \)」で比べることで、自由度が異なるカイ2乗値同士のばらつき度合いを、公平に比べることができるようにしています。
標本2を基準として、標本1のばらつき度合いを相対的に表したもの\[
F = \frac{ \frac{ \chi_1^2 }{k_1 } }{ \frac{ \chi_2^2 }{k_2 } }
\]は、F分布に従う。(自由度: \( ( k_1, k_2 ) \))
【変数の意味】
- 標本1について
- \( \chi_1^2 \) … カイ2乗値
- \( k_1 \) … 自由度
- 標本2について
- \( \chi_2^2 \) … カイ2乗値
- \( k_2 \) … 自由度
※ 自由度が \( ( k_1, k_2 ) \) については、2章の「F分布表の使い方」にて詳しく説明します。
スポンサードリンク
2. F分布表の使い方
F分布を用いた推定や仮説検定を実施する場合は、t分布、正規分布、カイ2乗分布のときと同じように専用の表(F分布表)から値を読み取り、読み取った値と計算されたF統計量から推定、仮説結果を出します。
例題、練習問題を解く際にお使いください。
ポイント1. グラフが左右対称ではない
F分布のグラフは、カイ2乗分布のグラフと同じように、左右対称ではありません。
そのため、F分布を用いた区間推定や両側検定を実施するときには、2つの値(上側の点、下側の点)を確認する必要があります。
※ 上側、下側は上位、下位みたいなものです。例えば、上側5%の点というのは、ある値が上位5%に属するときの値を指しています。
ポイント2. 2標本の自由度によって、形が変わる
F分布のグラフは、2つの自由度 \( ( k_1, k_2 ) \) によってグラフの概形が変化します。
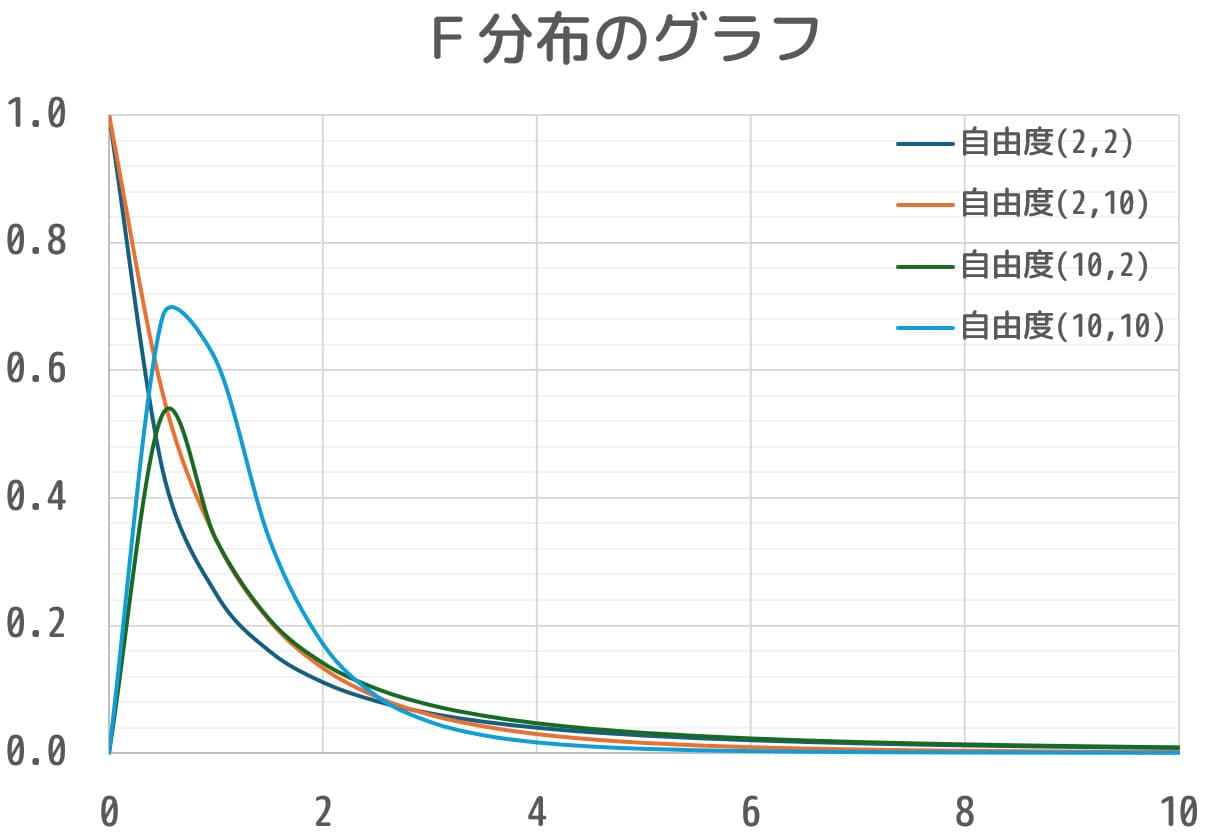
そのため、F分布表から値を読み取る際には
- 上側確率(与えられた信頼度 or 有意水準から計算する)
- 標本1の自由度 \( k_1 \)
- 標本2の自由度 \( k_2 \)
の3つの要素を把握する必要があります。
F分布表の構造としては、各上側確率 \( \alpha \) ごとに、「標本1の自由度 \( k_1 \)、標本2の自由度 \( k_2 \) 」表があります。
表.F分布表(\( \alpha = 0.050 \) のとき、\( \alpha = 0.025 \) の2つの表がある
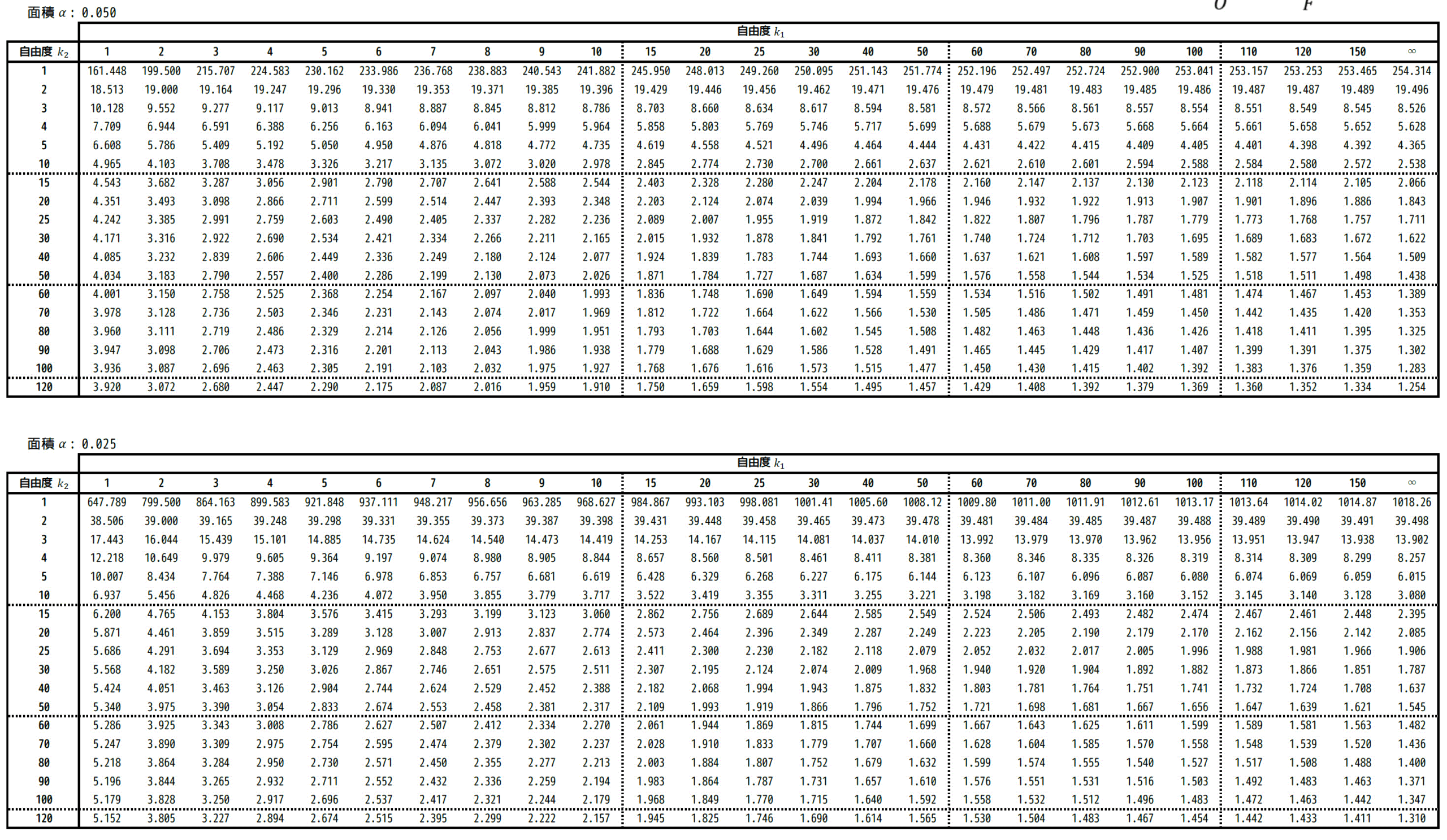
今まで出てきたt分布、カイ2乗分布では、2つの要素(信頼度 or 有意水準、自由度1つ)を用いて表から値を読み取っていたのに対し、F分布表では、自由度が2つになっているため、分布表を読み取るが少し大変かもしれません[1]例題や練習問題で、表の読み方も書いているので、ご安心を!。
※ 表の読み方は、例題や練習問題にて改めて解説します。
ポイント3. 下側確率の読み取り方にはひと工夫必要
F分布表では、上側確率 5%, 2.5%(表によっては1%, 0.5%もあり)での値のみが与えられ、下側確率 5%, 2.5%, (1%, 0.5%)の値は与えられません。
そのため、下側確率 \( \alpha \) の値をF分布表から読み取る際には、ひと工夫が必要です。
下側確率 \( \alpha \)、自由度 \( (\textcolor{red}{k_1}, \textcolor{blue}{k_2}) \) の値は、以下のStep1〜2の手順で読み取る。
Step1. 上側確率 \( \alpha \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。(自由度が入れ替わるので注意!)
Step2. 読み取った値の逆数(1/F値)を取る。
【仕組み】
まず、下側確率が \( \alpha \) ということは、上側確率は \( 1 - \alpha \) となります。
よって、\[
P ( F > f ) = 1 - \alpha
\]を満たすような \( f \) を求めることがゴールとなります。
ここで、確率の合計は1なので、\[
P ( F \leqq f ) = \alpha
\]が成り立ちますね。
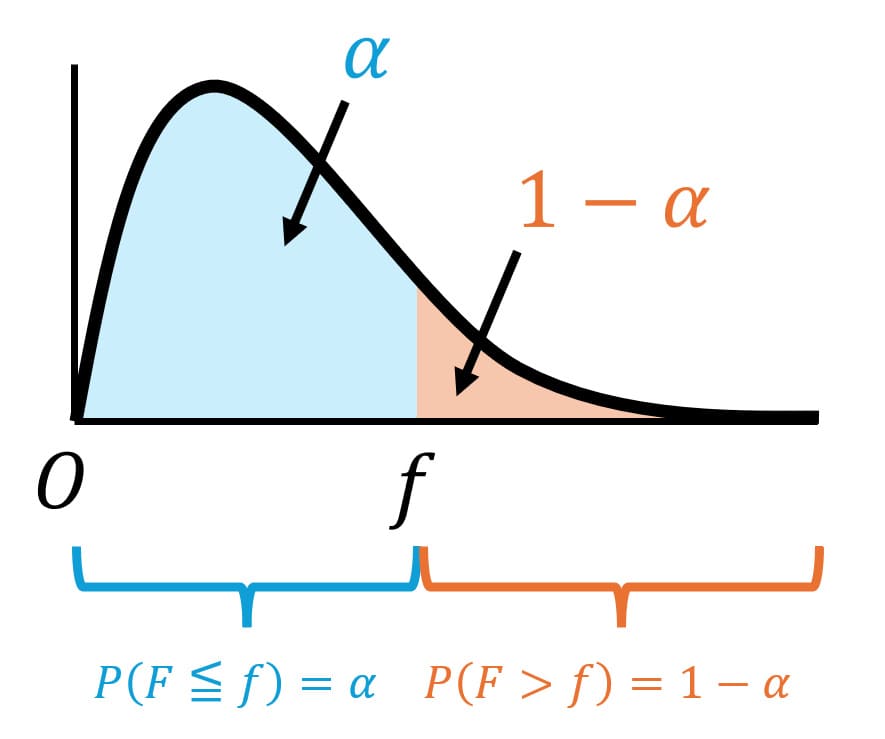
ここで、不等号にイコールがあったりなかったりするとややこしいので、イコールを消して\[
P ( F < f ) = \alpha \tag{1}
\]としておきましょう。
つぎに、\( P ( F < f ) \) の左辺を右辺に、右辺を左辺に入れ替えて\[
P \left( \frac{1}{f} < \frac{1}{F} \right)
\]とすることで、(1)式を\[
P \left( \frac{1}{F} > \frac{1}{f} \right) = \alpha
\]と変形できます。
ここで、F分布に従う変数 \( F \) は、定義より\[
F = \frac{ \textcolor{red}{\frac{ \chi_1^2 }{k_1 }} }{ \textcolor{blue}{\frac{ \chi_2^2 }{k_2 }} }
\]と、分子分母に「各標本ごとのカイ2乗値 ÷ 各標本ごとの自由度」の形を取るのでしたね。(自由度 \( (\textcolor{red}{k_1}, \textcolor{blue}{k_2}) \))
すると、\( \frac{1}{F} \) も\[\begin{align*}
\frac{1}{F} & = \frac{1}{ \frac{ \frac{ \chi_1^2 }{k_1 } }{ \frac{ \chi_2^2 }{k_2 } } }
\\ & = \frac{ \textcolor{blue}{\frac{ \chi_2^2 }{k_2 }} }{ \textcolor{red}{\frac{ \chi_1^2 }{k_1 }} }
\end{align*}\]と、\( F \) と同じように分子分母に「各標本ごとのカイ2乗値 ÷ 各標本ごとの自由度」の形を取っていますね。
そのため、変数 \( F \) が自由度 \( (\textcolor{red}{k_1}, \textcolor{blue}{k_2}) \) のF分布に従うのであれば、\( \frac{1}{F} \) は自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のF分布に従うといえますね。
※ 分子分母が入れ替わっているので、自由度も \( (\textcolor{red}{k_1}, \textcolor{blue}{k_2}) \) から \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) と入れ替わる点に注意!
ここで、一旦 \( F' = \frac{1}{F} \), \( f' = \frac{1}{f} \) とおき、\[
P \left( F' > f' \right) = \alpha
\]とします。
ここで、F分布表には\[
P \left( F > f \right) = \alpha
\]となるような \( f \) が確率 \( \alpha \)、自由度 \( (k_1,k_2) \) に記されています。
そのため、F分布表から、確率 \( \alpha \) 、自由度 \( (k_2, k_1) \) となる \( f' \) も、F分布表から読み取ることができます。
最後に読み取った値を、\[
f = \frac{1}{f'}
\]とすることで、下側確率 \( \alpha \) のときの値 \( f \) を求める事ができます。
スポンサードリンク
3. 母分散の比が推定できる仕組み
では、2標本の母分散の比 \( \frac{ \sigma_1^2 }{ \sigma_2^2 } \) を区間推定する方法について見ていきましょう。
まずは結論を紹介し、なぜその結論が導出できるか、の順で説明していきます。
以下の表の通りに、2標本の標本サイズ、不偏分散、母分散の文字をおく。
| 標本1 | 標本2 | |
|---|---|---|
| 標本サイズ (既知) | \( n_1 \) | \( n_2 \) |
| 不偏分散 (既知) | \( s_1^2 \) | \( s_2^2 \) |
| 母分散 (未知) | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
このとき、以下の手順にて、標本分散 \( n_1 \), \( n_2 \) および、不偏分散 \( s_1^2 \), \( s_2^2 \) を用いて、母分散の比率 \( \frac{\sigma_1^2}{ \sigma_2^2} \) の信頼区間を推定できる。
Step1. 信頼度 \( a \) %、および2標本に対する自由度 \( (k_1, k_2) = (n_1-1, n_2-1) \) に対して、F値の下側の点 \( F_1 \)、上側の点 \( F_2 \) を、F分布表から読み取る。
(1) 上側の点 \( F_2 \)
→ \( \alpha = a/2 \% = a/200 \)、自由度 \( (\textcolor{red}{k_1}, \textcolor{blue}{k_2}) \) に対応する値をF分布表から読み取る。
(2) 下側の点 \( F_1 \)
→ \( \alpha = a/2 \% = a/200 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) に対応する値をF分布表から読み取り、その逆数を取る。
Step2. 信頼度 \( a \) % の信頼区間をF分布の世界で表すと\[
F_1 \leqq F \leqq F_2
\]となる。
ここで、\[
F = \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } }
\]が成立するので、\[
F_1 \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } \leqq F_2
\]となる。
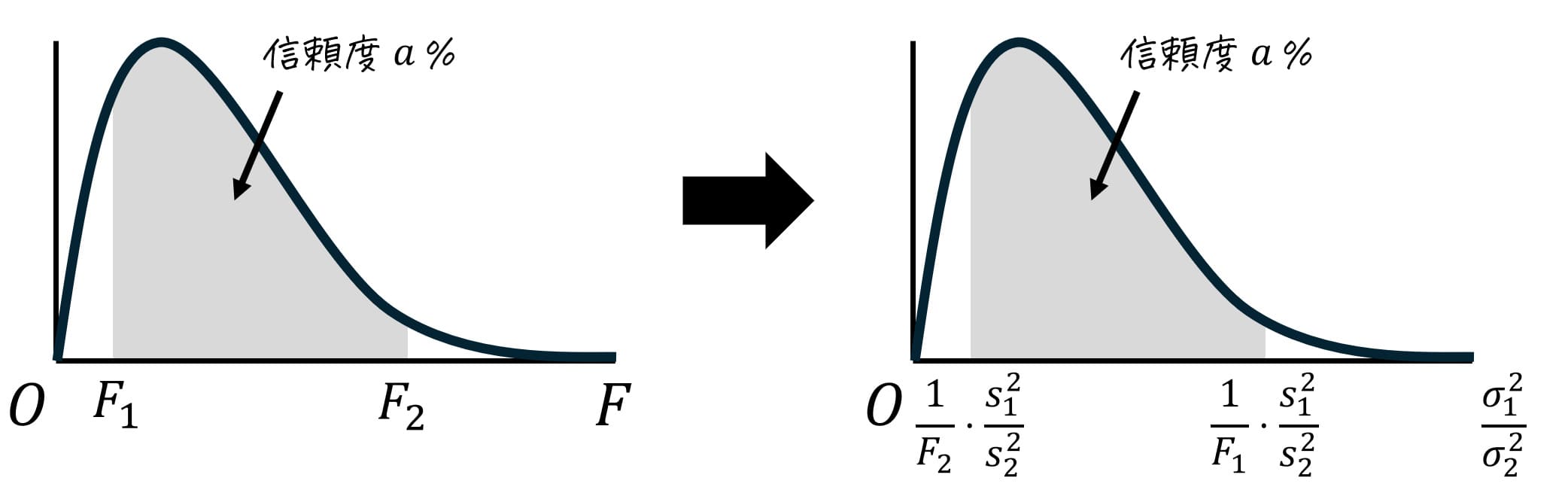
よって、信頼度 \( a \) %における2標本の母分散の比 \( \frac{\sigma_1^2}{ \sigma_2^2} \) の信頼区間は、\[
\frac{1}{F_2} \cdot \frac{ s_1^2 }{ s_2^2 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{1}{F_1} \cdot \frac{s_1^2 }{ s_2^2 }
\]と求められる。

※ 2標本の母分散の比を \( \frac{\sigma_2^2}{ \sigma_1^2} \) とした場合の信頼区間は、\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]となる。
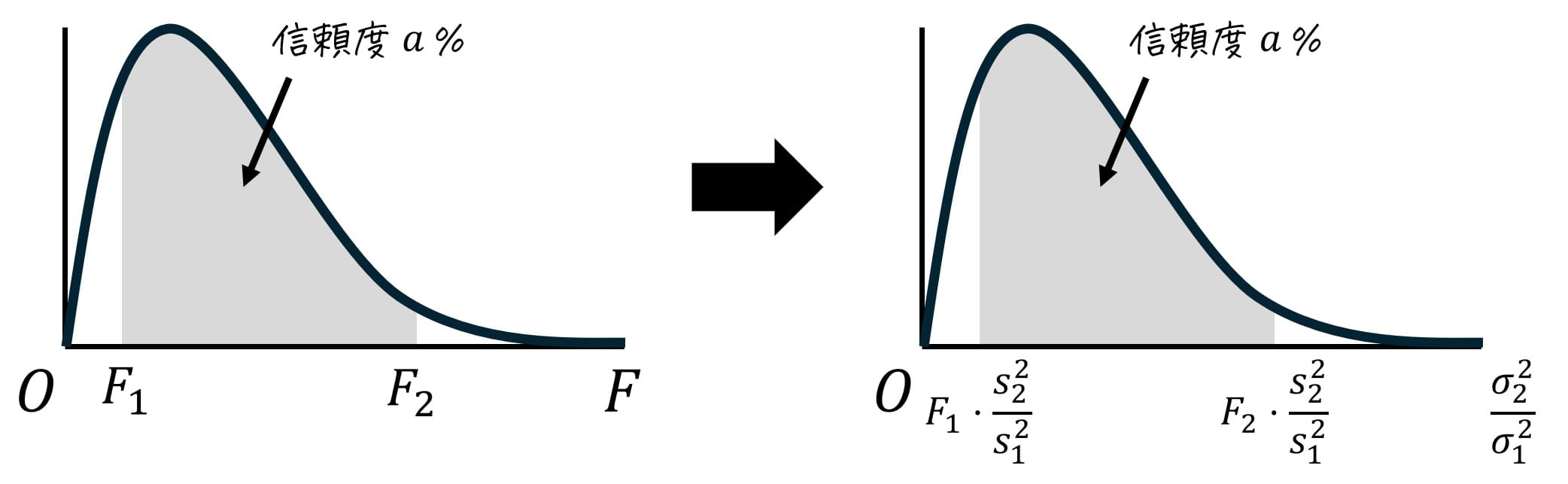
信頼区間を、母分散の比 \( \frac{\sigma_2^2}{\sigma_1^2} \) の形に変形
【母分散の信頼区間の導出】
まず、ある標本サイズ \( n \) のカイ2乗値 \( \chi^2 \) (自由度: \( k = n - 1 \))に対して\[\begin{align*}
\chi^2 & = \frac{ (n-1) s^2 }{ \sigma^2 }
\\ & = \frac{ k s^2 }{ \sigma^2 } \tag{2}
\end{align*}\]の関係が成り立ちます。
※ 標本サイズ \( n \)、不偏分散 \( s^2 \)、母分散 \( \sigma^2 \)
ここで、標本1、標本2の標本サイズ、不偏分散、母分散、自由度を下の表に通りにおきます。
| 標本1 | 標本2 | |
|---|---|---|
| 標本サイズ (既知) | \( n_1 \) | \( n_2 \) |
| 自由度 | \( k_1 = n_1 - 1 \) | \( k_2 = n_2 - 1 \) |
| 不偏分散 (既知) | \( s_1^2 \) | \( s_2^2 \) |
| 母分散 (未知) | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
すると、(2)式と同じように\[
\chi_1^2 = \frac{ k_1 s_1^2 }{ \sigma_1^2 } \tag{3}
\]\[
\chi_2^2 = \frac{ k_2 s_2^2 }{ \sigma_2^2 } \tag{4}
\]の2式が成立します。
つぎに、式(3), 式(4)をF分布の定義式に代入します。\[\begin{align*}
F & = \frac{ \frac{ \chi_1^2 }{k_1 } }{ \frac{ \chi_2^2 }{k_2 } }
\\ & = \frac{ \frac{ \frac{ k_1 s_1^2 }{ \sigma_1^2 } }{k_1 } }{ \frac{ \frac{ k_2 s_2^2 }{ \sigma_2^2 } }{k_2 } }
\\ & = \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } }
\end{align*}\]
あとは、信頼区間に対応する下側の点 \( F_1 \) と上側の点 \( F_2 \) を読み取り、\[
F_1 \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } \leqq F_2 \tag{5}
\]となる \( \frac{ \sigma_1^2 }{ \sigma_2^2 }\) の範囲を見つければOKです。
あとは、式(5)の\[
F_1 \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } , \ \ \ \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } \leqq F_2
\]をそれぞれ変形して、\( a \leqq \frac{ \sigma_1^2 }{ \sigma_2^2 } \leqq b \) の形にしていきます。
まず、\[
F_1 \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } }
\]は、両辺を \( \frac{\sigma_1^2}{ F_1 \sigma_2^2} \) 倍して、\[
\frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{s_1^2 }{F_1 s_2^2 } \tag{6}
\]とします。
同様に、\[
\frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } \leqq F_2
\]に対して、両辺を \( \frac{\sigma_1^2}{ F_2 \sigma_2^2} \) 倍して、\[
\frac{ s_1^2 }{ F_2 s_2^2 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \tag{7}
\]とします。
あとは、式(6), 式(7)を合わせて\[
\frac{ s_1^2 }{ F_2 s_2^2 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{s_1^2 }{F_1 s_2^2 }
\]\[
\frac{1}{F_2} \cdot \frac{ s_1^2 }{ s_2^2 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{1}{F_1} \cdot \frac{s_1^2 }{ s_2^2 }
\]とすれば、母分散の比 \( \frac{ \sigma_1^2 }{ \sigma_2^2 } \) に関する信頼区間の導出完了です。
【母分散の比率を \( \frac{ \sigma_2^2 }{ \sigma_1^2 } \) とした場合の信頼区間】
母分散の比率を \( \frac{ \sigma_2^2 }{ \sigma_1^2 } \) の信頼区間は、式(5)を分割した\[
F_1 \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } , \ \ \ \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2 } } \leqq F_2
\]の2つの不等式の各両辺に \( \frac{s_2^2}{s_1^2} \) を掛けると導出できます。
実際に2つの不等式の各両辺に \( \frac{s_2^2}{s_1^2} \) を掛けると、\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2^2 } } \cdot \frac{s_2^2}{s_1^2}
\]\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2^2 } } \cdot \frac{ \frac{1}{s_1^2} }{ \frac{1}{s_2^2} }
\]\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \frac{1}{\sigma_1^2} }{ \frac{1}{\sigma_2^2} } \tag{8}
\]\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 }
\]および\[
\frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2^2 } } \cdot \frac{s_2^2}{s_1^2} \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]\[
\frac{ \frac{ s_1^2 }{ \sigma_1^2 } }{ \frac{ s_2^2 }{ \sigma_2^2 } } \cdot \frac{ \frac{1}{s_1^2} }{ \frac{1}{s_2^2} } \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]\[
\frac{ \frac{1}{\sigma_1^2} }{ \frac{1}{\sigma_2^2} } \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]\[
\frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq F_2 \cdot \frac{s_2^2}{s_1^2} \tag{9}
\]となるので、式(8), 式(9)を合わせて\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]と導出できます。
4. 例題を解いてみよう!(母分散の比の推定)
ある大学では、1年生は1類、2類、3類の3つのクラスに分かれており、桃山先生は1類の1年生の講義「解析学1」の担当をしている。
桃山先生が受け持った1類の「解析学1」の成績分布について、以下のことがわかっている。
| 2024年度 | 2023年度 | |
|---|---|---|
| 履修人数 | 61 | 41 |
| 平均点 | 72 | 75 |
| 不偏分散 | 100 | 50 |
ある日、桃山先生は「解析学1」の点数のばらつき具合が2023年度と2024年度でどれくらい変化したかを調べようとしたが、桃山先生が担当していない2類、3類の「解析学1」の成績データは残っていない。
そこで、桃山先生は、自身が受け持った1類の成績データから、1年生の「解析学」の点数のばらつき具合が、2023年度に比べてどのように変わったか調べることにした。
2023年度に比べて、2024年度の「解析学」の母分散は何倍になったか。信頼度95%にて区間推定を行い、結果を小数第2位まで記しなさい。
※ 必要であれば、こちらからF分布表をダウンロードできます。
まず、各データから、変数をつぎのようにおきます。
| 2024年度 | 2023年度 | |
|---|---|---|
| 履修人数 | \( n_1 = 61 \) | \( n_2 = 41 \) |
| 不偏分散 | \( s_1^2 = 100 \) | \( s_2^2 = 50 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
求めたいものは、2023年度の母分散 \( \sigma_2^2 \) に比べて、2024年度の母分散 \( \sigma_1^2 \) は何倍になったかなので、\( \sigma_2^2 \) に対する \( \sigma_1^2 \) の倍率、つまり\[
\frac{ \sigma_1^2 }{ \sigma_2^2 }
\]が取りうる区間を信頼度95%で求めていきます。
Step1. 使用する分布、自由度の確認
今回は、母分散の比率 \( \frac{ \sigma_1^2 }{ \sigma_2^2 } \) を区間したいので、F分布を使います。
また、自由度 \( (k_1,k_2) \) は \( n_1 = 61 \)、\( n_2 = 41 \) なので、\[\begin{align*}
(k_1,k_2) & = (n_1 - 1, n_2 - 1)
\\ & = (60, 40)
\end{align*}\]となります。
Step2. 分布表からの値読み取り
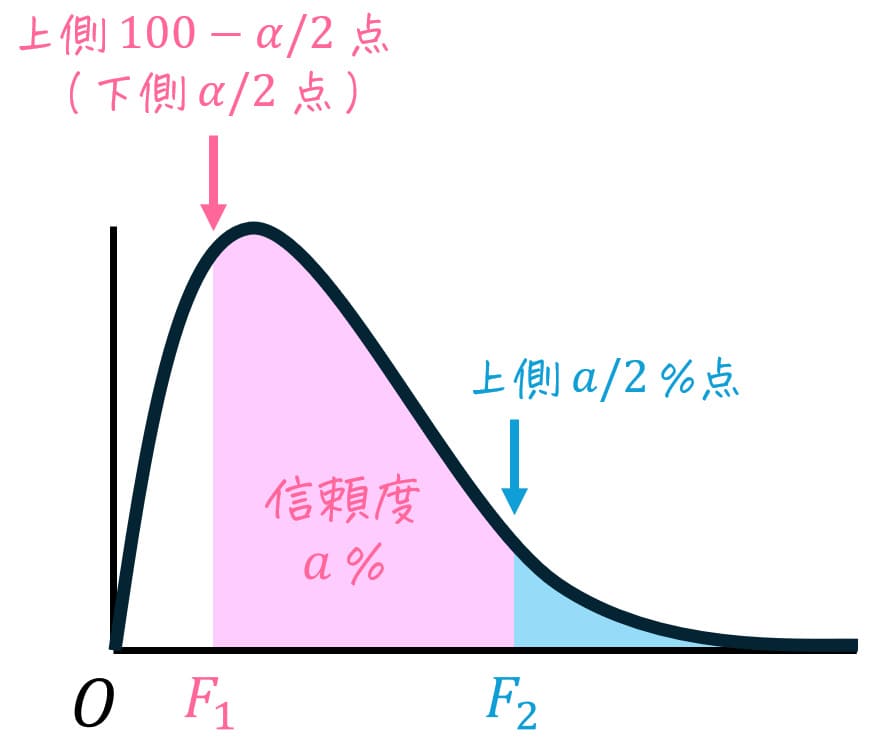
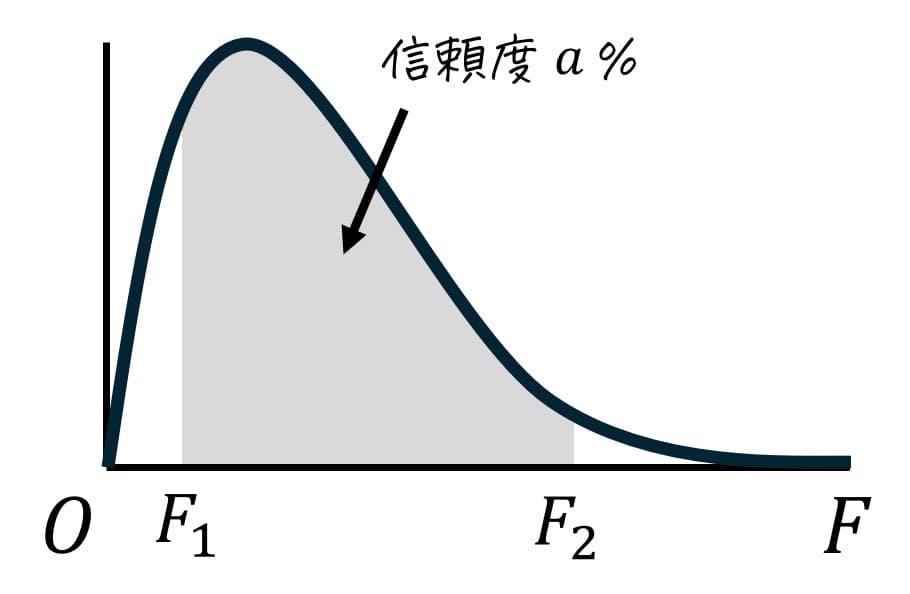
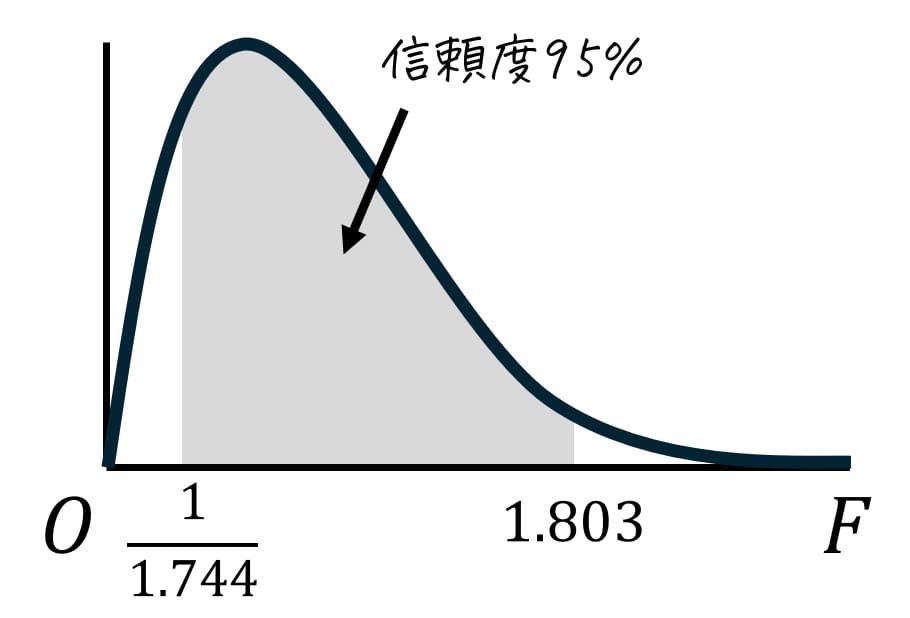
今回は、信頼度95%の推定を実施するため、下の図のように分布の中心から両端に合計95%の確率が含まれるようにします。
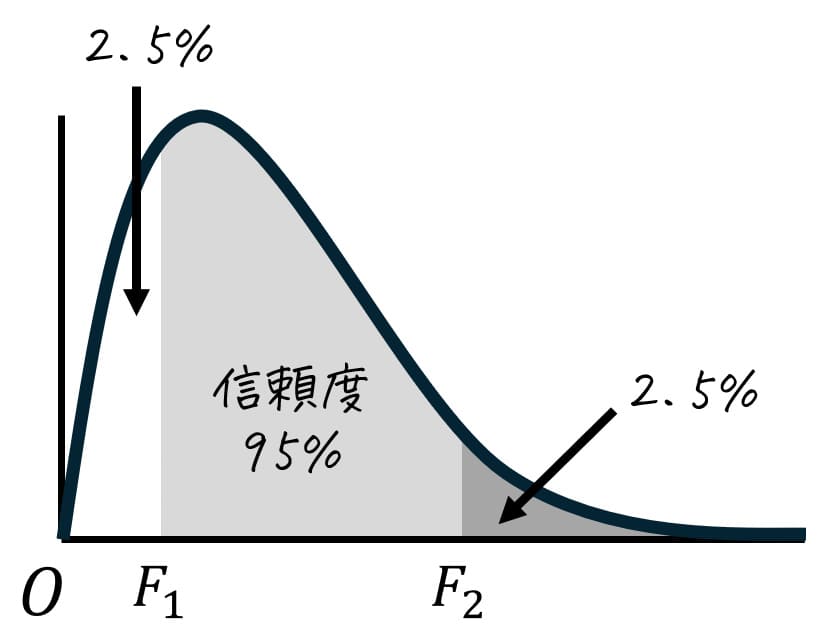
分布の中心から両端に取った薄い灰色部分の面積は95%なので、残りの5%は半分(2.5%)ずつ上側2.5%と下側2.5%に分けられます。
ここで、上側97.5%(=下側2.5%)部分のF値の境界値を \( F_1 \)、上側2.5%のF値の境界値を \( F_2 \) とおきます。つまり、\( F_1 \) 上側97.5%点(=下側2.5%点)、\( F_2 \) は上側2.5%点となります。
[1] \( F_2 \) の読み取り
\( F_2 \) は上側2.5%点なので、上側確率2.5%に相当する、\( \alpha = 0.025 \) の表を使います。
あとは、自由度は \( (k_1,k_2) = (60,40) \) に対応するところを表から読めばOKです。
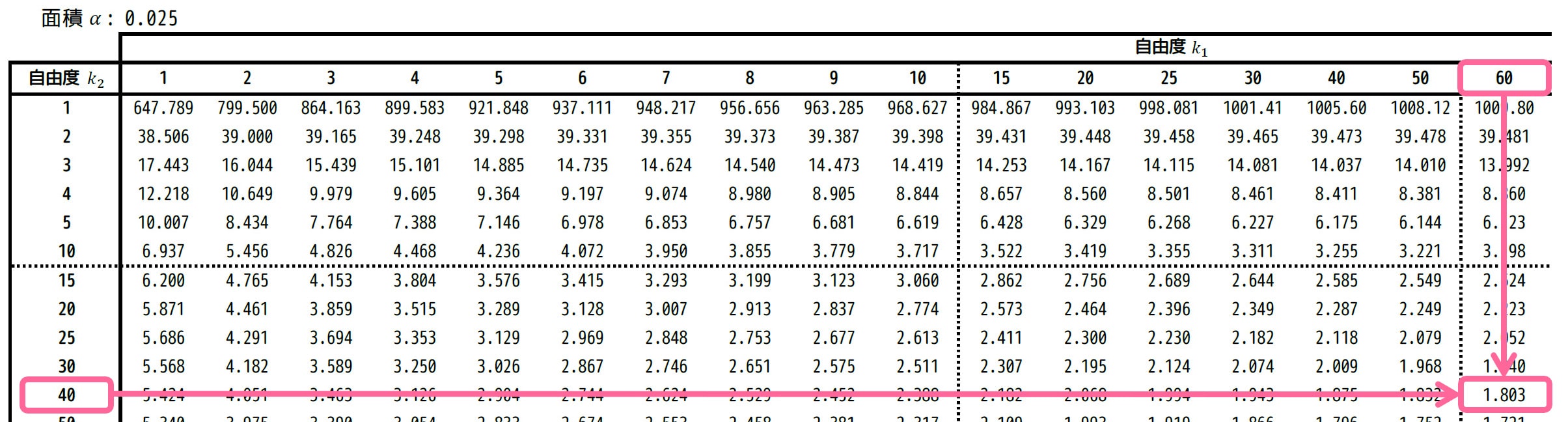
結果、1.803と読み取れます。\( F_2 = 1.803 \) としましょう。
[2] \( F_1 \) の読み取り
\( F_1 \) は下側2.5%点(上側97.5%点)ですが、\( \alpha = 0.975 \) の表はありません。
なので、次の手順で下側2.5%点 \( F_1 \) の値を読み取ります。
- 上側確率 \( \alpha = 0.025 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。
- 読み取った値の逆数(1/F値)を取る。
まず、自由度 \( (k_2,k_1) = (40,60) \)、つまり \( (k_1,k_2) = (40,60) \) に対応するところを表から読みます。
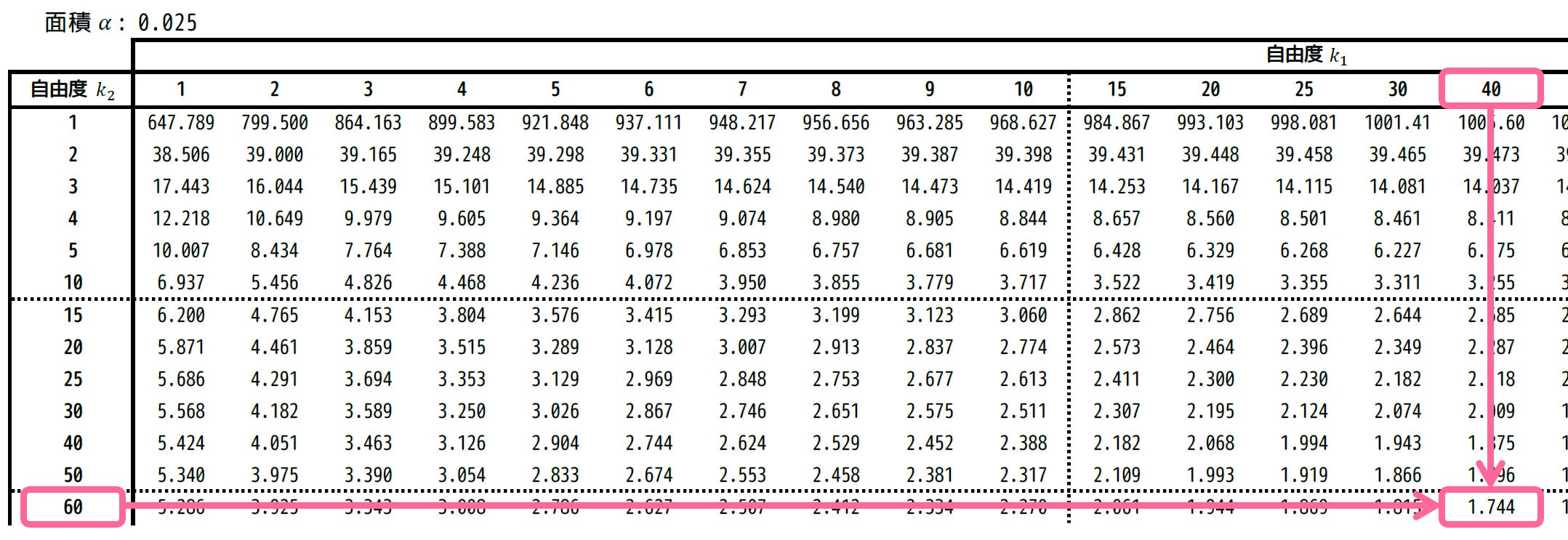
結果、1.744と読み取れます。この値の逆数が \( F_1 \) となるので、\[
F_1 = \frac{1}{1.744}
\]となります。(Step2で、再び \( 1/F_1 \) を計算するので、\( F_1 \) は分数表記のままにしておきます。
Step3. 区間推定の実施
あとは、推定公式\[
\frac{1}{F_2} \cdot \frac{ s_1^2 }{ s_2^2 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{1}{F_1} \cdot \frac{s_1^2 }{ s_2^2 }
\]に入れればOKです。
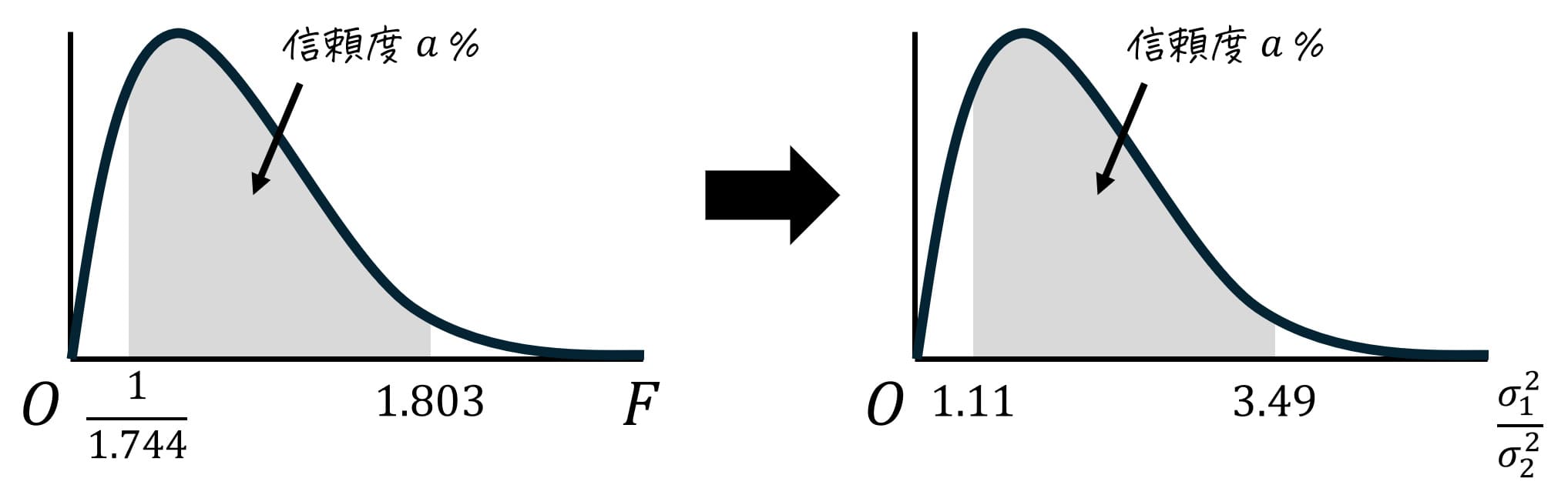
実際に代入していくと、\[
\frac{1}{1.803} \cdot \frac{ 100 }{ 50 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{1}{ \frac{1}{1.744} } \cdot \frac{100}{ 50 }
\]\[
\frac{1}{1.803} \cdot 2 \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 1.744 \cdot 2
\]\[
\frac{2}{1.803} \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 1.744 \cdot 2
\]\[
1.109 \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 3.488
\]となります。
よって、信頼度95%での信頼区間 \( \frac{ \sigma_1^2 }{ \sigma_2 ^2} \) が\[
1.11 \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 3.49
\]となったことにより、 2023年度に比べて、2024年度の「解析学」の母分散は 1.11~3.49 倍 になったと推定できます。
別解.変数のおきかたを変えた場合
2023年度と2024年度のデータを、以下のようにおいた人もいると思います。
| 2023年度 | 2024年度 | |
|---|---|---|
| 履修人数 | \( n_1 = 41 \) | \( n_2 = 61 \) |
| 不偏分散 | \( s_1^2 = 50 \) | \( s_2^2 = 100 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
このようにおいた場合、2023年度の母分散 \( \sigma_1^2 \) に比べて、2024年度の母分散 \( \sigma_2^2 \) は何倍になったか、つまり\[
\frac{ \sigma_2^2 }{ \sigma_1^2 }
\]が取りうる区間を信頼度95%で求めればOKです。
ただし、自由度 \( (k_1,k_2) \) が \( n_1 = 41 \)、\( n_2 = 61 \) なので、\[\begin{align*}
(k_1,k_2) & = (n_1 - 1, n_2 - 1)
\\ & = (40, 60)
\end{align*}\]となる点に注意が必要です。
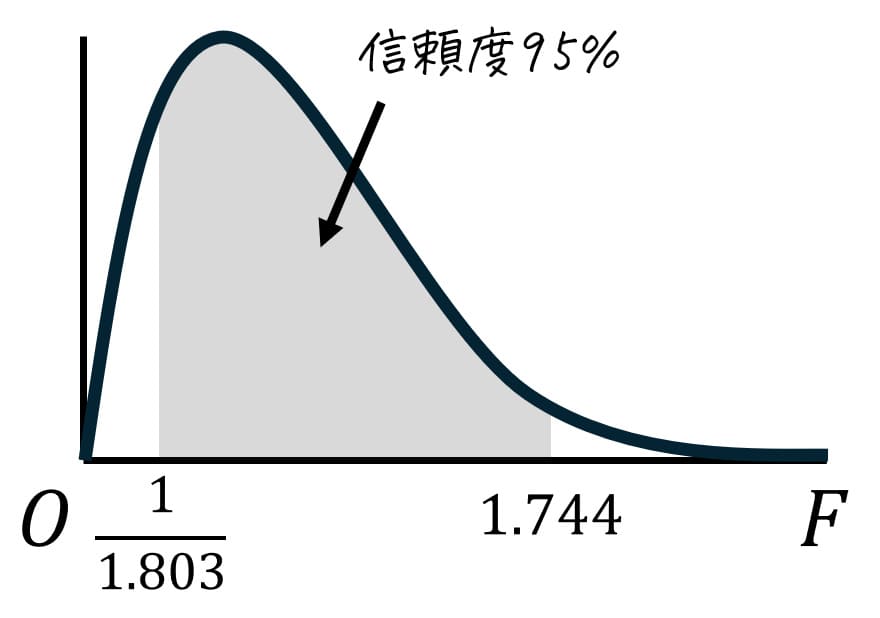
また、上側2.5%点 \( F_2 \) は \( \alpha = 0.025 \) の表の自由度は \( (k_1,k_2) = (40,60) \) に対応するところを表から読めばOKです。
すると、1.744と読み取れます。\( F_2 = 1.744 \) としましょう。

また、下側2.5%点(上側97.5%点) \( F_1\) は、次の手順で読み取ります。
- 上側確率 \( \alpha = 0.025 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。
- 読み取った値の逆数(1/F値)を取る。
自由度 \( (k_2,k_1) = (40,60) \)、つまり \( (k_1,k_2) = (60,40) \) に対応するところを表から読むと、1.803と読めます。

1.803の逆数が \( F_1 \) となるので、\[
F_1 = \frac{1}{1.803}
\]となります。
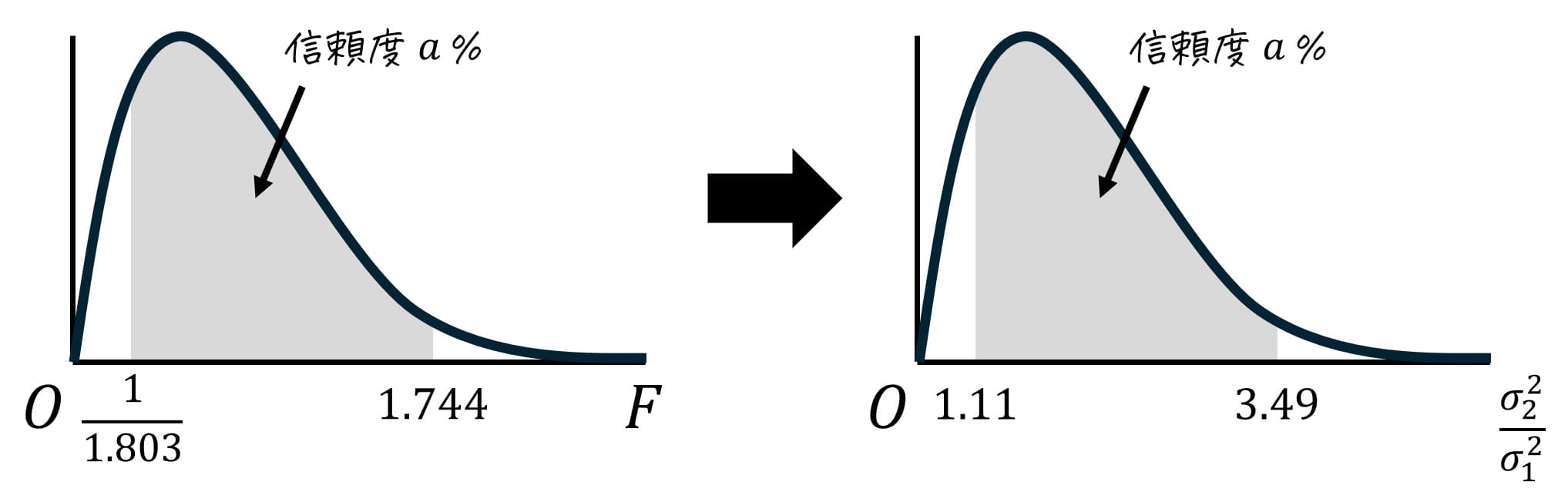
あとは、公式\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]に代入すると、\[
\frac{1}{1.803} \cdot \frac{100}{50} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq 1.744 \cdot \frac{100}{50}
\]\[
\frac{2}{1.803} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq 1.744 \cdot 2
\]\[
1.109 \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq 3.488
\]となるので、 2023年度に比べて、2024年度の「解析学」の母分散は 1.11~3.49 倍 になったと推定できます。
5. 練習問題チャレンジ!(母分散の比の推定)
桃山食堂では、ご飯を自動で一定量盛り付ける機械を導入している。この食堂では、最近、新型の機械を導入し、旧型の機械と比較して盛り付けられるご飯の重さのばらつき具合がどのように変わったかを調査した。
実際に、新しい機械、古い機械からランダムにご飯を盛り付けて、その重さを測定したところ、以下のデータを得ることができた。(ただしお椀の重さは入っていない)
| 新型 | 旧型 | |
|---|---|---|
| サンプル数 | 21 | 16 |
| 平均 [g] | 120 | 118 |
| 不偏分散 [g2] | 20 | 50 |
旧型の機械に比べて、新型の機械で盛り付けられるご飯の重さの母分散は何倍になったか。区間推定をし、結果を小数第2位まで示しなさい。
※ 必要であれば、こちらからF分布表をダウンロードできます。
6. 練習問題の解説
まず、各データから、変数をつぎのようにおきます。
| 新型 | 旧型 | |
|---|---|---|
| サンプル数 | \( n_1 = 21 \) | \( n_2 = 16 \) |
| 不偏分散 | \( s_2^2 = 20 \) | \( s_2^2 = 50 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
旧型の母分散 \( \sigma_2^2 \) に比べて、新型の母分散 \( \sigma_1^2 \) は何倍になったかなので、\( \sigma_2^2 \) に対する \( \sigma_1^2 \) の倍率、つまり\[
\frac{ \sigma_1^2 }{ \sigma_2^2 }
\]が取りうる区間を信頼度95%で求めていきます。
Step1. 使用する分布、自由度の確認
母分散の比率 \( \frac{ \sigma_1^2 }{ \sigma_2^2 } \) を区間したいので、F分布を使います。
また、自由度 \( (k_1,k_2) \) は \( n_1 = 21 \)、\( n_2 = 16 \) なので、\[\begin{align*}
(k_1,k_2) & = (n_1 - 1, n_2 - 1)
\\ & = (20, 15)
\end{align*}\]です。
Step2. 分布表からの値読み取り
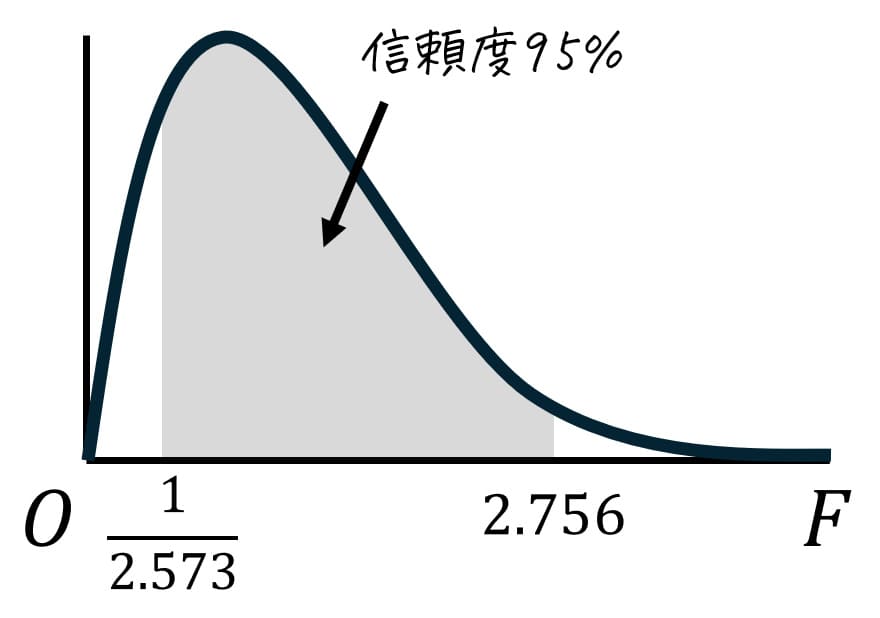
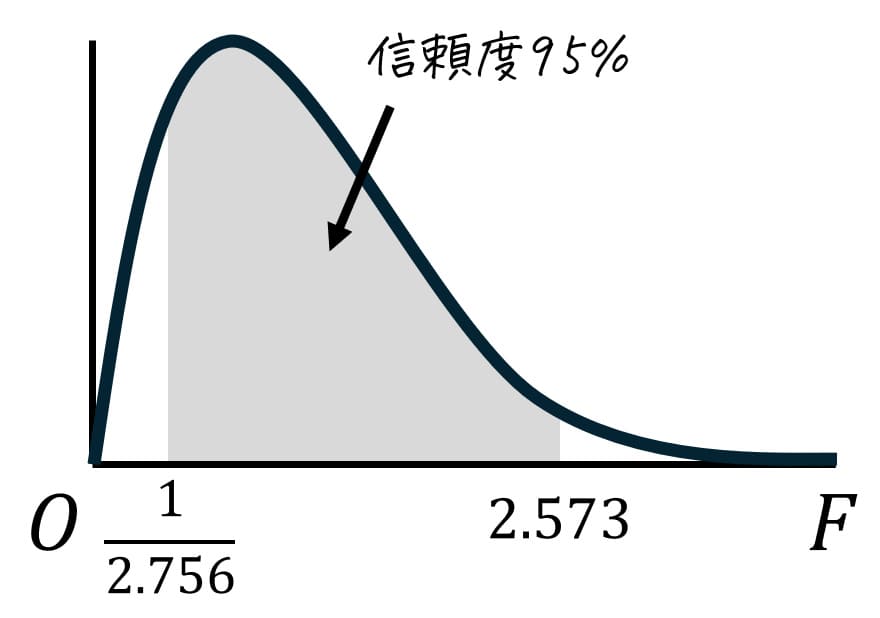
例題と同じく、信頼度95%の推定を実施するため、下の図のように分布の中心から両端に合計95%の確率が含まれるようにします。

上側97.5%(=下側2.5%)部分のF値の境界値を \( F_1 \)、上側2.5%のF値の境界値を \( F_2 \) して、\( F_1 \), \( F_2 \) の値をF分布表から読み取ります。
[1] 上側2.5%点 \( F_2 \)
\( \alpha = 0.025 \) の表の自由度から、\( (k_1,k_2) = (20,15) \) に対応するところを表から読めばOKです。
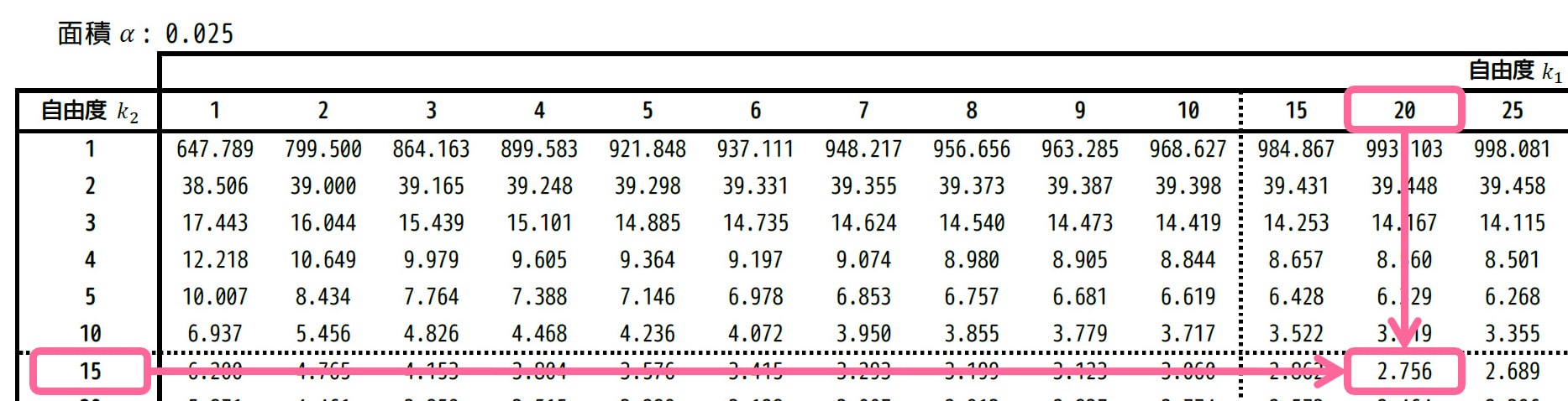
すると、2.756と読み取れます。\( F_2 = 2.756 \) としましょう。
[2] 下側2.5%(上側97.5%)点 \( F_2 \)
次の手順で下側2.5%点 \( F_1 \) の値を読み取ります。
- 上側確率 \( \alpha = 0.025 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。
- 読み取った値の逆数(1/F値)を取る。
自由度 \( (k_2,k_1) = (20,15) \)、つまり \( (k_1,k_2) = (15,20) \) に対応するところを表から読むと、2.573と読めます。
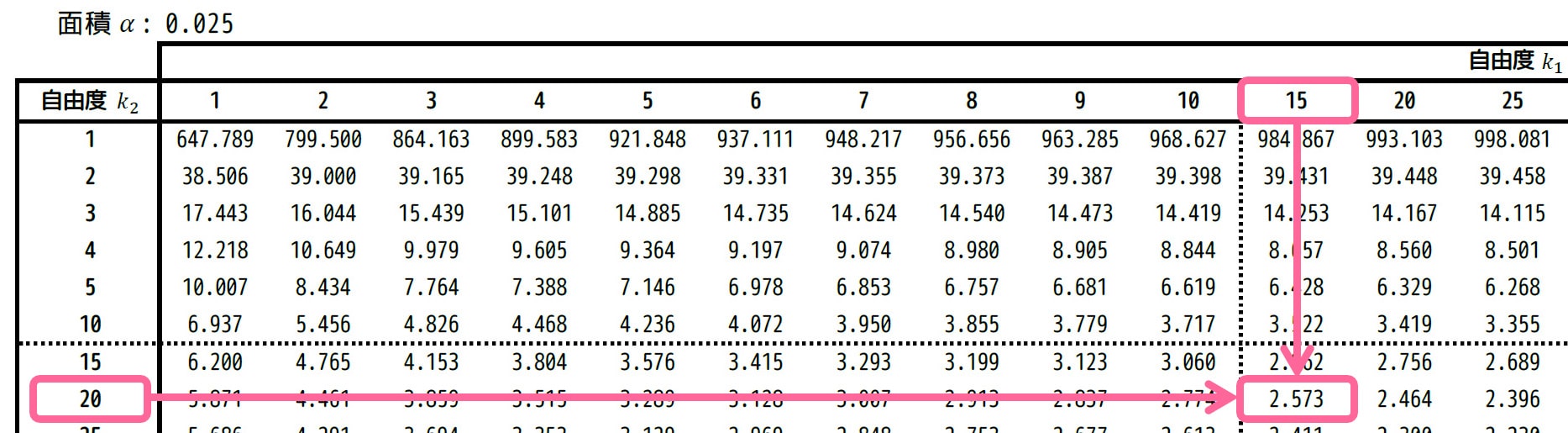
2.573の逆数が \( F_1 \) となるので、\[
F_1 = \frac{1}{2.573}
\]となります。
Step3. 区間推定の実施
| 新型 | 旧型 | |
|---|---|---|
| サンプル数 | \( n_1 = 21 \) | \( n_2 = 16 \) |
| 不偏分散 | \( s_2^2 = 20 \) | \( s_2^2 = 50 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
推定公式\[
\frac{1}{F_2} \cdot \frac{ s_1^2 }{ s_2^2 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{1}{F_1} \cdot \frac{s_1^2 }{ s_2^2 }
\]に各データの値を代入していくと、\[
\frac{1}{2.756} \cdot \frac{ 20 }{ 50 } \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq \frac{1}{\frac{1}{2.573}} \cdot \frac{20 }{ 50 }
\]\[
\frac{1}{2.756} \cdot \frac{2}{5} \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 2.573 \cdot \frac{2}{5}
\]\[
\frac{2}{2.756 \cdot 5} \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 2.573 \cdot 0.4
\]\[
0.145 \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 1.029
\]となります。
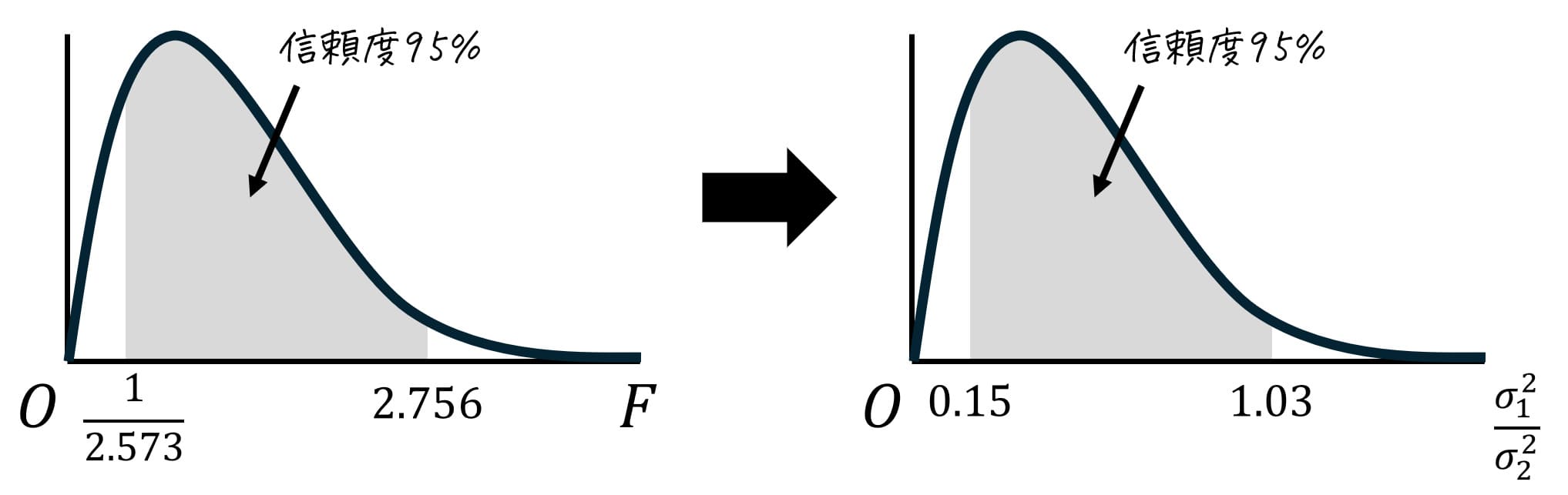
よって、信頼度95%での信頼区間 \( \frac{ \sigma_1^2 }{ \sigma_2 ^2} \) が\[
0.15 \leqq \frac{ \sigma_1^2 }{ \sigma_2 ^2} \leqq 1.03
\]となったことにより、 「旧型のご飯盛り付け器で盛り付けたご飯の重量」に比べて、「新型のご飯盛り付け器で盛り付けたご飯の重量」の母分散は 0.15~1.03 倍 になったと区間推定できます。
別解.変数のおきかたを変えた場合
旧型と新型のデータを、つぎのように置いた場合の計算過程も見ていきましょう。
| 旧型 | 新型 | |
|---|---|---|
| サンプル数 | \( n_1 = 16 \) | \( n_2 = 21 \) |
| 不偏分散 | \( s_2^2 = 50 \) | \( s_2^2 = 20 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
このようにおいた場合、旧型の母分散 \( \sigma_1^2 \) に比べて、新型の母分散 \( \sigma_2^2 \) は何倍になったか、つまり\[
\frac{ \sigma_2^2 }{ \sigma_1^2 }
\]が取りうる区間を信頼度95%で求めればOKです。自由度 \( (k_1,k_2) \) は、\( n_1 = 16 \)、\( n_2 = 21 \) なので、\[\begin{align*}
(k_1,k_2) & = (n_1 - 1, n_2 - 1)
\\ & = (15, 20)
\end{align*}\]となる点に注意が必要です。
まず、上側2.5%点 \( F_2 \) は \( \alpha = 0.025 \) の表の自由度は \( (k_1,k_2) = (15,20) \) に対応するところを表から読めばOKです。
すると、 2.573 と読み取れます。\( F_2 = 2.573 \) としましょう。

つぎに下側2.5%点(上側97.5%点) \( F_1\) は、次の手順で読み取ります。
- 上側確率 \( \alpha = 0.025 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。
- 読み取った値の逆数(1/F値)を取る。
自由度 \( (k_2,k_1) = (15,20) \)、つまり \( (k_1,k_2) = (20,15) \) に対応するところを表から読むと、2.756と読めます。

2.756の逆数が \( F_1 \) となるので、\[
F_1 = \frac{1}{2.756}
\]となります。
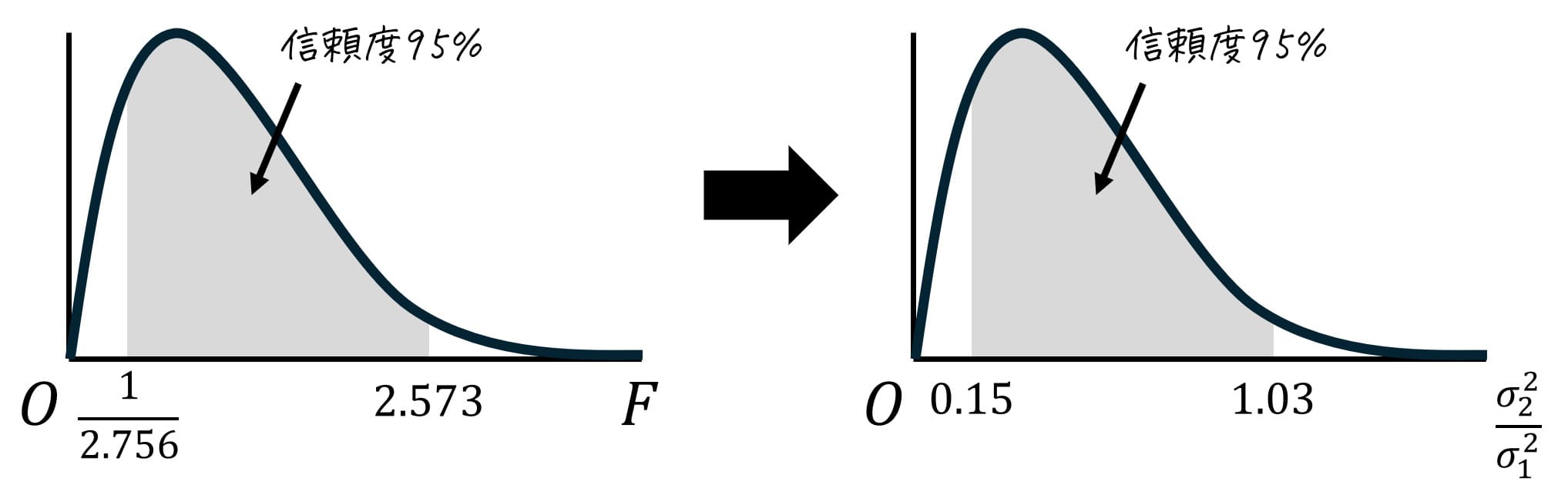
あとは、公式\[
F_1 \cdot \frac{s_2^2}{s_1^2} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq F_2 \cdot \frac{s_2^2}{s_1^2}
\]に代入すると、\[
\frac{1}{2.756} \cdot \frac{20}{50} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq 2.573 \cdot \frac{20}{50}
\]\[
\frac{2}{2.756 \cdot 5} \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq 2.573 \cdot 0.4
\]\[
0.145 \leqq \frac{ \sigma_2^2 }{ \sigma_1^2 } \leqq 1.029
\]となるので、「旧型のご飯盛り付け器で盛り付けたご飯の重量」に比べて、「新型のご飯盛り付け器で盛り付けたご飯の重量」の母分散は 0.15~1.03 倍 になったと区間推定できます。
注釈
| ↑1 | 例題や練習問題で、表の読み方も書いているので、ご安心を! |
|---|
関連広告・スポンサードリンク