スポンサードリンク
こんにちは、ももやまです。
今回は、t分布を使って母平均の仮説検定をする方法について、例題や練習問題を通じて一緒に学習していきましょう!
例題、練習問題を解く際にお使いください。
※ 使っている参考書や授業に合わせて、両側t分布表、片側t分布表を選択することをおすすめします。なお、統計検定の場合、与えられる表は片側t分布表です。
スポンサードリンク
1. t分布の特徴
実際に仮説検定の問題を解く前に、t分布の特徴を確認しましょう。
1.t分布はどんな時に使えるか?
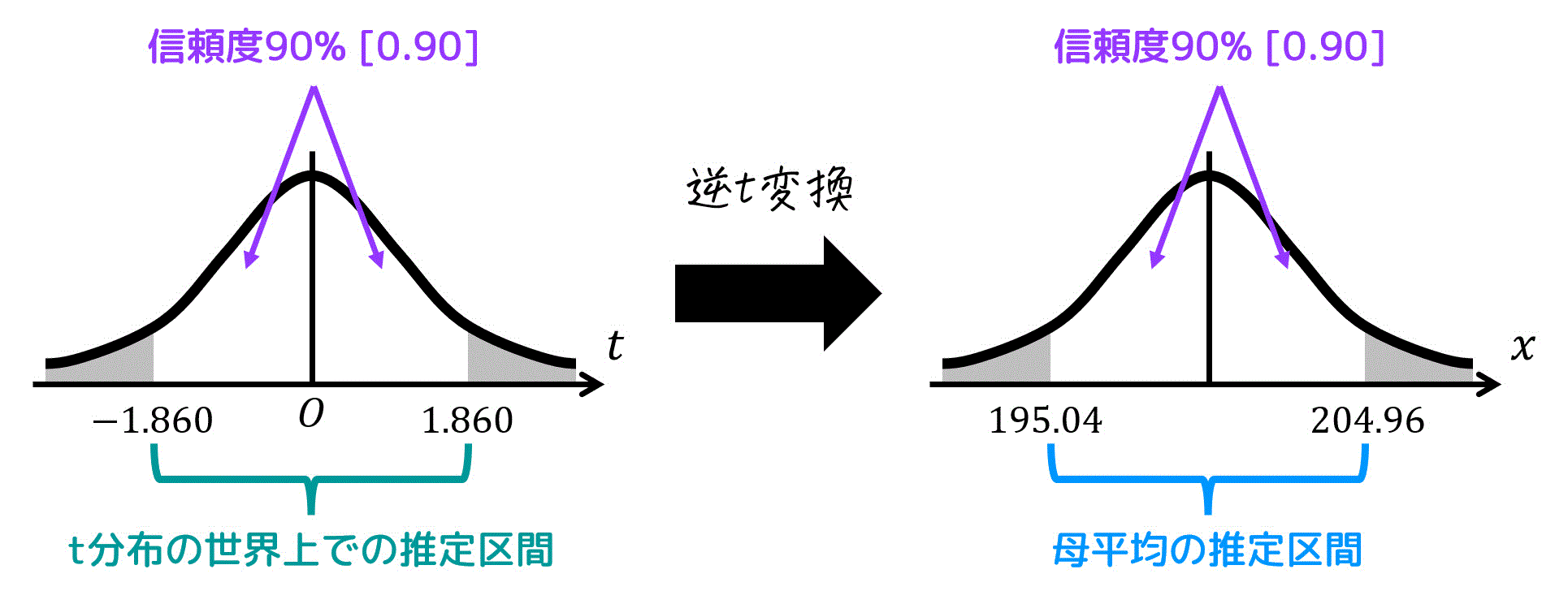
t分布は、標本のデータ(標本平均・不偏分散)から母平均を仮説検定する際に使える道具である。
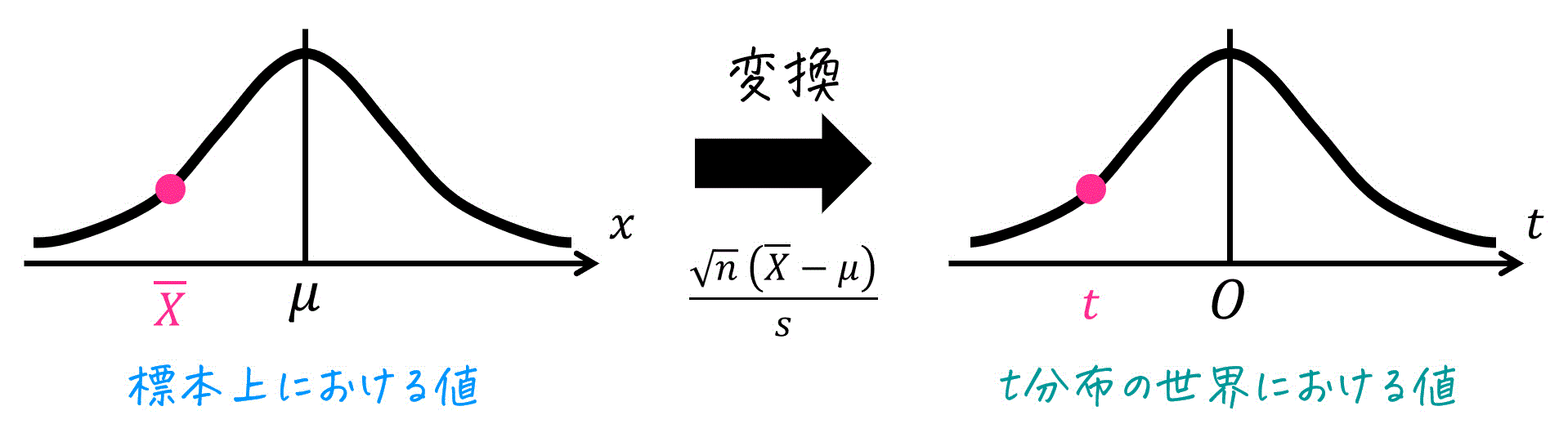
2.t分布の変換公式
ある標本のデータを、t分布の世界の値に変えるときの変換式は\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\end{align*}\]である。

※ 母平均: \( \mu \)、標本サイズ: \( n \)、標本平均: \( \overline{X} \)、不偏分散 \( s^2 \) [不偏標準偏差: \( s \)]
※ 不偏分散\[
s^2 = \frac{1}{n-1} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]の代わりに標本分散\[
S^2 = \frac{1}{n} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]を使った場合は、変換式は\[
\frac{ \sqrt{n-1} \ (\overline{X} - \mu) }{S}
\]となる[1]基本的には不偏分散 \( s^2 \)(不偏標準偏差 \( s \) を使った形で公式が記載されていますが、参考書によっては標本分散 \( S^2 \)(標本標準偏差 \( s … Continue reading。
3.t分布と自由度
単一の標本(母分散不明)について、母平均を推定する場合の自由度は次の通りである[2]標本の中で、1つ値が分からないものがあっても、標本平均や不偏分散から復元できるため、情報量は「標本のサイズ」より1小さい値となる。。
(自由度) = (標本のサイズ) - 1
t分布の復習をさらに詳細にしたい人は、以下の記事をご覧ください。
スポンサードリンク
2. 例題で理解! t分布を用いた母平均の仮説検定
母分散が不明で、標本の情報(平均、不偏分散)しか分からないときに、t分布を用いて仮説検定をする方法について、実際に例題で見ていきましょう。
※ 仮説検定については、下の記事にて詳しく説明しています。例題を解く前に仮説検定の復習や確認をしたい人は、下の記事をご覧ください。
ある農家で取れたのニンジンの重さを調査をするために、ランダムに選んだ9個のニンジンの重さを測定ところ、重さの平均は196g、重さの不偏分散は36g2だった。ニンジンの重量の母平均を200gと考えて良いか、仮説検定したい。
(1) 帰無仮説 \( H_0 \)、対立仮説 \( H_1 \) を述べなさい。
(2) 重さの区間推定を行うために必要な分布、および自由度として最も適切なものを、①〜④の中から1つ選びなさい。
① 正規分布
② 自由度8のt分布
③ 自由度9のt分布
④ 自由度10のt分布
(3) 有意水準(危険率)5%で仮説検定しなさい。(途中過程も記すこと。)
※ 必要であれば、記事の上部にあるt分布表を用いても良い。
解説2
(1)
帰無仮説 \( H_0 \) と対立仮説 \( H_1 \) を考える際には、「あるデータを仮定して、その仮定を否定した際に何が言えるのか」を考えてたてるのが良いです。まとめると、
- 帰無仮説 \( H_0 \): 仮説検定をするにあたって、立てる仮定。
→ データの値が等しい、などと仮定することが多い。
(背理法でいう仮定を立てる部分。) - 対立仮説 \( H_1 \): 帰無仮説が否定されたときに、言えること。
→ 本来証明したい内容をここに持ってくる。
(背理法でいう、否定できた際に言えることに相当。)
と言えますね。
帰無仮説 \( H_0 \) : 仮説検定をするにあたって、立てる仮定
→ 母平均が200g( \( \mu = 200 \) )
※ 母平均が200gと仮定した上で仮説検定を行う。
対立仮説 \( H_1 \) : 帰無仮説に反する仮定
→ 母平均が200gとは言えない。( \( \mu \not = 200 \) )
(2)
解答:②
今回は、母分散が未知(かつ標本サイズが小さい)状態で、母平均を推定したいため、t分布を使用します。
今回与えられた標本サイズ(データ数)は9のため、自由度は 9 - 1 = 8 となり、答えは②となります。
(3)
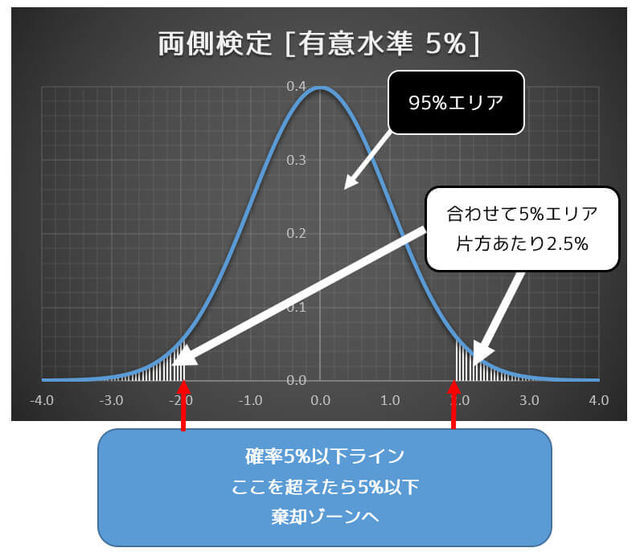
Step1. 片側検定 or 両側検定の確認
今回は対立仮説が「母平均が200gではない」なので、母平均200gよりも「軽すぎる場合」、「重すぎる場合」ともに帰無仮説 \( H_0 \) を否定する必要があります。
そのため、この問題では両側検定をする必要があります。
Step2. 採択 or 棄却ギリギリの \( t \) の値をt分布表から読み取る
まず、有意水準5%(灰色の面積部分が0.05)の判定ラインとなる \( t \) の値を表から調べます。
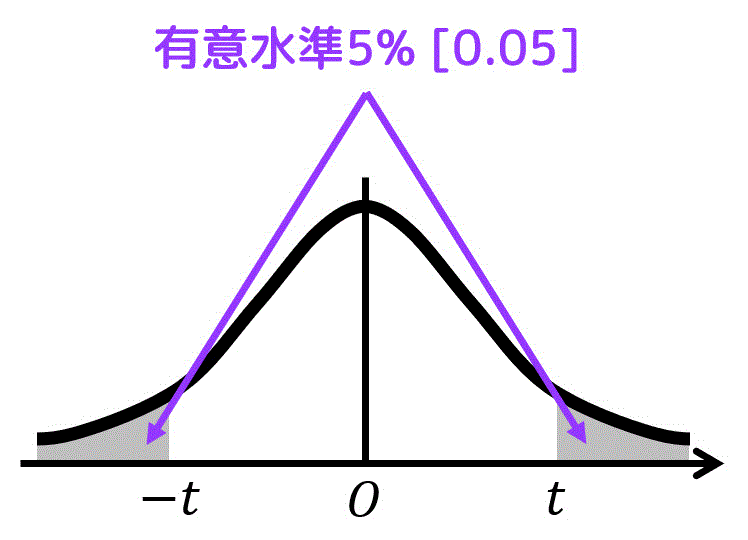
[i] 両側t分布表の場合
自由度8、灰色部分の面積の和 \( \alpha \) が 0.05 の場合をt分布表から読み取ればOKです。
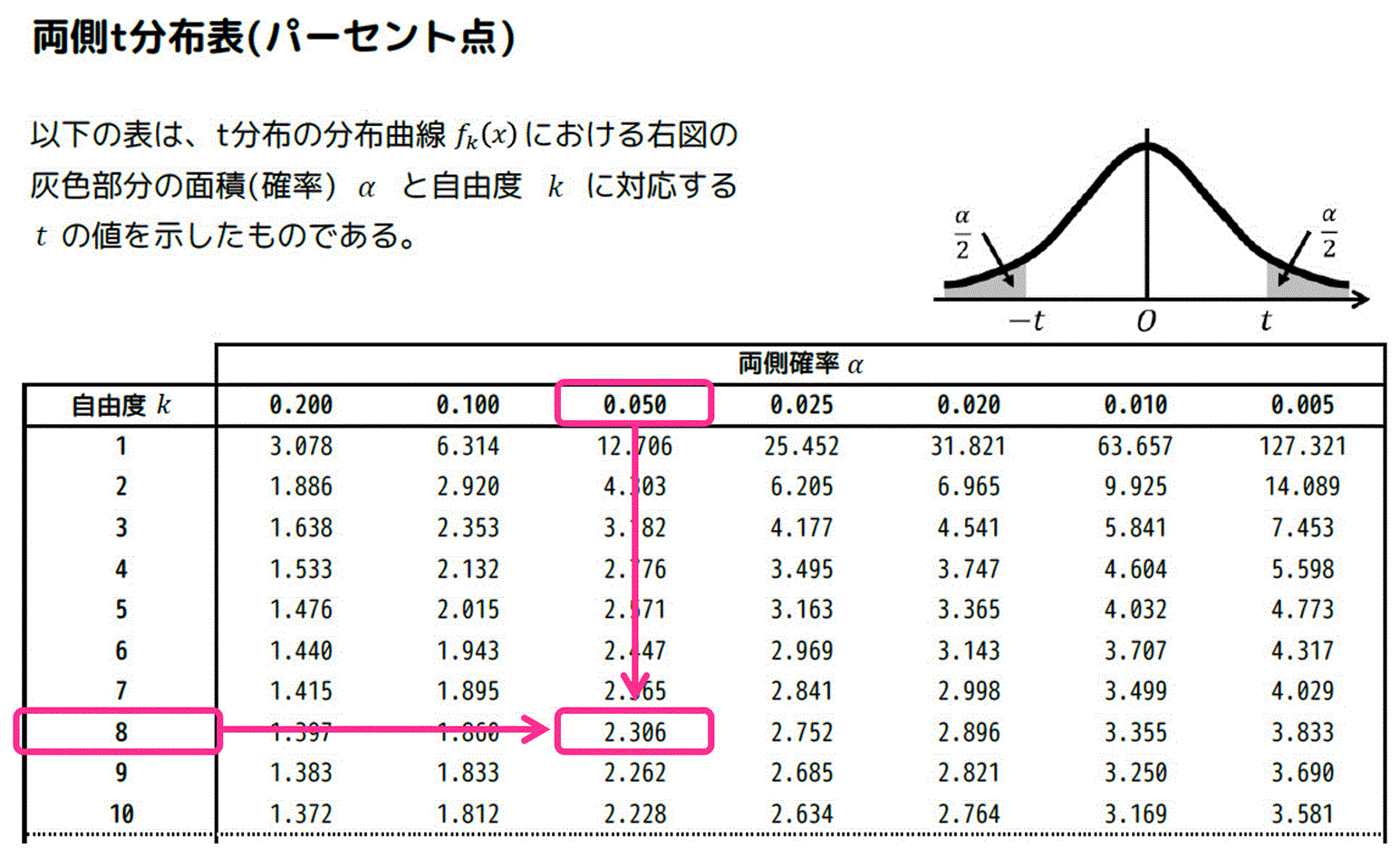
結果、\( t = 2.306 \) と読み取ることが出来ます。
[ii] 片側t分布表の場合
片側t分布表では、青色部分の面積のみが書かれているため、\( \alpha = 0.025 \) の部分を読み取る必要がある点に注意が必要です。
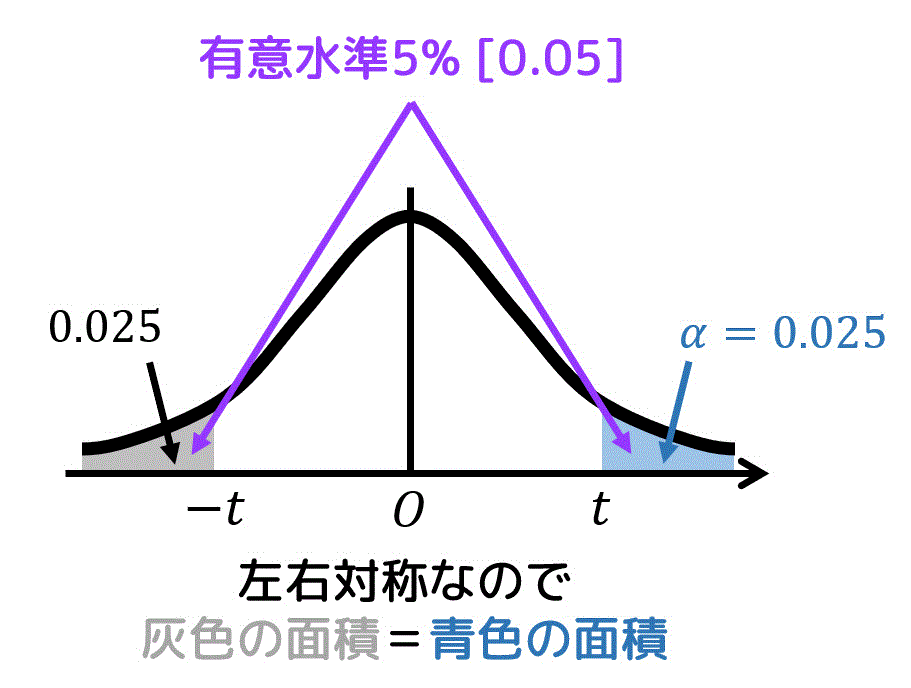
※ グラフが左右対称なので、青色部分の面積=灰色部分の面積。なので、読み取る際に使う \( \alpha \) の値は有意水準5%の半分に相当する 0.025 となる。
あとは、自由度8、\( \alpha = 0.025 \) の部分を片側t分布表から読み取ればOK。
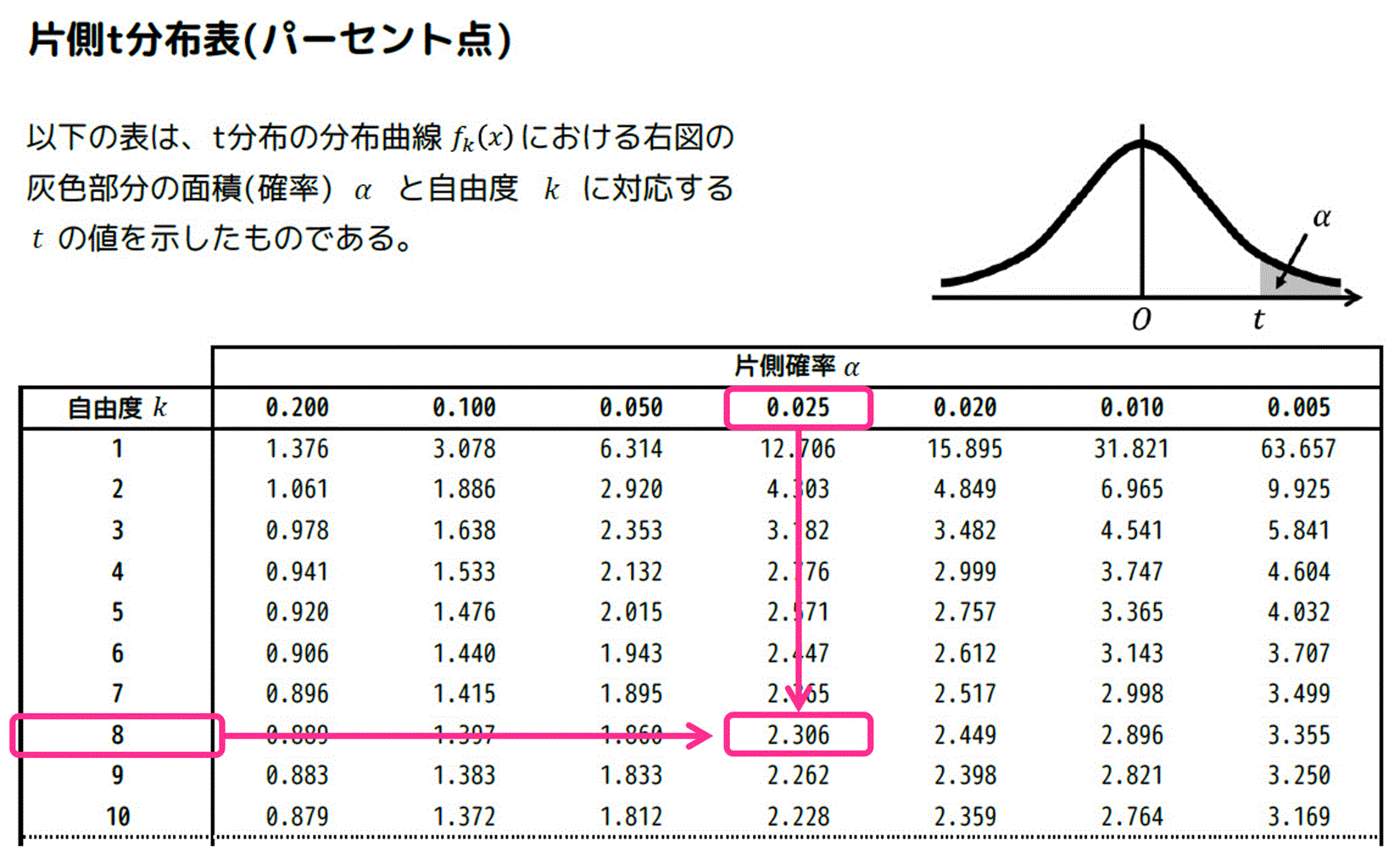
結果、\( t = 2.306 \) と読み取れます。
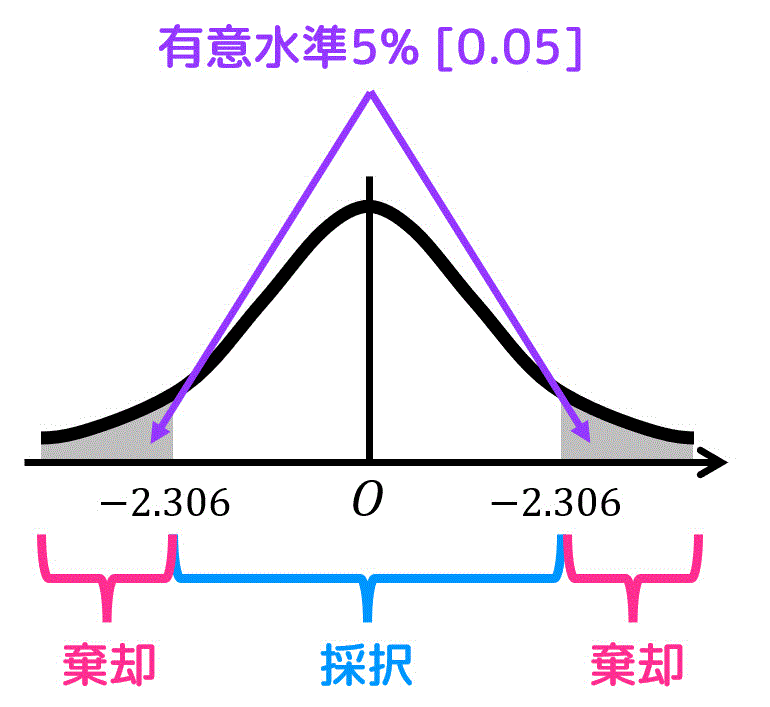
Step3. 与えられたデータ、仮定したデータから仮説検定を行う
Step2より、今回の標本の情報、および帰無仮説での仮定 \( \mu = 200 \) をt分布の変換式\[
t = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\]で変換した際に、その値が\[
- 2.306 \leqq t \leqq 2.306
\]に収まれば仮定 \( H_0 \) は採択(誤りとは言えない)と言え、収まらなければ仮定 \( H_0 \) は棄却(誤り)と言うことができます。
実際に、今回の標本の各情報
- 標本サイズ \( n \): 9
- 標本平均 \( \overline{X} \): 196
- 不偏分散 \( s^2 \): 36(不偏標準偏差 \( s \): 6)
および仮説 \( \mu = 200 \) を式に入れると、\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\\ & = \frac{ \sqrt{9} \ (196 - 200) }{ 6 }
\\ & = \frac{ 3 \cdot (-4) }{ 6 }
\\ & = -2
\end{align*}\]となり、\[
-2.306 \leqq -2 \leqq 2.306
\]と判定ラインに収まっていますね。
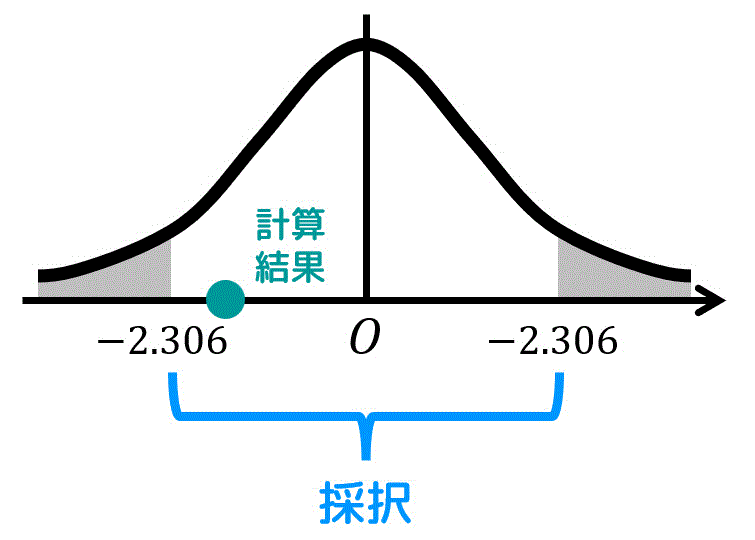
よって、帰無仮説 \( H_0 \) は採択(誤りとは言えない)となります。
母集団の母分散が未知で、かつ標本サイズが小さい(目安: 30未満)のときに母平均に関する仮説検定は、つぎの流れで行う。
Step1. 帰無仮説 \( H_0 \)、対立仮説 \( H_1 \) を立てる
帰無仮説: 母平均に関する仮定(例: 母平均が60である。)
対立仮説: 帰無仮説を否定することで、示したいもの。
(例: 母平均が60でない、母平均は60より大きい)
Step2. 有意水準(危険率)に対応する \( t \) の値を読み取る
自由度 \( n - 1 \)、信頼度に対応する \( \alpha \) の値から、信頼度に対応する \( t \) の値を読み取る。
ただし、\( \alpha \) の値は両側検定をするかによって変わるので注意。
[a] 両側検定をするとき(対立仮説が \( \mu \not = a \) のように、"仮定ではない" の形になっている場合)
- 両側t分布表の場合
→ \( \alpha \) の値: 有意水準
→ 例: 有意水準10%であれば、\( \alpha = 0.1 \) - 片側t分布表の場合
→ \( \alpha \) の値: 有意水準 ÷ 2
→ 例: 有意水準10%であれば、\( \alpha = 0.1 \div 2 = 0.05 \)
(対立仮説が \( \mu > a \) のように、"仮定より大きい/小さい" の形になっている場合)
- 両側t分布表の場合
→ \( \alpha \) の値: 有意水準×2
→ 例: 有意水準10%であれば、\( \alpha = 0.1 \times 2 = 0.2 \) - 片側t分布表の場合
→ \( \alpha \) の値: 有意水準
→ 例: 有意水準10%であれば、\( \alpha = 0.1 \)
ここで読み取った \( t \) の値を \( t_0 \) とする。
Step3. 標本の情報、および帰無仮説の仮定をt分布の値に変換する
標本の各情報について、標本のサイズを \( n \)、標本平均が \( \overline{X} \)、不偏分散が \( s^2 \) (不偏標準偏差が \( s \) )とする。
標本の情報および帰無仮説での仮定 \( \mu = 200 \) をt分布の変換式\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{s}
\end{align*}\]で変換する。
ただし、
※ 不偏分散 \( s^2 \) の代わりに標本分散\[
S^2 = \frac{1}{n} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]が与えられた場合、\( t \) の値は\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ S }{ \sqrt{n-1} } }
\\ & = \frac{ \sqrt{n-1} \ (\overline{X} - \mu) }{S}
\end{align*}\]で計算できる。
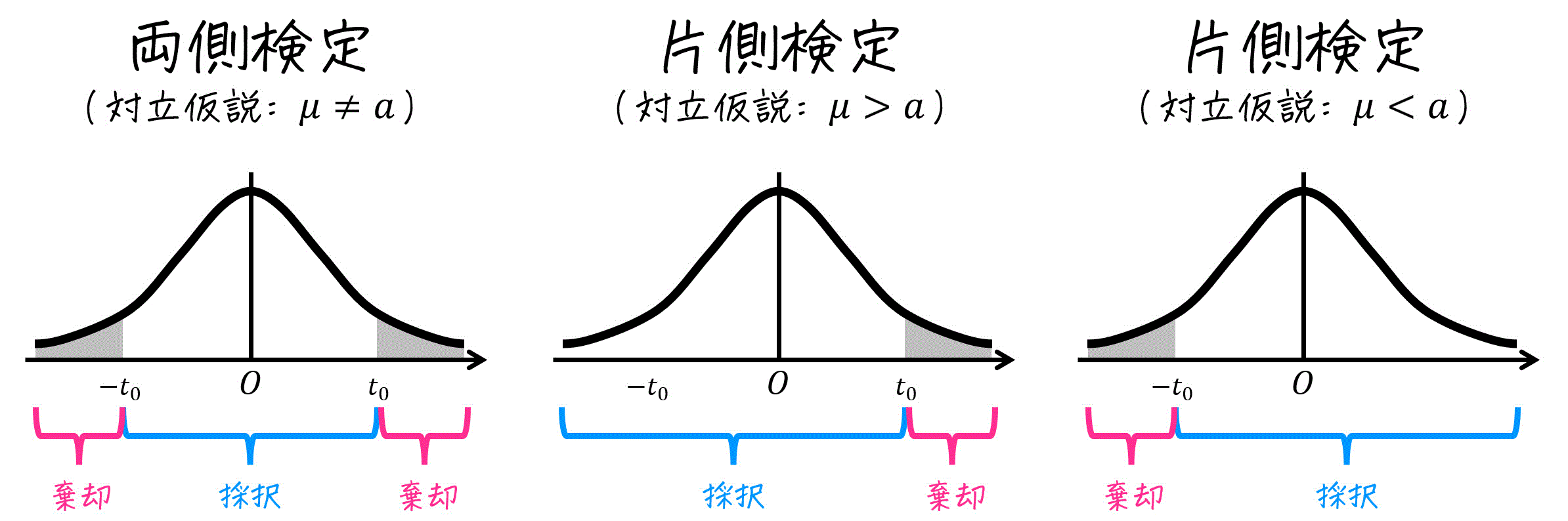
Step4. 採択 or 棄却の判定をする
\( t \) の値、および読み取った値 \( t_0 \) から採択 or 棄却の判定をする。
- 両側検定のとき
→ \( -t_0 \leqq t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu > a \) のとき (母平均が仮定よりも大きいとき)
→ \( t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu < a \) のとき (母平均が仮定よりも小さいとき)
→ \( t_0 \leqq t \) であれば採択。それ以外で棄却。
スポンサードリンク
3. 理解度チェック! 練習問題
では、「t分布の仮説検定の仕方」について理解できているか、実際に練習問題を解くことで確認してみましょう!
あるお菓子の内容量は、製造元によると 70g とされている。しかし、一部の購入者から「実際の容量よりも少ないのではないか?」と問い合わせがあったため、残っている9つのお菓子について、テストすることにした。
「お菓子の内容量を70gと表記してもよいか」の結論を出すために、9つの商品の内容量を測定したところ、中身の容量はそれぞれ以下の通りであった。
41g, 61g, 67g, 66g, 70g, 57g, 62g, 69g, 56g
この結果から、お菓子の内容量を70gと表記するのは誇大広告に該当しないか調査したい。
(1) 4つのお菓子の内容量について、平均、および不偏分散を求めなさい。
(2) 帰無仮説 \( H_0 \)、対立仮説 \( H_1 \) を述べなさい。
(3) 仮説検定を行うために、必要な分布を答えなさい。自由度がある分布については、自由度も答えなさい。
(4) 有意水準(危険率)1%で仮説検定しなさい。(途中過程も記すこと。)
※ 必要であれば、記事の上部にあるt分布表を用いても良い。
4. 練習問題の解答
(1)
解答: 標本平均: 61 [g] 不偏分散: 81 [g2]
標本の平均\[\begin{align*}
\overline{X} & = \frac{1}{n} \sum^{n}_{k=1} x_k
\\ & = \frac{1}{9} (41 + 61 + 67 + 66 + 70 + 57 + 62 + 69 + 56)
\\ & = 61
\end{align*}\]
データ数も多いので、いったん \( a = 60 \) とおいて、\[\begin{align*}
\overline{X} & = \frac{1}{9} \left\{ (a-19) + (a+1) + (a+7) + (a+6) + (a+10) + (a-3) + (a+2) + (a+9) + (a-4) \right\}
\\ & = \frac{1}{9} (9a + 9)
\\ & = a + 1
\\ & = 61
\end{align*}\]と計算するのがおススメです。
不偏分散
\[\begin{align*}
s^2 & = \frac{1}{n-1} \sum^{n}_{k=1} (x_k - \overline{X})
\\ & = \frac{1}{9-1} \left\{ (41-61)^2 + (61-61)^2 + (67-61)^2 + (66-61)^2 + (70-61)^2 + (57-61)^2 + (62-61)^2 + (69-61)^2 + (56-61)-2 \right\}
\\ & = \frac{1}{8} \left\{ (-20)^2 + 0^2 + 6^2 + 5^2 + 9^2 + (-4)^2 + 1^2 + 8^2 + (-5)^2 \right\}
\\ & = \frac{1}{8} \cdot 648
\\ & = 81
\end{align*}\]※ 不偏分散は割る数が \( n \) ではなく \( n-1 \) なので注意!
(2)
帰無仮説 \( H_0 \): お菓子の内容量 \( \mu \) は70gである。( \( \mu = 70 \) )
※ 仮説検定をするにあたって、立てる仮定。
対立仮説 \( H_0 \): お菓子の内容量 \( \mu \) は70gよりも少ない。( \( \mu < 70 \) )
※ 帰無仮説を否定して証明したいもの。
(3)
母平均に関する検定を、母分散が未知の状態でしたいので、t分布を使います。
また、今回与えられた標本サイズ(データ数)は9のため、自由度は 9 - 1 = 8 となります。
(4)
Step1. 片側検定 or 両側検定の確認
今回は対立仮説が \( \mu < 70 \) なので、母平均70gよりも「軽すぎる場合」場合のみ、帰無仮説 \( H_0 \) を否定します。
そのため、この問題では片側検定をする必要があります。
Step2. 採択 or 棄却ギリギリの \( t \) の値をt分布表から読み取る
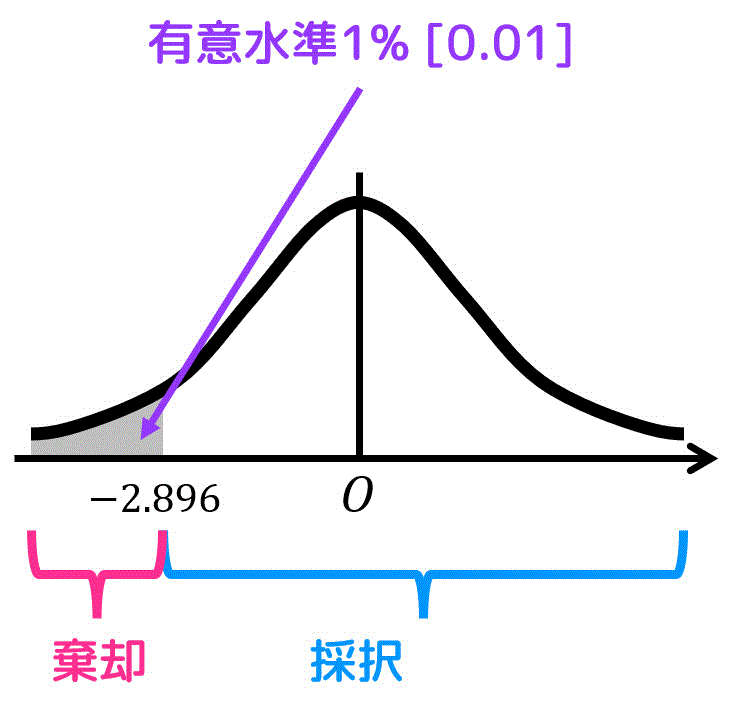
まず、有意水準1%(青色の面積部分が0.01)の判定ラインとなる \( t \) の値を表から調べます。
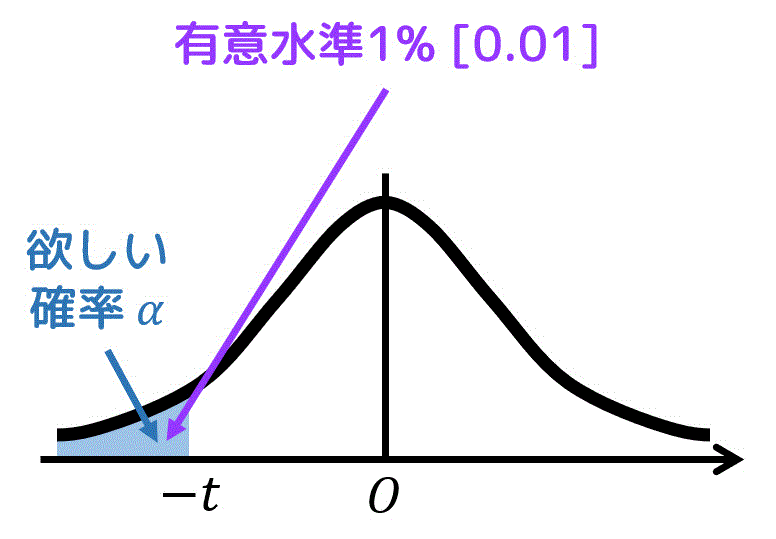
[i] 両側t分布表の場合
両側 \( t \) 分布表に表示されている \( \alpha \) は必要な青色の面積部分のほかに、不要な灰色部分の面積が含まれています。
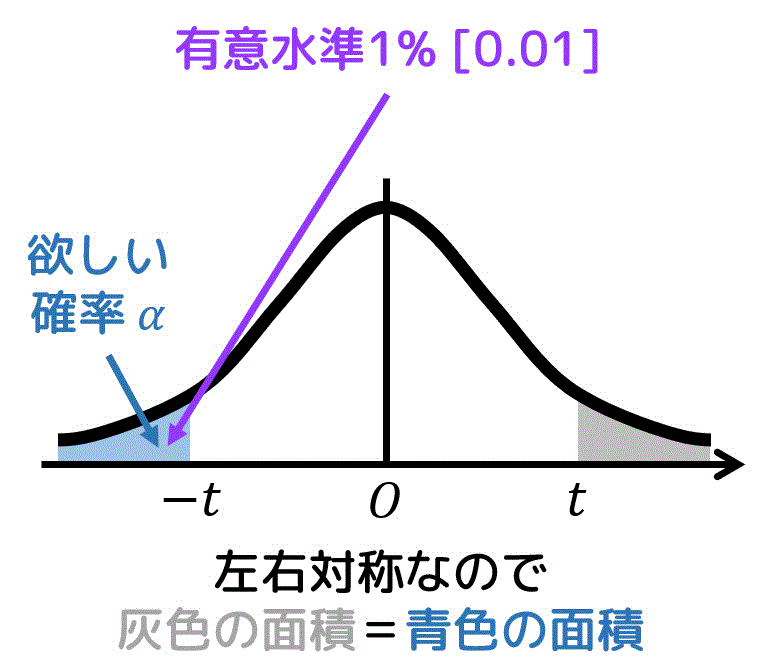
青色部分の面積と灰色部分の面積は同じなので、\( \alpha = 0.01 + 0.01 = 0.02 \) の値を使います。
また、自由度は8なので、\( k = 8 \), ( \alpha = 0.02 \) 灰色部分の面積の和 \( \alpha \) が 0.05 の場合をt分布表から読み取ればOKです。
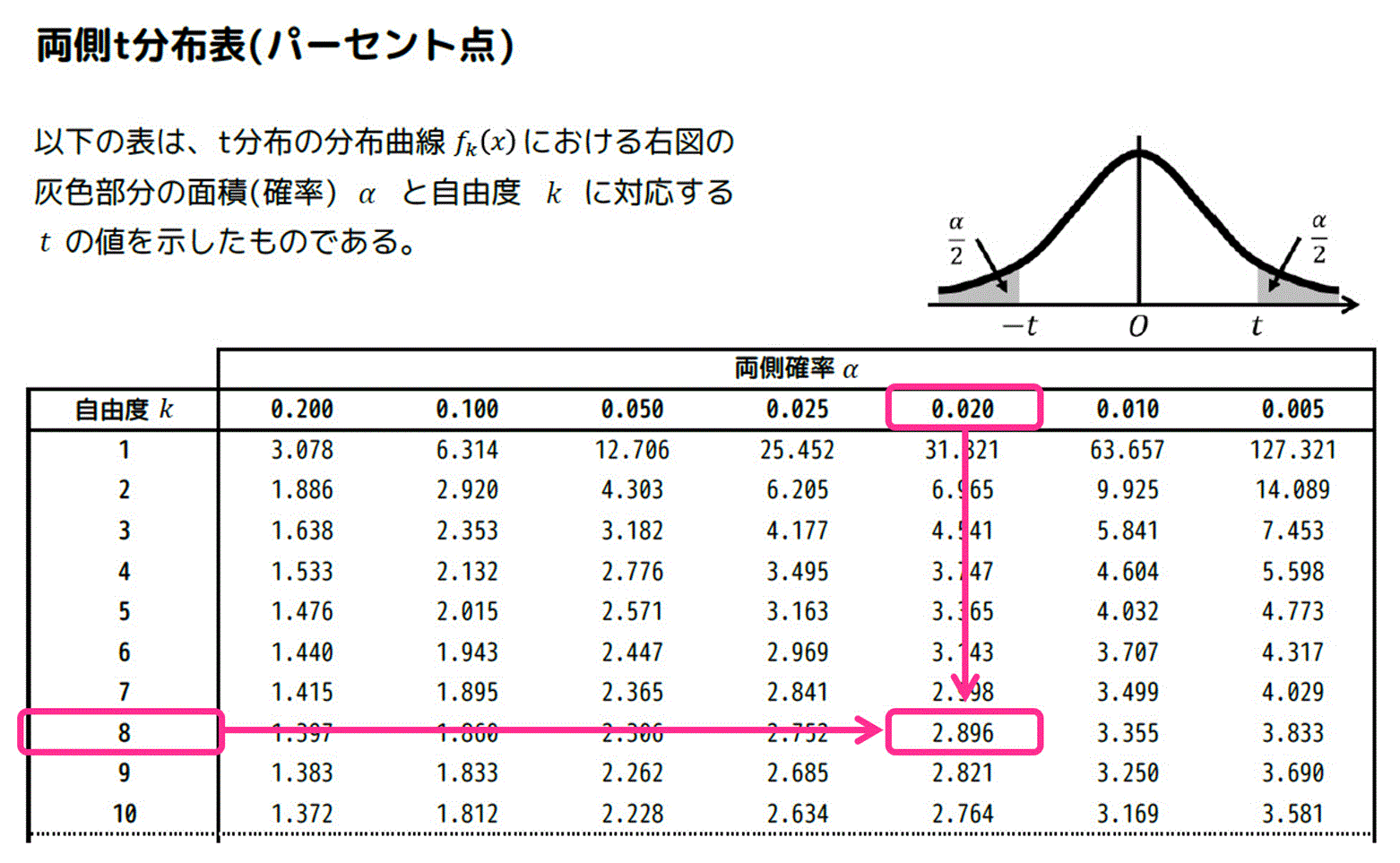
結果、\( t = 2.896 \) と読み取ることが出来ます。
[ii] 片側t分布表の場合
片側t分布表では、緑色部分の確率 \( \alpha \) が示されています。
しかし、緑色部分の面積と今回欲しい確率(青色部分の面積)は同じなので、有意水準1% \( \alpha = 0.01 \) の部分をそのまま読めばOKです。
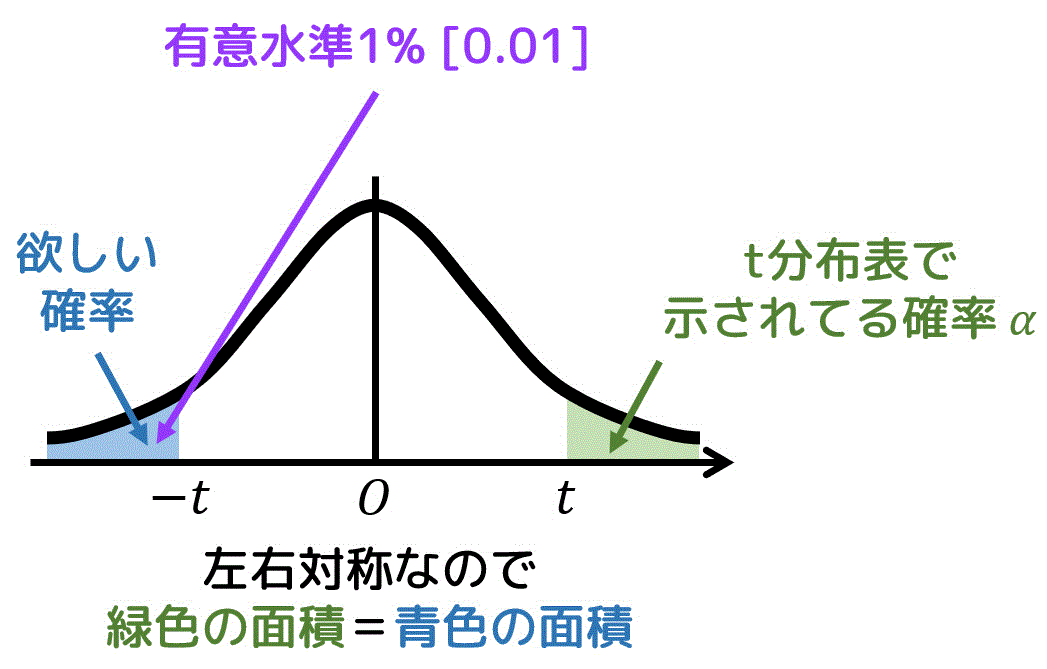
あとは、自由度 \( k = 8 \)、\( \alpha = 0.01 \) の部分を片側t分布表から読み取ればOK。
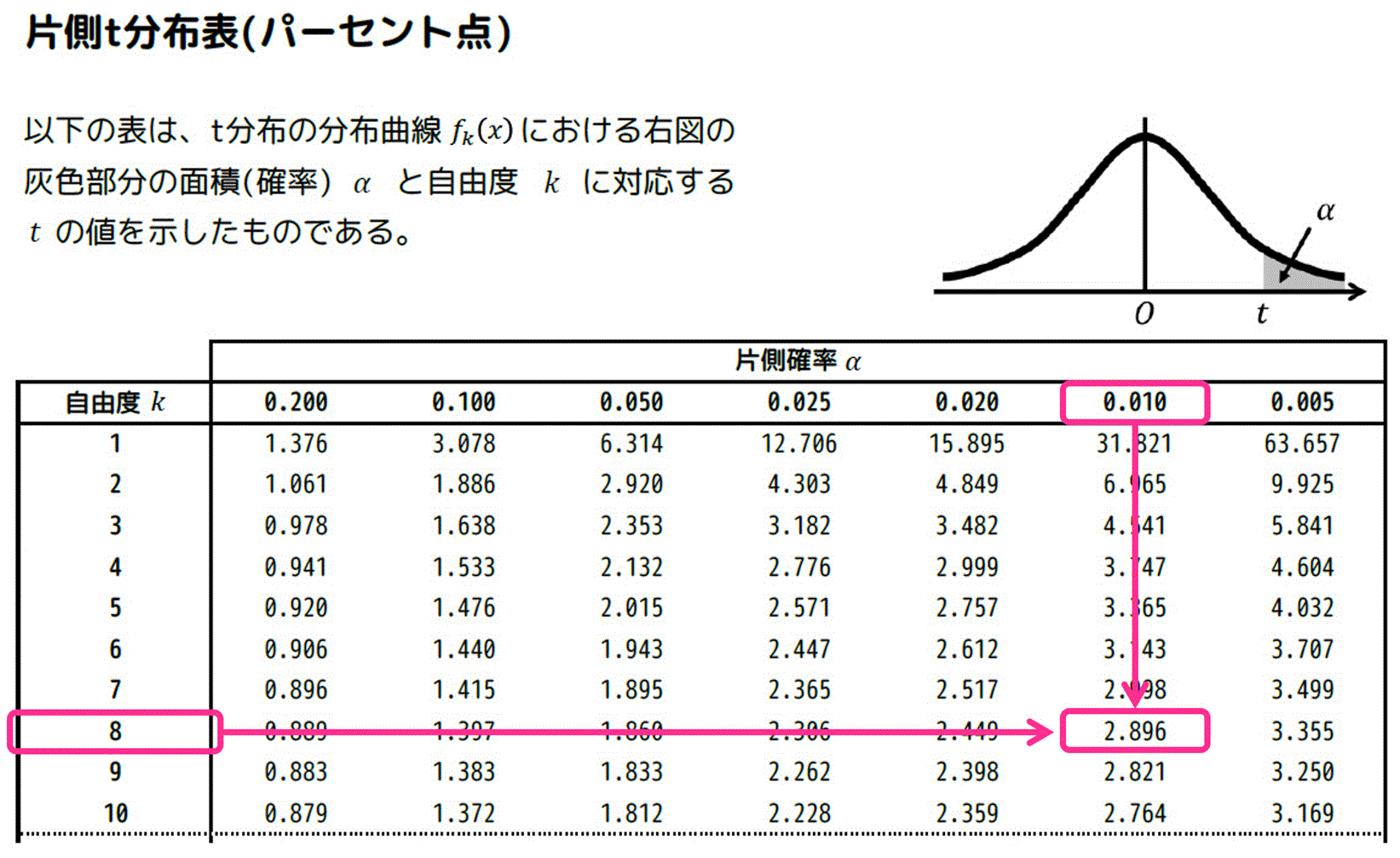
結果、\( t = 2.896 \) と読み取れます。
Step3. 与えられたデータ、仮定したデータから仮説検定を行う
あとは今回の標本の情報、および帰無仮説での仮定 \( \mu = 70 \) をt分布の変換式\[
t = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\]で変換したときに、値が\[
- 2.896 < t
\]に収まるかどうか確認し、次の2つの結論のどちらになるかを確認します。
- 収まった場合: 仮定は \( H_0 \) は採択。(誇張広告とは言えない)
- 収まらなかった場合: 仮定は \( H_0 \) は棄却。(誇張広告と言える)
あとは、今回の標本の各情報
- 標本サイズ \( n \): 9
- 標本平均 \( \overline{X} \): 61
- 不偏分散 \( s^2 \): 81(不偏標準偏差 \( s \): 9)
および仮説 \( \mu = 70 \) を式に入れると、\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\\ & = \frac{ \sqrt{9} \ (61 - 70) }{ 9 }
\\ & = \frac{ 3 \cdot (-9) }{ 9 }
\\ & = -3
\end{align*}\]となり、\[
- 2.896 \not \leqq -3
\]と判定ラインに収まっていません。
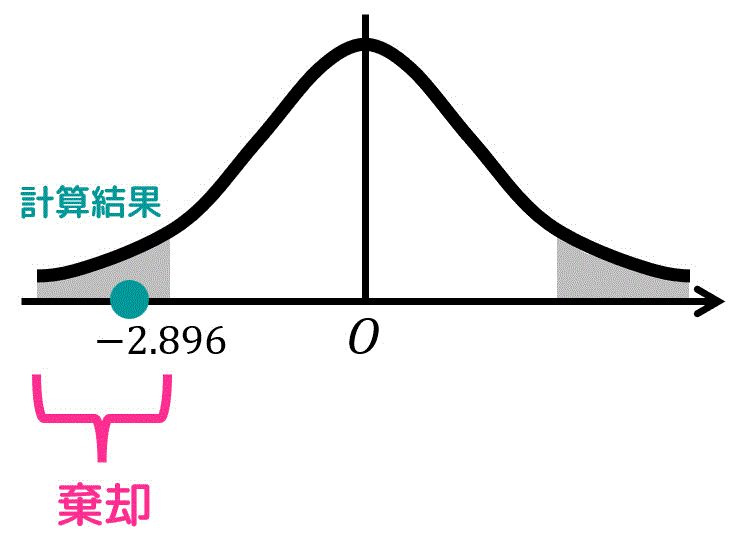
よって、帰無仮説 \( H_0 \) は棄却され、誇張広告であると言えます。
関連広告・スポンサードリンク