スポンサードリンク
こんにちは、ももやまです。
前回までの「t分布のいろは①・②」では1つの標本の標本平均、不偏分散から、母平均を推定・仮説検定していく方法について勉強しました。
t分布のいろは①(標本平均、不偏分散から母平均を区間推定)
t分布のいろは②(標本平均、不偏分散から母平均に関する仮説検定実施)
今回は、標本が2つで、なおかつその2つが対応している場合の仮説検定の仕方について、勉強していきましょう。
※ 「2つの標本が対応している」って何?? と思った人もいるかもしれませんが、2章にて説明していますので、ご安心ください。
例題、練習問題を解く際にお使いください。
※ 使っている参考書や授業に合わせて、両側t分布表、片側t分布表を選択することをおすすめします。なお、統計検定の場合、与えられる表は片側t分布表です。
目次
スポンサードリンク
1. t分布のおさらい
まずは、t分布を用いて母平均の検定をする方法について復習しましょう。
1.仮説検定でt分布はどんな時に使えるか?
標本のデータ(標本平均・不偏分散)から母平均の仮説検定をするときに使える。
2.t分布と自由度
単一の標本(母分散不明)について、母平均を検定する場合の自由度は次の通りである[1]標本の中で、1つ値が分からないものがあっても、標本平均や不偏分散から復元できるため、情報量は「標本のサイズ」より1小さい値となる。。
(自由度) = (標本のサイズ) - 1
3.t分布の変換公式
ある標本のデータを、t分布の世界の値に変えるときの変換式は\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\end{align*}\]である。
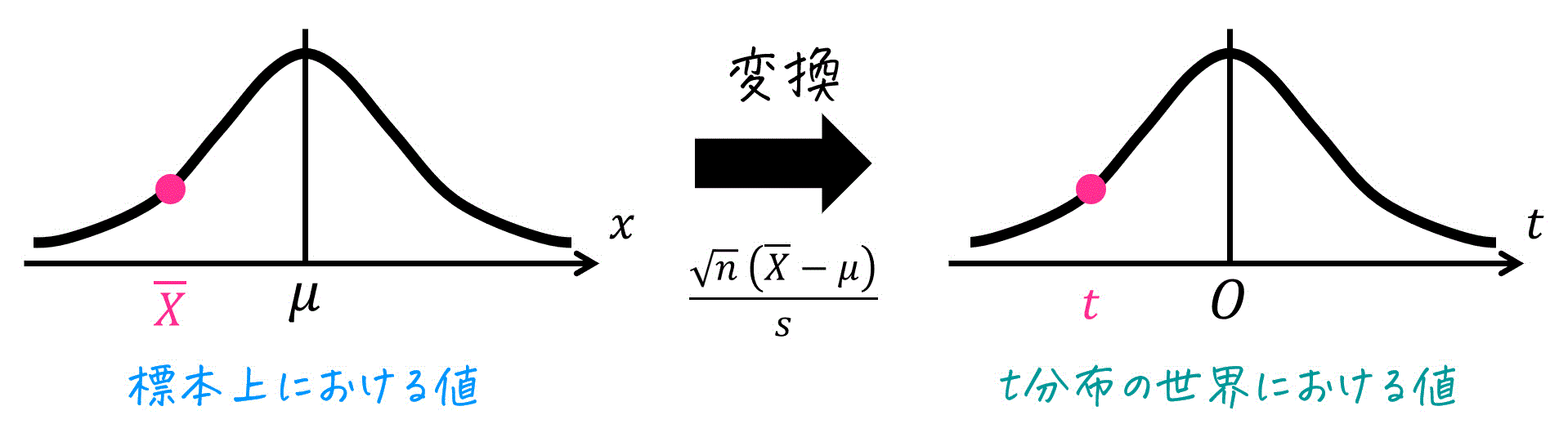
※ 母平均: \( \mu \)、標本サイズ: \( n \)、標本平均: \( \overline{X} \)、不偏分散 \( s^2 \) [不偏標準偏差: \( s \)]
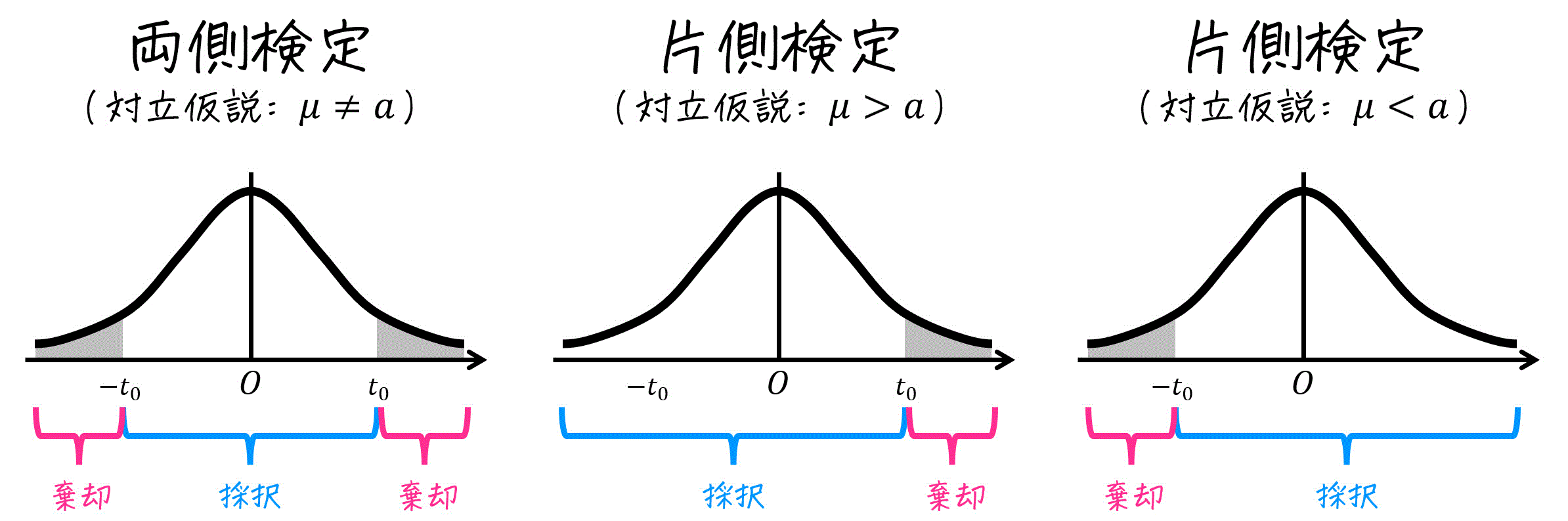
検定の結果(採択/棄却)を判断するときは、上の式の \( t \) 値への変換式、および読み取った値 \( t_0 \) から採択 or 棄却の判定をする。
- 両側検定のとき
→ \( -t_0 \leqq t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu > a \) のとき (母平均が仮定よりも大きいとき)
→ \( t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu < a \) のとき (母平均が仮定よりも小さいとき)
→ \( t_0 \leqq t \) であれば採択。それ以外で棄却。
※ 不偏分散\[
s^2 = \frac{1}{n-1} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]の代わりに標本分散\[
S^2 = \frac{1}{n} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]を使った場合は、変換式は\[
\frac{ \sqrt{n-1} \ (\overline{X} - \mu) }{S}
\]となる[2]基本的には不偏分散 \( s^2 \)(不偏標準偏差 \( s \) を使った形で公式が記載されていますが、参考書によっては標本分散 \( S^2 \)(標本標準偏差 \( s … Continue reading。
スポンサードリンク
2. 対応のある2標本の検定とは?
実際に例題を解く前に、まずは「対応のある2標本の検定」とはどのような検定なのかを、学習しましょう。
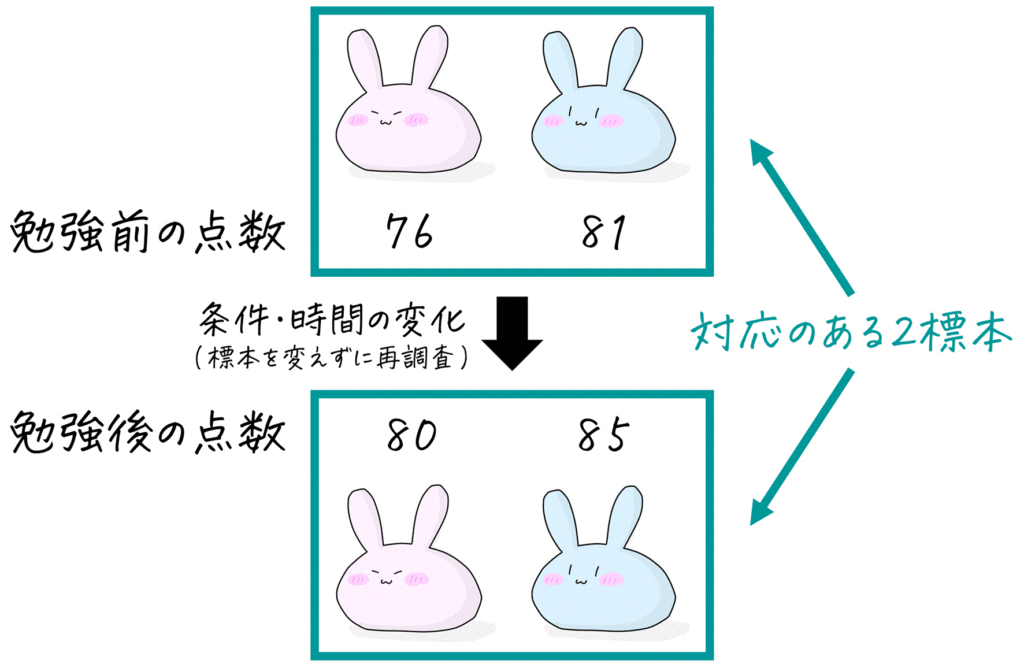
(1) 対応がある標本の検定
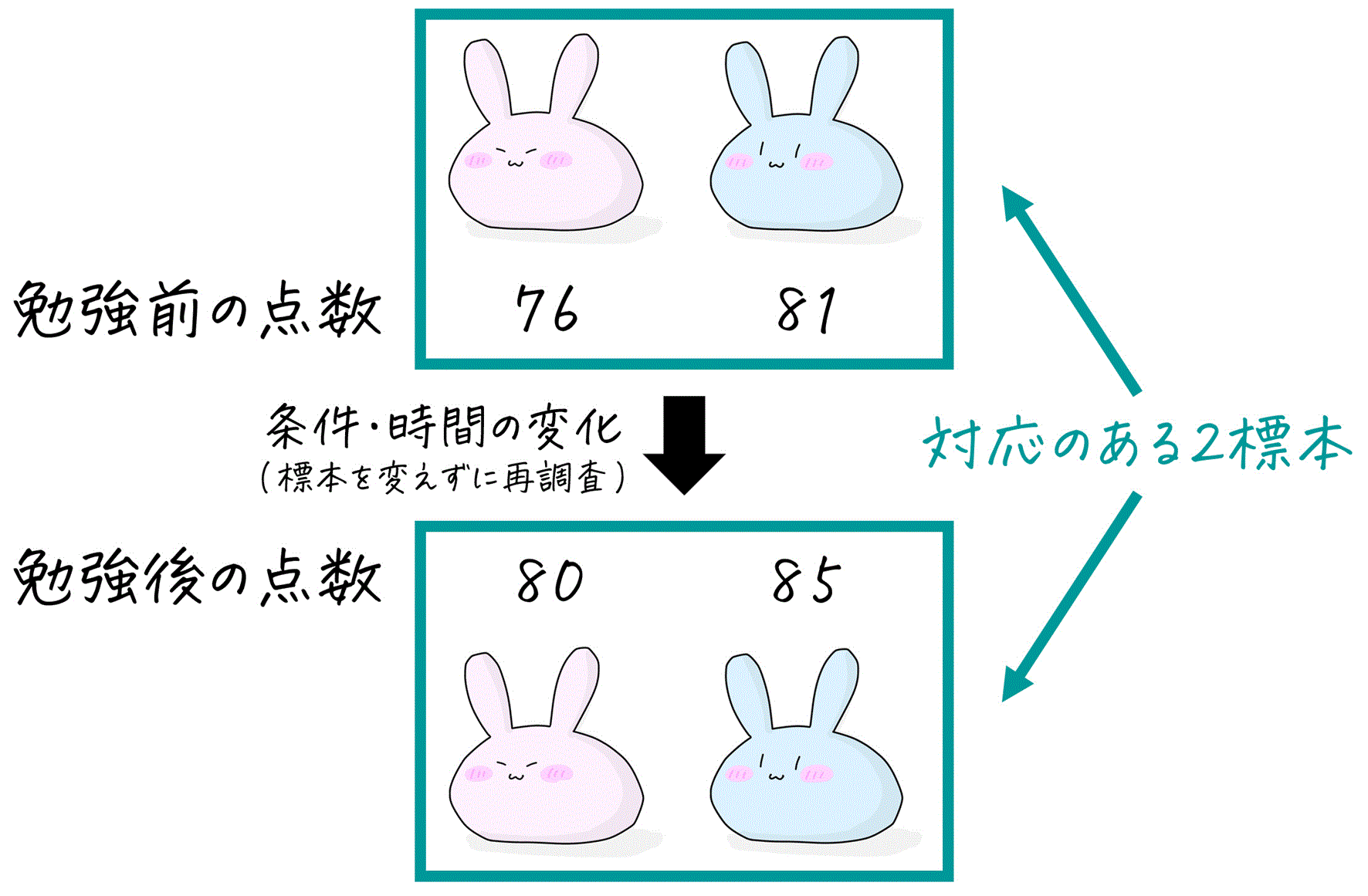
対応のある2標本の検定とは、全く同じ標本に対して、条件や時間を変えた2つのデータが与えられるた検定は、対応のある2標本の検定と呼びます。
例えば、「勉強前の山田くんと花子さんの点数」と「勉強後の山田くんと花子さんの点数」は、同じ標本(山田くんの点数、花子さんの点数)に対して条件(勉強前・勉強後)をが変わっているので、対応のある2標本といえます。
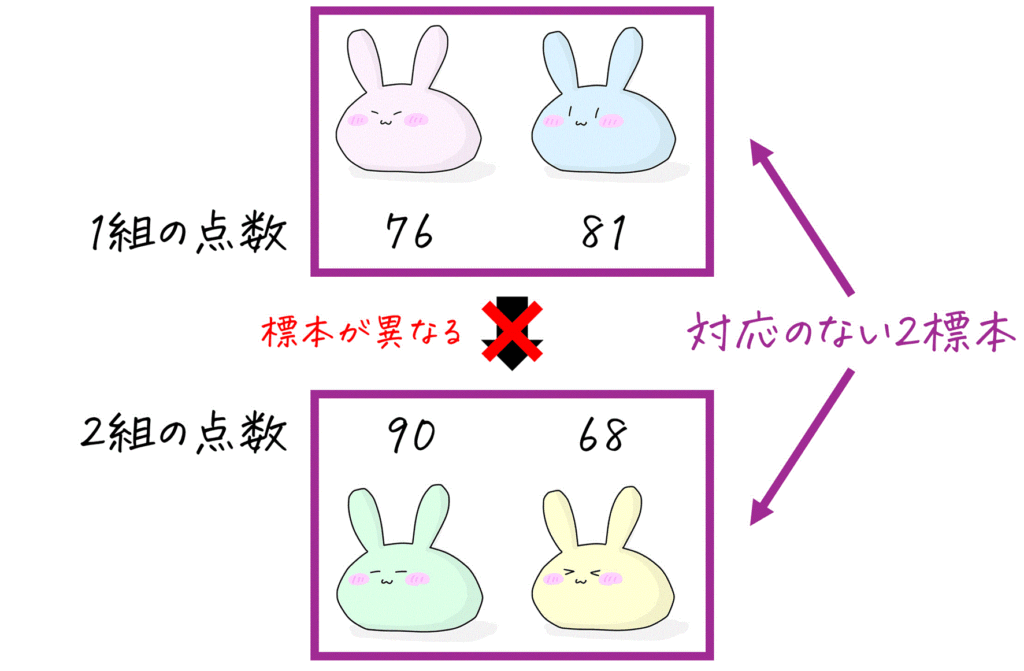
(2) 対応がない2標本とは?
一方、対象の異なる標本が2つある場合、これは対応がない2標本となります。
例えば、「1組の点数の標本」と「2組の点数の標本」を考えてみましょう。
この2つ(1組の点数の標本、2組の点数の標本)は異なる標本ですね。なので、この2標本は対応がない2標本と言えます。
対応がない2標本について、母平均の仮説検定を行っていく方法は、別の記事にて説明します。
スポンサードリンク
3. 例題で対応がある2標本のt検定方法を学ぼう
ここからは、実際に例題を使って対応のある2標本の検定をt分布で実施する方法について学習していきましょう。
新しく開発したトレーニングプログラムが、体重減少の効果を発揮するか検証するために、同じ大学に所属している4名の学生に、「1日15分でできる運動プログラム」を1年間試してもらった。トレーニングプログラム開始前と開始後で体重を測定してもらったところ、以下のデータが得られた。
| 名前 | 開始前 [kg] | 開始後 [kg] |
|---|---|---|
| 浅山 | 76 | 74 |
| 上杉 | 69 | 67 |
| 鈴木 | 83 | 77 |
| 渡辺 | 66 | 64 |
このデータをもとに、トレーニングプログラムに体重減少の効果があるといえるか、有意水準5%で検定したい。つぎの(1), (2)の問いに答えなさい。
(1) 帰無仮説 \( H_0 \), 対立仮説 \( H_1 \) を答えなさい。
(2) 有意水準5%で検定を行い、結果を答えなさい。過程も示すこと。
対応のある2標本についての検定の方針
今回の例題は、「4人のトレーニングプログラム実施前の体重」と「4人のトレーニングプログラム実施後の体重」のように、同じ4人(浅山さん、上杉さん、鈴木さん、渡辺さん)に対して実験前と実験後で結果に影響を与えるのかを調べる問題となっています。
そのため、この問題は対応のある2標本に対する検定の問題だと言えますね。
対応のある2標本の仮説検定では、「2つの標本データの対応するデータごとに差分を取り、それを新たな1つの標本する」というのがポイントです。
今回の問題の場合、各個人ごとの「開始後のデータ」から「開始前のデータ」を引いたものを新たらしいデータとします。「変化 (開始後 - 開始前)」とでも名付けましょうか。
| 名前 | 開始前 [kg] | 開始後 [kg] | 変化 (開始後 - 開始前) [kg] |
|---|---|---|---|
| 浅山 | 76 | 74 | -2 |
| 上杉 | 69 | 67 | -2 |
| 鈴木 | 83 | 77 | -6 |
| 渡辺 | 66 | 64 | -2 |
この新しいデータ「変化 (開始後 - 開始前)」に関する標本について仮説検定をすることで、1標本の母平均の仮説検定と同じ流れで仮説検定をすることが出来ます。
対応のある2標本の検定の方針
まず、実験後と実験前の条件の変化や時間が影響を与えない(つまり、影響がない)という仮定を立てます。
この「影響がない」という仮定は、「実験前の母集団と実験後の母集団は全く変化がない(つまり、母平均も同じ)」と言い換えることができます。さらに言い換えると、「実験後の母平均と実験前の母平均の差が0である」となりますね。
今回の例題の場合は、以下の表の「変化 (開始後 - 開始前)」の母平均が0であると仮定します。
| 名前 | 開始前 [kg] | 開始後 [kg] | 変化 (開始後 - 開始前) [kg] |
|---|---|---|---|
| 浅山 | 76 | 74 | -2 |
| 上杉 | 69 | 67 | -2 |
| 鈴木 | 83 | 77 | -6 |
| 渡辺 | 66 | 64 | -2 |
また、対立仮説は「帰無仮説を否定することで示したいもの」を設定します。
今回の例題の場合は、トレーニングプログラムの効果があることを示したいので、対立仮説は「トレーニングプログラムの効果がある」とありますね。
この対立仮説を数式で書くと、「"変化 (開始後 - 開始前)" の母平均が0未満である」となりますね。
(1)の答え [帰無仮説・対立仮説のまとめ]
まとめると、帰無仮説 \( H_0 \) と対立仮説 \( H_1 \) は、次の通りになります。
帰無仮説 \( H_0 \)
→ トレーニング開始後と開始前の体重の差(開始後 - 開始前) の母平均 \( \mu \) について、\( \mu = 0 \) である。
※ トレーニングプログラムの効果がない場合。
対立仮説 \( H_1 \)
→ トレーニング開始後と開始前の体重の差(開始後 - 開始前) の母平均 \( \mu \) について、\( \mu < 0 \) である。
※ トレーニングプログラムの効果がある場合。今回は、トレーニングプログラムが体重減少に効果があるのかを調べたいので、母平均が0より小さいとなる(片側検定)。
解説(2). 帰無仮説と対立仮説の決め方
Step1. "開始後 - 開始前" の標本平均、不偏分散を求める
まずは、トレーニング開始後と開始前の体重の差(開始後 - 開始前)の標本平均、不偏分散を求めていきます。
| 名前 | 開始前 [kg] | 開始後 [kg] | 変化 (開始後 - 開始前) [kg] |
|---|---|---|---|
| 浅山 | 76 | 74 | -2 |
| 上杉 | 69 | 67 | -2 |
| 鈴木 | 83 | 77 | -6 |
| 渡辺 | 66 | 64 | -2 |
標本平均 \( \overline{X} \)
\[\begin{align*}
\overline{X} & = \frac{1}{n} \sum^{n}_{k = 1} x_k
\\ & = \frac{1}{4} (-2 -2 -6 -2)
\\ & = \frac{1}{4} \cdot (-12)
\\ & = -3
\end{align*}\]
不偏分散 \( s^2 \)
\[\begin{align*}
s^2 & = \frac{1}{n-1} \sum^{n}_{k=1} (x_k - \overline{X})
\\ & = \frac{1}{4-1} \left[ \{ -2 - (-3) \}^2 + \{ -2 - (-3) \}^2 + \{ -6 - (-3) \}^2 + \{ -2 - (-3) \}^2 \right]
\\ & = \frac{1}{3} \left\{ 1^2 + 1^2 + (-3)^2 + 1^2 \right\}
\\ & = \frac{1}{3} \cdot 12
\\ & = 4
\end{align*}\]
Step2. 使う分布(必要であれば自由度)を確認
今回は、トレーニング開始後と開始前の体重の差(開始後 - 開始前)の母平均の仮説検定を、母分散を使わずで推定します。
なので、t分布を使用します。
また、自由度は (標本サイズ) - 1 にて求められるので、自由度3となります。
どのような検定で、どのような分布を使うかを復習しておきましょう。
| t分布 | 正規分布 | |
|---|---|---|
| 必要な情報 | 標本平均・不偏分散 | 標本平均・母分散 |
| 検定対象 | 母平均 | 母平均 |
Step3. 有意水準(危険率)5%に対応する t の値を求める
つぎに、有意水準5%に対応する \( t \) の値 \( t_0 \) を求めていきます。
今回の対立仮説は、「母平均が0より小さい」なので、母平均が大きい側を考える必要はありません。つまり、片側検定となります。
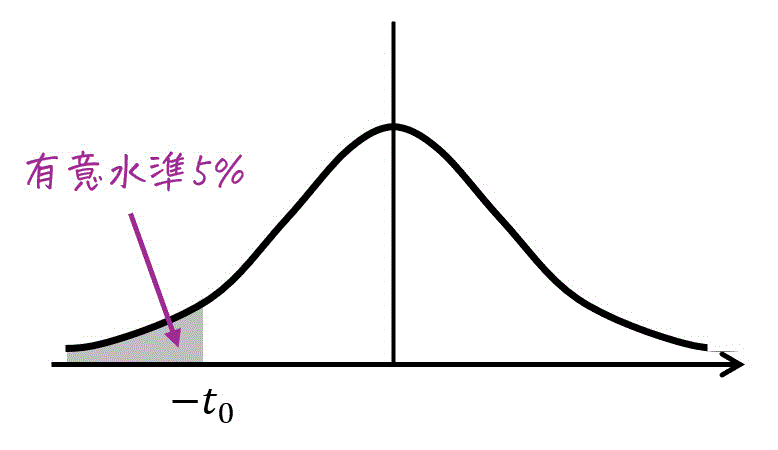
あとは、与えられた表から有意水準5%に相当する \( t = t_0 \) の値を求めればOKです。
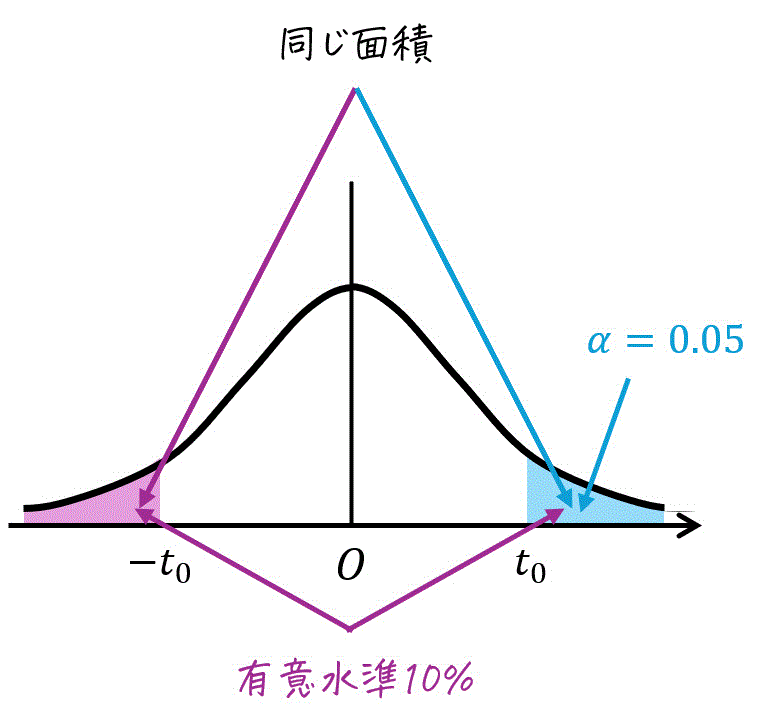
★ 両側t分布表が与えられた場合
両側 \( t \) 分布表に表示されている \( \alpha \) は必要な紫色の面積部分のほかに、不要な水色部分の面積が含まれています。
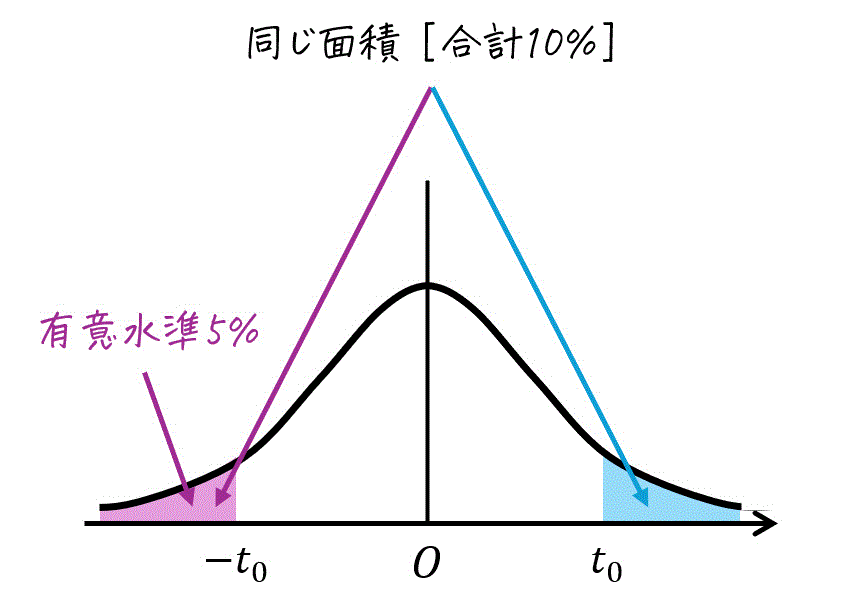
ここで、青色部分の面積と灰色部分の面積は同じなので \( \alpha = 0.05 + 0.05 = 0.10 \) の値を使えばOKです。
また、自由度は3でしたね。なので、あとは \( k = 3 \)、\( \alpha = 0.10 \) に相当する \( t \) の値を求めるだけです。
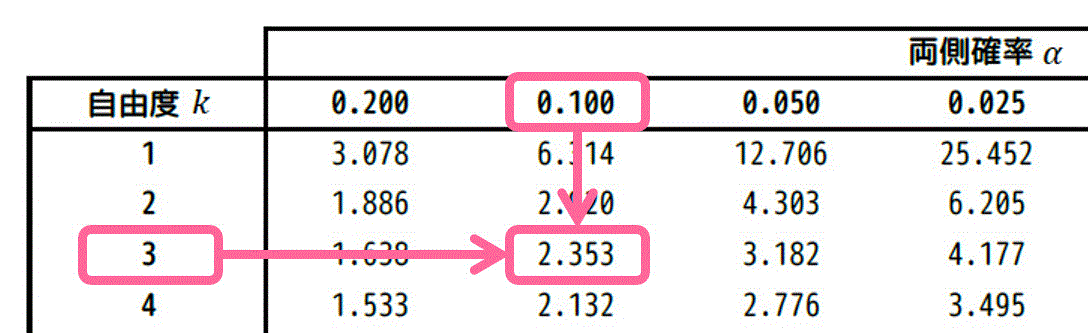
よって、\( t_0 = 2.353 \) と求まります。
★ 片側t分布表が与えられた場合
片側t分布表では、緑色部分の確率 \( \alpha \) が示されています。
しかし、緑色部分の面積と今回欲しい確率(青色部分の面積)は同じなので、有意水準1% \( \alpha = 0.05 \) の部分をそのまま読めばOKです。
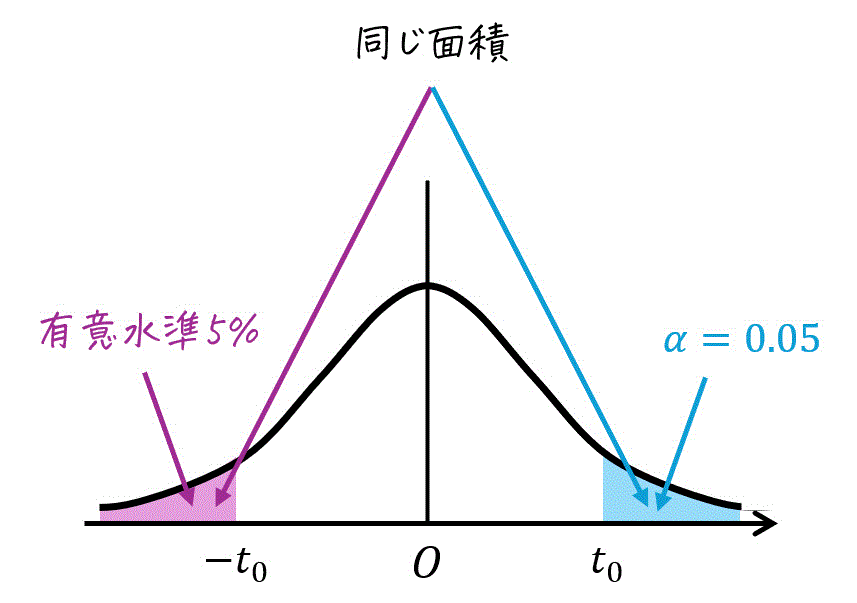
あとは、自由度 \( k = 3 \)、\( \alpha = 0.05 \) の部分を片側t分布表から読み取りましょう。
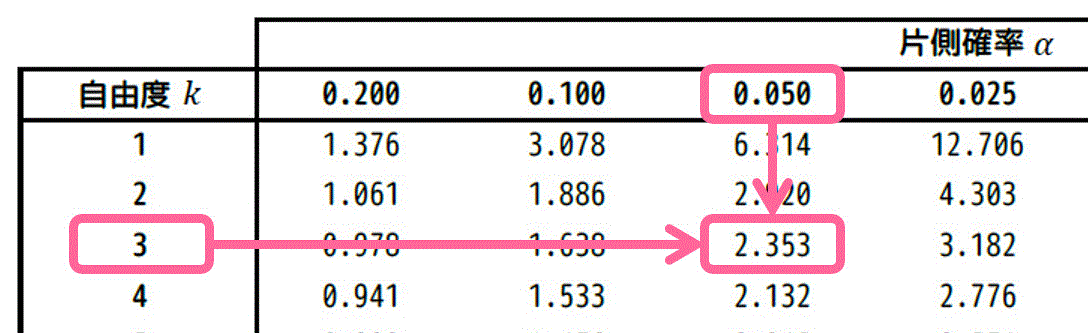
よって、\( t_0 = 2.353 \) と求まります。
Step4. 標本の情報をt変換し、結果 (採択/棄却) を判定する
標本サイズ \( n = 4 \)、標本平均 \( \overline{X} = -3 \)、不偏分散 \( s^2 = 4 \)(不偏標準偏差 \( s = 2 \))、帰無仮説の仮定 \( \mu = 0 \) をt分布の変換式\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\end{align*}\]に入れて、t分布の世界での値に変換しましょう。
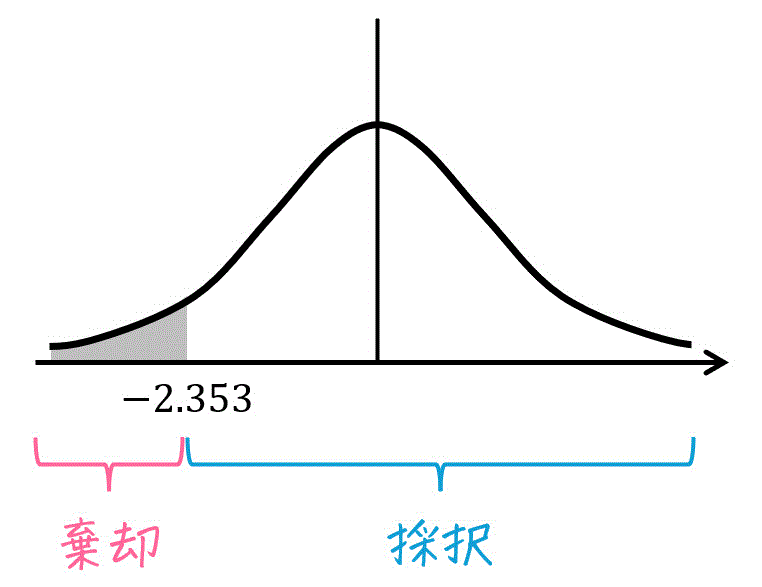
この変換結果が、Step3で求めた値 \( -t_0 = -2.353 \) と比べて
- \( - t_0 \leqq t \) となれば仮説は採択(仮定は誤りとはいえない)
- \( - t_0 > t \) となれば、仮定は棄却(仮定が誤りといえる)
となります。
変換をすると、\[\begin{align*}
t & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\\ & = \frac{ \sqrt{4} \ (-3 - 0) }{s}
\\ & = \frac{-6}{2}
\\ & = -3 > -2.353
\end{align*}\]となります。
よって、仮説 \( \mu = 0 \) は棄却されます。
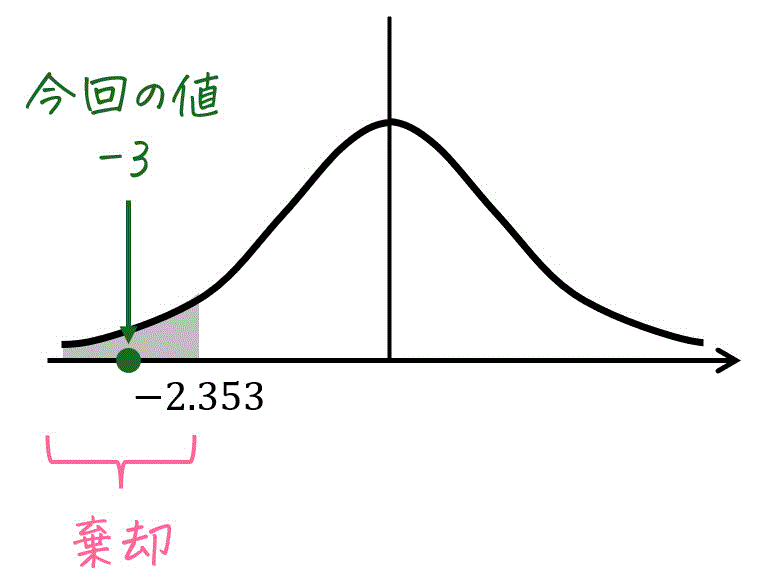
つまり、トレーニングプログラムの効果があると言えます。
4. 練習問題で理解度チェック!
では、対応のある2標本から母平均の推定をする方法の理解度を、練習問題で確認してみましょう。
睡眠時間が計算力に影響を与えるかを調べるために、9人の学生に
- 睡眠時間が7時間のとき
- 睡眠時間が8時間のとき
で同じ計算テストを時間を空けて2回実施した。結果、睡眠時間が8時間のときと6時間のときで、次のような結果が得られた。
| 名前 | 睡眠時間7h時の点数 [点] | 睡眠時間8h時の点数 [点] |
|---|---|---|
| 浅岡 | 66 | 70 |
| 上田 | 81 | 84 |
| 笠井 | 66 | 69 |
| 幸田 | 70 | 70 |
| 鈴木 | 69 | 70 |
| 奈良 | 77 | 77 |
| 新田 | 85 | 83 |
| 乃木 | 69 | 70 |
| 矢田 | 55 | 54 |
このデータをもとに、睡眠時間の変化は、計算力に(良い方向、悪い方向に関わらず)影響を与えるといえるか、検定したい。つぎの(1), (2)の問いに答えなさい。
(1) 帰無仮説 \( H_0 \), 対立仮説 \( H_1 \) を答えなさい。
(2) 有意水準10%で検定を行い、結果を答えなさい。過程も示すこと。
5. 練習問題の答え
(1)
この練習問題も、同じ標本に対して条件(睡眠時間)を変えることで、結果に影響を与えるかどうかを調べるパターンの問題ですね。なので、対応のある2標本の検定の解き方で解いていきます。
まず、帰無仮説 \( H_0 \) と対立仮説 \( H_1 \) は、"睡眠時間8時間のときの点数 - 睡眠時間7時間のときの点数" の母平均 \( \mu \) を使って、次のようにします。
帰無仮説 \( H_0 \)
→ \( \mu = 0 \) ※ 睡眠時間が計算力に影響を与えない
対立仮説 \( H_1 \)
→ \( \mu \not = 0 \) ※ 睡眠時間が計算力に影響を与える
※ 今回は、睡眠時間が良くも悪くも計算力に影響に与えるかを確認したいので、母平均が0ではないとなる(両側検定)
(2)
帰無仮説と対立仮説を設定したら、検定をはじめていきます。
Step1. "開始後 - 開始前" の標本平均、不偏分散を求める
まずは、睡眠時間が8時間のときの点数と睡眠時間が7時間のときの点数(睡眠8h時 - 睡眠7h時)の標本平均、不偏分散を求めていきます。
| 名前 | 睡眠時間7h時の点数 [点] | 睡眠時間8h時の点数 [点] | 変化 (睡眠8h時 - 睡眠7h時) [点] |
|---|---|---|---|
| 浅岡 | 66 | 70 | 4 |
| 上田 | 81 | 84 | 3 |
| 笠井 | 66 | 69 | 3 |
| 幸田 | 70 | 70 | 0 |
| 鈴木 | 69 | 70 | 1 |
| 奈良 | 77 | 77 | 0 |
| 新田 | 85 | 83 | -2 |
| 乃木 | 69 | 70 | 1 |
| 矢田 | 55 | 54 | -1 |
標本平均 \( \overline{X} \)
\[\begin{align*}
\overline{X} & = \frac{1}{n} \sum^{n}_{k = 1} x_k
\\ & = \frac{1}{9} (4 + 3 + 3 + 0 + 1 + 0 -2 + 1 - 1)
\\ & = \frac{1}{9} \cdot 9
\\ & = 1
\end{align*}\]
不偏分散 \( s^2 \)
\[\begin{align*}
s^2 & = \frac{1}{n-1} \sum^{n}_{k=1} (x_k - \overline{X})
\\ & = \frac{1}{9-1} \left\{ (4-1)^2+(3-1)^2+(3-1)^2+(0-1)^2+(1-1)^2+(0-1)^2+(-2-1)^2+(1-1)^2 + (-1-1)^2 \right\}
\\ & = \frac{1}{8} \left\{ 3^2 + 2^2 + 2^2 + (-1)^2 + 0^2 + (-1)^2 + (-3)^2 + 0^2 + (-2)^2 \right\}
\\ & = \frac{1}{8} \cdot 32
\\ & = 4
\end{align*}\]
Step2. 使う分布(必要であれば自由度)を確認
今回は、睡眠時間が8時間のときの点数と睡眠時間が7時間のときの点数の差について、母平均の仮説検定をしていきますが、母分散は与えられていませんね。
なので、t分布を使用します。
自由度は (標本サイズ) - 1 なので、8となります。
Step3. 有意水準(危険率)10%に対応する t の値を求める
つぎに、有意水準10%に対応する \( t \) の値を求めていきます。
今回の対立仮説は、「母平均が0ではない」なので、母平均が大きい場合と小さい場合の両方を考える必要があります。つまり、両側検定となります。
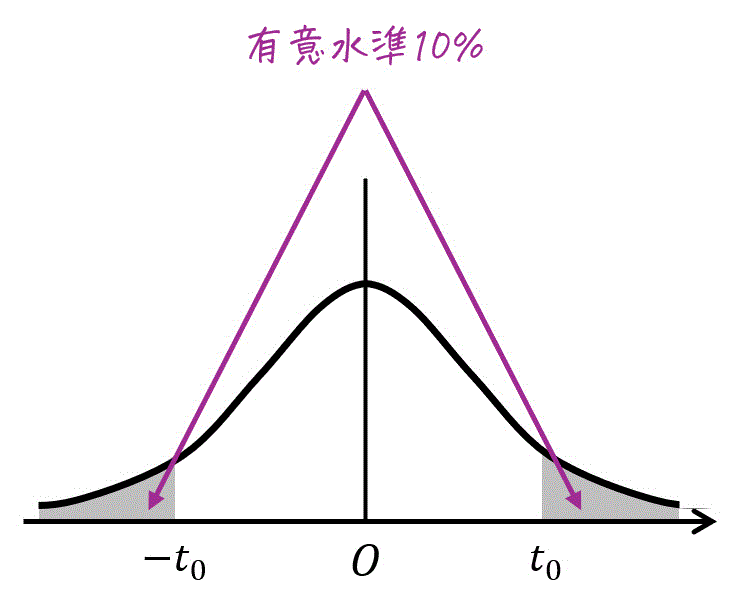
あとは、与えられた表から有意水準10%に相当する \( t = t_0 \) の値を求めればOKです。
★ 両側t分布表が与えられた場合
自由度 \( k = 8 \)、灰色部分の面積の和 \( \alpha \) が 0.10 の場合をt分布表から読み取ればOKです。
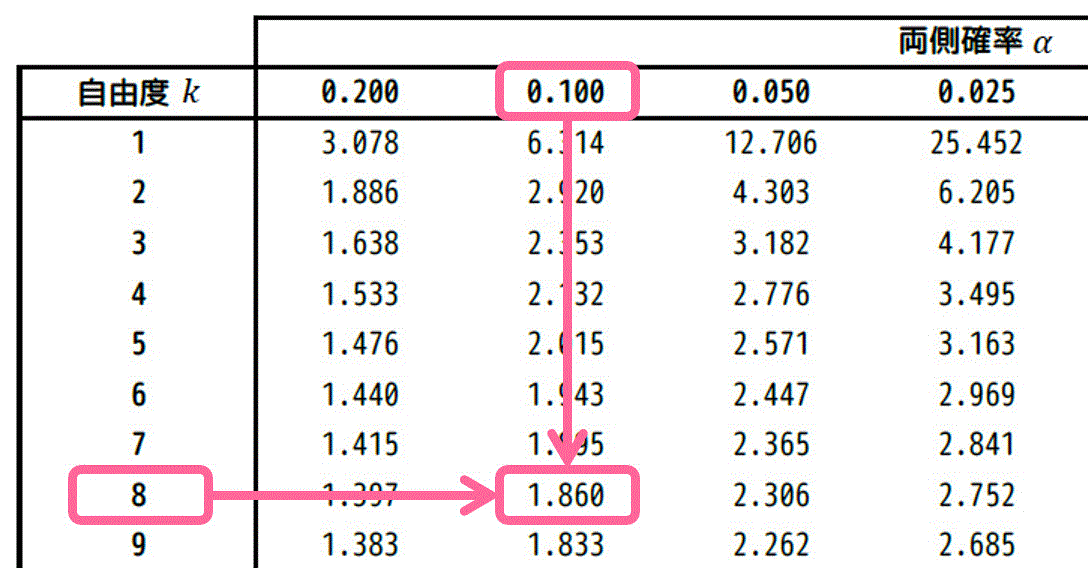
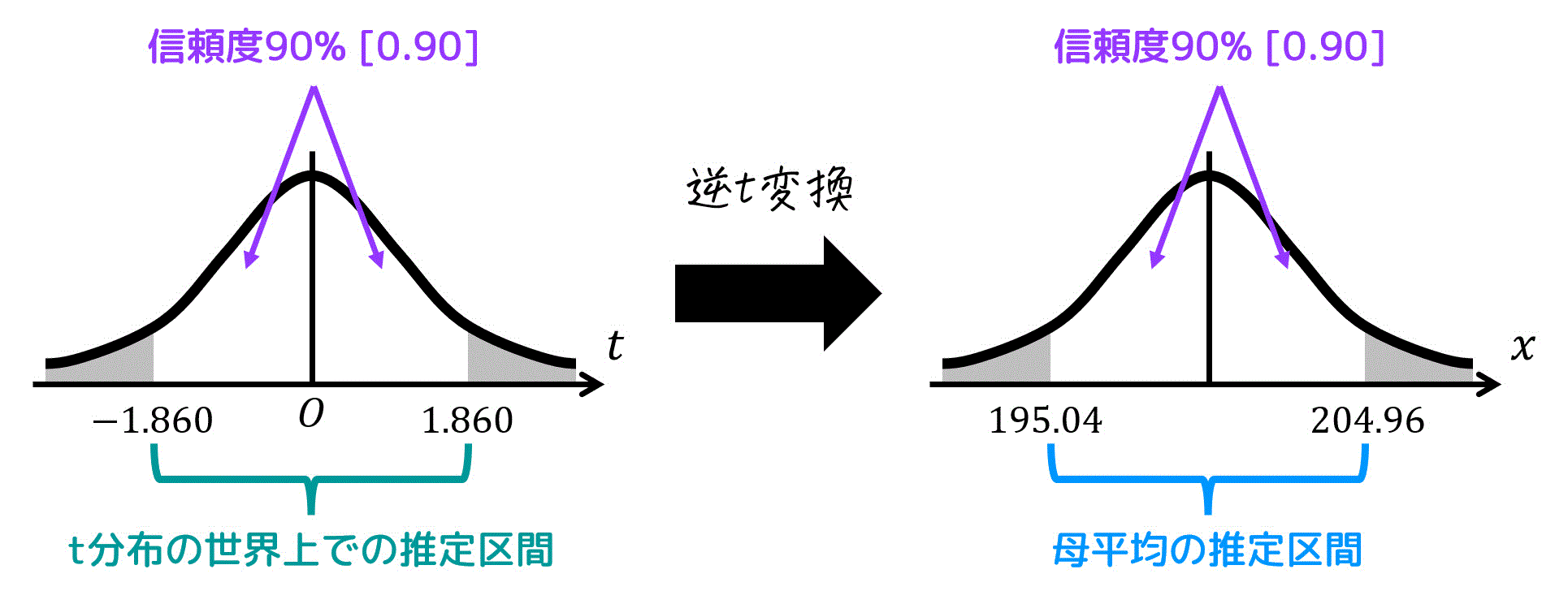
よって、\( t = 1.860 \) と求まります。
★ 片側t分布表が与えられた場合
片側t分布表の場合、青色部分の面積のみが書かれているため、半分の面積部分に相当する \( \alpha = 0.50 \) の部分を読み取る必要がある点に注意が必要です。
あとは、自由度8、\( \alpha = 0.05 \) の部分を片側t分布表から読み取ればOKです。
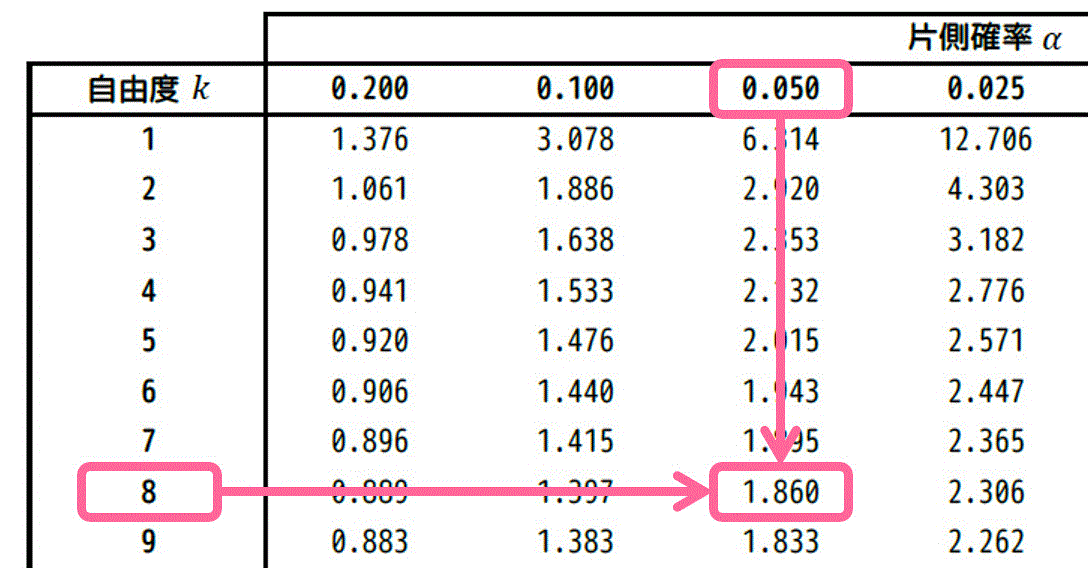
よって、\( t = 1.860 \) と求まります。
Step4. 標本の情報をt変換し、結果 (採択/棄却) を判定する
標本サイズ \( n = 9 \)、標本平均 \( \overline{X} = 1 \)、不偏分散 \( s^2 = 4 \)(不偏標準偏差 \( s = 2 \))、帰無仮説の仮定 \( \mu = 0 \) をt分布の変換式\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\end{align*}\]に入れて、t分布の世界での値に変換しましょう。
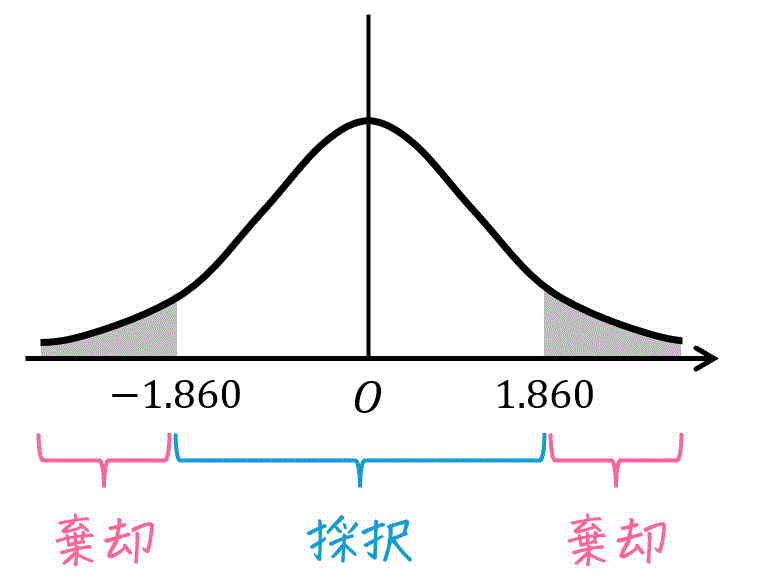
ここで、結果(採択/棄却)は、変換結果がStep3で求めた値 \( t_0 = 1.860 \) に対して、
- \( - t_0 \leqq t \leqq t_0 \) となれば仮説は採択(仮定は誤りとはいえない)
- \( - t_0 > t \) もしくは \( t_0 < t \) となれば、仮定は棄却(仮定が誤りといえる)
となります。
変換をすると、\[\begin{align*}
t & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\\ & = \frac{ \sqrt{9} \ (1 - 0) }{2}
\\ & = \frac{3}{2}
\\ & = 1.5 \leqq 1.860
\end{align*}\]となるため、仮説 \( \mu = 0 \) は採択されます。
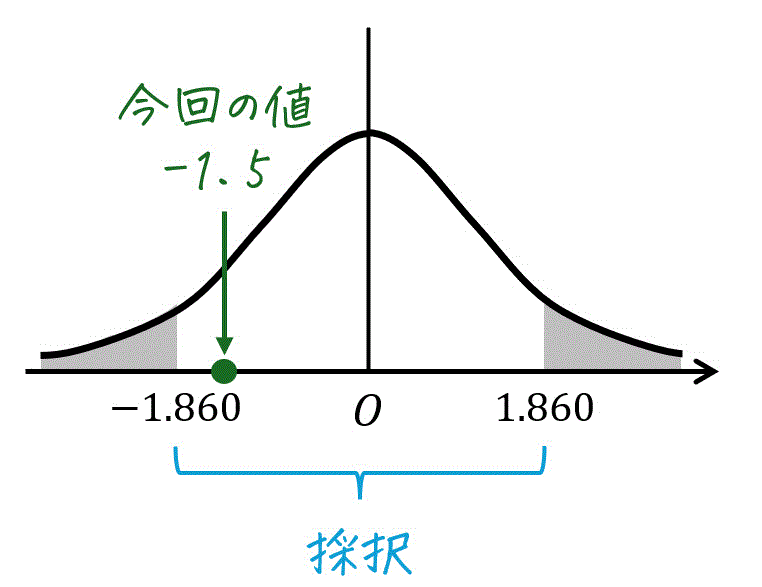
つまり、「睡眠時間7時間と睡眠時間8時間では、計算力に影響があるとは言えない」となります。
関連広告・スポンサードリンク