スポンサードリンク
こんにちは、ももやまです。
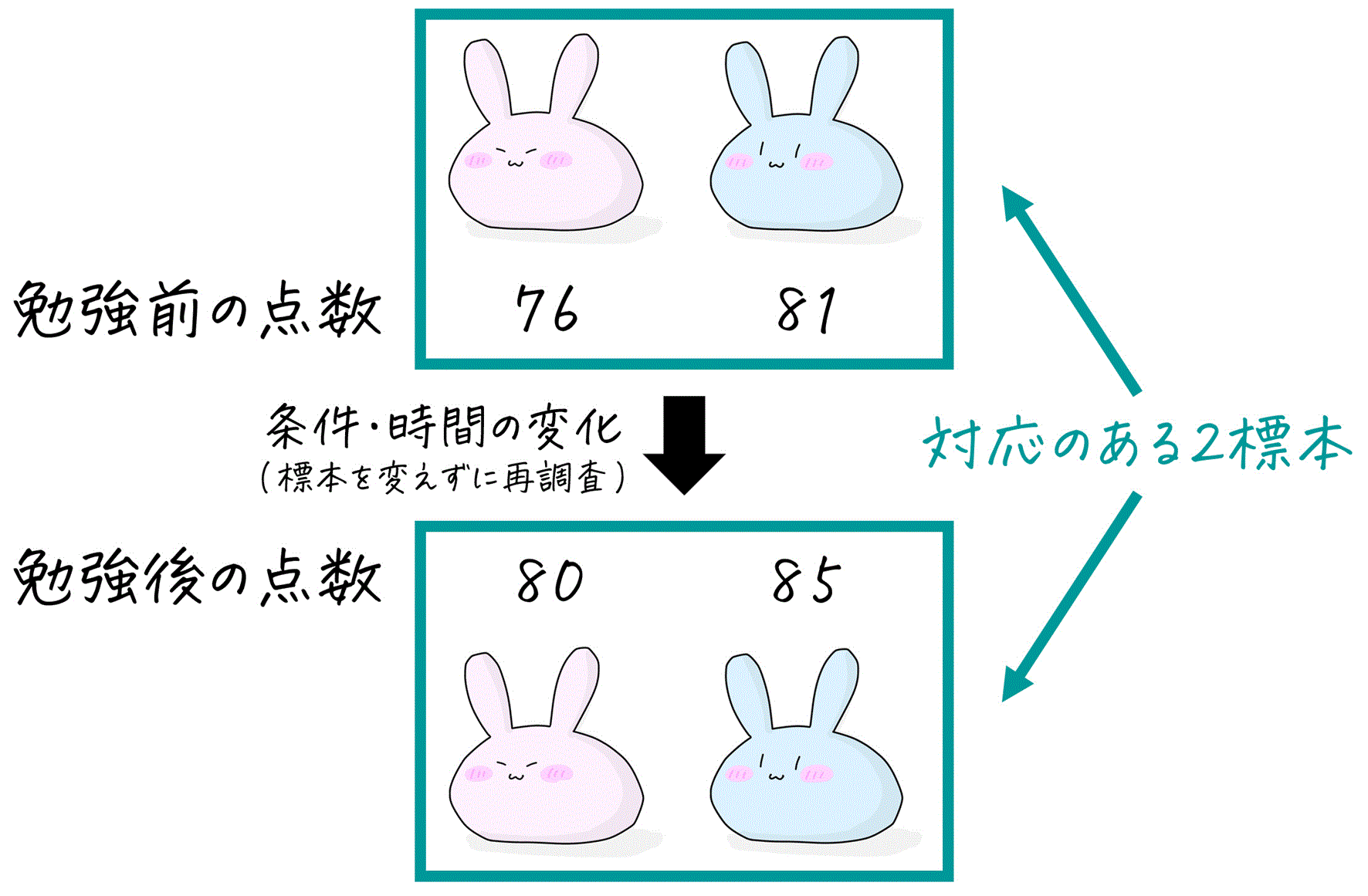
前回は「対応のある2標本」の母平均を、t分布を使って求めていく方法について説明していきましたね。
今回は、「対応のない2標本の母平均検定」を、t分布を使って求めていく方法について説明していきます。
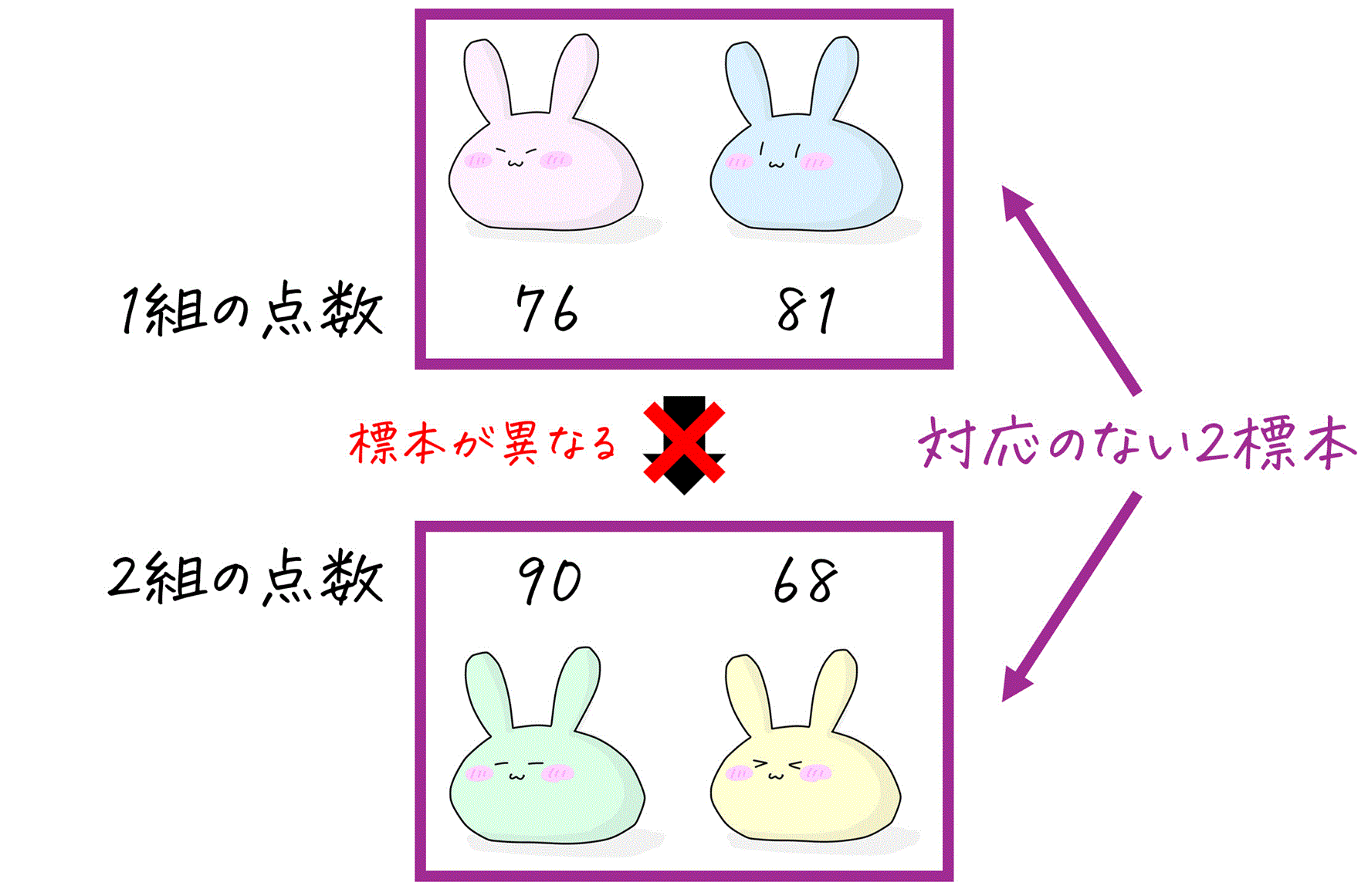
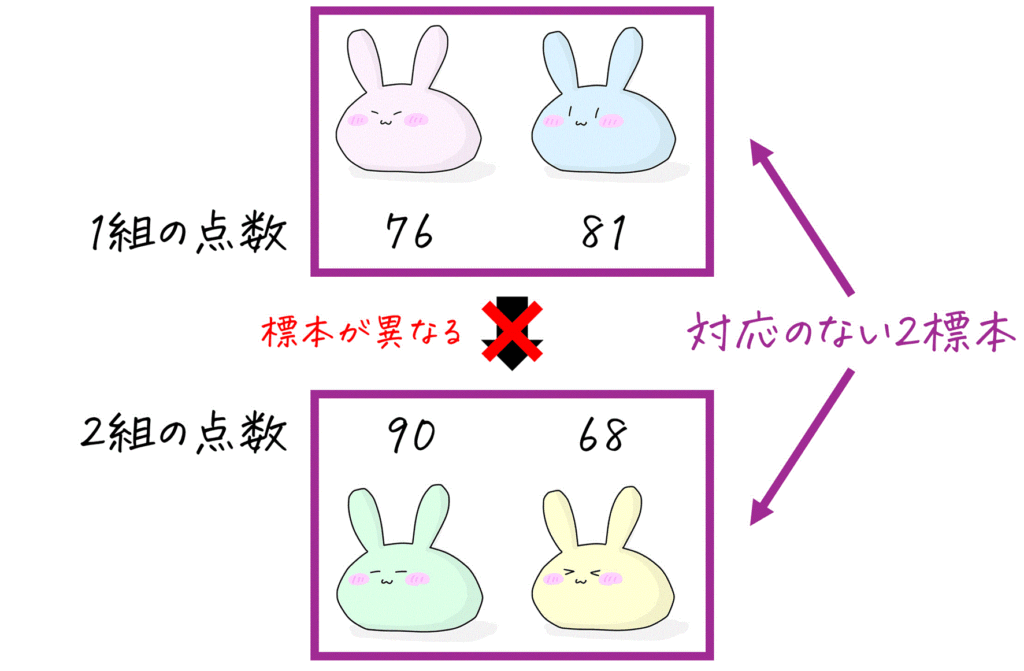
※ 対応のない2標本というのは、「1組の点数の標本」と「2組の点数の標本」のように、対象の異なる標本だと思っていただけたらOKです。
※ t分布を用いた仮説検定のことを「t検定」と記載している箇所があります。
例題、練習問題を解く際にお使いください。
※ 使っている参考書や授業に合わせて、両側t分布表、片側t分布表を選択することをおすすめします。なお、統計検定の場合、与えられる表は片側t分布表です。
目次
スポンサードリンク
1.t分布のおさらい
まずは、t分布を用いて母平均を推定する方法について、仮説検定をしていきましょう。
1.仮説検定でt分布はどんな時に使えるか?
標本のデータ(標本平均・不偏分散)から母平均の仮説検定をするときに使える。
2.t分布と自由度
単一の標本(母分散不明)について、母平均を検定する場合の自由度は次の通りである[1]標本の中で、1つ値が分からないものがあっても、標本平均や不偏分散から復元できるため、情報量は「標本のサイズ」より1小さい値となる。。
(自由度) = (標本のサイズ) - 1
3.t分布の変換公式
ある標本のデータを、t分布の世界の値に変えるときの変換式は\[\begin{align*}
t & = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\\ & = \frac{ \sqrt{n} \ (\overline{X} - \mu) }{ s }
\end{align*}\]である。
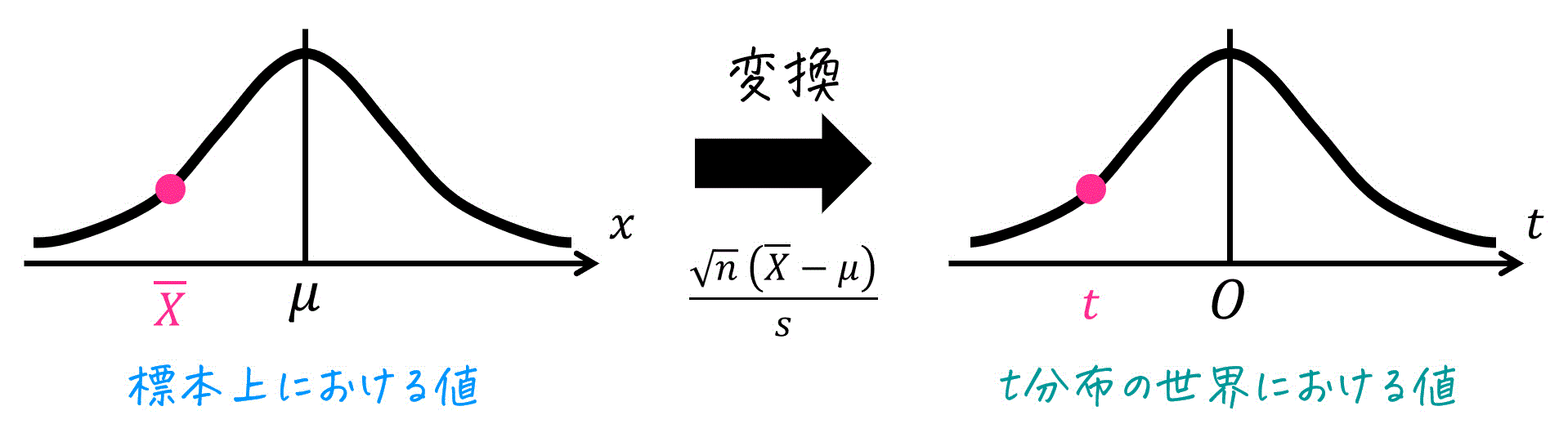
※ 母平均: \( \mu \)、標本サイズ: \( n \)、標本平均: \( \overline{X} \)、不偏分散 \( s^2 \) [不偏標準偏差: \( s \)]
4.t分布を使った母平均の仮説検定(t検定)
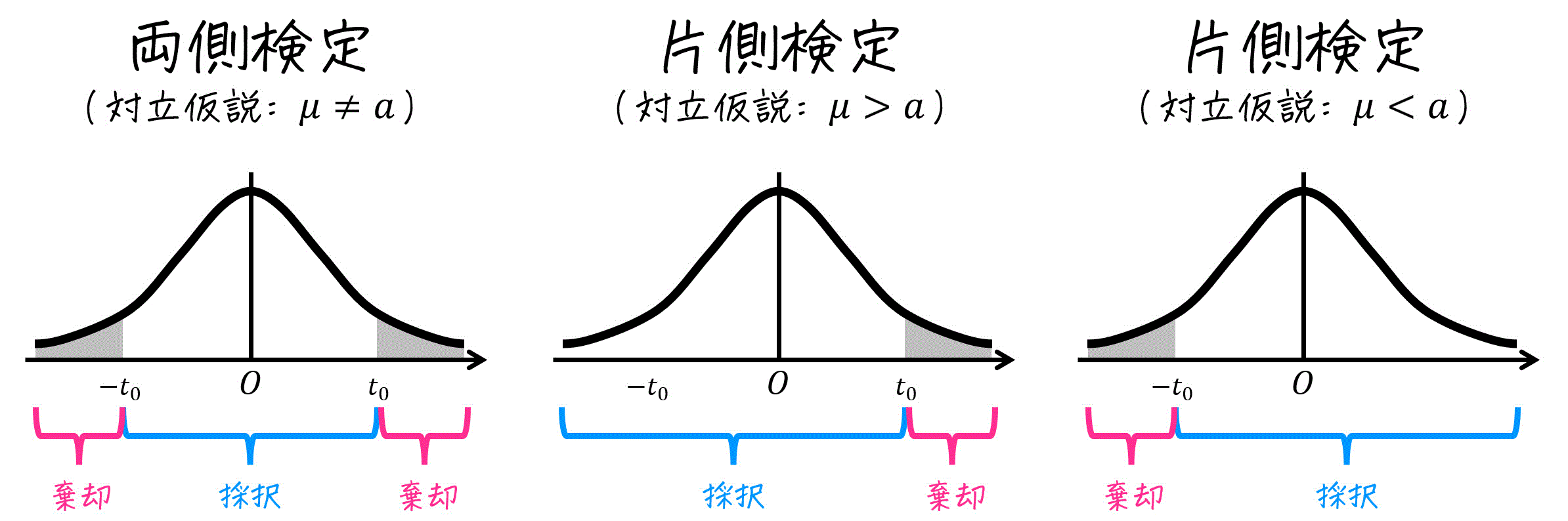
検定の結果(採択/棄却)を判断するときは、上の式の \( t \) 値への変換式、および読み取った値 \( t_0 \) から採択 or 棄却の判定をする。
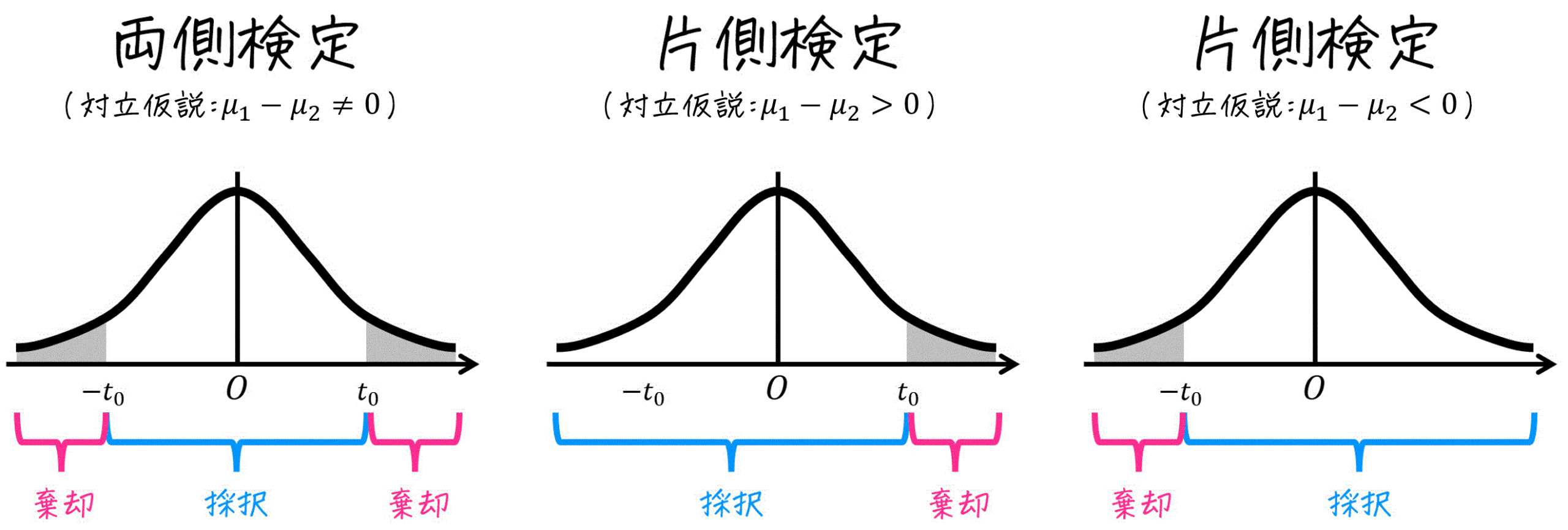
- 両側検定のとき
→ \( -t_0 \leqq t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu > a \) のとき (母平均が仮定よりも大きいとき)
→ \( t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu < a \) のとき (母平均が仮定よりも小さいとき)
→ \( t_0 \leqq t \) であれば採択。それ以外で棄却。
※ 不偏分散\[
s^2 = \frac{1}{n-1} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]の代わりに標本分散\[
S^2 = \frac{1}{n} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]を使った場合は、変換式は\[
\frac{ \sqrt{n-1} \ (\overline{X} - \mu) }{S}
\]となる[2]基本的には不偏分散 \( s^2 \)(不偏標準偏差 \( s \) を使った形で公式が記載されていますが、参考書によっては標本分散 \( S^2 \)(標本標準偏差 \( s … Continue reading。
↓↓↓母平均の仮説検定方法についての詳しい解説は、こちらから↓↓↓
スポンサードリンク
2. 例題で確認!
では実際に、例題を1問使って実際に「対応のない2標本の母平均検定」の流れを見ていきましょう。
※ 対応のない2標本の計算の流れを分かりやすくするために、例題の小問を多めに設定しています。
例題.
ある塾では、1組(生徒数: \( n_1 = 11 \))と2組(生徒数: \( n_2 = 6 \))に分けて授業をしている。この2つのクラスに学力差があるかどうか調べるために、数学の抜き打ちテストを実施した。その結果、クラスの平均点と不偏分散は以下の表の通りになった。
| 組 | 生徒数 | 平均点 | 不偏分散 |
|---|---|---|---|
| 1組 | 11 | 69 | 19 |
| 2組 | 6 | 75 | 10 |
※ 1組の平均点を \( \overline{X}_1 = 69 \)、2組の平均点を \( \overline{X}_2 = 75 \)、1組の不偏分散を \( s_1^2 = 19 \)、2組の不偏分散を \( s_2^2 = 10 \) とする。
このとき、1組、2組の数学の平均点に差があるかどうかを、有意水準1%で仮説検定したい。つぎの(1)~(6)を解き、仮説検定をしなさい。
(1) 帰無仮説 \( H_0 \)、対立仮説 \( H_1 \) を述べなさい。
(2) 以下の式で計算される「ブールされた分散 \( s_p \)」を求めなさい。\[
s_p^2 = \frac{ (n_1 -1 ) s_1^2 + (n_2 - 1) s_2^2}{n_1 + n_2 - 2}
\]
(3) 区間推定を行うために必要な自由度を答えなさい。
(4) t分布表から (3)で求めた自由度、および有意水準1%に対応する値 \( t = t_0 \) を求めなさい。必要であれば、以下からt分布表をダウンロードすること。
(5) 1組の平均点 \( \overline{X}_1 = 69 \)、2組の平均点 \( \overline{X}_2 = 75 \)、およびブールされた分散 \( s_p^2 \) を以下の式\[
t = \frac{ \overline{X}_1 - \overline{X}_2 }{ s_p \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }
\]に代入することで、t変換をしなさい。必要であれば、\( \sqrt{30} = 5.477 \), \( \sqrt{1122} = 33.50 \) とすること。
(6) (4), (5)から、有意水準(危険率)1%での仮説検定の結果を述べなさい。
対応のない2標本を解くための方針.
対応のない2標本の仮説検定では、異なる2つの標本から値を取得しています。
そのため、対応のある2標本で出来た「2つの標本データの対応するデータごとに差分を取り、それを新たな1つの標本する」ということが出来ません。
そこで、対応のない2標本の仮説検定では「2つの標本から得られた情報の差[3]標本平均、不偏分散など。をとって、それを新たな1つの標本にする」ということをしていきます。
(1) 帰無仮説、対立仮説の設定
まずは帰無仮説と対立仮説を立てましょう。(この過程は対応のある2標本の検定と同じです。)
帰無仮説 \( H_0 \) : 仮説検定をするにあたって、立てる仮定
→ 1組の平均点と2組の平均点に差はない。
→ 1組のテスト結果の母平均 \( \mu_1 \) と2組のテスト結果の母平均 \( \mu_2 \) に差はない。
→ \( \mu_1 = \mu_2 \)、つまり \( \mu_1 - \mu_2 = 0 \)
※ 平均点が等しい → 平均点の差が0、と持っていく。
対立仮説 \( H_1 \) : 帰無仮説を否定して証明したいもの。
→ 1組の平均点と2組の平均点に差がある。
→ 1組のテスト結果の母平均 \( \mu_1 \) と2組のテスト結果の母平均 \( \mu_2 \) に差がある。
→ \( \mu_1 \not = \mu_2 \)、つまり \( \mu_1 - \mu_2 \not = 0 \)
※ \( X_1 \) と \( X_2 \) の平均点に差がある → 平均点が等しくない → 平均点の差が0、と持っていく。
(2) ブールされた分散 \( s_p \) の計算
「対応のない2つの標本を1つの標本にまとめる」際には、新たな標本に対する
- 標本の不偏分散 \( s_p^2 \)
(ブールされた分散と呼ばれます) - 標本に対する自由度 \( k_p \)
を求める必要があります。
まず、(2) ではまとめた標本の不偏分散(ブールされた分散) \( s_p^2 \) がどのように計算されるかを確認しましょう。
具体的には、2つの標本の不偏分散 \( s_1^2 \), \( s_2^2 \) を1つにまとめて平均を取ったもの、新たな標本の分散 \( s_p^2 \) とみなします。
しかし、単に2つの不偏分散 \( s_1^2 \), \( s_2^2 \) の平均を取るのではなく、それぞれの自由度 \( k_1 \), \( k_2 \) で重みづけした加重平均をブールされた分散 \( s_p^2 \) とする点に注意が必要です。
具体的には、ブールされた分散 \( s_p^2 \) は、自由度 \( k_1 = n_1 - 1 \)、\( k_2 = n_2 - 1 \) を使って\[\begin{align*}
s_p^2 & = \frac{k_1 s_1^2 + k_2 s_2^2}{k_1 + k_2}
\\ & = \frac{ (n_1 - 1) s_1^2 + (n_2 - 1) s_2^2}{ (n_1 - 1) + (n_2 - 1) }
\\ & = \frac{ (n_1 - 1) s_1^2 + (n_2 - 1) s_2^2}{ n_1 + n_2 - 2}
\end{align*}\]と計算します。
今回は、\( n_1 = 11 \), \( s_1^2 = 19 \), \( n_2 = 6 \), \( s_2^2 = 10 \) なので、ブールされた分散は\[\begin{align*}
s_p^2 & = \frac{ (n_1 - 1) s_1^2 + (n_2 - 1) s_2^2}{ n_1 + n_2 - 2}
\\ & = \frac{10 \cdot 19 + 5 \cdot 10}{11 + 6 - 2}
\\ & = \frac{240}{15}
\\ & = 16
\end{align*}\]となり、ブールされた分散は \( s_p^2 = 16 \) と求まります。
※ 2乗を取って \( s_p \) としたものをブールされた標準偏差と呼ぶことにしましょうか。今回の場合は、ブールされた標準偏差は \( s_p = 4 \) です。
(3) 自由度の計算
つぎは、「対応のない2つの標本を、1つの標本にまとめたとき」のまとめた標本に対する自由度 \( k_p \) を求めていきましょう。
まず、統計の世界では、"自由度 = 標本が持つ情報量" でした。
ここで、対応のない2標本での仮説検定では、「2つの標本を1つにまとめる」ということをしています。
そのため、1つにまとめられた標本が持つ情報量は、2つの標本の情報量の和となります。
よって、区間推定を行うために必要な自由度 \( k_p \) は、\[\begin{align*}
k_p & = k_1 + k_2
\\ & = (n_1 - 1) + (n_2 - 1)
\\ & = n_1 + n_2 - 2
\end{align*}\]となります。
今回は、\( n_1 = 11 \), \( n_2 = 6 \) なので、自由度は\[\begin{align*}
k_p & = n_1 + n_2 - 2
\\ & = 11 + 6 - 2
\\ & = 15
\end{align*}\]となります。
(4) t分布表から、(3)で求めた自由度と有意水準に対応する値の読み取り
自由度15、有意水準1%に対応する \( t = t_0 \) の値を求めていきます。
今回の対立仮説は、「母平均が0ではない」なので、母平均が大きい場合と小さい場合の両方を考える必要があります。つまり、両側検定となります。
★ 両側t分布表の場合
自由度15、灰色部分の面積の和 \( \alpha \) が 0.01 の場合をt分布表から読み取ればOKです。
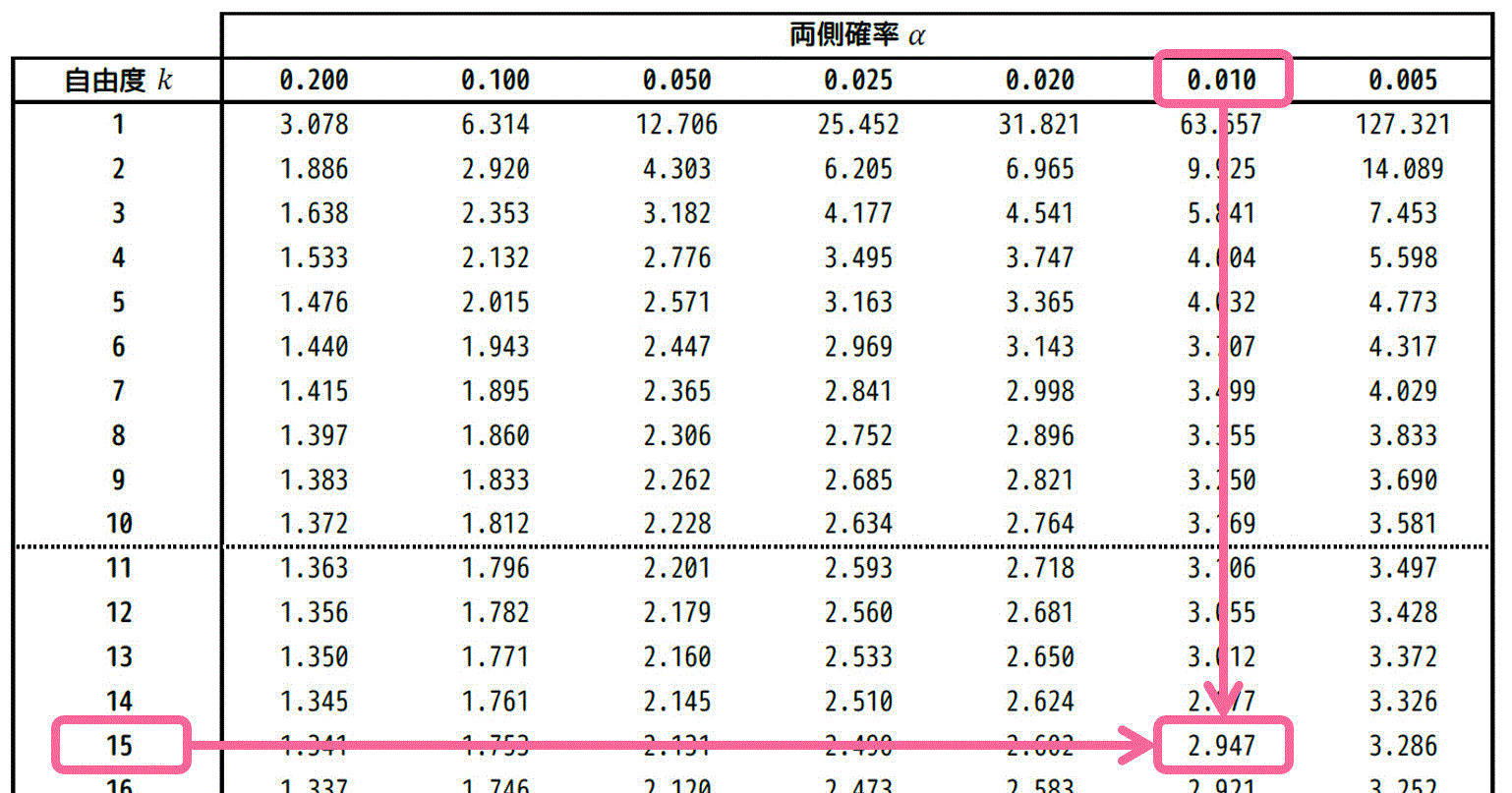
結果、2.947と読めます。読み取った値を \( t_0 = 2.947 \) としておきましょう。
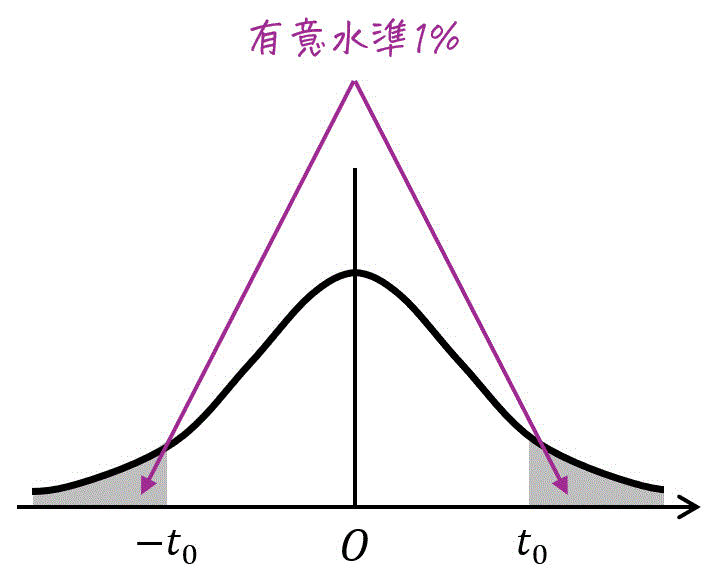
★ 片側t分布表の場合
片側t分布表に記載されている確率 \( \alpha \) は、青色部分の面積だけで、紫色部分の面積は入っていません。
青色部分の面積と紫色部分の面積は同じなので、\( \alpha \) を読み取る際には、1%を半分にした \( \alpha = 0.005 \) を読み取る必要がある点に注意です。
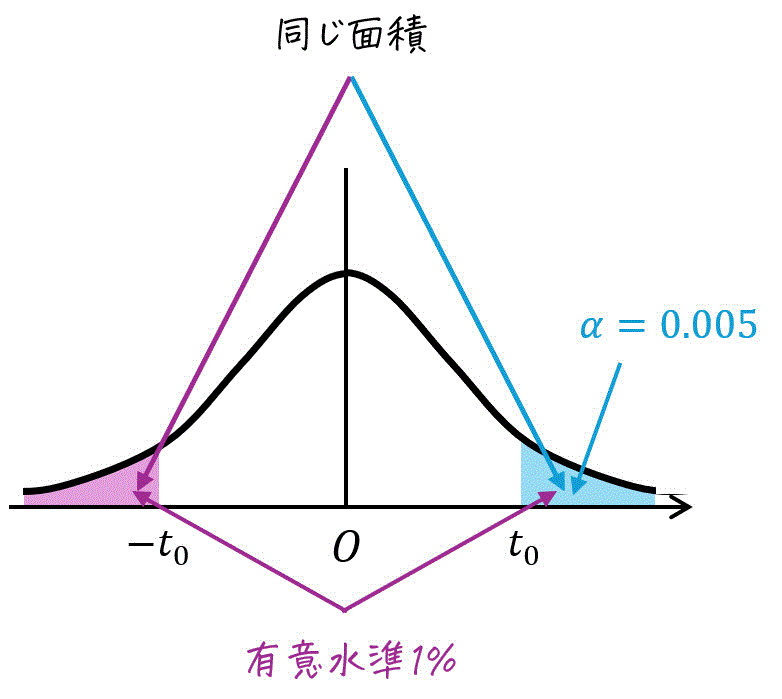
そのため、自由度15、片側確率 \( \alpha = 0.005 \) の部分の \( t \) の値を読み取ればOKです。
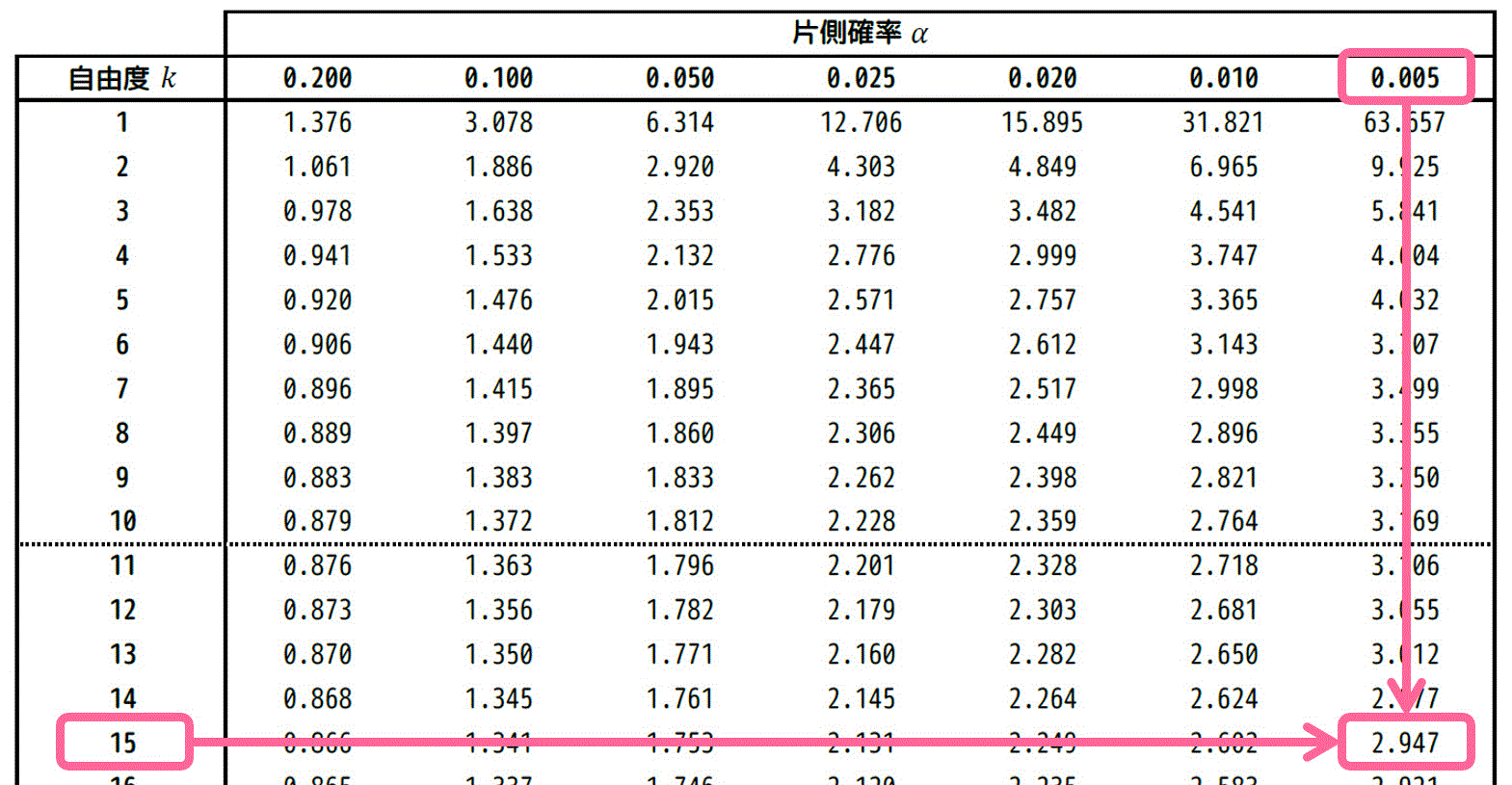
結果、2.947と読めます。読み取った値を \( t_0 = 2.947 \) としておきましょう。
(5) t変換の実施
与えられた2つの標本の各標本平均、標本サイズ、および(2)で求めたブールされた分散をt変換式に代入します。
- ブールされた分散 \( s_p^2 = 16 \)(ブールされた不偏標準偏差 \(s_p = 4 \))
- 自由度 \( k_p = 15 \)
| 組 | 標本サイズ (生徒数) | 標本平均 (平均点) |
|---|---|---|
| 1組 | \( n_1 = 11 \) | \( X_1 = 69 \) |
| 2組 | \( n_2 = 6 \) | \( X_2= 75 \) |
実際に代入すると、\[\begin{align*}
t & = \frac{ \overline{X}_1 - \overline{X}_2 }{ s_p \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }
\\ & = \frac{69 - 75}{ 4 \sqrt{ \frac{1}{11} + \frac{1}{6} } }
\\ & = \frac{-6}{4 \sqrt{ \frac{6}{66} + \frac{11}{66} } }
\\ & = \frac{-3}{2 \sqrt{ \frac{17}{66} } }
\\& = - \frac{3 \sqrt{66} }{2 \sqrt{17} }
\\ & = - \frac{3 \sqrt{66} \cdot \sqrt{17} }{2 \cdot 17}
\\ & = - \frac{3 \sqrt{1122} }{34}
\\ & \fallingdotseq - \frac{3 \cdot 33.50 }{34}
\\ & \fallingdotseq - 2.956
\end{align*}\]と計算できます。
※ t変換式の導出の仕組みは、3章にて説明しています。
(6) 仮説検定の結果判定
最後に、
- t分布表から読み取った値 \( t_0 = 2.947 \)
- t分布の変換式から計算して求めた \( t = -2.956 \)
の2つを比べて、採択/棄却を決めます。
【確認方法】
- \( - t_0 \leqq t \leqq t_0 \) となれば仮説は採択(仮定は誤りとはいえない)
- \( - t_0 > t \) もしくは \( t_0 < t \) となれば、仮定は棄却(仮定が誤りといえる)
今回は、\( t = -2.956 < -2.947 = - t_0 \) となるため、仮説は棄却されます。
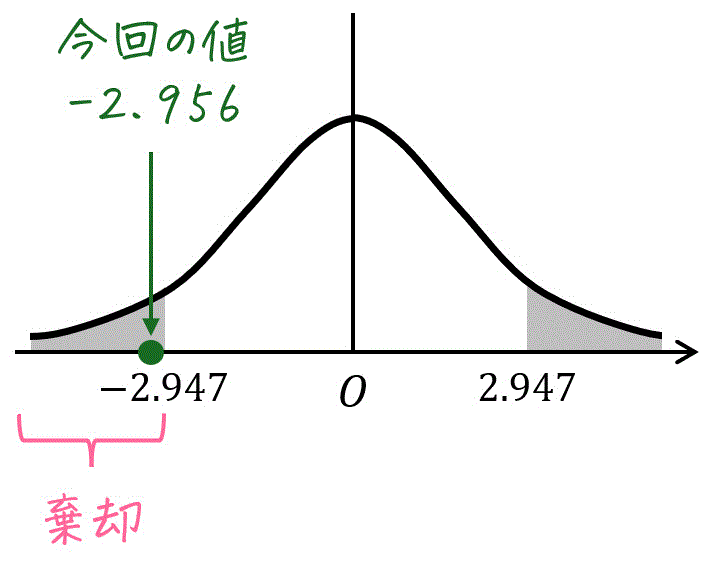
つまり、1組、2組の平均点に差があることが言えます。(=1組と2組の学力差がある。)
Step1. 帰無仮説、対立仮説を立てる。
- 帰無仮説:2つの標本の母平均 \( \mu_1 \), \( \mu_2 \) に差がない。
→ つまり、\( \mu_1 - \mu_2 = 0 \)(\( \mu_1 = \mu_2 \)) - 対立仮説
- 2つの標本の母平均 \( \mu_1 \), \( \mu_2 \) に差がある [両側検定]
→ つまり、\( \mu_1 - \mu_2 = 0 \)(\( \mu_1 = \mu_2 \)) - 2つの標本の母平均 \( \mu_1 \), \( \mu_2 \) のうち、片方が大きい [片側検定]
→ つまり、\( \mu_1 - \mu_2 > 0 \)(\( \mu_1 > \mu_2 \))
もしくは \( \mu_1 - \mu_2 < 0 \)(\( \mu_1 < \mu_2 \))
- 2つの標本の母平均 \( \mu_1 \), \( \mu_2 \) に差がある [両側検定]
Step2. ブールされた分散 \( s_p^2 \) を求める(まとめた標本の不偏分散の算出)
\[\begin{align*}
s_p^2 & = \frac{k_1 s_1^2 + k_2 s_2^2}{k_1 + k_2}
\\ & = \frac{ (n_1 - 1) s_1^2 + (n_2 - 1) s_2^2}{ (n_1 - 1) + (n_2 - 1) }
\\ & = \frac{ (n_1 - 1) s_1^2 + k_2 s_2^2}{ n_1 + n_2 - 2}
\end{align*}\]
【各変数の意味】
| 1つ目の標本 | 2つ目の標本 | |
|---|---|---|
| サイズ(データ数) | \( n_1 \) | \( n_2 \) |
| 自由度 | \( k_1 \) | \( k_2 \) |
※ \( s_p \) をブールされた標準偏差と呼ぶことにします。
Step3. 1つにまとめた標本の自由度 \( k_p \) を求める
\[\begin{align*}
k_p & = k_1 + k_2
\\ & = (n_1 - 1) + (n_2 - 1)
\\ & = n_1 + n_2 - 2
\end{align*}\]
【各変数の意味】
| 1つ目の標本 | 2つ目の標本 | |
|---|---|---|
| サイズ(データ数) | \( n_1 \) | \( n_2 \) |
| 自由度 | \( k_1 \) | \( k_2 \) |
Step4. t分布表から、自由度 \( k_p \) と有意水準に対応した \( t = t_0 \) の値を求める。
Step5. 与えられた2標本の標本平均、サイズ、およびブールされた分散を、t分布の変化式に代入する。
\[
t = \frac{ \overline{X}_1 - \overline{X}_2 }{ s_p \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }
\]
【各変数の意味】
| 1つ目の標本 | 2つ目の標本 | |
|---|---|---|
| サイズ(データ数) | \( n_1 \) | \( n_2 \) |
| 標本平均 | \( \overline{X}_1 \) | \( \overline{X}_2 \) |
Step6. Step5で求めた \( t \) を、Step4で読み取った \( t_0 \) と比べて採択/棄却を判断する。
- 両側検定のとき
→ \( -t_0 \leqq t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( \mu_1 - \mu_2 > 0 \) のとき (\( \mu_1 > \mu_2 \) のとき)
→ \( t \leqq t_0 \) であれば採択。それ以外で棄却。 - 片側検定 \( mu_1 - \mu_2 < 0 \) のとき (\( \mu_1 < \mu_2 \) のとき)
→ \( t_0 \leqq t \) であれば採択。それ以外で棄却。
スポンサードリンク
3. 対応のない2標本の母平均検定で使うt変換式導出
1標本での、t分布のt変換式\[
t = \frac{ \textcolor{deepskyblue}{ \overline{X} - \mu } }{\textcolor{magenta}{\frac{ s }{ \sqrt{n} } } }
\]から、対応のない2検定で使うt分布のt変換式\[
\frac{ \textcolor{deepskyblue}{ \overline{X}_1 - \overline{X}_2 } }{ \textcolor{magenta}{ s_p \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } } }
\]の導出の仕方をここで確認しましょう。
※ 厳密な証明ではないのでご注意ください。
復習.1標本のとき
t分布の変換式の変化 (分子部分)
元々のt分布の変化式の分子部分は、標本平均 \( \overline{X} \) から、母平均 \( \mu \) を引いていますね。
t分布の変換式の変化 (分母部分)
まず、元々のt分布の変化式の分母部分\[
\frac{ s }{ \sqrt{n} }
\]がどのように導出されたか復習しましょう。
Step1. 母平均 \( \mu \)、母分散 \( \sigma^2 \) の母集団から大きさ \( n \) の標本を選び、その標本平均を \( \overline{X} \) とした際の分散は、\[
V ( \overline{X} ) = \frac{ \sigma^2 }{ n }
\]となります。
Step2. 母分散 \( \sigma^2 \) を下の式のように、標本分散 \( s^2 \) に置きかえます。\[
\frac{ s^2 }{ n }
\]
Step3. この式の平方根を取ったものが、t部分の分母部分でしたね。\[
\frac{ s }{ \sqrt{n} }
\]
1標本のとき → 対応のない2標本へ拡張
1標本のときの復習ができたので、対応のない2標本へ拡張していきましょう。
【ポイント】
- 2つの標本から得られた情報の差をとったものを、新たな標本とする
- 作成した新たな標本に対して、t検定をする
→ t検定で使う新たな標本に対するt変換式を導出する
t分布のt変換式の変化 (分子部分)
「2つの標本から得られた情報の差をとって、それを新たな1つの標本にする」場合、1つにまとめた標本の標本平均 \( \overline{X}_p \)、母平均 \( \mu_p \) は、標本平均、母平均は2つの標本の差となります[4] \( E(X \pm Y) = E(X) \pm E(Y) \) を使用。[複号同順です。]。\[
\overline{X}_p = \overline{X_1} - \overline{X_2}
\]\[
\mu_p = \mu_1 - \mu_2
\]さらに、帰無仮説で、\( \mu_1 - \mu_2 = 0 \) を仮定しているため、t分布の変換式の分子は、\[\begin{align*}
\overline{X}_p - \mu_p & = ( \overline{X_1} - \overline{X_2}) - (\mu_1 - \mu_2)
\\ & = \textcolor{deepskyblue}{ \overline{X_1} - \overline{X_2}}
\end{align*}\]となります。
t分布のt変換式の変化 (分母部分)
- 標本1の情報: サイズ \( n_1 \)、母分散 \( \sigma_1^2 \)、標本分散 \( s_1^2 \)
- 標本2の情報: サイズ \( n_2 \)、母分散 \( \sigma_2^2 \)、標本分散 \( s_2^2 \)
Step1. 新たな標本の分散は、元の分散の和となります[5]2つの標本は対応がない(=独立)ため、2つの標本を引くと、分散は2つの標本の和となります。\[V( \overline{X}_1 + \overline{X}_2 ) = V( \overline{X}_1 ) + V … Continue reading。つまり、新たな標本の標本平均を \( \overline{X} \) とした際の分散は、\[
\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}
\]となります。
Step2. 標本1について母分散 \( \sigma_1^2 \) を標本分散 \( s_1^2 \)に、標本2について母分散 \( \sigma_2^2 \) を標本分散 \( s_2^2 \)におきかえます。\[
\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}
\]
Step3. さらに、標本分散 \( s_1^2 \)、標本分散 \( s_2^2 \) を、先ほど求めたブールされた分散 \( s_p^2 \) におきかえます。\[
\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}
\]
Step4. あとは、この式の平方根を取ることで、\[\begin{align*}
\sqrt{ \frac{s_p^2}{n_1} + \frac{s_p^2}{n_2} } & = \sqrt{ s_p^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right) }
\\ & =
\textcolor{magenta}{ s_p \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }
\end{align*}\]と導出できます。
4. 練習問題にチャレンジ
ある製品を製造している2つのライン(ラインA、ラインB)がある。この2つのラインの製造情報は、以下の表の通りであると伝えられた。
| ライン | 生産数 [個] | 平均 [g] | 不偏分散 [g2] |
|---|---|---|---|
| A | 11 | 104 | 7 |
| B | 16 | 101 | 12 |
このデータから、ラインAとラインBで作られた製品の重量に差があるかどうかを有意水準1%で判定しなさい。
※ 必要であれば、\( \sqrt{15} = 3.873 \), \( \sqrt{330} = 18.17 \) とすること。
※ 必要であれば、以下からt分布表をダウンロードすること。
5. 練習問題の答え
Step1. 帰無仮説と対立仮説を立てる
帰無仮説 \( H_0 \) : 仮説検定をするにあたって、立てる仮定
→ 「ラインAで作られた製品の重量」と「ラインBで作られた製品の重量」に差はない。
→ ラインAで作られた製品の重量の母平均 \( \mu_1 \) とラインBで作られた製品の重量の母平均 \( \mu_2 \) に差はない。
→ \( \mu_1 = \mu_2 \)、つまり \( \mu_1 - \mu_2 = 0 \)
※ 製品の重量が等しい → 製品の重量の差が0、と持っていく。
対立仮説 \( H_1 \) : 帰無仮説を否定して証明したいもの。
→ 「ラインAで作られた製品の重量」と「ラインBで作られた製品の重量」に差がある。
→ ラインAで作られた製品の重量の母平均 \( \mu_1 \) とラインBで作られた製品の重量の母平均 \( \mu_2 \) に差がある。
→ \( \mu_1 \not = \mu_2 \)、つまり \( \mu_1 - \mu_2 \not = 0 \)
※ 製品の重量が等しくない → 製品の重量の差が0ではない、と持っていく。
Step2. ブールされた分散 \( s_p^2 \) を求める
| ライン | 生産数 [個] | 不偏分散 [g2] |
|---|---|---|
| A | \( n_1 = 11 \) | \( s_1^2 = 7 \) |
| B | \( n_2 = 16 \) | \( s_2^2 = 12 \) |
\[\begin{align*}
s_p^2 & = \frac{ (n_1 - 1) s_1^2 + (n_2 - 1) s_2^2}{ (n_1 - 1) + (n_2 - 1) }
\\ & = \frac{ 10 \cdot 7 + 15 \cdot 12 }{11 + 16 - 2}
\\ & = \frac{ 70 + 180 }{25}
\\ & = \frac{ 250 }{25}
\\ & = 10
\end{align*}\]
※ ブールされた標準偏差: \( s_p = \sqrt{10} \)
Step3. 1つにまとめた標本の自由度 \( k_p \) を求める
\[\begin{align*}
k_p & = n_1 + n_2 - 2
\\ & = 16 + 11 - 2
\\ & = 25
\end{align*}\]
Step4. 表の読み取り
自由度25、有意水準1%に対応する \( t = t_0 \) の値を求めていきます。
今回の対立仮説も、例題と同じように「母平均が0ではない」なので、母平均が大きい場合と小さい場合の両方を考える必要があります。つまり、両側検定となります。
★ 両側t分布表の場合
自由度15、灰色部分の面積の和 \( \alpha \) が 0.01 の場合をt分布表から読み取ればOKです。
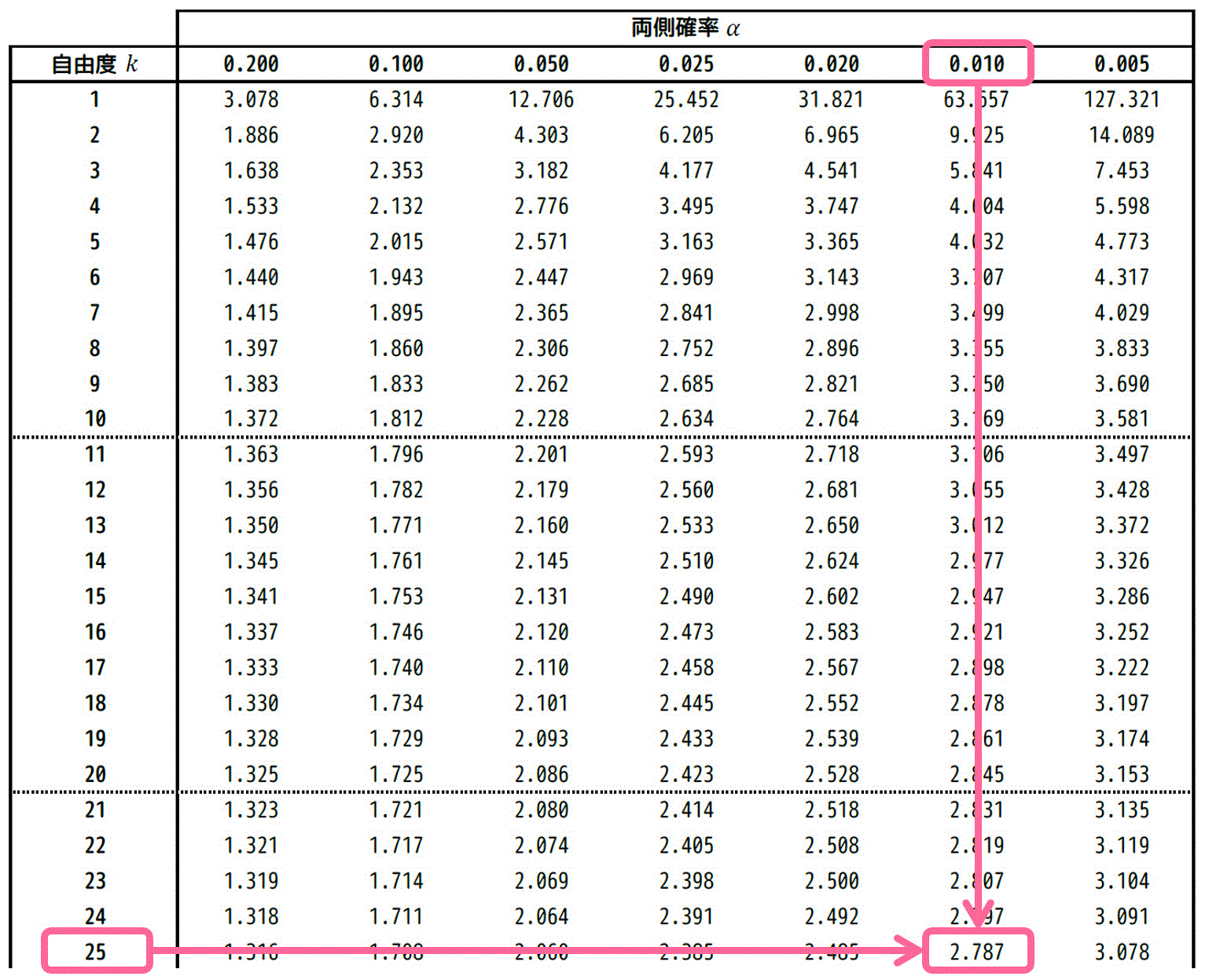
結果、2.787と読めます。読み取った値を \( t_0 = 2.787 \) としておきましょう。
★ 片側t分布表の場合
片側t分布表に記載されている確率 \( \alpha \) は、青色部分の面積だけで、紫色部分の面積は入っていません。
青色部分の面積と紫色部分の面積は同じなので、\( \alpha \) を読み取る際には、1%を半分にした \( \alpha = 0.005 \) を読み取る必要がある点に注意です。

そのため、片側分布表の場合は自由度25、片側確率 \( \alpha = 0.005 \) の部分の \( t \) の値を読み取ればOKです。
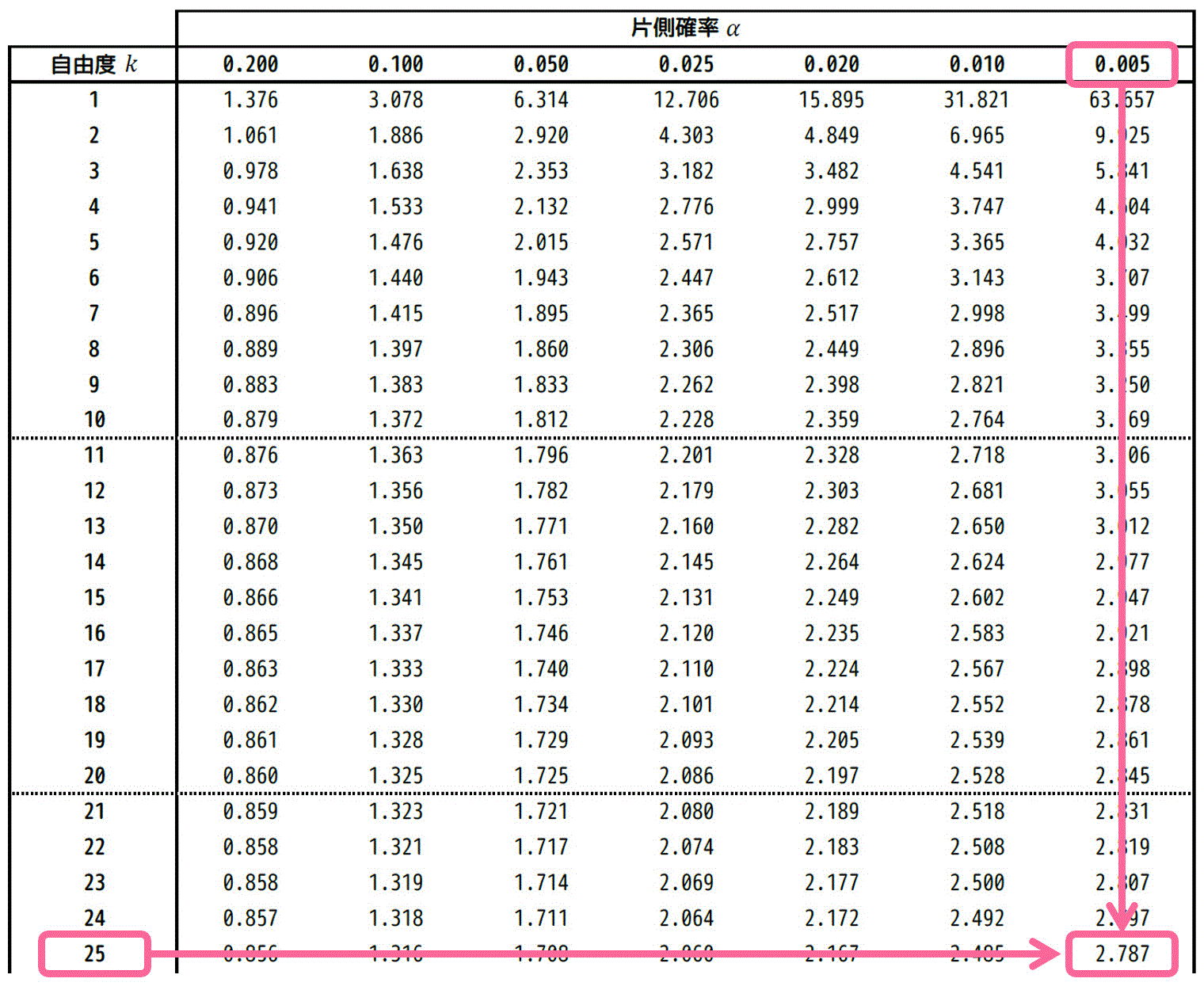
結果、2.787と読めます。読み取った値を \( t_0 = 2.787 \) としておきましょう。
Step5. t変換式の計算
以下の標本の情報、およびブールされた分散 \( s_p^2 = 10 \)(ブールされた標準偏差 \( s_p = \sqrt{10} \) をt変換式に代入し、t変換しましょう。
| ライン | 生産数 [個] | (標本)平均 [g] |
|---|---|---|
| A | \( n_1 = 11 \) | \( s_1^2 = 7 \) |
| B | \( n_2 = 16 \) | \( s_2^2 = 12 \) |
計算過程は、以下の通り。(ルートの処理が少し複雑です。)
\[\begin{align*}
t & = \frac{ \overline{X}_1 - \overline{X}_2 }{ s_p \sqrt{ \frac{1}{n_1} + \frac{1}{n_2} } }
\\ & = \frac{ 104 - 101 }{ \sqrt{10} \sqrt{ \frac{1}{11} + \frac{1}{16} } }
\\ & = \frac{ 3 }{ \sqrt{10} \sqrt{ \frac{16}{176} + \frac{11}{176} } }
\\ & = \frac{ 3 }{ \sqrt{10} \sqrt{ \frac{27}{176} } }
\\ & = \frac{ 3 }{ \sqrt{10} \cdot \frac{ 3 \sqrt{3} }{4 \sqrt{11} } }
\\ & = \frac{ 3 }{ \frac{ 3 \sqrt{30} }{4 \sqrt{11} } }
\\ & = \frac{ 12 \sqrt{11} }{ 3 \sqrt{30} }
\\ & = \frac{ 4 \sqrt{11} }{ \sqrt{30} }
\\ & = \frac{ 4 \sqrt{11} \cdot \sqrt{30} }{ \sqrt{30} \cdot \sqrt{30} }
\\ & = \frac{ 4 \sqrt{330} }{ 30 }
\\ & = \frac{ 2 \sqrt{330} }{ 15 }
\\ & \fallingdotseq \frac{ 2 \cdot 18.17 }{ 15 }
\\ & = \frac{ 36.34 }{ 15 }
\\ & \fallingdotseq 2.422
\end{align*}\]
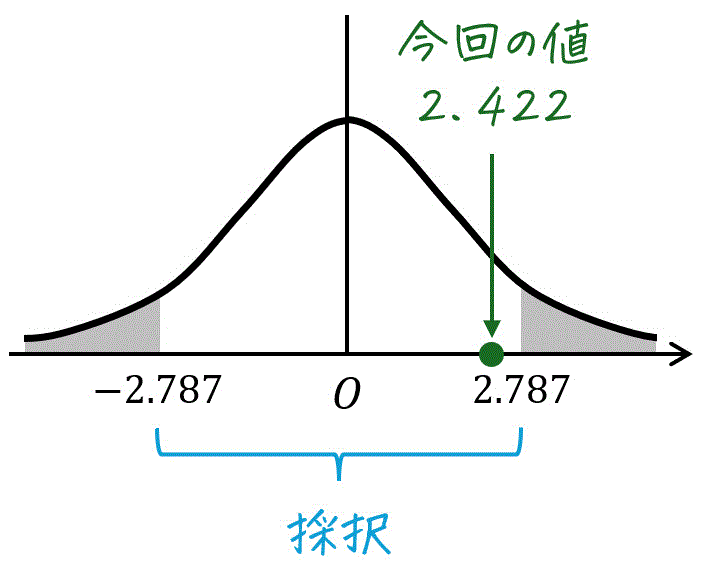
Step6. 仮説検定の結果判定
あとは、
- t分布表から読み取った値 \( t_0 = 2.787 \)
- t分布の変換式から計算して求めた \( t = 2.422 \)
の2つを比べて、採択/棄却を確認すればOKです。
【確認方法】
- \( - t_0 \leqq t \leqq t_0 \) となれば仮説は採択(仮定は誤りとはいえない)
- \( - t_0 > t \) もしくは \( t_0 < t \) となれば、仮定は棄却(仮定が誤りといえる)
今回は、\( - 2.787 \leqq 2.422 \leqq 2.787 \) となるため、仮説は採択されます。(=ラインAとラインBで作られた製品の重量に差があるとは言えません。)
注釈
| ↑1 | 標本の中で、1つ値が分からないものがあっても、標本平均や不偏分散から復元できるため、情報量は「標本のサイズ」より1小さい値となる。 |
|---|---|
| ↑2 | 基本的には不偏分散 \( s^2 \)(不偏標準偏差 \( s \) を使った形で公式が記載されていますが、参考書によっては標本分散 \( S^2 \)(標本標準偏差 \( s \))の形で記載されていることもあるので、注意しましょう。また、参考書によっては不偏分散 \( s^2 \) のことを標本分散と呼んでいるものもあるため、こちらも注意が必要です。 |
| ↑3 | 標本平均、不偏分散など。 |
| ↑4 | \( E(X \pm Y) = E(X) \pm E(Y) \) を使用。[複号同順です。] |
| ↑5 | 2つの標本は対応がない(=独立)ため、2つの標本を引くと、分散は2つの標本の和となります。\[ V( \overline{X}_1 + \overline{X}_2 ) = V( \overline{X}_1 ) + V (\overline{X}_2 ) \] |
関連広告・スポンサードリンク





![うさぎでもわかる計算機システム Part02 2の補数表現 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190615204157-1-150x150.gif)