うさぎでもわかる仮説検定のコツ（統計学）

2019年6月4日 2024年10月28日 19分47秒

ももうさ

スポンサードリンク

こんにちは、ももやまです！
今回は統計学の中でもよく使われる「仮説検定」についてまとめてみました！

★ 本記事の内容を、以下にリニューアルしています。仮説検定の方法を確認したい人は、以下の記事をご覧ください。

１．仮説検定とは
２．仮説検定の仕方
- (1) 帰無仮説
- (2) 対立仮説
３．両側検定と片側検定
- (1) 両側検定
- (2) 片側検定
４．例題
５．練習
- 問題
- 解答
６．さいごに

スポンサードリンク

１．仮説検定とは

あなたはとある人（Mくん）にこんな勝負を持ちかけられたとします。

サイコロ勝負しようぜ！　10回連続で6が出たら俺の勝ちな！　1億円ちょーだい！

サイコロで6の目が10回連続で出る確率はとてつもなく低い*1です。当然、そんなのありえないありえないと思いながらこの勝負受けます。しかし、10回連続で6が出てしまい、あなたは負けてしまいました。

このとき、2パターンの解釈があります。

こんな奇跡ありえない！　絶対にサイコロに細工がされているはず！
今回は奇跡が起こっただけ、確率に0％はありえない！

あなたはMくんに1億円は払いたくないでしょう。なので普通はインチキサイコロ*2である可能性を疑いますねよね。

これ*3を統計的に行うのが仮説検定です。

スポンサードリンク

２．仮説検定の仕方

仮説検定を行うためには、検定を行うための仮説を立てる必要があります。
仮説には帰無仮説と対立仮説の２つがあります。

(1) 帰無仮説

帰無仮説は、検定時に立てる仮説のことを表します。記号で \( H_0 \) と表すこともあります。

例えば、上のインチキサイコロの例で行くと、「サイコロがまとも」・「6の目が出る確率が1/6」が帰無仮説となります。

検定時にはこの仮説をもとに実際に検定を行います。なので、簡単に検証できる帰無仮説を立てる必要があります。

（だめな例：サイコロで6の目の出る確率が1/6ではない → このような設定にしてしまうと、サイコロの目が1/6で出ないことをもとに検定を行う必要があるため、全然簡単には検証できない。）

(2) 対立仮説

対立仮説は、帰無仮説に対する（反する）仮説となります。記号で \( H_1 \) と表すこともあります。

本来証明したいものを対立仮説にもっていくのがポイントです。

例えば、１のサイコロの例で行くと、「サイコロがまともでない（インチキサイコロ）」・「6の目が出る確率が1/6ではない」が対立仮説となります。

POINT1帰無仮説：検定時に立てる仮説（帰無仮説をもとに検証）
対立仮説：帰無仮説に対する仮説（本来証明したいもの）

仮説を立て終わったら実際に検定を行います。

帰無仮説を基に検定を行い、計算結果が一定の確率以下であればその仮説は正しくないと言えますね。この一定の確率のことを有意水準、危険率と言います。
例えば、有意水準5%で推定すると言えば、帰無仮説を用いて事象が発生する確率が5%以下かどうかを推定します。

確率を調べた結果、有意水準に満たない確率だった場合は正しくないと言えます。正しくないということを統計学的には棄却されるといいます。逆に計算結果が一定の確率を超えていた場合、その仮説は正しくないとは言えませんね*4。この場合は統計学的には採択されるといいます。

一般的に仮説は棄却される（つまり、無に帰する）ときに意味を持ちます*5。

そのため、対立仮説には「本来証明したいもの」を持ってきます。

スポンサードリンク

３．両側検定と片側検定

仮説検定の方法として、片側検定と両側検定の２つがあります。
今回は有意水準を5％として説明していきたいと思います。

片側検定と両側検定の違いは、対立仮説の置き方、つまり示したいものがなにかによって変化します。

例えばコイントスを100回し、このときの表が出る回数について考えましょう。

この場合の帰無仮説は、表が出る確率を \( p \) として、\( p = 1/2 \) となります。

(1) 両側検定

両側検定では、名前の通り「極端に表が出る」・「極端に裏が出る」の2パターン両方を対立仮説としてもっていく方法です。

このパターンの場合の対立仮説は、「コインがまともでない」となります。

数式で表すと、\( p \not = 1/2 \) となります。

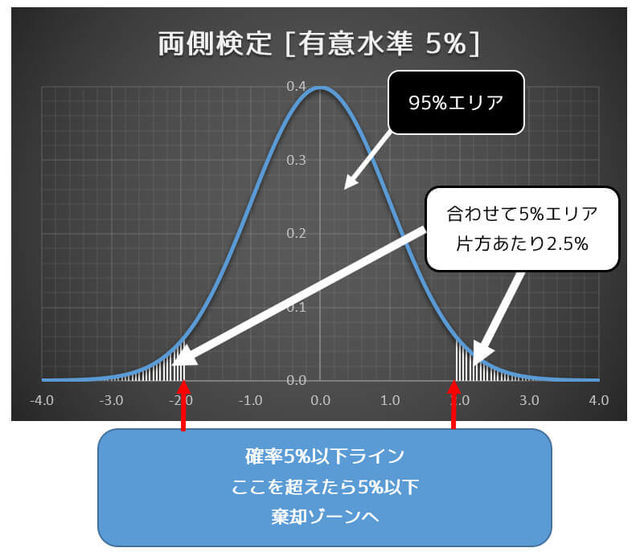
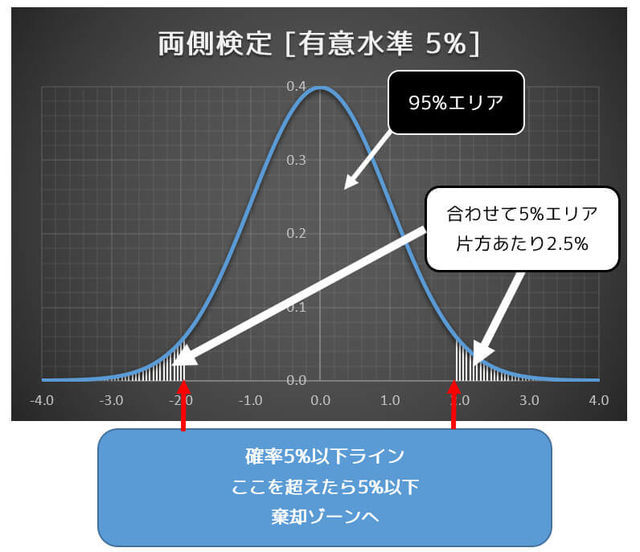
両側水準の場合、有意水準は左側と右側の合計の面積の値になることに注意してください。

今回の例でいくと、有意水準は5％なので、片方の面積は2.5％分になりますね*6。

(2) 片側検定

片側検定では、名前の通り片側の場合しか考えません。片側だけしか考えないので対立仮説は、

表が出やすい \( p \gt 1/2 \)
表が出にくい \( p \lt 1/2 \)

の2パターンとなります。片側検定の場合、対立仮説は「帰無仮説の単なる否定」とはならないことに注意が必要です*7。

両側検定と異なり、面積は片方側しか考えなくてよいので、片方で有意水準すべての面積となります。どちら側の面積を考えるかは示したいもの、つまり対立仮説によります。

(i) 表が出やすいことを示したい場合（対立仮説：表が出やすい）

表が出やすいことを示したい場合は、このように右側に棄却エリアを設定した片側検定を使います。極端に（棄却エリアに入るほど）表が出た場合のみ棄却されます。

この場合は、表が出にくい場合は考えないので、極端に表が出なかった場合でも棄却はされません。

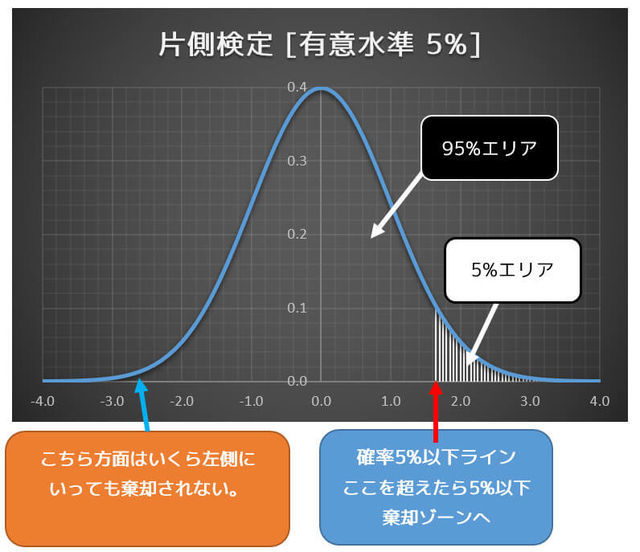
このように、帰無仮説で設定した値よりも「大きくなる」ことを示したい場合は、こちらの片側検定（私は右の片側検定と呼んでいます）を使います。

(ii) 表が出にくいことを示したい場合（対立仮説：表が出にくい）

表が出にくいことを示したい場合は、左側に棄却エリアを設定した片側検定を使います。(i)の逆パターンですね。
この場合、極端に（棄却エリアに入るほど）表が出なかった場合のみ棄却されます。

この場合は、表が出やすい場合は考えないので、極端に表が出た場合でも棄却はされません。

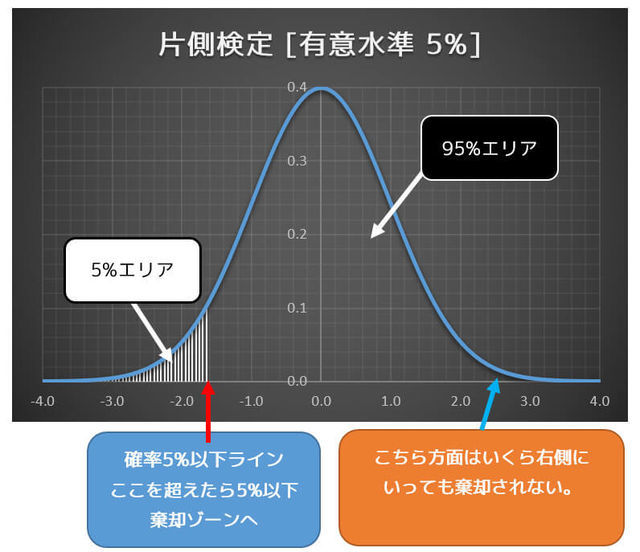
このように、帰無仮説で設定した値よりも「小さくなる」ことを示したい場合は、こちらの片側検定（私は左の片側検定と呼んでいます）を使います。

今の2つをまとめると、

対立仮説 \( p \not = 1/2 \) なら両側検定
対立仮説 \( p \gt 1/2 \) なら（右側）片側検定
対立仮説 \( p \lt 1/2 \) なら（左側）片側検定

となります。

このように、単に帰無仮説に対する仮説を立てる場合は両側検定、帰無仮説で設定した値よりも大きいことや小さいことを示したい場合は片側検定を使います。

片側検定は、片方あたりの棄却エリアが広くなるため、両側検定よりも棄却される可能性が高くなります。
ですが、棄却される可能性が上がるからといって後から検定法を「両側検定」から「片側検定」に変えるのは好ましくありません。辻褄を合わせようとしたと思われてしまうので……。

４．例題

ではここで両側検定と片側検定の2つの例題を解いてみましょう。

例題1

とある部の5人の身長を測定したところ、163[cm], 159[cm], 161[cm], 165[cm], 162[cm] となった。このとき、部の平均身長を160[cm]と考えてよいか検定したい。次の問いに答えなさい。

(1) 帰無仮説と対立仮説を述べなさい。
(2) この仮説検定では、どの分布を用いて検定を行うのがよいか。次の1～4から選んで番号で答えなさい。

1. 正規分布　　2. \( \chi^2 \) 分布　　3. F分布　　4. t分布

(3) 有意水準10%で検定をしなさい。結論だけでなく、根拠も記述すること。
（分布表は他のサイトなどで調べてください……）

解説1

まず、帰無仮説は、検定の際に立てる仮説でしたね。
今回は、部の平均身長が160[cm]であるが帰無仮説となります。

つぎに、対立仮説は、帰無仮説に対する仮説ですが、今回はただ「平均身長を160[cm]と考えてよいか。」だけなので対立仮説は部の平均身長が160[cm]でないとなります。部の（母集団の）平均身長を \( \mu \) [cm] とすると、

帰無仮説：\( \mu = 160 \)
対立仮説：\( \mu \not = 160 \)

となります。

(2) このように、母集団（今回の場合は部内全体）の分散が判明せず、かつデータ数も多く集まっていない場合はt分布を用います。よって答えは4。

(3) 実際に検定を行います。

まずは、5人の平均 \( \bar{X} \) と標準偏差 \( s \) を求めます。\[ \bar{X} = \frac{1}{5} (163 + 159 + 161 + 165 + 162) = 162\] \[ s^2 = \frac{1}{5} (1^2 + (-3)^2 + (-1)^2 + 3^2 + 0^2) = \frac{20}{5} = 4 \] \[ s = \sqrt{4} = 2 \]

と計算することができます。あとはこれをt分布の公式に入れるだけです。\[
T = \frac{\sqrt{n-1}(\bar{X} - \mu)}{s} = \frac{\sqrt{4}(162-160)}{2} = 2 \]

つぎにt分布の表を読み取ります。両側検定なので、それぞれの端は5%であることに気を付けてください*8。表を読み取ると2.132となります。

つまり、2.132以上であれば確率が5%以下となり、棄却、そうでなければ確率が5%以上となり採択となりますね。今回は2ちょうどなので採択となります。

つまり、結論は「採択、平均身長160[cm]でないとは言えない。」となります。

例題2

あるコインを投げる。そのコインは表がでやすいかどうかを検定したい。
このとき、つぎの問いに答えなさい。

必要ならば確率変数 \( Z \) が平均0、標準偏差1の正規分布に従う場合、

\( Z \leqq 1.65 \) となる確率95%
\( |Z| \leqq 1.96 \) となる確率95%
\( Z \leqq 2.05 \) となる確率98%
\( |Z| \leqq 2.33 \) となる確率98%
\( Z \leqq 2.33 \) となる確率99%
\( |Z| \leqq 2.58 \) となる確率99%

を用いてもよい。

(1) 帰無仮説、対立仮説を答えなさい。
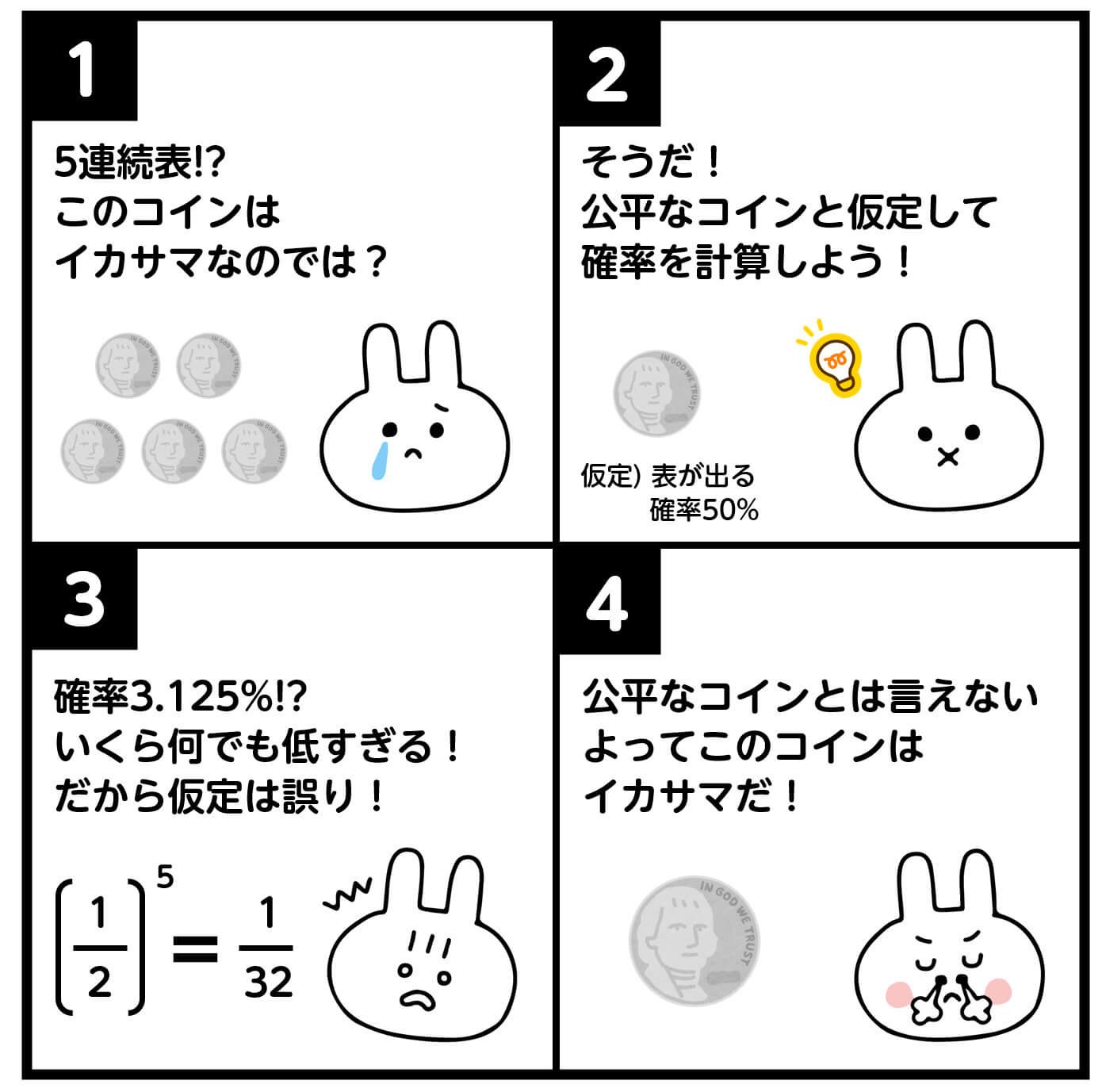
(2) このコインを5回投げた結果、5回とも表がでた。このとき、表が出やすいかどうか有意水準5%で検定しなさい。過程も書くこと。
(3) このコインを100回投げた結果、表が58回、裏が42回出た。このとき、表が出やすいかどうか有意水準5%で検定しなさい。

解説2

(1)

帰無仮説は、検定をする際に立てる仮説なので、表がでる確率 \( p \) を1/2（まともなコイン）となる。

対立仮説は、表が出やすいかどうかを検定したいため、\( p \not = 1/2 \) ではなく、\( p \gt 1/2 \) となることに要注意！！

帰無仮説：表が出る確率が1/2（まともなコイン）
対立仮説：表が出る確率が1/2を超えている（表が出やすいコイン）

(2)

5回投げたとき、5回とも表が出る確率は、\[ \left( \frac{1}{2} \right)^5 = \frac{1}{32} \]となる。\[ \frac{1}{32} < \frac{1}{20} \]なので、表が出る確率は5%以下となり、仮説は棄却され、表が出やすいコインといえる。

(3)

100回投げたときは、(2)のように \( 2^{100} \) を計算するのはめんどくさいし、100回は十分大きい回数*9と言えるので、正規分布を使う。

まずは、コインを100回投げたときの期待値 \( \mu \) と、標準偏差 \( \sigma \) を求める。コインは、表か裏の2つの事象しか起こらないため、二項分布を使ってこれら2つの計算をすることができる。\[ (平均) = 100 \times \frac{1}{2} = 50 \] \[ (分散) = 100 \times \frac{1}{2} \left(1 - \frac{1}{2} \right) = 25 \] \[ (標準偏差) = \sqrt{25} = 5 \]と計算ができる。

今回は、片側検定（コインが出やすいかどうか）で有意水準5%で検定すればいい*10ので、問題文の「\( Z \leqq 1.65 \) となる確率95%*11」を使う。すると1.65の値が読み取れる。つまり、平均から標準偏差1.65個分以上離れたデータであれば、棄却されたと言え、それ以外であれば採択されたといえる。

実際に平均から標準偏差何個分離れているかを計算してみる。\[ \frac{58-50}{5} = 1.600 < 1.65 \]となる。標準偏差1.6個分しか離れていないため、仮説は採択され、表が出やすいとは言えない。