スポンサードリンク
[お詫び] 2022/07/31 追記
データ数が偶数のときの四分位数の求め方の説明に誤りがありました。申し訳ございません。
誤) 中央値を求めるのに使ったデータ2つを無視し、第1, 第3四分位数を計算する。
正) 中央値は無視せず、「前半半分のデータ」から第1四分位数を、「後半半分のデータ」から第3四分位数を計算する。
こんにちは、ももやまです。
今回は数1範囲の「データの分析」の単元を、試験前1時間でさくっと復習できるように5つの単元にまとめました。
期末テスト、共通テストなどの試験直前に確認、普段の勉強、大学進学後に忘れてしまった人の復習などにぜひご利用ください!
目次
スポンサードリンク
1.平均・分散・標準偏差
平均、分散、標準偏差の意味と計算方法について復習しましょう。
(1) 平均
「データの値をすべて足したもの」を「データの個数」で割ることで求められます。
(記号表記: \( \bar{x} \), \( \mu \) など)

例えば、上の7つのデータの場合、総和は\[
3+6+1+4+7+5+2=28
\]となるので、平均は下のような計算式で計算できます。

計算を楽にするコツ(仮平均)
下のように各データの値が大きい場合、データの総和を求める際の計算が少し大変ですね。

そこで、平均がどれくらいか予測し、予測した平均を仮の平均とします。
上のデータ例の場合、平均が60に近そうなので仮平均を60とします。
つぎに、各データが予測した値(仮平均)とどれくらい離れているかを求め、さらに平均も求めます。
先程の例の場合、予想(60)との差の平均は+3となります。
最後に、予測した平均に先程求めた「予想との差の平均」を加えることで、平均点を求める計算量を減らすことができます!

(2) 分散
データがどれくらいばらついているのかを表します。
(記号は \( s^2 \) が用いられる。)
求め方は2通りあるので、それぞれ紹介します。
(i) 各データの偏差の2乗平均から求める
以下の1~4の手順で分散を計算できます。
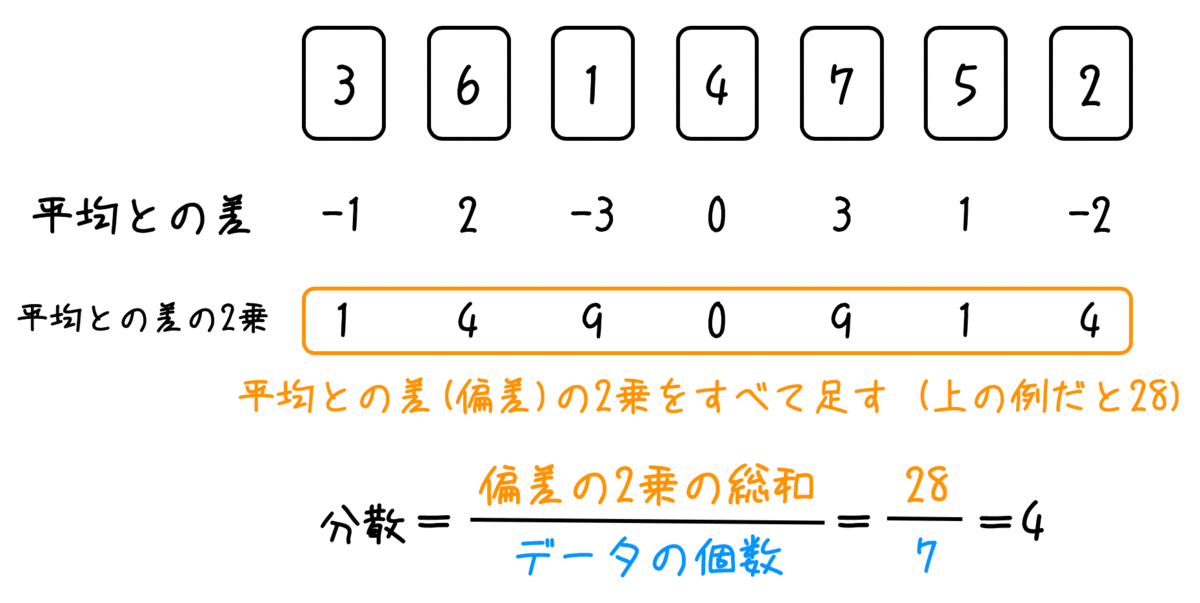
- それぞれのデータにおいて、平均からどれくらい離れているか(偏差)を求める
- それぞれの偏差を2乗する
- 2乗したものをすべて足す(下の例の場合は28)
- データの個数で割ったものが分散となる
(ii) 各データの2乗平均 - 平均の2乗から求める
それぞれのデータの値が大きくなく(-10~10程度)、かつ平均が小数や分数になる場合は、こちらの公式のほうが分散を早く求めることができます。
以下の1~3の手順で分散を計算できます。
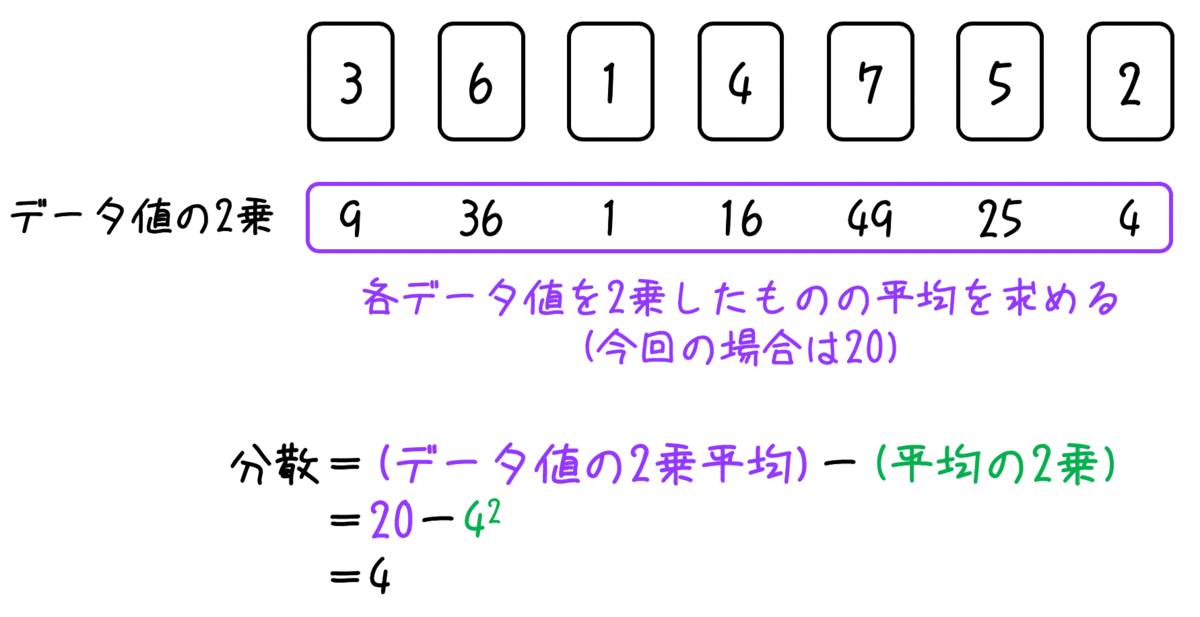
- それぞれのデータを2乗する
- 各データを2乗したものの平均(データ値の2乗平均)を求める
- 2で求めた(データ値を2乗平均)から(平均)を2乗したものを引くことで分散を求められる。
[注意]
分散は、必ず正の値になります(2乗したものを平均しているため)。
そのため、負になった場合は必ず計算ミスをしています。
(多くの場合、(データ値の2乗平均)と(平均の2乗)を引く順番を間違えているため、正負を逆にすれば正解になることが多いです)
(3) 標準偏差
分散では計算の際に2乗になってしまうため、ばらつきの単位が「単位の2乗」となってし、散らばり具合を比較するのにちょっと不便です。
そこで、分散のルート\[
(標準偏差) = \sqrt{ (分散) }
\]を取ることで、散らばり具合を比較しやすくしたものが、標準偏差です。
(記号は \( s \) が用いられる。)
スポンサードリンク
2.箱ひげ図を用いたデータの分析
つぎに、データの分析で必ず出てくる箱ひげ図についての復習です。
(1) 用語復習
箱ひげ図の前に、まずは箱ひげ図で使うデータの復習をしましょう。
最大値・最小値・中央値
最大値は名前の通り、データの中で一番大きい値を表し、最小値はデータの中で一番小さい値を表します。これは簡単。
中央値は、データの中で中央に位置する値です。メジアンとも呼ばれます。
具体的に言うと、データを小さい順に並べたときにちょうど真ん中に来る値が中央値となります。
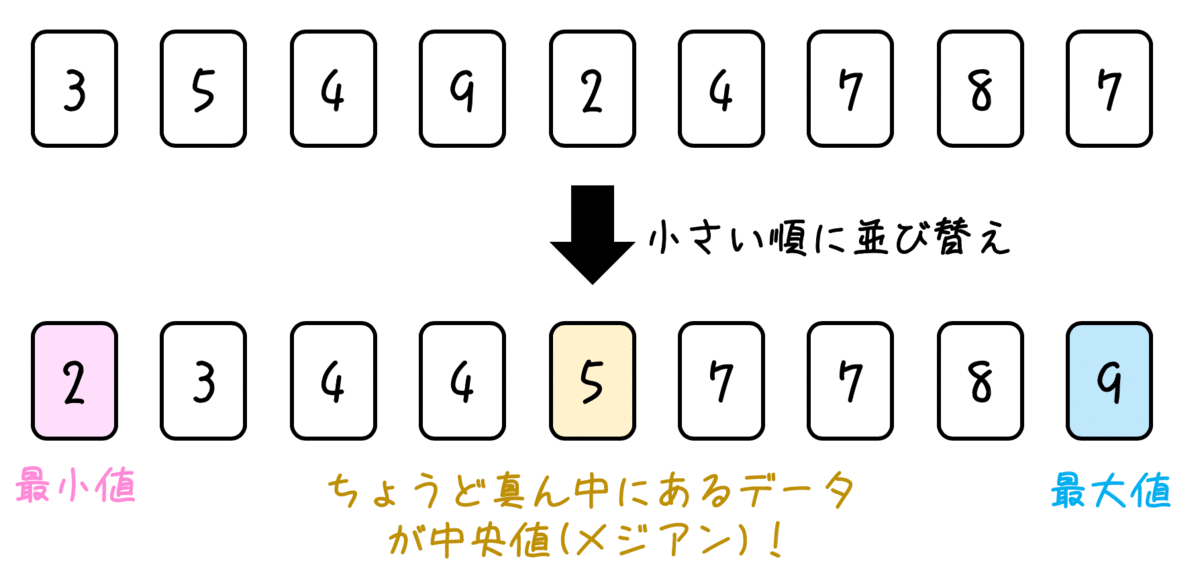
データの個数が奇数であれば「ちょうどど真ん中にあるデータ」がそのまま中央値となります。
もう少し厳密に書くと、データ数が \( 2n+1\) 個のときは \( n+1 \) 番目のデータが中央値です。
しかし、データの個数が偶数のときは少し大変です。
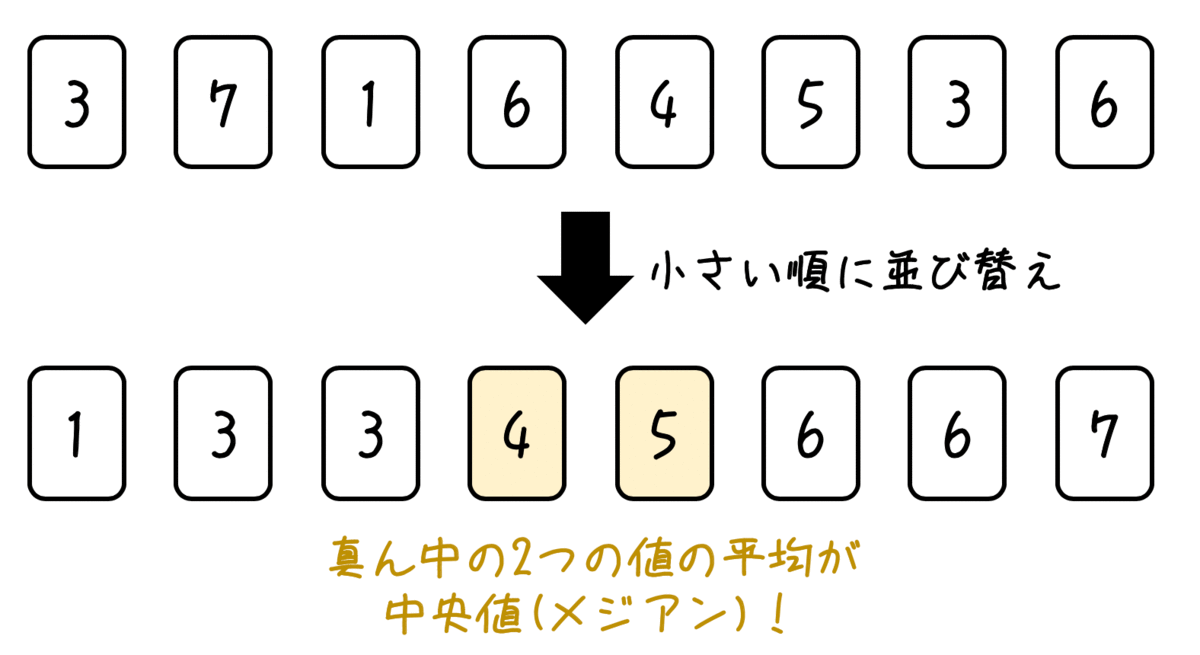
このときは、真ん中にある2つの値を平均したものが中央値です。(上の例だと4.5)
厳密に書くと、データ数が \( 2n\) 個のときは \( n \) 番目と \( n+1 \) 番目のデータを平均したものが中央値です。
最頻値(モード)
箱ひげ図では出てこないが、念のため復習しましょう。
最頻値は、データの中で一番出てくる数字が何かを表します。モードとも呼ばれます。
(一番出てくる数字の個数ではないので注意!)
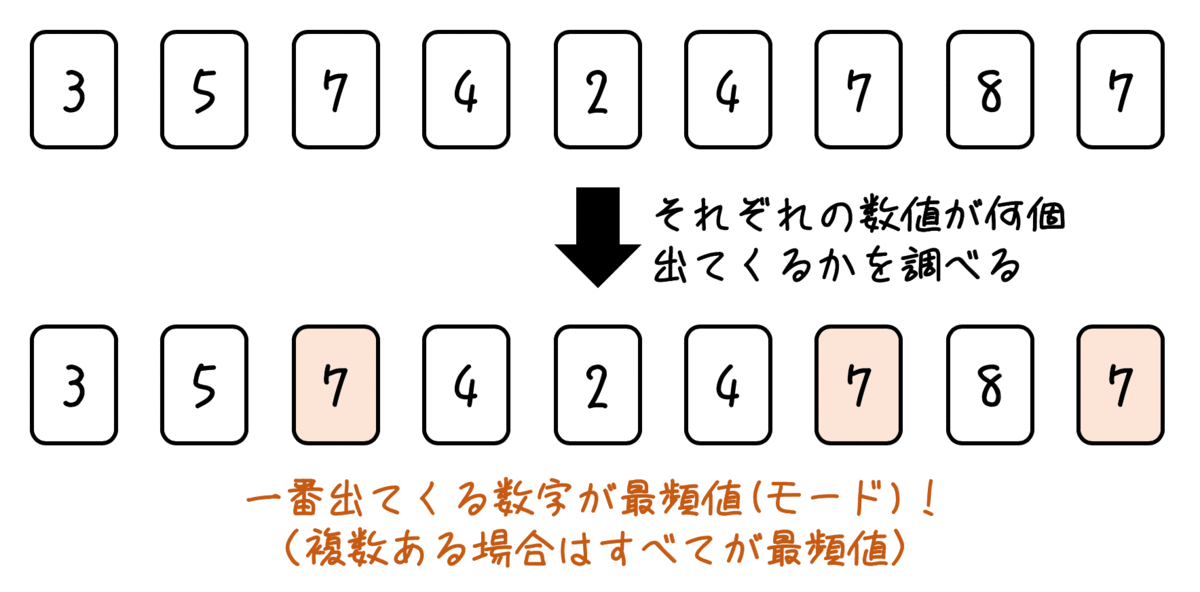
上の例だと、7が3回、4が2回、それ以外の数字が1回ずつ出てきてるから、最頻値は7ですね。
ちなみに一番出てくる数字が複数あるときは、全部最頻値となることに注意*1!
四分位数
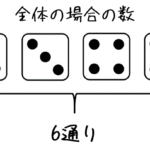
四分位数とは、データを4等分したときにその区切りのデータが何になるのかを示したものです。
区切りの場所によって、第1四分位数、第2四分位数、第3四分位数の3つの四分位数が生まれます*2。
ここからは、第1四分位数、第2四分位数、第3四分位数の求め方です。
突然ですが、皆さんはケーキを縦に切って4等分するときに、
- まず真ん中に包丁を1回入れて2等分に
- 2等分したものそれぞれに包丁を1回ずつ入れて4等分に
すると思います。
四分位数を求めるときも同じように、データを2等分し、さらに2等分したものを半分にすることで求めていきます。
まずデータを小さい順に並べます。
つぎに、中央値、つまり真ん中の区切りを見つけます。
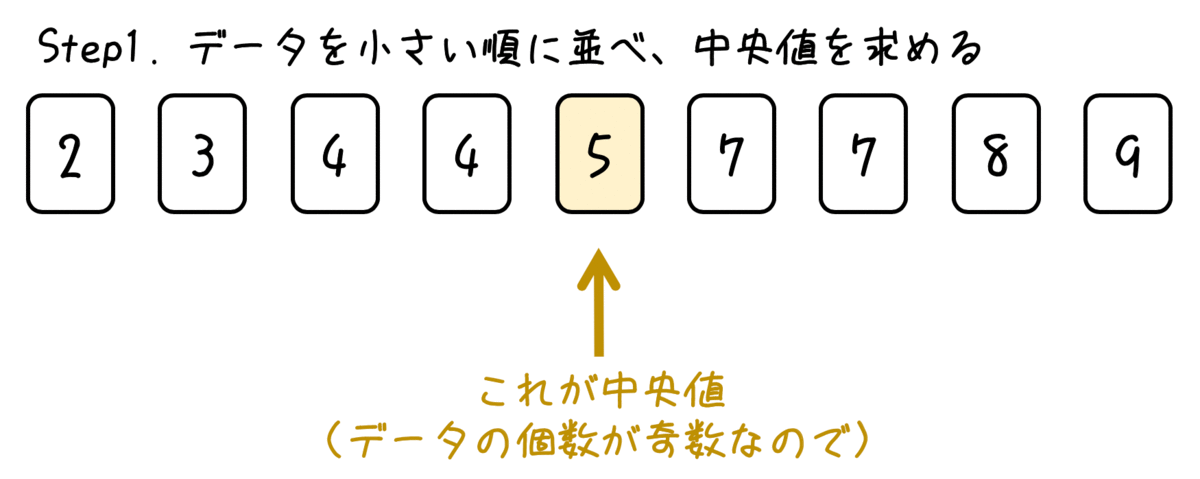
この真ん中の区切りが中央値、つまり第2四分位数です。
区切りを入れると、中央値よりも前の前半グループと中央値より後の後半グループの2つにわかれるますね。
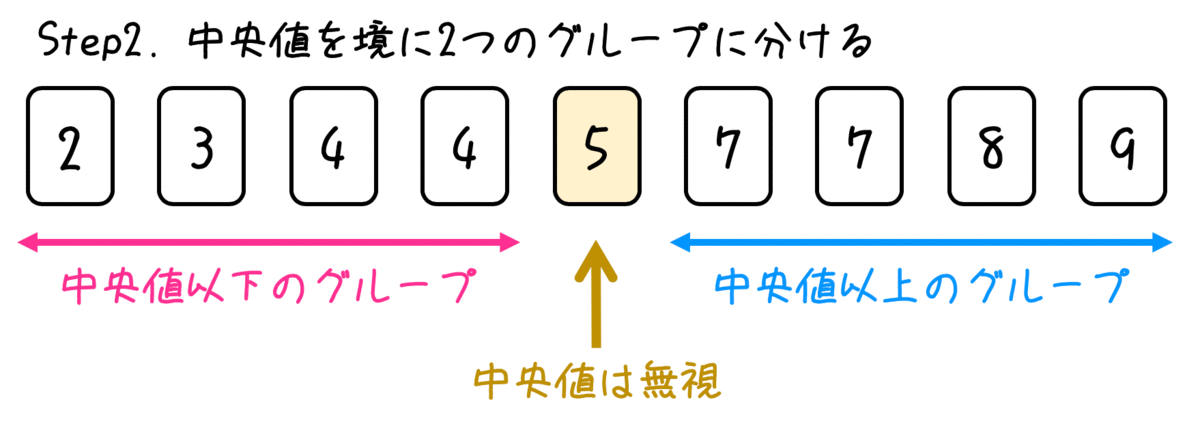
このとき注意してほしいポイントが、
- 区切りを入れるために使ったデータ(中央値)は無視
- 2つのグループのデータの個数は必ず同じ
の2点です。
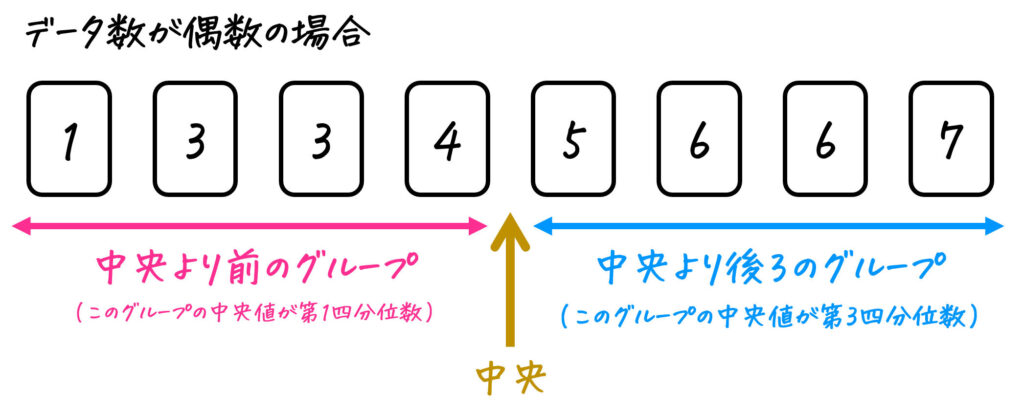
[注意] データ数が偶数のときは、- 前半半分のグループ(下の例の場合、1~4番目)
- 後半半分のグループ(下の例の場合、5~8番目)
となるように分けます。
[2022/07/31 追記] 中央値を求める際に使ったデータを無視してから第1, 第3四分位数を計算するという誤った表記をしておりました。申し訳ございません。
2つのグループに分けることができたら、あとはそれぞれのグループの区切りとなる中央値を求めればOK。
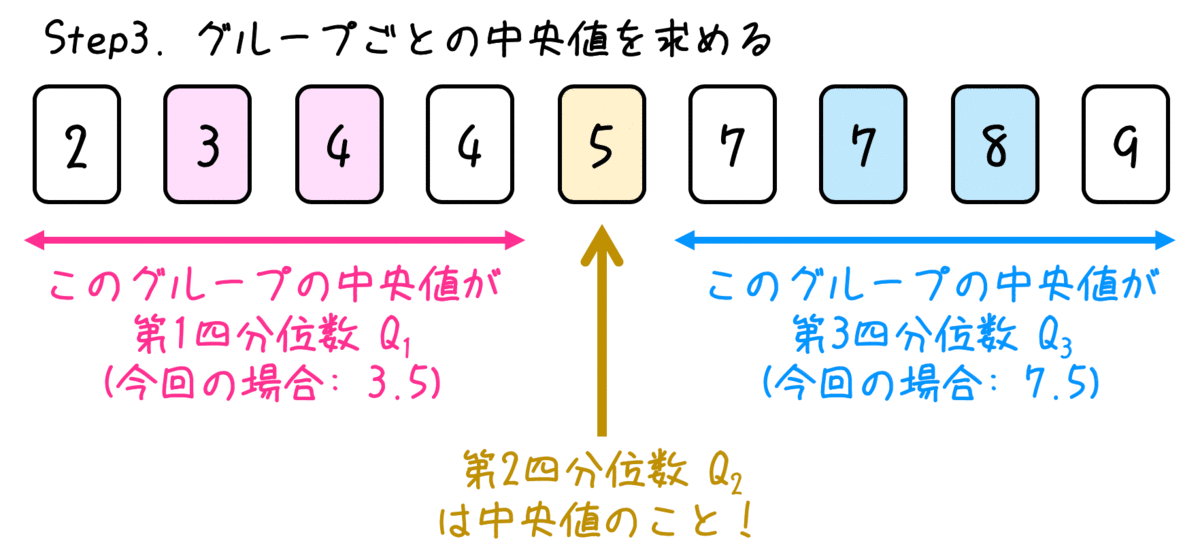
「中央値以下のグループ」の中央値が第1四分位数 \( Q_1 \)、「中央値以上のグループ」の中央値が第3四分位数 \( Q_3 \) です。
(上の例の場合、第1四分位数が3.5、第2四分位数が5.0、第3四分位数が7.5となる)
なお、先程も言った通り、第2四分位数 \( Q_2 \) は中央値となります。
(2) 箱ひげ図
用語説明が終わったので箱ひげ図を見ていきましょう。
箱ひげ図は、最大値、最小値、四分位数を用いて各データがどのように分布しているのかを表した図です。
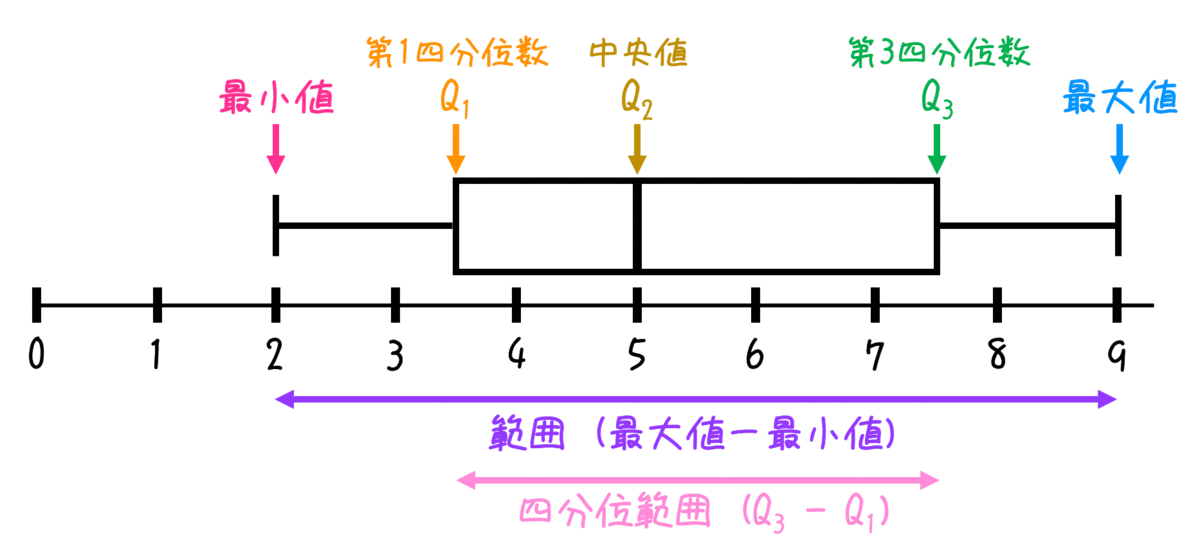
共通テストでは、箱ひげ図を読み取って解く問題が必ず出るので、それぞれの部分が何を表しているのかを頭に入れておきましょう。
ここで、先程説明していなかった3つの用語について復習しましょう。
範囲
データの最大値と最小値の差(最大 - 最小)を表します。
四分位範囲
第3四分位数と第1四分位数の差 \( Q_3 - Q_1 \) を表します。
四分位偏差
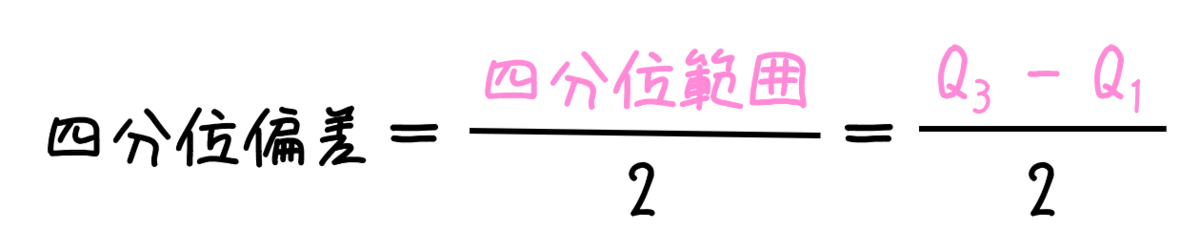
で計算できます。
スポンサードリンク
3.共分散と相関係数
2つのデータをペアと見て、あるデータ(A)ともう一方のデータ(B)にどれくらい関係性があるのかを見たものが相関係数です。
相関係数については、共通テストで使う
- 共分散を用いた直接計算
- 散布図を見てだいたいの相関係数を見積もる
の2点を確認しておきましょう。
(1) 共分散
共分散は、2つのデータA, Bのばらつき(分散)の積を平均したものを表します。
(記号は \( s_{xy} \) が用いられる。)
求め方が2つあるので、どちらも紹介しましょう。
その1 データA, Bの偏差の積の平均から求める(定義)
求める流れとしては、
- 2つのデータの平均を求める
- 各データごとに平均からのばらつき(偏差)を求める
- データA、データBの偏差の積の平均を求める
の1~3で求められます。
例えば、下の5つのデータの共分散を求めてみましょう。
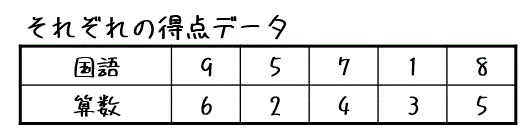
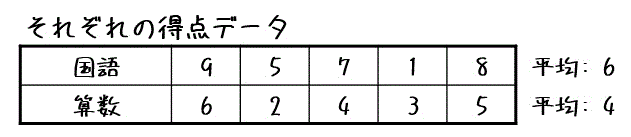
まず、2つのデータの平均を求めます。
すると、国語の平均点が6、算数の平均点が4と求められます。
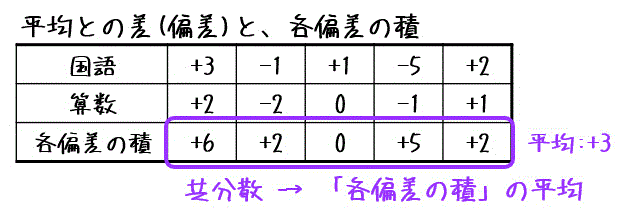
つぎに、国語、算数それぞれの平均からの差(ばらつき)を求めましょう。
さらに、各偏差の積を求め、それを平均したものが共分散となります。
計算すると、\[\begin{align*}
s_{xy} & = \frac{1}{5} \left\{ (9-6)(6-4) + (5-6)(2-4) + (7-6)(4-4) + (1-6)(3-4) + (8-6)(5-4) \right\}
\\ & = \frac{1}{5} \left\{ 6 + 2 + 0 + 5 + 2 \right\}
\\ & = \frac{1}{5} \cdot 15
\\ & = 3
\end{align*}\]となるので、共分散は3ですね。
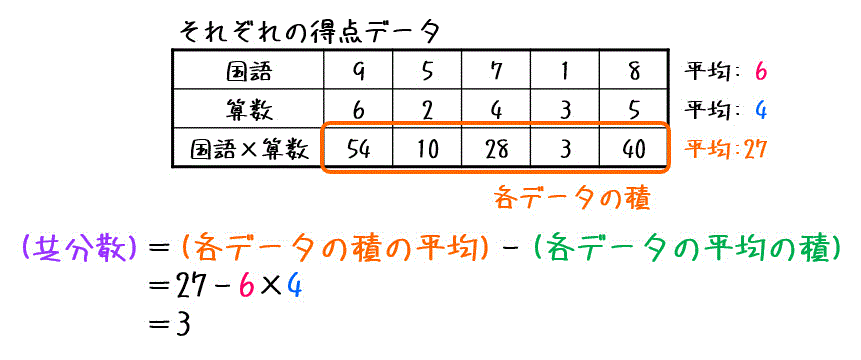
その2 (各データの積の平均) - (各データの平均の積) から求める
この方法の場合、
- 各データの平均を求める
- データA, Bそれぞれの値の積を平均したもの(各データの積の平均)を求める
- (各データの積の平均)-(データAの平均)×(データBの平均)を計算して共分散を求める。
の3ステップで求められます。
2つのデータに大きな値があまり含まれない場合はこちらの方法のほうがおすすめです。
(2) 相関係数(厳密に求める)
相関係数は、共分散と各データの標準偏差を求めることで計算ができます。
具体的には、相関係数は以下の式で計算できます。

なお、記号だと \( r \) などが使われることが多いです。
先程出てきた下のデータで、相関係数を求めてみましょう。
(このデータの共分散は3)

まず、国語の点数の標準偏差 \( s_x \) と 算数の標準偏差 \( s_y \) を求めましょう。
すると、\[
s_x = 2 \sqrt{2} , \ \ \ s_y = \sqrt{2}
\]と求められます。
なので、相関係数は\[\begin{align*}
r & = \frac{ s_{xy} }{ s_x s_y }
\\ & = \frac{ 3 }{ 2 \sqrt{2} \cdot \sqrt{2} }
\\ & = \frac{3}{4}
\\ & = 0.75
\end{align*}\]と計算できます。
[注意]
相関係数は、必ず-1以上1以下の値 \( (-1 \leqq r \leqq 1) \) となります。
なので、3.5とか-2のような-1以上1以下の値になったときは100%計算ミスをしています。
(3) 散布図から相関係数を読み取る
共通テストでは、散布図から相関係数を読み取る問題が頻出します。
ということで、相関係数と散布図の特徴を確認しておきましょう。
(i) 相関係数が1に近くなると…
相関係数が1に近づけば近づくほど、下の図のようにデータが正の傾きの直線に近くなります。
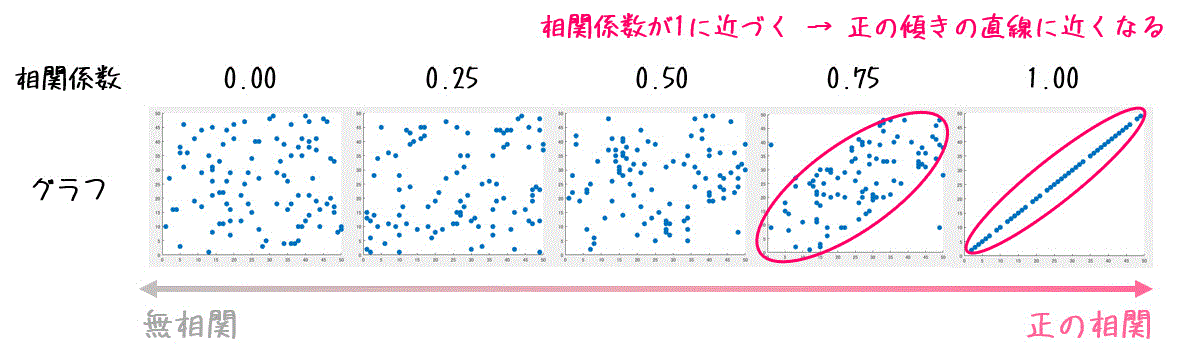
なお、相関係数が1.00(完全に1)のときはデータは(正の傾きを持った)直線上に並びます。
(ii) 相関係数が-1に近くなると…
相関係数が-1に近づけば近づくほど、下の図のようにデータが負の傾きの直線に近くなります。
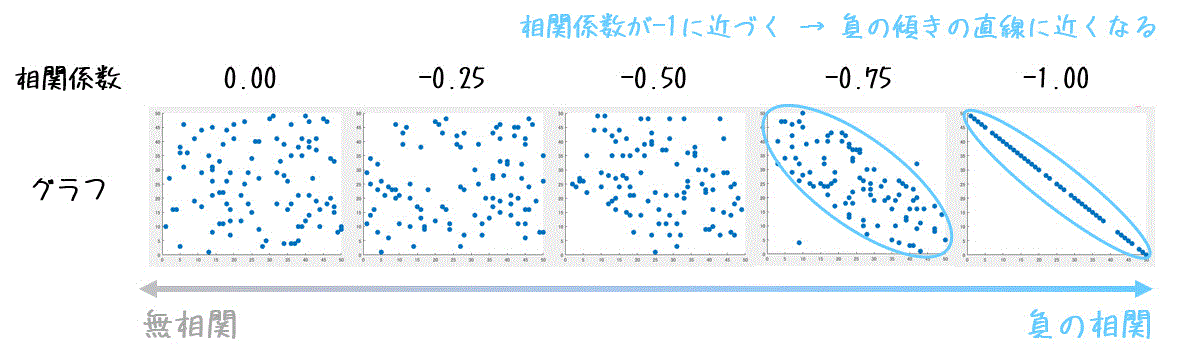
なお、相関係数が-1.00(完全に1)のときはデータは(負の傾きを持った)直線上に並びます。
最後に、相関係数-1から1まで変化させたときのそれぞれの散布図をチェックしておきましょう。

4.度数分布表とヒストグラム
次に度数分布表とヒストグラムについての確認をしておきましょう。
度数分布表:それぞれのデータをある範囲ごとに区切った(階級)ときにそれぞれのデータがどこに属するのかを表したもの。
ヒストグラム:度数分布表を図にしたもの

ここで、度数分布表の用語を復習しておこう。
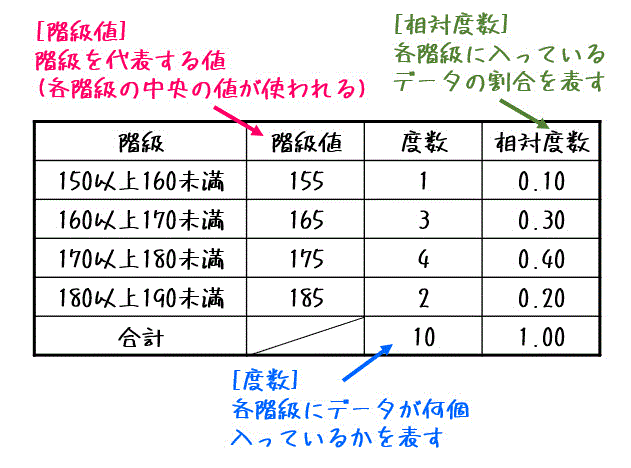
度数分布表で注意するポイントは、中央値や四分位数、平均などを求める際には各階級の中央の値(階級値)で計算することです。
例えば、上のデータであれば
155, 165, 165, 165, 175, 175, 175, 175, 185
の10個のデータがあるものとして中央値などを求めます。
5.データの操作による変化(応用)
(もし復習の時間がある人はこの章もぜひ確認しましょう!)
最後に、
- 全データに定数を加算・減算
- 全データを定数倍(2倍、3倍…)
したときに平均、分散、標準偏差、共分散、相関係数がどうなるかを確認しておきましょう。
まず、結論から書きます。
あるデータ全体に、
- 定数を加算
- 定数倍
したときの平均、分散、標準偏差、共分散、相関係数の変化は以下の通りである。
[平均]定数を加算:加算した分だけ平均が上がる
定数倍 :平均も定数倍される(2倍したら平均も2倍)
定数を加算:変わらない
定数倍 :定数倍の2乗される(2倍したら分散は4倍)
定数を加算:変わらない
定数倍:標準偏差も定数倍される
片方のデータ全体に定数を加算:変わらない
片方のデータ全体を定数倍 :共分散は定数倍される
(データAを2倍したら、共分散は2倍に)
片方のデータ全体に定数を加算:変わらない
片方のデータ全体を定数倍 :変わらない
※「相関係数が何倍になりますか」と聞かれたときはだいたい1倍(変わらない)と答えればほぼ確実に当たります。理由としては、相関係数は-1以上1以下の値しかとらないため、1倍以外の値だと-1以上1以下の値以外になってしまう可能性が出てくるため*3。
次に、なぜそう変化するのかを簡単に説明したいと思います。
(1) 平均の変化
定数を加算
例えば、平均点が6点の小テストがあります。
この小テストの点数が全員2点上がったらどうなるでしょうか。
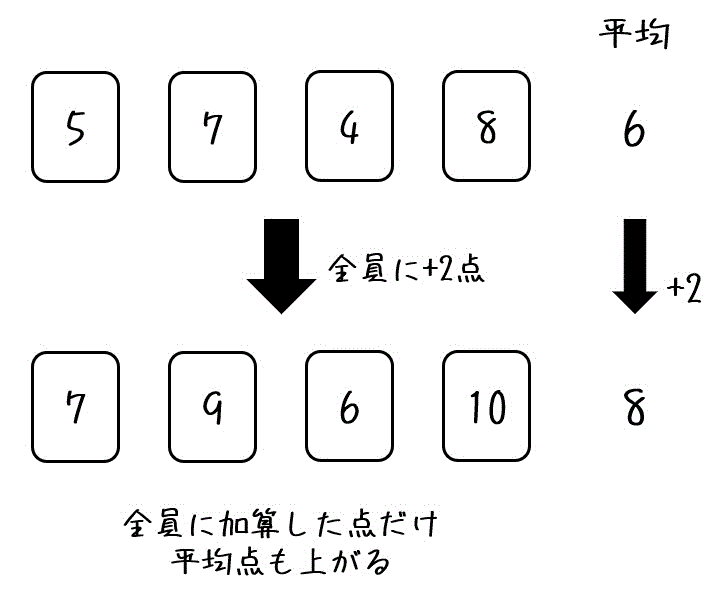
すると、全員の点数の和は「(上がった点数)×(人数)」だけ増えますね。
なので、平均点も「(上がった点数)×(人数)÷(人数)」、つまり「上がった点数」だけ増えますね。
なので、全部のデータに定数 \( a \) を加えると、平均も \( a \) だけ上がるのです!
定数倍
先程と同じ、平均点が6点の小テストがあります。
この小テストの点数が全員2倍になったらどうなるでしょうか。
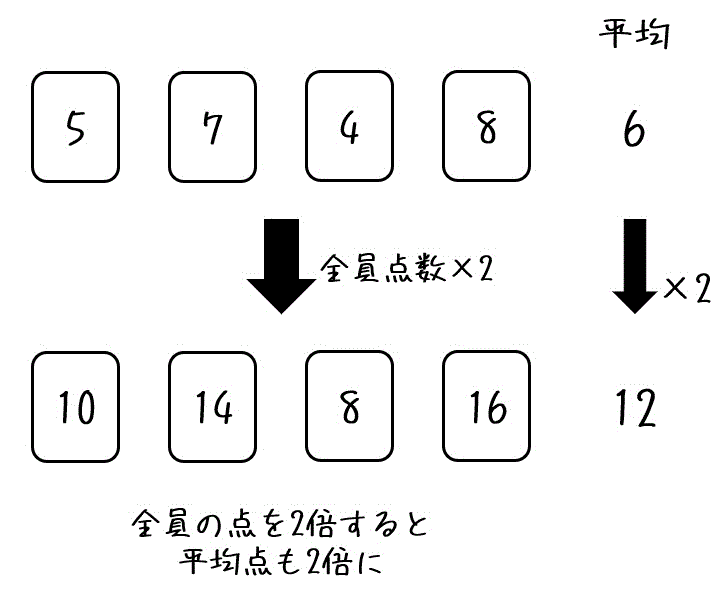
すると、先程と同じように全員の点数の和も2倍になるので、平均点も当然2倍になりますね。
なので、全部のデータを \( a \) 倍すると、平均も \( a \) 倍になるのです!
(2) 分散・標準偏差の変化
定数を加算
先程と同じ、平均点が6点の小テストがあります。
この小テストの点数が全員2点上がったらどうなるでしょうか。
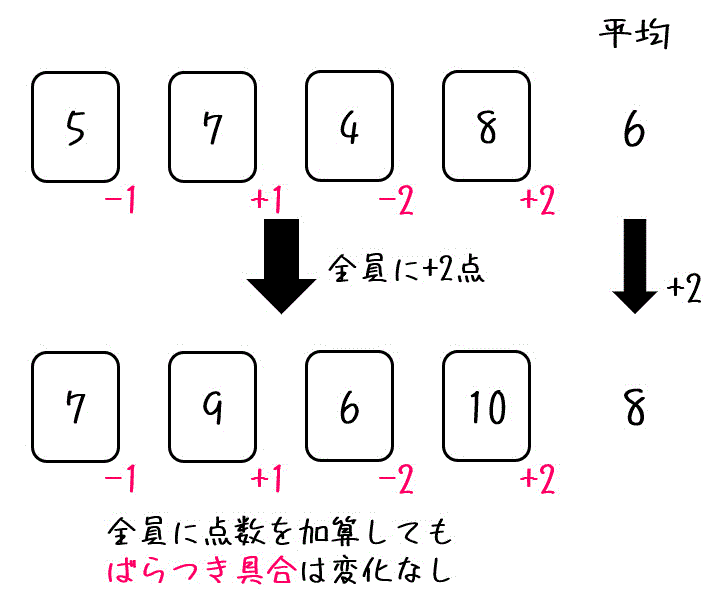
全員の点数を増やしても、点数のばらつき自体は変化しませんよね。
そのため、全員の点数を増やしても分散、標準偏差は一切変化しません。
定数倍
先程と同じ、平均点が6点の小テストがあります。
この小テストの点数が全員2倍になったらどうなるでしょうか。
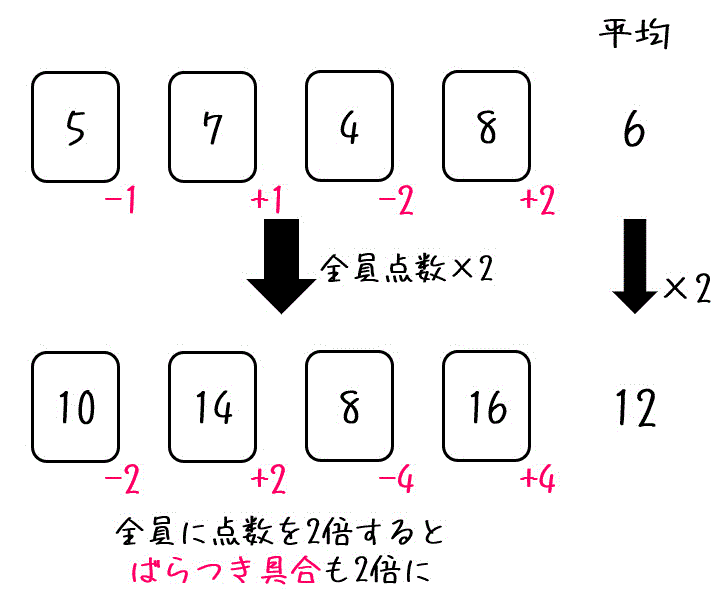
全員の点数を2倍にすると、点数のばらつき具合も2倍になりますね。
そのため、ばらつき具合を示す標準偏差は2倍に、ばらつき具合の2乗を示す分散は4倍になりますね。
なので、全部のデータを \( a \) 倍すると、標準偏差は \( a \) 倍、分散は \( a^2 \) 倍となります!
(3) 共分散
片方のデータ全体に定数を加算
国語の小テストと算数の小テストのそれぞれの点数の共分散を考えます。
ここで、全員の国語の点数を1点増やしたとき、共分散はどうなるでしょうか。
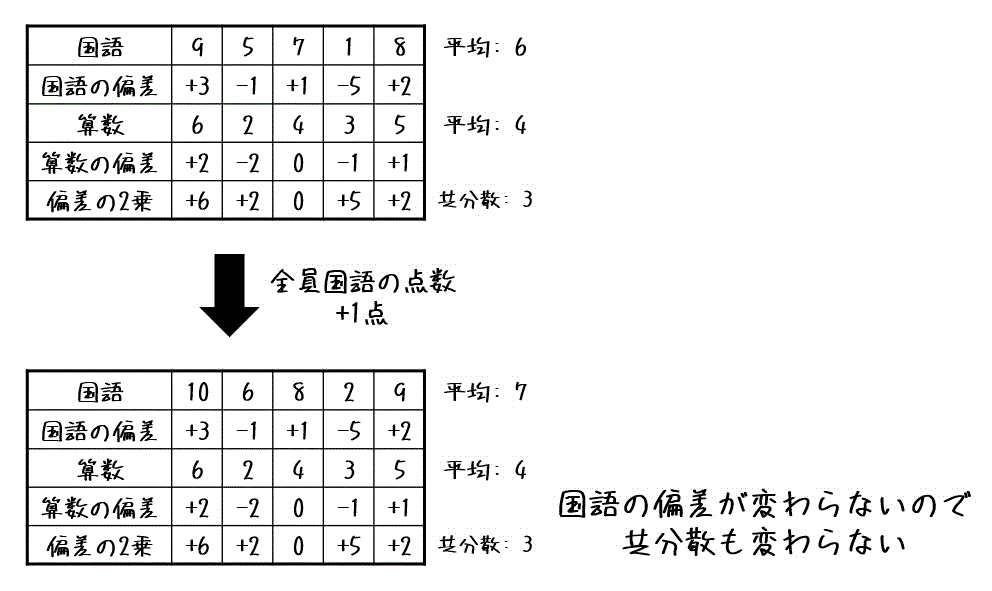
全員に国語の点数を加算しても、国語の偏差(ばらつき具合)は変化しませんね。
そのため、片方のデータ全体に定数を加算しても共分散は変化しないことがわかりますね。
片方のデータ全体を定数倍
先程と同じ国語の小テストと算数の小テストのそれぞれの点数の共分散を考えます。
ここで、全員の国語の点数2倍にしたとき、共分散はどうなるでしょうか。
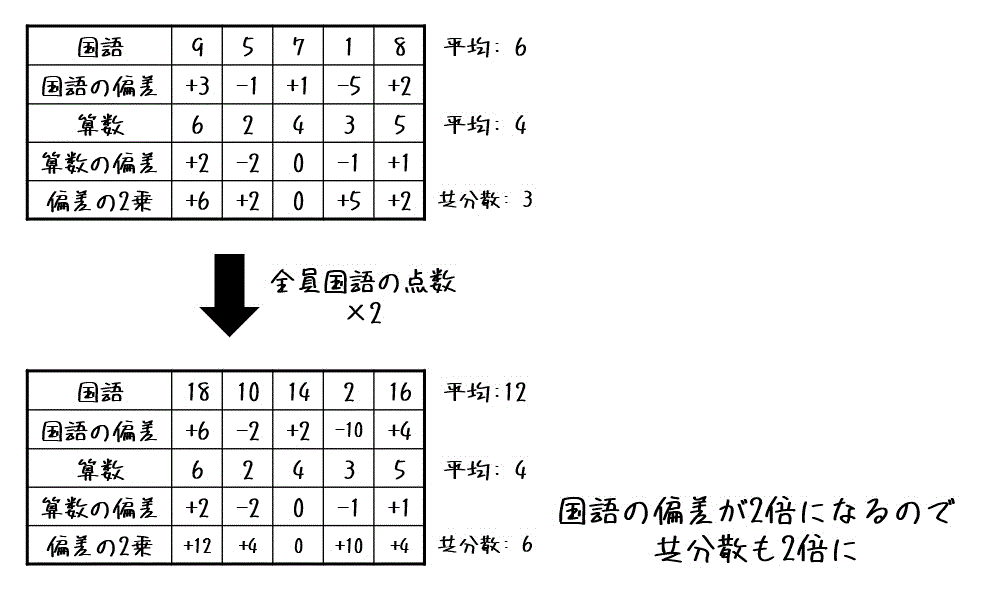
全員に国語の点数を2倍にすると、国語の偏差(ばらつき具合)も2倍になりますね。
そのため、(国語の偏差)×(算数の偏差)の総和、平均も2倍となり、共分散も2倍になりますね。
なので、片方のデータを \( a \) 倍すると、共分散も \( a \) 倍となります!
(4) 相関係数
相関係数は、下の式で求めることができましたね。

この式を用いて片方のデータに定数倍、定数を加算したときの相関係数の変化を見ていきましょう。
片方のデータ全体に定数を加算
例えばデータA全体に定数が加えられたとします。
しかし、データAの標準偏差、共分散ともに変化しませんね。(当然データBの標準偏差も変化しない)
そのため、片方のデータ全体に定数が加えられても相関係数は変化しません。
片方のデータ全体を定数倍
例えばデータA全体が定数倍になったとします。
すると、データAの標準偏差と、共分散は定数倍されます。
しかし、相関係数を求める式の分子側、分母側ともに同じ定数倍されているため、打ち消し合って相関係数は変化しません。
そのため、片方のデータ全体が定数倍になっても相関係数は変化しません。
6.最後に
今回は、データの分析の総復習を行うための記事でした。
もし需要があれば、演習問題編も公開したいと思います。
では、試験ふぁいと!
関連広告・スポンサードリンク