スポンサードリンク
こんにちは、ももやまです。
「うさぎ塾 微積分総復習」では、数3の中で特に重要な
の総復習問題を提供します。
Part2の今回は、微分に関する総復習問題を厳選して用意しました。
- 数3で極限を一通り習った人
- 模試・試験・入試前の直前演習
- 大学で解析学を学ぶ前のリハビリ
などにご使用ください。
なお、問題のPDFはこちらからダウンロードできます。
解答は、この記事の後ろにまとめて用意しています。
※ \( \log x \) は、\( \log_{e} x \)(底が \( e \) の対数、自然対数)を表します。
目次
スポンサードリンク
問題1.定義微分・微分可能性
つぎの(1), (2) の問いに答えなさい。(配点 10)
(1) 関数 \( f(x) = x^3 \) の導関数 \( f'(x) \) を定義に基づいて求めなさい。
(2) 関数 \( f(x) = |x| \) について、(i), (ii) の問いに答えなさい。
(i) \( f(x) \) は \( x = 0 \) で連続か。理由も踏まえて答えなさい。
(ii) \( f(x) \) は \( x = 0 \) で微分可能か。理由も踏まえて答えなさい。
スポンサードリンク
解答1.
(1) [5点]
導関数の定義・微分係数の定義を確認しておきましょう。
\[
f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}
\]
\[
f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
\]
今回は、\( f(x) = x^3 \) を定義に従って求めればいいので、\[\begin{align*}
f'(x) & = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
\\ & = \lim_{h \to 0} \frac{(x+h)^3 - x^3}{h}
\\ & = \lim_{h \to 0} \frac{x^3 + 3x^2 h + 3xh^2 + h^3 - x^3}{h}
\\ & = \lim_{h \to 0} 3x^2 + 3xh + h^2
\\ & = 3x^2
\end{align*}\]となる。
(式があっているが計算ミスであれば2点)
(2)
おなじみ連続性、微分可能性の判定問題ですね。
まずは、連続性の判定方法、微分可能性の判定方法を確認しておきましょう。
関数 \( f(x) \) が \( x = a \) で連続であるということは、\[ \lim_{x \to a+0 } f(x) = \lim_{x \to a-0 } f(x) = f(a) \]が成立することである。
関数 \( f(x) \) が \( x = a \) で微分可能ということは、\[ \lim_{h \to +0} \frac{f(a+h) - f(a)}{h} = \lim_{h \to -0} \frac{f(a+h) - f(a)}{h} \]
なお、関数 \( f(x) \) が \( x = a \) で微分可能である場合、\( x = a \) で連続である。
(微分可能であれば連続であることは言えるがその逆(連続であれば微分可能)は言えないので要注意!)
(i) [2点]
\( f(0) = 0 \) である。
また、\[ \lim_{x \to +0} |x| = \lim_{x \to +0} x = 0 \]\[ \lim_{x \to -0} |x| = \lim_{x \to -0} -x = 0 \]より、\[ \lim_{x \to +0} f(x) = \lim_{x \to -0} f(x) = f(0) \]を満たすので連続であるといえる。
(ii) [3点]
\[ \lim_{h \to +0} \frac{f(0+h) - f(0)}{h} = \frac{h}{h} = 1 \]\[ \lim_{h \to -0} \frac{f(0+h) - f(0)}{h} = \frac{-h}{h} = -1\]となり、\[ \lim_{h \to +0} \frac{f(0+h) - f(0)}{h} \not = \lim_{h \to -0} \frac{f(0+h) - f(0)}{h} \]なので微分可能ではない。
\( f(x) = |x| \) は、連続なものであっても微分可能ではない珍しい関数であることがわかりましたとさ。
スポンサードリンク
問題2.微分の基礎
つぎの(1)~(8)を微分しなさい。(目標時間:20分)
(1) \[
f(x) = (2x + 7)(3x + 11)
\]
(2) \[
f(x) = \frac{ 3x^2 + x + 12}{ 2x + 1}
\]
(3) \[
f(x) = (x^2 + 3x + 1)^5
\]
(4) \[
f(x) = \frac{x}{ \sqrt{x^2 + x + 1} }
\]
(5) \[
f(x) = \sin x + 2 \cos 2x + 3 \tan 3x
\]
(6) \[
f(x) = x \log x
\]
(7) \[
f(x) = 2^x \log_a x
\]
(8) \[
\left\{ \begin{array}{l} \ \ x = 4 \sin t \cos t \\ y = 12 \cos^2 t - 6 \end{array}\right.
\]
( \( \frac{dy}{dx} \) を \( t \) を用いて表すこと。)
解答2.
すべての問題が各5点で、合計40点満点です。
(1)
まず、式を展開しましょう。\[\begin{align*}
(2x+7)(3x +11) & = 6x^2 + (22+21)x +77
\\ & = 6x^2 + 43x + 77
\end{align*} \]なので、微分すると、\[
f'(x) = 12x + 43
\]となる。
基本的に\[
\left( x^n \right)' = n x^{n-1}
\]を覚えていたらOK!(\( n \) は自然数でなくてもOK)
この公式は、数2で習う\[
\left( x^4 \right)' = 4x^3
\]のような多項式・整式だけでなく、\[\begin{align*}
\left( \frac{1}{x} \right)' & = x^{-1}
\\ & = -x^{-2}
\\ & = - \frac{1}{x^2}
\end{align*} \]や、\[\begin{align*}
\left( \sqrt{x} \right)' & = x^{ \frac{1}{2} }
\\ & = \frac{1}{2} x^{ - \frac{1}{2} }
\\ & = \frac{1}{2 \sqrt{x} }
\end{align*} \]のように、分数やルートの式でも使うこともできます!
2つの積の微分公式を使って計算する方法もあります。
この場合、\[\begin{align*}
f'(x) & = (2x+7)' (3x+11) + (2x+7)(3x+11)'
\\ & = 2(3x+11) + (2x+7) \cdot 3
\\ & = 6x + 22 + 6x + 21
\\ & = 12x + 43
\end{align*}\]となります。
関数が \( f(x) g(x) \) の2つの和で示される場合、微分すると\[
\left\{ f(x) g(x) \right\}' = f'(x) g(x) + f(x) g'(x)
\]となる。
(2)
そのまま分数関数の微分公式に持ち込むのもありですが、分子 \( 3x^2 + x + 12 \) のほうが分母 \( 2x + 1 \) の次数*1以上となっていますね。なので、
\[\begin{align*}
f(x) & = \frac{ 3x^2 + x + 12}{ 2x + 1}
\\ & = \frac{3}{2} x - \frac{1}{4} + \frac{1}{4} \cdot \frac{49}{2x+1}
\end{align*} \]と変形します。
ここで、分数関数の微分公式を使います。
関数が \( \frac{f(x)}{g(x)} \) と表される場合、微分すると\[
\left\{ \frac{ f(x) }{ g(x) } \right\}' = \frac{f'(x)g(x) \color{red}{-} f(x)g'(x)}{ \left\{ g(x) \right\}^2 }
\]となる。
この公式で、\[
h(x) = \frac{49}{2x+1}
\]を微分すると、\[\begin{align*}
h'(x) & = \frac{ (49)' (2x+1) - 49 (2x+1)' }{(2x+1)^2}
\\ & = \frac{ 0 - 49 \cdot 2}{(2x+1)^2}
\\ & = - \frac{98}{(2x+1)^2}
\end{align*} \]となる。
よって、\( f(x) \) を微分すると、\[\begin{align*}
f'(x) & = \frac{3}{2} + \frac{1}{4} h'(x)
\\ & = \frac{3}{2} + \frac{1}{4} \left( - \frac{98}{(2x+1)^2} \right)
\\ & = \frac{3}{2} - \frac{49}{2 (2x+1)^2}
\end{align*} \]となります。
もちろん変形せずに計算してもOKです。この場合、\[\begin{align*}
f'(x) & = \frac{(6x + 1) (2x+1) - (3x^2 + x + 12) \cdot 2}{(2x+1)^2}
\\ & = \frac{12x^2 + 8x + 1 - 6x^2 - 2x - 24}{(2x+1)^2}
\\ & = \frac{6x^2 + 6x - 23}{(2x+1)^2}
\end{align*} \]と計算ができます。
案外こっちほうがいいのかも。
(3)
合成関数の微分法に関する問題です。
関数 \( y = f(x) \) を \( u = f(x) \) とおいたとき、\( f'(x) \) は、\[
f'(x) = \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}
\]で求められる。
今回の場合は、\( u = x^2 + 3x + 1 \) とおくことで、\( y = u^5 \) とできるので、\[\begin{align*}
f'(x) & = \frac{dy}{dx} \\ & = \frac{dy}{du} \frac{du}{dx}
\\ & = 5u^4 \cdot (2x + 3)
\\ & = 5 (x^2+3x+1)^4 (2x+3)
\\ & = (10x+15) (x^2+3x+1)^4
\end{align*}\]と計算できます。
なお、実際には \( u \) を括弧の中身として、(中身の微分)×(外の係数の微分)として、
\[\begin{align*}
f'(x) & = 5 \cdot (2x+3) \cdot (x^2+3x+1)^4
\\ & = (10x+15) (x^2+3x+1)^4
\end{align*}\]
と計算するのが基本です。(いちいち \( u \) とおかない!)
(4)
(2)と同じ分数関数の微分の問題です。\[\begin{align*}
\left( \sqrt{x^2 + x + 1} \right)' & = (x^2 + x + 1)^{ \frac{1}{2} }
\\ & = \frac{1}{2} (2x+1) (x^2 + x + 1)^{ - \frac{1}{2} }
\\ & = \frac{2x+1}{ 2 \sqrt{x^2 + x + 1} }
\end{align*}\]に注意すると、\[\begin{align*}
f'(x) & = \frac{1 \sqrt{x^2 + x + 1} - x \cdot \frac{2x+1}{ 2 \sqrt{x^2 + x + 1} } }{x^2+x+1}
\\ & = \frac{ 2(x^2 + x + 1) - x(2x+1) }{ 2 (x^2 + x + 1) \sqrt{x^2 + x + 1} }
\\ & = \frac{x + 2} { 2 (x^2 + x + 1) \sqrt{x^2 + x + 1} }
\end{align*} \]と計算できます。
(2行目の変形で分子分母に \( 2 \sqrt{x^2 + x + 1} \) を掛けるのがポイント)
(5)
三角関数の微分の問題です。
まずは、公式の確認をしましょう。
覚えておきたい三角関数の公式\[
\left( \sin ax \right)' = a \cos ax \]\[
\left( \cos ax \right)' = \color{red}{-} a \sin ax \]\[
\left( \cos ax \right)' = \color{red}{-} a \sin ax \]\[
\left( \tan ax \right)' = \frac{a}{a \cos^2 ax} \]\[
\left( \frac{1}{\tan ax} \right)' = - \frac{a}{a \sin^2 ax}
\]
教科書では、\( \sin x \) の微分が… と説明していますが、私的には \( \sin ax \) の形で頭にいれておいたほうがいいと思うので覚えておきましょう。
注意点としては、他の微分(積分)公式でも言えますが、\[
( \sin x )' = \cos x
\]などの公式の \( x \) の部分を他の文字に書き換えても成立しません。
つまり、公式と全く同じ形であったときのみ公式を適用することができます。
例えば、\[
( \sin 5 x )' = \cos 5x
\]とするのはダメです。(正しくは \( 5 \cos 5x \))
正しく \( \sin x \) や \( \cos x \) などの公式を使って \( \sin ax \) や \( \cos ax \) を微分するためには、合成関数の微分の知識を使います。例えば、\[
y = \sin 5x
\]を \( x \) で微分するのであれば、\( u = 5x \) として、\( y = \sin u \) の形にしてから、\[\begin{align*}
\frac{dy}{dx} & = \frac{du}{dx} \cdot \frac{dy}{du}
\\ & = 5 \cdot \cos u
\\ & = 5 \cos 5x
\end{align*} \]と計算します。
また、\( \tan ax \) の公式導出は積の微分公式を使います。具体的には、\[\begin{align*}
\left( \tan ax \right)' & = \left( \frac{\sin ax}{\cos ax} \right)'
\\ & = \frac{a \cos ax \cdot \cos ax + \sin ax \cdot \sin ax}{\cos^2 ax}
\\ & = \frac{a \cos^2 ax + \sin^2 ax}{\cos^2 ax}
\\ & = \frac{a}{\cos^2 ax}
\end{align*} \]と導出できます。
(\( \frac{1}{\tan ax} \) も同じように積の微分公式で導出できます。)
今回の問題の場合、\[\begin{align*}
f'(x) = \cos x - 4 \sin 2x + \frac{9}{\cos^2 3x}
\end{align*} \]と計算できます。
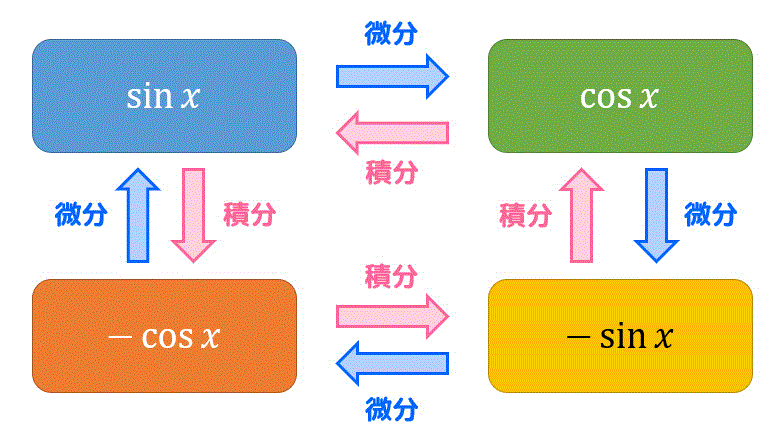
なお、三角関数の微分積分の関係は、下のような図の関係になっていることを頭に入れておくと公式を忘れにくいかと思います。
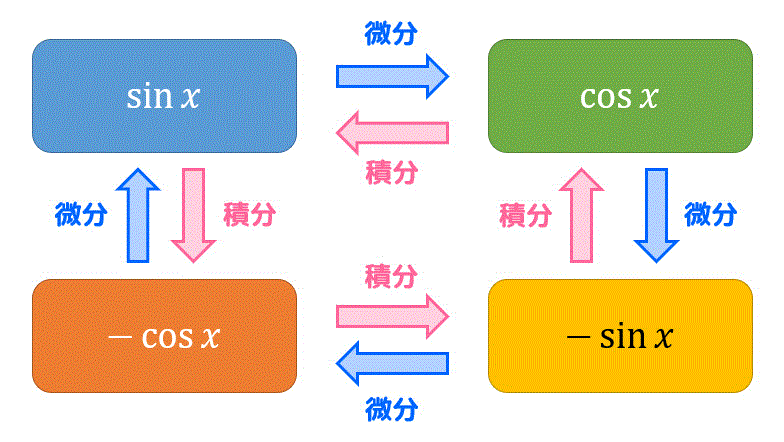
(6)
積の微分公式+自然対数 \( \log x \) の微分の問題です。
ここで、対数関数と指数関数の微分公式を抑えておきましょう。
覚えておきた対数関数・指数関数の公式\[
\left( \log x \right)' = \frac{1}{x} \]\[
\left( e^{x} \right)' = e^{x}
\]
今回の場合、\[\begin{align*}
f'(x) & = 1 \cdot \log x + x \cdot \frac{1}{x}
\\ & = \log x + 1
\end{align*}\]と微分できます。
必須ではないですが、下のように拡張したVerの対数関数・指数関数の公式を覚えておくと計算が早くなっておすすめです。
できれば頭に入れておきたい対数関数・指数関数の公式\[
\left( \log f(x) \right)' = \frac{f'(x)}{f(x)} \]\[
\left( \log | f(x) | \right)' = \frac{f'(x)}{f(x)} \]\[
\left( e^{f(x)} \right)' = f'(x) e^{f(x)}
\]
対数関数・指数関数の微分拡張公式
例えば、\[
g(x) = \log (x^2 + 1) , \ \ \ h(x) = e^{x^2}
\]の微分はそれぞれ、\[
g'(x) = \frac{2x}{x^2+1}, \ \ \ h'(x) = 2x e^{x^2}
\]と計算できます。
(7)
対数微分法、底が \( e \) ではない対数の微分の問題です。
どちらも導けるので、暗記は不要です。
微分したい対数関数が、\[
g(x) = \log_a x
\]のように底が \( e \) でなくても、\[\begin{align*}
\log_a x = \frac{\log_e x}{\log_e a}
\end{align*}\]と底を変換することで、\[
g'(x) = \frac{1}{x \log a}
\]と計算ができる。
例えば、\( g(x) = \log_2 x \) を微分するのであれば、\[
g(x) = \frac{\log x}{\log 2} = \frac{1}{\log 2} \log x
\]と変換することで、\[
g'(x) = \frac{1}{x \log 2}
\]と計算できます。
微分したい関数が、\[
y = f(x)^{g(x)}
\]と、変数の変数乗になっているとき、両辺の \( \log \) を取り、\[
\log |y| = \log \left| f(x)^{g(x)} \right| = | g(x) \log f(x) |
\]の形にし、両辺を \( x \) で微分することで、\[
\frac{y'}{y} = \left( g(x) \log f(x) \right)' \]\[
y' = y \left( g(x) \log f(x) \right)'
\]と計算することができる。
例えば、\( g(x) = 2^x \) を微分するのであれば、\[
g(x) = 2^x \]\[
\log g(x) = x \log 2 \]\[
\frac{g'(x)}{g(x)} = \log 2 \]\[
g'(x) = g(x) \log 2
y = 2^x \log 2
\]と計算ができます。
(\( g(x) \gt 0 \) なので \( \log g(x) \) の絶対値は省略しています。)
よって、今回の \( f(x) \) の場合、\[\begin{align*}
f'(x) & = \left( 2^x \log 2 \right) \cdot \log_a x + 2^x \cdot \frac{1}{x \log 2}
\\ & = 2^x \log 2 \cdot \log_a x + \frac{2^x}{x \log 2}
\end{align*} \]と計算できます。
対数微分法は、\[
g(x) = \frac{ (3x+5)^2 }{ \sqrt{2x + 3} }
\]のような、複雑な関数の積で表されるときにも使えます。
両辺の対数を取ると、\[
\log | g(x) | = 2 \log |3x + 5| - \frac{1}{2} \log | 2x + 3 |
\]となります。両辺を \( x \) で微分すると、\[\begin{align*}
\frac{g'(x)}{g(x)} & = 2 \cdot \frac{3}{3x + 5} - \frac{1}{2} \cdot \frac{2}{2x + 3}
\\ & = \frac{6}{3x + 5} - \frac{1}{2x+3}
\\ & = \frac{6(2x+3) - (3x + 5)}{(3x+5)(2x+3)}
\\ & = \frac{9x + 13}{(3x+5)(2x+3)}
\end{align*} \]と計算できます。
よって、\[\begin{align*}
g'(x) & = \frac{9x + 13}{(3x+5)(2x+3)} \cdot g(x)
\\ & = \frac{9x + 13}{(3x+5)(2x+3)} \cdot \frac{ (3x+5)^2 }{ \sqrt{2x + 3} }
\\ & = \frac{(3x+5)(9x+13)}{(2x+3) \sqrt{2x+3}}
\end{align*}\]と計算できます。
(8)
まず、両辺を \( t \) で微分します。\[\begin{align*}
\frac{dx}{dt} & = 4 ( \sin t )' \cos t + 4 \sin t ( \cos t )'
\\ & = 4 \cos^2 t - 4 \sin^2 t
\\ & = 4 \cos 2t
\end{align*} \]
\[\begin{align*}
\frac{dy}{dt} & = 12 \cdot (-2 \sin t) \cdot \cos t
\\ & = -24 \sin 2t
\\ & = -12 \sin 2t
\end{align*} \]
となるので、\[\begin{align*}
\frac{dy}{dx} & = \frac{ \frac{dy}{dt} }{ \frac{dx}{dt} }
\\ & = \frac{ -12 \sin 2t }{ 4 \cos 2t }
\\ & = -3 \tan 2t
\end{align*}\]となる。
問題3.接線の方程式
つぎの(1), (2)で与えられた曲線・点における接線の方程式を求めなさい。(配点 10)
(1)
\[ y = e^{-2x} \ \ \ \left( 0, 1 \right) \]
(2)
\[ y = \frac{ \log x }{ \sqrt{x} } \ \ \ \left( e, \frac{1}{ \sqrt{e} } \right) \]
解答3.
まずは接線の方程式を求め方を確認しておきましょう。
曲線 \( y = f(x) \) の点 \( ( t, f(t) ) \) における接線の方程式は\[
y = f'(t) (x-t) + f(t)
\]となる。
ついでに法線の求め方も確認しておきましょう。
曲線 \( y = f(x) \) の点 \( ( t, f(t) ) \) における法線の方程式は、\[
y = - \frac{1}{f'(t)} (x-t) + f(t) \ \ \ \left( f'(t) \not = 0 \right)
\]となる。
(\( f'(t) = 0 \) のときの法線は \( x = t \) となる)
(1)
\( f(x) = e^{-2x} \) とすると、\[
f'(x) = -2 e^{-2x}
\]となるので、\( f'(0) =-2 \) となる。
よって、接線の方程式は、\[\begin{align*}
y & = -2(x-0)+1
\\ & = -2x + 1
\end{align*} \]となる。[5点]
(2)
\[
f(x) = \frac{\log x}{ \sqrt{x} }
\]とすると、\[\begin{align*}
f'(x) & = \frac{\frac{1}{x} \cdot \sqrt{x} - \log x \cdot \frac{1}{2 \sqrt{x}}}{x}
\\ & = \frac{\frac{2}{x} \cdot x - \log x }{2x \sqrt{x} }
\\ & = \frac{2 - \log x }{2x \sqrt{x} }
\end{align*}\]となるので、\[\begin{align*}
f'(e) & = \frac{2 - \log e }{2e \sqrt{e} }
\\ & = \frac{1}{2 e \sqrt{e} }
\end{align*}\]となる。
よって、接線の方程式は、\[\begin{align*}
y & = \frac{1}{2 e \sqrt{e} } (x - e) + \frac{1}{\sqrt{e}}
\\ & = \frac{1}{2 e \sqrt{e} } + \frac{1}{2 \sqrt{e}}
\end{align*} \]となる。[5点]
問題4.陰関数表記の微分
つぎの(1), (2)の方程式で定められる \( x \) の関数 \( y \) について、\( \frac{dy}{dx} \) を求めなさい。(配点 10)
(1)
\[ \frac{x^2}{4} + \frac{y^2}{9} = 1 \]
(2)
\[ x^2 - xy + y^2 = 1 \]
解答4.
(1)
両辺を \( x \) で微分すると、\[
\frac{d}{dx} \left( \frac{x^2}{4} \right) + \frac{d}{dx} \left( \frac{y^2}{9} \right) = \frac{d}{dx} 1 \]\[
\frac{x}{2} + \frac{dy}{dx} \cdot \frac{d}{dy} \left( \frac{y^2}{9} \right) = 0 \]\[
\frac{x}{2} + \frac{y}{3} \frac{dy}{dx} = 0
\]となるので、\[
\frac{dy}{dx} = - \frac{3x}{2y}
\]となる。[5点]
(ただし \( 2y \not = 0 \))
(2)
両辺を \( x \) で微分すると、\[
2x - \frac{d}{dx} \left( xy \right) + \frac{dy}{dx} \frac{d}{dy} \left( y^2 \right) = 0 \]\[
2x - \left( \frac{d}{dx} (x) \cdot y + x \frac{dy}{dx} \frac{d}{dy} (y) \right) + 2y \frac{dy}{dx} = 0 \]\[
2x - y - x \frac{dy}{dx} + 2y \frac{dy}{dx} = 0 \]\[
(2y-x) \frac{dy}{dx} = -(2x-y)
\]となるので、\[
\frac{dy}{dx} = \frac{2x-y}{x-2y}
\]となる。[5点]
(ただし \( x - 2y \not = 0 \))
※ 分母 ≠ 0 の条件には念のため気を付けましょう(なくても不問です)
問題5.逆関数の導関数
つぎの(1)~(3)で表される逆関数の導関数 \( \frac{dy}{dx} \) を求めなさい。ただし、(2), (3)については \( x \) のみの式で表すこと。(配点 15)
(1) \[
x = y^2 + 5y + 1
\]
(2) \[
x = \sin y \ \ \ \left( - \frac{\pi}{2} \leqq y \leqq \frac{\pi}{2} \right)
\]
(3) \[
x = \tan y \ \ \ \left( - \frac{\pi}{2} \lt y \lt \frac{\pi}{2} \right)
\]
解答5.
逆関数の導関数に関する問題です。
逆関数の微分は、\[
\frac{dy}{dx} = \frac{1}{ \frac{dx}{dy} }
\]で計算することができる。
(1)
まずは簡単な問題。
\[ \begin{align*}
\frac{dy}{dx} & = \frac{1}{2y + 5}
\end{align*} \][5点]
(2)
\[ \begin{align*}
\frac{dy}{dx} & = \frac{1}{ \frac{dx}{dy} }
\\ & = \frac{1}{\cos y}
\\ & = \frac{1}{\sqrt{ \cos^2 y } }
\\ & = \frac{1}{\sqrt{ 1 - \sin^2 y} }
\\ & = \frac{1}{\sqrt{1 - x^2} }
\end{align*} \]と計算できる。[5点]
(3)
\[ \begin{align*}
\frac{dy}{dx} & = \frac{1}{ \frac{dx}{dy} }
\\ & = \frac{1}{ \frac{1}{\cos^2 y} }
\\ & = \frac{1}{ 1 + \tan^2 y }
\\ & = \frac{1}{1 + x^2}
\end{align*} \]と計算できる。[5点]
[余談:逆三角関数]
大学に入ると解析学などの最初の授業で、逆三角関数について習います。
ちょっとだけ説明すると\[
x = \sin y, \ \ \ x = \cos y, \ \ \ x = \tan y
\]の逆関数を取ったものを逆三角関数と呼び、それぞれ\[
y = \sin^{-1} x, \ \ \ y = \cos^{-1} x, \ \ \ y = \tan^{-1} x
\]で表します。
今回の(2), (3)の問題は、逆三角関数の微分公式\[
\left( \sin^{-1} x \right)' = \frac{1}{\sqrt{1-x^2}} \]\[
\left( \tan^{-1} x \right)' = \frac{1}{1+x^2}
\]を導く問題ともいえます。
逆三角関数について興味がある人は、こちらの記事をご覧ください。
問題6.
つぎの関数\[
y = \frac{1-x}{1+x^2}
\]の増減、極値、凹凸を調べ、グラフの概形を書きなさい。(配点 10)
解答6.
皆さんおなじみ増減表に関する問題です。
まずは極値を調べましょう。すると、\[\begin{align*}
\lim_{x \to \infty} \frac{1-x}{1+x^2} & = \lim_{x \to \infty} \frac{\frac{1}{x^2} - \frac{1}{x} }{ \frac{1}{x^2} + 1}
\\ & = 0
\end{align*} \]\[\begin{align*}
\lim_{x \to - \infty} \frac{1-x}{1+x^2} & = \lim_{x \to \infty} \frac{\frac{1}{x^2} - \frac{1}{x} }{ \frac{1}{x^2} + 1}
\\ & = 0
\end{align*} \]となる。[各2点×2 = 4点]
つぎに、極値の点を調べるために1回微分しましょう。\[ \begin{align*}
y' & = \frac{-1(1+x^2)-(1-x) \cdot 2x}{(1+x^2)^2}
\\ & = \frac{x^2 - 2x + 1}{(1+x^2)^2}
\end{align*} \]となるので、\[
\frac{x^2 - 2x + 1}{(1+x^2)^2} = 0
\]を満たす点、つまり \( x^2 - 2x + 1 = 0 \) となる点\[
x = 1 \pm \sqrt{2}
\]が極値となる点である。[微分結果:1点 極値となる点:1点×2]
さらにに変曲点を調べるために2回微分を行う。\[\begin{align*}
y'' & = \frac{x^2 - 2x - 1}{(1+x^2)^2}
\\ & = \frac{(2x-2) \cdot (1+x^2)^2 - (x^2 - 2x - 1) \cdot 2 \cdot 2x(1+x^2)}{(1+x^2)^4}
\\ & = \frac{(2x-2) \cdot (1+x^2) - 4x (x^2 - 2x - 1)}{(1+x^2)^3}
\\ & = \frac{2x^3 - 2x^2 + 2x - 2 - 4x^3 + 8x^2 + 4x}{(1+x^2)^3}
\\ & = \frac{-2(x^3 - 3x^2 - 3x + 1)}{(1+x^2)^3}
\\ & = \frac{-2(x+1)(x^2 - 4x + 1)}{(1+x^2)^3}
\end{align*} \]となるので、\[
\frac{-2(x+1)(x^2 - 4x + 1)}{(1+x^2)^3} = 0
\]つまり \( (x+1)(x^2 - 4x + 1) = 0 \) となる点\[
x = -1, 2 \pm \sqrt{3}
\]が変曲点である。[微分結果:1点 変曲点となる点:1点×3]
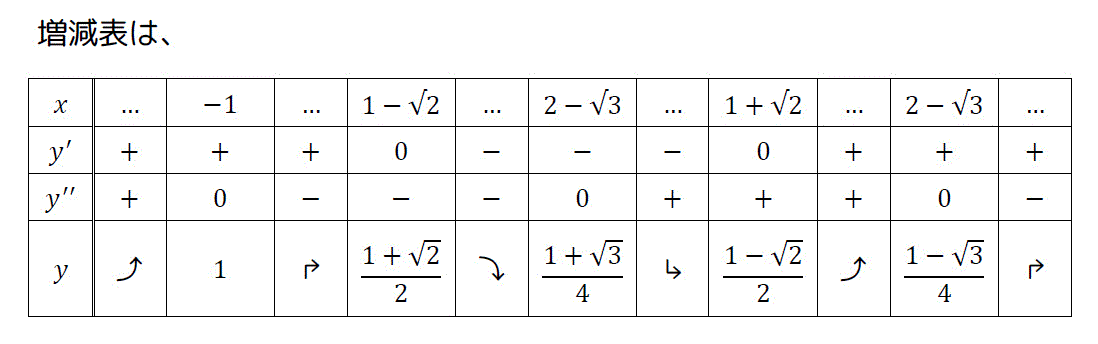
となるので、グラフの概形は
となる。(心電図みたいですね。)
[概形・増減表がうまくかけていれば:4点(多少のミスは不問)]さいごに
今回は、微積分の総復習として、微分の計算演習を18問用意しました。
練習で間違えた問題は、必ず復習して解けるようにしておきましょう。
また、もし忘れている公式などがあれば、必ず頭にいれておくようにしましょう。
次回は、総復習の積分編を用意したいと思います。
*1:それぞれの項の中で掛けあわされている文字の個数の中で最大のものを表します。例えば、\( 3x^2 + x + 12 \) であれば、\( 3x^2 \) の次数は2、\( x \) の次数は1、\( 12 \) の次数は0(定数項)なので、\( 3x^2 + x + 12 \) の次数は2となります。
関連広告・スポンサードリンク