スポンサードリンク
こんにちは、ももやまです。
前回の「うさぎでもわかる解析」で変数変換を用いた2重積分の求め方について説明しましたね。
今回は変数変換の中でも特に重要で期末試験や院試や数検1級などにも出題される極座標変換を用いた2重積分について説明していきたいと思います。
前回の解析の記事(Part24)はこちら!
変数変換の方法やヤコビアンなどについて書いてあるので変数変換の方法を忘れてしまった人はこちらの記事で確認しましょう!
スポンサードリンク
1.極座標変換
積分範囲が\[
D = \{ (x,y) \mid 1 \leqq x^2 +y^2 \leqq 4, \ x \geqq 0, \ y \geqq 0 \ \}
\]のような円で表されるものに対しては極座標変換を用いると積分範囲を\[
D' = \{ (r,\theta) \mid a' \leqq r \leqq b', \ c' \leqq \theta \leqq d' \ \}
\]の形にでき、2重積分を計算することができます。
(範囲に \( x^2 + y^2 \) が入っているのが目印です!)
例題を1つ出しながら説明していきましょう。
例題1
つぎの2重積分\[
\iint_D xy \ dxdy \]\[ D = \{ (x,y) \mid 1 \leqq x^2 +y^2 \leqq 4, \ x \geqq 0, \ y \geqq 0 \ \}
\]を計算しなさい。
解説1
積分範囲の中に円\[
1 \leqq x^2 +y^2 \leqq 4
\]が含まれていますね。
このように円が含まれているときには極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]とおきましょう。
(\( r \) は半径なので必ず0以上、\( \theta \) は最大でも1周分なので \( 0 \leqq \theta \leqq 2 \pi \) や \( - \pi \leqq \theta \leqq \pi \) の制約がかかる点に注意。)
ここで変数変換をおこなったのでヤコビアンを計算して \( dxdy \) と \( dr d\theta \) の関係式を求める必要があります。\[\begin{align*}
J = & \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right|
\\ = & \left| \begin{array}{ccc} \cos \theta & - r \sin \theta \\ \sin \theta & r \cos \theta \end{array} \right|
\\ = & \ r \left( \cos^2 \theta + \sin^2 \theta \right)
\\ = & \ r
\end{align*}\]と計算できますね。よって、\[
dxdy = r \ dr d \theta
\]となりますね。
(極座標変換のヤコビアンはなるべく覚えておきましょう。)
2重積分の積分領域が円で表される場合、 \( x = r \cos \theta \), \( y = r \sin \theta \) と置き換えることで2重積分を計算することができる。
またこのときのヤコビアン \( J \) は\[
J = \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right| = r
\]と表せる。よってこのときの変数変換における \( dxdy \) と \( drd \theta \) の関係は\[
dxdy = r \ drd \theta
\]となる。(できれば覚えておきましょう。)
また、積分範囲は\[
1 \leqq r^2 \leqq 4, \ \ \ r \cos \theta \geqq 0, \ \ \ r \sin \theta \geqq 0
\]となり、\( r \geqq 0 \) のため、\[
1 \leqq r \leqq 2, \ \ \ \cos \theta \geqq 0, \ \ \ \sin \theta \geqq 0
\]となります。\( \cos \theta \geqq 0 \) かつ \( \sin \theta \geqq 0 \) を満たすような \( \theta \) は\[
0 \leqq \theta \leqq \frac{\pi}{2}
\]なので、変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \ \middle| \ 1\leqq r \leqq 2, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]の形にでき、2重積分を計算することができます。
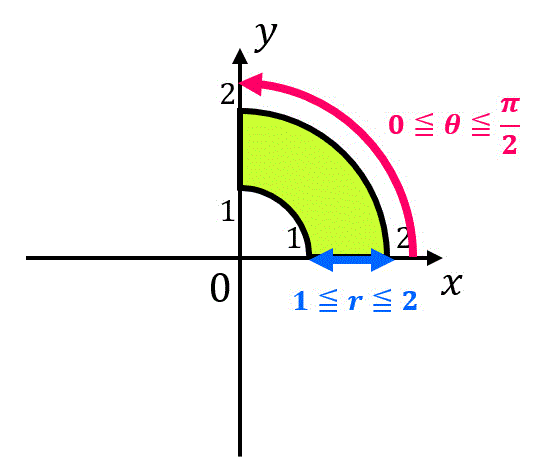
なお、積分範囲を図示すると変数変換の際に積分範囲 \( D' \) を求めるミスが減るので慣れないうちは図示してもいいかもしれません。今回の場合は、
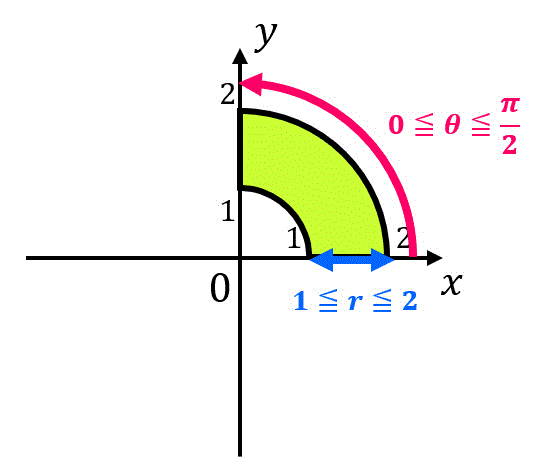
となります。
あとは今までの2重積分と同じように計算するだけ。\[\begin{align*} &
\iint_D xy \ dxdy
\\ = & \iint_{D'} r^3 \sin \theta \cos \theta \ drd \theta
\\ = & \int^2_1 r^3 \ dr \cdot \int^{ \frac{\pi}{2} }_0 \sin \theta \cos \theta \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^2_1 r^3 \ dr = & \left[ \frac{1}{4} r^4 \right]^2_1
\\ = & \ 4 - \frac{1}{4}
\\ = & \ \frac{15}{4}
\end{align*} \]\[\begin{align*}
\int^{ \frac{\pi}{2} }_0 \sin \theta \cos \theta \ d \theta = & \frac{1}{2} \int^{ \frac{\pi}{2} }_0 \sin 2 \theta \ d \theta
\\ = & \ \frac{1}{2} \left[ - \frac{1}{2} \cos 2 \theta \right]^{ \frac{\pi}{2} }_0
\\ = & \ \frac{1}{2} \cdot 1
\\ = & \ \frac{1}{2}
\end{align*} \]となるので、\[\begin{align*}
\iint_D xy \ dxdy
= & \ \frac{15}{4} \cdot \frac{1}{2}
\\ = & \ \frac{15}{8}
\end{align*} \]となる。
スポンサードリンク
2.領域が楕円の場合の変換
領域が円ではなく楕円だった場合でも極座標変換を少し変えるだけで2重積分を行うことができます。
例題2
つぎの2重積分\[
\iint_D y \ dxdy \]\[ D = \{ (x,y) \mid \ \frac{x^2}{a^2} + \frac{y^2}{b^2} \leqq 1, \ x \geqq 0, \ y \geqq 0 \ \}
\]を計算しなさい。
解説2
領域が楕円の場合、分母にある \( a^2 \), \( b^2 \) を消すために極座標変換\[
x = a r \cos \theta , \ \ \ y = b r \sin \theta \\ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]とおきましょう。
ヤコビアンを計算して \( dxdy \) と \( dr d\theta \) の関係式を求める。\[\begin{align*}
J = & \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right|
\\ = & \left| \begin{array}{ccc} a \cos \theta & - a r \sin \theta \\ b \sin \theta & b r \cos \theta \end{array} \right|
\\ = & \ abr \left( \cos^2 \theta + \sin^2 \theta \right)
\\ = & \ abr
\end{align*}\]と計算できますね。よって、\[
dxdy = abr \ dr d \theta
\]となります。
2重積分の積分領域が楕円\[
\alpha \leqq \frac{x^2}{a^2} + \frac{y^2}{b^2} \leqq \beta
\]で表される場合、 \( x = a r \cos \theta \), \( y = b r \sin \theta \) と置き換えることで2重積分を計算することができる。
またこのときのヤコビアン \( J \) は\[
J = \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right| = abr
\]と表せる。よってこのときの変数変換における \( dxdy \) と \( drd \theta \) の関係は\[
dxdy = abr \ drd \theta
\]となる。(導出過程がわかればOKです。)
また、積分範囲は\[
0 \leqq r^2 \leqq 1, \ \ \ r \cos \theta \geqq 0, \ \ \ r \sin \theta \geqq 0
\]となるので、変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \mid 0 \leqq r \leqq 1, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]の形にでき、2重積分を計算することができます。
あとは今までの2重積分と同じように計算するだけ。\[\begin{align*} &
\iint_D y \ dxdy
\\ = & \iint_{D'} ab^2 r^2 \sin \theta \ drd \theta
\\ = & ab^2 \int^1_0 r^2 \ dr \cdot \int^{ \frac{\pi}{2} }_0 \sin \theta \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^1_0 r^2 \ dr = & \left[ \frac{1}{3} r^3 \right]^1_0
\\ = & \ \frac{1}{3}
\end{align*} \]\[\begin{align*}
\int^{ \frac{\pi}{2} }_0 \sin \theta \ d \theta = & \ \left[ - \cos \theta \right]^{ \frac{\pi}{2} }_0
\\ = & 1
\end{align*} \]となるので、\[\begin{align*}
\iint_D xy \ dxdy
= & ab^2 \cdot \frac{1}{3} \cdot 1
\\ = & \ \frac{1}{3} ab^2
\end{align*} \]となる。
スポンサードリンク
3.練習問題
では練習をしていきましょう。
練習1
つぎの2重積分\[
\iint_D \sqrt{4-x^2-y^2} \ dxdy \]\[ D = \{ (x,y) \mid \ x^2 + y^2 \leqq 4, \ y \geqq 0 \ \}
\]を計算しなさい。
練習2
つぎの2重積分\[
\iint_D \frac{x}{x^2+y^2 + 9} \ dxdy \]\[ D = \{ (x,y) \mid \ x^2 + y^2 \leqq 9, \ x + y \geqq 0 \ \}
\]を計算しなさい。
練習3
つぎの2重積分\[
\iint_D xy^2 \ dxdy \]\[ D = \{ (x,y) \mid \ x^2 + y^2 \leqq 2y, \ x \geqq 0 \ \}
\]を計算しなさい。
4.練習問題の答え
解説1
積分範囲が円になっているので極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \]\[ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行う。
また、このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。
また、積分範囲は\[
r^2 \leqq 4, \ \ \ r \sin \theta \geqq 0
\]となり、\( r \geqq 0 \) のため、\[
0 \leqq r \leqq 2, \ \ \ \sin \theta \geqq 0
\]となる。よって変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \mid 0 \leqq r \leqq 2, \ 0 \leqq \theta \leqq \pi \ \right\}
\]の形となる。
(積分範囲を図示すると
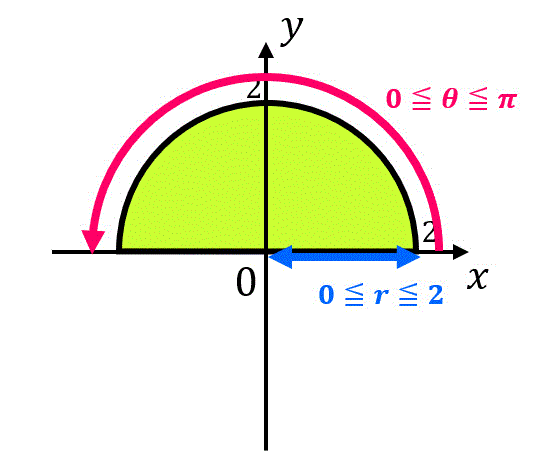
となり、確かに範囲が正しいことが確認できる。
よって、\[\begin{align*} &
\iint_D \sqrt{4-x^2-y^2} \ dxdy
\\ = & \iint_{D'} r \sqrt{4 - r^2} \ drd \theta
\\ = & \int^2_0 r \sqrt{4 - r^2} \ dr \cdot \int^{ \pi }_0 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^2_0 r \sqrt{4 - r^2} \ dr = & -\frac{1}{2} \int^2_0 -2r \sqrt{4 - r^2} \ dr
\\ = & - \frac{1}{2} \left[ \frac{2}{3} (4 - r^2)^{ \frac{3}{2} } \right]^2_0
\\ = & \ - \frac{1}{2} \cdot \left( - \frac{2}{3} \cdot 4^{ \frac{3}{2} } \right)
\\ = & \ \frac{8}{3}
\end{align*} \]\[\begin{align*}
\int^{ \pi }_0 1 \ d \theta = & \left[ \theta \right]^{ \pi }_0
\\ = & \pi
\end{align*} \]となるので、\[\begin{align*}
\iint_D \sqrt{4-x^2-y^2} \ dxdy
= & \ \frac{8}{3} \pi
\end{align*} \]となる。
解答2
積分範囲が円になっているので極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ - \pi \leqq \theta \leqq \pi \right)
\]を行う。( \( 0 \leqq \theta \leqq 2 \pi \) と置くと途中で積分が切れてしまうためおすすめではない。)
また、このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。
また、積分範囲は\[
r^2 \leqq 9, \ \ \ r \cos \theta + r \sin \theta \geqq 0
\]となり、\( r \geqq 0 \) のため、\[
0 \leqq r \leqq 3 \\
\sin \theta + \cos \theta =
\sqrt{2} \sin \left( \theta + \frac{\pi}{4} \right) \geqq 0 \]となる。よって変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \mid 0 \leqq r \leqq 3, \ - \frac{\pi}{4} \leqq \theta \leqq \frac{3}{4} \pi \ \right\}
\]の形となる。
(積分範囲を図示すると
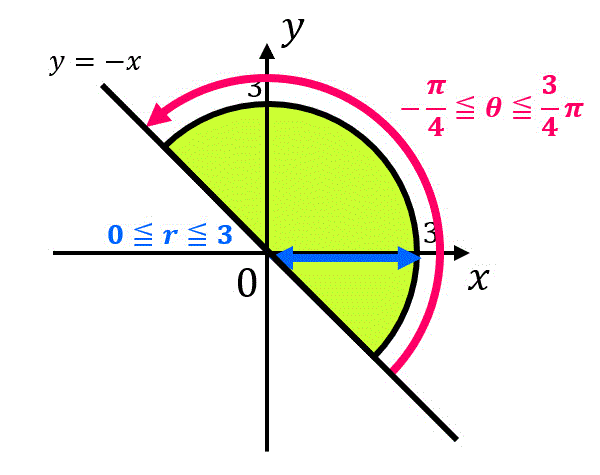
となり、確かに範囲が正しいことが確認できる。
よって、\[\begin{align*} &
\iint_D \frac{x}{x^2+y^2 + 9} \ dxdy
\\ = & \iint_{D'} \frac{r^2 \cos \theta}{r^2 + 9} \ drd \theta
\\ = & \int^3_0 \frac{r^2}{r^2+9} \ dr \cdot \int^{ \frac{3}{4} \pi }_{ - \frac{\pi}{4} } \cos \theta \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^3_0 \frac{r^2}{r^2+9} \ dr = & \int^2_0 r \int^3_0 \frac{r^2+9 - 9}{r^2+9}
\\ = & \int^3_0 \left( 1 - \frac{9}{r^2+9} \right) \ dr
\\ = & \left[ r - 3 \tan^{-1} \frac{r}{3} \right]^3_0
\\ = & \ 3 - \frac{3}{4} \pi
\end{align*} \]\[\begin{align*}
\int^{ \frac{3}{4} \pi }_{ - \frac{\pi}{4} } \cos \theta \ d \theta = & \left[ \sin \theta \right]^{ \frac{3}{4} \pi }_{ - \frac{\pi}{4} }
\\ = & \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}
\\ = & \sqrt{2}
\end{align*} \]となるので、\[\begin{align*}
\iint_D \sqrt{4-x^2-y^2} \ dxdy
= & \left( 3 - \frac{3}{4} \pi \right) \cdot \sqrt{2}
\\ = & 3 \sqrt{2} \left( 1 - \frac{\pi}{4} \right)
\end{align*} \]となる。
解答3
とりあえず積分範囲を図示してみましょう。

解き方が2通りあるので2通りとも示します。
[解法1:素直に極座標変換]
積分範囲が円になっているので極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ - \pi \leqq \theta \leqq \pi \right)
\]を行う。このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。
また、積分範囲は\[
r^2 \leqq 2 r \sin \theta, \ \ \ r \cos \theta \geqq 0
\]となる。ここで \( r \geqq 0 \) のため、\[
0 \leqq r \leqq 2 \sin \theta ,\ \ \ 0 \leqq \theta \leqq \frac{\pi}{2}
\]となる。( \( 2 \sin \theta \geqq 0 \) にも要注意!!)
よって変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \mid 0 \leqq r \leqq 2 \sin \theta, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]の形となる。
↓積分範囲を図示して正しいかどうか慣れないうちは確認しましょう
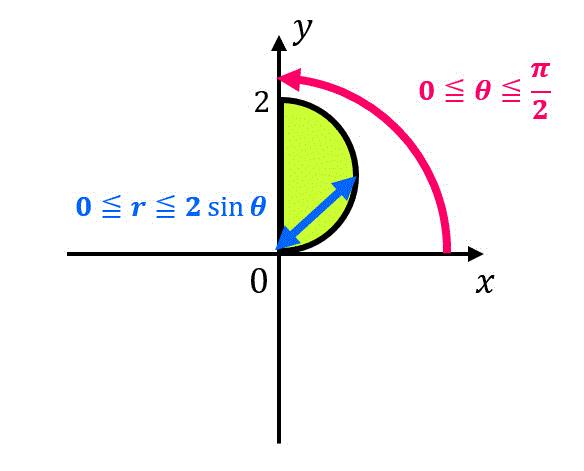
よって、\[\begin{align*} &
\iint_D xy^2 \ dxdy
\\ = & \iint_{D'} r^4 \cos \theta \sin^2 \theta \ drd \theta
\\ = & \int^{ \frac{\pi}{2} }_0 \left( \int^{2 \sin \theta}_0 r^4 \cos \theta \sin^2 \theta \ dr \right) \ d \theta
\end{align*} \]を計算すればよい。
ここで、\[\begin{align*} &
\int^{2 \sin \theta}_0 r^4 \cos \theta \sin^2 \theta \ dr
\\ = & \cos \theta \sin^2 \theta \left[ \frac{1}{5} r^5 \right]^{2 \sin \theta}_0
\\ = & \ \frac{32}{5} \cos \theta \sin^7 \theta
\end{align*} \]なので、\[\begin{align*} &
\int^{ \frac{\pi}{2} }_0 \left( \int^{2 \sin \theta}_0 r^4 \cos \theta \sin^2 \theta \ dr \right) \ d \theta
\\ = & \ \frac{32}{5} \int^{ \frac{\pi}{2} }_0 \cos \theta \sin^7 \theta \ d \theta
\\ = & \ \frac{32}{5} \left[ \frac{1}{8} \sin^8 \theta \ d \theta \right]^{ \frac{\pi}{2} }_0
\\ = & \ \frac{32}{5} \cdot \frac{1}{8}
\\ = & \ \frac{4}{5}
\end{align*} \]と計算できる。
[解法2:\( x^2 + y^2 \leqq a^2 \) の形にしてから極座標変換]
領域 \( D \) を変形すると、\[
D = \{ (x,y) \mid \ x^2 + (y-1)^2 \leqq 1, \ x \geqq 0 \ \}
\]となりますね。ここで \( y - 1 = t \) とおきます。すると \( dy = dt \) なので \( dxdy = dxdt \) ですね。さらに極座標変換\[
x = r \cos \theta , \ \ \ t = r \sin \theta \\ \left( r \geqq 0, \ \ - \pi \leqq \theta \leqq \pi \right)
\]を行う。このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。
また、積分範囲は\[
r^2 \leqq 1 , \ \ \ r \cos \theta \geqq 0
\]となる。ここで \( r \geqq 0 \) のため、\[
0 \leqq r \leqq 1 ,\ \ \ - \frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2}
\]となるので変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \ \middle| \ 0 \leqq r \leqq 1, \ - \frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]の形となる。
↓慣れないうちは図示することで積分範囲を確認しましょう
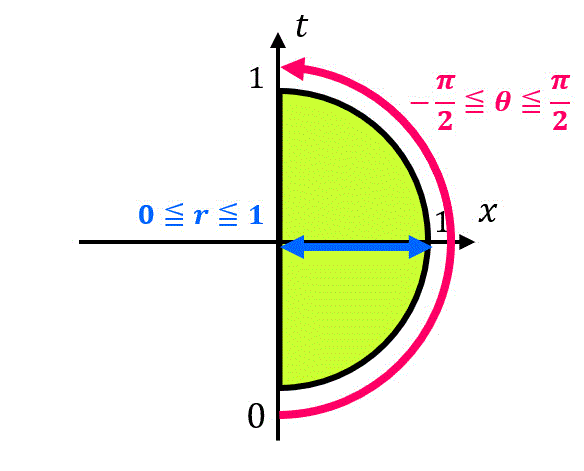
よって\[\begin{align*} &
\iint_D xy^2 \ dxdy
\\ = & \iint_D x (t+1)^2 \ dxdt
\\ = & \iint_{D'} r^2 \cos \theta \left( r \sin \theta + 1 \right)^2 \ drd \theta
\\ = & \int^{ \pi }_0 \left( \int^{1}_0 r^2 \cos \theta \left( r \sin \theta + 1 \right)^2 \ d \theta \right) \ dr
\end{align*} \]を計算すればよい。
ここで、\[\begin{align*} &
\int^{1}_0 r^2 \cos \theta \left( r \sin \theta + 1 \right)^2 \ d \theta
\\ = & \ r \left[ \frac{1}{3} \left( r \sin \theta + 1 \right)^3 \right]^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} }
\\ = & \ \frac{1}{3} r \left( (1+r)^3 - (1-r)^3 \right)
\\ = & \ \frac{1}{3} r \left( 1 + 3r + 3r^2 + r^3 - \left(1 - 3r + 3r^2 - r^3 \right) \right)
\\ = & \ \frac{1}{3} r \left( 6r + 2r^2 \right)
\\ = & \ \frac{2}{3} r^4 + 2r^2
\end{align*} \]なので、\[\begin{align*} &
\int^{ \pi }_0 \left( \int^{1}_0 r^2 \cos \theta \left( r \sin \theta + 1 \right)^2 \ d \theta \right) \ dr
\\ = & \int^{1}_0 \frac{2}{3} r^4 + 2r^2 \ dr
\\ = & \left[ \frac{2}{15} r^5 + \frac{2}{3} r^3 \right]^1_0
\\ = & \ \frac{2}{15} + \frac{2}{3}
\\ = & \ \frac{4}{5}
\end{align*} \]と計算できる。
2重積分の計算において、置換積分の省略技を頻繁に使用しています。
詳しくはこちらの記事をご覧ください。
5.さいごに
今回は、極座標変換を用いた2重積分の求め方についてまとめました。
極座標変換を行う2重積分は数検や院試や期末試験などに頻出するため必ずマスターしましょう。\( x = r \cos \theta \), \( y = r \sin \theta \) とおいたときのヤコビアンが \( r \) になることももう覚えちゃいましょう。
慣れるまでは積分範囲を考える際には図示などをすると計算ミスを防げるかと思います。
関連広告・スポンサードリンク