うさぎでもわかる解析　Part28　3重積分

こんにちは、ももやまです。

今回は、解析学のなかでも少し難易度が高めな3重積分について、計算方法を中心にうさぎでもわかるように基礎から説明していきます！

スポンサードリンク

１．2重積分の復習

3重積分の説明の前に、2重積分について軽く復習しておきましょう。

2重積分では、下のように \( x \) と \( y \) の2変数による積分で、積分領域 \( D \) は平面（2次元）になっているのでしたね。\[
\iint_D f(x,y) dxdy
\]

このような2重積分を解く際には、積分領域 \( D \) を\[
D = \{ (x,y) \mid a \leqq x \leqq b, \ c \leqq y \leqq d \ \}
\]と \( x \) 軸による積分、\( y \) 軸による積分の2つに分解し、\[
\iint_D f(x,y) dxdy = \int^d_c \left( \int^b_a f(x,y) \ dx \right)  \ dy
\]もしくは\[
\iint_D f(x,y) dxdy = \int^b_a \left( \int^d_c f(x,y) \ dy \right) \ dx
\]と定積分を2回する形に持ち込むのでした。

（この積分区間の変数 \( a \), \( b \), \( c \), \( d \) に定数以外、自分自身以外の積分変数を入れてもOK）

スポンサードリンク

２．3重積分と2重積分の2つの相違点

それでは、本題の3重積分に入っていきましょう。

まずは、3重積分と2重積分で変化する部分を説明していきましょう。

(1) 被積分関数が3変数関数に

3重積分では被積分関数が \( f(x,y,z) \) のような3変数関数となります。

（2重積分では \( f(x,y) \) の2変数関数でしたね）

(2) 積分領域が3次元に

3重積分では、積分領域 \( V \) が3次元（ \( xyz \) 空間）となります。

※教科書によっては3次元の領域も \( D \) と表しているものが多いですが、2次元の領域と区別をするため、本記事では3次元の領域を \( V \) で表すことにします。

（なお、2重積分では積分領域が2次元（ \(xy \) 平面）でしたね。）

3重積分では、2重積分の理解が必須です。

まだあまり理解できてないなと思ったら、下の記事で復習をすることを強くおすすめします。

www.momoyama-usagi.com

スポンサードリンク

３．3重積分の計算法

それでは、ここからは3重積分の計算法についてみていきましょう。

(1) 3重積分の基本計算

まずは、3重積分の中でも一番基本的な形を見てきましょう。

基本的には3回定積分を行うと思っていただけたらOKです。

少しだけ補足をしたいと思います。

[補足] (i)の方法

2重積分にあった\[
\iint_D f(x,y) dxdy = \int^d_c \left( \int^b_a f(x,y) \ dx \right)  \ dy
\]の形を3重積分に拡張して\[
\iiint_V f(x,y,z) \ dxdydz = \int^f_e \left( \int^d_c \left( \int^b_a f(x,y,z) \ dx \right)  \ dy \right) \ dz
\]と思っていただけたらOKです。

もちろん2重積分と同じように、まだ積分していない or 積分しようとしていない積分変数を入れることもできます*1。\[
\int^1_0 \left( \int^z_0 \left( \int^y_0 f(x,y,z) \ dx \right)  \ dy \right) \ dz
\]

また、積分順序は自由です。つまり、\( x \), \( y \), \( z \) どれから積分してもOKです。

例えば、\[
\iiint_V f(x,y,z) \ dxdydz = \int^f_e \left( \int^d_c \left( \int^b_a f(x,y,z) \ dx \right)  \ dy \right) \ dz \]の3重積分を\[
\iiint_V f(x,y,z) \ dxdydz = \int^b_a \left( \int^d_c \left( \int^f_e f(x,y,z) \ dz \right)  \ dy \right) \ dx
\]と入れ替えて計算することができます。

ただし、\[
\int^1_0 \left( \int^x_0 \left( \int^1_0 f(x,y,z) \ dx \right)  \ dy \right) \ dz
\]のようにすでに積分した変数 or これから積分しようとする変数を入れることはできません*2。

（積分順序に関するルールは2重積分のときと同じです）

[補足] (ii)の方法

被積分関数 \( f(x,y,z) \) を

• \( x \) だけの関数 \( p(x) \)
• \( y \) だけの関数 \( q(x) \)
• \( z \) だけの関数 \( r(x) \)

の3つの積で表され、なおかつ積分範囲が全部定数のときは、以下のように3つの定積分の式を計算することで答えを求めることができます。\[
\iiint_V f(x,y,z) \ dxdydz = \int^b_a p(x) \ dx \times \int^d_c q(y) \ dy \times \int^f_e r(z) \ dz
\]

計算については、実際に例題を解いてなれたほうが早いと思います。

ということで例題へLet's go!

解説1

(1)

積分範囲がすべて定数で表されているので、(ii)の方法で解いてみましょう。\[\begin{align*}
\iiint_V x^3 y^2 z \ dxdydz & = \int^{1}_{0} x^3 \ dx \cdot \int^{2}_{1} y^2 \ dy \cdot  \int^{3}_{2} z \ dz
\\ & = \left[ \frac{1}{4} x^4 \right]^{1}_{0} \cdot \left[ \frac{1}{3} y^3 \right]^{2}_{1} \cdot \left[ \frac{1}{2} z^2 \right]^{3}_{2}
\\ & = \frac{1}{4} \cdot \frac{1}{3} \left( 8 - 1 \right) \cdot \frac{1}{2} \left( 9 - 4 \right)
\\ & = \frac{1}{4} \cdot \frac{7}{3} \cdot \frac{5}{2}
\\ & = \frac{35}{24}
\end{align*}\]

(2)

積分範囲を見てみる。すると、積分順序に以下の2つの制限がかかる。

• \( z\) に \( y \) の積分範囲が存在する
  → \( y \) を積分する前に \( z \) を積分する必要あり
• \( y \) に \( x \) の積分範囲が存在する
  → \( x \) を積分する前に \( y \) を積分する必要あり

そのため、\( z \), \( y \), \( x \) の順に積分する必要がある。

\[\begin{align*}
& \iiint_V x^3 y^2 z \ dxdydz
\\ = \ & \int^1_0 \left( \int^x_0 \left( \int^y_0 x^3 y^2 z \ dz \right)  \ dy \right) \ dx
\\ = \ & \int^1_0 \left( \int^x_0 x^3 y^2 \left[ \frac{1}{2} z^2 \right]^{y}_{0}  \ dy \right) \ dx
\\ = \ & \frac{1}{2} \int^1_0 \left( \int^x_0 x^3 y^4 \ dy \right) \ dx
\\ = \ & \frac{1}{2} \int^1_0 x^3 \left[ \frac{1}{5} y^5 \right]^{x}_{0} \ dx
\\ = \ & \frac{1}{10} \int^1_0 x^8 \ dx
\\ = \ & \frac{1}{10} \left[ \frac{1}{9} x^{9} \right]^{1}_{0}
\\ = \ & \frac{1}{90}
\end{align*}\]

(2) 積分範囲が複雑な場合

実際の3重積分の問題では、(1)のように\[
V = \{ (x,y,z) \ \mid  a \leqq x \leqq b, \ c \leqq y \leqq d , \ e \leqq z \leqq f \}
\]のように、すぐに \( x \), \( y \), \( z \) の積分範囲に分けられるような問題は基本出てきません。

例えば、\[
V = \{ (x,y,z) \ \mid  0 \leqq x , \ 0 \leqq y , \ 0 \leqq z , \ x+y+z \leqq 1 \}
\]のようにひとひねりされた積分範囲であることがほとんどです。

このような問題の場合、\[
\iint_D \left( \int^{q(x,y)}_{p(x,y)} f(x,y,z) \ dz \right) \ dxdy
\]のように、

• どれか1変数を積分できるような形に変形
  （\( z \) を積分するのであれば \( p(x,y) \leqq z \leqq q(x,y) \) の形*3
• 残りの2変数を積分領域 \( D \) で表現
  （最初に \( z \) を積分したら、領域 \( D \) は \( xy \) 平面上になる

の形に持ちこんでから解きます。

積分範囲を 1変数＋2重積分 の形に変形する際に

• 積分範囲を解析的(?)に変形する方法
• 積分範囲（立体）を図示する方法

の2通りがあります。

実際に例題を1問解いて見ましょう。

解説2

\( x + y + z \leqq 1 \) を \( z \) 中心の形にすると、\( z \leqq 1 - x - y \) となります。

さらに \( V \) の範囲より、\( 0 \leqq z \) なので、\( z \) の積分範囲は\[
0 \leqq z \leqq 1-x-y
\]となります。

式変形で考えるのが難しいなと思う人は、下のように立体を図示してから考えるのもいいでしょう。（緑色の部分が領域 \( V \)）

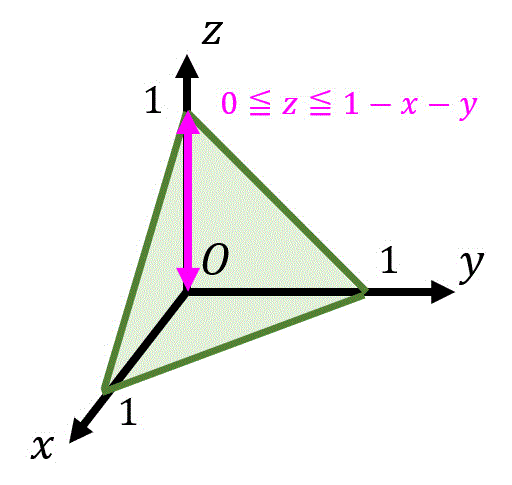
つぎに、残りの2重積分の範囲を考えましょう。

\( z \) がどんなに小さな値だったとしても \( z = 0 \) なので必ず \( x + y \leqq 1 \) となりますね。

また、\( 0 \leqq x \), \( 0 \leqq y \) なので \( 0 \leqq x + y \) ですね。なので、\[
0 \leqq x+y \leqq 1
\]が成り立ち、残りの2重積分の積分範囲 \( D \) は\[
D = \{ (x,y) \ \mid  0 \leqq x , \ 0 \leqq y , \ x+y \leqq 1 \}
\]となります。

さらに \( D \) の積分範囲を分解していくと、\[
D =  \{ (x,y) \ \mid  0 \leqq x \leqq 1, \ 0 \leqq y \leqq 1 - x \}
\]となりますね。

（2重積分の積分範囲を考えるときは図示してもOK）

なお、図形的に考える場合は、残りの2重積分の範囲 \( D \) は、領域 \( V \) を真上方向から見たものと同じと思うとわかりやすいかもしれません。

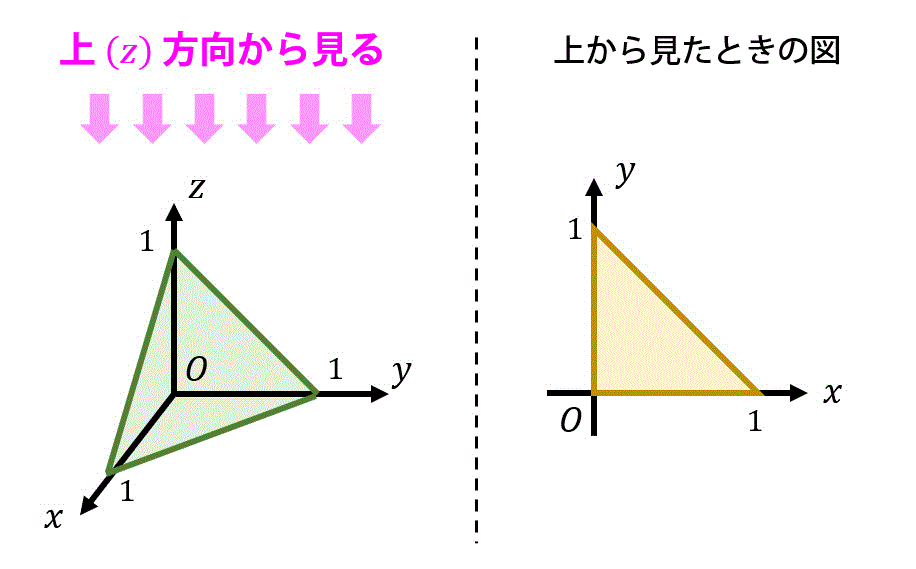
よって、\[\begin{align*}
\iiint_V 1 \ dxdydz & =  \iint_D \left( \int^{1-x-y}_{0} 1 \ dz \right) \ dxdy
\\ & = \iint_D 1-x-y \ dxdy
\\ & = \int^{1}_{0}  \left( \int^{1-x}_{0} 1-x-y \ dy \right) dx
\\ & = \int^{1}_{0}  \left[ y - xy - \frac{1}{2} y^2 \right]^{1 - x}_{0} \ dx
\\ & =  \int^{1}_{0}  1-x - x(1-x) - \frac{1}{2} (1-x)^2  \ dx
\\ & = \int^{1}_{0}  \frac{1}{2} x^2 - x + \frac{1}{2} \ dx
\\ & = \left[ \frac{1}{6} x^3 - \frac{1}{2} x^2 + \frac{1}{2} x \right]^{1}_{0}
\\ & = \frac{1}{6} - \frac{1}{2} + \frac{1}{2}
\\ & = \frac{1}{6}
\end{align*}\]と計算できる。

４．3重積分と変数変換（ヤコビアン）

2重積分に出てきたヤコビアン、実は3重積分でも出てきます。

（ヤコビアンってなんだっけという人はこちらの記事で復習をしましょう。）

www.momoyama-usagi.com

(1) ヤコビアンの公式

3重積分の場合にも、変数変換を用いて積分範囲を簡潔に表す方法が使えます。

例えば、\[
\left\{\begin{array}{l} x = 2p - 3q - r \\ y = -p + 3r \\ z = p + 2q + 2r    \end{array}\right.
\]とおきかえることを考えてみましょう。

このときのヤコビアンは、\[\begin{align*}
J & =  \left| \begin{array}{ccc} \frac{\partial x}{\partial p} & \frac{\partial x}{\partial q} & \frac{\partial x}{\partial r}  \\ \frac{\partial y}{\partial p} & \frac{\partial y}{\partial q} & \frac{\partial y}{\partial r} \\ \frac{\partial z}{\partial p} & \frac{\partial z}{\partial q} & \frac{\partial z}{\partial r}  \end{array} \right|
\\ & =  \left| \begin{array}{ccc} 2 & -3 & -1 \\ -1 & 0 & 3 \\ 1 & 2 & -2  \end{array} \right|
\\ & = -13
\end{align*}\]となるので、\[
dxdydz = 13 \ dpdqdr
\]の関係式が成り立つことがわかります。

(2) よく出る変数変換1　球面座標への変換

球面座標への変換とは、\[
\left\{\begin{array}{l} x = r \sin \theta \cos \phi \\ y = r \sin \theta \sin \phi \\ z = r \cos \theta    \end{array}\right.
\]のような変換を表します。

（※ただし \( 0 \leqq r \),  \( 0 \leqq \theta \leqq \pi \),  \( 0 \leqq \phi \leqq 2 \pi \) です。\( \phi \) は1周分の積分だが、\( \theta \) は1周分ではない点に注意。）

球面変換を図で表してみましょう。

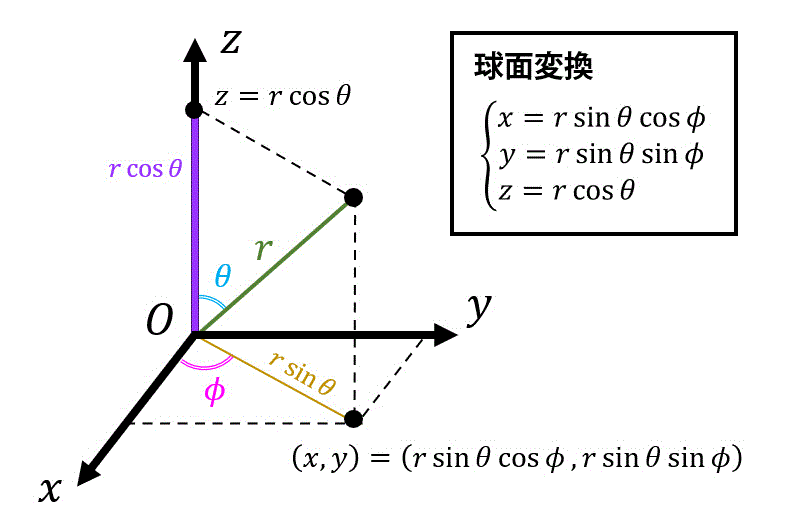
このときのヤコビアン \( J \) は\[\begin{align*}
J & =  \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \phi}  \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \phi} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \phi}  \end{array} \right|
\\ & =  \left| \begin{array}{ccc} \sin \theta \cos \phi & r \cos \theta \cos \phi & - r \sin \theta \sin \phi \\ \sin \theta \sin \phi & r \cos \theta \sin \phi & r \sin \theta \cos \phi \\ \cos \theta & - r \sin \theta & 0  \end{array} \right|
\\ & = r^2 \sin \theta \cos^2 \theta \cos^2 \phi + r^2 \sin^3 \theta \sin^2 \phi + r^2 \sin \theta \cos^2 \theta \sin^2 \phi + r^2 \sin^3 \theta \cos^2 \phi
\\ & = r^2 \sin \theta \left( \cos^2 \theta \cos^2 \phi + \sin^2 \theta \sin^2 \phi + \cos^2 \theta \sin^2 \phi + \sin^2 \theta \cos^2 \phi \right)
\\ & = r^2 \sin \theta \left( \cos^2 \theta + \sin^2 \theta  \right) \left( \cos^2 \phi + \sin^2 \phi  \right)
\\ & = r^2 \sin \theta
\end{align*}\]と計算できるので、ヤコビアンは \( r^2 \sin \theta \) となり、\[
dxdydz = r^2 \sin \theta \ dr d \theta d \phi
\]の関係式が成り立ちます。

1回自分で導出してみるとわかるのですが、かなり計算がえげつないのでヤコビアン \( r^2 \sin \theta \) は覚えておくことをつよくおすすめします。

球面座標への変数変換は、積分領域に \( x^2 + y^2 + z^2 \leqq a^2 \) のように \( x^2 + y^2 + z^2 \) が含まれる形のときに使われることが多いです。

積分範囲に \( x^2 + y^2 + z^2 \) が含まれている場合、球面変換をすることを疑ってください*4。

例題で球面座標の変換に慣れておきましょう。

解説3

積分領域が \( x^2 + y^2 + z^2 \) の形で設定されているので、\[
\left\{\begin{array}{l} x = r \sin \theta \cos \phi \\ y = r \sin \theta \sin \phi \\ z = r \cos \theta    \end{array}\right.
\]の変数変換をしましょう。

ここで、\( z \geqq 0 \)、つまり \( r \cos \theta \geqq 0 \) なので、\( \cos \theta \geqq 0 \) という制限が入りますね*5。

また、\[
x^2+y^2+z^2 = r^2 \leqq 1
\]より*6、変換後の積分領域 \( V' \) は\[
V' = \left\{ (r,\theta,\phi) \ \middle| 0 \leqq r \leqq 1 , \ 0 \leqq \theta \leqq \frac{\pi}{2} , \ 0 \leqq \phi \leqq 2 \pi \right\}
\]となります。

あとは、積分領域が \( r \), \( \theta \), \( \phi \) ともに定数範囲になったので3つの定積分に分解して解くだけでOK。

ヤコビアン \( r^2 \sin \theta \) の存在もお忘れなく。

すると、\[\begin{align*}
\iiint_V 1 \ dxdydz & = \iiint_{V'} r^2 \sin \theta  \ drd \theta d \phi
\\ & = \int^{1}_{0} r^2 \ dr \cdot \int^{\frac{\pi}{2}}_{0} \sin \theta \ d \theta \cdot \int^{2 \pi}_{0} 1 \ phi
\\ & = \left[ \frac{1}{3} r^3 \right]^{1}_{0} \cdot \left[ - \cos \theta \right]^{\frac{\pi}{2}}_{0} \cdot \left[ \phi \right]^{2 \pi}_{0}
\\ & = \frac{1}{3} \cdot 1 \cdot 2 \pi
\\ & = \frac{2}{3} \pi
\end{align*}\]と答えが求まります。

(3) よく出る変数変換2　円柱座標への変換

円柱座標への変換とは、\[
\left\{\begin{array}{l} x = r \cos \theta  \\ y = r \sin \theta \\ z = z   \end{array}\right.
\]のような変換を表します。

（※ただし \( 0 \leqq r \),  \( 0 \leqq \theta \leqq 2 \pi \)。\( \theta \) は1周分。）

円柱変換を図で表してみましょう。

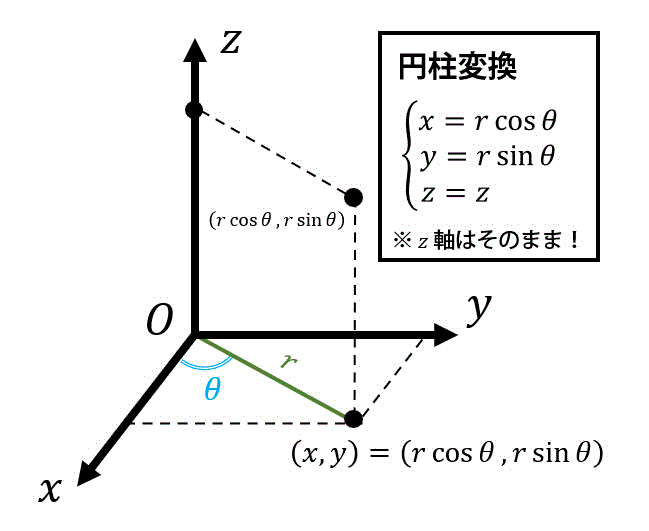
 \( xy \) 平面は極座標変換、\( z \) 軸に関しては一切変換をしません。

そのため、高さを変えない極座標変換だと思っていただけたらOKです。

このときのヤコビアン \( J \) は\[\begin{align*}
J & =  \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z}  \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}  \end{array} \right|
\\ & =  \left| \begin{array}{ccc} \cos \theta  & - r \sin \theta & 0 \\ \sin \theta & r \cos \theta & 0  \\ 0 & 0 & 1  \end{array} \right|
\\ & =  \left| \begin{array}{ccc} \cos \theta  & - r \sin \theta \\ \sin \theta & r \cos \theta   \end{array} \right|
\\ & = r \cos^2 \theta +r \sin^2 \theta
\\ & = r \left( \sin^2 \theta + \cos^2 \theta \right)
\\ & = r
\end{align*}\]と計算できるので、ヤコビアンは \( r \) となり、\[
dxdydz =r \ dr d \theta d z
\]の関係式が成り立ちます。

以下のような3重積分の場合、円柱変換をする可能性があります。

• 積分範囲に \( x^2 + y^2 \) が含まれている
• \( x^2 + y^2 + z^2 \) が式や積分範囲にあり、球面変換をしてもうまくいかない

この2パターンに当てはまった場合は「円柱変換をするかも…？」と思ってください。

では、円柱変換を行う例題を見てみましょう。

解説4

積分範囲に \( x^2 + y^2 \) が含まれているので、円柱変換\[
\left\{\begin{array}{l} x = r \cos \theta \\ y = r \sin \theta \\ z = z    \end{array}\right.
\]をしましょう。

ここで、\( x^2 + y^2 \leqq 2 \) なので、\( 0 \leqq r \leqq \sqrt{2} \) となりますね。

また、\( 0 \leqq z \leqq \sqrt{x^2+y^2} \) なので、\( 0 \leqq z \leqq r \) も成り立ちますね。

よって、領域変換後の積分領域 \( V' \) は\[
V' = \left\{ (r,\theta,\phi) \ \middle| 0 \leqq r \leqq \sqrt{2} , \ 0 \leqq \theta \leqq 2 \pi , \ 0 \leqq z \leqq r  \right\}
\]となります。

すると、\[\begin{align*}
\iiint_V (x^2+y^2) z^3 \ dxdydz & = \iiint_{V'} r^2 z^3 \cdot r  \ drd \theta dz
\\ & = \int^{2 \pi}_{0} \left( \int^{\sqrt{2}}_{0} r^3 \left( \int^{r}_{0} z^3  \ dz \right) \ d r \right) \ d \theta
\\ & = \int^{2 \pi}_{0} \left( \int^{\sqrt{2}}_{0} r^3 \left[ \frac{1}{4} z^4 \right]^{r}_{0} \ dr \right) \ d \theta
\\ & = \frac{1}{4} \int^{2 \pi}_{0} \left( \int^{\sqrt{2}}_{0} r^7  \ dr \right) \ d \theta
\\ & = \frac{1}{4} \int^{2 \pi}_{0} \left[ \frac{1}{8} r^8 \right]^{ \sqrt{2} }{0} \ d \theta
\\ & = \frac{1}{32} \int^{2 \pi}_{0} 16 \ d \theta
\\ & = \frac{1}{32} \cdot 32 \pi
\\ & = \pi
\end{align*}\]と答えが求まります。

５．練習問題

では、何問か練習問題を用意したのでチャレンジしてみましょう。

練習1

つぎの3重積分の値を計算しなさい。\[
\iiint_V z \ dxdydz \]\[
V = \{ (x,y,z) \ \mid 0 \leqq x \leqq y \leqq z \leqq 1 \}
\]

練習2

つぎの3重積分の値を計算しなさい。\[
\iiint_V e^{x+y+z} \ dxdydz \]\[
V = \{ (x,y,z) \ \mid  0 \leqq x , \ 0 \leqq y , \ 0 \leqq z , \ x+y+z \leqq 2 \}
\]

練習3

つぎの3重積分の値を計算しなさい。\[
\iiint_V z \ dxdydz \]\[
V = \{ (x,y,z) \ \mid 0 \leqq x , \ 0 \leqq y , \ 0 \leqq z  , \ x^2 + y^2 + z^2 \leqq 4 \}
\]

練習4 [難問]

つぎの3重積分の値を計算しなさい。\[
\iiint_V 1 \ dxdydz \\
V = \{ (x,y,z) \ \mid x^2 + y^2 \leqq x  , \ x^2 + y^2 + z^2 \leqq 1 \}
\]

６．練習問題の答え

解答1

積分順序によって計算量が結構変わります。

おすすめの積分順序(1)と、例題2と同じ積分順序で計算するパターン両方を紹介したいと思います。

(1) \( x \), \( y \), \( z \) の順で積分する方法 [おすすめ]

まず、\( 0 \leqq x \leqq y \leqq z \leqq 1 \) より \( 0 \leqq x \leqq y \) となることがわかる。

また、残りの2変数の積分領域 \( D \) は、\( 0 \leqq x \), \( y+z \leqq 1 \) より\[
D =  \{ (y,z) \ \mid 0 \leqq y \leqq z \leqq 1 \}
\]となります。

さらに積分領域 \( D \) は \( 0 \leqq y \leqq z \) より\[
D =  \{ (y,z) \ \mid 0 \leqq y \leqq z , \ 0 \leqq z \leqq 1 \}
\]と分解ができます。

よって、\[\begin{align*}
\iiint_V z \ dxdydz & =  \iint_D \left( \int^{y}_{0} z \ dx \right) \ dydz
\\ & = \iint_D z \left[ x \right]^{y}_{0} \ dydz
\\ & = \iint_D yz \ dydz
\\ & = \int^{1}_{0} \left( \int^{z}_{0} yz \ dy \right) dz
\\ & = \int^{1}_{0} z \left[ \frac{1}{2} y^2 \ dy \right]^{z}_{0} \ dz
\\ & = \frac{1}{2} \int^{1}_{0} z^3 \ dz
\\ & = \frac{1}{2} \left[ \frac{1}{4} z^4 \right]^{1}_{0}
\\ & = \frac{1}{8}
\end{align*}\]と計算できます。

(2) \( z \), \( y \), \( x \) の順で積分する方法 [ちょい大変]

計算量を比較するために、こちらの方法でもやってみましょう。

\( 0 \leqq x \leqq y \leqq z \leqq 1 \) に注目すると \( z \) の積分範囲は \( y \leqq z \leqq 1 \) となります。

また、残りの2変数の積分領域 \( D \) は、 \( z \leqq 1 \) より\[
D =  \{ (y,z) \ \mid 0 \leqq x \leqq y \leqq 1 \}
\]となります。

さらに積分領域 \( D \) は \( x \leqq y \leqq 1\) より\[
D =  \{ (y,z) \ \mid x \leqq y \leqq 1 , \ 0 \leqq x \leqq 1 \}
\]と分解ができます。

よって、\[\begin{align*}
\iiint_V z \ dxdydz & =  \iint_D \left( \int^{1}_{y} z \ dz \right) \ dxdy
\\ & = \iint_D \left[ \frac{1}{2} z^2 \right]^{1}_{y} \ dxdy
\\ & = \frac{1}{2} \iint_D 1 - y^2 \ dxdy
\\ & = \frac{1}{2} \int^{1}_{0} \left( \int^{1}_{x} \frac{1}{x} 1 - y^2 \ dy \right) dx
\\ & = \frac{1}{2}  \int^{1}_{0} \left[ y - \frac{1}{3} y^3 \ dy \right]^{1}_{x} \ dx
\\ & = \frac{1}{2} \int^{1}_{0} \frac{2}{3} - x + \frac{1}{3} x^3 dz
\\ & = \frac{1}{2} \left[ \frac{2}{3} x - \frac{1}{2} x^2 + \frac{1}{12} x^4 \right]^{1}_{0}
\\ & = \frac{1}{2} \left( \frac{2}{3} - \frac{1}{2} + \frac{1}{12} \right)
\\ & = \frac{1}{2} \cdot \frac{1}{4}
\\ & = \frac{1}{8}
\end{align*}\]と計算できます。

解答2

積分範囲の分解の仕方は例題2とほぼ同じです。

\( z \), \( y \), \( x \) の順に積分しましょうか。

\( x + y + z \leqq 2 \) を \( z \) 中心の形にすると、\( z \leqq 2 - x - y \) となります。

また、\( 0 \leqq z \) なので、\( z \) の積分範囲は\[
0 \leqq z \leqq 2-x-y
\]となります。

ここで、\[
0 < x + y < 2 - z
\]の範囲を \( z \) を使わずに表すことを考えましょう。

\( z \) の範囲は \( z \geqq 0 \) なので、\( x + y < 2 \) となるので、残りの2重積分の積分範囲 \( D \) は\[
D = \{ (x,y) \ \mid  0 \leqq x , \ 0 \leqq y , \ x+y \leqq 2 \}
\]となります。

さらに \( D \) の積分範囲を分解していくと、\[
D =  \{ (x,y) \ \mid  0 \leqq x \leqq 2, \ 0 \leqq y \leqq 2 - x \}
\]となります。

よって、\[\begin{align*}
\iiint_V e^{x+y+z} \ dxdydz & =  \iint_D \left( \int^{2-x-y}_{0} e^{x+y+z} \ dz \right) \ dxdy
\\ & = \iint_D \left[ e^{x+y+z} \right]^{2-x-y}_{0} \ dxdy
\\ & = \iint_D e^{2} - e^{x+y} \ dxdy
\\ & = \int^{2}_{0} \left( \int^{2-x}_{0} e^{2} - e^{x+y} \ dy \right) dx
\\ & = \int^{2}_{0} \left[ x e^{2} - e^{x+y} \ dy \right]^{2-x}_{0} \ dx
\\ & = \int^{2}_{0} (2-x) e^{2} - e^2 + e^x
\\ & = \int^{2}_{0} e^x + e^2 - e^{2} x
\\ & = \left[ e^x + e^2 x - \frac{1}{2} e^2 x^2 \right]^{2}_{0}
\\ & = e^2 + 2e^2 - 2e^2 - 1
\\ & = e^2 - 1
\end{align*}\]と計算できます。

解答3

積分領域が \( x^2 + y^2 + z^2 \) の形で設定されているので、\[
\left\{\begin{array}{l} x = r \sin \theta \cos \phi \\ y = r \sin \theta \sin \phi \\ z = r \cos \theta    \end{array}\right.
\]の変数変換をしましょう。

まず、\( x^2 + y^2 + z^2 = r^2 \leqq 4 \) より \( 0 \leqq r \leqq 2 \) という制限が入ります。

つぎに、\( z = r \cos \theta \geqq 0 \)、\( \cos \theta \geqq 0 \) という条件が領域にありますね。よって、\( 0 \leqq \theta \leqq \pi / 2 \) の制限が入ります。

さらに \( x = r \sin \theta \cos \phi \geqq 0 \), \( y = r \sin \theta \sin \phi \geqq 0 \) という条件も領域に入りますね。

ここで、\( r \geqq 0 \), \( \sin \theta \geqq 0 \) なので、\( \cos \phi \geqq 0 \), \( \sin \phi \geqq 0 \) を満たすような \( \phi \) は \( 0 \leqq \theta \leqq \phi / 2 \) となります*7。

よって、新たな積分領域 \( V' \) は\[
V' = \left\{ (r,\theta,\phi) \ \middle| \ 0 \leqq r \leqq 2 , \ 0 \leqq \theta \leqq \frac{\pi}{2} , \ 0 \leqq \phi \leqq \frac{ \pi }{2} \right\}
\]となります。

ヤコビアン \( r^2 \sin \theta \) の存在もお忘れなく。

よって、\[\begin{align*}
\iiint_V z \ dxdydz & = \iiint_{V'} r \cos \theta \cdot r^2 \sin \theta  \ drd \theta d \phi
\\ & = \int^{2}_{0} r^3 \ dr \cdot \int^{\frac{\pi}{2}}_{0} \sin \theta \cos \theta \ d \theta \cdot \int^{ \frac{\pi}{2} }_{0} 1 \phi
\end{align*}\]を解けば答えが求まりますね。

ここで、それぞれの積分は\[\begin{align*}
\int^{2}_{0} r^3 \ dr & = \left[ \frac{1}{4} r^4 \right]^{2}_{0}
\\ & = 4
\end{align*}\]\[\begin{align*}
\int^{ \frac{\pi}{2} }_{0} \sin \theta \cos \theta \ d \theta & = \frac{1}{2} \int^{ \frac{\pi}{2} }_{0} \sin 2 \theta \ d \theta
\\ & = \frac{1}{2} \left[ - \frac{1}{2} \cos 2 \theta \right]^{\frac{\pi}{2}}_{0}
\\ & = \frac{1}{2}
\end{align*}\]\[\begin{align*}
\int^{ \frac{\pi}{2} }_{0} 1 \ d \phi = \frac{\pi}{2}
\end{align*}\]と計算できる*8。

よって、\[\begin{align*}
\iiint_V z \ dxdydz & =  \int^{2}_{0} r^3 \ dr \cdot \int^{\frac{\pi}{2}}_{0} \sin \theta \cos \theta \ d \theta \cdot \int^{ \frac{\pi}{2} }_{0} 1 \ \phi
\\ & = 4 \cdot \frac{1}{2} \cdot \frac{\pi}{2}
\\ & = \pi
\end{align*}\]となる。

解答4

積分領域が \( x^2 + y^2 + z^2 \) の形で設定されているので、\[
\left\{\begin{array}{l} x = r \sin \theta \cos \phi \\ y = r \sin \theta \sin \phi \\ z = r \cos \theta    \end{array}\right.
\]の変数変換をしようと変形すると、\[
x^2 +y^2 \leqq x  \\
r^2 \sin \theta  \leqq r \cos \theta \\
r \sin \theta \leqq \cos \theta \\
r \leqq \frac{ \cos \theta }{ \sin \theta } = \frac{1}{ \tan \theta }
\]となるため、しんどそうな積分になりそうな気がしますね。

そこで、円柱変換\[
\left\{\begin{array}{l} x = r \cos \theta \\ y = r \sin \theta \\ z = z    \end{array}\right.
\]をしてみましょう。

すると、\( x^2 + y^2 \leqq x \) を \( r^2 \leqq r \cos \theta \) と変形できるので、\( r \geqq 0 \) より、\( r \leqq \cos \theta \) が成立します。

よって、\( r \) の積分範囲は \( 0 \leqq r \leqq \cos \theta \) となります。

さらに、\( 0 \leqq \cos \theta \) より、\( \theta \) の積分範囲は \( - \pi / 2 \leqq \theta \leqq \pi / 2 \) となります。

また、\[
x^2 + y^2 + z^2 = r^2 + z^2 \leqq 1
\]より、\[
z^2 \leqq 1 - r^2 \\
- \sqrt{1 - r^2} \leqq z \leqq \sqrt{1 - r^2}
\]と \( z \) の積分範囲が決まります。（\( r \) と異なり正でなくてもよいため、負の範囲が入ることに注意！）

よって、新たな積分領域 \( V' \) は\[
V' = \left\{ (r,\theta, z) \ \middle| \ 0 \leqq r \leqq \cos \theta , \ - \frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2} , \ - \sqrt{1 - r^2} \leqq z \leqq \sqrt{1 - r^2} \right\}
\]

となる。

また、以下の2つの条件を考慮するために \( z \), \( r \), \( \theta \) の順に積分をする必要がある。

• \( \theta \) の積分前に \( r \) を積分
  （\( r \) の範囲に \( \theta \) が含まれているため）
• \( \ r \) の積分前に \( z \) を積分
  （\( z \) の積分範囲に \( r \) が含まれているため）

ヤコビアン \( r \) も忘れずに。

よって、\[\begin{align*}
\iiint_V 1 \ dxdydz & = \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \left( \int^{ \cos \theta }_{0} \left( \int^{ \sqrt{1 - r^2} }_{ - \sqrt{1-r^2} } r \ dz \right) dr \right) d \theta
\\ & =  \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \left( \int^{ \cos \theta }_{0} 2r \sqrt{ 1 - r^2 } dr \right) d \theta
\\ & =  \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \left[ - \frac{2}{3} ( 1 - r^2 )^{ \frac{3}{2} } \right]^{ \cos \theta }_{0} d \theta
\\ & =  \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } - \frac{2}{3} \left(  ( \cos^2 - 1 )^{ \frac{3}{2} } - 1 \right)    d \theta
\\ & =  \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} }  \frac{2}{3} \left(  ( 1 - \cos^2 )^{ \frac{3}{2} } - 1 \right)    d \theta
\\ & = \frac{2}{3} \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } 1 - | \sin^3 \theta |    d \theta
\\ & = \frac{4}{3} \int^{ \frac{\pi}{2} }_{ 0 } 1 - \sin^3 \theta  \  d \theta
\\ & = \frac{4}{3} \int^{ \frac{\pi}{2} }_{ 0 } 1 -\frac{1}{4} ( 3 \sin \theta - \sin 3 \theta )  \  d \theta
\\ & = \frac{4}{3} \left[ \theta + \frac{3}{4} \cos \theta - \frac{1}{12} \cos 3 \theta   \right]^{ \frac{\pi}{2} }_{ 0 }
\\ & = \frac{4}{3} \left( \frac{\pi}{2} - \left( \frac{3}{4} - \frac{1}{12} \right) \right)
\\ & = \frac{4}{3} \left( \frac{\pi}{2} - \frac{2}{3} \right)
\\ & =  \frac{2}{3} \pi - \frac{8}{9}
\end{align*}\]と計算できる*9。

注意点としては、\[\begin{align*}
\left( 1 - \cos^2 \theta \right)^{ \frac{3}{2} } & = | \sin^3 \theta |
\\ & \neq \sin^3 \theta
\end{align*}\]があります。絶対値の存在を忘れないようにしましょう。

\[
\int^{ \frac{\pi}{2} }_{ \frac{\pi}{2} } | \sin^3 \theta | \neq \int^{ \frac{\pi}{2} }_{ \frac{\pi}{2} }  \sin^3 \theta
\]ですからね。

７．さいごに

今回は、3重積分について説明しました。

最後に、3重積分について重要なポイントを5つおさらいしておきましょう。

• 2重積分より積分する変数が1つ増えただけ
• すでに積分した変数を積分しなければ、積分の順序は任意
• 範囲が複雑であれば式を変形して定積分＋残りの領域で2重積分の形に。
• 球面変換のヤコビアンは \( r^2 \sin \theta \)、\( \theta \) の範囲は1周分ではなく、\( 0 \leqq \theta \leqq \pi \)
• 円柱変換のヤコビアンは \( r \)、極座標変換＋高さを変化させない変換だと思えばOK

うさぎでもわかる解析は今回が最終回となります。

Part28までお付き合いいただき、ありがとうございました！