スポンサードリンク
こんにちは、ももやまです。
前回(Part3)では複素関数の収束半径を求めたり、べき級数の収束円内における総和を求める方法を説明しました。
今回はある複素関数をマクローリン展開・テイラー展開してべき級数展開する方法について簡単にですがまとめていきたいと思います。
前回のうさぎでもわかる複素関数(Part3)はこちら!
収束半径やべき級数の総和(マクローリン展開・べき級数展開の逆)の方法をまとめているので、まだ収束半径がよくわかっていない人はこちらの記事で復習しましょう。
スポンサードリンク
1.複素関数のマクローリン展開
複素関数も実数関数と同じようにマクローリン展開をすることができます! しかも実数関数とそっくりなのです!
もし実数関数のマクローリン展開ってどんなのだっけとか忘れちゃったという人は下の記事でいったん復習しましょう。
複素関数のマクローリン展開の公式は下に示しておきます。
複素関数 \( f(z) \) が \( |z| \lt R \) (収束円内)で収束するとき、\[ \begin{align*}
f(z) & = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} z^n
\\ & = f(0) + \frac{f'(0)}{1!} z + \frac{f''(0)}{2!} z^2 + \frac{f'''(0)}{3!} z^3 + \cdots + \frac{f^{(n)}(0)}{n!} z^n + \cdots
\end{align*} \]
とマクローリン展開することができる。
実数のマクローリン展開とそっくりですよね!
しかし1つ異なるのは、実数関数 \( f(x) \) のマクローリン展開は \( f(x) \) が無限回微分可能であることが条件となっているのに対し、複素関数は無限回微分可能であることは条件には入っていませんよね。
実は複素関数の場合は、1回でも微分できるような複素関数は、必ず無限回微分することができるのです!
(実数関数だと1回微分できたからといって無限回微分できるとは限りませんよね。)
なので1回でも微分できるような複素関数はマクローリン展開することができるのです!
代表的な複素関数のマクローリン展開を紹介します。
主要な複素関数のマクローリン展開(べき級数展開)とその収束半径 \( R \) は以下のようになる。\[
\frac{1}{1-z} = \sum^{\infty}_{n = 0} z^n = 1 + z + z^2 + z^3 + \cdots \ \ \ \left( R = 1 \right) \\
e^z = \sum^{\infty}_{n = 0} \frac{1}{n!} z^n = 1 + z + \frac{1}{2!} z^2 + \frac{1}{3!} z^3 + \cdots \ \ \ \left( R = \infty \right) \\
\sin z = \sum^{\infty}_{n = 0} \frac{(-1)^n}{(2n)!} z^{2n} = z - \frac{1}{3!} z^3 + \frac{1}{5!} z^5 - \cdots \ \ \ \left( R = \infty \right) \\
\cos z = \sum^{\infty}_{n = 0} \frac{(-1)^n}{(2n+1)!} z^{2n} = 1 - \frac{1}{2!} z^2 + \frac{1}{4!} z^4 - \cdots \ \ \ \left( R = \infty \right) \\
\]
特に\[
\frac{1}{1-z} = 1 + z + z^2 + z^3 + \cdots
\]は頻繁に使うのでぜひ頭にいれておきましょう!
スポンサードリンク
2.複素関数のテイラー展開
原点 \( z = 0 \) 以外でもべき級数展開を行うことができます。この展開を \( z = a \) まわりのテイラー展開と呼びます。
(マクローリン展開は原点 \( z = 0 \) まわりのテイラー展開です)
複素関数 \( f(z) \) が \( |z-a| \lt R \)(収束円内)で収束するとき、\[ \begin{align*}
f(x) & = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (z-a)^n
\\ & = f(a) + \frac{f'(a)}{1!} (z-a) + \frac{f''(a)}{2!}(z-a)^2 + \frac{f'''(a)}{3!}(z-a)^3 + \cdots
\end{align*} \]
と \( z = a \) まわりでテイラー展開することができる。
マクローリン展開と同じく、1回でも微分できるような複素関数はテイラー展開することができます!
スポンサードリンク
3.べき級数の収束半径
例えば、複素関数\[
f(z) = \frac{1}{1-z}
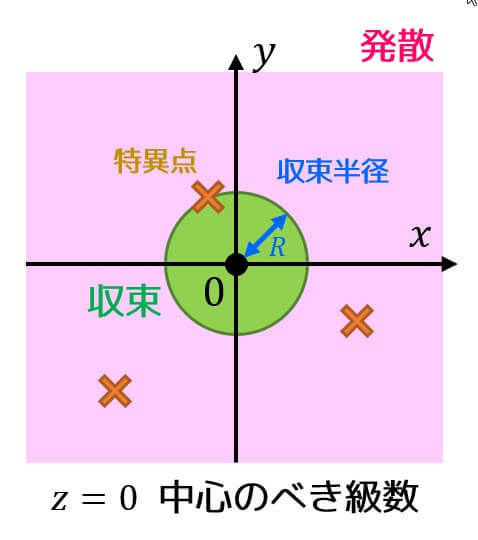
\]は、\( z = 1 \) のとき、分母が0になり、定義されませんね。このような点のことを特異点と呼びます。
マクローリン展開やテイラー展開で求めたべき級数の収束半径は展開の中心から最も近い特異点までの距離となるのでわざわざダランベールの公式などを適用しなくても簡単に求めることができます。
イメージ図を用意しました
(Part3と同じ図です。また、\( x \) 軸が実軸、\( y \) 軸が虚軸です。)
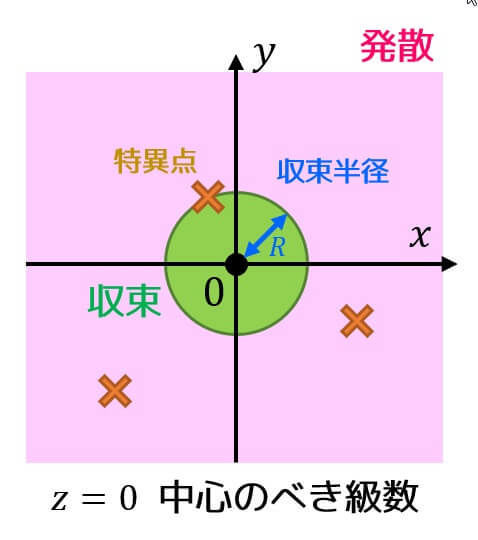
例えば、べき級数\[
\frac{1}{1-z}
\]の特異点は \( z = 1 \) なので、展開の中心(原点 \( z = 0 \))からの距離が1となり、収束半径 \( R = 1 \) を導くことができます。
ここで1問例題を解いてみましょう。
例題
複素関数\[
f(z) = \frac{1}{1+4z}
\]をべき級数展開し、さらにべき級数の収束半径を求めなさい。
解説
方法は2パターン
その1:\( n \) 次導関数を使って求める
\( f(z) \) の \( n \) 次導関数を求める\[
f(z) = (1+4z)^{-1}
\]なので、\[
f(0) = 1 \\
f'(z) = 1 \cdot (-4) (1+4z)^{-2} \ \ \ \ f'(0) = -4 \\
f''(z) = 2 \cdot 16 (1+4z)^{-3} \ \ \ f''(0)= 2 \cdot 16 \\
f'''(z) = 6 \cdot (-64) (1+4z)^{-4} \ \ \ f'''(0) = 6 \cdot (-64) \\
f^n (z) = n! \cdot (-4)^n (1+4z)^{-1-n} \ \ \ f^n (0) = n! \cdot (-4)^n
\]となるのでべき級数展開は、\[ \begin{align*}
f(z) & = 1 - 4z + 16z^2 - 64z^3 + \cdots
\\ & = \sum_{n=0}^{\infty} (-4)^n z^n
\end{align*} \]となる。
その2:すでにある公式を利用
マクローリン展開公式\[
\frac{1}{1-z} = \sum^{\infty}_{n = 0} z^n = 1 + z + z^2 + z^3 + \cdots
\]を利用します。
この \( z \) を \( -4z \) に置き換えると、\[\begin{align*}
\frac{1}{1-(-4z)} & =
\frac{1}{1+4z} \\ & = \sum^{\infty}_{n = 0} (-4)^n z^n = 1 - 4z + 16 z^2 - 64 z^3 + \cdots
\end{align*} \]
べき級数の収束半径
また、べき級数の収束半径は展開の中心(原点)から最も近い特異点までの距離である。ここで特異点は \( 1 + 4z = 0 \) より \( z = -1/4 \) に存在する。よって収束半径 \( R \)は\[
R = \frac{1}{4}
\]となる。
ダランベールの公式で確認
本当に収束半径が 1/4 になるのかをダランベールの公式で確認してみましょう。\[
R = \lim_{n \to \infty} \left| \frac{ c_n }{ c_{n+1} } \right| = \lim_{n \to \infty} \left| \frac{ (-4)^n }{ (-4)^{n+1} } \right| = \frac{1}{4}
\]より、たしかに \( R = 1/4 \) となりますね!
4.練習問題
では2問だけですが練習してみましょう。
練習1
複素関数\[
f(z) = \frac{1}{(a+z)^3}
\]をべき級数展開(マクローリン展開)し、さらにべき級数の収束半径を求めなさい。
練習2
複素関数\[
f(z) = \frac{1}{(a+bz)^2}
\]をべき級数展開(マクローリン展開)し、さらにべき級数の収束半径を求めなさい。
5.練習問題の答え
解答1
まずは収束半径
べき級数の収束半径は展開の中心(原点)から最も近い特異点までの距離である。ここで特異点は \( (a+z)^3 = 0 \) より \( z = -a \) に存在する。よって収束半径 \( R \) は\[
R = a
\]となる。
その1:\( n \) 次導関数を使って求める
\( f(z) \) の \( n \) 次導関数を求める\[
f(z) = (a+z)^{-3}
\]なので、\[
f(0) = a^{-3} \\
f'(z) = -3 (a+z)^{-4} \ \ \ \ f'(0) = -3 a^{-4} \\
f''(z) = 12 (a+z)^{-5} \ \ \ f''(0)= 3 \cdot 4 a^{-5} \\
f'''(z) = -60 (a+z)^{-6} \ \ \ f'''(0) = -3 \cdot 4 \cdot 5 a^{-6} \\
f^n (z) = \frac{(-1)^n (n+2)!}{2(a+z)^{n+3}} \ \ \ f^n (0) = \frac{(n+2)!}{2a^{n+3}} (-1)^n
\]となるのでべき級数展開は、\[ \begin{align*}
f(z) & = \frac{1}{a^3} - \frac{3}{a^4} z + \frac{6}{a^5} z^2 - \frac{10}{a^6} z^3 + \cdots + \frac{(n+2)!}{n! \cdot 2a^{n+3}} (-1)^n z^n + \cdots
\\ & = \sum_{n=0}^{\infty} \frac{ (-1)^n (n+2)(n+1)}{2a^{n+3}} z^n
\end{align*} \]となる。
その2:すでにある公式を利用
公式\[
\frac{1}{1-z} = \sum^{\infty}_{n = 0} z^n = 1 + z + z^2 + z^3 + \cdots
\]を2回微分します。
収束半径内なら項別微分できるので、\[\begin{align*}
\frac{d}{dz} \frac{1}{1-z} & = \frac{1}{(1-z)^2}
\\ & = \frac{d}{dz} (1 + z + z^2 + z^3 + z^4 + \cdots z^n + \cdots)
\\ & = 1 + 2z + 3z^2 + 4z^3 + \cdots + (n+1) z^n + \cdots
\end{align*} \]となる。
さらにもう1回項別微分すると、\[\begin{align*}
\frac{d}{dz} \frac{1}{(1-z)^2} & = \frac{2}{(1-z)^3}
\\ & = \frac{d}{dz} (1 + 2z + 3z^2 + 4z^3 + \cdots + (n+1) z^n + \cdots)
\\ & = 2 + 2 \cdot 3z + 3 \cdot 4z^2 + \cdots + (n+1)(n+2) z^n + \cdots
\end{align*} \]となる。
ここで、\( z \) を \( -z/a \) に置き換えると、\[\begin{align*}
\frac{2}{\left( 1- \left( -\frac{z}{a} \right) \right)^3 } & = \frac{2}{ \left( 1 + \frac{z}{a} \right)^3 }
\\ & = \frac{2}{ \left( \frac{a+z}{a} \right)^3 }
\\ & = \frac{2 a^3}{(a+z)^3}
\\ & = 2 + 2 \cdot 3 \left( - \frac{z}{a} \right) + 3 \cdot 4 \left( - \frac{z}{a} \right)^2 + \cdots + (n+1)(n+2) \left( - \frac{z}{a} \right)^n + \cdots
\\ & = 2 - \frac{2 \cdot 3}{a} z + \frac{3 \cdot 4}{a^2} z^2 - \cdots + \frac{(n+1)(n+2)}{a^n} z^n + \cdots
\end{align*}\]
となるので両辺を \( 2a^3 \) で割ると \( f(z) \) のべき級数展開は、\[ \begin{align*}
\frac{1}{(a+z)^3} & = \frac{1}{a^3} - \frac{3}{a^4} z + \frac{6}{a^5} z^2 - \frac{10}{a^6} z^3 + \cdots + \frac{(n+1) (n+2)}{ \cdot 2a^{n+3}} (-1)^n z^n + \cdots
\\ & = \sum_{n=0}^{\infty} \frac{ (-1)^n (n+2)(n+1)}{2a^{n+3}} z^n
\end{align*} \]と求めることができる。
解答2
まずは収束半径
べき級数の収束半径は展開の中心(原点)から最も近い特異点までの距離である。ここで特異点は \( (a+bz)^3 = 0 \) より \( z = -a/b \) に存在する。よって収束半径 \( R \) は\[
R = \frac{a}{b}
\]となる。
その1:\( n \) 次導関数を使って求める
\( f(z) \) の \( n \) 次導関数を求める\[
f(z) = (a+bz)^{-2}
\]なので、\[
f(0) = a^{-2} \\
f'(z) = -2b (a+bz)^{-3} \ \ \ \ f'(0) = -2b a^{-3} \\
f''(z) = 6b^2 (a+bz)^{-4} \ \ \ f''(0)= 2b^2 \cdot 3 a^{-4} \\
f'''(z) = -24 (a+bz)^{-5} \ \ \ f'''(0) = -2b^3 \cdot 3 \cdot 4 a^{-5} \\
f^n (z) = \frac{(-b)^n (n+1)!}{(a+bz)^{n+2}} \ \ \ f^n (0) = \frac{(n+1)!}{a^{n+2}} (-b)^n
\]となるのでべき級数展開は、\[ \begin{align*}
f(z) & = \frac{1}{a^2} - \frac{2b}{a^3} z + \frac{3b^2}{a^4} z^2 - \frac{4b^3}{a^5} z^3 + \cdots + \frac{(n+1)!}{n! \cdot a^{n+2}} (-b)^n z^n + \cdots
\\ & = \sum_{n=0}^{\infty} \frac{ (n+1)(-b)^n }{a^{n+2}} z^n
\end{align*} \]となる。
その2:すでにある公式を利用
公式\[
\frac{1}{1-z} = \sum^{\infty}_{n = 0} z^n = 1 + z + z^2 + z^3 + \cdots
\]を1回項別微分する。
収束半径内なら項別微分できるので、\[\begin{align*}
\frac{d}{dz} \frac{1}{1-z} & = \frac{1}{(1-z)^2}
\\ & = \frac{d}{dz} (1 + z + z^2 + z^3 + z^4 + \cdots z^n + \cdots)
\\ & = 1 + 2z + 3z^2 + 4z^3 + \cdots + (n+1) z^n + \cdots
\end{align*} \]となる。
ここで、\( z \) を \( -bz/a \) に置き換えると、\[\begin{align*}
\frac{1}{\left( 1- \left( -\frac{bz}{a} \right) \right)^2 } & = \frac{1}{ \left( 1 + \frac{bz}{a} \right)^2 }
\\ & = \frac{1}{ \left( \frac{a+bz}{a} \right)^2 }
\\ & = \frac{a^2}{(a+bz)^2}
\\ & = 1 + 2 \left( - \frac{bz}{a} \right) + 3 \left( - \frac{bz}{a} \right)^2 + \cdots + (n+1) \left( - \frac{bz}{a} \right)^n + \cdots
\\ & = 1 - \frac{2b}{a} z + \frac{3b^2}{a^2} z^2 - \cdots + \frac{(n+1) b^n}{a^n} z^n + \cdots
\end{align*}\]
となるので両辺を \( a^2 \) で割ると \( f(z) \) のべき級数展開は、\[ \begin{align*}
\frac{1}{(a+bz)^2} & = \frac{1}{a^2} - \frac{2b}{a^3} z + \frac{3b^2}{a^4} z^2 - \frac{4b^3}{a^5} z^3 + \cdots + \frac{(n+1) b^n}{a^{n+2}} (-b)^n z^n+ \cdots
\\ & = \sum_{n=0}^{\infty} \frac{ (-b)^n (n+1)}{a^{n+2}} z^n
\end{align*} \]と求めることができる。
6.さいごに
今回は複素関数をマクローリン展開やテイラー展開を行うことでべき級数展開する方法についてまとめました。
複素関数もほぼ実数関数と同じようにマクローリン展開ができるのでここの計算はほぼ実数の場合と同じです!
次回は複素関数ならではの展開として特異点まわりでの展開(ローラン展開)についてまとめていきたいと思います。
Next Part05 ローラン展開はこちら↓
関連広告・スポンサードリンク