スポンサードリンク
--- お詫び --- [2023/6/12追記]
すべての例題・練習問題の途中過程において、本来は\[
\frac{1}{1- \frac{z}{a} } = \frac{a}{a - z}
\]とすべきところを、\[
\frac{1}{1- \frac{z}{a} } = \frac{1}{a - z}
\]と誤って記載しておりました。大変申し訳ございません。
※ この誤りにつきましては、すべて修正し、正しい途中式に直しております。
-----------------------------------------------------------------------------------------------------
こんにちは、ももやまです。
前回(Part4)は複素数のマクローリン展開・テイラー展開について説明しましたね。
今回はテイラー展開をさらに拡張した複素関数ならではの展開方法としてローラン展開についてまとめていきたいと思います。
さらにローラン展開を用いた特異点の分類法についてもまとめています。
前回の記事はこちら!
ローラン展開を行うためにはマクローリン展開・テイラー展開の知識が必須なのでまだマクローリン展開・テイラー展開が理解できていない人はこちらの記事で復習しましょう。
目次
スポンサードリンク
1.ローラン展開
(1) ローラン展開とは
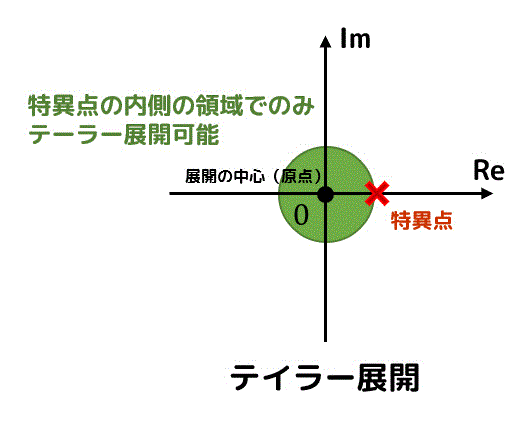
テイラー展開が可能な正則な点まわりでの級数展開に加えて、正則ではない点(特異点)まわりでも級数展開をできるようにしたものをローラン展開と呼びます。
テイラー展開可能な領域範囲
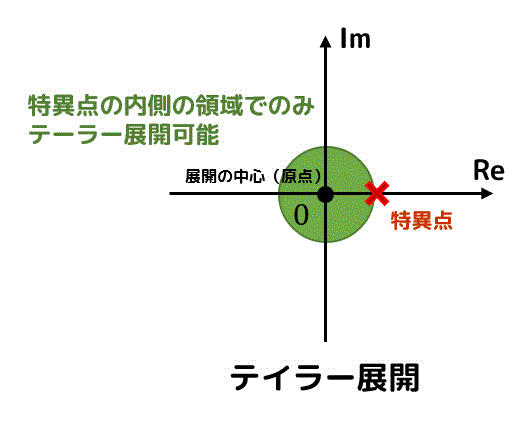
ローラン展開可能な領域範囲
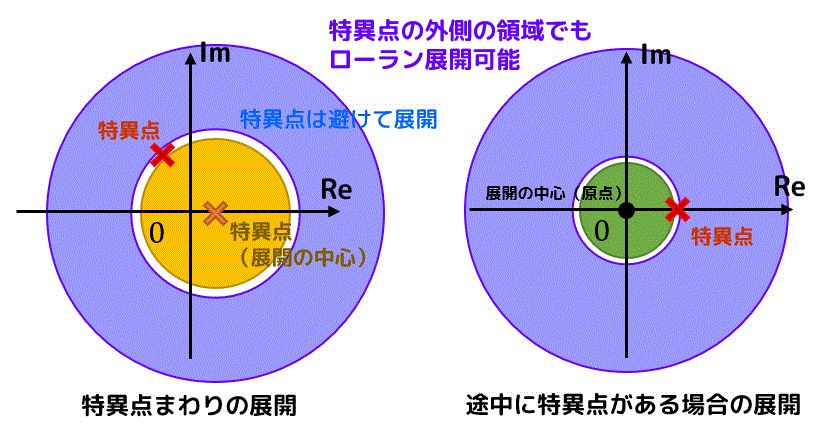
緑色の領域がテイラー展開・ローラン展開ともに可能な領域、黄色や紫色の領域がローラン展開のみ可能な領域を表します。
ただし、ローラン展開の場合でも領域内は正則である必要があります。
(領域内に特異点が含まれているなどで正則でない場合はローラン展開できません。)
テイラー展開:正則な点のまわりに限定した展開
ローラン展開:正則な点に限定しない展開
(ローラン展開は正則ではない点(特異点)まわりでも展開可能)
ローラン展開の公式を見てみましょう。

テイラー展開の部分に加えて負のべき乗の項 \( a_{-1} \), \( a_{-2} \), … が加わっているところがポイントです。この負のべき乗の項のことを特異部もしくは主要部と呼びます。
特異部(主要部)は正則ではない点を中心に展開した場合や、正則な点を中心に展開した場合でもテイラー展開では求められない特異点の外側の領域の点に対してローラン展開を行うと発生します。

逆にテイラー展開可能な領域(緑色部分)でローラン展開を行った場合は、主要部のすべての項が消えてテイラー展開とローラン展開の答えが同じになります。
(2) ローラン展開の求め方
テイラー展開を求めるときには、実際に複素関数を何回か微分していくことで求めましたね。
しかし、ローラン展開では正則ではない点のまわりでも展開を行うので微分でローラン展開を求めることができません。
その代わり、\[
\frac{1}{1-z} = \sum^{\infty}_{n = 0} z^n = 1 + z + z^2 + z^3 + \cdots \ \ \ \left( R = 1 \right)
\]のようなマクローリン展開の公式を使うことでローラン展開を求めることができます。
では1問実際にローラン展開を行ってみましょう。
例題1
つぎの複素関数\[
f(z) = \frac{ \cos z }{z^2}
\]を \( z = 0 \) を中心にローラン展開しなさい。
解説1
\( \cos z \) のマクローリン展開(\( z = 0 \) におけるテイラー展開)の公式は、\[
\cos z = \sum^{\infty}_{n = 0} \frac{(-1)^n}{(2n+1)!} z^{2n} = 1 - \frac{1}{2!} z^2 + \frac{1}{4!} z^4 - \cdots
\]なので \( z = 0 \) 中心のローラン展開は\[\begin{align*}
f(z) & = \frac{ \cos z }{z^2} \\ & = \frac{1}{z^2} \sum^{\infty}_{n = 0} \frac{(-1)^n}{(2n+1)!} z^{2n}
\\ & = \frac{1}{z^2} \left( 1 - \frac{1}{2!} z^2 + \frac{1}{4!} z^4 - \cdots + \frac{(-1)^n}{(2n+1)!} z^{2n} \right) + \cdots
\\ & = \frac{1}{z^2} - \frac{1}{2!} + \frac{1}{4!} z^2 - \cdots + \frac{(-1)^n}{(2n+1)!} z^{2n-2} + \cdots
\end{align*} \]となる。
(今回の場合は \( \frac{1}{z^2} \) が特異部になります。)
(3) 場合分けが必要なローラン展開
下の図のように展開の中心部分以外に何個かの特異点がある場合を考えます。
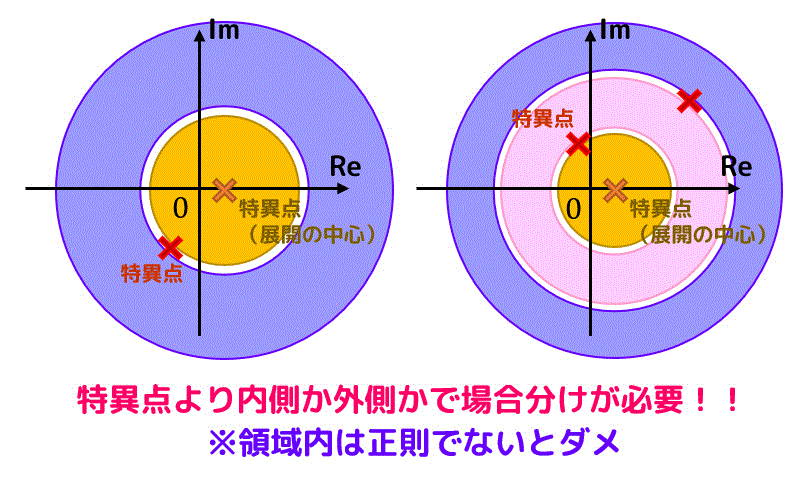
この場合、特異点の内側と外側でローラン展開が異なるので、それぞれの特異点の前後で場合分けを行う必要があります。
(例えば \( z = 0 \) 中心にローラン展開を行い、\( z = 1 \), \( z = 3 \) に特異点がある場合は \( 0 \lt |z| \lt 1 \), \( 1 \lt |z| \lt 3 \), \( 3 \lt |z| \) の3つに場合分けをする必要がある。)
また、領域内は正則である必要があるので、特異点をローラン展開の領域に含むことはできないので注意しましょう。
では1問実際に場合分けが必要なローラン展開を行ってみましょう。
例題2
つぎの複素関数\[
f(z) = \frac{1}{z(z-2)}
\]を \( z = 0 \) を中心にローラン展開しなさい。
解説2
特異点は \( z = 0 \), \( z = 2 \) の2か所にありますね。
\( z = 0 \) は展開の中心なので場合分けには影響しませんが、 \( z = 2 \) の前後で場合分けをする必要があります。
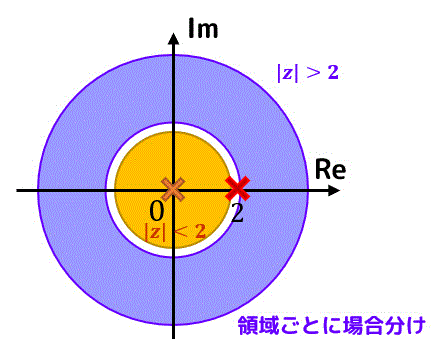
なので、\( 0 \lt |z| \lt 2 \) と \( 2 \lt |z| \) で場合分けをします。
( \( |z| = 2 \) は特異点が含まれてしまうのでローラン展開の領域には含めません)
(1) \( 0 \lt |z| \lt 2 \) のとき
\( |a| \lt 1 \) において\[
\frac{1}{1-a} = \sum^{\infty}_{n = 0} a^n = 1 + a + a^2 + a^3 + \cdots
\]なので、\( a \) を \( z/2 \) に変えると\[
\left| \frac{z}{2} \right| < 1 \ つまり \ \left| z \right| < 2
\]において、\[\begin{align*}
\frac{1}{1- \frac{z}{2} } & = \frac{2}{2-z}
\\ & = \sum^{\infty}_{n = 0} \left(\frac{z}{2} \right)^n
\\ & = 1 + \frac{1}{2} z + \frac{1}{4} z^2 + \frac{1}{8} z^3 + \cdots
\end{align*}\]となる。よって、\[\begin{align*}
f(z) & = \frac{1}{z(z-2)}
\\ & = \frac{1}{2z} \cdot \frac{2}{z-2}
\\ & = - \frac{1}{2z} \cdot \frac{2}{2-z}
\\ & = - \frac{1}{2z} \left(1 + \frac{1}{2} z + \frac{1}{4} z^2 + \frac{1}{8} z^3 + \cdots \right)
\\ & = - \frac{1}{2z} - \frac{1}{4} - \frac{1}{8} z - \frac{1}{16} z^2 - \cdots
\\ & = - \frac{1}{2z} \sum^{\infty}_{n = 0} \left(\frac{z}{2} \right)^n
\end{align*}\]となる。
(2) \( 2 \lt |z| \) のとき
\( 2 \lt |z| \) そのままの形だと\[
\frac{1}{1-a} = \sum^{\infty}_{n = 0} a^n = 1 + a + a^2 + a^3 + \cdots
\]の公式に当てはめることができません。そこで、\[
\frac{1}{|z|} = \left| \frac{1}{z} \right| < \frac{1}{2}
\]とし、2倍をすることで\[
\left| \frac{2}{z} \right| < 1
\]となるので\[\begin{align*}
\frac{1}{1- \frac{2}{z}}
& = \frac{1}{z} \left( 1 + \frac{2}{z} + \frac{4}{z^2} + \frac{8}{z^3} + \cdots \right)
\\ & = \frac{1}{z} \sum^{\infty}_{n = 0} \left( \frac{2}{z} \right)^n
\end{align*}\]と公式を適用することができる。(\( a \) が \( 2/z \) に変わっただけ)
よって、\[\begin{align*}
f(z) & = \frac{1}{z} \cdot \frac{1}{z-2}
\\ & = \frac{1}{z} \cdot \frac{1}{z} \cdot \frac{1}{1 - \frac{2}{z} }
\\ & = \frac{1}{z^2} \left( 1 + \frac{2}{z} + \frac{4}{z^2} + \frac{8}{z^3} + \cdots \right)
\\ & = \frac{1}{z^2} + \frac{2}{z^3} + \frac{4}{z^4} + \frac{8}{z^5} + \cdots
\\ & = \frac{1}{z^2} \sum^{\infty}_{n = 0} \left( \frac{2}{z} \right)^n
\end{align*}\]となる。
(1), (2) よりローラン展開は
\( 0 \lt |z| \lt 2 \) のとき\[
f(z) = - \frac{1}{2z} \sum^{\infty}_{n = 0} \left(\frac{z}{2} \right)^n
\]\( 2 \lt |z| \) のとき\[
f(z) = \frac{1}{z^2} \sum^{\infty}_{n = 0} \left( \frac{2}{z} \right)^n
\]となる。
[別解]
部分分数分解を使って分解する方法もあり\[
\frac{1}{z(z-2)} = - \frac{1}{2} \cdot \frac{1}{z} + \frac{1}{2} \cdot \frac{1}{z-2}
\]と部分分数分解を行う。
部分分数分解の方法を忘れてしまった人や不安な人はこちらから復習しましょう。
(1) \( 0 \lt |z| \lt 2 \) のとき
\[\begin{align*}
\frac{1}{1- \frac{z}{2} } & = \frac{2}{2-z}
\\ & = \sum^{\infty}_{n = 0} \left(\frac{z}{2} \right)^2
\end{align*}\]となる。よって、\[\begin{align*}
f(z) & = - \frac{1}{2} \cdot \frac{1}{z} + \frac{1}{2} \cdot \frac{1}{z-2}
\\ & = - \frac{1}{2} \cdot \frac{1}{z} - \frac{1}{4} \cdot \frac{2}{2-z}
\\ & = - \frac{1}{2z} - \frac{1}{4} \sum^{\infty}_{n = 0} \left(\frac{z}{2} \right)^2
\end{align*}\]となる。
(2) \( 2 \lt |z| \) のとき
\[\begin{align*}
\frac{1}{1- \frac{2}{z}}
& = \frac{1}{z} \left( 1 + \frac{2}{z} + \frac{4}{z^2} + \frac{8}{z^3} + \cdots \right)
\\ & = \frac{1}{z} \sum^{\infty}_{n = 0} \left( \frac{2}{z} \right)^n \ \ \ \left( \left| \frac{2}{z} \right| < 1 \right)
\end{align*}\]より、\[\begin{align*}
f(z) & = - \frac{1}{2z} + \frac{1}{2} \cdot \frac{1}{z-2}
\\ & = - \frac{1}{2z} + \frac{1}{2z} \cdot \frac{1}{1-\frac{2}{z} }
\\ & = - \frac{1}{2z} + \frac{1}{2z} \sum^{\infty}_{n = 0} \left( \frac{2}{z} \right)^n
\\ & = \frac{1}{2z} \sum^{\infty}_{n = 1} \left( \frac{2}{z} \right)^n
\end{align*}\]となる。
別解で解くと見た目の答えが別解ではない解き方と微妙に異なりますが、両方とも同じ答えなのでどちらで答えてもOKです。
(\( n = 0,1,2 \) くらいで実際に確かめると同じ答えになることがわかると思います。)
スポンサードリンク
2.特異点
(1) 特異点とは(復習)
複素関数 \( f(z) \) がある点 \( z = a \) において正則ではないとき、点 \( a \) のことを特異点と呼びましたね。例えば、\[
\frac{1}{z(z-2)}
\]は \( z = 0,2 \) のとき、分母が0になってしまい \( f(z) \) が定義されませんよね。なので当然正則でもありません。
(2) 孤立特異点と集積特異点
特異点 \( a \) のまわりに他の特異点が存在しないような特異点のことを孤立特異点と呼びます。
一方特異点のまわりにどんなに狭い範囲を考えても特異点が存在してしまうような特異点のことを集積特異点と呼びます。
集積特異点の例としては\[
f(z) = \tan \frac{1}{z}
\]がいいでしょう。例えば \( z = 0 \) は特異点の1つですね。このとき、\[
f(z) = \tan \frac{\pi}{2}, \ \frac{3}{2} \pi, \ \frac{5}{2} \pi , \ \cdots
\]と特異点が存在しますね。なので、どんなに \( z = 0 \) に近づけたとしても \( z = 0 \) 以外に\[
z = \frac{2}{\pi}, \ \frac{2}{3 \pi}, \ \frac{2}{ 5 \pi} , \ \cdots
\]の特異点が存在しますね。
なので \( z = 0 \) は集積特異点となります。
(3) 孤立特異点の3つの分類
さらに孤立特異点はローラン展開の特異部(負のべき乗部分)によって極・除去可能な特異点・真性特異点の3つに分類されます。
(1) 極
特異点 \( a \) まわりでローラン展開を行ったときに特異部(負のべき乗)が存在はするものの無限に続かないとき、\( a \) を極と呼びます。例えば、\[
f(z) = \frac{ \cos z }{z^2}
\]をローラン展開すると、\[
f(z) = \frac{1}{z^2} - \frac{1}{2!} + \frac{1}{4!} z^2 - \cdots + \frac{(-1)^n}{(2n+1)!} z^{2n-2} + \cdots
\]となりましたね(例題1より)。この場合の特異部は \( \frac{1}{z^2} \) だけですね。なので極となります。
さらに、極は特異部(負のべき乗)がどこまで続いているかによって極の位数もセットで表すこともあります。
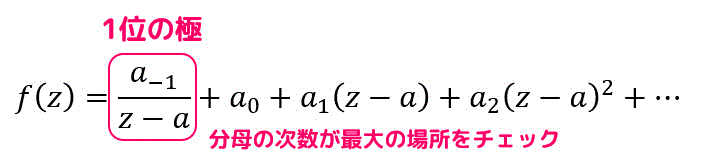
例えば、上のようなローラン展開だった場合、\( a_{-1} \) が負のべき乗となっていることがわかりますね。なので1位の極となります。
(基本的に分母の次数が最大になっているところが極の位数の基準となります。)
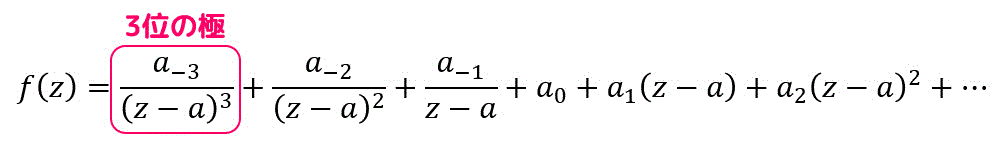
さらにもう1つ例をみてみましょう。
特異部は \( a_{-1} \), \( a_{-2} \), \( a_{-3} \) の3つなので一番分母の次数が大きい \( a_{-3} \) が基準となり、3位の極になります。
なので、下のように負のべき乗が \( n \) 乗まで続いていれば、\( n \) 位の極になりますね。
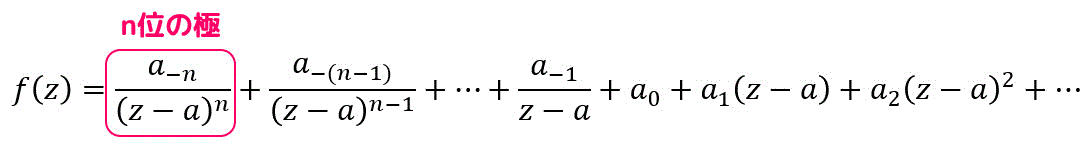
ちなみに\[
f(z) = \frac{ \cos z }{z^2}
\]は \( \frac{1}{z^2} \) が特異部なので、2位の極となります。
(2) 除去可能な特異点
たとえば複素関数\[
f(z) = \frac{\sin z}{z}
\]は \( z = 0 \) を特異点に持ちそうですね。なのでローラン展開してみましょう。\[
\sin z = z - \frac{1}{3!} z^3 + \frac{1}{5!} z^5 - \cdots
\]なので、\[\begin{align*}
f(z) & = \frac{\sin z}{z}
\\ & = \frac{z - \frac{1}{3!} z^3 + \frac{1}{5!} z^5 - \cdots}{z}
\\ & = 1 - \frac{1}{3!} z^2 + \frac{1}{5!} z^4 - \cdots
\end{align*}\]とローラン展開できますね。
特異点を持ちそうに見えるのにローラン展開の特異部(負のべき乗)が存在しませんね。
このように(分母が0になるなど)一見特異点そうに見える点でもローラン展開を行うと特異部が消えるような特異点のことを除去可能な特異点と呼びます。
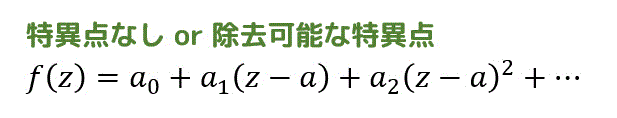
(3) 真性特異点
たとえば複素関数\[
f(z) = e^{ \frac{1}{z} }
\]を \( z = 0 \) まわりでローラン展開してみましょう。\[
e^z = 1 + z + \frac{1}{2!} z^2 + \frac{1}{3!} z^3 + \cdots
\]となるので \( z \) を \( 1/z \) にかえると\[
e^{ \frac{1}{z} } = 1 + \frac{1}{z} + \frac{1}{2!} \cdot \frac{1}{z^2} + \frac{1}{3!} \cdot \frac{1}{z^3} + \cdots
\]となり、負のべき乗が無限に続くような結果になりますね。
このようにローラン展開の特異部が無限に続くような特異点のことを真性特異点と呼びます。

特異点のまとめを下に記します。
特異点は孤立特異点・集積特異点の2つに分類できる。
孤立特異点:まわりに他の特異点がないような特異点
集積特異点:どんなに狭いまわりを考えても他の特異点が存在するような特異点
さらに孤立特異点はローラン展開の負のべき乗部分(特異部)によって3つに分けることができる
\( n \) 位の極:特異部が \( -n \) 次の項まで続くような特異点
除去可能な特異点:特異部が存在しないような特異点
真性特異点:特異部が無限に続くような特異点
スポンサードリンク
3.留数定理
ローラン展開を用いることで留数を求めることができます。
留数とは、特異点からすぐ近くの正則な領域で展開したローラン展開を行ったときに出てくる \( \frac{1}{z-a} \) の項の係数(\( a_{-1} \))のことを表します。
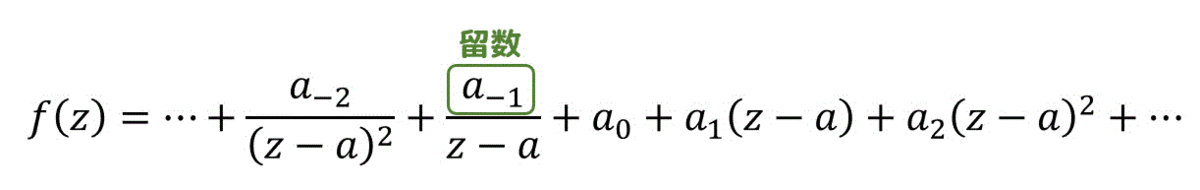
複素関数 \( f(z) \) を特異点からすぐ近くの正則な領域 \( 0 \lt |z-a| \lt R \) でローラン展開した結果\[
f(z) = \cdots + \frac{ a_{-2} }{ (z-a)^2 } + \frac{a_{-1} }{z-a} + \sum^{\infty}_{n = 0} a_n (z-a)^n
\]の \( \frac{1}{z-a} \) の項の係数 \( a_{-1} \) を \( f(z) \) の \( z = a \) における留数と呼ぶ。
留数を求めることで不定積分を計算することなく周積分を行ったり、Part6で説明する実関数の積分を複素解析の力を借りて計算できるようになります。
ですが、毎回留数を求めるためにローラン展開するのはかなりめんどくさいので実際に留数を求めるときには簡単に留数を求めるための定理として留数定理を使うことが多いです。
留数定理の説明、および複素解析の力を借りて実関数の積分を行う方法などについてはこちらの記事をご覧ください。
4.練習問題
では2問ほど練習してみましょう。
どちらも場合分けが必要な問題となっております。
練習1
つぎの複素関数\[
f(z) = \frac{1}{(z-1)(z-5)}
\]を \( z = 5 \) を中心にローラン展開し、留数を求めなさい。
練習2
つぎの複素関数\[
f(z) = \frac{z-5}{(z-1)(z-3)}
\]を \( z = 1 \) を中心にローラン展開し、留数を求めなさい。
5.練習問題の答え
解答1
\( t = z-5 \) とする。すると、\[
f(t) = \frac{1}{t(t+4)}
\]となる。 \( t \) を基準にすると \( t = 0 \) 中心のローラン展開を求めればよい。
特異点は \( z = 1,5 \)、つまり \( t = 0,4 \) なので距離が4未満か4を超えるかで場合分けが必要。(距離4ちょうどは特異点が含まれるのでダメ)
(1) \( 0 \lt |t| \lt 4 \)、つまり \( 0 \lt |z-5| \lt 4 \) のとき
\[
\frac{1}{1-a} = \sum^{\infty}_{n = 0} a^n = 1 + a + a^2 + \cdots \ \ \ \left( |a| < 1 \right)
\]の \( a \) を \( -t/4 \) に変えると、\[\begin{align*}
\frac{1}{1+ \frac{t}{4} } & = \frac{4}{4+t}
\\ & = \frac{4}{t+4}
\\ & = 1 - \frac{1}{4} t + \frac{1}{16} t^2 + \cdots
\\ & =\sum^{\infty}_{n = 0} \left( - \frac{t}{4} \right)^n
\end{align*}\]となる。
よって、\[ \begin{align*}
f(t) & = \frac{1}{t(t+4)}
\\ & = \frac{1}{t} \cdot \frac{1}{4} \cdot \frac{4}{t+4}
\\ & = \frac{1}{4t} \left(1 - \frac{1}{4} t + \frac{1}{16} t^2 + \cdots \right)
\\ & = \frac{1}{4t} - \frac{1}{16} + \frac{1}{64} t + \cdots
\\ & = \frac{1}{4t} \sum^{\infty}_{n = 0} \left( - \frac{t}{4} \right)^n
\end{align*}\]となる。
ここで、\( z \) の形にもどすと\[\begin{align*}
f(z) & = \frac{1}{4(z-5)} \sum^{\infty}_{n = 0} \left( - \frac{z-5}{4} \right)^n
\end{align*} \]となる。
留数は特異点にごく近い(距離0付近)のローラン展開の \( \frac{1}{z-5} \) の項の係数となる。
よって留数は \( \frac{1}{4} \) となる。
(2) \( 4 \lt |t| \)、つまり \( 4 \lt |z-5| \) のとき
\( 4 \lt |z| \) そのままの形だと\[
\frac{1}{1-a} = \sum^{\infty}_{n = 0} a^n = 1 + a + a^2 + a^3 + \cdots
\]の公式に当てはめることができません。そこで、\[
\frac{1}{|t|} = \left| \frac{1}{t} \right| < \frac{1}{4}
\]とし、4倍をすることで\[
\left| \frac{4}{t} \right| = \left| - \frac{4}{t} \right| < 1
\]となるので\[\begin{align*}
\frac{1}{1 + \frac{4}{t}}
& = \frac{1}{t} \left( 1 - \frac{4}{t} + \frac{16}{t^2} - \frac{64}{t^3} + \cdots \right)
\\ & = \frac{1}{t} \sum^{\infty}_{n = 0} \left( - \frac{4}{t} \right)^n
\end{align*}\]と公式を適用することができる。(\( a \) が \( -4/t \) に変わっただけ)
よって、\[\begin{align*}
f(t) & = \frac{1}{t} \cdot \frac{1}{t-4}
\\ & = \frac{1}{t} \cdot \frac{1}{t} \cdot \frac{1}{1 - \frac{4}{t} }
\\ & = \frac{1}{t^2} \left( 1 - \frac{4}{t} + \frac{16}{t^2} - \frac{64}{t^3} + \cdots \right)
\\ & = \frac{1}{t^2} - \frac{4}{t^3} + \frac{16}{t^4} - \frac{64}{t^5} + \cdots
\\ & = \frac{1}{t^2} \sum^{\infty}_{n = 0} \left( - \frac{4}{t} \right)^n
\end{align*}\]となる。
ここで、\( z \) の形にもどすと\[\begin{align*}
f(z) & = \frac{1}{(z-5)^2} \sum^{\infty}_{n = 0} \left(- \frac{4}{z-5} \right)^n
\end{align*} \]となる。
(1), (2) よりローラン展開は
\( 0 \lt |z| \lt 4 \) のとき\[
f(z) = \frac{1}{4(z-5)} \sum^{\infty}_{n = 0} \left( - \frac{z-5}{4} \right)^n
\]\( 4 \lt |z| \) のとき\[
f(z) = \frac{1}{(z-5)^2} \sum^{\infty}_{n = 0} \left( - \frac{4}{z-5} \right)^n
\]となり、留数は \( 1/4 \) と求められる。
[別解]
部分分数分解を行い、\[
\frac{1}{4} \cdot \frac{1}{z-5} - \frac{1}{4} \cdot \frac{1}{z-1}
\]と変形を行い、\( z = t-5 \) とする。
(1) \( 0 \lt |t| \lt 4 \)、つまり \( 0 \lt |z-5| \lt 4 \) のとき
\[\begin{align*}
\frac{1}{1 + \frac{t}{4} } & = \frac{4}{4+t}
\\ & = \frac{4}{t+4}
\\ & = \sum^{\infty}_{n = 0} \left( - \frac{t}{4} \right)^n
\end{align*}\]となる。よって、\[\begin{align*}
f(t) & = \frac{1}{4t} - \frac{1}{4} \cdot \frac{1}{t+4}
\\ & = \frac{1}{4t} - \frac{1}{16} \cdot \frac{4}{t+4}
\\ & = \frac{1}{4t} - \frac{1}{16} \sum^{\infty}_{n = 0} \left(- \frac{t}{4} \right)^n
\end{align*}\]となる。
\( z \) に戻すと、\[
f(z) = \frac{1}{4(z-5)} - \frac{1}{16} \sum^{\infty}_{n = 0} \left(- \frac{z-5}{4} \right)^n
\]となる。
(2) \( 4 \lt |t| \)、つまり \( 4 \lt |z-5| \) のとき
\[\begin{align*}
\frac{1}{1 + \frac{4}{t}}
& = \frac{1}{t} \left( 1 - \frac{4}{t} + \frac{16}{t^2} - \frac{64}{t^3} + \cdots \right)
\\ & = \frac{1}{t} \sum^{\infty}_{n = 0} \left( \frac{4}{t} \right)^n \ \ \ \left( \left| \frac{4}{t} \right| < 1 \right)
\end{align*}\]より、\[\begin{align*}
f(t) & = \frac{1}{4t} - \frac{1}{4} \cdot \frac{1}{t+4}
\\ & = \frac{1}{4t} - \frac{1}{4t} \cdot \frac{1}{1+\frac{4}{t}}
\\ & = \frac{1}{4t} - \frac{1}{4t} \sum^{\infty}_{n = 0} \left( - \frac{4}{t} \right)^n
\\ & = - \frac{1}{4t} \sum^{\infty}_{n = 1} \left( - \frac{4}{t} \right)^n
\end{align*}\]となる。
\( z \) に戻すと、\[
f(z) = - \frac{1}{4(z-5)} \sum^{\infty}_{n = 1} \left( - \frac{4}{z-5} \right)^n
\]となる。
解答2
\( t = z-1 \) とする。すると、\[
f(t) = \frac{t-4}{t(t-2)}
\]となる。\( t = 0 \) まわりのローラン展開を求めればよい。
さらに\[\begin{align*}
\frac{t-4}{t(t-2)} & = \frac{t-2}{t(t-2)} - \frac{2}{t(t-2)}
\\ & = \frac{1}{t} - \frac{2}{t} \cdot \frac{1}{t-2}
\end{align*} \]と変形できる。
特異点は \( z = 1,3 \)、つまり \( t = 0,2 \) なので距離が2未満か2を超えるかで場合分けが必要。(距離2ちょうどは特異点が含まれるのでダメ)
(1) \( 0 \lt |t| \lt 2 \)、つまり \( 0 \lt |z-1| \lt 2 \) のとき
\[
\frac{1}{1-a} = \sum^{\infty}_{n = 0} a^n = 1 + a + a^2 + \cdots \ \ \ \left( |a| < 1 \right)
\]の \( a \) を \( t/2 \) に変えると、\[\begin{align*}
\frac{1}{1 - \frac{t}{2} } & = \frac{2}{2-t}
\\ & = 1 + \frac{1}{2} t + \frac{1}{4} t^2 + \frac{1}{8} t^3 + \cdots
\\ & = \sum^{\infty}_{n = 0} \left( \frac{t}{2} \right)^n
\end{align*}\]となる。
よって、\[ \begin{align*}
f(t) & = \frac{t-4}{t(t-2)}
\\ & = \frac{1}{t} - \frac{2}{t} \cdot \frac{1}{t-2}
\\ & = \frac{1}{t} + \frac{2}{t} \cdot \frac{1}{2-t}
\\ & = \frac{1}{t} + \frac{1}{t} \cdot \frac{2}{2-t}
\\ & = \frac{1}{t} + \frac{1}{t} \left(1 + \frac{1}{2} t + \frac{1}{4} t^2 + \frac{1}{8} t^3 + \cdots \right)
\\ & = \frac{2}{t} + \frac{1}{2} + \frac{1}{4} t + \frac{1}{8} t^2 + \cdots
\\ & = \frac{1}{t} + \frac{1}{t} \sum^{\infty}_{n = 0} \left(\frac{t}{2} \right)^n
\end{align*}\]となる。
ここで、\( z \) の形にもどすと\[\begin{align*}
f(z) & = \frac{1}{z-1} + \frac{1}{z-1} \sum^{\infty}_{n = 0} \left(\frac{z-1}{2} \right)^n
\\ & = \frac{2}{z-1} + \frac{1}{z-1} \sum^{\infty}_{n = 1} \left(\frac{z-1}{2} \right)^n
\end{align*} \]となる。
また、留数は特異点にごく近い(距離0付近)のローラン展開の \( \frac{1}{z-1} \) の項の係数となる。
よって留数は 2 となる。
(2) \( 2 \lt |t| \)、つまり \( 2 \lt |z-1| \) のとき
\( 2 \lt |t| \) そのままの形だと\[
\frac{1}{1-a} = \sum^{\infty}_{n = 0} a^n = 1 + a + a^2 + a^3 + \cdots
\]の公式に当てはめることができません。そこで、\[
\frac{1}{|t|} = \left| \frac{1}{t} \right| < \frac{1}{2}
\]とし、2倍をすることで\[
\left| \frac{2}{t} \right| < 1
\]となるので\[\begin{align*}
\frac{1}{1 - \frac{2}{t}}
& = \frac{1}{t} \left( 1 + \frac{2}{t} + \frac{4}{t^2} + \frac{8}{t^3} + \cdots \right)
\\ & = \frac{1}{t} \sum^{\infty}_{n = 0} \left( \frac{2}{t} \right)^n
\end{align*}\]と公式を適用することができる。(\( a \) が \( 2/t \) に変わっただけ)
よって、\[\begin{align*}
f(t) & = \frac{1}{t} - \frac{2}{t} \cdot \frac{1}{t-2}
\\ & = \frac{1}{t} - \frac{2}{t^2} \cdot \frac{1}{1 - \frac{4}{t} }
\\ & = \frac{1}{t} - \frac{2}{t^2} \left( 1 + \frac{2}{t} + \frac{4}{t^2} + \frac{8}{t^3} + \cdots \right)
\\ & = \frac{1}{t} - \frac{2}{t^2} - \frac{4}{t^3} - \frac{8}{t^4} + \cdots
\\ & = \frac{1}{t} - \frac{2}{t^2} \sum^{\infty}_{n = 0} \left( \frac{2}{t} \right)^n
\end{align*}\]となる。
ここで、\( z \) の形にもどすと\[\begin{align*}
f(z) & = \frac{1}{z-1} - \frac{2}{(z-1)^2} \sum^{\infty}_{n = 0} \left( \frac{2}{z-1} \right)^n
\end{align*} \]となる。
[別解 部分分数分解を用いた解き方]
部分分数分解を行い、\[
\frac{z-5}{(z-1)(z-3)} = \frac{2}{z-1} - \frac{1}{z-3}
\]と変形を行い、\( z-1 = t \) とする。すると、\[
\frac{2}{t} - \frac{1}{t-2}
\]となる。
(1) \( 0 \lt |t| \lt 2 \)、つまり \( 0 \lt |z-1| \lt 2 \) のとき
\[\begin{align*}
\frac{1}{1 - \frac{t}{2} } & = \frac{2}{2-t}
\\ & = \sum^{\infty}_{n = 0} \left( \frac{t}{2} \right)^n
\end{align*}\]となる。よって、\[\begin{align*}
f(t) & = \frac{2}{t} - \frac{1}{t-2}
\\ & = \frac{2}{t} + \frac{1}{2} \cdot \frac{2}{2-t}
\\ & = \frac{2}{t} + \frac{1}{2} \sum^{\infty}_{n = 0} \left( \frac{t}{2} \right)^n
\end{align*}\]となる。
\( z \) に戻すと、\[
f(z) = \frac{2}{z-1} + \frac{1}{2} \sum^{\infty}_{n = 0} \left( \frac{z-1}{2} \right)^n
\]となる。
(よって留数は2となる。)
(2) \( 2 \lt |t| \)、つまり \( 2 \lt |z-1| \) のとき
\[\begin{align*}
\frac{1}{1 - \frac{2}{t}}
= \sum^{\infty}_{n = 0} \left( \frac{2}{t} \right)^n \ \ \ \left( \left| \frac{2}{t} \right| < 1 \right)
\end{align*}\]より、\[\begin{align*}
f(t) & = \frac{2}{t} - \frac{1}{t-2}
\\ & = \frac{2}{t} - \frac{1}{t} \cdot \frac{1}{1- \frac{2}{t} }
\\ & = \frac{2}{t} - \frac{1}{t} \sum^{\infty}_{n = 0} \left( \frac{2}{t} \right)^n
\end{align*}\]となる。
\( z \) に戻すと、\[
f(z) = \frac{2}{z-1} - \frac{1}{z-1} \sum^{\infty}_{n = 0} \left( \frac{2}{z-1} \right)^n
\]となる。
6.さいごに
今回はテイラー展開の拡張バージョンのローラン展開についてまとめました。
ローラン展開も見た目は複雑そうな形をしていますが、実際やると大したことがないなと思っていただければありがたいです。
次回は留数を複素関数を積分する方法、および実関数の積分に応用する方法についてまとめていきたいと思います。
では、また次回。
Part6はこちら!
関連広告・スポンサードリンク