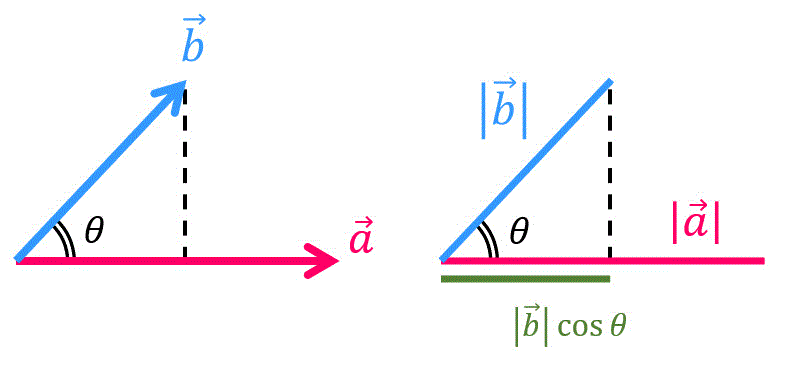
うさぎでもわかる線形代数　補充1　線形代数におけるベクトル　内積と外積

2020年5月14日 2020年5月14日 47分49秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

今回は大学の線形代数で最初に習うベクトルについて、具体的には

高校生までのベクトルの違い
ベクトルの内積
ベクトルの外積

について説明していきたいと思います。

目次 [hide]

１．高校までのベクトルとの違い
２．内積（スカラー積）・ベクトルの大きさ
３．外積（ベクトル積）
４．外積を用いた三角形・三角錐の面積の求め方
- (1) 三角形の面積
- (2) 三角錐の面積
５．練習問題
- 問題
６．練習問題の答え
７．さいごに

スポンサードリンク

１．高校までのベクトルとの違い

(1) ベクトルってなんだろう

皆さんは、数Bで「ベクトル」を習ったときに、ベクトルは向きや大きさを持った矢印 $\vec{a}$ として定義していましたね。

しかし、線形代数で出てくるベクトルは、矢印 $\vec{a}$ ではなく、いくつかの数字が縦、もしくは横に並んでおり、 $(\begin{array}{ccc} 1 \\ 2 \\ 3 \end{array}) + (\begin{array}{ccc} 3 \\ 2 \\ 1 \end{array}) = (\begin{array}{ccc} 4 \\ 4 \\ 4 \end{array}) 3 (\begin{array}{ccc} 1 \\ 1 \\ 1 \end{array}) = (\begin{array}{ccc} 3 \\ 3 \\ 3 \end{array})$ のように足し算や定数倍ができるようなものと定義します。

また、ベクトルの表記の仕方も高校までで使った $\vec{a}$ から、ただの太文字 $a$ に変化します。

（※ただし、本ブログにおいてはベクトル表記 $\vec{a}$ を見やすくするため、あえて太字表記 $a$ ではなく矢印表記 $\vec{a}$ を使って表現します。）

線形代数におけるベクトル

その1. ベクトルの定義

$n$ 個の実数 $a_{1}$ , $a_{2}$ , …, $a_{n}$ を並べた $(\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array})$ を $n$ 次元のベクトルと呼ぶ。

また、 $n$ 次元実数ベクトルの集合を $R^{n}$ と表す。

その2. ベクトルの表記

線形代数におけるベクトルは $a$ , $b$ のような大文字で表記することが多い*1。

その3. ベクトルの和と定数倍

ベクトル $a$ , $b$ を $a = (\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array}), b = (\begin{array}{ccc} b_{1} \\ b_{2} \\ ⋮ \\ b_{n} \end{array})$ とする。

このとき、ベクトルの和 $a$ , $b$ は $a + b = (\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array}) + (\begin{array}{ccc} b_{1} \\ b_{2} \\ ⋮ \\ b_{n} \end{array}) = (\begin{array}{ccc} a_{1} + b_{1} \\ a_{2} + b_{2} \\ ⋮ \\ a_{n} + b_{n} \end{array})$ と定められ、ベクトル $a$ の定数倍（ $k$ 倍）を $k a = k (\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array}) = (\begin{array}{ccc} k a_{1} \\ k a_{2} \\ ⋮ \\ k a_{n} \end{array})$ と定められる。

高校数学では、 $\vec{a} = (\begin{array}{ccc} 1 \\ 2 \end{array})$ のような2次元ベクトル $R^{2}$ や $\vec{b} = (\begin{array}{ccc} 3 \\ 3 \\ 4 \end{array})$ のような3次元ベクトル $R^{3}$ のように、線形代数におけるベクトルの一部分を習っていたのです！

大学の線形代数では、 $a = (\begin{array}{ccc} 1 \\ 2 \\ 3 \\ 4 \end{array})$ のように、高校では出てこなかった4次元以上のベクトルなども出てくるので、頭にいれておきましょう。

(2) 縦ベクトルと横ベクトル

高校数学では $\vec{a} = (1, 2), \vec{b} = (3, 3, 4)$ のように横方向にベクトルを表記している人が大半だと思います。

この表記は、横方向に数字を書いているので横ベクトル（列ベクトル）と呼ばれます。

一方線形代数におけるベクトルでは、 $\vec{a} = (\begin{array}{ccc} 1 \\ 2 \end{array}), \vec{b} = (\begin{array}{ccc} 3 \\ 3 \\ 4 \end{array})$ のように縦方向にベクトルを表記することが多いです。

この表記は、縦方向に数字を書いているので縦ベクトル（行ベクトル）と呼ばれます。

(3) ゼロベクトル

成分がすべて0のベクトル $(\begin{array}{ccc} 0 \\ 0 \\ ⋮ \\ 0 \end{array})$ をゼロベクトルと呼び、太字表記であれば $0$ 、矢印表記であれば $\vec{0}$ と表します。

(4) ベクトルの計算法則

最後にベクトルの計算法則を確認しておきましょう。

とは言っても、高校数学のときと変わらないので特に身構える必要はありません。

ベクトルの計算法則

ある $n$ 次元ベクトル $a$ , $b$ , $c$ および、実数 $k$ , $l$ において以下の法則が成り立つ。

その1. 足し算を入れ替えても計算結果は変わらない $a + b = b + a$

その2. 3個以上ベクトルが並んでいればどこから計算してもOK $(a + b) + c = a + (b + c)$

その3. 定数 k を分配することができる $k (a + b) = k a + k b$

その4. 2つ以上の定数を分離することができる $(k + l) a = k a + l a$

どれも当たり前なのでささっと終わらせましょう。

スポンサードリンク

２．内積（スカラー積）・ベクトルの大きさ

ここからは、ベクトルをわかりやすく表記するため、矢印表記 $\vec{a}$ で表記していきます。

(1) 線形代数における内積

高校数学では、内積 $\vec{a} \cdot \vec{b}$ を $\vec{a}$ と $\vec{b}$ のなす角 $θ$ を用いて $\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos θ$ と定義していましたね。

しかし、線形代数のベクトルは4次元以上のものが出てきます。

4次元のベクトルがなす角度の想像はちょっときついですね。

そこで、線形代数におけるベクトルでは、2つのベクトルのなす角ではなく、成分を用いて $(\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array}) \cdot (\begin{array}{ccc} b_{1} \\ b_{2} \\ ⋮ \\ b_{n} \end{array}) = a_{1} b_{1} + a_{2} b_{2} \dots + a_{n} b_{n}$ で定義します。

成分計算で定義すれば、4次元ベクトルの角度を想像する必要はありませんよね。

ベクトルの内積

ベクトル $\vec{a} = (\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array}) \vec{b} = (\begin{array}{ccc} b_{1} \\ b_{2} \\ ⋮ \\ b_{n} \end{array})$ とすると、内積 $\vec{a} \cdot \vec{b}$ は $\vec{a} \cdot \vec{b} = a_{1} b_{1} + a_{2} b_{2} + \dots + a_{n} b_{n} = \sum_{i = 1}^{n} a_{i} b_{i}$ と定義される。

また、 $n$ 次元ベクトル $\vec{a}$ , $\vec{b}$ がなす角 $θ$ は、内積 $\vec{a} \cdot \vec{b}$ を用いて $\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos θ (0^{\circ} ≦ θ ≦ 180^{\circ}, \vec{a} \neq \vec{0}, \vec{b} \neq \vec{0})$ という等式を満たす $θ$ で定義される。

ちなみに内積はスカラー積とも呼ばれます。頭の片隅にでも入れておけばOKです。

(2) 内積と直交

ベクトル $\vec{a}$ , $\vec{b}$ がなす角が90度になるとき、つまり、 $\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos 90^{\circ} = 0$ となるとき、ベクトル $\vec{a}$ , $\vec{b}$ は直交します。

ベクトルの内積を成分表示

$\vec{0}$ でないベクトル $\vec{a}$ , $\vec{b}$ が $\vec{a} \cdot \vec{b} = 0$ を満たすとき、2つのベクトルは直交し、 $\vec{a} ⊥ \vec{b}$ で表す。

高校数学で出てきたベクトルと同じですね！

(3) 内積の計算法則

内積の計算法則を確認しておきましょう。

ベクトルの内積には、下のような法則が成り立ちます。

ベクトルの内積における定理

ベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ および行列 $A$ に対し、以下の3つの定理が成立する。

その1. 順番を入れ替えても内積の値はかわらない $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$

その2. 内積の分解公式 $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} + \vec{c}$

その3. 定数倍を分離できる $k \vec{a} \cdot \vec{b} = k (\vec{a} \cdot \vec{b})$

(4) ベクトルの大きさ

高校数学で出てきたベクトル（2次元・3次元ベクトル）は、始点からの終点までの距離を表していましたね。

4次元以上のベクトルにおいても、始点から終点までの距離を求めるように成分で定義されます。

ベクトルの大きさ（ノルム）

$n$ 次元のベクトル $\vec{a} = (\begin{array}{ccc} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{array})$ の大きさ（ $| \vec{a} |$ もしくは $‖ \vec{a} ‖$ ）は、 $| \vec{a} | = \sqrt{a_{1}^{2} + a_{2}^{2} + \dots + a_{n}^{2}}$ で表せる。

なお、大きさが1のベクトルのことを単位ベクトルと呼ぶので頭にいれておきましょう。

(5) ベクトルの正規化

最後に正規化について説明しておきましょう。

ベクトルの向きをそのままにして、大きさを1（単位ベクトル）にする処理のことを正規化といいます。

ベクトルの正規化

ベクトル $\vec{a}$ を正規化（単位化）したベクトル $\vec{u}$ は、 $\vec{u} = \frac{\vec{a}}{| \vec{a} |}$ で求められる。

スポンサードリンク

３．外積（ベクトル積）

内積があれば外積ってないの…？と思った人もいるかもしれません。

安心してください、あります。しかも、大学の物理などでも使われる重要な分野なので、頭にいれておきましょう。

（数検1級を受ける人は、外積の問題が計算問題で出ることがあるので確実に得点源にできるようにしましょう！）

ただし、3次元ベクトル以外の外積を使う機会はほぼないので、今回は3次元ベクトルに限定して外積の説明をしたいと思います。

（期末試験でも3次元ベクトル以外の外積を求める機会はないと思ってOKです）

(1) 外積（ベクトル積）の定義

まず、成分を用いた外積の定義から見ていきましょう。

外積の定義（公式）

3次元実ベクトル $R^{3}$ $\vec{a} = (\begin{array}{ccc} a_{1} \\ a_{2} \\ a_{3} \end{array}), \vec{b} = (\begin{array}{ccc} b_{1} \\ b_{2} \\ b_{3} \end{array})$ に関して外積 $\vec{a} \times \vec{b}$ を $\vec{a} \times \vec{b} = (\begin{array}{ccc} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{array})$ と定義する。

外積は計算結果がベクトルとなるのが特徴です。内積は、計算結果がスカラーでしたね。

（なので内積のことをスカラー積、外積のことをベクトル積と呼ぶ。）

ところで、少し公式が覚えにくいですね。

なので、下のようなたすき掛けの形で頭にいれておきましょう。

（ $a_{3}$ と $a_{1}$ 、 $b_{3}$ と $b_{1}$ はつながっていると考えてください。イメージはドラクエとかのRPGのマップと同じです）

ちなみに、たすき掛けの右下方向が足し算、右上方向が引き算なので逆にしないように気を付けましょう。

1問計算練習をしてみましょう。

例題1

次の3次元ベクトル $\vec{a} = (\begin{array}{ccc} 1 \\ 1 \\ 2 \end{array}), \vec{b} = (\begin{array}{ccc} 2 \\ - 1 \\ 1 \end{array})$ の外積 $\vec{a} \times \vec{b}$ と $\vec{b} \times \vec{a}$ を求めなさい。

解説1

$\vec{a} \times \vec{b}$ の計算をすると、 $\begin{aligned} \vec{a} \times \vec{b} & = (\begin{array}{ccc} 1 \cdot 1 - 2 \cdot (- 1) \\ 2 \cdot 2 - 1 \cdot 1 \\ 1 \cdot (- 1) - 1 \cdot 2 \end{array}) \\ = (\begin{array}{ccc} 3 \\ 3 \\ - 3 \end{array}) \end{aligned}$ と求められる。

同様に、 $\vec{b} \times \vec{a}$ を $\begin{aligned} \vec{b} \times \vec{a} & = (\begin{array}{ccc} - 1 \cdot 2 - 1 \cdot 1 \\ 1 \cdot 1 - 2 \cdot 2 \\ 2 \cdot 1 - 1 \cdot (- 1) \end{array}) \\ = (\begin{array}{ccc} - 3 \\ - 3 \\ 3 \end{array}) \end{aligned}$ と計算できる。

あれ、 $\vec{a} \times \vec{b}$ と $\vec{b} \times \vec{a}$ の答えが一致しませんでした。符号が入れ替わっていますね。

実は上の計算のように、外積 $\vec{a} \times \vec{b}$ では、計算順序を入れ替えると符号が逆になるのです。要注意ポイントですね。

(2) 外積（ベクトル積）の計算法則

つぎに、外積の計算法則を確認しておきましょう。

外積の計算法則

3次元実ベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ に対し、以下の3つの計算法則が成り立つ。

その1. 定数倍は分離できる $k (\vec{a} \times \vec{b}) = (k \vec{a}) \times \vec{b} = \vec{a} \times (k \vec{b})$

その2. 計算順序を入れ替えると符号が変わる $\vec{a} \times \vec{b} = - (\vec{b} \times \vec{a})$

その3. 括弧を外しても計算結果は変わらない $\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} (\vec{a} + \vec{b}) \times \vec{c} = \vec{a} \times \vec{c} + \vec{b} \times \vec{c}$

(1)で説明した通り、計算順序を入れ替えると符号が逆になる点が要注意ポイントです。

(3) 外積（ベクトル積）のイメージ

外積のイメージは、

ベクトル $\vec{a}$ , $\vec{b}$ の両方に直交するベクトル
（向きのイメージ）
2つのベクトル $\vec{a}$ , $\vec{b}$ が張る平行四辺形がそのまま外積の大きさ
（大きさのイメージ）

を満たすようなベクトルとなります。

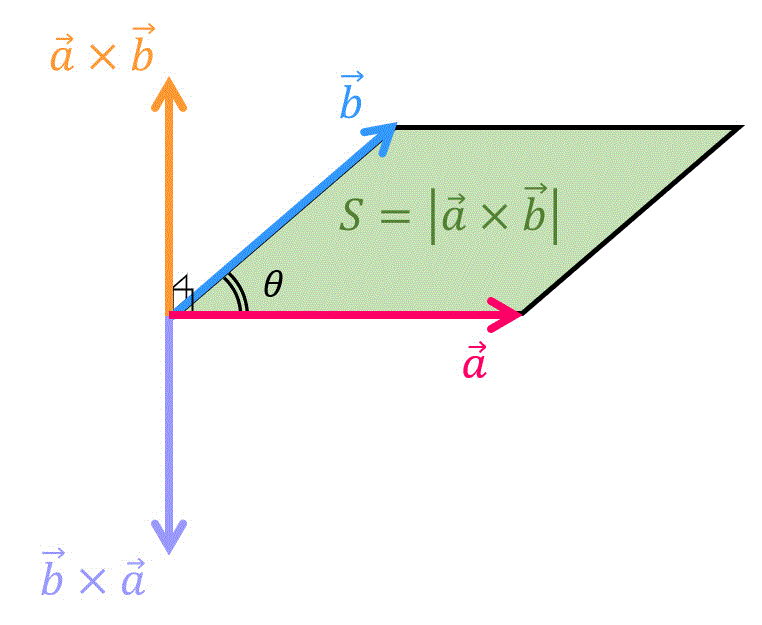
つまり、ベクトル $\vec{a}$ 、 $\vec{b}$ の両方に直交し、長さが2つのベクトル $\vec{a}$ , $\vec{b}$ で張られる平行四辺形の面積 $S$ となるものが外積の直観的イメージです！

(4) 外積の検算テクニック（期末試験で使える！）

ベクトル $\vec{a}$ , $\vec{b}$ の外積 $\vec{a} \times \vec{b}$ は、ベクトル $\vec{a}$ , $\vec{b}$ に垂直であると先程説明しましたね。

（ $(\vec{a} \times \vec{b}) ⊥ \vec{a}$ と $(\vec{a} \times \vec{b}) ⊥ \vec{b}$ が成立する）

垂直であるということは、内積が0になると言い換えられますね。

この性質を外積の検算に利用します。外積 $\vec{a} \times \vec{b}$ を求めたあとに $(\vec{a} \times \vec{b}) \cdot \vec{a} = 0 (\vec{a} \times \vec{b}) \cdot \vec{b} = 0$ を確かめることで、外積が合っていることを確かめることができます。

期末試験や数検の試験などで「答えが合っている安心感」を得たい人は、必ず検算するようにしましょう。

ベクトル $\vec{a}$ , $\vec{b}$ の外積 $\vec{a} \times \vec{b}$ の性質として、 $(\vec{a} \times \vec{b}) ⊥ \vec{a} (\vec{a} \times \vec{b}) ⊥ \vec{b}$ が成り立つ。つまり、 $(\vec{a} \times \vec{b}) \cdot \vec{a} = 0 (\vec{a} \times \vec{b}) \cdot \vec{b} = 0$ を確かめることで外積が合っているかどうかを確かめることができる。

（ただし符号が正しいかどうかは判定できないので注意）

外積の検算

例題2

次の3次元ベクトル $\vec{a} = (\begin{array}{ccc} 1 \\ 1 \\ 2 \end{array}), \vec{b} = (\begin{array}{ccc} 2 \\ - 1 \\ 1 \end{array})$ の外積 $\vec{a} \times \vec{b}$ は $\vec{a} \times \vec{b} = (\begin{array}{ccc} 3 \\ 3 \\ - 3 \end{array})$ で求められる。（例題1より）

外積 $\vec{a} \times \vec{b}$ がベクトル $\vec{a}$ , $\vec{b}$ と直交する、つまり $(\vec{a} \times \vec{b}) ⊥ \vec{a} (\vec{a} \times \vec{b}) ⊥ \vec{b}$ となることを確かめ、例題1で求めた外積が確かに合っていることを確かめなさい。

解説2

内積を計算すると $\begin{aligned} (\vec{a} \times \vec{b}) ⊥ \vec{a} & = (\begin{array}{ccc} 3 \\ 3 \\ - 3 \end{array}) \cdot (\begin{array}{ccc} 1 \\ 1 \\ 2 \end{array}) \\ = 3 + 3 - 6 \\ = 0 \end{aligned}$ $\begin{aligned} (\vec{a} \times \vec{b}) ⊥ \vec{b} & = (\begin{array}{ccc} 3 \\ 3 \\ - 3 \end{array}) \cdot (\begin{array}{ccc} 2 \\ - 1 \\ 1 \end{array}) \\ = 6 - 3 - 3 \\ = 0 \end{aligned}$ となるので、確かに外積 $\vec{a} \times \vec{b}$ がベクトル $\vec{a}$ , $\vec{b}$ と直交していることがわかる。

(5) 行列式を用いた外積の表し方

外積の公式は、下のように行列式を用いて表すこともできます。

（ $\vec{i}$ , $\vec{j}$ , $\vec{k}$ は単位ベクトル）

サラスの公式を習った後は、こちらの表記で頭にいれておくことをおすすめします。

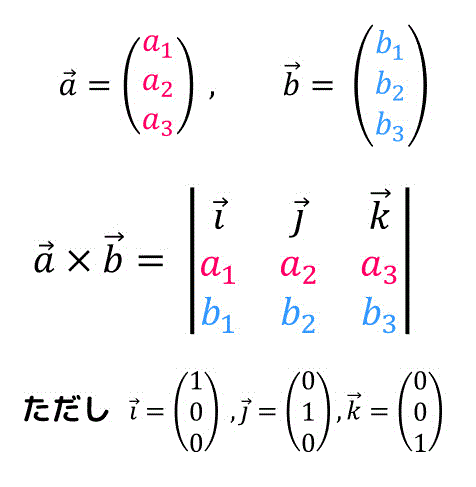
実際にサラスの公式を使って計算すると、 $\begin{aligned} \vec{a} \times \vec{b} & = | \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array} | \\ = (a_{2} b_{3} - a_{3} b_{2}) \vec{i} + (a_{3} b_{1} - a_{1} b_{3}) \vec{j} + (a_{1} b_{3} - a_{2} b_{1}) \vec{k} \\ = (\begin{array}{ccc} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{array}) \end{aligned}$ となり、確かに同じ結果が得られますね。

行列式を（予習・復習）したい人はこちらの記事で復習ができるので、ぜひご覧ください。

www.momoyama-usagi.com

(6) 平行四辺形の面積・平行六面体の体積

外積を用いることで、ベクトルが張る平行四辺形の面積、ベクトルが張る平行六面体の体積を求めることができます。

(i) 平行四辺形の面積

2つのベクトル $\vec{a}$ , $\vec{b}$ が張る平行四辺形の面積 $S$ は $S = | \vec{a} \times \vec{b} |$ で計算することができます。

[導出過程]

下の2つのベクトル $\vec{a}$ , $\vec{b}$ で張られる平行四辺形があるとします。

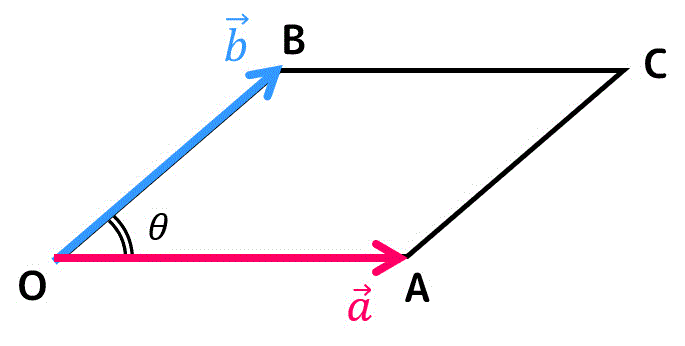
平行四辺形の面積は、底辺 OA × 高さ BH で求めることができますね。

底辺は $| \vec{a} |$ 、高さは $| \vec{b} | \sin θ$ となるので、平行四辺形の面積 $S$ は $S = | \vec{a} | | \vec{b} | \sin θ$ で求めることができます。

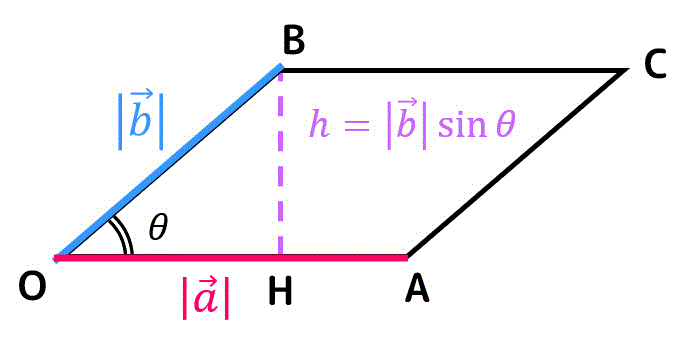
ここで、ベクトル $\vec{a}$ , $\vec{b}$ を $\vec{a} = (\begin{array}{ccc} a_{1} \\ a_{2} \\ a_{3} \end{array}), \vec{b} = (\begin{array}{ccc} b_{1} \\ b_{2} \\ b_{3} \end{array})$ とすると、 $\begin{aligned} S^{2} & = | \vec{a} |^{2} | \vec{b} |^{2} \sin^{2} θ \\ = | \vec{a} |^{2} | \vec{b} |^{2} (1 - \cos^{2} θ) \\ = | \vec{a} |^{2} | \vec{b} |^{2} - | \vec{a} |^{2} | \vec{b} |^{2} \cos^{2} θ \\ = | \vec{a} |^{2} | \vec{b} |^{2} - (\vec{a} \cdot \vec{b})^{2} \\ = (a_{1}^{2} + a_{2}^{2} + a_{3}^{2}) (b_{1}^{2} + b_{2}^{2} + b_{3}^{2}) - (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3})^{2} \\ = (a_{2} b_{3} - a_{3} b_{2})^{2} + (a_{3} b_{1} - a_{1} b_{3})^{2} + (a_{1} b_{2} - a_{2} b_{1})^{2} \\ = | \vec{a} \times \vec{b} |^{2} \end{aligned}$ となるので、 $S = | \vec{a} \times \vec{b} |$ を導出することができます。

平行四辺形の面積

ベクトル $\vec{a}$ , $\vec{b}$ に張られる平行四辺形の面積 $S$ は $\begin{aligned} S & = | \vec{a} \times \vec{b} | \\ = | \vec{a} | | \vec{b} | \sin θ \end{aligned}$ で求めることができる。

(ii) 平行六面体の体積

3つのベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ が張る平行六面体の体積 $V$ は $V = | (\vec{a} \times \vec{b}) \cdot \vec{c} |$ で計算することができます。

[導出過程]

下の3つのベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ で張られる平行六面体があるとします。

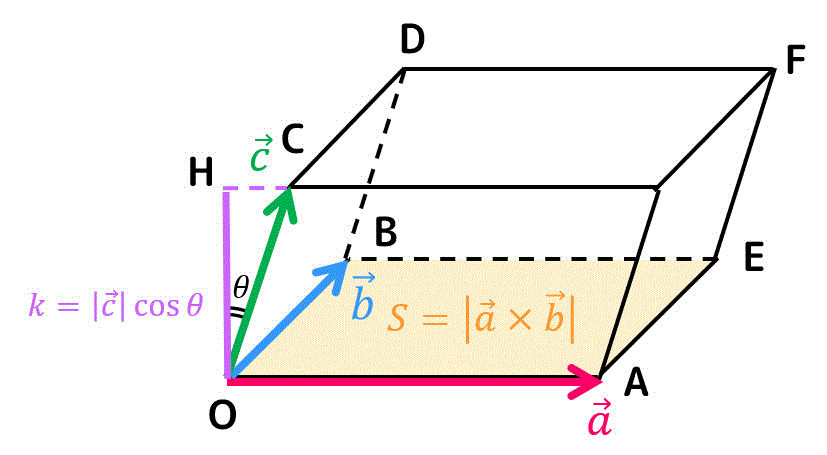
平行六面体の面積は、ベクトル $\vec{a}$ , $\vec{b}$ で張られる底面 $S$ と高さに相当する OH の積で求められますね。

底目は $| \vec{a} \times \vec{b} |$ 、高さは $| \vec{c} | \cos θ$ となるので、平行六面体の体積 $V$ は $V = | \vec{a} \times \vec{b} | | \vec{c} | \cos θ$ で求めることができます。

式を変形していくと、 $\begin{aligned} V & = | \vec{a} \times \vec{b} | | \vec{c} | \cos θ \\ = | | \vec{a} \times \vec{b} | | \vec{c} | \cos θ | \\ = | (\vec{a} \times \vec{b}) \cdot \vec{c} | \end{aligned}$ となり、式を導出することができました。

平行六面体の面積

ベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ に張られる平行六面体の体積 $V$ は $\begin{array}{r} V = | (\vec{a} \times \vec{b}) \cdot \vec{c} | \end{array}$ で求めることができる。

４．外積を用いた三角形・三角錐の面積の求め方

外積を応用することで、三角形や三角錐の面積を簡単に求めることができます。

(1) 三角形の面積

ベクトル $\vec{a}$ , $\vec{b}$ に張られる平行四辺形の面積 $S$ は $\begin{aligned} S & = | \vec{a} \times \vec{b} | \\ = | \vec{a} | | \vec{b} | \sin θ \end{aligned}$ で求めることができましたね。

三角形OABの面積を求めるためには、下のように平行四辺形の面積 $S$ を半分にした部分の面積を求めればいいですね。

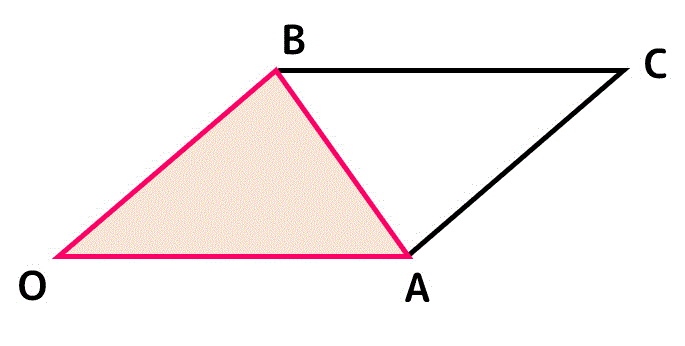
よって、ベクトル $\vec{a}$ , $\vec{b}$ が張る三角形の面積 $S^{'}$ は、 $\begin{aligned} S^{'} & = \frac{1}{2} \\ = \frac{1}{2} | \vec{a} \times \vec{b} | \\ = \frac{1}{2} | \vec{a} | | \vec{b} | \sin θ \end{aligned}$ と求められます。

（数1で出てきた面積公式 $S = \frac{1}{2} a b \sin θ$ が導出できましたね。）

(2) 三角錐の面積

ベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ に張られる平行六面体の体積 $V$ は $\begin{array}{r} V = | (\vec{a} \times \vec{b}) \cdot \vec{c} | \end{array}$ で求めることができましたね。

三角錐OABCの体積を求めるためには、

平行六面体に比べて底面の大きさが1/2（三角形）
三角錐なので三角柱に比べて面積が1/3

されることを踏まえると、平行六面体の面積を1/6することで求めることができますね。

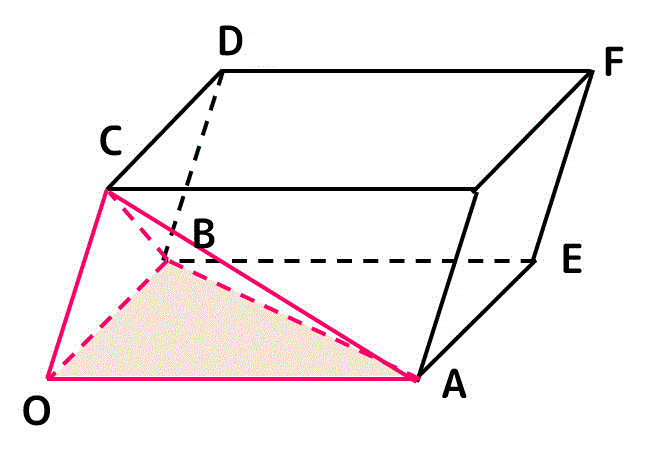
よって、三角錐OABCの体積 $V^{'}$ は $\begin{aligned} V^{'} & = \frac{1}{6} V \\ = \frac{1}{6} | (\vec{a} \times \vec{b}) \cdot \vec{c} | \end{aligned}$ で求めることができます。

５．練習問題

では、最後に練習問題を1問用意してみました。

理解できたかどうかのチャレンジにどうぞ！

問題

3次元ベクトル $\vec{a}$ , $\vec{b}$ , $\vec{c}$ を $\vec{a} = (\begin{array}{ccc} 2 \\ 1 \\ - 3 \end{array}), \vec{b} = (\begin{array}{ccc} - 3 \\ 2 \\ 1 \end{array}), \vec{c} = (\begin{array}{ccc} 1 \\ 1 \\ 4 \end{array})$ とし、さらに $\vec{O A} = \vec{a}$ , $\vec{O B} = \vec{b}$ , $\vec{O C} = \vec{c}$ とする。次の問いに答えなさい。

(1) ベクトル $\vec{a}$ , $\vec{b}$ の大きさ $| \vec{a} |$ , $| \vec{b} |$ を求めなさい。

(2) ベクトル $\vec{a}$ , $\vec{b}$ がなす角の大きさを求めなさい。

(3) $\vec{a} \times \vec{b}$ と $(\vec{a} \times \vec{b}) \cdot \vec{c}$ を求めなさい。

(4) $\vec{a}$ と $\vec{b}$ の両方に直交するような単位ベクトルを1つ求めなさい。

(5) 三角形OABの面積 $S$ を求めなさい。

(6) 三角錐OABCの体積 $V$ を求めなさい。

６．練習問題の答え

(1)

まずはウォーミングアップ。 $\begin{aligned} | \vec{a} | & = \sqrt{2^{2} + 1^{2} + (- 3)^{2}} \\ = \sqrt{14} \end{aligned}$ $\begin{aligned} | \vec{b} | & = \sqrt{(- 3)^{2} + 2^{2} + 1^{2}} \\ = \sqrt{14} \end{aligned}$ となる。

(2)

内積 $\vec{a} \cdot \vec{b}$ は $\begin{aligned} \vec{a} \cdot \vec{b} & = 2 \cdot (- 3) + 1 \cdot 2 + (- 3) \cdot 1 \\ = - 6 + 2 - 3 \\ = - 7 \end{aligned}$ と計算できるので、なす角 $θ$ に $\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos θ - 7 = 14 \cos θ \cos θ = - \frac{1}{2}$ の関係式が成り立つ。よって、 $θ = 120^{\circ}$ となる。

(3)

$\vec{a} \times \vec{b}$ は $\begin{aligned} \vec{a} \times \vec{b} & = (\begin{array}{ccc} 1 \cdot 1 - (- 3) \cdot 2 \\ - 3 \cdot (- 3) - 2 \cdot 1 \\ 2 \cdot 2 - 1 \cdot (- 3) \end{array}) \\ = (\begin{array}{ccc} 7 \\ 7 \\ 7 \end{array}) \end{aligned}$ と計算できる。

[検算]

内積を計算すると $\begin{aligned} (\vec{a} \times \vec{b}) ⊥ \vec{a} & = (\begin{array}{ccc} 7 \\ 7 \\ 7 \end{array}) \cdot (\begin{array}{ccc} 2 \\ 1 \\ - 3 \end{array}) \\ = 14 + 7 - 21 \\ = 0 \end{aligned}$ $\begin{aligned} (\vec{a} \times \vec{b}) ⊥ \vec{b} & = (\begin{array}{ccc} 7 \\ 7 \\ 7 \end{array}) \cdot (\begin{array}{ccc} - 3 \\ 2 \\ 1 \end{array}) \\ = - 21 + 14 + 7 \\ = 0 \end{aligned}$ より、外積が合っていることがわかる。

また、 $(\vec{a} \times \vec{b}) \cdot \vec{c}$ は、 $\begin{aligned} (\begin{array}{ccc} 7 \\ 7 \\ 7 \end{array}) \cdot (\begin{array}{ccc} 1 \\ 1 \\ 4 \end{array}) \\ = & 7 + 7 + 28 \\ = & 42 \end{aligned}$ と計算できる。

(4)

外積 $\vec{a} \times \vec{b}$ はベクトル $\vec{a}$ , $\vec{b}$ に直交するので、 $\vec{a} \times \vec{b}$ を大きさ1に正規化すればよい。

（大きさ1のベクトルは2つ存在するので注意！　逆方向を忘れないように！）

ここで、 $\vec{a} \times \vec{b} = \vec{u}$ とすると、正規化したベクトル $\vec{v}$ は、 $\begin{aligned} \vec{v} & = \frac{1}{| \vec{v} |} \\ = \frac{1}{\sqrt{3}} (\begin{array}{ccc} 1 \\ 1 \\ 1 \end{array}) \end{aligned}$ となり、これが答えとなる。

(5)

パターン1. 外積で求める方法

三角形OABの面積 $S$ は、 $\begin{aligned} S & = \frac{1}{2} | \vec{a} \times \vec{b} | \\ = \frac{1}{2} | (\begin{array}{ccc} 7 \\ 7 \\ 7 \end{array}) | \\ = \frac{1}{2} \sqrt{7^{2} + 7^{2} + 7^{2}} \\ = \frac{7 \sqrt{3}}{2} \end{aligned}$ となる。

パターン2. $θ$ を使う方法

三角形OABの面積 $S$ は、 $\begin{aligned} S & = \frac{1}{2} | \vec{a} | | \vec{b} | \sin 120^{\circ} \\ = \frac{1}{2} \cdot \sqrt{14} \cdot \sqrt{14} \frac{\sqrt{3}}{2} \\ = \frac{7 \sqrt{3}}{2} \end{aligned}$ となる。